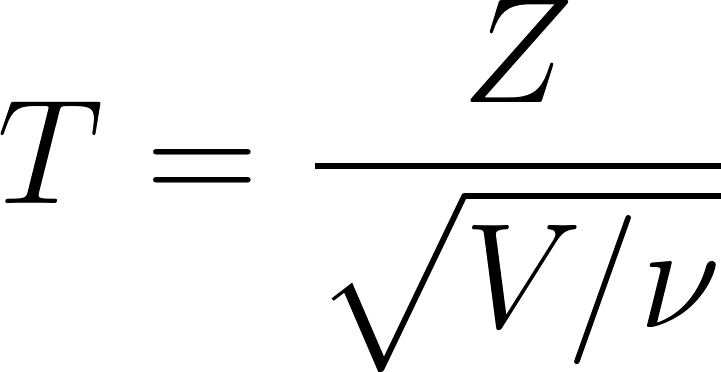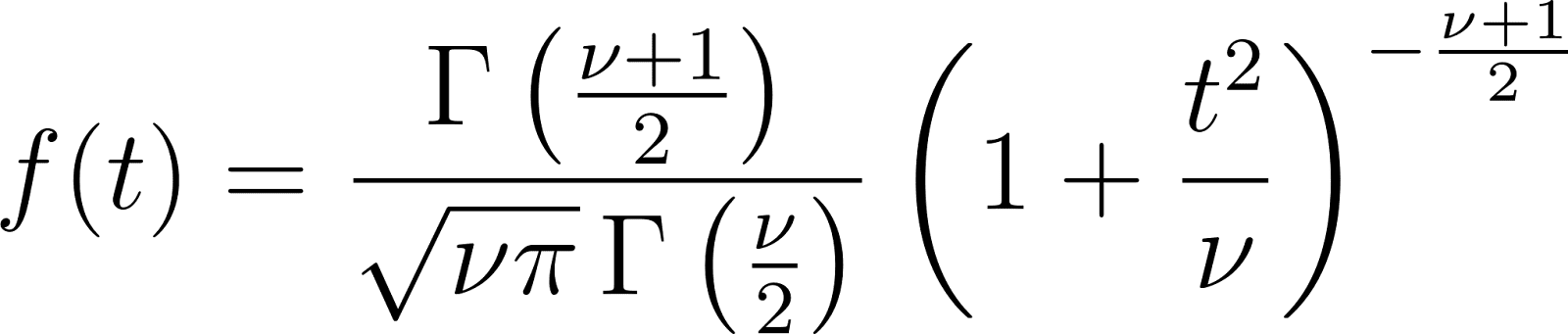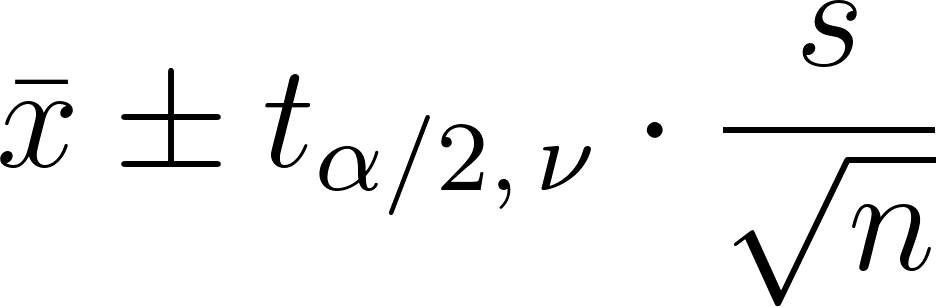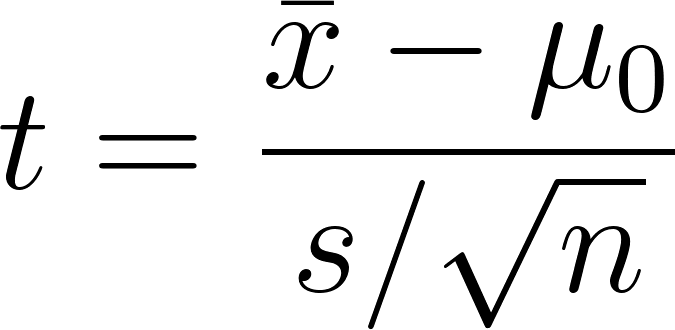Lorsque vous travaillez avec des données réelles, il arrive souvent que la taille des échantillons soit faible ou que la variance de la population soit inconnue. C'est dans ces conditions que les techniques statistiques traditionnelles basées sur la distribution normale peuvent ne pas fonctionner. C'est là que la distribution t, également connue sous le nom de distribution t de Student, devient utile. C'est un outil puissant qui permet de faire des déductions statistiques fiables lorsque les données sont limitées ou que l'incertitude est élevée.
Dans cet article, nous allons étudier ce qu'est la distribution t, comment elle se compare à d'autres distributions similaires, ses principales propriétés mathématiques et comment elle est utilisée dans la pratique, en particulier dans les tests d'hypothèse et les intervalles de confiance. J'ai également inclus un tableau de distribution t à la fin pour une référence rapide.
Qu'est-ce que la distribution en T ?
Tout comme la distribution normale, la distribution t est également symétrique et en forme de cloche. Cependant, les queues sont plus lourdes, ce qui reflète l'incertitude plus grande qui accompagne souvent les échantillons de petite taille.
En outre, il existe un autre facteur clé qui distingue la distribution t : elle est définie par ses degrés de liberté (df). Cette valeur, df, est calculée comme la taille de l'échantillon moins un (n - 1) et influence la forme de la distribution.
Au fur et à mesure que les degrés de liberté augmentent, la distribution t se rapproche de la distribution normale. Lorsque la taille de l'échantillon est importante (par exemple, n > 30), la différence devient si faible que la distribution t commence à ressembler à la courbe normale standard.
Distribution en T vs. Autres distributions similaires
Il est utile de comparer la distribution t à d'autres distributions similaires.
Distribution en T ou distribution normale
Bien que nous ayons noté que les deux distributions sont en forme de cloche, la distribution t ayant des queues plus lourdes et étant plus adaptée aux petits échantillons et à la variance inconnue de la population, il est particulièrement important de souligner sa tolérance à l'égard des valeurs aberrantes.
|
Fonctionnalité |
t-distribution |
Distribution normale |
|
Forme |
En forme de cloche, queues plus lourdes |
En forme de cloche, queues plus fines |
|
Cas d'utilisation |
Petits échantillons, σ inconnu |
Grands échantillons, σ connu |
|
Degrés de liberté |
Exigée |
Sans objet |
|
Sensibilité aux valeurs aberrantes |
Plus tolérant |
Moins tolérant |
Pour les échantillons plus importants, le théorème de la limite centrale justifie l'utilisation de la distribution normale, car les moyennes des échantillons tendent à suivre une distribution normale quelle que soit la forme de la population.
Distribution en T vs. Z-distribution
La distribution Z fait référence à la distribution normale standard, dont la moyenne est de 0 et l'écart-type de 1.
|
Fonctionnalité |
t-distribution |
Z-distribution |
|
Variance connue ? |
Non |
Oui |
|
Épaisseur de la queue |
Plus lourd |
Plus mince |
|
Test commun |
T-tests |
Z-tests |
|
Utilisation pour de petits échantillons |
Oui |
Non |
Comprenons cela à l'aide d'un exemple de code Python :
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, norm
# X-axis range
x = np.linspace(-5, 5, 1000)
# Standard Normal (Z) Distribution
z_dist = norm.pdf(x)
# Plotting
plt.figure(figsize=(10, 6))
plt.plot(x, z_dist, label='Z-Distribution (Standard Normal)', color='black', linewidth=2)
# T-Distributions with different degrees of freedom
dfs = [1, 3, 5, 10, 30]
colors = ['red', 'orange', 'green', 'blue', 'purple']
for df, color in zip(dfs, colors):
t_dist = t.pdf(x, df)
plt.plot(x, t_dist, label=f'T-Distribution (df={df})', color=color, linestyle='--')
plt.title('T-Distribution vs Z-Distribution: Heavier Tails for Smaller Sample Sizes')
plt.xlabel('x')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.show()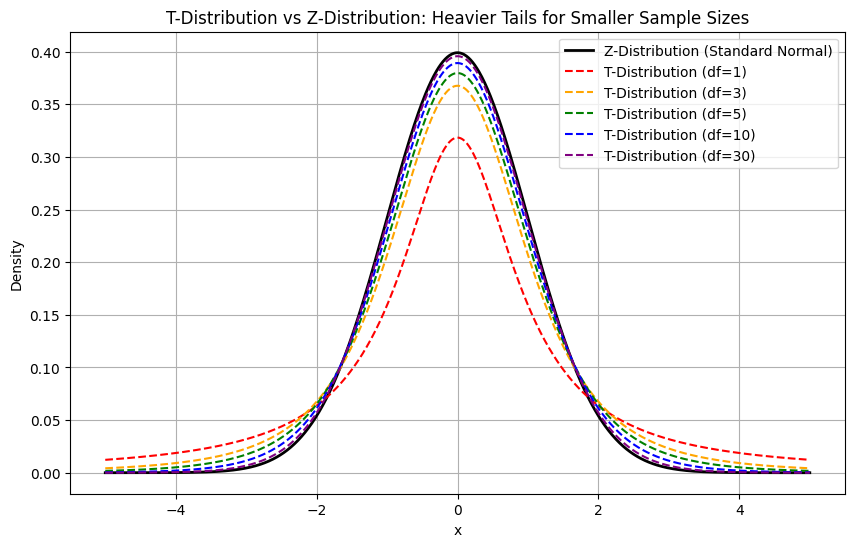
Cas particuliers et distributions connexes
La distribution t est étroitement liée à plusieurs autres distributions de probabilité :
- Distribution normale standard (comme df → ∞) : La distribution t converge vers la distribution normale lorsque les degrés de liberté augmentent.
- Distribution de Cauchy (df = 1): Une distribution t à un degré de liberté est équivalente à la distribution de Cauchy, connue pour avoir une moyenne et une variance non définies, ce qui signifie qu'une distribution t à un degré de liberté est rarement utilisée dans la pratique.
- Distribution F : Le carré d'une variable distribuée en t avec ν degrés de liberté suit une distribution F avec (1, ν) degrés de liberté.
- Distribution t non centrale: Utilisée dans l'analyse de puissance et les applications statistiques avancées, cette version intègre un paramètre de non-centralité, qui apparaît lorsque l'hypothèse nulle est fausse.
Limites de la distribution en T
La distribution t suppose que les données sous-jacentes sont approximativement distribuées normalement. Dans le cas de données très asymétriques ou non normales, elle peut ne pas être appropriée. Les techniques statistiques robustes ou les méthodes non paramétriques peuvent être mieux adaptées dans de tels scénarios.
Comparons maintenant le comportement du test t sur des données normales et sur des données asymétriques, les deux ayant la même moyenne.
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
np.random.seed(42)
# Generate data
normal_data = np.random.normal(loc=0, scale=1, size=30)
skewed_data = np.random.exponential(scale=1.0, size=30) - 1 # Shift to mean ≈ 0
# Perform one-sample t-tests (test if mean == 0)
t_stat_normal, p_normal = stats.ttest_1samp(normal_data, popmean=0)
t_stat_skewed, p_skewed = stats.ttest_1samp(skewed_data, popmean=0)
# Plot histograms
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.hist(normal_data, bins=15, color='skyblue', edgecolor='black')
plt.title(f'Normal Data\np-value = {p_normal:.3f}')
plt.axvline(0, color='red', linestyle='--')
plt.subplot(1, 2, 2)
plt.hist(skewed_data, bins=15, color='salmon', edgecolor='black')
plt.title(f'Skewed Data\np-value = {p_skewed:.3f}')
plt.axvline(0, color='red', linestyle='--')
plt.suptitle("Impact of Data Shape on t-test")
plt.tight_layout()
plt.show()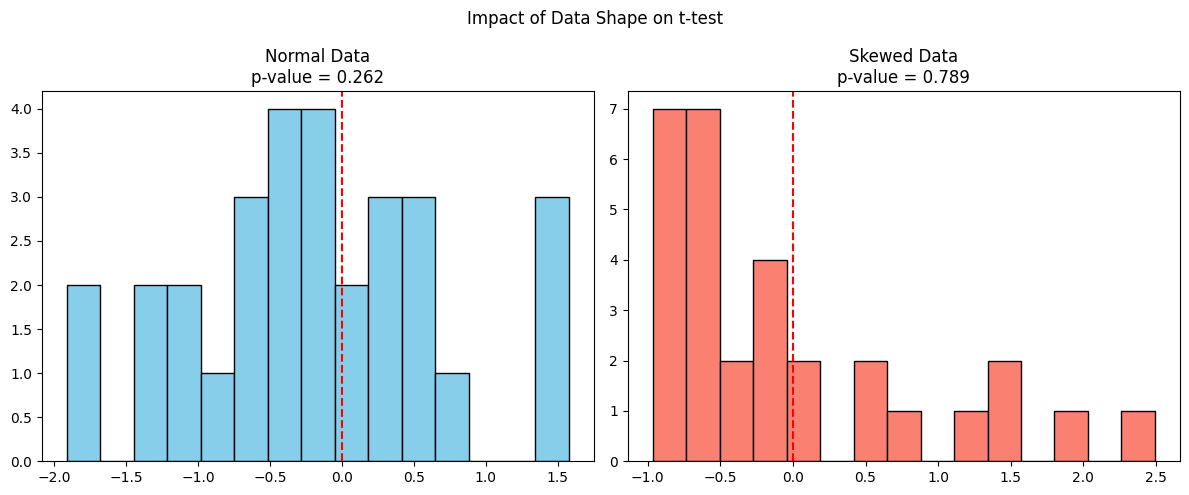
Le graphique de gauche montre des données issues d'une distribution normale pour laquelle le test t est valide et la valeur p est digne de confiance. Alors que le graphique de droite montre des données asymétriques issues d'une distribution exponentielle, bien que la moyenne de l'échantillon puisse être similaire, le test t suppose une symétrie et ne tient pas compte de l'asymétrie, ce qui peut donner une valeur p inexacte.
Propriétés mathématiques de la distribution T
La distribution t est définie comme suit :
Où ?
- T est la valeur résultante qui suit une distribution t de Student avec ν degrés de liberté
- Z est une variable aléatoire normale standard Z∼N(0,1)
- V est une variable aléatoire distribuée selon le principe du chi-carré avec ν degrés de liberté, V∼χ2(ν)
- v est le paramètre des degrés de liberté, souvent égal à n-1, où n est la taille de l'échantillon.
Fonction de densité de probabilité (PDF)
Propriétés principales
- Moyenne: 0 (pour v > 1 )
- Variance: v /(v - 2) (pour v > 2)
- Skewness: 0 (distribution symétrique)
- Kurtosis: Distribution supérieure à la normale (leptokurtique)
Simulation
Les méthodes de Monte Carlo sont fréquemment utilisées pour simuler des variables aléatoires distribuées en t, notamment pour évaluer la signification statistique ou créer des données synthétiques.
Simulons cela à l'aide de Python.
Ici, notre objectif est de simuler un grand nombre d'expériences sur de petits échantillons (taille de l'échantillon = 10), de calculer la statistique t pour chacune d'entre elles et de comparer la distribution obtenue à la distribution t théorique.
Pour ce faire, nous devons suivre l'approche suivante:
- Générez de nombreux échantillons à partir d'une distribution normale (moyenne = 0, std = 1).
- Pour chaque échantillon, calculez la statistique t : (Soustraire la moyenne de la population μ de la moyenne de l'échantillon xˉpuis divisez le résultat par l'erreur type de la moyenne, qui est l'écart type de l'échantillon s divisé par la racine carrée de la taille de l'échantillon n)
- Graphique de l'histogramme des valeurs t simulées.
- Superposez la distribution t théorique à des fins de comparaison.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t
# Simulation parameters
n = 10 # sample size
mu = 0 # population mean
sigma = 1 # population std deviation (not used directly)
df = n - 1 # degrees of freedom
num_simulations = 10000 # number of Monte Carlo simulations
# Monte Carlo simulation
t_stats = []
for _ in range(num_simulations):
sample = np.random.normal(loc=mu, scale=sigma, size=n)
sample_mean = np.mean(sample)
sample_std = np.std(sample, ddof=1) # sample std dev with Bessel's correction
t_stat = (sample_mean - mu) / (sample_std / np.sqrt(n))
t_stats.append(t_stat)
# Plot histogram of simulated t-statistics
x = np.linspace(-5, 5, 1000)
plt.figure(figsize=(10, 6))
plt.hist(t_stats, bins=50, density=True, alpha=0.6, label='Simulated t-Statistics')
# Overlay theoretical t-distribution
plt.plot(x, t.pdf(x, df), label=f'Theoretical t-Distribution (df={df})', color='red', linewidth=2)
plt.title('Monte Carlo Simulation of t-Distribution (n=10)')
plt.xlabel('t-value')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.show()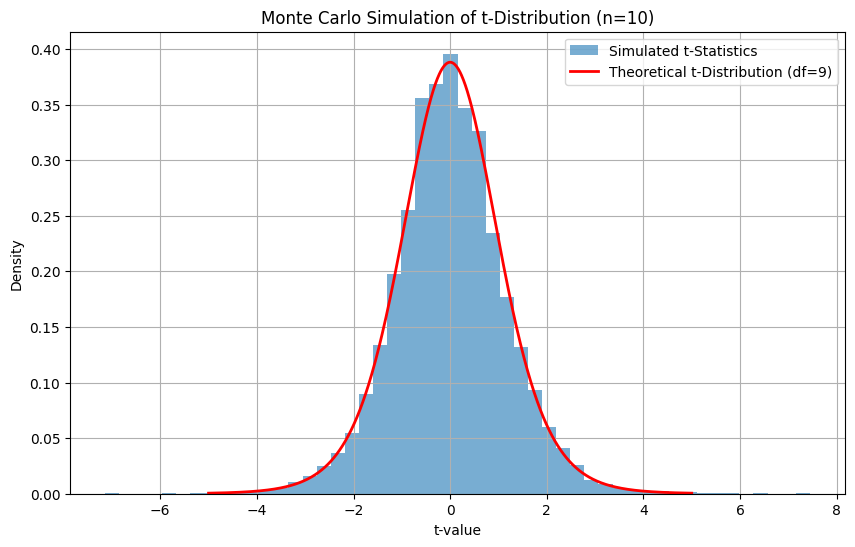
Les valeurs t simulées forment une distribution qui correspond étroitement à la distribution t théorique avec df = 9. Il s'agit d'un moyen pratique de comprendre et de valider la distribution t par le biais d'un échantillonnage aléatoire. Il s'agit également d'un concept fondamental derrière le bootstrapping et l'inférence basée sur le rééchantillonnage.
Quand utiliser la distribution en T
La distribution t est fondamentale dans de nombreuses applications statistiques :
- Estimation des moyennes de population lorsque l'écart-type est inconnu
- Tests d'hypothèses à l'aide de tests t
- Intervalles de confiance pour les petits échantillons
- Analyse de régression, où les coefficients suivent une distribution t
- Inférence bayésienne, en particulier lorsque les paramètres de variance sont marginalisés
Intervalles de confiance avec la distribution t
Un intervalle de confiance pour la moyenne est calculé comme suit :
Où ?
- x est la moyenne de l'échantillon
- s est l'écart-type de l'échantillon
- n est la taille de l'échantillon
- Et la partie centrale est la valeur critique de la distribution t. (alpha est le niveau de signification, et alpha divisé par deux parce que la distribution est bilatérale).(alpha est le niveau de signification, et alpha divisé par deux parce qu'il s'agit d'une distribution bilatérale).
Utilisez un tableau de distribution t ou une calculatrice pour trouver la valeur critique.
Tests d'hypothèses avec la distribution t
Dans les tests t, la statistique du test est :
Vous comparez cette valeur à une valeur t critique pour accepter ou rejeter l'hypothèse nulle. Les tests T peuvent être :
- A l'échelle de l'échantillon
- Deux échantillons
- Échantillon apparié
Des illustrations graphiques permettent de visualiser les régions critiques dans les tests unilatéraux et bilatéraux.
Tableau de distribution en T
Un tableau de distribution t tableau les valeurs critiques de la distribution t pour différents niveaux de confiance et degrés de liberté. Il est essentiel pour :
- Détermination des intervalles de confiance
- Réalisation de tests t
- Vérification de la signification d'une régression
Si cela peut vous être utile, j'ai inclus une version condensée d'un tableau de distribution t que vous pouvez consulter ici :
| df | 80 % (unilatéral) | 90 % (bilatéral) | 95 % (bilatéral) | 98% (bilatéral) | 99% (bilatéral) |
|---|---|---|---|---|---|
| 1 | 3.078 | 6.314 | 12.706 | 31.821 | 63.657 |
| 2 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 |
| 5 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 |
| 10 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 |
| 20 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 |
| 30 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 |
| 60 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 |
| ∞ | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 |
Conclusion
J'espère que cet article vous a permis de bien comprendre la distribution t et de combler le fossé entre la théorie et la pratique. Il s'agit d'un concept fondamental en statistique qui traite de l'incertitude, en particulier avec des échantillons de petite taille ou des paramètres de population inconnus.
En outre, la distribution t continuera à apparaître lorsque nous travaillerons sur des données plus avancées, telles que celles impliquant des statistiques robustes et des méthodes bayésiennes. Je vous recommande de vous inscrire à notre cursus de statisticien en R pour devenir réellement un expert.

Je suis un stratège de l'IA et un éthicien qui travaille à l'intersection de la science des données, du produit et de l'ingénierie pour construire des systèmes d'apprentissage automatique évolutifs. Considéré comme l'un des 200 plus grands innovateurs commerciaux et technologiques au monde, je me suis donné pour mission de démocratiser l'apprentissage automatique et de briser le jargon pour que tout le monde puisse participer à cette transformation.
FAQ sur la distribution en T
Qu'est-ce que la distribution t et quand doit-elle être utilisée ?
La distribution t, ou distribution t de Student, est une distribution de probabilité utilisée lorsque l'on travaille avec des échantillons de petite taille ou lorsque la variance de la population est inconnue. Il est particulièrement utile pour les tests d'hypothèses et la construction d'intervalles de confiance dans ces conditions.
En quoi la distribution t diffère-t-elle de la distribution normale (z) ?
Bien qu'elles soient toutes deux en forme de cloche et symétriques, la distribution t a des queues plus lourdes, ce qui la rend plus robuste pour les petits échantillons et les données comportant des valeurs aberrantes potentielles. La distribution normale suppose une variance de population connue et convient mieux aux grands échantillons.
Que sont les degrés de liberté (df) et comment affectent-ils la distribution t ?
Les degrés de liberté, généralement calculés comme n - 1 pour un échantillon de taille n, déterminent la forme de la distribution t. Lorsque df augmente, la distribution t se rapproche de la distribution normale, ce qui les rend presque identiques pour les grands échantillons.
La distribution t peut-elle traiter des données asymétriques ou non normales ?
La distribution t suppose que les données sont approximativement normales. Pour les données fortement asymétriques ou non normales, son utilisation peut conduire à des résultats inexacts. Dans ce cas, des méthodes statistiques robustes ou non paramétriques peuvent être plus appropriées.
Quelles sont les applications de la distribution t dans le monde réel ?
Il est couramment utilisé dans les tests t (par exemple, les tests t à un échantillon, à deux échantillons et par paires) pour déterminer si les moyennes diffèrent de manière significative. Elle est également utilisée pour construire des intervalles de confiance lorsque la taille de l'échantillon est faible ou que la variance est inconnue.