Distribución de Cauchy: Comprender los datos de cola pesada

La distribución de Cauchy plantea un intrigante enigma estadístico. Aunque comparte la conocida forma curva de campana con muchas otras distribuciones continuas de probabilidad, desafía el análisis convencional al carecer tanto de media como de varianza definidas. Llamada así por el matemático Augustin-Louis Cauchy, esta distribución surge de forma natural en campos que van desde la modelización financiera a la estadística bayesiana.

Como herramienta didáctica, la distribución de Cauchy ilustra conceptos estadísticos fundamentales con notable claridad. Demuestra la no convergencia de las medias muestrales, subraya la importancia de los supuestos distribucionales y muestra cómo se comportan los estimadores en condiciones variables.

¿Quieres dominar estos conceptos estadísticos y sus aplicaciones en la ciencia de datos? Explora nuestro itinerario profesional de Científico de Aprendizaje Automático en R, donde aprenderás a poner en práctica estas ideas utilizando la programación en R.

¿Qué es la distribución de Cauchy?

La distribución de Cauchy es una distribución de probabilidad continua famosa por sus propiedades únicas y sus colas pesadas. Se caracteriza por dos parámetros clave:

1. Parámetro de localización (θ): Este parámetro determina dónde se sitúa el pico (o centro) de la distribución en el eje x. Piensa que es como desplazar toda la distribución a la izquierda o a la derecha sin cambiar su forma.
2. Parámetro de escala (σ): Este parámetro controla el grado de dispersión de la distribución. Los valores mayores de σ crean distribuciones más amplias y planas, con colas más pesadas. Puedes pensar que es como estirar o apretar horizontalmente la distribución.

La distribución se define matemáticamente por su función de densidad de probabilidad (FDP):

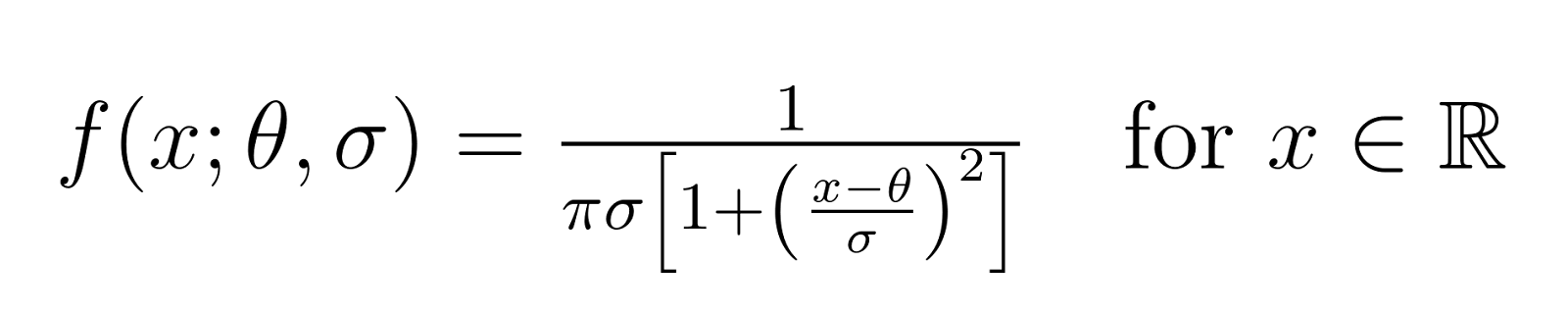
Cuando fijamos θ = 0 y σ = 1, obtenemos lo que se llama la distribución estándar de Cauchy. Ésta es la forma más sencilla de la distribución y sirve como punto de referencia para comprender casos más complejos.

Características principales de la distribución de Cauchy

Las propiedades definitorias de las distribuciones de Cauchy

Colas pesadas

Piensa en la distribución de Cauchy como la distribución de los "sucesos extremos". Mientras que una distribución normal sugiere que los valores alejados del centro son muy raros (como encontrar a una persona que mida 7 pies), la distribución de Cauchy nos dice que los valores extremos se dan con más frecuencia de lo que cabría esperar. 

Por ejemplo, en los rendimientos del mercado bursátil, los cambios masivos de precios en un solo día (como durante los desplomes o repuntes del mercado) ocurren más a menudo de lo que predeciría una distribución normal. Las colas pesadas de la distribución de Cauchy pueden captar mejor estos sucesos de "cisne negro".

Media y varianza indefinidas

Ésta es quizá la propiedad más fascinante de la distribución de Cauchy. A diferencia de la mayoría de las distribuciones con las que te has encontrado, la distribución de Cauchy no tiene un promedio (media ) ni una dispersión (varianza) significativos. 

Para entender por qué esto es importante: si tomas muestras repetidas de una distribución de Cauchy e intentas calcular su media, no convergerás a ningún valor concreto, ni siquiera con millones de muestras. Esto tiene implicaciones para el análisis estadístico, ya que los métodos estadísticos tradicionales que se basan en medias y varianzas (como las pruebas t o ANOVA) no funcionan con datos distribuidos en Cauchy.

Simetría

La distribución de Cauchy está perfectamente equilibrada en torno a su parámetro de localización (θ), como una imagen especular a ambos lados. Sin embargo, esta simetría no significa que se comporte como la conocida distribución normal. Aunque ambas distribuciones son simétricas, la distribución de Cauchy reparte mucho más su probabilidad. Esto significa que, aunque tenga un centro claro, los valores pueden alejarse mucho de este centro con una probabilidad significativa.

Estabilidad

La distribución de Cauchy tiene una propiedad notable: cuando sumas dos variables independientes con distribución de Cauchy, ¡obtienes otra distribución de Cauchy! Esta propiedad, conocida como estabilidad, sólo la comparten algunas otras distribuciones (como la distribución normal). Es especialmente útil en física y modelización financiera, donde a menudo necesitamos comprender cómo se comportan los procesos aleatorios combinados a lo largo del tiempo.

Aspectos a tener en cuenta al utilizar la distribución de Cauchy

Manejo de valores atípicos

La distribución de Cauchy es excelente en el manejo de valores atípicos porque espera que se produzcan. Esto lo hace especialmente útil en situaciones en las que los valores extremos son partes naturales de los datos, no errores que haya que eliminar. En estos casos, los métodos tradicionales de detección de valores atípicos podrían ser demasiado agresivos, marcando indebidamente puntos de datos legítimos para su eliminación. La distribución de Cauchy proporciona un marco para construir modelos robustos que no se verán indebidamente influidos por observaciones extremas, lo que la convierte en una herramienta valiosa cuando se trabaja con conjuntos de datos en los que los valores atípicos son una característica inherente y no una anomalía que hay que eliminar.

Selección del modelo

La elección de utilizar o no una distribución de Cauchy depende de tus datos y objetivos. La distribución de Cauchy es especialmente valiosa cuando tus datos muestran con frecuencia valores extremos, cuando trabajas con relaciones de variables distribuidas normalmente o cuando necesitas un modelo robusto que pueda manejar datos con colas pesadas. Sin embargo, debes tener cuidado al utilizar la distribución de Cauchy en determinadas situaciones: cuando necesites basarte en medias y varianzas, cuando tus datos sigan en realidad una distribución de colas más ligeras, o cuando la eficiencia computacional sea una preocupación primordial. Comprender estas compensaciones es útil para tomar decisiones informadas sobre si la distribución de Cauchy es adecuada para tus necesidades específicas de análisis.

Eficacia informática

Aunque la fórmula matemática de la distribución de Cauchy es sencilla, trabajar con ella computacionalmente puede ser un reto. La estimación de los parámetros suele requerir técnicas especializadas, como Markov Chain Monte Carlo (MCMC), y los métodos estándar de máxima verosimilitud pueden tener problemas con las colas pesadas. Afortunadamente, los paquetes de software estadístico modernos suelen incluir herramientas específicas para manejar las distribuciones de Cauchy, lo que hace más factible trabajar con esta distribución en la práctica a pesar de sus complejidades computacionales.

Propiedades matemáticas de la distribución de Cauchy

La distribución de Cauchy posee varias propiedades matemáticas importantes que la hacen única y útil:

• Una distribución estable con un comportamiento interesante: cuando sumas dos variables con distribución de Cauchy, obtienes otra distribución de Cauchy con parámetros escalados. Esto lo hace útil para estudiar los efectos acumulativos en física y finanzas.
• Momentos indefinidos, incluidas la media y la varianza, lo que la convierte en un contraejemplo fascinante en teoría de la probabilidad. Esta propiedad ayuda a los alumnos a comprender por qué el Teorema Central del Límite requiere una varianza finita.
• Unaforma matemáticaelegantemente simple, con una PDF y una función característica sencillas. A pesar de su complejo comportamiento, su descripción matemática básica es sorprendentemente manejable.
• La propiedad de razón: si divides una variable aleatoria normal por otra variable aleatoria normal independiente, obtienes una distribución de Cauchy. Esto la hace naturalmente adecuada para modelar relaciones y proporciones.
• Fuertes aplicaciones bayesianas, en particular como distribución a priori en modelos jerárquicos. Sus colas pesadas la convierten en una elección excelente para parámetros de escala en los que la robustez es importante.

Visualizar la Distribución de Cauchy en R y Python

El comportamiento de la distribución de Cauchy se comprende mejor mediante la visualización. Utilicemos R para crear gráficos de distintas distribuciones de Cauchy, demostrando cómo los parámetros de localización (θ) y escala (σ) afectan a la forma y posición de la distribución.

Distribución de Cauchy en R

R proporciona funciones para trabajar con las distribuciones de Cauchy a través de su paquete stats. También utilizaremos ggplot2 para crear elementos visuales claros y con calidad de publicación:

# Load required libraries
library(ggplot2)  # for plotting
# Note: dcauchy is from the stats package which is loaded by default in R

# Create a sequence of x values
x <- seq(-10, 10, length.out = 1000)

# Generate different Cauchy distributions using stats::dcauchy
# Standard Cauchy (θ = 0, σ = 1)
standard_cauchy <- dcauchy(x, location = 0, scale = 1)

# Location and Scale Adjusted (θ = 2, σ = 3)
adjusted_cauchy <- dcauchy(x, location = 2, scale = 3)

# Highly Scaled (θ = -1, σ = 5)
scaled_cauchy <- dcauchy(x, location = -1, scale = 5)

# Create a data frame for plotting
plot_data <- data.frame(
  x = rep(x, 3),
  density = c(standard_cauchy, adjusted_cauchy, scaled_cauchy),
  distribution = rep(c("Standard (θ=0, σ=1)", 
                      "Adjusted (θ=2, σ=3)", 
                      "Scaled (θ=-1, σ=5)"), 
                    each = length(x))
)

# Create the plot
ggplot(plot_data, aes(x = x, y = density, color = distribution)) +
  geom_line(size = 1) +
  theme_minimal() +
  labs(title = "Comparison of Cauchy Distributions",
       x = "x",
       y = "Density",
       color = "Parameters") +
  theme(legend.position = "bottom",
        plot.title = element_text(hjust = 0.5)) +
  scale_color_brewer(palette = "Set1")

Este código genera un gráfico comparativo de tres distribuciones de Cauchy diferentes:

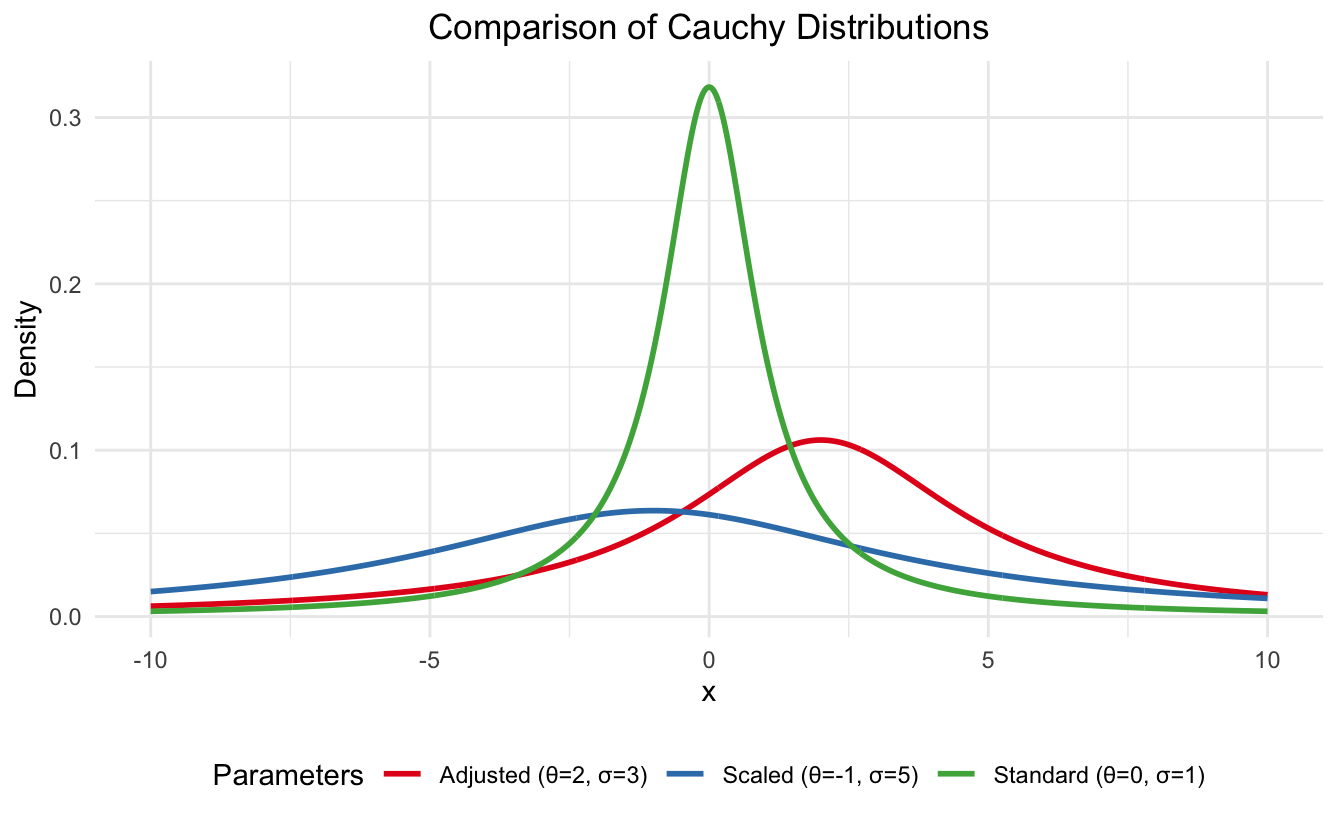
Distribución de Cauchy en R. Imagen del Autor

1. Cauchy estándar (línea verde): Con θ = 0 y σ = 1, esto representa el caso base. Observa su pico agudo en x = 0 y sus colas pesadas simétricas.
2. Cauchy ajustado a la localización (línea roja): Ajustar θ = 2 desplaza el pico hacia la derecha manteniendo la forma. Esto demuestra cómo el parámetro de localización afecta al centro de la distribución sin cambiar su dispersión.
3. Cauchy de alta escala (línea azul): Con θ = -1 y σ = 5, se muestra una distribución desplazada y mucho más plana. El parámetro de escala mayor crea colas más anchas y pesadas y reduce la altura del pico, lo que ilustra cómo σ controla la dispersión.

La visualización muestra claramente cómo el aumento del parámetro de escala (σ) conduce a una distribución más plana y extendida, mientras que el parámetro de localización (θ) simplemente desplaza toda la distribución hacia la izquierda o la derecha.

Distribución de Cauchy en Python

Después de explorar los parámetros de la distribución de Cauchy en R, vamos a utilizar Python para comparar la distribución de Cauchy con su prima más familiar, la distribución Normal. La pila de cálculo científico de Python, en particular scipy.stats, proporciona excelentes herramientas para trabajar con distribuciones de probabilidad.

Mientras que el paquete stats de R nos daba acceso directo a las funciones de la distribución de Cauchy, el módulo scipy.stats de Python ofrece una funcionalidad similar con una interfaz ligeramente diferente. Utilizaremos matplotlib, la principal biblioteca de trazado de Python, para crear una visualización clara:

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Set style parameters for better visualization
plt.style.use('seaborn')
plt.rcParams.update({
    'font.size': 16,
    'axes.labelsize': 18,
    'axes.titlesize': 24,
    'xtick.labelsize': 16,
    'ytick.labelsize': 16,
    'legend.fontsize': 16,
})

# Create data
x = np.linspace(-10, 10, 1000)
cauchy = stats.cauchy.pdf(x, loc=0, scale=1)
normal = stats.norm.pdf(x, loc=0, scale=1)

# Create the plot
plt.figure(figsize=(12, 8))

# Plot distributions
plt.plot(x, cauchy, 'b-', linewidth=2.5, label='Cauchy(0,1)')
plt.plot(x, normal, 'r--', linewidth=2.5, label='Normal(0,1)')

# Customize the plot
plt.title('Cauchy vs Normal Distribution', pad=20)
plt.xlabel('x', labelpad=10)
plt.ylabel('Density', labelpad=10)

# Customize legend
plt.legend(fontsize=16, bbox_to_anchor=(0.99, 0.99), 
          loc='upper right', borderaxespad=0.)

# Add grid and adjust layout
plt.grid(True, alpha=0.3)
plt.tight_layout()

plt.show()

El código anterior crea una comparación entre la distribución Cauchy estándar (línea continua azul) y la distribución Normal estándar (línea discontinua roja), ambas centradas en 0 con un parámetro de escala de 1.

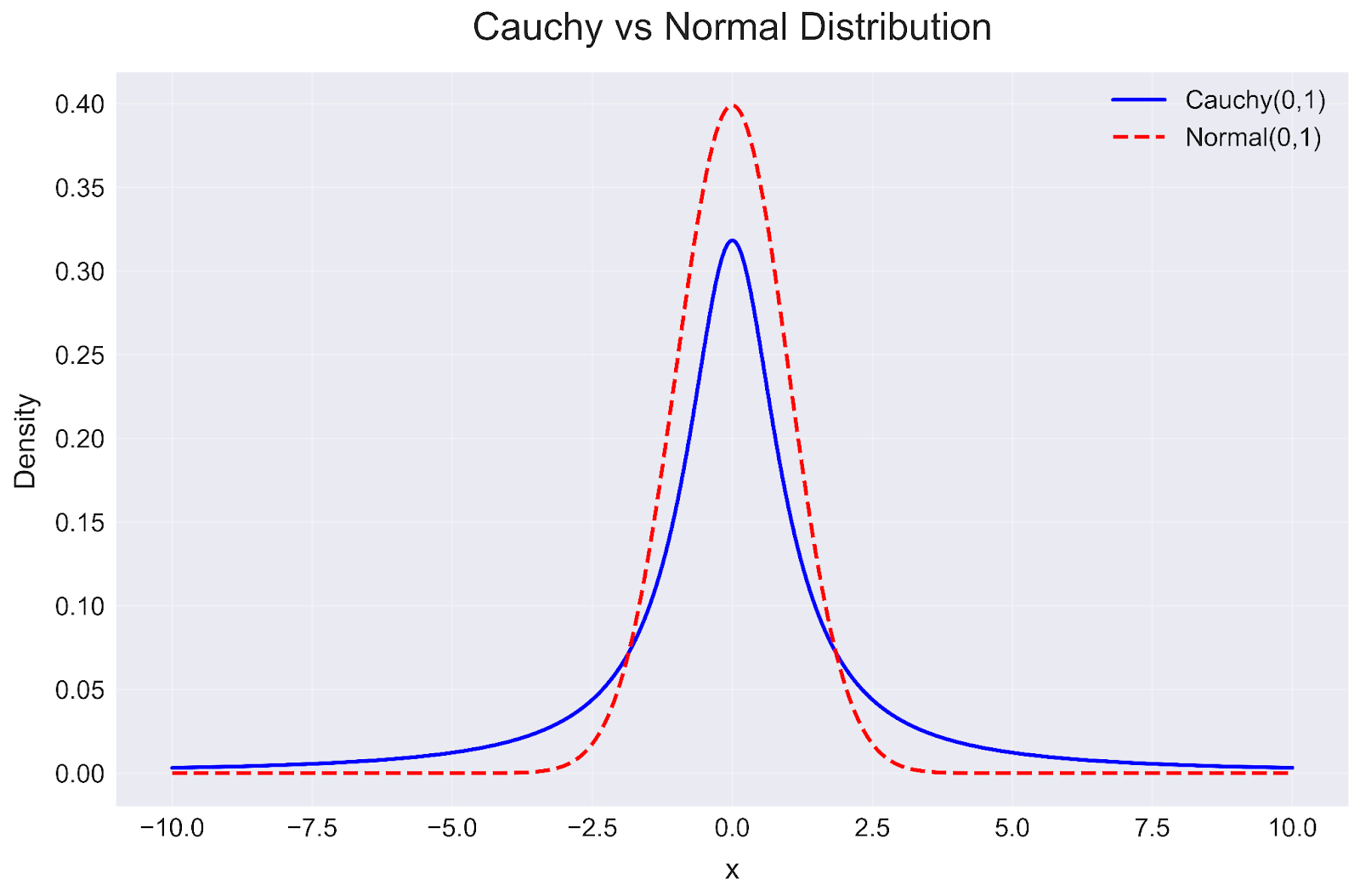
Distribución de Cauchy en Python. Imagen del autor

Esta visualización revela varias ideas clave:

1. Altura máxima: La distribución Normal alcanza una densidad de picos mayor (aproximadamente 0,4) que la distribución Cauchy (aproximadamente 0,32), lo que indica que los valores están más concentrados alrededor del centro en la distribución Normal.
2. Colas pesadas: Observa cómo la línea azul de la distribución de Cauchy se mantiene más alta que la línea discontinua roja de la distribución Normal a medida que nos alejamos del centro. Estas "colas pesadas" significan que los valores extremos son mucho más probables en una distribución Cauchy que en una distribución Normal.
3. Implicaciones prácticas: Las colas más pesadas de la distribución Cauchy la hacen más adecuada para modelizar fenómenos en los que los sucesos extremos ocurren con más frecuencia de lo que predeciría una distribución Normal, como los rendimientos de los mercados financieros o ciertos fenómenos físicos.

Esta comparación ayuda a explicar por qué la distribución Cauchy se utiliza a menudo en situaciones en las que la distribución Normal subestima la probabilidad de sucesos extremos. Aunque ambas distribuciones son simétricas en torno a su centro, las colas gruesas de la distribución de Cauchy la hacen más apropiada para modelar sistemas en los que los valores atípicos son habituales y no raras excepciones.

Cuándo es útil la distribución de Cauchy

La distribución de Cauchy sirve para fines específicos en el análisis y modelización de datos. Examinemos cómo se utiliza eficazmente en distintos ámbitos.

Finanzas: Gestionar la incertidumbre del mercado

Rendimientos del modelado

Los mercados financieros son conocidos por su naturaleza impredecible, y a menudo experimentan oscilaciones drásticas de precios que se considerarían "imposibles" según los supuestos de una distribución normal. La distribución de Cauchy brilla aquí porque:

• Naturalmente, capta los acontecimientos de "cisne negro", como las caídas del mercado o las subidas repentinas.
• Refleja mejor la realidad de que los movimientos extremos del mercado ocurren con más frecuencia de lo que predicen los modelos tradicionales.
• No subestimes el riesgo de grandes movimientos de precios.

Por ejemplo, durante la crisis financiera de 2008, muchos modelos tradicionales fallaron porque suponían distribuciones normales. Un modelo basado en Cauchy habría previsto mejor la posibilidad de movimientos tan extremos del mercado.

Evaluación de riesgos

Al evaluar los riesgos de inversión, la distribución de Cauchy proporciona una visión más conservadora y realista. Ayuda a los gestores de riesgos a establecer reservas de capital más apropiadas al tener en cuenta escenarios extremos, estima mejor la probabilidad de pérdidas o ganancias significativas y proporciona un modelo más realista para las pruebas de estrés de las carteras. Este enfoque de la evaluación de riesgos ayuda a las instituciones financieras a prepararse para acontecimientos de mercado improbables pero impactantes.

Estadística bayesiana: Inferencia estadística robusta

Distribuciones anteriores

En el análisis bayesiano, elegir la distribución a priori adecuada es fundamental. La distribución de Cauchy es especialmente valiosa aquí porque:

• Sus colas pesadas hacen que sea menos probable descartar accidentalmente valores importantes de los parámetros
• Es especialmente útil para los parámetros de escala (como las desviaciones típicas) en modelos jerárquicos
• Ayuda a evitar que el modelo confíe demasiado en sus estimaciones

Por ejemplo, al analizar la eficacia de un nuevo tratamiento médico, utilizar un previo de Cauchy para el tamaño del efecto ayuda a garantizar que no subestimamos la posibilidad de grandes efectos del tratamiento.

Regresión robusta

La regresión tradicional puede verse muy influida por los valores atípicos. Utilizar términos de error distribuidos en Cauchy ayuda a construir modelos más robustos, haciendo que el modelo sea menos sensible a las observaciones extremas. Los resultados siguen siendo fiables incluso cuando los datos contienen valores atípicos, y las predicciones son más estables en presencia de puntos de datos inusuales. Esta robustez hace que los términos de error distribuidos de Cauchy sean especialmente valiosos cuando se trabaja con conjuntos de datos reales que a menudo contienen valores inesperados o extremos.

Aprendizaje automático y ciencia de datos: Construir modelos resilientes

Algoritmos robustos

El aprendizaje automático moderno a menudo trata con datos ruidosos del mundo real. La distribución de Cauchy ayuda a construir algoritmos más resistentes mediante:

• Proporcionar un modelo mejor para el ruido en los datos de los sensores
• Ayudar a manejar los valores atípicos en los datos de entrenamiento sin eliminarlos
• Hacer que los algoritmos de aprendizaje sean más resistentes a los puntos de datos corruptos

Por ejemplo, en visión por ordenador, utilizar modelos de ruido distribuido de Cauchy puede ayudar a los algoritmos a manejar mejor los artefactos de la imagen o los fallos del sensor.

Modelos generativos

En aplicaciones avanzadas de aprendizaje automático, la distribución de Cauchy ayuda a crear modelos más flexibles. Es útil en autocodificadores variacionales en los que los datos pueden tener características de cola pesada, ayuda a generar datos sintéticos más realistas que incluyen valores extremos ocasionales, y es valioso para modelar espacios latentes en los que las distribuciones normales pueden ser demasiado restrictivas. Esta flexibilidad hace que la distribución de Cauchy sea especialmente útil en tareas de modelado generativo en las que es importante captar toda la gama de posibles variaciones de los datos.

Confundir la distribución de Cauchy con otras distribuciones

Es frecuente confundir la distribución de Cauchy con otras distribuciones similares. Exploremos las principales diferencias para ayudarte a hacer la elección correcta para tu análisis.

Distribución de Cauchy vs. distribución normal

La distribución normal suele ser la elección por defecto para muchos análisis, pero hay diferencias importantes entre ella y la distribución de Cauchy:

Comportamiento de la cola 

Aunque ambas distribuciones son simétricas, sus colas cuentan historias muy diferentes: La distribución normal sugiere que los valores superiores a tres desviaciones típicas son extremadamente raros. La distribución de Cauchy nos dice que los valores extremos son mucho más frecuentes de lo que cabría esperar.

Propiedades estadísticas 

Estas distribuciones difieren fundamentalmente en la forma en que podemos analizarlas: La distribución normal tiene momentos bien definidos (media = μ, varianza = σ²). La distribución de Cauchy no tiene media ni varianza definidas, lo que hace inutilizables los métodos estadísticos tradicionales.

Implicaciones prácticas 

Esta diferencia es importante en las aplicaciones reales: Utiliza la distribución normal cuando tus datos se agrupen en torno a un valor central con una dispersión predecible. Utiliza la distribución de Cauchy cuando tus datos muestren con frecuencia valores extremos que serían "imposibles" bajo supuestos normales.

Cauchy vs. Distribución de Laplace

La distribución de Laplace puede parecer similar a la de Cauchy a primera vista, pero hay diferencias clave que las diferencian:

Comportamiento de la cola 

Ambas distribuciones tienen colas más pesadas que la distribución normal, pero difieren en su peso: Las colas de la distribución de Laplace decaen exponencialmente. Las colas de la distribución de Cauchy decaen más lentamente (polinómicamente), lo que hace que los valores extremos sean aún más probables.

Simetría 

Ambas distribuciones son simétricas en torno a su centro, pero difieren en cómo se comportan sus colas: La distribución de Laplace muestra un decaimiento exponencial en sus colas. La distribución de Cauchy muestra un decaimiento polinómico, lo que hace que sus colas sean más pesadas que las de Laplace.

Casos prácticos 

Comprender estas diferencias ayuda a elegir la herramienta adecuada: Utiliza la distribución de Laplace cuando esperes valores atípicos ocasionales, pero sigas necesitando momentos definidos. Utiliza la distribución de Cauchy cuando esperes valores extremos frecuentes y no necesites calcular medias.

Conclusión

La distribución de Cauchy, aunque no se aplica tan ubicuamente como la distribución normal, tiene una importancia significativa en áreas en las que los datos presentan un comportamiento de colas pesadas, se requiere solidez frente a los valores atípicos o interesan las propiedades teóricas de las distribuciones estables. Ya sea en física, finanzas o estadística bayesiana, comprender la distribución de Cauchy mejora la capacidad de modelar e interpretar datos que presentan una variabilidad significativa y valores atípicos.

Para una comprensión más profunda de las distribuciones de probabilidad relacionadas, puede que te resulte valiosa la serie siguiente: Nuestra guía de la Distribución Gaussiana explora la distribución de probabilidad más utilizada, que sirve de excelente contraste con el comportamiento de cola pesada de la distribución Cauchy. Nuestra guía de la Distribución de Poisson se sumerge en el modelado de sucesos discretos en el tiempo o el espacio, mientras que nuestra guía de la Distribución Binomial explica las matemáticas que hay detrás de las secuencias de ensayos independientes. Para los interesados en los fundamentos de la teoría de la probabilidad, nuestra guía de la Distribución de Bernoulli proporciona una visión de los componentes básicos de distribuciones más complejas.