Descomposición de series temporales: Comprender las tendencias, la estacionalidad y el ruido

La descomposición es una de las cosas más interesantes de la ciencia de datos. En esencia, la descomposición consiste en dividir algo complejo en partes más sencillas e interpretables. Esto puede ocurrir con una matriz, un modelo o una señal. 

Como es una idea general, puede adoptar muchas formas. En álgebra lineal, existen la descomposición QR, la eigendecomposición, la descomposición del valor singular y la descomposición de Cholesky, por nombrar algunas. En otros ámbitos, existe la transformada de Fourier, el análisis de componentes principales e incluso el modelado de temas mediante métodos como el LDA. La variabilidad de los modelos de regresión puede descomponerse en componentes de la suma de cuadrados: SST, SSR y SSE. Incluso pensamos en los árboles de decisión como una forma de descomposición. 

Aquí repasaremos una de nuestras favoritas: la descomposición de series temporales. Si, al final, hemos despertado tu curiosidad al respecto, sigue nuestro curso Previsión en R con el profesor Rob Hyndman.

¿Qué es la descomposición de series temporales?

La descomposición de las series temporales es un método utilizado para descomponer una serie temporal en componentes separados denominados tendencia o tendencia-ciclo, estacionalidad y residuos. 

El objetivo de la descomposición de las series temporales es comprender mejor los patrones subyacentes y mejorar la precisión de las previsiones.

¿Cuáles son los componentes de una serie temporal?

Echemos un vistazo a los componentes de las series temporales. 

Componente de tendencia

La tendencia de una serie temporal (como su nombre indica) es el movimiento a largo plazo. Debemos decir que el componente de tendencia suele considerarse en realidad como el ciclo-tendencia, entendiendo por ciclos las pautas largas e irregulares. Históricamente se entendía que las ventas de coches se movían en ciclos de siete años (por la razón que fuera), aunque probablemente, con el movimiento hacia los coches eléctricos, ya no sea así.

La gran conclusión que la gente saca de la tendencia suele ser ésta: Los datos aumentan o disminuyen, o permanecen estables, a largo plazo. El aumento global de la temperatura de los océanos en las últimas décadas es una tendencia clara (léase: mala).

Componente estacional

El componente estacional va a llevar un poco más de tiempo explicarlo porque es un poco más complicado. El componente estacional de una serie temporal son los ciclos repetitivos a corto plazo de los datos que se producen a intervalos regulares. Piensa en diario, mensual, semanal, trimestral. La clave aquí es que los intervalos tienen que ser bastante regulares. Podrías ver, por ejemplo, que los pedidos de las cafeterías siguen una estacionalidad semanal si a la gente le gusta prepararse el café en casa los domingos. (Exploraremos esta cuestión sobre los pedidos de las cafeterías en la siguiente sección).

Lo que ocurre con la estacionalidad es que puede ser más complicada de lo que parece. Piensa que el número de semanas de un año no es un número entero (~52,18). O piensa que los meses no están espaciados uniformemente: Febrero tiene 28 (o 29) días, pero julio siempre tiene 31.

Es más, como cada año tiene algo más de 52 semanas, y como los meses también varían, no puedes dividir la mayoría de los meses uniformemente en semanas. Esto es evidente cuando estudias un calendario. Pero lo que es menos obvio para un analista de datos es que, cuando observas los datos a nivel semanal y luego los agregas a nivel mensual, puedes ver cosas incoherentes, como que un mes de enero puede tener cuatro lunes, pero el siguiente puede tener cinco, y así las comparaciones pueden ser difíciles.

El componente residual / irregular / resto

Todo lo que queda después de extraer la tendencia-ciclo y el componente estacional lo llamamos, apropiadamente, componente residual, que incluye cosas anómalas en los datos, como un gran acontecimiento, y ruido aleatorio. El componente residual no es un artefacto inútil. Todos los datos tienen una variabilidad inexplicable, y cuantificar el tamaño de esa variabilidad es importante. Curiosamente,los residuales suelen adoptar la forma de una distribución gaussiana en una serie bien comportada, en cuyo caso podríamos evaluar los sucesos de cisne negro con pruebas de hipótesis.

Modelos de descomposición de series temporales

Ahora que ya hemos tratado las partes constituyentes de una serie temporal, debemos mencionar que en realidad hay dos tipos generales distintos de descomposición de series temporales. Empezaremos con el modelo aditivo.

Descomposición aditiva

Aquí tienes la fórmula de la descomposición aditiva:

Fíjate en los signos más. Lo que dice esta fórmula es que si tomas la tendencia y la sumas al componente estacional, y lo añades a los residuos, vuelves a obtener la serie temporal original. En general, utilizamos una descomposición aditiva cuando la variación estacional es constante en el tiempo.

Descomposición multiplicativa

Aquí tienes la fórmula de la descomposición multiplicativa. Observa los signos de multiplicación en esta versión. 

Utilizamos un modelo multiplicativo cuando la variación estacional escala con la tendencia. Es decir, cuando veas que el tamaño de los efectos estacionales aumenta a medida que la serie general sube o baja. En realidad, se trata de una forma de heteroscedasticidad.

Técnicas de descomposición de series temporales

Hasta ahora, hemos tratado lo que implica una descomposición de series temporales, y los dos tipos generales principales. Más adelante, tenemos que hablar de los dos métodos más comunes. Cada uno de ellos puede aplicarse como modelo aditivo o multiplicativo. 

Descomposición clásica

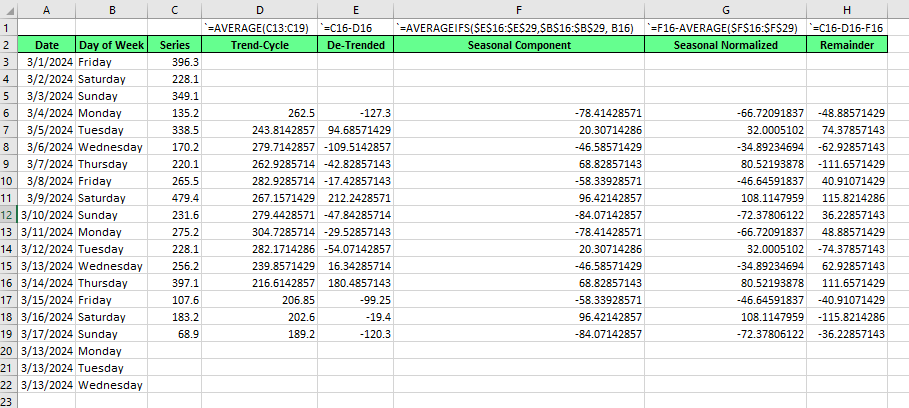
La descomposición clásica es la más fácil de entender. Es de los años 20, pero sigue siendo relevante hoy en día. Para mostrar la descomposición clásica, utilicemos Excel. La descomposición clásica, como la STL, que mostraremos a continuación, puede realizarse con un modelo aditivo o multiplicativo. Para este ejemplo, crearemos una versión aditiva.

Si quieres probar por ti mismo, utiliza el CSV index_1 en este interesantísimo conjunto de datos de ventas de café que puedes encontrar en Kaggle. Para tu referencia, hemos agregado y resumido las ventas por día.

• Primero, calculamos la tendencia-ciclo. Estamos identificando una estacionalidad semanal, y en una semana hay siete días, por lo que el periodo estacional es impar, lo que significa que nuestra media móvil debe centrarse utilizando una ventana simétrica. Es decir, una media móvil de 7 días. Ten cuidado con la alineación y el centrado de .

• A continuaciónhallamos la serie detrendida restando la tendencia de la original.

• A continuación,, para hallar el componente estacional, promediamos los valores detrendentes de cada periodo estacional. Una adición importante: Yverás que el componente estacional probablemente no sume exactamente cero. Asegúrate de ajustarlo:

  • Calcula la media de tu componente estacional.

  • Resta la media estacional de cada valor estacional.

• Por últimopara el resto, restamos la tendencia y el periodo estacional de la serie original.

Si hubiéramos visto que nuestra serie tenía un efecto estacional que cambiaba con el nivel de datos, habríamos considerado en su lugar una descomposición multiplicativa. Los pasos para la descomposición multiplicativa son muy parecidos, salvo que utilizamos la división en lugar de la resta. En concreto, encontraríamos la serie detrendida dividiendo la serie original por la tendencia-ciclo. Luego, más adelante, para hallar el resto, dividiríamos la serie original por el producto de los componentes tendencial y estacional. (Como alternativa, podríamos haber tomado el logaritmo natural de la serie original y aplicado una descomposición aditiva. Esto sería funcionalmente lo mismo).

Descomposición STL 

La descomposición STL, que significa descomposición estacional y de tendencia mediante LOESS, es una versión más moderna de la descomposición. Es más difícil de explicar, pero en general es más flexible que el método clásico. STL funciona utilizando un método llamado LOESS, que ajusta modelos de regresión simples a pequeños trozos superpuestos de los datos. Aplica esta regresión ponderada localmente para aislar por separado los componentes tendencial y estacional.

Este método aborda inconvenientes específicos de la descomposición clásica, a saber, que en la versión clásica no se dispone de estimaciones de tendencia-ciclo o resto para la primera y la última observación. Puedes verlo en los espacios en blanco de Excel, en las filas 3, 4, 5, y 20, 21 y 22, arriba.

También hay que decir que la tendencia-ciclo identificada por la descomposición clásica suaviza las subidas y bajadas rápidas, por lo que puede pasar por alto cosas importantes que ocurren en la serie. Por último, la descomposición clásica da por sentada la idea de que existe un patrón estacional, pero, con datos suficientes, a veces podemos ver que el patrón estacional cambia.

Empecemos por crear una trama temporal de la serie original. Como antes, como primer paso, estamos agregando y resumiendo el conjunto de datos Kaggle antes de descomponer las series.

coffee_sales_data <- read.csv("/Users/x/Desktop/index_1.csv")
coffee_sales_data <- as.data.frame(coffee_sales_data)

library(dplyr)
library(ggplot2)

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  ggplot(aes(x = as.Date(date), y = money)) +
  geom_line(color = '#01ef63') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Time series")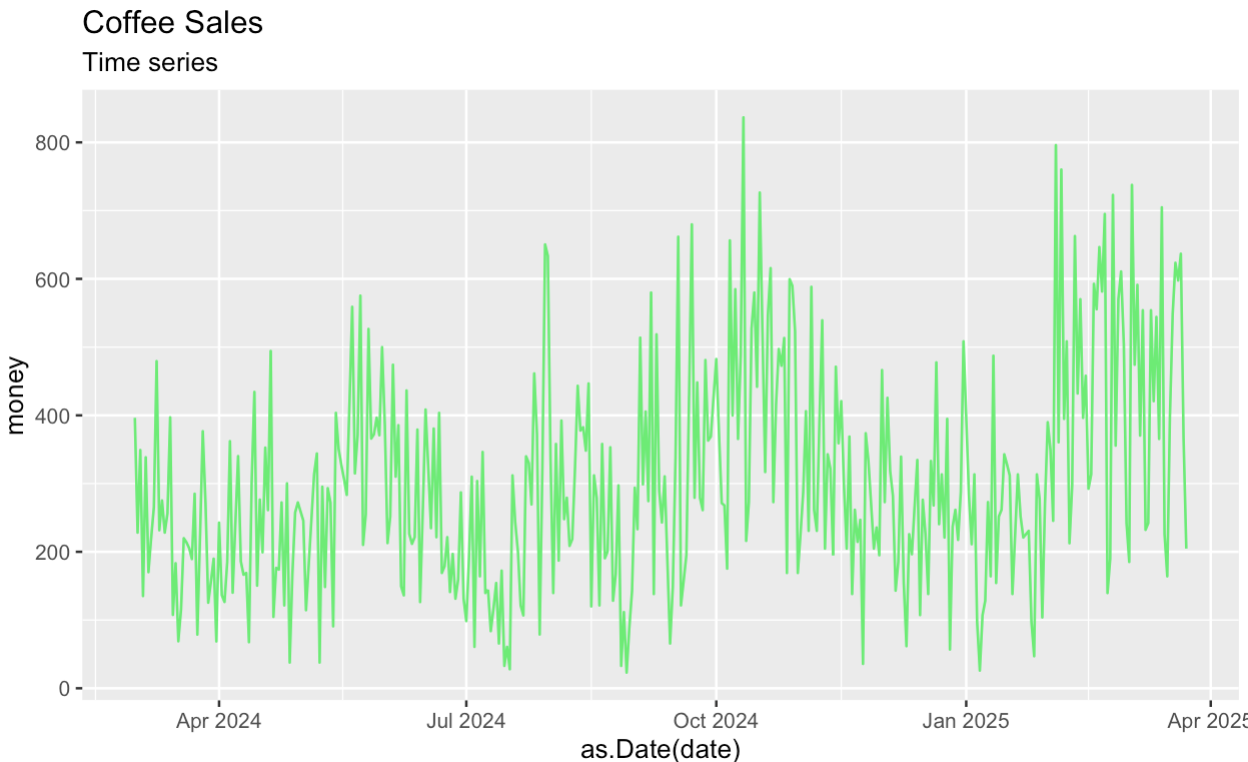

A continuación, descomponemos nuestras series en componentes de tendencia, estacionales y de resto. El recuadro de la parte superior del gráfico de descomposición muestra la serie original, aunque un poco aplastada.

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  mutate(date = as.Date(date)) |>
  as_tsibble() |>
  filter(date > '2024-02-28') |>
  filter(date < '2024-05-01') |>
  model(
      STL(money ~ season(window = "periodic"))
  ) |>
  components() |>
  autoplot(color = '#203147') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Classical additive decomposition")

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  mutate(date = as.Date(date)) |>
  as_tsibble() |>
  filter(date > '2024-02-28') |>
  filter(date < '2024-05-01') |>
  model(
      STL(money ~ season(window = "periodic"))
  ) |>
  components() -> ts_components

ts_components |>
  autoplot(color = '#203147') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Classical additive decomposition")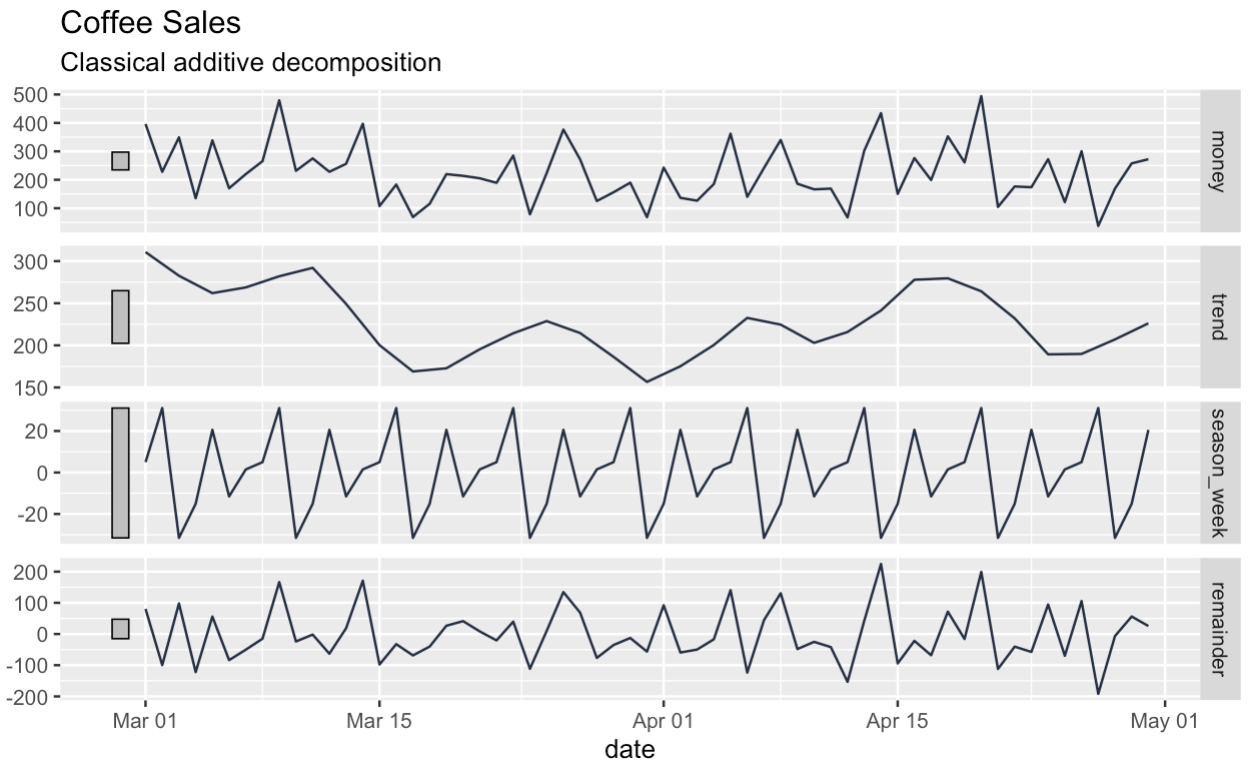

Observa que, a diferencia de la descomposición clásica, el marco de datos que obtenemos no tiene huecos al principio ni al final.  

print(ts_components)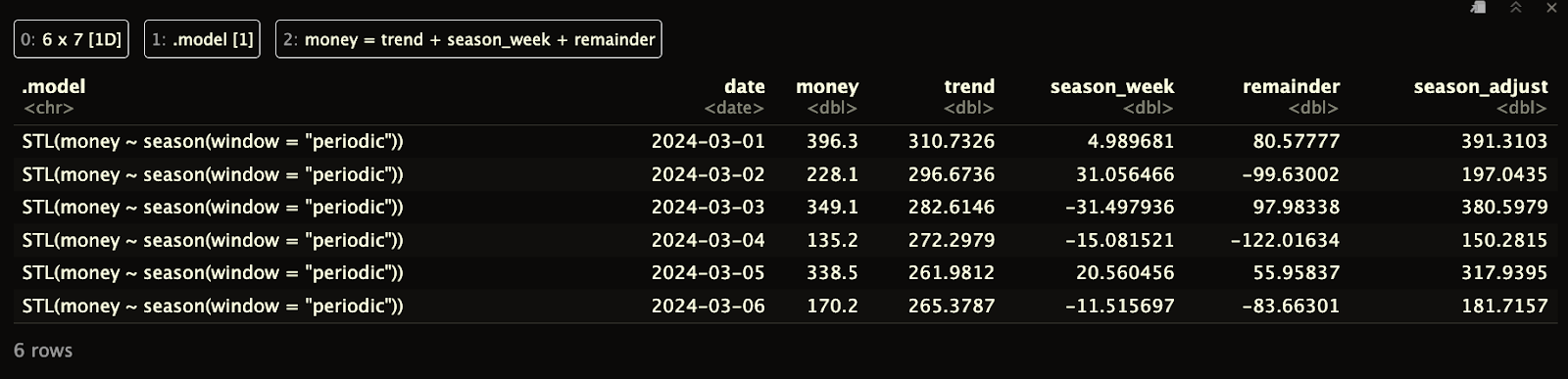

También hay algunos inconvenientes con la descomposición STL y, si te interesa, hemos añadido esa información en nuestras FAQ. 

Descomposición de series temporales y ajustes estacionales

A menudo, es útil crear una versión ajustada estacionalmente de los datos. Para ello, podemos sumar los componentes de la tendencia y del resto. O bien, podríamos restar el componente estacional de la serie original; en ambos casos llegaríamos a lo mismo.

seasonally_adjusted <- components |>
  mutate(seasonally_adjusted = money - season_week)

season_adjust_data <- seasonally_adjusted |>
  select(date, money, season_adjust) |>
  pivot_longer(cols = c(money, season_adjust), names_to = "series", values_to = "value")

season_adjust_data |>
  autoplot() + facet_wrap(~series) +
  scale_color_manual(values = c(
    "money" = '#203147',          # blue
    "season_adjust" = '#01ef63'   # orange
  )) +
  facet_wrap(~series) +
  labs(title = "Coffee Sales: Original vs Seasonally Adjusted")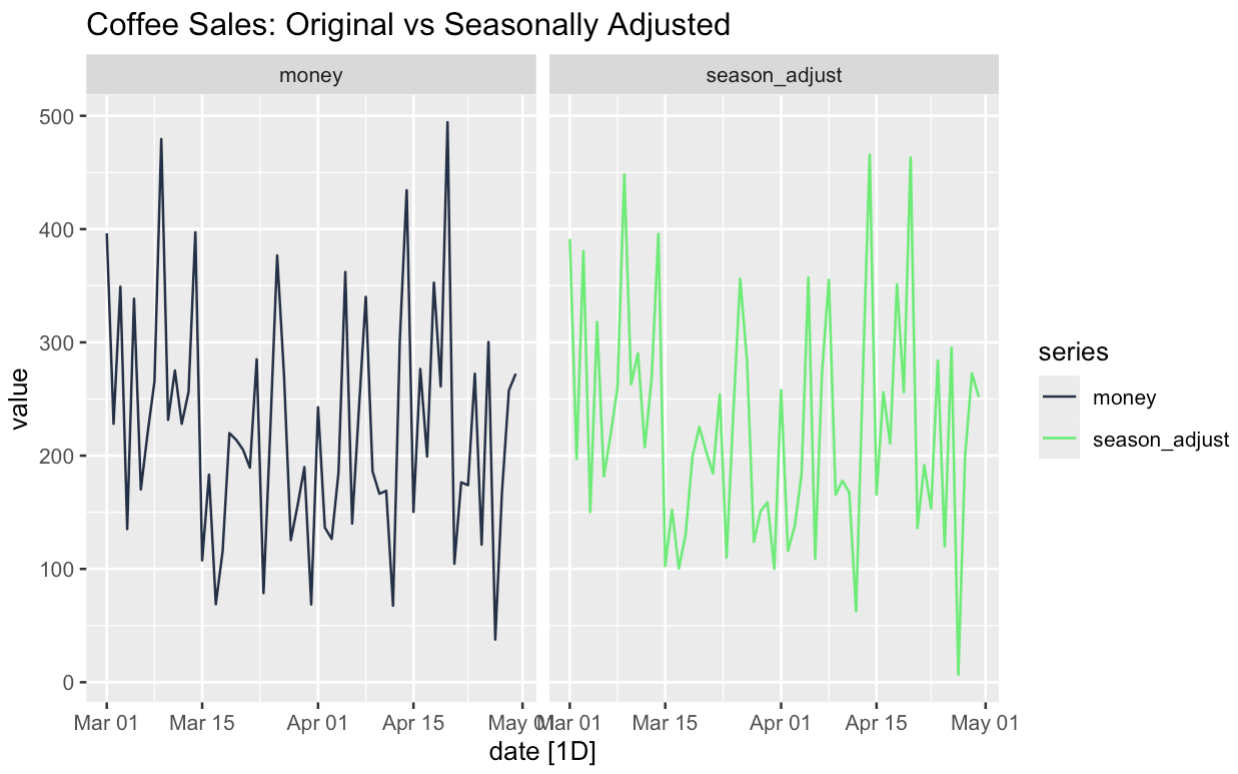

El poder de los datos ajustados estacionalmente es que pueden ayudarnos a comprender ciertas características de nuestras series. Podemos ver si la tendencia subyacente es el resultado de la estacionalidad, por ejemplo. En segundo lugar, podemos examinar más de cerca los sucesos inusuales en los datos. ¿Creemos que nuestra promoción del viernes funcionó porque era viernes o porque era una promoción? Pues bien, utilizando la descomposición de las series temporales y los ajustes estacionales, podemos poner a prueba preguntas como ésa.

Descomposición y previsión de series temporales

Quizá te sorprenda saber que la descomposición de las series temporales también es útil para hacer previsiones. Pensamos en ello de dos formas principales. En primer lugar, queremos comprender los componentes de nuestras series temporales para ayudarnos a decidir qué modelo de previsión debemos utilizar. Si observamos una fuerte estacionalidad, podríamos inclinarnos por modelos como el suavizado exponencial de Holt-Winters o los métodos ETS, que están específicamente construidos para manejar tanto la tendencia como los componentes estacionales.

En segundo lugar, podemos incluso utilizar datos descompuestos como parte de nuestra previsión, lo que nos da opciones. Podemos, por ejemplo, ejecutar un modelo de previsión no estacional sobre una versión ajustada estacionalmente de nuestros datos. (Podemos reintroducir el componente estacional más adelante). El ajuste estacional es especialmente útil cuando queremos utilizar modelos flexibles, como el ARIMA estándar y la regresión lineal. 

Aquí creamos un modelo ARIMA sencillo para prever los datos ajustados estacionalmente. 

season_adjust_data_filtered <- season_adjust_data |>
  filter(series == "season_adjust") |>
  as_tsibble(index = date)

seasonal_adjust_arima_model <- season_adjust_data_filtered |>
  model(
    ARIMA(value)
  )

seasonal_adjust_arima_model |>
  forecast(h = "14 days") |>  
  autoplot(season_adjust_data_filtered, color = '#01ef63') +
  labs(title = "Forecast of Seasonally Adjusted Coffee Sales",
       subtitle = "Simple ARIMA Model",
       y = "Money (Seasonally Adjusted)",
       x = "Date")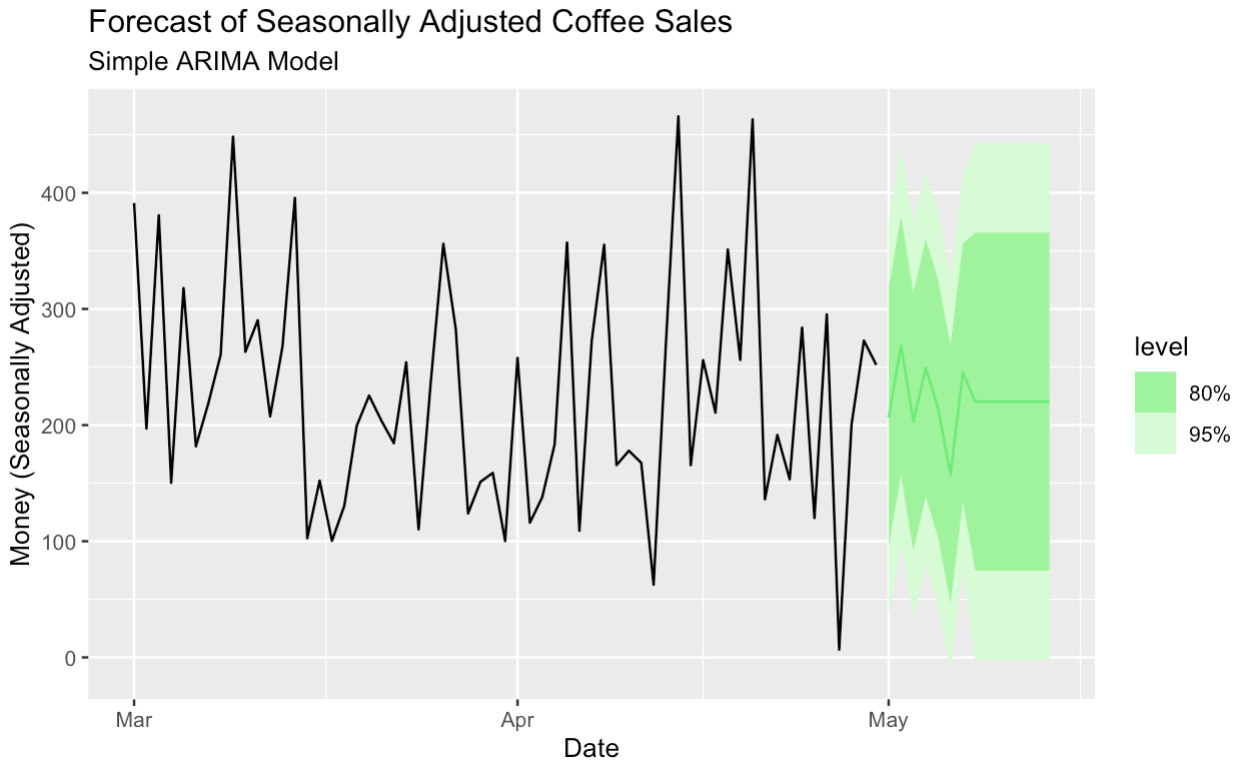

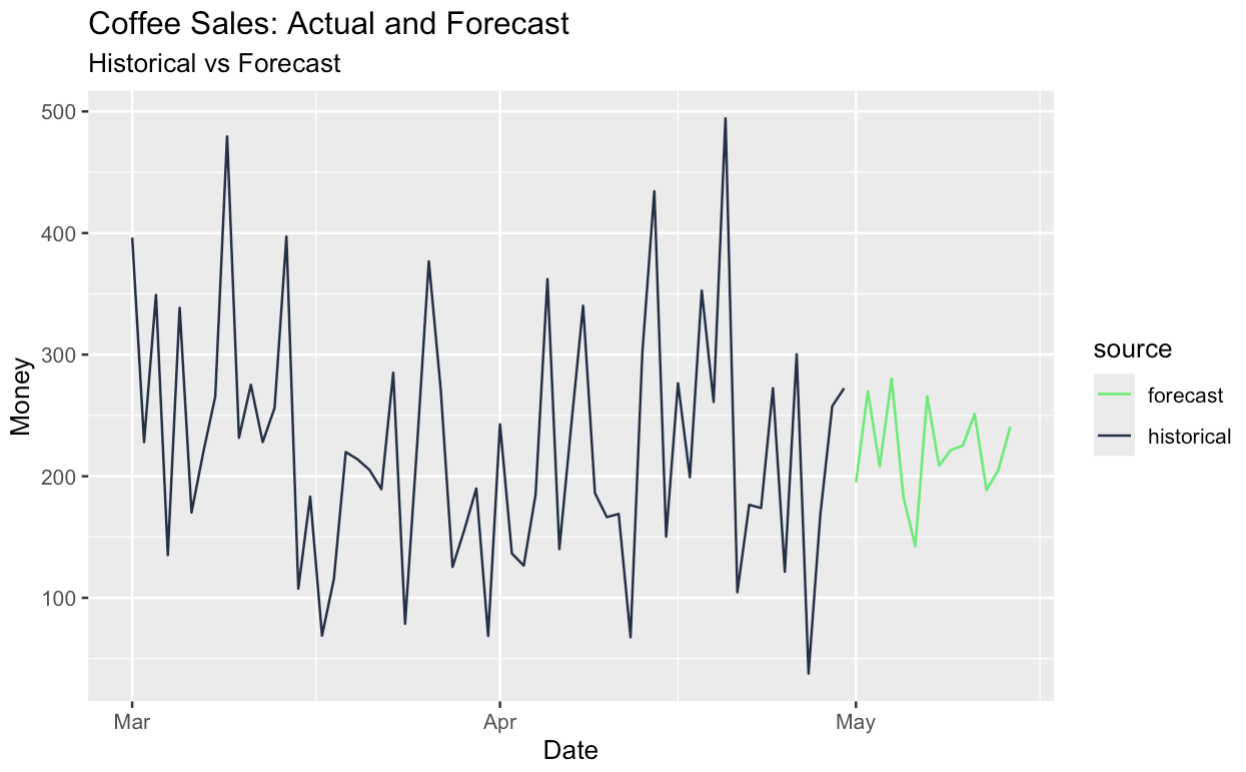
También podemos prever la serie ajustada estacionalmente y volver a añadir el componente estacional, lo que nos da efectivamente una previsión estacional. Todo esto ha sido posible gracias a nuestra original descomposición de series temporales.

# Build tagged historical and forecast data
historical_data <- components |>
  as_tibble() |>
  select(date, money) |>
  mutate(source = "historical")

forecast_data <- final_forecast |>
  as_tibble() |>
  transmute(date, money = money_forecast) |>
  mutate(source = "forecast")

# Bind and create tsibble
full_data <- bind_rows(historical_data, forecast_data) |>
  as_tsibble(index = date, validate = FALSE)

# Plot with color by source
full_data |>
  ggplot(aes(x = date, y = money, color = source)) +
  geom_line() +
  scale_color_manual(values = c(
    "historical" = "#203147",   # dark blue for real data
    "forecast" = "#01ef63"      # green for forecast
  )) +
  labs(
    title = "Coffee Sales: Actual and Forecast",
    subtitle = "Historical vs Forecast",
    y = "Money",
    x = "Date"
  )

Reflexiones finales

¡Espero que te haya gustado nuestro artículo sobre la descomposición de las series temporales! Recuerda que la descomposición es sólo una parte del análisis de series temporales, así que para convertirte en un experto, matricúlate en el curso Previsión en R con el profesor Rob Hyndman, que ayudó a desarrollar los paquetes de R que utilizamos para nuestros visuales. También tenemos un curso de Visualización de Datos de Series Temporales en Python si te han parecido interesantes las ideas de este artículo pero prefieres Python, que también es muy bueno para este tipo de cosas.