Decomposição de séries temporais: Entenda as tendências, a sazonalidade e o ruído

A decomposição é um dos aspectos mais interessantes da ciência de dados. Em sua essência, a decomposição consiste em dividir algo complexo em partes mais simples e mais interpretáveis. Isso pode acontecer com uma matriz, um modelo ou um sinal. 

Por ser uma ideia geral, pode assumir várias formas. Na álgebra linear, há a decomposição QR, a decomposição eigend, a decomposição de valor singular e a decomposição de Cholesky, para citar algumas. Em outros domínios, há a transformada de fourier, a análise de componentes principais e até mesmo a modelagem de tópicos usando métodos como o LDA. A variabilidade nos modelos de regressão pode ser decomposta em componentes de soma de quadrados: SST, SSR e SSE. Podemos até pensar nas árvores de decisão como uma forma de decomposição. 

Aqui, analisaremos um de nossos favoritos: a decomposição de séries temporais. Se, no final, tivermos despertado sua curiosidade, faça nosso curso de Previsão em R com o professor Rob Hyndman.

O que é decomposição de séries temporais?

A decomposição de séries temporais é um método usado para dividir uma série temporal em componentes separados chamados de tendência ou ciclo de tendência, sazonalidade e resíduos. O objetivo da decomposição de séries temporais é entender melhor os padrões subjacentes e melhorar a precisão da previsão.

Quais são os componentes de uma série temporal?

Vamos dar uma olhada nos componentes da série temporal. Essa pode ser a melhor maneira de você entender a ideia.

Componente de tendência

A tendência de uma série temporal (como o nome sugere) é o movimento de longo prazo. Devemos dizer que o componente de tendência é frequentemente considerado como o ciclo de tendência, em que os ciclos são entendidos como padrões longos e irregulares. Historicamente, entende-se que as vendas de carros se movem em ciclos de sete anos (por qualquer motivo), embora provavelmente, com o movimento em direção aos carros elétricos, não mais.

A grande conclusão que as pessoas obtêm da tendência geralmente é a seguinte: Os dados estão aumentando ou diminuindo, ou permanecendo estáveis, a longo prazo? O aumento global da temperatura dos oceanos nas últimas décadas é uma tendência clara (leia-se: ruim).

Componente sazonal

O componente sazonal levará um pouco mais de tempo para ser explicado, pois é um pouco mais complicado. O componente sazonal de uma série temporal é a repetição de ciclos de curto prazo nos dados que ocorrem em intervalos regulares. Pense diariamente, mensalmente, semanalmente, trimestralmente. O segredo aqui é que os intervalos devem ser bastante regulares. Você pode ver, por exemplo, que os pedidos de cafeterias seguem uma sazonalidade semanal se as pessoas gostam de fazer café em casa aos domingos. (Exploraremos essa questão sobre os pedidos da cafeteria na próxima seção).

O problema da sazonalidade é que ela pode ser mais complicada do que parece. Pense em como o número de semanas em um ano não é um número inteiro (~52,18). Ou pense em como os meses não são espaçados uniformemente: Fevereiro tem 28 (ou 29) dias, mas julho sempre tem 31.

Além disso, como cada ano tem um pouco mais de 52 semanas, e como os meses também variam, você não pode dividir a maioria dos meses igualmente em semanas. Isso é óbvio quando você estuda um calendário. Mas o que é menos óbvio para um analista de dados é que, ao analisar os dados no nível semanal e agregá-los ao nível mensal, você pode ver coisas inconsistentes, como o fato de que um janeiro pode ter quatro segundas-feiras, mas o próximo pode ter cinco, e assim as comparações podem ser difíceis.

O componente residual / irregular / restante

Tudo o que sobra depois de retirar o ciclo de tendência e o componente sazonal é chamado, apropriadamente, de componente residual, que inclui coisas anômalas nos dados, como um grande evento, e ruído aleatório. O componente residual não é um artefato inútil. Todos os dados têm variabilidade inexplicável, e quantificar o tamanho dessa variabilidade é importante. É interessante notar que os residuais geralmente assumem a forma de uma distribuição gaussiana em uma série bem comportada e, nesse caso, podemos avaliar eventos de cisne negro com testes de hipóteses.

Modelos de decomposição de séries temporais

Agora que já abordamos as partes constituintes de uma série temporal, devemos mencionar que há, na verdade, dois tipos gerais diferentes de decomposição de séries temporais. Começaremos com o modelo aditivo.

Decomposição aditiva

Aqui está a fórmula para a decomposição aditiva:

Observe os sinais de mais. O que essa fórmula está dizendo é que, se você pegar a tendência e adicioná-la ao componente sazonal e adicioná-la aos resíduos, você terá de volta a série temporal original. De modo geral, usamos uma decomposição aditiva quando a variação sazonal é constante ao longo do tempo.

Decomposição multiplicativa

Aqui está a fórmula para a decomposição multiplicativa. Observe os sinais de multiplicação nessa versão. 

Usamos um modelo multiplicativo quando a variação sazonal é escalonada com a tendência. Ou seja, quando você vê que o tamanho dos efeitos sazonais se torna maior à medida que a série geral se move para cima ou para baixo. Essa é realmente uma forma de heterocedasticidade.

Técnicas de decomposição de séries temporais

Até o momento, abordamos o que faz parte de uma decomposição de série temporal e os dois principais tipos gerais. Para continuar, precisamos falar sobre os dois métodos mais comuns. Cada um deles pode ser aplicado como um modelo aditivo ou multiplicativo. 

Decomposição clássica

A decomposição clássica é a mais fácil de entender. É da década de 1920, mas ainda é relevante hoje. Para mostrar a decomposição clássica, vamos usar o Excel. A decomposição clássica, como a STL, que mostraremos a seguir, pode ser feita com um modelo aditivo ou multiplicativo. Para este exemplo, criaremos uma versão aditiva.

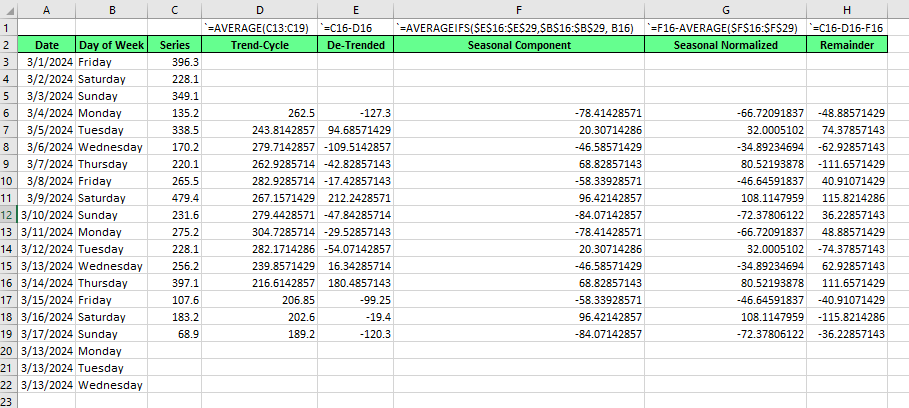
Se quiser tentar você mesmo, use o CSV index_1 neste conjunto de dados de vendas de café muito interessante que você pode encontrar no Kaggle. Para sua referência, agregamos e resumimos as vendas por dia.

• Primeiro, calculamos o ciclo de tendência. Estamos identificando uma sazonalidade semanal, e há sete dias em uma semana, portanto, o período sazonal é ímpar, o que significa que nossa média móvel deve ser centralizada usando uma janela simétrica. Ou seja, uma média móvel de 7 dias. Tenha cuidado com o alinhamento e a centralização do .

• Em seguidavocê encontrará a série com tendência detrendida subtraindo a tendência do original.

• Em seguida,, para encontrar o componente sazonal, calculamos a média dos valores detrendidos para cada período sazonal. Uma adição importante: Emvocê verá que o componente sazonal provavelmente não soma exatamente zero. Certifique-se de fazer o ajuste para isso:

  • Calcule a média de seu componente sazonal.

  • Subtraia a média sazonal de cada valor sazonal.

• Finalmentepara o restante, subtraímos a tendência e o período sazonal da série original.

Se percebêssemos que nossa série tinha um efeito sazonal que mudava com o nível dos dados, teríamos considerado uma decomposição multiplicativa. As etapas da decomposição multiplicativa são praticamente as mesmas, exceto pelo fato de usarmos a divisão em vez da subtração. Especificamente, encontraríamos a série com tendência detrendida dividindo a série original pelo ciclo de tendência. Então, mais tarde, para encontrar o restante, dividiríamos a série original pelo produto dos componentes de tendência e sazonais. (Como alternativa, poderíamos ter obtido o logaritmo natural da série original e aplicado uma decomposição aditiva. Isso seria funcionalmente o mesmo).

Decomposição STL 

A decomposição STL, que significa decomposição sazonal e de tendências usando LOESS, é uma versão mais moderna da decomposição. É mais difícil de explicar, mas geralmente é mais flexível do que o método clássico. O STL funciona usando um método chamado LOESS, que ajusta modelos de regressão simples a pequenas partes sobrepostas dos dados. Ele aplica essa regressão ponderada localmente para isolar a tendência e os componentes sazonais separadamente.

Esse método aborda desvantagens específicas da decomposição clássica, a saber, que, na versão clássica, não há estimativas de ciclo de tendência ou de resto disponíveis para a primeira e a última observação. Você pode ver isso nos espaços em branco do Excel, nas linhas 3, 4, 5, e 20, 21 e 22, acima.

Também devemos dizer que o ciclo de tendência, conforme identificado pela decomposição clássica, suaviza os rápidos aumentos e quedas, portanto, pode encobrir coisas importantes que estão acontecendo na série. Por fim, a decomposição clássica pressupõe a ideia de que há um padrão sazonal, mas, com dados suficientes, às vezes podemos ver o padrão sazonal mudar.

Vamos começar criando uma trama temporal da série original. Como antes, como primeira etapa, estamos agregando e resumindo o conjunto de dados do Kaggle antes de decompor a série.

coffee_sales_data <- read.csv("/Users/x/Desktop/index_1.csv")
coffee_sales_data <- as.data.frame(coffee_sales_data)

library(dplyr)
library(ggplot2)

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  ggplot(aes(x = as.Date(date), y = money)) +
  geom_line(color = '#01ef63') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Time series")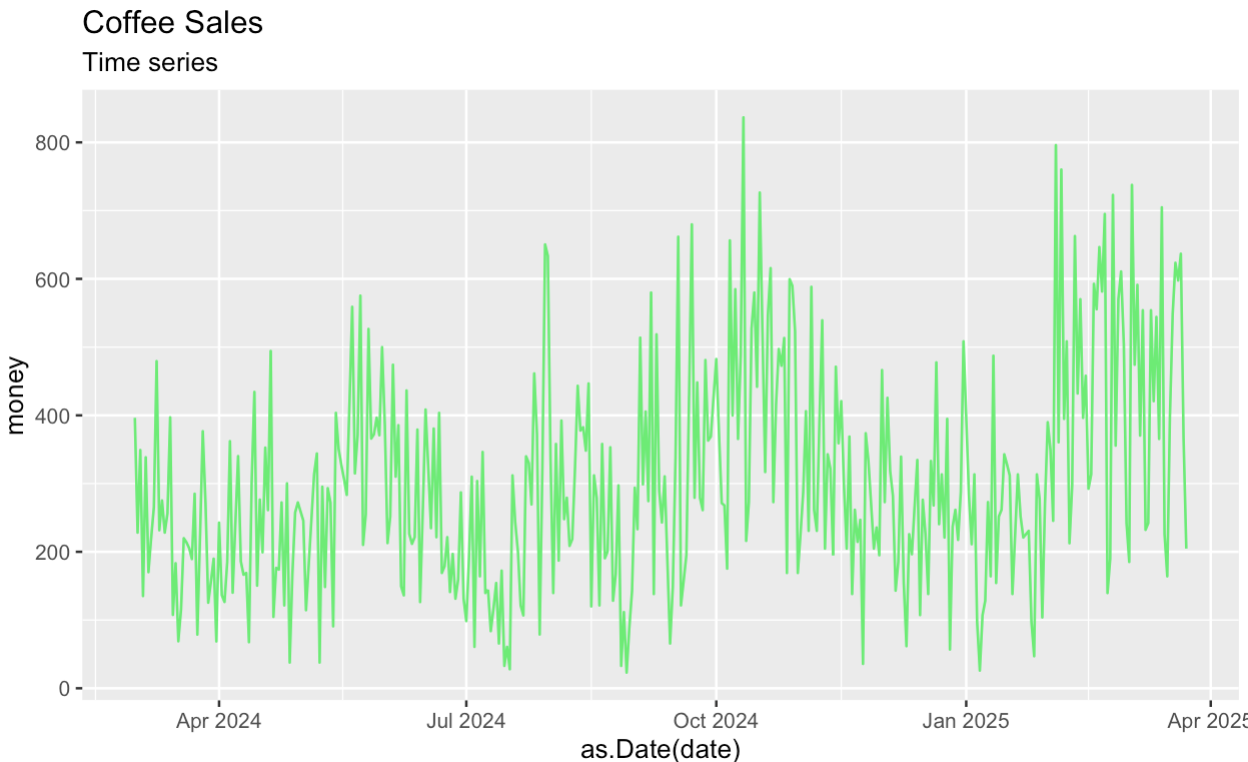

Em seguida, decompomos nossa série em componentes de tendência, sazonais e remanescentes. A caixa na parte superior do gráfico de decomposição mostra a série original, embora um pouco esmagada.

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  mutate(date = as.Date(date)) |>
  as_tsibble() |>
  filter(date > '2024-02-28') |>
  filter(date < '2024-05-01') |>
  model(
      STL(money ~ season(window = "periodic"))
  ) |>
  components() |>
  autoplot(color = '#203147') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Classical additive decomposition")

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  mutate(date = as.Date(date)) |>
  as_tsibble() |>
  filter(date > '2024-02-28') |>
  filter(date < '2024-05-01') |>
  model(
      STL(money ~ season(window = "periodic"))
  ) |>
  components() -> ts_components

ts_components |>
  autoplot(color = '#203147') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Classical additive decomposition")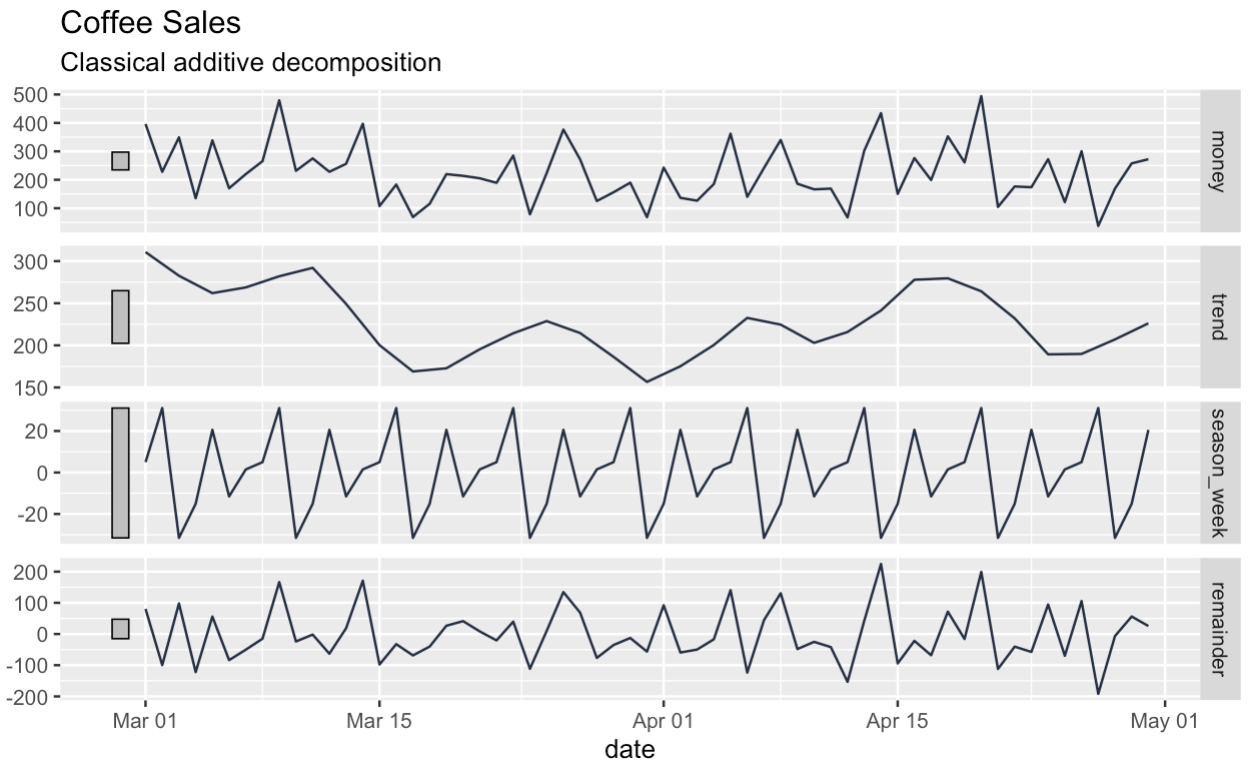

Observe que, diferentemente da decomposição clássica, o DataFrame que recebemos de volta não tem lacunas no início ou no final.  

print(ts_components)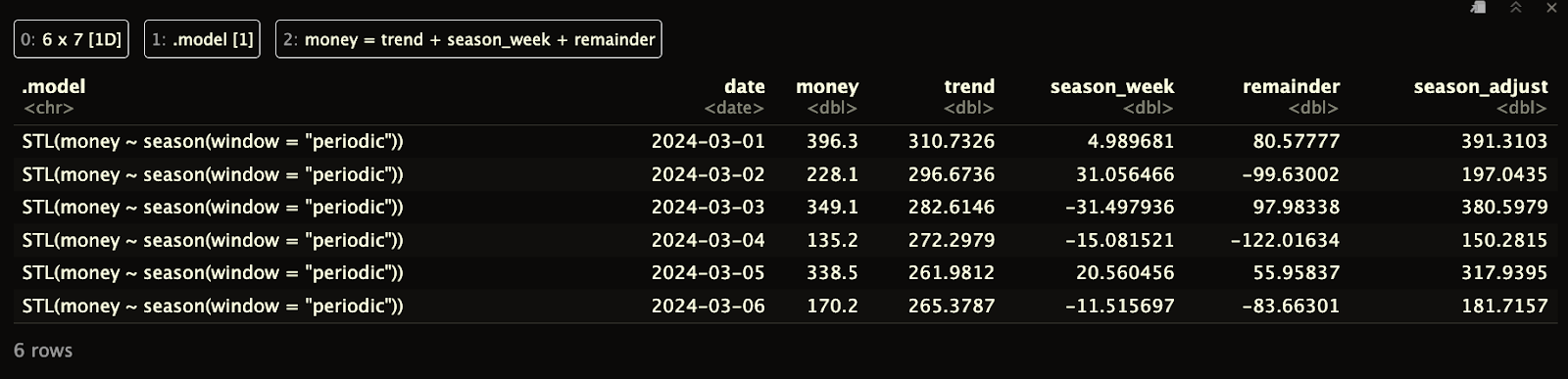

Também há algumas desvantagens na decomposição STL e, se você tiver interesse, adicionamos essas informações às nossas perguntas frequentes. 

Decomposição de séries temporais e ajustes sazonais

Muitas vezes, é útil criar uma versão dos dados com ajuste sazonal. Para isso, podemos adicionar a tendência e os componentes restantes juntos. Ou então, poderíamos subtrair o componente sazonal da série original; ambos chegariam ao mesmo resultado.

seasonally_adjusted <- components |>
  mutate(seasonally_adjusted = money - season_week)

season_adjust_data <- seasonally_adjusted |>
  select(date, money, season_adjust) |>
  pivot_longer(cols = c(money, season_adjust), names_to = "series", values_to = "value")

season_adjust_data |>
  autoplot() + facet_wrap(~series) +
  scale_color_manual(values = c(
    "money" = '#203147',          # blue
    "season_adjust" = '#01ef63'   # orange
  )) +
  facet_wrap(~series) +
  labs(title = "Coffee Sales: Original vs Seasonally Adjusted")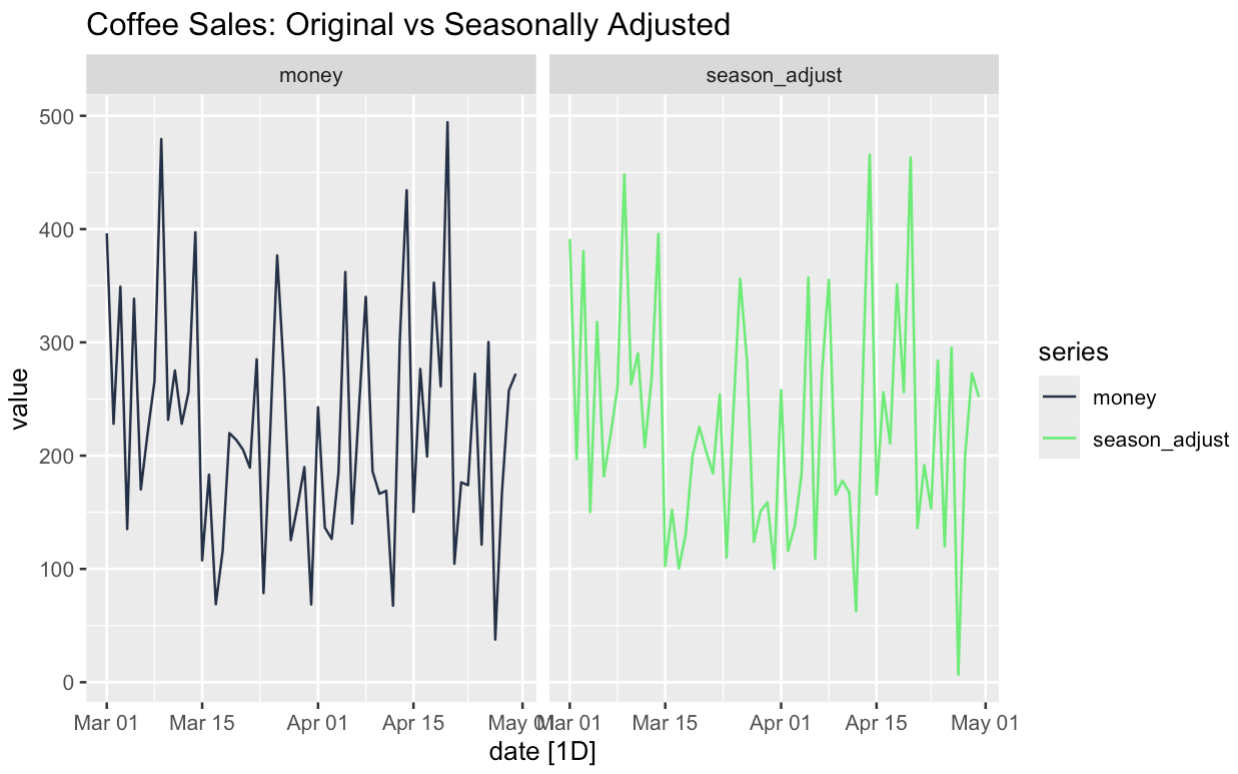

O poder dos dados com ajuste sazonal é que eles podem nos ajudar a entender certas características de nossa série. Podemos ver se a tendência subjacente é o resultado da sazonalidade, por exemplo. Por dois motivos, podemos examinar mais de perto as ocorrências incomuns nos dados. Você acha que nossa promoção de sexta-feira funcionou porque era uma sexta-feira ou porque era uma promoção? Bem, usando a decomposição de séries temporais e ajustes sazonais, podemos testar perguntas como essa.

Decomposição e previsão de séries temporais

Talvez você se surpreenda ao saber que a decomposição de séries temporais também é útil na previsão. Pensamos nisso de duas maneiras principais. Primeiro, queremos entender nossos componentes de série temporal para nos ajudar a decidir qual modelo de previsão devemos usar. Se observarmos uma forte sazonalidade, podemos nos inclinar para modelos como a suavização exponencial de Holt-Winters ou os métodos ETS, que são especificamente desenvolvidos para lidar com componentes de tendência e sazonais.

Em segundo lugar, podemos até mesmo usar dados decompostos como parte de nossa previsão, o que nos dá opções. Podemos, por exemplo, executar um modelo de previsão não sazonal em uma versão ajustada sazonalmente de nossos dados. (Podemos reintroduzir o componente sazonal mais tarde). O ajuste sazonal é especialmente útil quando queremos usar modelos flexíveis, como o ARIMA padrão e a regressão linear. 

Aqui, criamos um modelo ARIMA simples para prever os dados ajustados por sazonalidade. 

season_adjust_data_filtered <- season_adjust_data |>
  filter(series == "season_adjust") |>
  as_tsibble(index = date)

seasonal_adjust_arima_model <- season_adjust_data_filtered |>
  model(
    ARIMA(value)
  )

seasonal_adjust_arima_model |>
  forecast(h = "14 days") |>  
  autoplot(season_adjust_data_filtered, color = '#01ef63') +
  labs(title = "Forecast of Seasonally Adjusted Coffee Sales",
       subtitle = "Simple ARIMA Model",
       y = "Money (Seasonally Adjusted)",
       x = "Date")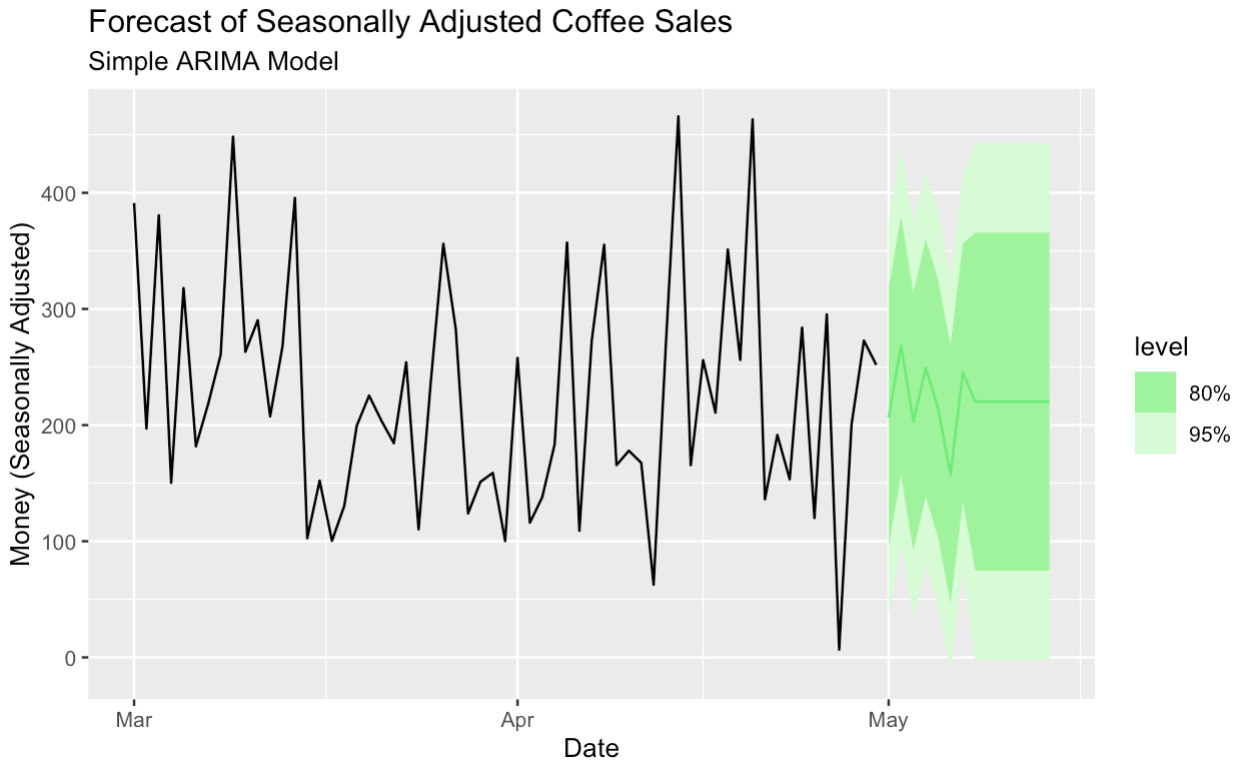

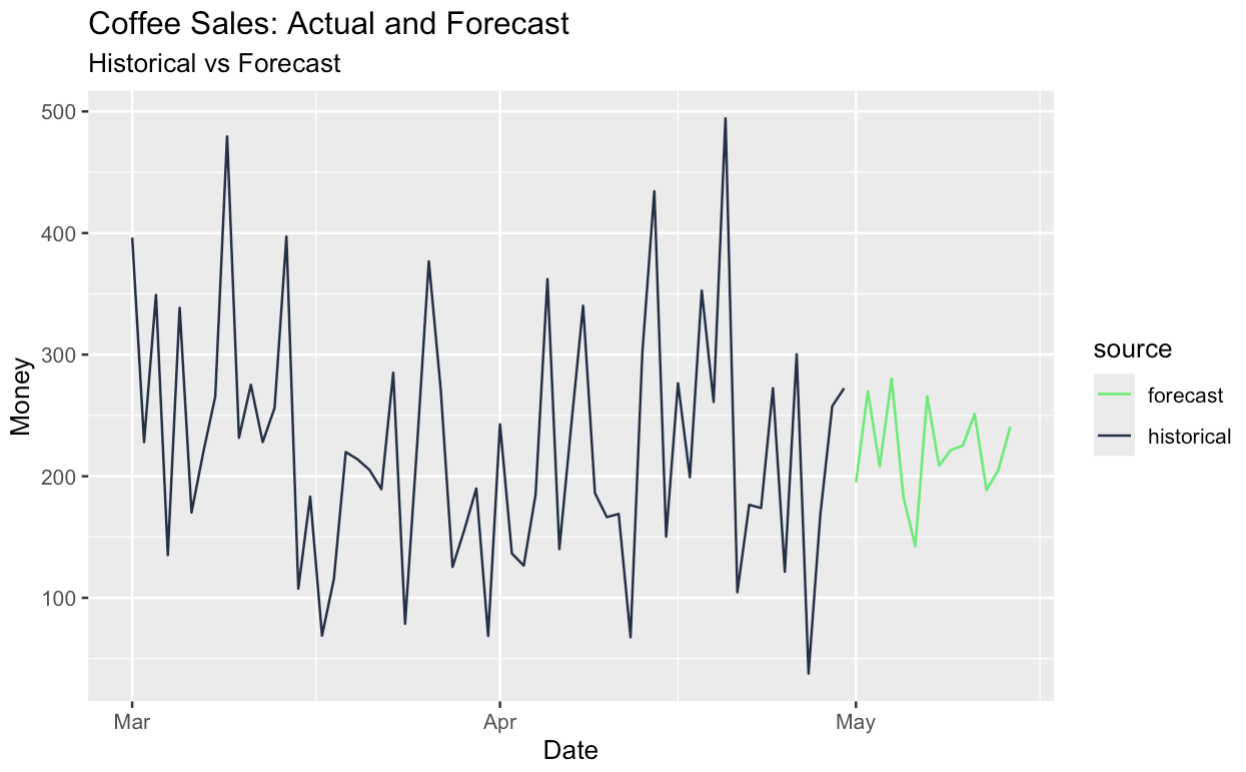
Também podemos prever a série com ajuste sazonal e adicionar o componente sazonal de volta, o que efetivamente nos dá uma previsão sazonal. Tudo isso foi possível graças à nossa decomposição original de séries temporais.

# Build tagged historical and forecast data
historical_data <- components |>
  as_tibble() |>
  select(date, money) |>
  mutate(source = "historical")

forecast_data <- final_forecast |>
  as_tibble() |>
  transmute(date, money = money_forecast) |>
  mutate(source = "forecast")

# Bind and create tsibble
full_data <- bind_rows(historical_data, forecast_data) |>
  as_tsibble(index = date, validate = FALSE)

# Plot with color by source
full_data |>
  ggplot(aes(x = date, y = money, color = source)) +
  geom_line() +
  scale_color_manual(values = c(
    "historical" = "#203147",   # dark blue for real data
    "forecast" = "#01ef63"      # green for forecast
  )) +
  labs(
    title = "Coffee Sales: Actual and Forecast",
    subtitle = "Historical vs Forecast",
    y = "Money",
    x = "Date"
  )

Considerações finais

Espero que você tenha gostado do nosso artigo sobre decomposição de séries temporais! Lembre-se de que a decomposição é apenas uma parte da análise de séries temporais; portanto, para se tornar um especialista, inscreva-se no curso Forecasting in R (Previsão em R ) com o professor Rob Hyndman, que ajudou a desenvolver os pacotes R que usamos em nossos visuais. Também temos um curso Visualizing Time Series Data in Python se você achou as ideias deste artigo interessantes, mas prefere Python, que também é muito bom para esse tipo de coisa.