Décomposition des séries temporelles : Comprendre les tendances, la saisonnalité et le bruit

La décomposition est l'un des aspects les plus intéressants de la science des données. À la base, la décomposition consiste à diviser un élément complexe en parties plus simples et plus faciles à interpréter. Cela peut arriver à une matrice, un modèle ou un signal. 

Parce qu'il s'agit d'une idée générale, elle peut prendre de nombreuses formes. En algèbre linéaire, il existe la décomposition QR, la décomposition d 'Eigend, la décomposition des valeurs singulières et la décomposition de Cholesky, pour n'en citer que quelques-unes. Dans d'autres domaines, il y a la transformée de Fourier, l'analyse en composantes principales et même la modélisation de sujets à l'aide de méthodes telles que LDA. La variabilité dans les modèles de régression peut être décomposée en composantes de la somme des carrés : SST, SSR et SSE. On peut même considérer les arbres de décision comme une forme de décomposition. 

Nous allons ici passer en revue l'un de nos favoris : la décomposition des séries temporelles. Si, à la fin, nous avons piqué votre curiosité, suivez notre cours Forecasting in R avec le professeur Rob Hyndman.

Qu'est-ce que la décomposition des séries temporelles ?

La décomposition des séries temporelles est une méthode utilisée pour décomposer une série temporelle en composantes distinctes appelées tendance ou tendance-cycle, saisonnalité et résidus. L'objectif de la décomposition des séries temporelles est de mieux comprendre les modèles sous-jacents et d'améliorer la précision des prévisions.

Quelles sont les composantes d'une série temporelle ?

Examinons les composantes de la série temporelle. C'est peut-être la meilleure façon de comprendre l'idée.

Composante tendancielle

La tendance d'une série chronologique (comme son nom l'indique) est le mouvement à long terme. Il convient de préciser que la composante "tendance" est souvent considérée comme la tendance-cycle, les cycles étant considérés comme des schémas longs et irréguliers. Historiquement, les ventes de voitures étaient considérées comme évoluant selon des cycles de sept ans (quelle qu'en soit la raison), mais ce n'est probablement plus le cas avec le mouvement vers les voitures électriques.

Le principal enseignement que les gens tirent de cette tendance est généralement le suivant : Les données augmentent-elles, diminuent-elles ou restent-elles stables à long terme ? L'augmentation globale de la température des océans au cours des dernières décennies est une tendance claire (lire : mauvaise).

Composante saisonnière

La composante saisonnière sera un peu plus longue à expliquer car elle est un peu plus compliquée. La composante saisonnière d'une série temporelle est la répétition de cycles à court terme dans les données qui se produisent à intervalles réguliers. Pensez au quotidien, au mois, à la semaine, au trimestre. L'essentiel est que les intervalles soient assez réguliers. Vous pouvez constater, par exemple, que les commandes des cafés suivent une saisonnalité hebdomadaire si les gens aiment faire du café à la maison le dimanche. (Nous examinerons cette question concernant les commandes des cafés dans la section suivante).

La saisonnalité est plus compliquée qu'il n'y paraît. Réfléchissez au fait que le nombre de semaines dans une année n'est pas un nombre entier (~52,18). Ou réfléchissez à la façon dont les mois ne sont pas espacés uniformément : Le mois de février compte 28 (ou 29) jours, mais le mois de juillet en compte toujours 31.

De plus, comme chaque année compte un peu plus de 52 semaines et que les mois varient également, vous ne pouvez pas diviser la plupart des mois en semaines. Cela est évident lorsque vous étudiez un calendrier. Mais ce qui est moins évident pour un analyste de données, c'est que, lorsque vous examinez des données au niveau hebdomadaire, puis que vous les agrégez au niveau mensuel, vous pouvez constater des incohérences, comme le fait qu'un mois de janvier peut avoir quatre lundis, mais que le suivant peut en avoir cinq, et que les comparaisons peuvent donc être difficiles.

La composante résiduelle / irrégulière / restante

Tout ce qui reste après avoir retiré la tendance-cycle et la composante saisonnière est appelé, à juste titre, la composante résiduelle, qui comprend des éléments anormaux dans les données, comme un grand événement, et du bruit aléatoire. La composante résiduelle n'est pas un artefact inutile. Toutes les données présentent une variabilité inexpliquée et il est important de quantifier l'ampleur de cette variabilité. Il est intéressant de noter que les residuels prennent souvent la forme d'une distribution gaussienne. distribution gaussienne Dans ce cas, nous pouvons évaluer les cygnes noirs à l'aide de tests d'hypothèse.

Modèles de décomposition des séries temporelles

Maintenant que nous avons abordé les éléments constitutifs d'une série temporelle, nous devons mentionner qu'il existe en fait deux types généraux différents de décomposition des séries temporelles. Nous commencerons par le modèle additif.

Décomposition additive

Voici la formule de la décomposition additive :

Notez les signes plus. Cette formule indique que si vous prenez la tendance, que vous l'ajoutez à la composante saisonnière et que vous l'ajoutez aux résidus, vous retrouvez la série temporelle originale. D'une manière générale, nous utilisons une décomposition additive lorsque les variations saisonnières sont constantes dans le temps.

Décomposition multiplicative

Voici la formule de décomposition multiplicative. Notez les signes de multiplication dans cette version. 

Nous utilisons un modèle multiplicatif lorsque la variation saisonnière s'échelonne avec la tendance. C'est-à-dire lorsque vous constatez que l'ampleur des effets saisonniers augmente à mesure que la série globale évolue à la hausse ou à la baisse. Il s'agit en fait d'une forme d'hétéroscédasticité.

Techniques de décomposition des séries temporelles

Jusqu'à présent, nous avons abordé ce qui entre dans la composition d'une décomposition de série temporelle et les deux principaux types de décomposition. Pour aller plus loin, nous devons parler des deux méthodes les plus courantes. Chacun d'entre eux peut être appliqué en tant que modèle additif ou multiplicatif. 

Décomposition classique

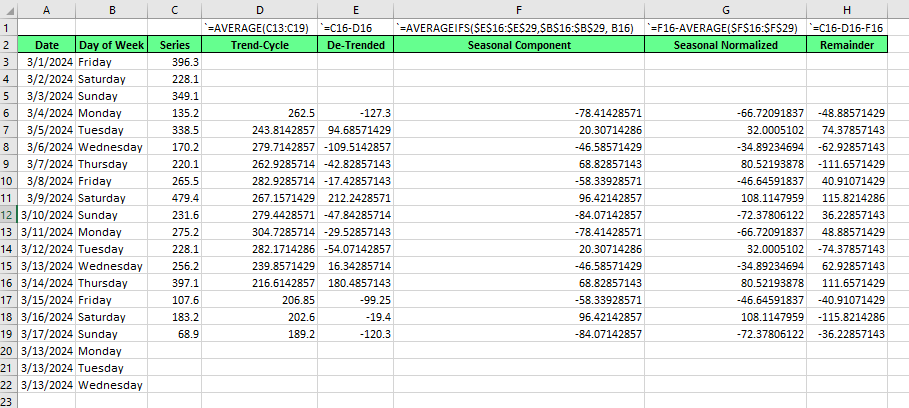
La décomposition classique est la plus facile à comprendre. Il date des années 1920, mais il est toujours d'actualité. Pour illustrer la décomposition classique, utilisons Excel. La décomposition classique, comme la STL, que nous montrerons ensuite, peut être effectuée avec un modèle additif ou multiplicatif. Pour cet exemple, nous allons créer une version additive.

Si vous voulez essayer par vous-même, utilisez le CSV index_1 dans cet ensemble de données très intéressant sur les ventes de café que vous pouvez trouver sur Kaggle. Pour votre information, nous avons regroupé et résumé les ventes par jour.

• Tout d'abord, nous calculons la tendance-cycle. Nous identifions une saisonnalité hebdomadaire, et il y a sept jours dans une semaine, donc la période saisonnière est impaire, ce qui signifie que notre moyenne mobile doit être centrée en utilisant une fenêtre symétrique. Il s'agit d'une moyenne mobile sur 7 jours. Faites attention à l'alignement et au centrage de .

• Ensuite, nous trouvons la série détriangée en soustrayant la tendance de l'original.nous obtenons la série détriangée en soustrayant la tendance de la série originale.

• Ensuite,, pour trouver la composante saisonnière, nous faisons la moyenne des valeurs détendues pour chaque période saisonnière. Un ajout important : Yous verrez que la somme de la composante saisonnière n'est probablement pas égale à zéro. Veillez à tenir compte de ce facteur :

  • Calculez la moyenne de votre composante saisonnière.

  • Soustrayez la moyenne saisonnière de chaque valeur saisonnière.

• Enfin, pour le reste, nous soustrayons la tendance et la période saisonnière de la série originale.pour le reste, nous soustrayons la tendance et la période saisonnière de la série originale.

Si nous avions constaté que notre série avait un effet saisonnier qui changeait avec le niveau des données, nous aurions plutôt envisagé une décomposition multiplicative. Les étapes de la décomposition multiplicative sont à peu près les mêmes, sauf que nous utilisons la division au lieu de la soustraction. Plus précisément, nous trouverions la série tendancielle en divisant la série originale par la tendance-cycle. Puis, plus tard, pour trouver le reste, nous diviserons la série originale par le produit de la tendance et des composantes saisonnières. (Nous aurions également pu prendre le logarithme naturel de la série originale et appliquer une décomposition additive. Cela reviendrait à la même chose sur le plan fonctionnel).

Décomposition STL 

La décomposition STL (seasonal and trend decomposition using LOESS) est une version plus moderne de la décomposition. Elle est plus difficile à expliquer, mais elle est généralement plus souple que la méthode classique. Le STL utilise une méthode appelée LOESS, qui ajuste des modèles de régression simples à de petits morceaux de données qui se chevauchent. Il applique cette régression pondérée localement pour isoler séparément les composantes tendancielles et saisonnières.

Cette méthode répond aux inconvénients spécifiques de la décomposition classique, à savoir que, dans la version classique, aucune estimation de la tendance-cycle ou du reste n'est disponible pour la première et la dernière observation. Vous pouvez le constater dans les espaces vides d'Excel, aux lignes 3, 4, 5, et 20, 21 et 22, ci-dessus.

Il convient également de préciser que la tendance-cycle, telle qu'identifiée par la décomposition classique, lisse les hausses et les baisses rapides, et peut donc masquer des éléments importants de la série. Enfin, la décomposition classique prend pour acquis l'idée qu'il existe un schéma saisonnier mais, si l'on dispose de suffisamment de données, on peut parfois voir le schéma saisonnier changer.

Commençons par créer un graphique temporel de la série originale. Comme précédemment, nous commençons par agréger et résumer l'ensemble des données Kaggle avant de décomposer les séries.

coffee_sales_data <- read.csv("/Users/x/Desktop/index_1.csv")
coffee_sales_data <- as.data.frame(coffee_sales_data)

library(dplyr)
library(ggplot2)

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  ggplot(aes(x = as.Date(date), y = money)) +
  geom_line(color = '#01ef63') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Time series")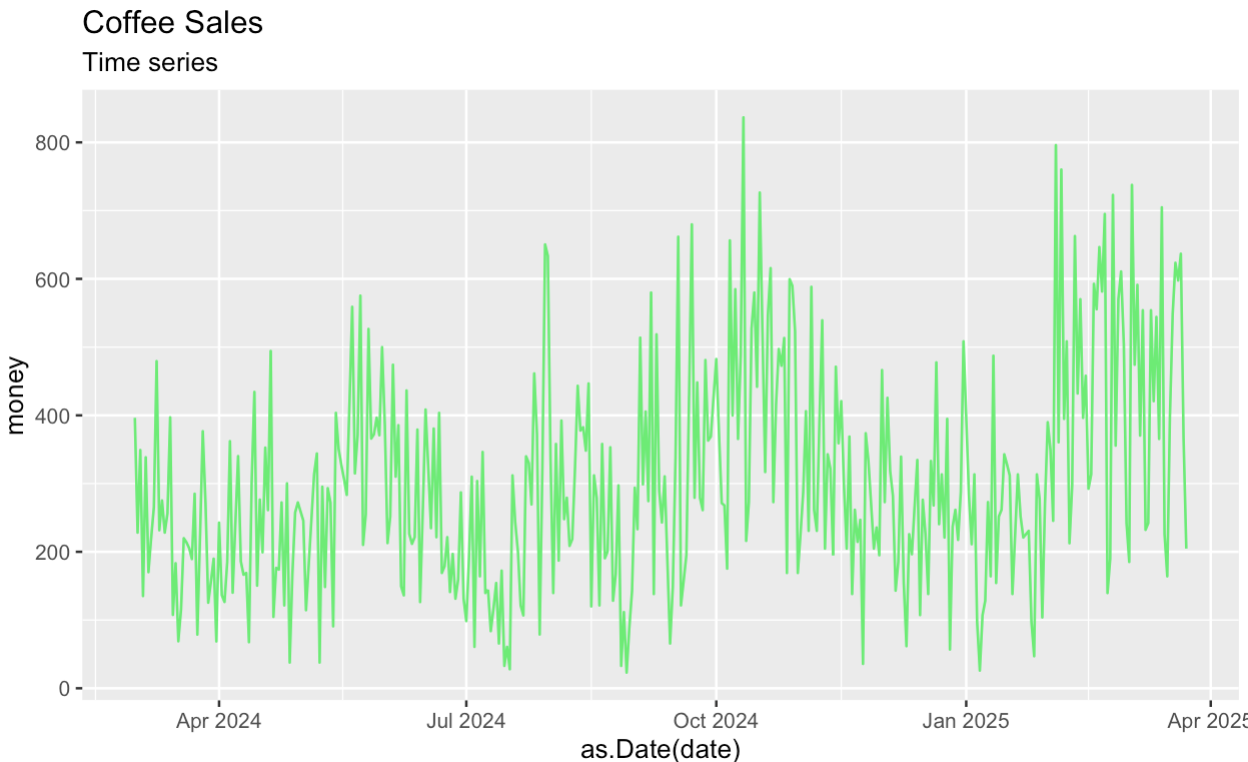

Ensuite, nous décomposons nos séries en composantes tendancielles, saisonnières et résiduelles. La boîte en haut du graphique de décomposition montre la série originale, même si elle est un peu réduite.

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  mutate(date = as.Date(date)) |>
  as_tsibble() |>
  filter(date > '2024-02-28') |>
  filter(date < '2024-05-01') |>
  model(
      STL(money ~ season(window = "periodic"))
  ) |>
  components() |>
  autoplot(color = '#203147') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Classical additive decomposition")

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  mutate(date = as.Date(date)) |>
  as_tsibble() |>
  filter(date > '2024-02-28') |>
  filter(date < '2024-05-01') |>
  model(
      STL(money ~ season(window = "periodic"))
  ) |>
  components() -> ts_components

ts_components |>
  autoplot(color = '#203147') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Classical additive decomposition")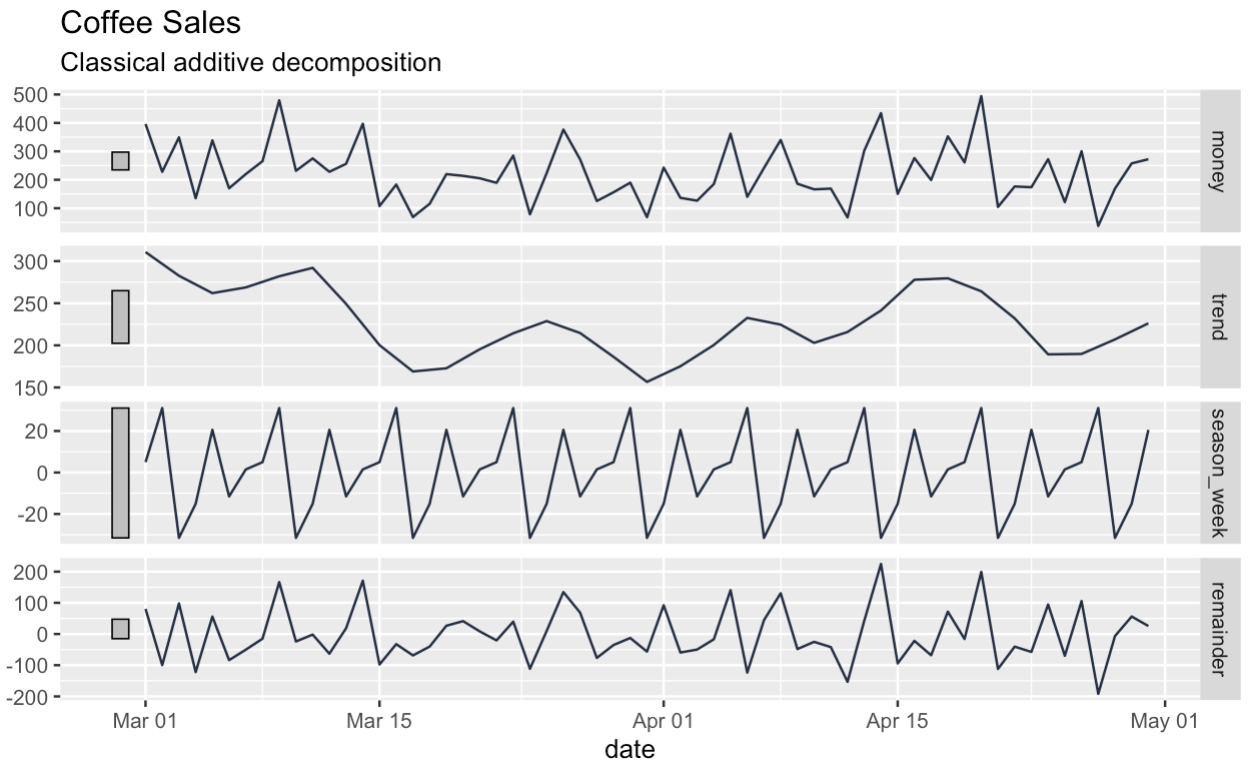

Remarquez que, contrairement à la décomposition classique, le DataFrame que nous obtenons en retour ne présente aucune lacune au début ou à la fin.  

print(ts_components)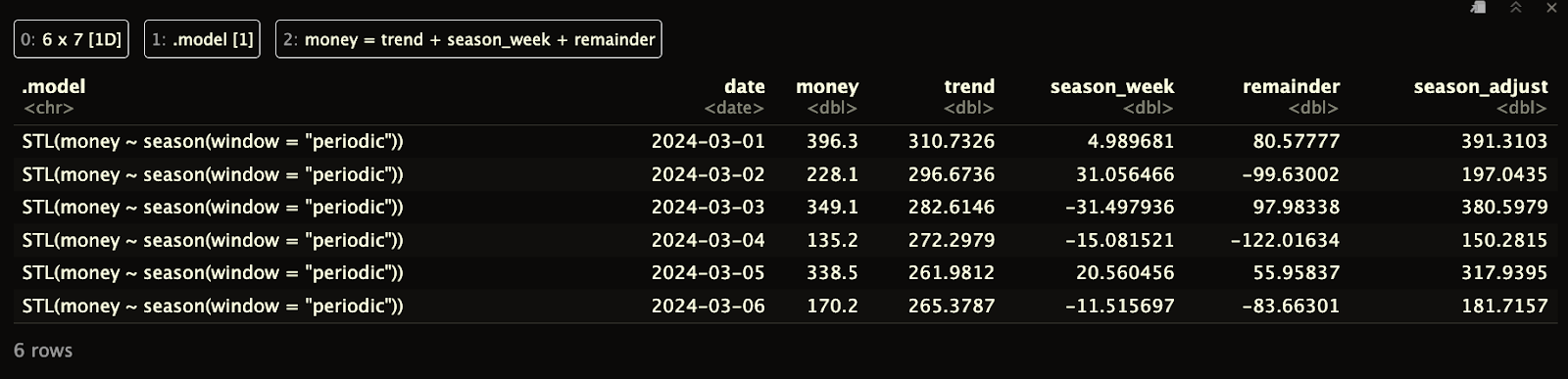

La décomposition STL présente également certains inconvénients et, si vous êtes intéressé, nous avons ajouté ces informations dans nos FAQ. 

Décomposition des séries temporelles et désaisonnalisation

Il est souvent utile de créer une version corrigée des variations saisonnières des données. Pour ce faire, nous pouvons additionner les composantes tendance et reste. Ou encore, nous pourrions soustraire la composante saisonnière de la série originale, ce qui aboutirait à la même chose.

seasonally_adjusted <- components |>
  mutate(seasonally_adjusted = money - season_week)

season_adjust_data <- seasonally_adjusted |>
  select(date, money, season_adjust) |>
  pivot_longer(cols = c(money, season_adjust), names_to = "series", values_to = "value")

season_adjust_data |>
  autoplot() + facet_wrap(~series) +
  scale_color_manual(values = c(
    "money" = '#203147',          # blue
    "season_adjust" = '#01ef63'   # orange
  )) +
  facet_wrap(~series) +
  labs(title = "Coffee Sales: Original vs Seasonally Adjusted")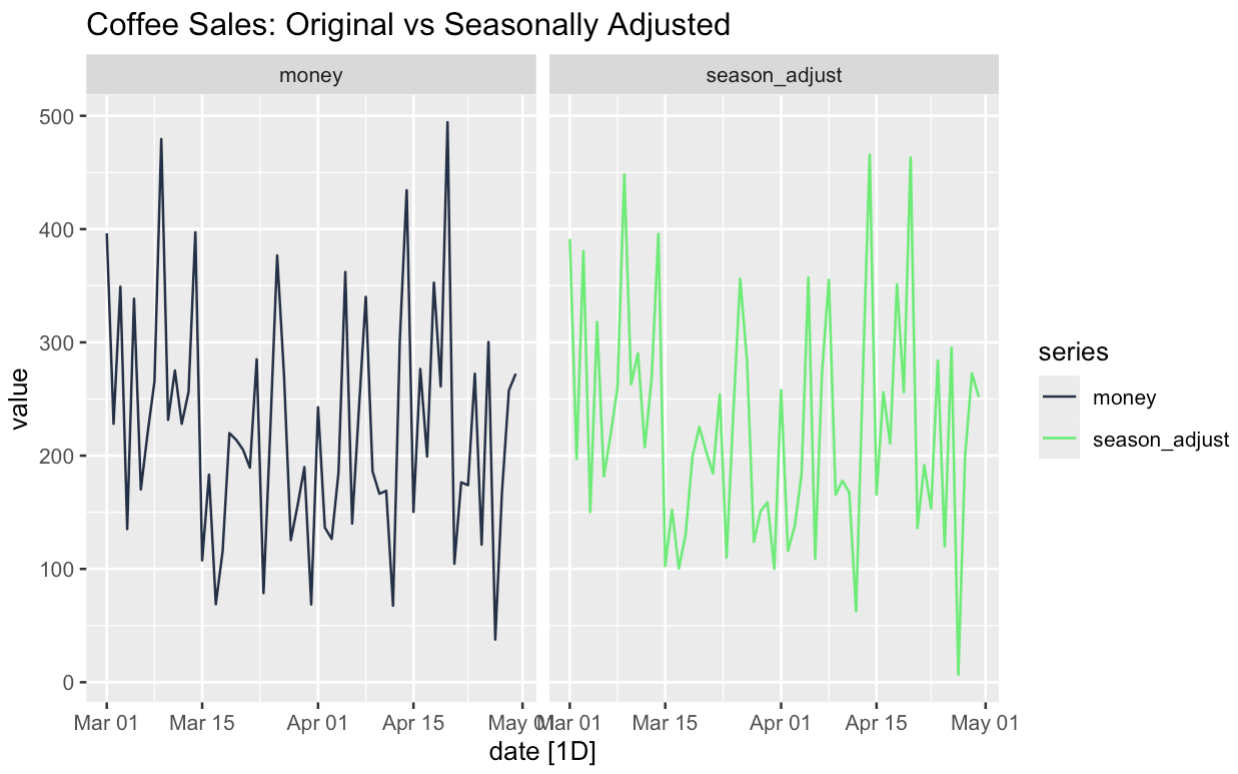

L'intérêt des données corrigées des variations saisonnières est qu'elles peuvent nous aider à comprendre certaines caractéristiques de nos séries. Nous pouvons voir si la tendance sous-jacente est le résultat de la saisonnalité, par exemple. Deuxièmement, nous pouvons examiner de plus près les occurrences inhabituelles dans les données. Pensons-nous que notre promotion du vendredi a fonctionné parce que c'était un vendredi ou parce qu'il s'agissait d'une promotion ? Grâce à la décomposition des séries temporelles et aux ajustements saisonniers, nous pouvons tester des questions de ce type.

Décomposition des séries temporelles et prévisions

Vous serez peut-être surpris d'apprendre que la décomposition des séries temporelles est également utile pour les prévisions. Nous envisageons cette question de deux manières principales. Tout d'abord, nous voulons comprendre les composantes de notre série temporelle pour nous aider à décider du modèle de prévision à utiliser. Si nous observons une forte saisonnalité, nous pourrions nous tourner vers des modèles tels que le lissage exponentiel de Holt-Winters ou les méthodes ETS, qui sont spécifiquement conçues pour traiter à la fois les tendances et les composantes saisonnières.

Deuxièmement, nous pouvons même utiliser des données décomposées dans le cadre de nos prévisions, ce qui nous donne des options. Nous pouvons, par exemple, exécuter un modèle de prévision non saisonnier sur une version corrigée des variations saisonnières de nos données. (Nous pourrons réintroduire la composante saisonnière plus tard). La désaisonnalisation est particulièrement utile lorsque l'on souhaite utiliser des modèles flexibles, tels que l'ARIMA standard et la régression linéaire. 

Nous créons ici un modèle ARIMA simple pour prévoir les données corrigées des variations saisonnières. 

season_adjust_data_filtered <- season_adjust_data |>
  filter(series == "season_adjust") |>
  as_tsibble(index = date)

seasonal_adjust_arima_model <- season_adjust_data_filtered |>
  model(
    ARIMA(value)
  )

seasonal_adjust_arima_model |>
  forecast(h = "14 days") |>  
  autoplot(season_adjust_data_filtered, color = '#01ef63') +
  labs(title = "Forecast of Seasonally Adjusted Coffee Sales",
       subtitle = "Simple ARIMA Model",
       y = "Money (Seasonally Adjusted)",
       x = "Date")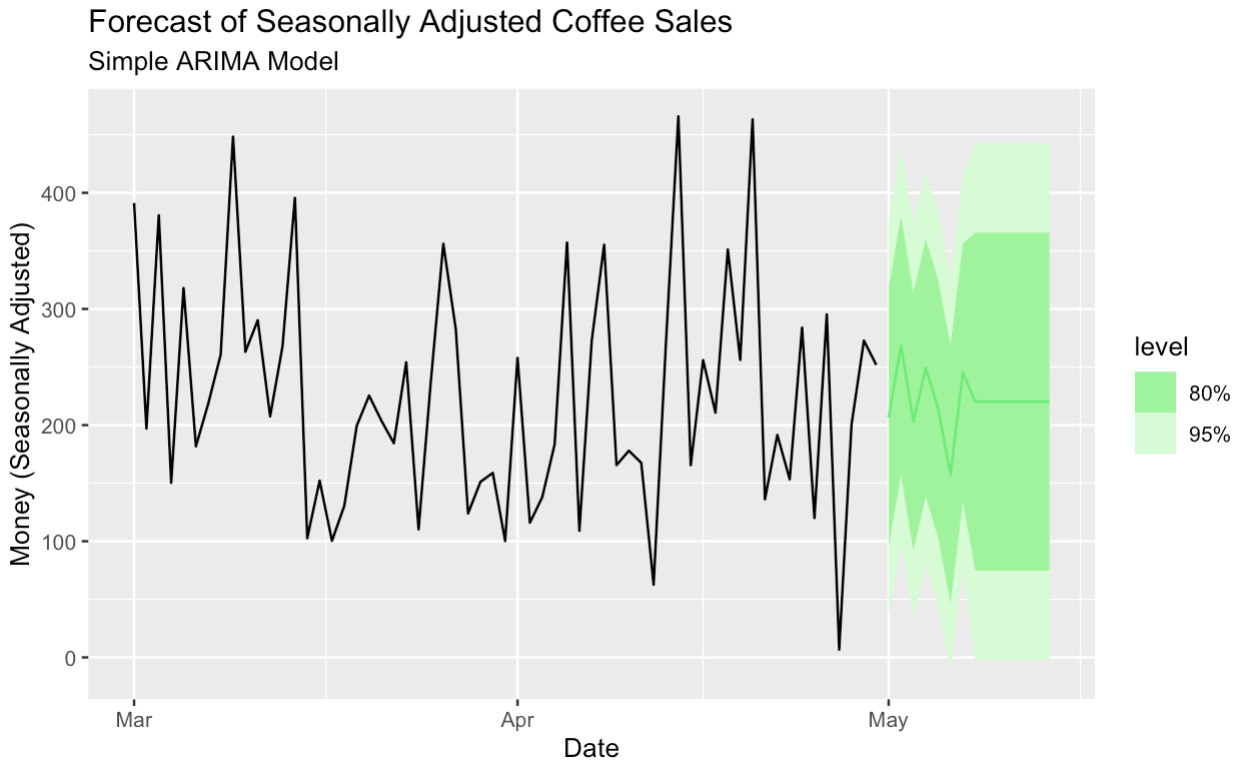

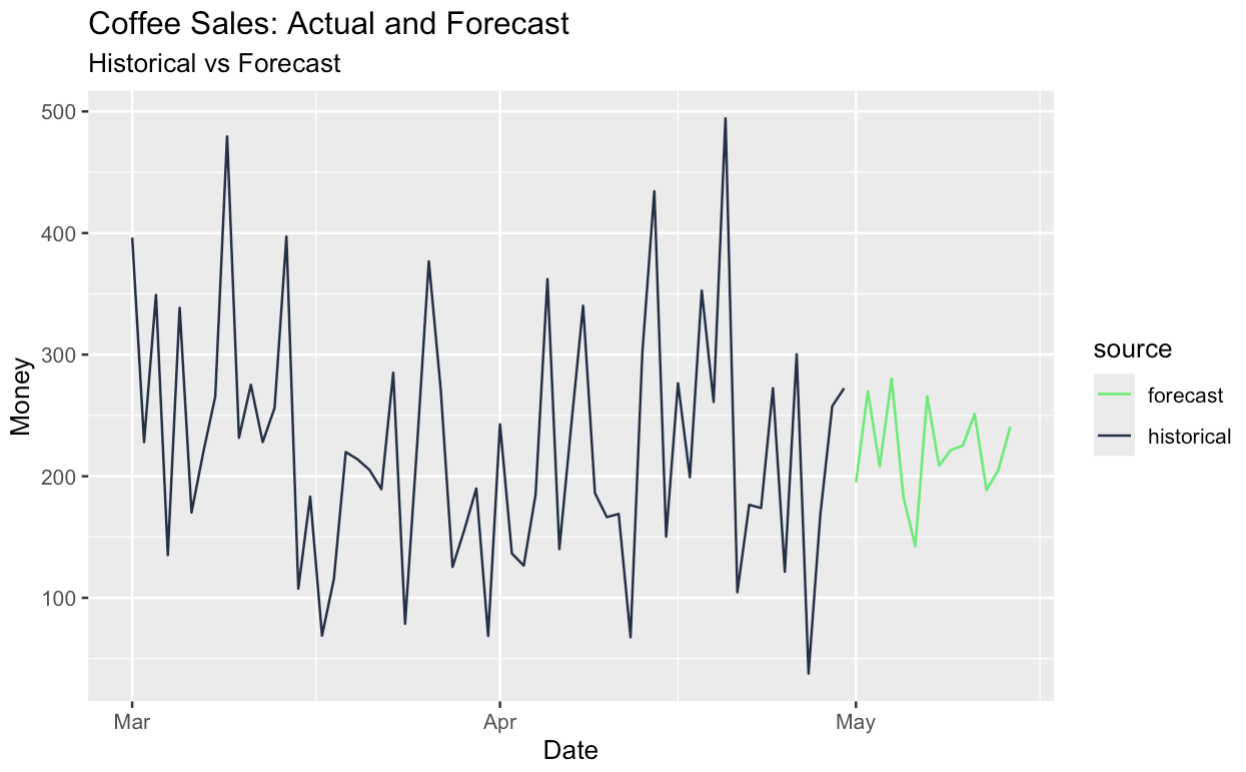
Nous pouvons également prévoir la série corrigée des variations saisonnières et ajouter la composante saisonnière, ce qui nous permet d'obtenir des prévisions saisonnières. Tout cela a été rendu possible grâce à notre décomposition originale des séries temporelles.

# Build tagged historical and forecast data
historical_data <- components |>
  as_tibble() |>
  select(date, money) |>
  mutate(source = "historical")

forecast_data <- final_forecast |>
  as_tibble() |>
  transmute(date, money = money_forecast) |>
  mutate(source = "forecast")

# Bind and create tsibble
full_data <- bind_rows(historical_data, forecast_data) |>
  as_tsibble(index = date, validate = FALSE)

# Plot with color by source
full_data |>
  ggplot(aes(x = date, y = money, color = source)) +
  geom_line() +
  scale_color_manual(values = c(
    "historical" = "#203147",   # dark blue for real data
    "forecast" = "#01ef63"      # green for forecast
  )) +
  labs(
    title = "Coffee Sales: Actual and Forecast",
    subtitle = "Historical vs Forecast",
    y = "Money",
    x = "Date"
  )

Réflexions finales

J'espère que vous avez apprécié notre article sur la décomposition des séries temporelles ! N'oubliez pas que la décomposition n'est qu'une partie de l'analyse des séries temporelles. Pour devenir un expert, inscrivez-vous au cours Forecasting in R du professeur Rob Hyndman, qui a contribué au développement des paquets R que nous avons utilisés pour nos visuels. Nous avons également un cours Visualisation des données de séries temporelles en Python si vous avez trouvé les idées de cet article intéressantes mais que vous préférez Python, qui est également très bon pour ce genre de choses.