Zeitreihenzerlegung: Verstehe Trends, Saisonalität und Rauschen

Die Dekomposition ist eine der interessantesten Dinge in der Datenwissenschaft. Im Kern geht es bei der Dekomposition darum, etwas Komplexes in einfachere, besser interpretierbare Teile zu zerlegen. Das kann mit einer Matrix, einem Modell oder einem Signal passieren. 

Weil es eine allgemeine Idee ist, kann sie viele Formen annehmen. In der linearen Algebra gibt es die QR-Zerlegung, die Eigenwertzerlegung, die Singulärwertzerlegung und die Cholesky-Zerlegung, um nur einige zu nennen. In anderen Bereichen gibt es die Fourier-Transformation, die Hauptkomponentenanalyse und sogar die Themenmodellierung mit Methoden wie LDA. Die Variabilität in Regressionsmodellen kann in Summe der Quadrate Komponenten zerlegt werden: SST, SSR und SSE. Wir können Entscheidungsbäume sogar als eine Form der Dekomposition betrachten. 

Hier werden wir einen unserer Favoriten unter die Lupe nehmen: die Zerlegung von Zeitreihen. Wenn wir dich am Ende neugierig gemacht haben, besuche unseren Kurs Forecasting in R mit Professor Rob Hyndman.

Was ist die Zeitreihenzerlegung?

Die Zeitreihenzerlegung ist eine Methode, mit der eine Zeitreihe in einzelne Komponenten, den Trend oder Trend-Zyklus, die Saisonalität und die Residuen, zerlegt wird. Der Zweck der Zeitreihenzerlegung ist es, die zugrunde liegenden Muster besser zu verstehen und die Prognosegenauigkeit zu verbessern.

Was sind die Bestandteile einer Zeitreihe?

Werfen wir einen Blick auf die Zeitreihenkomponenten. Das ist vielleicht der beste Weg, um die Idee zu verstehen.

Trend-Komponente

Der Trend einer Zeitreihe (wie der Name schon sagt) ist die langfristige Bewegung. Wir sollten erwähnen, dass die Trendkomponente oft als Trendzyklus bezeichnet wird, wobei unter Zyklen lange, unregelmäßige Muster verstanden werden. In der Vergangenheit wurden die Autoverkäufe in Sieben-Jahres-Zyklen abgewickelt (aus welchen Gründen auch immer), aber mit der Entwicklung hin zu Elektroautos ist das wahrscheinlich nicht mehr der Fall.

Die wichtigste Erkenntnis, die die Menschen aus dem Trend mitnehmen, ist in der Regel diese: Nehmen die Daten langfristig zu oder ab, oder bleiben sie stabil? Der weltweite Anstieg der Meerestemperaturen in den letzten Jahrzehnten ist ein eindeutiger (sprich: schlechter) Trend.

Saisonale Komponente

Die saisonale Komponente wird ein bisschen länger dauern, weil sie ein bisschen komplizierter ist. Die saisonale Komponente einer Zeitreihe sind die sich wiederholenden kurzfristigen Zyklen in den Daten, die in regelmäßigen Abständen auftreten. Denke täglich, monatlich, wöchentlich, vierteljährlich. Der Schlüssel dazu ist, dass die Intervalle ziemlich regelmäßig sein müssen. Du könntest zum Beispiel sehen, dass die Bestellungen in den Coffee Shops einer wöchentlichen Saisonalität folgen, wenn die Leute sonntags gerne zu Hause Kaffee kochen. (Wir werden diese Frage zu den Bestellungen im Café im nächsten Abschnitt untersuchen).

Die Sache mit der Saisonalität ist, dass sie komplizierter sein kann, als sie scheint. Denke daran, dass die Anzahl der Wochen in einem Jahr keine ganze Zahl ist (~52,18). Oder denke daran, dass die Monate nicht gleichmäßig verteilt sind: Der Februar hat 28 (oder 29) Tage, aber der Juli hat immer 31.

Und da jedes Jahr etwas mehr als 52 Wochen hat und auch die Monate variieren, kannst du die meisten Monate nicht gleichmäßig in Wochen unterteilen. Das wird deutlich, wenn du einen Kalender studierst. Aber was für einen Datenanalysten weniger offensichtlich ist, ist, dass, wenn du Daten auf wöchentlicher Ebene betrachtest und sie dann auf die monatliche Ebene aggregierst, du vielleicht uneinheitliche Dinge siehst, wie z.B. dass ein Januar vier Montage hat, der nächste aber fünf, und so können Vergleiche schwierig sein.

Die restliche / unregelmäßige / verbleibende Komponente

Alles, was übrig bleibt, nachdem wir den Trend-Zyklus und die saisonale Komponente herausgezogen haben, nennen wir passenderweise die Restkomponente, die anomale Dinge in den Daten, wie ein großes Ereignis, und zufälliges Rauschen beinhaltet. Die Restkomponente ist kein nutzloses Artefakt. Alle Daten weisen unerklärliche Schwankungen auf, und es ist wichtig, das Ausmaß dieser Schwankungen zu bestimmen. Interessanterweise nehmen residuals oft die Form einer Gauß-Verteilung In diesem Fall können wir die Ereignisse des schwarzen Schwans mit Hypothesentests bewerten.

Modelle zur Zerlegung von Zeitreihen

Nachdem wir uns nun mit den Bestandteilen einer Zeitreihe befasst haben, sollten wir erwähnen, dass es eigentlich zwei verschiedene allgemeine Arten der Zeitreihenzerlegung gibt. Wir beginnen mit dem additiven Modell.

Additive Zersetzung

Hier ist die Formel für die additive Zersetzung:

Beachte die Pluszeichen. Diese Formel besagt, dass du die ursprüngliche Zeitreihe zurückbekommst, wenn du den Trend zur saisonalen Komponente und diese zu den Residuen addierst. Im Allgemeinen verwenden wir eine additive Zerlegung, wenn die saisonalen Schwankungen im Laufe der Zeit konstant sind.

Multiplikative Zerlegung

Hier ist die Formel für die multiplikative Dekomposition. Beachte die Multiplikationszeichen in dieser Version. 

Wir verwenden ein multiplikatives Modell, wenn die saisonalen Schwankungen mit dem Trend skalieren. Das heißt, wenn du siehst, dass die Größe der saisonalen Effekte größer wird, wenn sich die Gesamtreihe nach oben oder unten bewegt. Dies ist eigentlich eine Form der Heteroskedastizität.

Techniken zur Zerlegung von Zeitreihen

Bisher haben wir uns damit beschäftigt, was eine Zeitreihenzerlegung ausmacht und welche zwei Haupttypen es gibt. Im Folgenden müssen wir über die beiden gängigsten Methoden sprechen. Jedes dieser Modelle kann als additives oder multiplikatives Modell angewendet werden. 

Klassische Zersetzung

Die klassische Zersetzung ist einfacher zu verstehen. Es stammt aus den 1920er Jahren, ist aber auch heute noch aktuell. Um die klassische Zerlegung zu zeigen, verwenden wir Excel. Die klassische Dekompostierung, wie die STL, die wir im Folgenden zeigen werden, kann entweder mit einem additiven oder multiplikativen Modell durchgeführt werden. Für dieses Beispiel werden wir eine additive Version erstellen.

Wenn du es selbst ausprobieren möchtest, verwende die index_1 CSV in diesem sehr interessanten Kaffeeverkaufsdatensatz, den du auf Kaggle finden kannst. Zu deiner Information haben wir die Verkäufe nach Tagen zusammengefasst.

• Zuerst berechnen wir den Trend-Zyklus. Wir ermitteln eine wöchentliche Saisonalität, und da eine Woche sieben Tage hat, ist der saisonale Zeitraum ungerade, was bedeutet, dass unser gleitender Durchschnitt mit einem symmetrischen Fenster zentriert werden sollte. Das heißt, ein gleitender 7-Tage-Durchschnitt. Achte auf die Ausrichtung und Zentrierung von .

• Weiterfinden wir die umgekehrte Reihe, indem wir den Trend vom Original abziehen.

• Dann, um die saisonale Komponente zu finden, bilden wir den Durchschnitt der abgeleiteten Werte für jede saisonale Periode. Eine wichtige Ergänzung: Yie werden sehen, dass die Summe der saisonalen Komponente wahrscheinlich nicht genau Null ergibt. Achte darauf, dass du dies berücksichtigst:

  • Berechne den Mittelwert deiner saisonalen Komponente.

  • Ziehe den saisonalen Mittelwert von jedem saisonalen Wert ab.

• Schließlichziehen wir für den Rest den Trend und die saisonale Periode von der ursprünglichen Reihe ab.

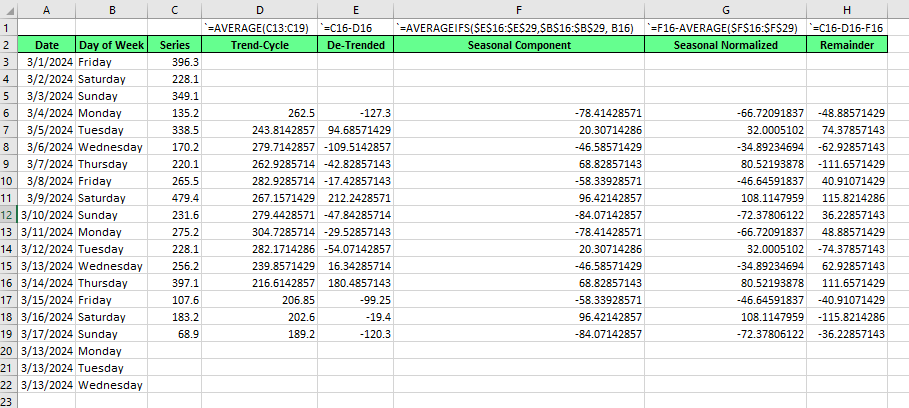
Wenn wir gesehen hätten, dass unsere Reihe einen saisonalen Effekt hat, der sich mit der Datenebene ändert, hätten wir stattdessen eine multiplikative Zerlegung in Betracht gezogen. Die Schritte für die multiplikative Zerlegung sind fast die gleichen, außer dass wir die Division statt der Subtraktion verwenden. Konkret würden wir die abweichende Reihe finden, indem wir die ursprüngliche Reihe durch den Trendzyklus dividieren. Um den Rest zu finden, würden wir später auf die ursprüngliche Reihe durch das Produkt aus Trend und saisonaler Komponente teilen. (Alternativ hätten wir auch den natürlichen Logarithmus der ursprünglichen Reihe nehmen und eine additive Zerlegung durchführen können. Das wäre funktional dasselbe.)

STL-Zerlegung 

Die STL-Zerlegung, die für Seasonal and Trend Decomposition using LOESS steht, ist eine modernere Version der Zerlegung. Sie ist schwieriger zu erklären, aber sie ist im Allgemeinen flexibler als die klassische Methode. STL arbeitet mit einer Methode namens LOESS, die einfache Regressionsmodelle auf kleine, sich überschneidende Teile der Daten anpasst. Sie wendet diese lokal gewichtete Regression an, um den Trend und die saisonalen Komponenten getrennt zu isolieren.

Diese Methode behebt bestimmte Nachteile der klassischen Zerlegung, nämlich dass in der klassischen Version keine Trendzyklus- oder Restschätzungen für die erste und letzte Beobachtung verfügbar sind. Du kannst dies in den leeren Excel-Feldern in den Zeilen 3, 4, 5 und 20, 21 und 22 oben sehen.

Wir sollten auch sagen, dass der Trend-Zyklus, wie er durch die klassische Zerlegung ermittelt wird, schnelle Anstiege und Rückgänge glättet, so dass er wichtige Dinge, die in den Reihen passieren, überdecken könnte. Schließlich geht die klassische Zerlegung davon aus, dass es ein saisonales Muster gibt, aber wenn wir genügend Daten haben, können wir manchmal sehen, dass sich das saisonale Muster ändert.

Beginnen wir damit, einen Zeitplan für die Originalserie zu erstellen. Wie zuvor fassen wir in einem ersten Schritt den Kaggle-Datensatz zusammen, bevor wir die Reihen zerlegen.

coffee_sales_data <- read.csv("/Users/x/Desktop/index_1.csv")
coffee_sales_data <- as.data.frame(coffee_sales_data)

library(dplyr)
library(ggplot2)

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  ggplot(aes(x = as.Date(date), y = money)) +
  geom_line(color = '#01ef63') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Time series")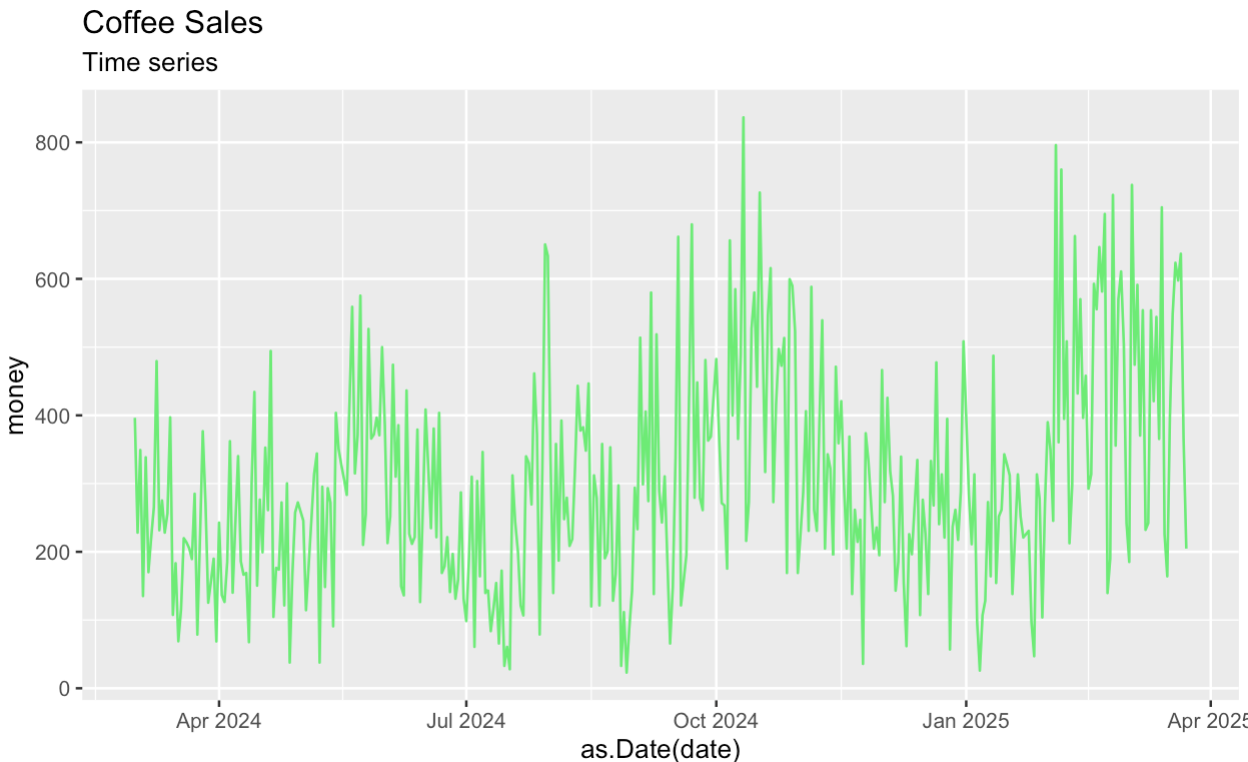

Als nächstes zerlegen wir unsere Reihen in Trend-, Saison- und Restkomponenten. Das Kästchen am oberen Rand des Zerlegungsdiagramms zeigt die ursprüngliche Reihe, wenn auch etwas gequetscht.

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  mutate(date = as.Date(date)) |>
  as_tsibble() |>
  filter(date > '2024-02-28') |>
  filter(date < '2024-05-01') |>
  model(
      STL(money ~ season(window = "periodic"))
  ) |>
  components() |>
  autoplot(color = '#203147') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Classical additive decomposition")

coffee_sales_data |>
  group_by(date) |>
  summarize(money = sum(money)) |>
  mutate(date = as.Date(date)) |>
  as_tsibble() |>
  filter(date > '2024-02-28') |>
  filter(date < '2024-05-01') |>
  model(
      STL(money ~ season(window = "periodic"))
  ) |>
  components() -> ts_components

ts_components |>
  autoplot(color = '#203147') +
  labs(title = "Coffee Sales") +
  labs(subtitle = "Classical additive decomposition")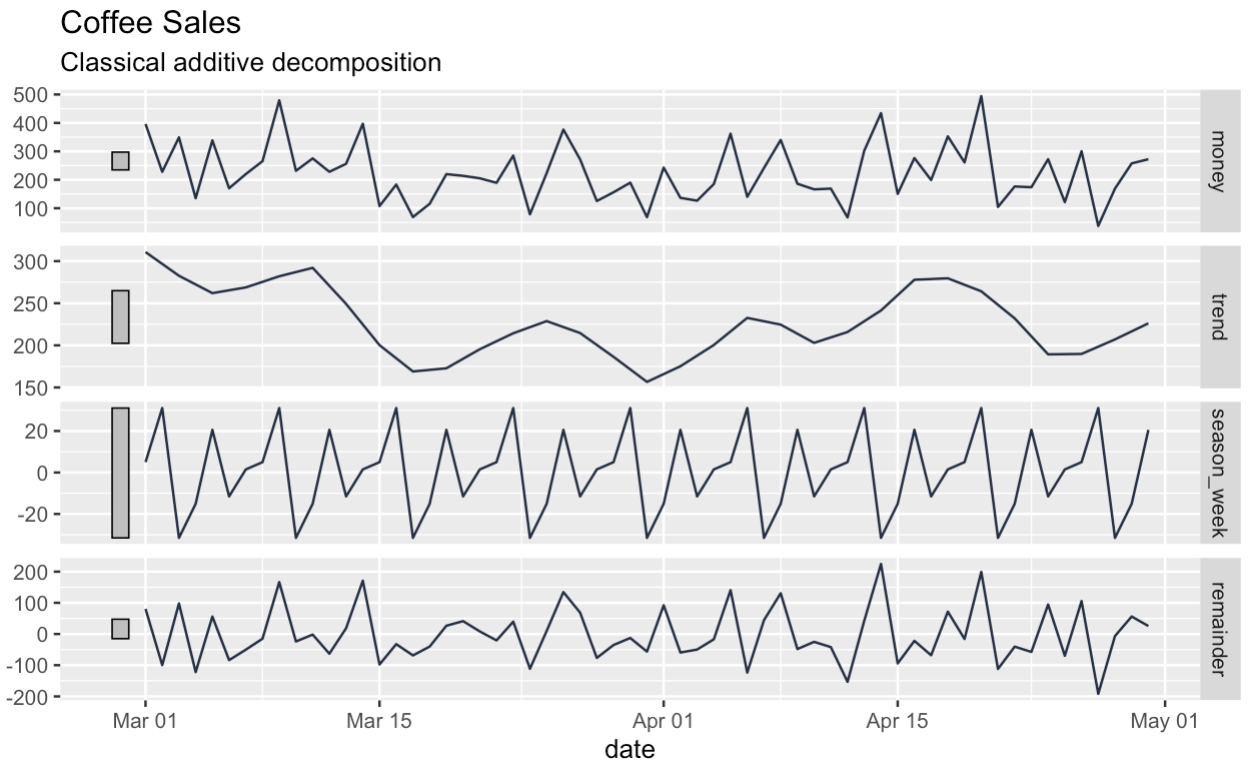

Beachte, dass der DataFrame, den wir zurückbekommen, anders als bei der klassischen Zerlegung keine Lücken am Anfang oder Ende hat.  

print(ts_components)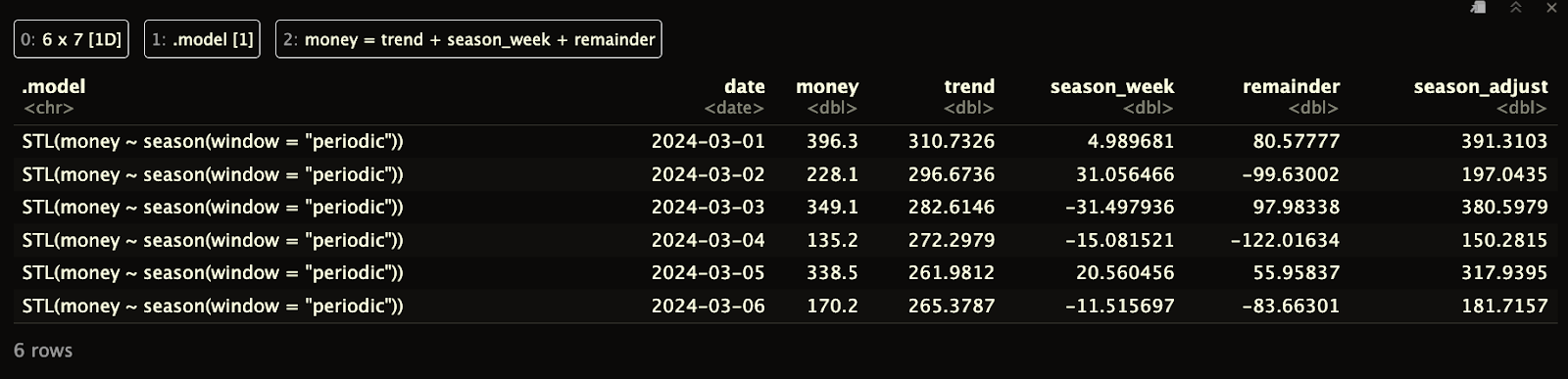

Es gibt auch einige Nachteile bei der STL-Zerlegung, und wenn du daran interessiert bist, haben wir diese Informationen in unsere FAQs aufgenommen. 

Zeitreihenzerlegung und saisonale Anpassungen

Oft ist es hilfreich, eine saisonbereinigte Version der Daten zu erstellen. Dazu können wir die Trend- und die Restkomponente zusammenzählen. Oder wir könnten die saisonale Komponente von der ursprünglichen Reihe abziehen; beides würde auf dasselbe hinauslaufen.

seasonally_adjusted <- components |>
  mutate(seasonally_adjusted = money - season_week)

season_adjust_data <- seasonally_adjusted |>
  select(date, money, season_adjust) |>
  pivot_longer(cols = c(money, season_adjust), names_to = "series", values_to = "value")

season_adjust_data |>
  autoplot() + facet_wrap(~series) +
  scale_color_manual(values = c(
    "money" = '#203147',          # blue
    "season_adjust" = '#01ef63'   # orange
  )) +
  facet_wrap(~series) +
  labs(title = "Coffee Sales: Original vs Seasonally Adjusted")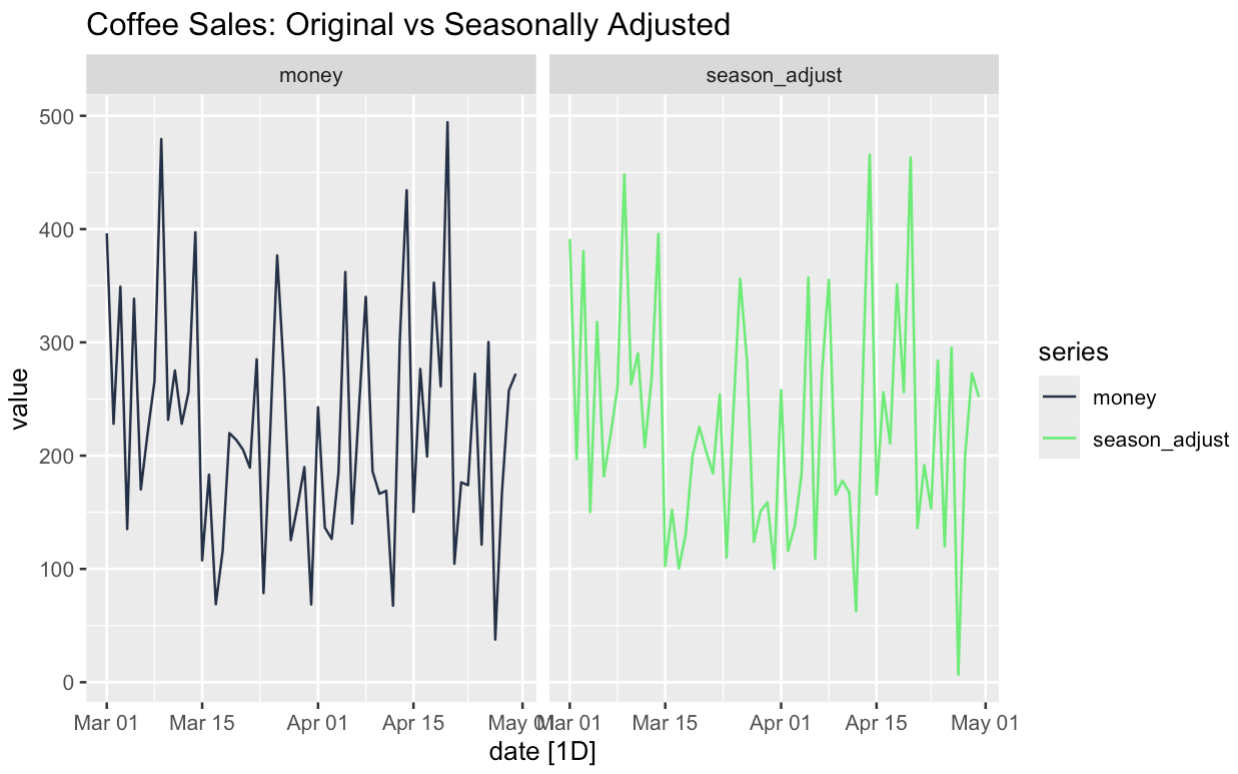

Die Stärke der saisonbereinigten Daten ist, dass sie uns helfen können, bestimmte Merkmale unserer Reihen zu verstehen. Wir können zum Beispiel sehen, ob der zugrunde liegende Trend das Ergebnis von Saisonalität ist. Zweitens können wir ungewöhnliche Vorkommnisse in den Daten genauer untersuchen. Denken wir, dass unsere Freitagsaktion funktioniert hat, weil es ein Freitag war oder weil es eine Aktion war? Nun, mit Hilfe der Zeitreihenzerlegung und der Saisonbereinigung können wir solche Fragen testen.

Zeitreihendekomposition und Vorhersage

Es wird dich vielleicht überraschen zu hören, dass die Zeitreihenzerlegung auch bei Prognosen hilfreich ist. Wir denken darüber auf zwei Arten nach. Zunächst wollen wir unsere Zeitreihenkomponenten verstehen, damit wir entscheiden können, welches Prognosemodell wir verwenden sollten. Wenn wir eine starke Saisonabhängigkeit feststellen, können wir zu Modellen wie der exponentiellen Glättung nach Holt-Winters oder der ETS-Methode greifen, die speziell dafür entwickelt wurden, sowohl Trend- als auch saisonale Komponenten zu berücksichtigen.

Zweitens können wir sogar zerlegte Daten als Teil unserer Prognosen verwenden, was uns Optionen eröffnet. Wir können zum Beispiel ein nicht saisonales Prognosemodell auf eine saisonbereinigte Version unserer Daten anwenden. (Wir können die saisonale Komponente später wieder einführen). Die Saisonbereinigung ist besonders hilfreich, wenn wir flexible Modelle wie die Standard-ARIMA und die lineare Regression verwenden wollen. 

Hier erstellen wir ein einfaches ARIMA-Modell zur Prognose der saisonbereinigten Daten. 

season_adjust_data_filtered <- season_adjust_data |>
  filter(series == "season_adjust") |>
  as_tsibble(index = date)

seasonal_adjust_arima_model <- season_adjust_data_filtered |>
  model(
    ARIMA(value)
  )

seasonal_adjust_arima_model |>
  forecast(h = "14 days") |>  
  autoplot(season_adjust_data_filtered, color = '#01ef63') +
  labs(title = "Forecast of Seasonally Adjusted Coffee Sales",
       subtitle = "Simple ARIMA Model",
       y = "Money (Seasonally Adjusted)",
       x = "Date")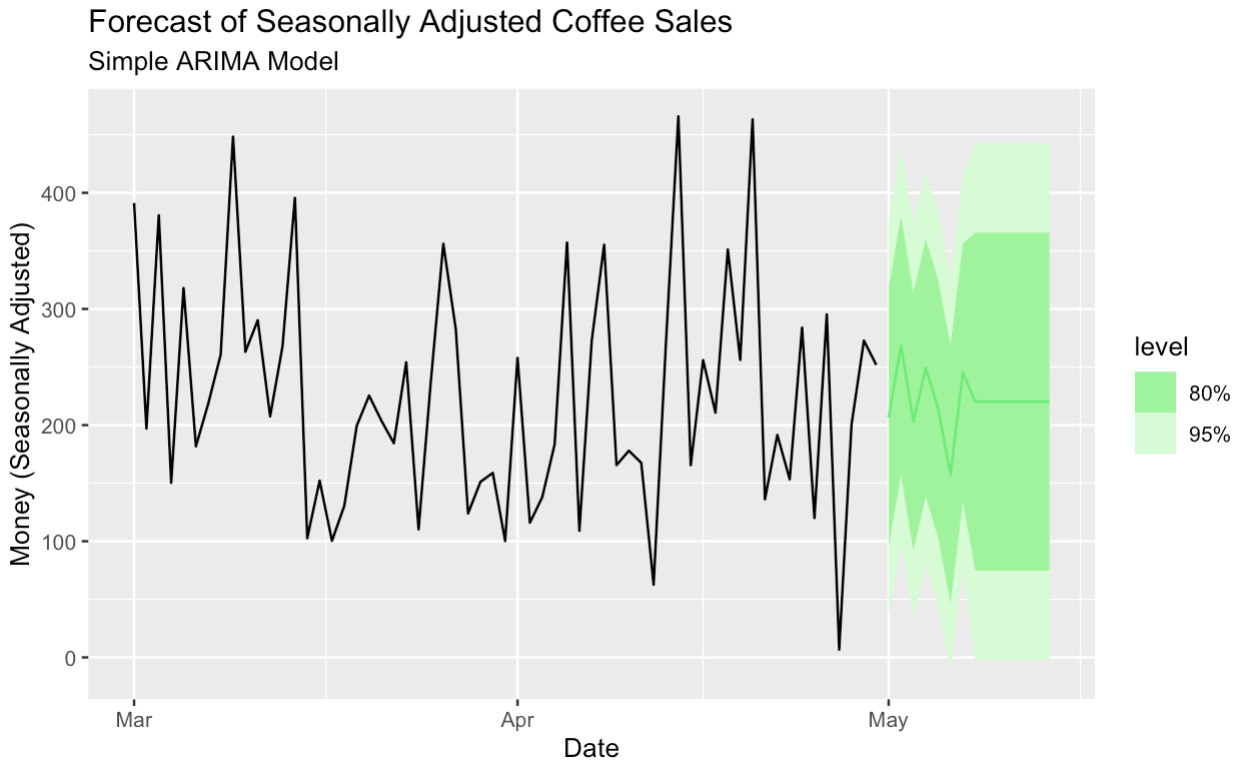

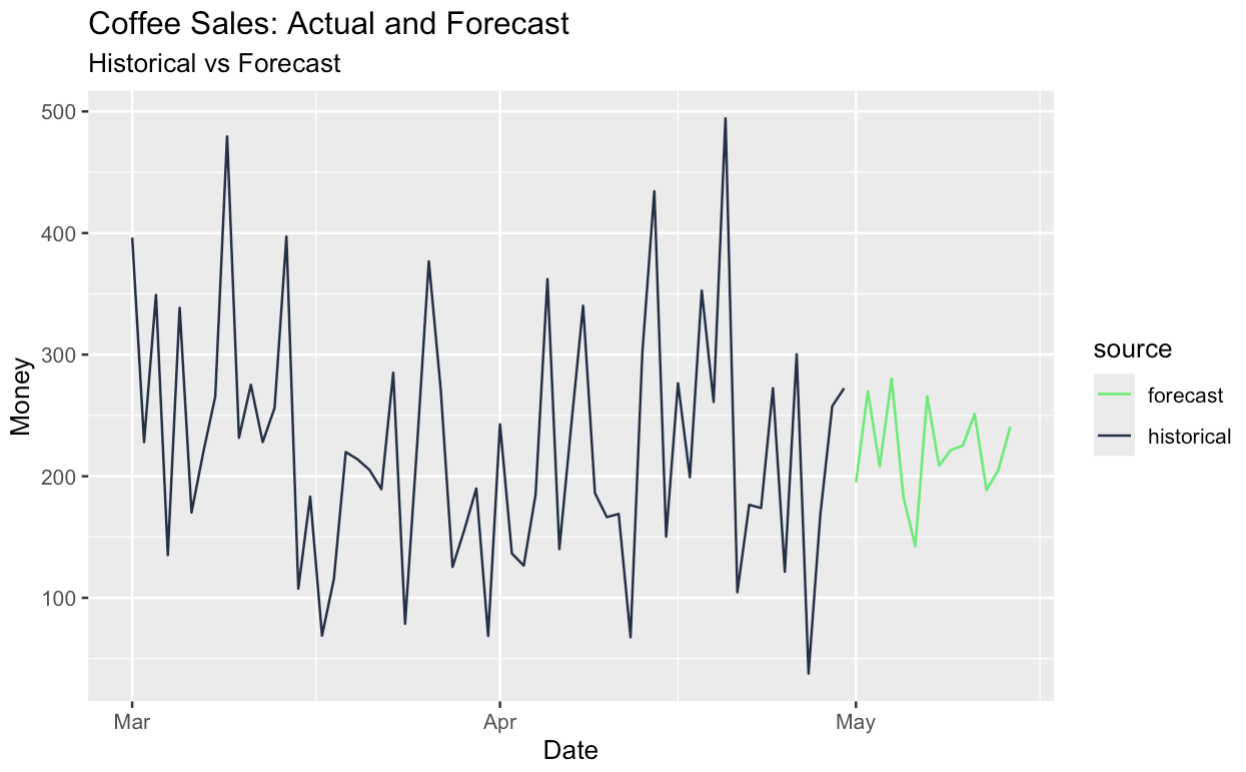
Wir können auch die saisonbereinigte Reihe prognostizieren und die saisonale Komponente wieder hinzufügen, wodurch wir effektiv eine saisonale Prognose erhalten. All dies wurde durch unsere originelle Zeitreihenzerlegung möglich.

# Build tagged historical and forecast data
historical_data <- components |>
  as_tibble() |>
  select(date, money) |>
  mutate(source = "historical")

forecast_data <- final_forecast |>
  as_tibble() |>
  transmute(date, money = money_forecast) |>
  mutate(source = "forecast")

# Bind and create tsibble
full_data <- bind_rows(historical_data, forecast_data) |>
  as_tsibble(index = date, validate = FALSE)

# Plot with color by source
full_data |>
  ggplot(aes(x = date, y = money, color = source)) +
  geom_line() +
  scale_color_manual(values = c(
    "historical" = "#203147",   # dark blue for real data
    "forecast" = "#01ef63"      # green for forecast
  )) +
  labs(
    title = "Coffee Sales: Actual and Forecast",
    subtitle = "Historical vs Forecast",
    y = "Money",
    x = "Date"
  )

Schlussgedanken

Ich hoffe, unser Artikel über die Zerlegung von Zeitreihen hat dir gefallen! Vergiss nicht, dass die Zerlegung nur ein Teil der Zeitreihenanalyse ist. Um ein Experte zu werden, solltest du den Kurs "Forecasting in R" bei Professor Rob Hyndman belegen, der bei der Entwicklung der R-Pakete geholfen hat, die wir für unsere Visualisierungen verwendet haben. Wir haben auch einen Kurs über die Visualisierung von Zeitreihendaten in Python, falls du die Ideen in diesem Artikel interessant findest, aber Python bevorzugst, das für diese Art von Aufgaben ebenfalls sehr gut geeignet ist.