Distribution de Cauchy : Comprendre les données à queue lourde

La distribution de Cauchy constitue une énigme statistique intrigante. Bien qu'elle partage la forme familière en cloche avec de nombreuses autres distributions de probabilités continues, elle défie l'analyse conventionnelle en n'ayant pas de moyenne ni de variance définies. Nommée d'après le mathématicien Augustin-Louis Cauchy, cette distribution apparaît naturellement dans des domaines allant de la modélisation financière aux statistiques bayésiennes.

En tant qu'outil pédagogique, la distribution de Cauchy illustre les concepts statistiques fondamentaux avec une clarté remarquable. Il démontre la non-convergence des moyennes d'échantillon, souligne l'importance des hypothèses de distribution et montre comment les estimateurs se comportent dans différentes conditions.

Vous souhaitez maîtriser ces concepts statistiques et leurs applications dans le domaine de la science des données ? Explorez notre cursus de carrière Machine Learning Scientist in R, où vous apprendrez à mettre en œuvre ces idées à l'aide de la programmation R.

Qu'est-ce que la distribution de Cauchy ?

La distribution de Cauchy est une distribution de probabilité continue célèbre pour ses propriétés uniques et ses queues lourdes. Il se caractérise par deux paramètres clés :

1. Paramètre de localisation (θ) : Ce paramètre détermine où se situe le pic (ou centre) de la distribution sur l'axe des x. Il s'agit de déplacer l'ensemble de la distribution vers la gauche ou vers la droite sans en modifier la forme.
2. Paramètre d'échelle (σ) : Ce paramètre détermine le degré d'étalement de la distribution. Des valeurs plus élevées de σ créent des distributions plus larges et plus plates avec des queues plus lourdes. Vous pouvez considérer cela comme un étirement ou une compression horizontale de la distribution.

La distribution est définie mathématiquement par sa fonction de densité de probabilité (PDF) :

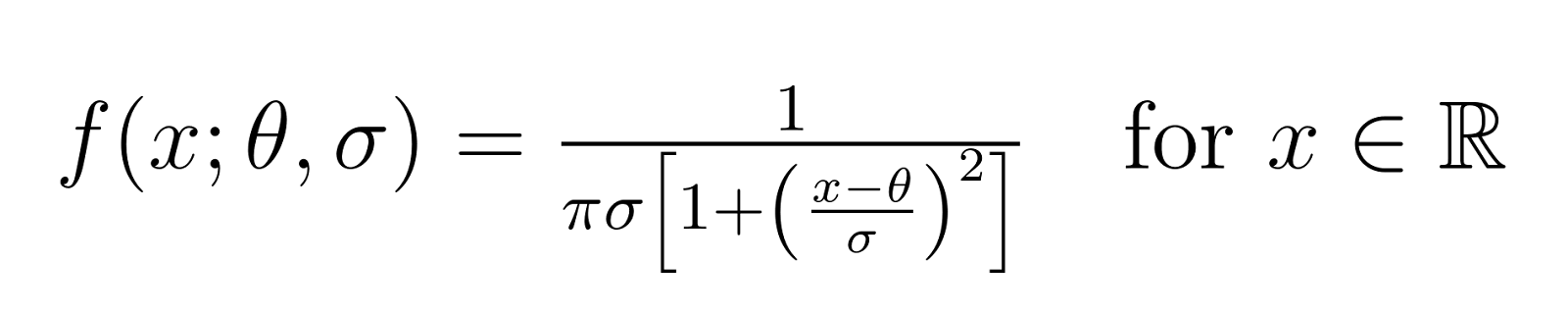
Lorsque nous fixons θ = 0 et σ = 1, nous obtenons ce que l'on appelle la distribution standard de Cauchy. Il s'agit de la forme la plus simple de la distribution, qui sert de point de référence pour comprendre les cas plus complexes.

Les principales caractéristiques de la distribution de Cauchy

Propriétés déterminantes des distributions de Cauchy

Queues lourdes

Considérez la distribution de Cauchy comme la distribution des "événements extrêmes". Alors qu'une distribution normale suggère que les valeurs éloignées du centre sont très rares (comme trouver une personne mesurant 1,80 m), la distribution de Cauchy nous indique que les valeurs extrêmes sont plus fréquentes qu'on ne pourrait le penser. 

Par exemple, en ce qui concerne les rendements des marchés boursiers, les variations massives de prix en une seule journée (comme lors de krachs ou de rallyes boursiers) sont plus fréquentes que ce que prévoirait une distribution normale. Les queues lourdes de la distribution de Cauchy permettent de mieux rendre compte de ces "cygnes noirs".

Moyenne et variance non définies

C'est peut-être la propriété la plus fascinante de la distribution de Cauchy. Contrairement à la plupart des distributions que vous avez rencontrées, la distribution de Cauchy n'a pas de moyenne (moyenne) ou de dispersion (variance) significative. 

Pour comprendre pourquoi cela est important : si vous prenez des échantillons répétés d'une distribution de Cauchy et que vous essayez de calculer leur moyenne, vous ne convergerez pas vers une valeur spécifique, même avec des millions d'échantillons. Cela a des implications pour l'analyse statistique, car les méthodes statistiques traditionnelles qui s'appuient sur les moyennes et les variances (comme les tests t ou l' ANOVA) ne fonctionnent pas avec des données distribuées selon la loi de Cauchy.

Symétrie

La distribution de Cauchy est parfaitement équilibrée autour de son paramètre de localisation (θ), comme une image miroir des deux côtés. Toutefois, cette symétrie ne signifie pas qu'elle se comporte comme la distribution normale habituelle. Bien que les deux distributions soient symétriques, la distribution de Cauchy répartit ses probabilités de manière beaucoup plus large. Cela signifie que même si elle a un centre clair, les valeurs peuvent s'éloigner de ce centre avec une probabilité significative.

Stabilité

La distribution de Cauchy possède une propriété remarquable : lorsque vous additionnez deux variables indépendantes distribuées par Cauchy, vous obtenez une autre distribution de Cauchy ! Cette propriété, connue sous le nom de stabilité, n'est partagée que par quelques autres distributions (comme la distribution normale). Elle est particulièrement utile en physique et en modélisation financière, où nous devons souvent comprendre comment des processus aléatoires combinés se comportent dans le temps.

Ce qu'il faut savoir lorsque l'on utilise la distribution de Cauchy

Traitement des valeurs aberrantes

La distribution de Cauchy excelle dans le traitement des valeurs aberrantes car elle s'attend à ce qu'elles se produisent. Il est donc particulièrement utile dans les scénarios où les valeurs extrêmes sont des éléments naturels des données, et non des erreurs à supprimer. Dans ce cas, les méthodes traditionnelles de détection des valeurs aberrantes peuvent être trop agressives et signaler de manière inappropriée des points de données légitimes à supprimer. La distribution de Cauchy fournit un cadre pour la construction de modèles robustes qui ne seront pas indûment influencés par des observations extrêmes, ce qui en fait un outil précieux pour travailler avec des ensembles de données où les valeurs aberrantes sont une caractéristique inhérente plutôt qu'une anomalie à éliminer.

Sélection du modèle

Le choix d'une distribution de Cauchy dépend de vos données et de vos objectifs. La distribution de Cauchy est particulièrement utile lorsque vos données présentent fréquemment des valeurs extrêmes, lorsque vous travaillez avec des ratios de variables normalement distribuées ou lorsque vous avez besoin d'un modèle robuste capable de traiter des données à queue lourde. Cependant, vous devez faire preuve de prudence dans l'utilisation de la distribution de Cauchy dans certaines situations : lorsque vous devez vous appuyer sur les moyennes et les variances, lorsque vos données suivent en réalité une distribution à queue plus légère, ou lorsque l'efficacité des calculs est une préoccupation majeure. Comprendre ces compromis est utile pour décider en connaissance de cause si la distribution de Cauchy est adaptée à vos besoins d'analyse spécifiques.

Efficacité informatique

Si la formule mathématique de la distribution de Cauchy est simple, son utilisation informatique peut s'avérer difficile. L'estimation des paramètres nécessite souvent des techniques spécialisées telles que la méthode de Monte Carlo par chaîne de Markov (MCMC), et les méthodes standard du maximum de vraisemblance peuvent avoir des difficultés avec les queues lourdes. Heureusement, les logiciels statistiques modernes comprennent souvent des outils spécifiques pour traiter les distributions de Cauchy, ce qui permet de travailler plus facilement avec cette distribution dans la pratique, malgré ses complexités informatiques.

Propriétés mathématiques de la distribution de Cauchy

La distribution de Cauchy possède plusieurs propriétés mathématiques importantes qui la rendent unique et utile :

• Une distribution stable a un comportement intéressant : lorsque vous ajoutez deux variables à distribution de Cauchy, vous obtenez une autre distribution de Cauchy avec des paramètres mis à l'échelle. Il est donc utile pour étudier les effets cumulatifs en physique et en finance.
• Moments non définis, y compris la moyenne et la variance, ce qui en fait un contre-exemple fascinant en théorie des probabilités. Cette propriété aide les élèves à comprendre pourquoi le théorème de la limite centrale exige une variance finie.
• Une forme mathématiqueélégamment simple, avec un PDF direct et une fonction caractéristique. Malgré son comportement complexe, sa description mathématique de base est étonnamment simple.
• La propriété du rapport: si vous divisez une variable aléatoire normale par une autre variable aléatoire normale indépendante, vous obtenez une distribution de Cauchy. Il est donc naturellement adapté à la modélisation des rapports et des proportions.
• De solides applications bayésiennes, notamment en tant que distribution préalable dans les modèles hiérarchiques. Ses queues lourdes en font un excellent choix pour les paramètres d'échelle où la robustesse est importante.

Visualisation de la distribution de Cauchy en R et Python

La meilleure façon de comprendre le comportement de la distribution de Cauchy est de la visualiser. Utilisons R pour créer des graphiques de différentes distributions de Cauchy, en montrant comment les paramètres de localisation (θ) et d'échelle (σ) affectent la forme et la position de la distribution.

Distribution de Cauchy dans R

R fournit des fonctions permettant de travailler avec les distributions de Cauchy grâce à son paquetage stats. Nous utiliserons également le site ggplot2 pour créer des visuels clairs et de qualité :

# Load required libraries
library(ggplot2)  # for plotting
# Note: dcauchy is from the stats package which is loaded by default in R

# Create a sequence of x values
x <- seq(-10, 10, length.out = 1000)

# Generate different Cauchy distributions using stats::dcauchy
# Standard Cauchy (θ = 0, σ = 1)
standard_cauchy <- dcauchy(x, location = 0, scale = 1)

# Location and Scale Adjusted (θ = 2, σ = 3)
adjusted_cauchy <- dcauchy(x, location = 2, scale = 3)

# Highly Scaled (θ = -1, σ = 5)
scaled_cauchy <- dcauchy(x, location = -1, scale = 5)

# Create a data frame for plotting
plot_data <- data.frame(
  x = rep(x, 3),
  density = c(standard_cauchy, adjusted_cauchy, scaled_cauchy),
  distribution = rep(c("Standard (θ=0, σ=1)", 
                      "Adjusted (θ=2, σ=3)", 
                      "Scaled (θ=-1, σ=5)"), 
                    each = length(x))
)

# Create the plot
ggplot(plot_data, aes(x = x, y = density, color = distribution)) +
  geom_line(size = 1) +
  theme_minimal() +
  labs(title = "Comparison of Cauchy Distributions",
       x = "x",
       y = "Density",
       color = "Parameters") +
  theme(legend.position = "bottom",
        plot.title = element_text(hjust = 0.5)) +
  scale_color_brewer(palette = "Set1")

Ce code génère un graphique de comparaison de trois distributions de Cauchy différentes :

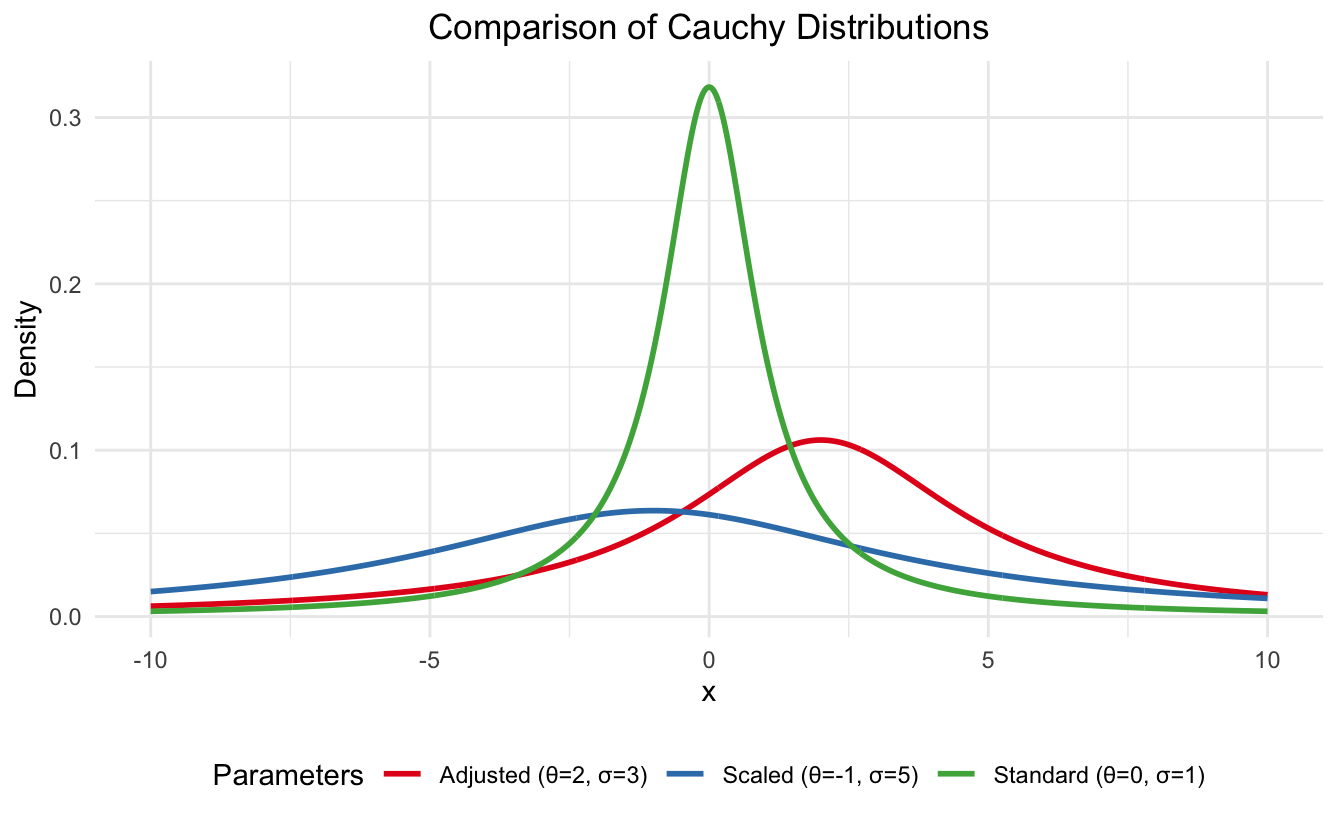
Distribution de Cauchy en R. Image par l'auteur

1. Cauchy standard (ligne verte) : Avec θ = 0 et σ = 1, il s'agit du cas de base. Remarquez le pic net à x = 0 et les queues lourdes et symétriques.
2. Cauchy ajusté à la localisation (ligne rouge) : Le réglage de θ = 2 déplace le pic vers la droite tout en conservant la forme. Cela montre comment le paramètre de localisation affecte le centre de la distribution sans en modifier l'étendue.
3. Cauchy à haute échelle (ligne bleue) : Avec θ = -1 et σ = 5, la distribution est décalée et beaucoup plus plate. L'augmentation du paramètre d'échelle crée des queues plus larges et plus lourdes et réduit la hauteur du pic, ce qui illustre la façon dont σ contrôle l'étalement.

La visualisation montre clairement comment l'augmentation du paramètre d'échelle (σ) conduit à une distribution plus plate et plus étalée, tandis que le paramètre de localisation (θ) déplace simplement l'ensemble de la distribution vers la gauche ou vers la droite.

Distribution de Cauchy en Python

Après avoir exploré les paramètres de la distribution de Python dans R, utilisons Python pour comparer la distribution de Python avec sa cousine plus familière, la distribution normale. La pile de calcul scientifique de Python, en particulier scipy.stats, fournit d'excellents outils pour travailler avec des distributions de probabilités.

Alors que le package stats de R nous a permis d'accéder directement aux fonctions de distribution de Python, le module scipy.stats de Python offre des fonctionnalités similaires avec une interface légèrement différente. Nous utiliserons matplotlib, la principale bibliothèque de traçage de Python, pour créer une visualisation claire :

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Set style parameters for better visualization
plt.style.use('seaborn')
plt.rcParams.update({
    'font.size': 16,
    'axes.labelsize': 18,
    'axes.titlesize': 24,
    'xtick.labelsize': 16,
    'ytick.labelsize': 16,
    'legend.fontsize': 16,
})

# Create data
x = np.linspace(-10, 10, 1000)
cauchy = stats.cauchy.pdf(x, loc=0, scale=1)
normal = stats.norm.pdf(x, loc=0, scale=1)

# Create the plot
plt.figure(figsize=(12, 8))

# Plot distributions
plt.plot(x, cauchy, 'b-', linewidth=2.5, label='Cauchy(0,1)')
plt.plot(x, normal, 'r--', linewidth=2.5, label='Normal(0,1)')

# Customize the plot
plt.title('Cauchy vs Normal Distribution', pad=20)
plt.xlabel('x', labelpad=10)
plt.ylabel('Density', labelpad=10)

# Customize legend
plt.legend(fontsize=16, bbox_to_anchor=(0.99, 0.99), 
          loc='upper right', borderaxespad=0.)

# Add grid and adjust layout
plt.grid(True, alpha=0.3)
plt.tight_layout()

plt.show()

Le code ci-dessus établit une comparaison entre la distribution standard de Cauchy (ligne continue bleue) et la distribution normale standard (ligne pointillée rouge), toutes deux centrées sur 0 avec un paramètre d'échelle de 1.

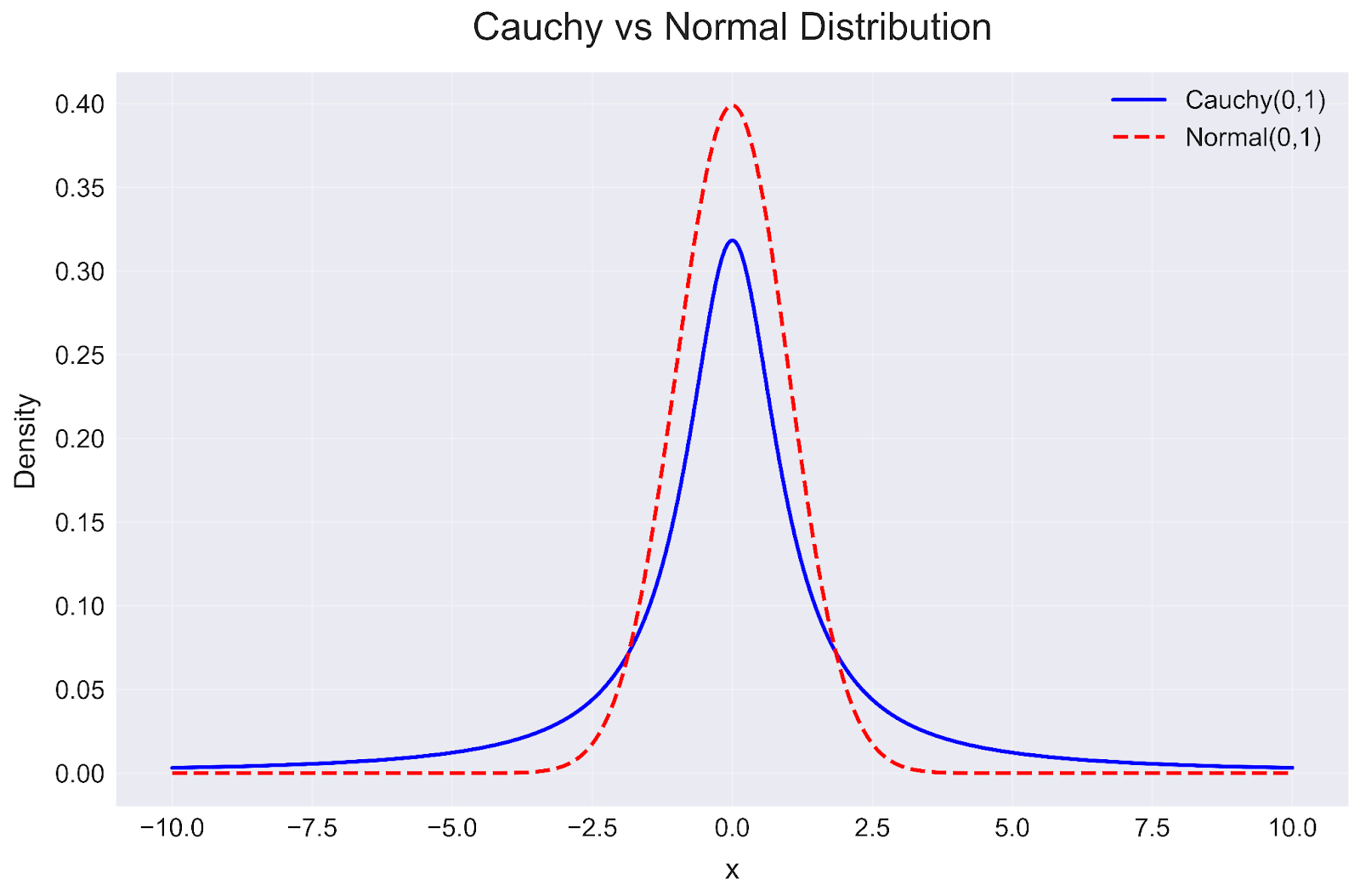
Distribution de Cauchy en Python. Image par l'auteur

Cette visualisation révèle plusieurs éléments clés :

1. Hauteur de la crête: La distribution normale atteint un pic de densité plus élevé (environ 0,4) que la distribution de Cauchy (environ 0,32), ce qui indique que les valeurs sont plus concentrées autour du centre dans la distribution normale.
2. Queues lourdes: Remarquez que la ligne bleue de la distribution de Cauchy reste plus élevée que la ligne pointillée rouge de la distribution normale à mesure que l'on s'éloigne du centre. Ces "queues lourdes" signifient que les valeurs extrêmes sont beaucoup plus probables dans une distribution de Cauchy que dans une distribution normale.
3. Implications pratiques: Les queues plus lourdes de la distribution de Cauchy la rendent plus adaptée à la modélisation de phénomènes où les événements extrêmes se produisent plus fréquemment que ne le prévoirait une distribution normale, comme les rendements des marchés financiers ou certains phénomènes physiques.

Cette comparaison permet d'expliquer pourquoi la distribution de Cauchy est souvent utilisée dans des scénarios où la distribution normale sous-estime la probabilité d'événements extrêmes. Bien que les deux distributions soient symétriques autour de leur centre, les queues lourdes de la distribution de Cauchy la rendent plus appropriée pour modéliser des systèmes où les valeurs aberrantes sont courantes plutôt que de rares exceptions.

Quand la distribution de Cauchy est utile

La distribution de Cauchy sert des objectifs spécifiques dans l'analyse des données et la modélisation. Examinons comment il est utilisé efficacement dans différents domaines.

Finances : Gérer l'incertitude du marché

Modélisation des rendements

Les marchés financiers sont connus pour leur nature imprévisible et connaissent souvent des fluctuations de prix spectaculaires qui seraient considérées comme "impossibles" dans le cadre d'hypothèses de distribution normales. La distribution de Cauchy brille ici par son efficacité :

• Il capture naturellement les événements de type "cygne noir", tels que les krachs boursiers ou les reprises soudaines.
• Il reflète mieux la réalité, à savoir que les mouvements extrêmes du marché sont plus fréquents que ne le prévoient les modèles traditionnels.
• Il ne sous-estime pas le risque de mouvements de prix importants.

Par exemple, lors de la crise financière de 2008, de nombreux modèles traditionnels ont échoué parce qu'ils supposaient des distributions normales. Un modèle basé sur Cauchy aurait mieux anticipé la possibilité de mouvements de marché aussi extrêmes.

Évaluation des risques

Lors de l'évaluation des risques d'investissement, la distribution de Cauchy offre une vision plus conservatrice et plus réaliste. Il aide les gestionnaires de risques à fixer des réserves de capital plus appropriées en tenant compte des scénarios extrêmes, à mieux estimer la probabilité de pertes ou de gains importants et fournit un modèle plus réaliste pour les tests de résistance des portefeuilles. Cette approche de l'évaluation des risques aide les institutions financières à se préparer à des événements peu probables mais ayant un impact sur le marché.

Statistiques bayésiennes : Inférence statistique robuste

Distributions antérieures

Dans l'analyse bayésienne, le choix de la bonne distribution préalable est essentiel. La distribution de Cauchy est particulièrement utile ici car :

• Grâce à ses queues lourdes, il est moins susceptible d'exclure accidentellement des valeurs de paramètres importantes
• Il est particulièrement utile pour les paramètres d'échelle (tels que les écarts types) dans les modèles hiérarchiques.
• Elle permet d'éviter que le modèle ne soit trop confiant dans ses estimations.

Par exemple, lors de l'analyse de l'efficacité d'un nouveau traitement médical, l'utilisation d'un a priori de Cauchy pour la taille de l'effet permet de s'assurer que nous ne sous-estimons pas la possibilité d'effets de traitement importants.

Régression robuste

La régression traditionnelle peut être fortement influencée par les valeurs aberrantes. L'utilisation de termes d'erreur distribués selon la méthode de Cauchy permet de construire des modèles plus robustes en rendant le modèle moins sensible aux observations extrêmes. Les résultats restent fiables même lorsque les données contiennent des valeurs aberrantes, et les prédictions sont plus stables en présence de points de données inhabituels. Cette robustesse rend les termes d'erreur distribués par Cauchy particulièrement utiles lorsque l'on travaille avec des ensembles de données réels qui contiennent souvent des valeurs inattendues ou extrêmes.

Apprentissage automatique et science des données : Construire des modèles résilients

Algorithmes robustes

L'apprentissage automatique moderne traite souvent des données bruyantes du monde réel. La distribution de Cauchy permet de construire des algorithmes plus résistants :

• Fournir un meilleur modèle pour le bruit dans les données des capteurs
• Aider à traiter les valeurs aberrantes dans les données d'apprentissage sans les supprimer
• Rendre les algorithmes d'apprentissage plus résistants aux données corrompues

Par exemple, dans le domaine de la vision artificielle, l'utilisation de modèles de bruit distribué de Cauchy peut aider les algorithmes à mieux gérer les artefacts d'image ou les défaillances du capteur.

Modèles génératifs

Dans les applications avancées d'apprentissage automatique, la distribution de Cauchy permet de créer des modèles plus souples. Il est utile dans les autoencodeurs variationnels lorsque les données peuvent présenter des caractéristiques de queues lourdes, aide à générer des données synthétiques plus réalistes qui comprennent des valeurs extrêmes occasionnelles, et est utile dans la modélisation des espaces latents lorsque les distributions normales peuvent être trop restrictives. Cette flexibilité rend la distribution de Cauchy particulièrement utile dans les tâches de modélisation générative où il est important de capturer toute la gamme des variations possibles des données.

Confusion de la distribution de Cauchy avec d'autres distributions

Il est fréquent de confondre la distribution de Cauchy avec d'autres distributions similaires. Examinons les principales différences afin de vous aider à faire le bon choix pour votre analyse.

Distribution de Cauchy et distribution normale

La distribution normale est souvent le choix par défaut pour de nombreuses analyses, mais il existe des différences importantes entre elle et la distribution de Cauchy :

Comportement de la queue 

Si les deux distributions sont symétriques, leurs queues racontent des histoires très différentes : La distribution normale suggère que les valeurs supérieures à trois écarts types sont extrêmement rares. La distribution de Cauchy nous apprend que les valeurs extrêmes sont beaucoup plus fréquentes que vous ne le pensez.

Propriétés statistiques 

Ces distributions diffèrent fondamentalement dans la manière dont nous pouvons les analyser : La distribution normale a des moments bien définis (moyenne = μ, variance = σ²). La distribution de Cauchy n'a pas de moyenne ni de variance définies, ce qui rend les méthodes statistiques traditionnelles inutilisables.

Implications pratiques 

Cette différence est importante dans les applications réelles : Utilisez la distribution normale lorsque vos données sont regroupées autour d'une valeur centrale avec une dispersion prévisible. Utilisez la distribution de Cauchy lorsque vos données présentent fréquemment des valeurs extrêmes qui seraient "impossibles" dans des conditions normales.

Cauchy vs. Distribution de Laplace

La distribution de Laplace peut sembler similaire à la distribution de Cauchy à première vue, mais il existe des différences essentielles qui les distinguent :

Comportement de la queue 

Les deux distributions ont des queues plus lourdes que la distribution normale, mais elles diffèrent dans leur intensité : Les queues de la distribution de Laplace décroissent de façon exponentielle. Les queues de la distribution de Cauchy se décomposent plus lentement (polynomialement), ce qui rend les valeurs extrêmes encore plus probables.

Symétrie 

Les deux distributions sont symétriques autour de leur centre, mais elles diffèrent par le comportement de leurs queues : La distribution de Laplace présente une décroissance exponentielle dans ses queues. La distribution de Cauchy présente une décroissance polynomiale, ce qui rend ses queues plus lourdes que celles de Laplace.

Cas pratiques 

Comprendre ces différences permet de choisir l'outil adéquat : Utilisez la distribution de Laplace lorsque vous vous attendez à des valeurs aberrantes occasionnelles mais que vous avez besoin de moments définis. Utilisez la distribution de Cauchy lorsque vous vous attendez à des valeurs extrêmes fréquentes et qu'il n'est pas nécessaire de calculer les moyennes.

Conclusion

La distribution de Cauchy, bien qu'elle ne soit pas aussi omniprésente que la distribution normale, revêt une importance significative dans les domaines où les données présentent des queues lourdes, où la robustesse contre les valeurs aberrantes est requise ou où les propriétés théoriques des distributions stables présentent un intérêt. Que ce soit en physique, en finance ou en statistiques bayésiennes, la compréhension de la distribution de Cauchy améliore la capacité à modéliser et à interpréter des données présentant une variabilité importante et des valeurs aberrantes.

Pour une compréhension plus approfondie des distributions de probabilités, vous pouvez consulter les séries suivantes : Notre guide sur la distribution gaussienne explore la distribution de probabilité la plus largement utilisée, qui offre un excellent contraste avec la distribution de Cauchy, dont la queue est lourde. Notre guide sur la distribution de Poisson se penche sur la modélisation d'événements discrets dans le temps ou l'espace, tandis que notre guide sur la distribution binomiale explique les mathématiques qui sous-tendent les séquences d'essais indépendants. Pour ceux qui s'intéressent aux fondements de la théorie des probabilités, notre guide sur la distribution de Bernoulli donne un aperçu des éléments constitutifs de distributions plus complexes.