Curso
Se você pegar várias amostras aleatórias de praticamente qualquer tipo de distribuição de dados, algo surpreendente acontecerá. A média dessas amostras começa a se parecer com uma distribuição normal - a conhecida curva em forma de sino. Esse é o teorema do limite central (CLT) em poucas palavras.
Isso é muito importante em probabilidade e estatística, pois significa que podemos fazer previsões precisas e tirar conclusões sobre populações inteiras, mesmo quando analisamos apenas pequenas amostras.
O que torna o CLT ainda mais útil é que ele funciona mesmo que os dados originais não sejam normalmente distribuídos. Vamos explorar isso em detalhes e ver como podemos calcular.
O que é o Teorema Central do Limite?
O teorema do limite central, ou CLT, é uma ideia em estatística que diz que, se pegarmos várias amostras aleatórias de qualquer população e observarmos as médias dessas amostras, essas médias começarão a formar uma curva normal em forma de sino, mesmo que a população original não pareça normal.
Isso está relacionado à lei dos grandes números, que nos diz que, à medida que coletamos mais dados, nossa média amostral fica cada vez mais próxima da média real de toda a população. O CLT leva isso um passo adiante - ele nos diz que a média da amostra se torna mais precisa e que o padrão dessas médias se torna previsível. Nosso curso de Introdução à Estatística tem exercícios práticos para que você se familiarize com a relação e as diferenças entre a CLT e a lei dos grandes números, caso queira explorar mais essa parte.
Uma ótima maneira de ver isso em ação é lançando um dado. Se você rolar apenas uma vez, obterá um número aleatório entre 1 e 6. Mas, depois de um número suficiente de lançamentos, a média ficará em torno de 3,5 (o verdadeiro valor médio de um dado justo). Se você fizer isso várias vezes, a distribuição dessas médias começará a se parecer com uma curva normal.
Fórmula do teorema do limite central
Aqui está a fórmula básica para o teorema do limite central:
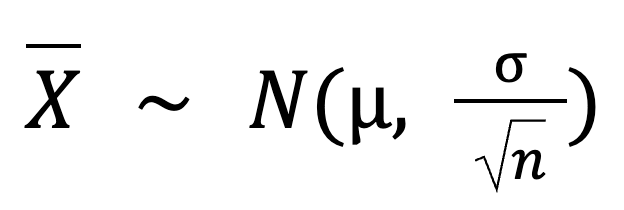
Nessa fórmula:
-
Xé a distribuição de amostragem da média da amostra, que segue uma distribuição normal. -
Né a distribuição normal. -
𝜇é a média da população. -
σé o desvio padrão da população. -
né o tamanho da amostra.
À medida que o tamanho da amostra aumenta, o desvio padrão da distribuição da amostra fica menor. Quanto mais dados forem coletados, mais as médias de nossas amostras se agruparão em torno da média real da população.
Condições do teorema do limite central
Agora, para que o teorema do limite central funcione da maneira que esperamos, há algumas condições a serem consideradas:
- Tamanho de amostra suficientemente grande: O tamanho da amostra deve ser grande o suficiente. Um tamanho de amostra de 30 ou mais é geralmente considerado bom. No entanto, se a população da qual estamos fazendo a amostragem for distorcida ou tiver muitos valores discrepantes, talvez seja necessária uma amostra maior para que apareça a bela curva em forma de sino.
- Amostras independentes e identicamente distribuídas (i.i.d.): As amostras que coletamos precisam ser independentes e identicamente distribuídas (i.i.d.). Isso significa que cada amostra é escolhida aleatoriamente e provém da mesma população. Se isso não for verdade, então os resultados podem não ser confiáveis.
- Variância de população finita: A população que estamos amostrando deve ter uma variação finita. Se os dados forem provenientes de uma distribuição com variância infinita, como a distribuição de Cauchy, o CLT não se aplicará a eles.
Exemplos do Teorema Central do Limite
Digamos que você queira saber quantas xícaras de café são vendidas por dia em uma cafeteria local. Ao longo dos anos, o número de copos vendidos por dia pode seguir uma distribuição semelhante à que estou incluindo aqui. Na maioria dos dias, eles vendem entre 80 e 120 xícaras. Mas em dias movimentados, como feriados ou eventos especiais, eles vendem 150 ou até 180 xícaras. Os dados estão um pouco distorcidos (desiguais) nesse caso.
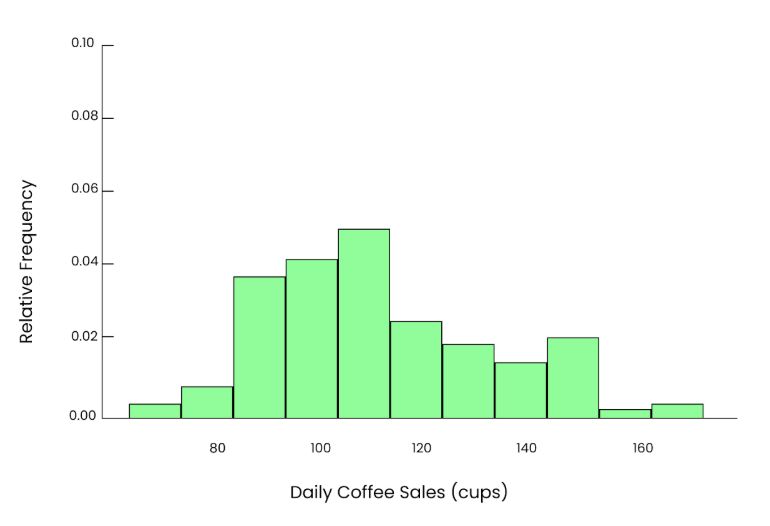
Gráfico irregular. Imagem do autor.
Digamos que você pegue uma pequena amostra. Escolhemos aleatoriamente 5 dias do ano e verificamos quantos copos foram vendidos nesses dias.
95, 102, 85, 110, 120A média que obtemos dessa amostra é:
Mean = 95+102+85+110+1205 = 102.4 cups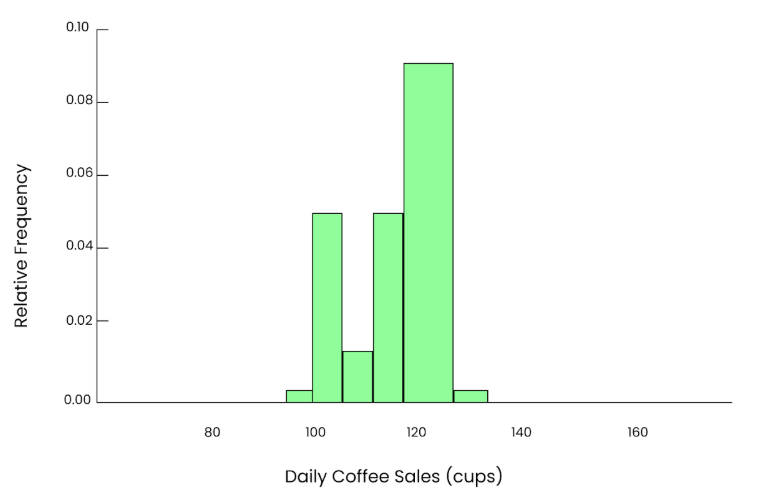
Gráfico de 5 xícaras. Imagem do autor.
Isso nos dá uma estimativa da média da população, mas como a amostra é pequena, ela pode não ser exata. Se você repetir esse processo 10 vezes, escolha aleatoriamente 5 dias de cada vez, calcule a média e anote os resultados. As médias de 10 amostras seriam:
97.6, 105.8, 93.4, 110.2, 99.0, 102.4, 101.2, 107.5, 96.3, 94.1Se traçarmos esses valores em um histograma, veremos uma forma aproximada de sino, mas ainda assim poderá parecer irregular. E a dispersão dessas médias é menor do que a dispersão na população.
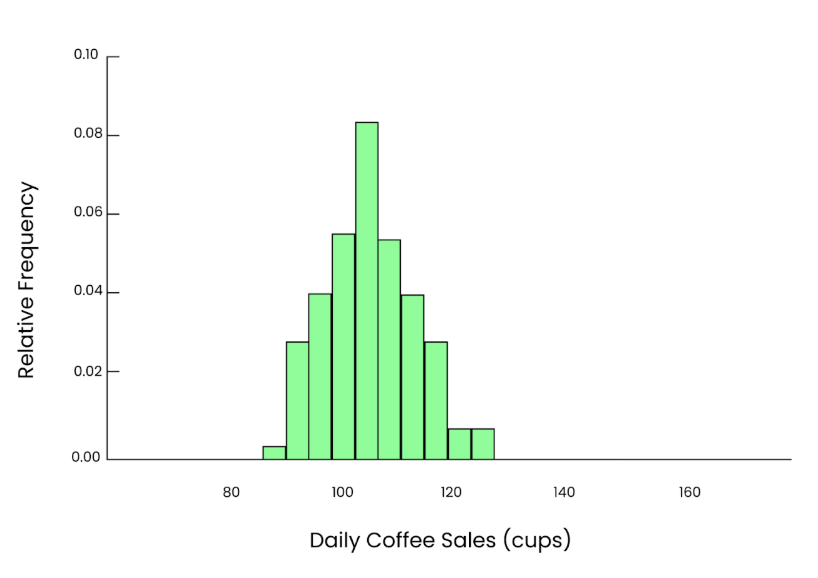
Gráfico de 10 xícaras. Imagem do autor.
Agora, vamos pegar uma amostra maior. Dessa vez, selecionamos aleatoriamente 50 dias e calculamos o número médio de copos vendidos:
98, 104, 87, 112, 105, 100, 108, 95, 102, 106,
92, 115, 97, 101, 109, 103, 96, 110, 104, 98,
100, 102, 89, 107, 94, 111, 108, 90, 100, 103,
106, 99, 96, 112, 105, 97, 100, 104, 93, 110,
107, 102, 95, 101, 99, 103, 109, 98, 94, 100Quando calculamos a média dessa amostra, obtemos o seguinte:
Mean = 101.2 cupsEssa estimativa está muito mais próxima da média populacional de 100 e, como o tamanho da nossa amostra é maior, é uma estimativa mais precisa.
Se repetirmos esse processo várias vezes, cada vez selecionando aleatoriamente 50 dias, calculando a média e plotando essas médias em um histograma, mesmo que os dados originais estejam distorcidos, veremos uma curva aparente e suave em forma de sino. Portanto, esse é o poder do teorema do limite central.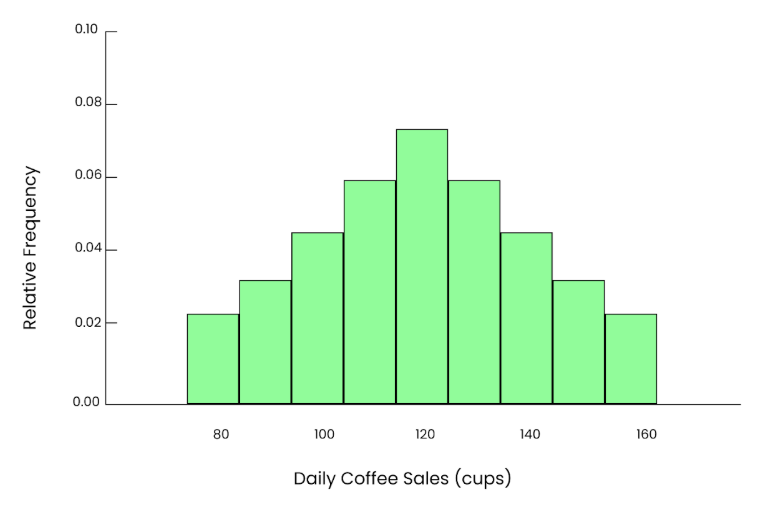
Até mesmo o gráfico. Imagem do autor.
Você pode até calcular esse spread usando esta fórmula:
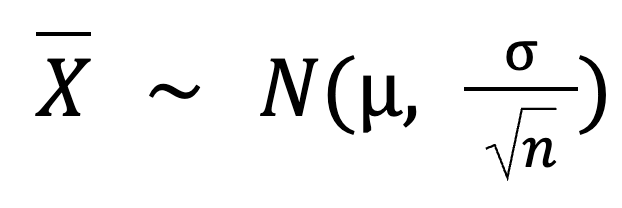 Aqui:
Aqui:
-
µ(média da população) = 100 -
σ(desvio padrão da população) = 15 -
n(tamanho da amostra) = 50
Portanto, o desvio padrão das médias de nossa amostra é:
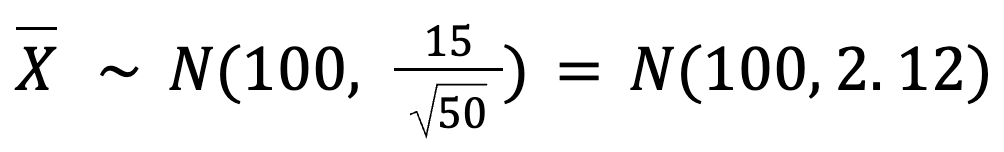
Isso nos diz que a média da amostra será muito próxima de 100 xícaras, com apenas uma pequena variação (cerca de 2,12 xícaras).
Por que o Teorema Central do Limite é importante
Agora sabemos que os dados no mundo real podem ser estranhos e imprevisíveis. Mas o teorema do limite central nos dá uma maneira confiável de entender o que está acontecendo e fazer escolhas melhores com base nisso. Vamos entender sua importância com mais detalhes.
Inferência estatística
Em estatística, o teorema do limite central é a razão pela qual os testes paramétricos, como testes t, ANOVA e regressão, funcionam da maneira que funcionam. Esses testes se baseiam na ideia de que os dados de amostra são provenientes de uma população com características fixas.
Sem o teorema do limite central, não poderíamos nos basear nesses testes. E, devido a esse teorema, os testes paramétricos geralmente são mais potentes do que os não paramétricos, que não fazem suposições sobre a distribuição dos dados.
Aplicativos do setor
Ele também aparece em muitas situações do mundo real. Em finanças, os analistas o utilizam para estimar os retornos médios das ações com base no desempenho anterior. Em sondagens e pesquisas, ele faz previsões sobre toda a população coletando uma amostra de respostas. No machine learning e no big data, usamos isso quando os modelos são treinados em amostras. Por exemplo, um aplicativo de filmes pode usar uma amostra da atividade do usuário para criar seu sistema de recomendação.
Calculadora do teorema do limite central
O desvio padrão é um número que nos informa o quanto os valores estão espalhados em relação à média. Quando analisamos as médias das amostras (as médias de diferentes amostras), queremos saber o quanto essas médias variam. Para isso, podemos usar esta fórmula:
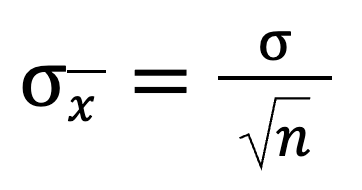
Isso nos diz que, quando dividimos o desvio padrão da população pela raiz quadrada do tamanho da amostra, obtemos o desvio padrão da distribuição da amostra. À medida que o tamanho da amostra aumenta, o valor geral fica menor.
Vamos dar uma olhada em um exemplo rápido:
| Tamanho da amostra (n) | Média da amostra (μₓ̄) | Std. Desvio (σₓ̄) |
|---|---|---|
| 5 | 17 | 1.788854 |
| 10 | 17 | 1.264911 |
| 25 | 17 | 0.800000 |
| 50 | 17 | 0.565685 |
| 100 | 17 | 0.400000 |
Você pode ver que a média permanece a mesma, mas o desvio padrão continua diminuindo. Isso mostra que quanto maior for a amostra, mais precisa e consistente ela será.
O teorema do limite central na ciência de dados
Na ciência de dados, geralmente lidamos com amostras, não com populações inteiras. O CLT nos ajuda a entender como esses resultados de amostra se comportam e nos diz que, se coletarmos amostras suficientes, suas médias começarão a se parecer com uma distribuição normal, mesmo que os dados originais não sejam nada disso.
Isso também traz algumas vantagens importantes para o mundo real. No machine learning, geralmente usamos técnicas como bootstrapping para estimar valores. Graças ao CLT, podemos ter certeza de que essas estimativas são precisas.
Ele também é um participante importante nos testes A/B. Quando uma empresa experimenta duas versões de uma página da Web ou de um recurso, o CLT nos ajuda a descobrir se os resultados são significativos ou ruídos aleatórios.
Mesmo no aprendizado por reforço, em que os sistemas aprendem por tentativa e erro, o CLT elimina o caos. À medida que mais dados chegam, as médias se tornam mais estáveis, o que ajuda o sistema a aprender mais rápido e melhor.
Por fim, você também verá o CLT em testes de hipóteses e análise de séries temporais. Com ele, você ajuda os cientistas de dados a testar ideias e a rastrear tendências com mais confiança.
Considerações finais
O teorema do limite central pode parecer técnico se você for novo em estatísticas, mas é um dos principais motivos pelos quais podemos fazer coisas inteligentes com os dados. Ela transforma a aleatoriedade em algo que podemos entender e confiar. Na verdade, esse é um dos elementos básicos da modelagem estatística e um conhecimento obrigatório para qualquer pessoa que trabalhe com dados.
Se você quiser explorar mais, leia sobre a lei dos grandes números e as distribuições de probabilidade - todas elas estão interligadas.
Sou um estrategista de conteúdo que adora simplificar tópicos complexos. Ajudei empresas como Splunk, Hackernoon e Tiiny Host a criar conteúdo envolvente e informativo para seus públicos.
Perguntas frequentes sobre o Teorema Central do Limite
O teorema do limite central pode ser usado com dados não numéricos?
Sim, mas não diretamente. O CLT se aplica a dados numéricos, especialmente médias e somas. Entretanto, para dados categóricos ou ordinais, você ainda pode usar princípios semelhantes convertendo os dados em formato numérico ou usando outras técnicas estatísticas.
Qual é a diferença entre a distribuição da amostragem e a distribuição da população?
A distribuição da população descreve o conjunto completo de dados, enquanto a distribuição da amostragem se refere à distribuição das estatísticas da amostra (como as médias) da amostragem repetida.
Como os valores discrepantes afetam o teorema do limite central?
Os outliers aumentam a assimetria e a variância, o que significa que talvez seja necessário um tamanho de amostra maior para que a distribuição da amostragem se aproxime da normalidade.


