Mesures de tendance centrale : Une vue d'ensemble complète

La tendance centrale est l'un des concepts les plus importants en statistiques. Elle décrit la valeur typique autour de laquelle les données ont tendance à se regrouper. Il fournit un chiffre unique et représentatif qui résume l'ensemble des données, rendant ainsi comparables de grandes quantités d'informations.

Historiquement, la notion de « valeur centrale » a évolué au fil des siècles. Les savants de l'Antiquité, tels que les Grecs, utilisaient des moyennes simples, tandis que les mathématiciens des XVIIe et XVIIIe siècles ont formalisé la moyenne, la médiane et le mode en tant qu'outils statistiques. Le XXe siècle a apporté davantage de sophistication, avec l'introduction de mesures spécialisées pour traiter les données asymétriques ou sujettes à des valeurs aberrantes. Aujourd'hui, la tendance centrale reste cruciale dans un large éventail de domaines, des sciences sociales et économiques à l'ingénierie et à l'apprentissage automatique.

Concepts fondamentaux de la tendance centrale

Avant d'aborder les variantes, passons en revue quelques termes techniques. Pour approfondir ce sujet et en savoir plus, veuillez vous inscrire à notre cours Introduction aux statistiques.

Définition et objectif

La tendance centrale désigne la mesure statistique qui identifie un point central dans un ensemble de données. Il sert de statistique sommaire, indiquant où la plupart des valeurs de la distribution ont tendance à se regrouper. En proposant une valeur unique et représentative, il simplifie la variabilité complexe inhérente aux données brutes.

L'un des principaux objectifs de la tendance centrale est de permettre la comparaison entre différents ensembles de données. Par exemple, à l'aide de mesures centralisées, nous pouvons comparer les revenus moyens entre différentes villes et mettre rapidement en évidence des tendances socio-économiques. Il est important de noter que la tendance centrale diffère des mesures de dispersion, qui décrivent la répartition des données autour du centre. Alors que la moyenne ou la médiane indique où se situe le centre des données, des mesures telles que la variance et l'écart type révèlent le degré de concentration ou de dispersion des données autour de ce centre.

Rôle dans les statistiques descriptives

En statistiques descriptives, la tendance centrale est utilisée pour résumer efficacement de grands ensembles de données. Qu'il s'agisse d'analyser les résultats d'examens, les délais de production ou les évaluations des clients, connaître la valeur typique est essentiel pour interpréter les tendances.

La tendance centrale est étroitement liée aux mesures de variabilité. Par exemple, deux ensembles de données peuvent avoir la même moyenne, mais présenter des écarts considérables, ce qui influe sur la fiabilité réelle de cette moyenne en tant que statistique récapitulative. 

Dans des situations réelles, la tendance centrale aide les décideurs politiques, les chefs d'entreprise et les chercheurs à prendre des décisions fondées sur des valeurs représentatives. Un détaillant peut analyser les ventes moyennes afin d'élaborer des stratégies d'inventaire, tandis qu'un chercheur dans le domaine de la santé peut examiner les durées de survie médianes afin d'évaluer l'efficacité d'un traitement.

Types de données et tendance centrale

Le choix d'une mesure appropriée de la tendance centrale dépend fortement du type de données. Les données se répartissent en quatre grandes catégories :

• Les données nominales représentent des catégories sans ordre inhérent (par exemple, les groupes sanguins, les couleurs).
• Les données ordinales indiquent un ordre de classement, mais sans intervalles cohérents (par exemple, les notes attribuées dans une enquête : médiocre, passable, bon).
• Les données d'intervalle ont des valeurs ordonnées avec des intervalles égaux, mais sans véritable zéro (par exemple, les températures en degrés Celsius).
• Les données de ratio sont caractérisées par des intervalles égaux et un zéro absolu (par exemple, le poids, la taille, le revenu).

Voici les mesures de tendance centrale les plus appropriées pour chaque type de données :

• Pour les données nominales, le mode est approprié car il est inutile de calculer la moyenne de catégories telles que « rouge », « bleu » et « vert ».
• Pour les données ordinales, la médiane est souvent le meilleur choix, car elle respecte le rang sans supposer des différences égales entre les rangs.
• Pour les données d'intervalle et de ratio données d'intervalle et de ratio, la moyenne, la médiane ou le mode peuvent tous être appropriés, selon la distribution des données et la présence de valeurs aberrantes.

Par exemple, le revenu médian des ménages est souvent utilisé car les données sur les revenus sont faussées par les revenus extrêmement élevés, tandis que la taille moyenne est une donnée raisonnable pour les tailles humaines normalement distribuées.

Mesures primaires de la tendance centrale

Il existe trois mesures principales de la tendance centrale : la moyenne arithmétique, la médiane et le mode. Examinons chacune d'entre elles en accordant une attention particulière à leurs points forts et à leurs limites.

Moyenne arithmétique

La moyenne arithmétique, souvent appelée simplementmoyenne ou moyenne arithmétique, est calculée en additionnant toutes les valeurs d'un ensemble de données et en divisant le résultat par le nombre d'observations :

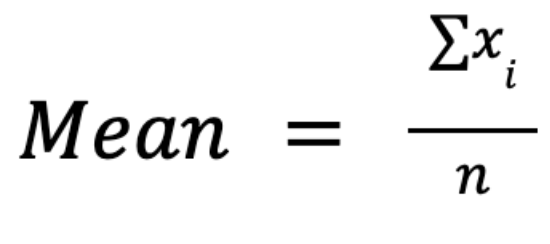
Le principal avantage de cette mesure réside dans ses propriétés mathématiques : elle est manipulable algébriquement, ce qui permet des formulations élégantes en statistiques inférentielles, en tests d'hypothèses et en analyse de régression. Par exemple, il s'intègre parfaitement aux calculs de variance et d'écart type.

Cependant, la moyenne est très sensible aux valeurs aberrantes : quelques valeurs extrêmes peuvent la fausser considérablement, la rendant non représentative des distributions asymétriques. Par exemple, dans les données sur les revenus, quelques milliardaires peuvent faire grimper la moyenne bien au-dessus de ce que gagne la plupart des gens.

En parlant de moyenne, il est essentiel de distinguer la moyenne de la population (μ) etla moyenne de l'échantillon (μ). moyenne échantillon (x̄). Le premier d'entre eux décrit l'ensemble de la population, tandis que le second l'estime à partir d'un sous-ensemble. Pour tirer des conclusions sur l'ensemble d'une population à partir d'un échantillon de données, nous utilisons un processus appelé « inférence statistique ».

Les scénarios dans lesquels la moyenne ne doit pas être utilisée comprennent les distributions fortement asymétriques, les données comportant des valeurs aberrantes significatives ou les données ordinales, où le calcul de la moyenne des rangs n'a aucune signification pratique.

Médiane

La médiane représente la valeur centrale d'un ensemble de données ordonnées. Pour un nombre impair de valeurs, il s'agit de la valeur centrale unique. Pour un ensemble de données pair, il s'agit de la moyenne des deux valeurs centrales.

Pour calculer la médiane, nous avons besoin de :

1. Pour classer les données de la plus petite à la plus grande.
2. Pour déterminer la valeur moyenne.

La principale force de la médiane réside dans sa robustesse face aux valeurs aberrantes : les valeurs extrêmes situées à chaque extrémité de la distribution n'ont aucune influence sur sa valeur, ce qui la rend idéale pour les données asymétriques telles que les revenus ou les prix de l'immobilier.

Cependant, la médiane est mathématiquement moins facile à manipuler que la moyenne. Il est moins utile dans les formules statistiques complexes ou la modélisation et ne s'intègre pas facilement dans les manipulations algébriques.

Mode

Le mode est la valeur qui apparaît le plus fréquemment dans un ensemble de données. Contrairement à l'e , la médiane peutégalement êtreutilisée avec des données nominales, ce qui la rend applicable à différents types de données.

Ce mode permet d'identifier les catégories à haute fréquence, telles que la couleur de produit la plus populaire ou la plainte la plus courante des clients. Cependant, il présente certaines limites :

• Dans les distributions uniformes, il peut ne pas y avoir de mode.
• Dans les distributions multimodales, il peut y avoir plusieurs modes, ce qui complique l'interprétation.
• Pour les données numériques, le mode peut être moins informatif, voire insignifiant si toutes les valeurs sont uniques.

Un tableau de distribution de fréquences aide souvent à déterminer le mode. Par exemple, dans le tableau de distribution de fréquences ci-dessous représentant les couleurs des pommes, « vert » est la mode me :

Analyse comparative des mesures primaires

Il est essentiel en statistiques de comprendre les différences entre la moyenne, la médiane et le mode en termes de performance et d'adéquation. Comparons-les :

Sensibilité aux valeurs aberrantes et à l'asymétrie

Parmi les trois mesures, la moyenne est la plus sensible aux valeurs aberrantes : une seule valeur extrême peut fausser considérablement la moyenne. La médiane, en revanche, reste stable à moins que suffisamment de valeurs extrêmes ne s'accumulent pour déplacer le point médian. Ce mode est totalement insensible aux valeurs aberrantes, car il dépend uniquement de la fréquence.

L'asymétrie influe également sur ces mesures. Dans les distributions asymétriques à droite (par exemple, les données sur les revenus), la moyenne est généralement supérieure à la médiane, qui est elle-même supérieure au mode.(Par mode, j'entends ici le mode dans une distribution continue, où le mode est le pic de la courbe de densité de probabilité, en supposant qu'il en existe un.)

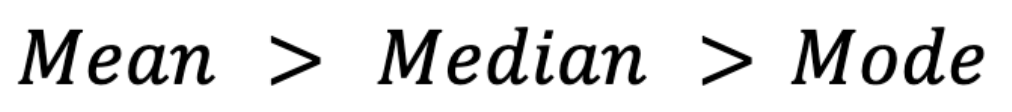
À l'inverse, dans les distributions asymétriques à gauche (par exemple, les notes d'examen où la plupart des élèves obtiennent des notes élevées), la moyenne est inférieure à la médiane et au mode :

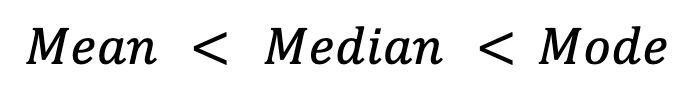
Les distributions symétriques, commela distribution normale,montrent idéalement une égalité entre les trois mesures :

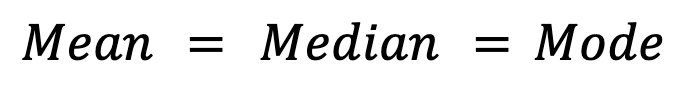
Dans la pratique, cependant, de légers écarts peuvent apparaître dans les distributions symétriques en raisonde la variabilité de l'échantillonnage.

Relations entre la moyenne, la médiane et le mode

Dans la section précédente, nous avons déjà examiné les relations générales entre la moyenne, la médiane et le mode dans les distributions normales et asymétriques. En général, les relations entre ces trois mesures constituent un outil de diagnostic de l'asymétrie. Dans les études empiriques, les statisticiens utilisent souvent le deuxième coefficient d'asymétrie de Pearson :

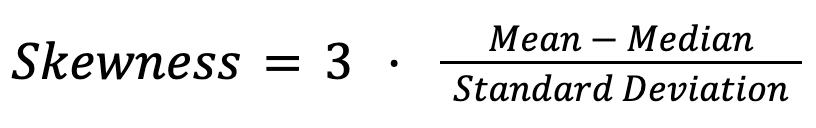
Par exemple, dans la répartition des salaires, un écart important entre la moyenne et la médiane indique une inégalité des revenus. De même, sur les marchés immobiliers, le prix médian des logements reflète souvent mieux les coûts habituels que la moyenne, qui peut être faussée par quelques propriétés extrêmement chères.

Applicabilité par type de données

Différentes mesures de tendance centrale conviennent à différents types de données. Le tableau ci-dessous résume les cas d'utilisation optimale et les limitations d'ons pour chaque mesure.

Comme nous pouvons le constater, il est essentiel d'aligner la mesure statistique sur la nature des données.

Mesures spécialisées de la tendance centrale

Outre les mesures primaires de tendance centrale, il existe des alternatives spécialisées qui répondent à des défis spécifiques liés aux données, tels que l'asymétrie, les valeurs aberrantes et la mise à l'échelle des données.

Moyenne ajustée et winsorisée

Une moyenne trimée ( ) exclut un pourcentage fixe de valeurs extrêmes aux deux extrémités de l'ensemble de données avant de calculer la moyenne. Par exemple, une moyenne tronquée de 10 % élimine les 10 % des valeurs les plus basses et les 10 % des valeurs les plus élevées.

Une moyenne winsorisée n' pas éliminer les valeurs extrêmes, mais les remplace par les valeurs restantes les plus proches. Cette mesure est utile dans des domaines tels que la finance, la fabrication et l'analyse d'enquêtes, où les données peuvent inclure des valeurs extrêmes rares mais influentes.

Les deux techniques réduisent l'influence des valeurs aberrantes, permettant ainsi d'atteindre un équilibre entre robustesse et conservation des données en combinant la sensibilité de la moyenne et la résilience de la médiane.

Moyennes géométriques et harmoniques

La moyenne géométrique multiplie tous les points de données et prend la racine n-ième (où n est le nombre de points de données). Il est particulièrement utile dans les processus multiplicatifs, tels que les taux de croissance, les rendements d'investissement et les mesures biologiques. La formule pour calculer les moyennes géométriques est la suivante :

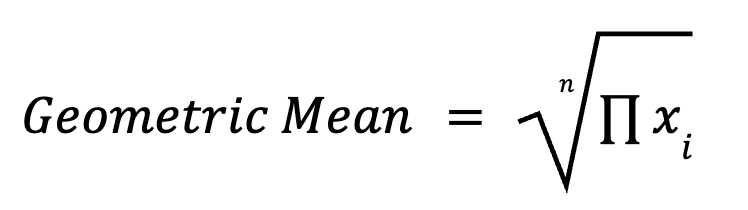
Par exemple, la croissance moyenne sur plusieurs années est mieux résumée par une moyenne géométrique que par une moyenne arithmétique.

La moyenne harmonique estcalculée comme suit :

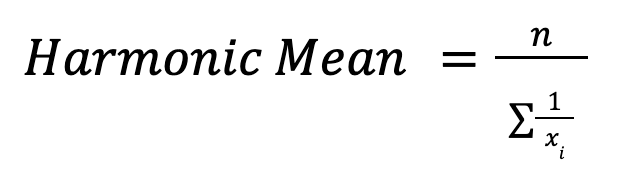
Il est utile pour calculer des moyennes, comme la vitesse ou les ratios financiers. Par exemple, pour calculer la vitesse moyenne sur différentes distances, la moyenne harmonique donne le taux global correct.

Mesures pondérées et trigénaires

Une moyenne pondérée attribue une importance variable aux points de données. Par exemple, la note finale d'un étudiant peut combiner les résultats d'examens et les travaux réalisés en cours, avec des pondérations différentes. Cette mesure corrige les biais et garantit que les observations les plus significatives ont davantage d'influence.

La trimédiane combine la médiane et les quartiles :

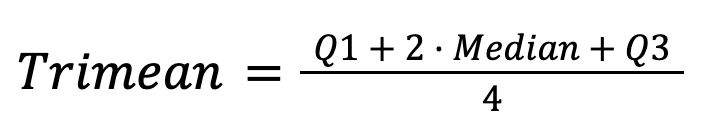
Il fournit une estimation stable et pertinente de la tendance centrale en combinant la robustesse de la médiane avec des informations sur la dispersion des données.

Pour maîtriser vos compétences en matière de raisonnement statistique, veuillez vous inscrireaux cours suivants : 

• Pensée statistique en Python (Partie 1)
• Pensée statistique en Python (Partie 2)
• Études de cas en raisonnement statistique

Robustesse des mesures de tendance centrale

La robustesse décrit la résistance d'une mesure de tendance centrale à la distorsion causée par des valeurs aberrantes ou des distributions non normales. Dans ce chapitre, nous approfondirons ce concept.

Analyse des points de rupture

Le point de rupture indique le niveau de contamination qu'une statistique peut supporter avant de commencer à fournir des résultats extrêmement inexacts. Par exemple :

• La moyenne présente un point de rupture de 0 %, car une valeur aberrante extrême peut la fausser.
• La médiane a un point de rupture de 50 %, ce qui signifie que jusqu'à la moitié des données peuvent être faussées avant que la médiane ne soit complètement invalidée.
• Les moyens ajustés présentent des points de rupture intermédiaires, car ils améliorent la robustesse tout en préservant l'efficacité des données.

Comprendre les points de rupture aide les analystes de données à choisir les statistiques appropriées lorsqu'ils sont confrontés à une contamination potentielle des données.

Compromis entre robustesse et sensibilité

Les mesures robustes telles que la médiane sacrifient une partie de l'efficacité statistique, ce qui signifie qu'elles peuvent nécessiter des échantillons plus importants pour atteindre la même précision que des mesures moins robustes telles que la moyenne.

Par exemple, bien que la médiane soit robuste, elle est moins efficace pour les distributions normales. À l'inverse, la moyenne est efficace pour les distributions normales, mais sensible aux données asymétriques. Les analystes de données doivent trouver un équilibre entre robustesse et efficacité, en fonction des caractéristiques des données.

Dans la pratique, la robustesse est privilégiée à l'efficacité dans des domaines tels que la finance ou la recherche biomédicale, où les anomalies dans les données sont courantes et les risques considérables.

Considérations avancées

Les défis posés par les données modernes poussent l'analyse de la tendance centrale au-delà de ses méthodes traditionnelles. Examinons de plus près certains sujets avancés.

Interactions de l'asymétrie

L'asymétrie affecte fondamentalement l'interprétation des mesures de tendance centrale. Le fait de ne rapporter que la moyenne dans un ensemble de données asymétrique peut être trompeur. Afin de mieux refléter l'asymétrie des données, les meilleures pratiques recommandent de communiquer à la fois la moyenne et la médiane. Par exemple, dans les études sur les revenus, la médiane offre souvent une image plus claire des revenus « typiques » que la moyenne.

Distributions multimodales

Les distributions multimodales comportent plusieurs pics, chacun pouvant représenter un sous-groupe différent. Se fier uniquement à une seule mesure telle que la moyenne peut masquer des informations essentielles.

Par exemple, dans les résultats d'un examen universitaire, deux modes peuvent indiquer deux groupes d'étudiants : ceux qui ont bien compris la matière et ceux qui ont rencontré des difficultés. Dans de tels cas, le fait de signaler plusieurs modes ou des médianes spécifiques à un groupe permet de mettre en évidence ces tendances.

Approches des données catégorielles

Les données nominales et ordinales rendent souvent difficile la synthèse numérique traditionnelle. Pour les données nominales, le mode reste l'outil principal. Cependant, des méthodes avancées telles que l'entropie de catégorie modale évaluent la diversité et la certitude au sein des données catégorielles, en quantifiant le degré de concentration ou de dispersion des réponses entre les catégories.

Pour les données ordinales, des techniques telles que les pourcentages cumulés ou les rangs médians offrent des informations plus approfondies sur la tendance centrale, en conservant l'ordre sans supposer des intervalles égaux.

Conclusion

Les nouvelles méthodes informatiques et les techniques de science des données continuent d'affiner notre compréhension de la tendance centrale. De nouvelles approches permettent des analyses plus nuancées, même dans des ensembles de données complexes et à haute dimension. Les recherches et développements futurs dans le domaine de la tendance centrale pourraient se concentrer sur des mesures adaptatives qui s'ajustent automatiquement en fonction de l'asymétrie ou de la contamination des données, garantissant ainsi une robustesse et une interprétabilité encore plus grandes.

Si vous souhaitez améliorer vos compétences en matière de données et acquérir des bases plus solides en statistiques avec Python et R, je vous recommande vivement de suivre nos cursus, que je recommande vivement :

• Principes fondamentaux des statistiques en Python
• Principes fondamentaux des statistiques dans R