Maße für die zentrale Tendenz: Ein umfassender Überblick

Die zentrale Tendenz ist eines der wichtigsten Konzepte in der Statistik und beschreibt den typischen Wert, um den sich Daten normalerweise gruppieren. Es gibt eine einzige, aussagekräftige Zahl, die einen ganzen Datensatz zusammenfasst, sodass man viele Infos besser verstehen und vergleichen kann.

Historisch gesehen hat sich die Idee eines „zentralen Wertes“ über Jahrhunderte hinweg entwickelt. Alte Gelehrte wie die Griechen haben einfache Durchschnittswerte genommen, während Matheprofis im 17. und 18. Jahrhundert Mittelwert, Median und Modus als statistische Werkzeuge eingeführt haben. Im 20. Jahrhundert wurde das Ganze noch besser und es kamen spezielle Methoden für den Umgang mit schief verteilten oder Ausreißer-anfälligen Daten dazu. Heutzutage ist die zentrale Tendenz in vielen Bereichen super wichtig, von den Sozialwissenschaften und der Wirtschaft bis hin zum Ingenieurwesen und maschinellem Lernen.

Grundlegende Konzepte der zentralen Tendenz

Bevor ich auf die Varianten eingehe, lass uns erst mal ein paar Begriffe klären. Wenn du mehr darüber erfahren willst, schreib dich in unseren Kurs „Einführung in die Statistik“ ein.

Was ist das und wozu ist es gut?

Die zentrale Tendenz ist ein statistisches Maß, das einen Mittelpunkt in einem Datensatz findet. Es ist wie eine Zusammenfassung, die zeigt, wo die meisten Werte in der Verteilung liegen. Durch die Angabe eines einzigen, repräsentativen Werts wird die komplexe Variabilität der Rohdaten vereinfacht.

Ein wichtiger Grund für die zentrale Tendenz ist, dass man Datensätze miteinander vergleichen kann. Mit zentralen Messgrößen können wir zum Beispiel die Durchschnittseinkommen verschiedener Städte vergleichen und schnell sozioökonomische Muster erkennen. Wichtig ist, dass sich die zentrale Tendenz von Streuungsmaßen unterscheidet, die beschreiben, wie sich Daten um den Mittelpunkt verteilen. Während der Mittelwert oder Median zeigt, wo das Rechenzentrum liegt, zeigen Sachen wie Varianz und Standardabweichung, wie eng oder weit die Daten um diesen Punkt verteilt sind.

Rolle in der deskriptiven Statistik

In der deskriptiven Statistik wird die zentrale Tendenz verwendet, um große Datensätze effektiv zusammenzufassen. Egal, ob du Prüfungsergebnisse, Produktionszeiten oder Kundenbewertungen checkst – den typischen Wert zu kennen, ist super wichtig, um Trends zu verstehen.

Die zentrale Tendenz hängt eng mit den Variabilitätsmaßen zusammen. Beispielsweise können zwei Datensätze denselben Mittelwert haben, sich jedoch in ihrer Streuung stark unterscheiden, was die Zuverlässigkeit dieses Mittelwerts als zusammenfassende Statistik beeinflusst. 

In der Praxis hilft die zentrale Tendenz Politikern, Unternehmenschefs und Forschern, Entscheidungen auf der Grundlage repräsentativer Werte zu treffen. Ein Einzelhändler kann die durchschnittlichen Verkaufszahlen checken, um seine Lagerbestände zu planen, während ein Gesundheitsforscher vielleicht die durchschnittliche Überlebenszeit anschaut, um zu sehen, wie gut eine Behandlung wirkt.

Arten von Daten und zentrale Tendenz

Die Wahl eines passenden Maßes für die zentrale Tendenz hängt stark vom Datentyp ab. Daten lassen sich in vier große Kategorien einteilen:

• Nominale Daten sind Kategorien ohne bestimmte Reihenfolge (z. B. Blutgruppen, Farben).
• Ordinaldaten zeigen eine Rangfolge an, aber ohne feste Abstände (z. B. Bewertungen in Umfragen wie schlecht, befriedigend, gut).
• Intervalldaten haben Werte, die in gleichen Abständen angeordnet sind, aber keinen echten Nullpunkt haben (z. B. Temperaturen in Celsius).
• Verhältnisdaten haben gleiche Abstände und einen absoluten Nullpunkt (z. B. Gewicht, Größe, Einkommen).

Hier sind die besten Mittelwerte für jede Art von Daten:

• Für nominale Datenist der Modus gut, weil es keinen Sinn macht, Kategorien wie „rot“, „blau“ und „grün“ zu mitteln.
• Für Ordinaldatenist der Median oft die beste Wahl, da er die Rangfolge berücksichtigt, ohne dass man davon ausgeht, dass die Unterschiede zwischen den Rängen gleich groß sind.
• Für Intervall- und Verhältnismessungenkönnen der Mittelwert, der Median oder der Modus gut sein, je nachdem, wie die Daten verteilt sind und ob es Ausreißer gibt.

Zum Beispiel wird oft das mittlere Haushaltseinkommen angegeben, weil die Einkommensdaten durch extrem hohe Verdiener verzerrt sind, während die durchschnittliche Körpergröße für normal verteilte Körpergrößen sinnvoll ist.

Primäre Maße der zentralen Tendenz

Es gibt drei Hauptmaße für die zentrale Tendenz: den arithmetischen Mittelwert, den Median und den Modus. Schauen wir uns die einzelnen Punkte genauer an und achten dabei besonders auf ihre Stärken und Schwächen.

Arithmetischer Mittelwert

Der arithmetische Mittelwert, oft einfachals Durchschnitt oder Mittelwert bezeichnet, wird berechnet, indem alle Werte in einem Datensatz addiert und durch die Anzahl der Beobachtungen geteilt werden:

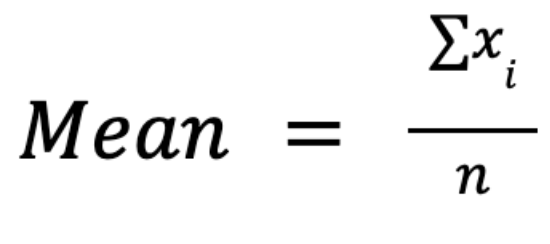
Der Hauptvorteil dieser Maßnahme liegt in ihren mathematischen Eigenschaften: Sie lässt sich algebraisch manipulieren und ermöglicht so elegante Formulierungen in der inferentiellen Statistik, Hypothesentests und Regressionsanalysen. Zum Beispiel lässt es sich super in Varianz- und Standardabweichungsberechnungen einbauen.

Der Mittelwert ist allerdings ziemlich empfindlich gegenüber Ausreißern: Ein paar extreme Werte können ihn stark verzerren, sodass er für schiefe Verteilungen nicht mehr repräsentativ ist. Zum Beispiel können bei den Einkommensdaten ein paar Milliardäre den Durchschnitt weit über das hinausziehen, was die meisten Leute verdienen.

Wenn wir über den Mittelwert reden, ist es wichtig, zwischen dem Populationsmittelwert (μ) unddem Stichprobenmittelwert Mittelwert einer Stichprobe (x̄). Der erste beschreibt die ganze Population, während der zweite sie anhand einer Teilmenge schätzt. Um aus einer Stichprobe von Daten Rückschlüsse auf die ganze Population zu ziehen, verwenden wir einen Prozess, der statistische Inferenz genannt wird.

Szenarien, in denen der Mittelwert nicht verwendet werden sollte, sind stark verzerrte Verteilungen, Daten mit deutlichen Ausreißern oder ordinale Daten, bei denen eine Mittelwertbildung keine praktische Bedeutung hat.

Median

Der Median ist der mittlere Wert einer geordneten Datenreihe. Bei einer ungeraden Anzahl von Werten ist es der mittlere Wert. Bei einem Datensatz mit gerader Anzahl ist es der Durchschnitt der beiden mittleren Werte.

Um den Median zu berechnen, brauchen wir:

1. Die Daten von klein nach groß sortieren.
2. Den Mittelwert ermitteln.

Die größte Stärke des Medians ist, dass er sich nicht von Ausreißern beeinflussen lässt: Extreme Werte an den Enden der Verteilung haben keinen Einfluss auf seinen Wert, was ihn super für schiefe Daten wie Einkommen oder Immobilienpreise macht.

Der Median ist aber mathematisch nicht so einfach zu handhaben wie der Mittelwert. Es ist weniger nützlich in komplizierten statistischen Formeln oder Modellen und lässt sich nicht so einfach in algebraische Berechnungen einbauen.

Modus

Der Modus ist der Wert, der in einem Datensatz am häufigsten vorkommt. Anders als der Median und der Medianwert kann der Unl-chmit nominalen Daten verwendet werden, sodass er für verschiedene Datentypen geeignet ist.

Der Modus hilft dabei, häufig vorkommende Kategorien zu erkennen, wie zum Beispiel die beliebteste Produktfarbe oder die häufigste Kundenbeschwerde. Allerdings gibt's ein paar Einschränkungen:

• Bei gleichmäßigen Verteilungen gibt es vielleicht keinen Modus.
• Bei multimodalen Verteilungen kann es mehrere Modi geben, was die Interpretation kompliziert macht.
• Bei Zahlen kann der Modus weniger aussagekräftig sein oder sogar ganz bedeutungslos, wenn alle Werte einzigartig sind.

Eine Häufigkeitsverteilungstabelle hilft oft dabei, den Modus zu bestimmen. In der folgenden Tabelle mit der Häufigkeitsverteilung der Apfelfarben ist beispielsweise „grün“ der mode:

Vergleichende Analyse der wichtigsten Maßnahmen

In der Statistik ist es echt wichtig zu wissen, wie sich Mittelwert, Median und Modus in ihrer Leistung und Eignung unterscheiden. Vergleichen wir sie mal:

Empfindlichkeit gegenüber Ausreißern und Schiefe

Von den drei Maßen ist der Mittelwert am empfindlichsten gegenüber Ausreißern: Ein einziger extremer Wert kann den Mittelwert stark verzerren. Der Median bleibt dagegen stabil, es sei denn, es sammeln sich so viele extreme Werte an, dass sich der Mittelwert verschiebt. Der Modus ist total unempfindlich gegenüber Ausreißern, weil er nur von der Häufigkeit abhängt.

Die Schiefe beeinflusst auch diese Maße. Bei rechts verschobenen Verteilungen (z. B. Einkommensdaten) ist der Mittelwert normalerweise höher als der Median, der wiederum höher ist als der Modus.(Mit Modus meine ich hier den Modus in einer kontinuierlichen Verteilung, wo der Modus der Höhepunkt der Wahrscheinlichkeitsdichtekurve ist, vorausgesetzt, dass es einen gibt.)

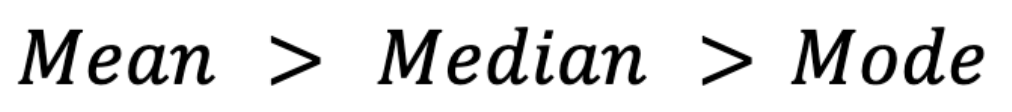
Umgekehrt liegt bei links verschobenen Verteilungen (z. B. bei Testnoten, bei denen die meisten Schüler gute Noten haben) der Mittelwert unter dem Median und dem Modus:

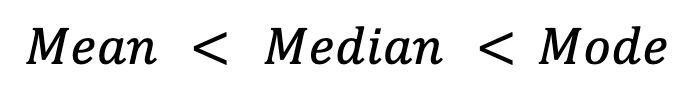
Symmetrische Verteilungen, wiedie Normalverteilung,zeigen im Idealfall Gleichheit zwischen allen drei Maßen:

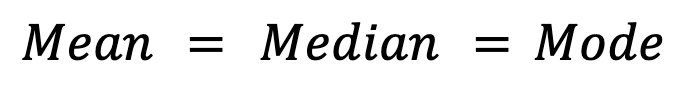
In der Praxis kann es aber bei symmetrischen Verteilungen wegenAbweichungen bei der Stichprobenahme zu kleinen Abweichungen kommen.

Zusammenhänge zwischen Mittelwert, Median und Modus

Im letzten Abschnitt haben wir schon die allgemeinen Beziehungen zwischen Mittelwert, Median und Modus in normalen und verzerrten Verteilungen gesehen. Im Allgemeinen helfen die Beziehungen zwischen den drei Messungen dabei, Schiefe zu erkennen. In empirischen Studien verwenden Statistiker oft den zweiten Schiefe-Koeffizienten von Pearson:

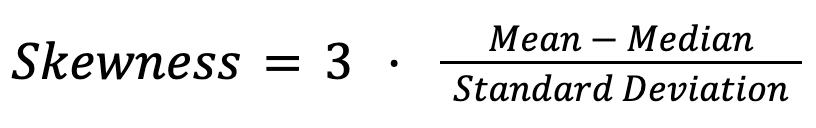
Bei der Verteilung der Gehälter zeigt zum Beispiel ein großer Unterschied zwischen dem Durchschnitts- und dem Medianwert, dass es Einkommensunterschiede gibt. Ähnlich ist es auf dem Wohnungsmarkt: Der Medianpreis für Häuser zeigt oft besser die typischen Kosten als der Durchschnittspreis, der durch ein paar extrem teure Immobilien verzerrt sein kann.

Anwendbarkeit nach Datentyp

Verschiedene Maße für die zentrale Tendenz passen zu unterschiedlichen Datentypen. Die Tabelle unten zeigt die besten Anwendungsfälle und Einschränkungen für jede Maßnahme.

Wie wir sehen, ist es wichtig, die statistische Messung an die Art der Daten anzupassen.

Spezielle Maße für die zentrale Tendenz

Neben den gängigen Maßen für die zentrale Tendenz gibt's auch spezielle Alternativen, die sich mit bestimmten Datenproblemen wie Schiefe, Ausreißern und Datenskalierung beschäftigen.

Getrimmt und winsorisiert bedeutet

Ein getrimmter Mittelwert, schmeißt einen festen Prozentsatz der Extremwerte von beiden Enden des Datensatzes raus, bevor er den Durchschnitt berechnet. Zum Beispiel werden bei einer Trimmung von 10 % die niedrigsten 10 % und die höchsten 10 % der Werte rausgenommen.

Ein winsorisierter Mittelwert löscht extreme Werte nicht, sondern ersetzt sie durch die nächstgelegenen Werte, die noch da sind. Diese Maßnahme ist nützlich in Bereichen wie Finanzen, Fertigung und Umfrageauswertung, wo Daten seltene, aber wichtige Extremwerte enthalten können.

Beide Techniken reduzieren den Einfluss von Ausreißern und schaffen so ein Gleichgewicht zwischen Robustheit und Datenerhaltung, indem sie die Sensitivität des Mittelwerts mit der Widerstandsfähigkeit des Medians kombinieren.

Geometrische und harmonische Mittelwerte

Der geometrische Mittelwert multipliziert alle Datenpunkte und zieht die n-te Wurzel (wobei n die Anzahl der Datenpunkte ist). Das ist besonders praktisch bei multiplizierenden Prozessen, wie zum Beispiel Wachstumsraten, Investitionsrenditen und biologischen Messungen. Die Formel für die Berechnung der geometrischen Mittelwerte lautet wie folgt:

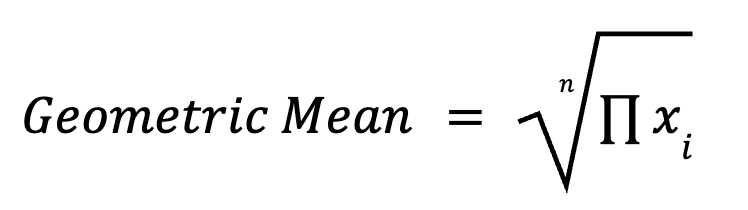
Zum Beispiel lässt sich das durchschnittliche Wachstum über mehrere Jahre besser mit einem geometrischen Mittelwert als mit einem arithmetischen Mittelwert zusammenfassen.

Der harmonische Mittelwert wirdso berechnet:

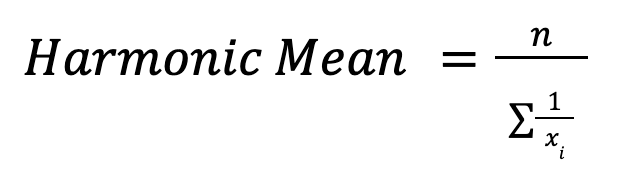
Das ist super, wenn du Durchschnittswerte berechnen willst, wie zum Beispiel Geschwindigkeiten oder Finanzkennzahlen. Wenn man zum Beispiel die Durchschnittsgeschwindigkeit über verschiedene Strecken berechnet, gibt der harmonische Mittelwert den richtigen Gesamtwert.

Gewichtete und Trimean-Maße

Ein gewichteter Mittelwert, gibt den Datenpunkten unterschiedliche Gewichte. Zum Beispiel kann die Endnote eines Schülers aus Prüfungsergebnissen und Kursarbeiten mit unterschiedlichen Gewichtungen bestehen. Diese Maßnahme gleicht Verzerrungen aus und sorgt dafür, dass wichtigere Beobachtungen mehr Einfluss haben.

Die Trimean ist der Mittelwert aus Median und Quartilen:

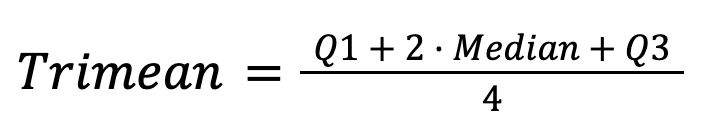
Es liefert eine stabile und aussagekräftige Schätzung der zentralen Tendenz, indem es die Robustheit des Medians mit Infos zur Datenverteilung kombiniert.

Um deine statistischen Denkfähigkeiten zu verbessern, melde dichfür die folgenden Kurse an: 

• Statistisches Denken in Python (Teil 1)
• Statistisches Denken in Python (Teil 2)
• Fallstudien zum statistischen Denken

Robustheit bei Maßen der zentralen Tendenz

Robustheit ist wie die Widerstandsfähigkeit eines Maßes für die zentrale Tendenz gegenüber Verzerrungen durch Ausreißer oder nicht normale Verteilungen. In diesem Kapitel schauen wir uns das Konzept genauer an.

Analyse der Bruchstellen

Der Breakdown-Punkt zeigt an, wie viel Verfälschung eine Statistik verkraften kann, bevor sie extrem ungenaue Ergebnisse liefert. Zum Beispiel:

• Der Mittelwert hat einen Breakdown-Punkt von 0 %, weil ein extremer Ausreißer ihn verzerren kann.
• Der Median hat einen Bruchpunkt von 50 %, was bedeutet, dass bis zur Hälfte der Daten verzerrt sein können, bevor der Median komplett versagt.
• Getrimmte Mittelwerte haben Zwischenbruchstellen, weil sie die Robustheit verbessern und gleichzeitig die Dateneffizienz erhalten.

Das Verständnis von Bruchstellen hilft Datenanalysten dabei, die richtigen Statistiken zu wählen, wenn sie mit möglichen Datenverfälschungen zu tun haben.

Abwägung zwischen Robustheit und Empfindlichkeit

Robuste Messgrößen wie der Median opfern ein bisschen statistische Effizienz, was bedeutet, dass sie möglicherweise größere Stichproben erfordern, um die gleiche Genauigkeit wie weniger robuste Messgrößen wie der Mittelwert zu erreichen.

Zum Beispiel ist der Median zwar robust, aber bei Normalverteilungen nicht so gut. Umgekehrt ist der Mittelwert gut für normale Verteilungen, aber nicht so toll bei schief verteilten Daten. Datenanalysten müssen je nach den Eigenschaften der Daten ein Gleichgewicht zwischen Robustheit und Effizienz finden.

In der Praxis ist Robustheit wichtiger als Effizienz, zum Beispiel in der Finanzbranche oder in der biomedizinischen Forschung, wo Datenanomalien häufig vorkommen und die Risiken ziemlich hoch sind.

Weitere Überlegungen

Die Herausforderungen moderner Daten bringen die Zentralwertanalyse über ihre traditionellen Methoden hinaus. Schauen wir uns ein paar fortgeschrittene Themen genauer an.

Schiefe Wechselwirkungen

Die Schiefe beeinflusst die Interpretation von Maßen der zentralen Tendenz ziemlich stark. Wenn man bei einem schief verteilten Datensatz nur den Mittelwert angibt, kann das irreführend sein. Um die Ungleichmäßigkeit der Daten besser zu zeigen, ist es besser, sowohl den Durchschnitt als auch den Median anzugeben. In Einkommensstudien zum Beispiel gibt der Median oft ein klareres Bild von „typischen“ Verdiensten als der Durchschnitt.

Multimodale Verteilungen

Multimodale Verteilungen haben mehrere Spitzen, die jede für sich eine andere Untergruppe darstellen können. Wenn man sich nur auf eine einzige Messung wie den Durchschnitt verlässt, kann man wichtige Erkenntnisse übersehen.

Bei den Prüfungsergebnissen einer Uni könnten zwei Modi zum Beispiel zwei Gruppen von Studierenden zeigen: die, die den Stoff gut verstanden haben, und die, die Probleme hatten. In solchen Fällen helfen die Angabe mehrerer Modi oder clusterspezifischer Mediane dabei, diese Muster aufzudecken.

Kategoriale Datenansätze

Nominale und ordinale Daten machen es oft schwierig, traditionelle numerische Zusammenfassungen zu erstellen. Bei nominalen Daten ist der Modus immer noch das wichtigste Werkzeug. Aber, fortgeschrittene Methoden wie die modale Kategorieentropie checken die Vielfalt und Sicherheit von Daten innerhalb von Kategorien und zeigen, wie konzentriert oder verteilt die Antworten über die Kategorien verteilt sind.

Bei Ordinaldaten helfen Techniken wie kumulative Prozentsätze oder Medianränge dabei, die zentrale Tendenz besser zu verstehen, ohne dass man gleiche Intervalle annehmen muss.

Fazit

Neue Computer-Methoden und Datenwissenschaftstechniken helfen uns immer besser, die zentrale Tendenz zu verstehen. Neue Ansätze ermöglichen selbst bei komplexen, hochdimensionalen Datensätzen differenziertere Analysen. Zukünftige Forschung und Entwicklung im Bereich der zentralen Tendenz könnten sich auf adaptive Maßnahmen konzentrieren, die automatisch Verzerrungen oder Datenverfälschungen ausgleichen und so für noch mehr Robustheit und Interpretierbarkeit sorgen.

Wenn du deine Datenkenntnisse verbessern möchtest und dir gründlichere Grundlagen in Statistik mit Python und R aneignen möchtest, empfehle ich dir unsere Lernpfade, die ich sehr empfehlen kann:

• Statistik-Grundlagen in Python
• Statistik-Grundlagen in R