Medidas de tendencia central: Una visión general completa

La tendencia central es uno de los conceptos más importantes de la estadística, ya que describe el valor típico en torno al cual tienden a agruparse los datos. Proporciona un número único y representativo que resume todo un conjunto de datos, lo que hace que grandes cantidades de información sean fáciles de digerir y comparar.

Históricamente, la idea de un «valor central» ha evolucionado a lo largo de los siglos. Los antiguos eruditos, como los griegos, consideraban los promedios simples, mientras que los matemáticos de los siglos XVII y XVIII formalizaron la media, la mediana y la moda como herramientas estadísticas. El siglo XX trajo consigo una mayor sofisticación, con la introducción de medidas especializadas para trabajar con datos sesgados o propensos a valores atípicos. Hoy en día, la tendencia central sigue siendo crucial en un amplio espectro de campos, desde las ciencias sociales y la economía hasta la ingeniería y el machine learning.

Conceptos fundamentales de la tendencia central

Antes de entrar en las variantes, repasemos algunos términos. Para obtener información más detallada y completa sobre este y otros temas, inscríbete en nuestro curso Introducción a la estadística.

Definición y finalidad

La tendencia central se refiere a la medida estadística que identifica un punto central dentro de un conjunto de datos. Funciona como una estadística resumida, indicando dónde tienden a agruparse la mayoría de los valores de la distribución. Al ofrecer un valor único y representativo, simplifica la compleja variabilidad inherente a los datos brutos.

Un objetivo clave de la tendencia central es permitir comparaciones entre conjuntos de datos. Por ejemplo, utilizando medidas centrales, podemos comparar los ingresos medios entre ciudades y revelar rápidamente patrones socioeconómicos. Es importante destacar que la tendencia central difiere de las medidas de dispersión, que describen cómo se distribuyen los datos alrededor del centro. Mientras que la media o mediana muestran dónde se encuentra el centro de datos, medidas como la varianza y la desviación estándar revelan cuán ajustada o dispersa es la distribución de los datos alrededor de ese centro.

Función en la estadística descriptiva

En estadística descriptiva, la tendencia central se utiliza para resumir eficazmente grandes conjuntos de datos. Ya sea que analices los resultados de un examen, los tiempos de producción o las valoraciones de los clientes, conocer el valor típico es muy valioso para interpretar las tendencias.

La tendencia central interactúa estrechamente con las medidas de variabilidad. Por ejemplo, dos conjuntos de datos pueden tener la misma media, pero diferir drásticamente en su dispersión, lo que influye en la fiabilidad real de esa media como estadística resumen. 

En situaciones reales, la tendencia central ayuda a los responsables políticos, los líderes empresariales y los investigadores a tomar decisiones basadas en valores representativos. Un minorista puede analizar las ventas medias para desarrollar estrategias de inventario, mientras que un investigador sanitario puede examinar los tiempos medios de supervivencia para evaluar la eficacia de un tratamiento.

Tipos de datos y tendencia central

La elección de una medida adecuada de la tendencia central depende en gran medida del tipo de datos. Los datos se dividen en cuatro grandes categorías:

• Datos nominales representan categorías sin un orden inherente (por ejemplo, tipos de sangre, colores).
• Los datos ordinales indican un orden clasificado, pero sin intervalos consistentes (por ejemplo, valoraciones en encuestas como malo, regular, bueno).
• Los datos de intervalos tienen valores ordenados con intervalos iguales, pero sin un cero verdadero (por ejemplo, las temperaturas en grados Celsius).
• Los datos de ratio presentan intervalos iguales y un cero absoluto (por ejemplo, peso, altura, ingresos).

Estas son las medidas de tendencia central más adecuadas para cada tipo de datos:

• Para datos nominales, la moda es adecuada porque promediar categorías como «rojo», «azul» y «verde» no tiene sentido.
• Para datos ordinales, la mediana suele ser la mejor opción, ya que respeta el rango sin suponer diferencias iguales entre los rangos.
• Para datos de intervalos y ratios, la media, la mediana o la moda pueden ser adecuadas, dependiendo de la distribución de los datos y de la presencia de valores atípicos.

Por ejemplo, la renta media por hogar se suele publicar porque los datos sobre los ingresos están sesgados por las rentas extremadamente altas, mientras que la estatura media es razonable para las estaturas humanas distribuidas normalmente.

Medidas primarias de tendencia central

Hay tres medidas principales de tendencia central: la media aritmética, la mediana y la moda. Consideremos cada uno de ellos, prestando especial atención a sus puntos fuertes y limitaciones.

media aritmética

La media aritmética, a menudo denominada simplementepromedio o media, se calcula sumando todos los valores de un conjunto de datos y dividiéndolos por el número de observaciones:

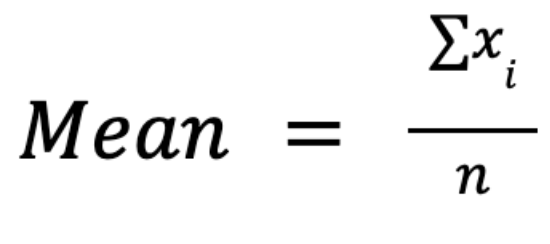
La principal ventaja de esta medida radica en sus propiedades matemáticas: es manipulable algebraicamente, lo que permite formulaciones elegantes en estadística inferencial, pruebas de hipótesis y análisis de regresión. Por ejemplo, se integra perfectamente en cálculos de varianza y desviación estándar.

Sin embargo, la media es muy sensible a los valores atípicos: unos pocos valores extremos pueden sesgarla significativamente, haciendo que no sea representativa de distribuciones sesgadas. Por ejemplo, en los datos sobre ingresos, varios multimillonarios pueden elevar la media muy por encima de lo que gana la mayoría de la gente.

Al hablar de la media, es fundamental distinguir entre la media poblacional (μ) yla muestra muestral (x̄). El primero de ellos describe a toda la población, mientras que el segundo la estima a partir de un subconjunto. Para sacar conclusiones sobre toda la población a partir de una muestra de datos, utilizamos un proceso denominado inferencia estadística.

Los casos en los que no se debe utilizar la media incluyen distribuciones muy sesgadas, datos con valores atípicos significativos o datos ordinales, en los que el promedio de las clasificaciones no tiene sentido práctico.

mediana

La mediana representa el valor medio de un conjunto de datos ordenados. Para un número impar de valores, es el valor central único. Para un conjunto de datos par, es la media de los dos valores centrales.

Para calcular la mediana, necesitamos:

1. Para ordenar los datos de menor a mayor.
2. Para identificar el valor medio.

La principal ventaja de la mediana es su solidez frente a los valores atípicos: los valores extremos en ambos extremos de la distribución no influyen en su valor, lo que la hace ideal para datos sesgados, como los ingresos o los precios de los inmuebles.

Sin embargo, la mediana es matemáticamente menos manejable que la media. Es menos útil en fórmulas estadísticas complejas o en la creación de modelos, y no se integra fácilmente en manipulaciones algebraicas.

Modo

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. A diferencia de la mediana, puedeutilizarse también con datos nominales, lo que la hace aplicable a diferentes tipos de datos.

El modo ayuda a identificar categorías de alta frecuencia, como el color más popular de un producto o la queja más habitual de los clientes. Sin embargo, tiene algunas limitaciones:

• En distribuciones uniformes, puede que no haya modo.
• En las distribuciones multimodales, puede haber varios modos, lo que complica la interpretación.
• En el caso de los datos numéricos, la moda puede ser menos informativa, hasta el punto de carecer de sentido si todos los valores son únicos.

Una tabla de distribución de frecuencias suele ayudar a determinar la moda. Por ejemplo, en la tabla de distribución de frecuencias de los colores de las manzanas que aparece a continuación, «verde» es la moda m:

Análisis comparativo de las medidas primarias

Comprender cómo difieren la media, la mediana y la moda en cuanto a rendimiento e idoneidad es fundamental en estadística. Comparémoslos:

Sensibilidad a valores atípicos y sesgos

De las tres medidas, la media es la más sensible a los valores atípicos: un solo valor extremo puede distorsionar significativamente la media. La mediana, por el contrario, permanece estable a menos que se acumulen suficientes valores extremos como para desplazar el punto medio. El modo es completamente insensible a los valores atípicos, ya que depende exclusivamente de la frecuencia.

La asimetría también afecta a estas medidas. En distribuciones sesgadas a la derecha (por ejemplo, datos sobre ingresos), la media suele ser superior a la mediana, que a su vez es superior a la moda.(Por moda me refiero a la moda en una distribución continua, donde la moda es el pico de la curva de densidad de probabilidad, suponiendo que exista).

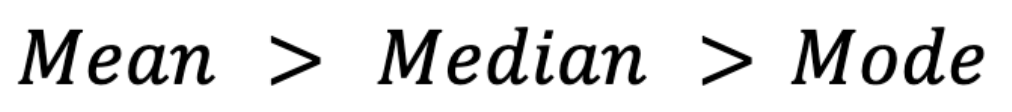
Por el contrario, en distribuciones sesgadas hacia la izquierda (por ejemplo, calificaciones en exámenes en las que la mayoría de los estudiantes obtienen calificaciones altas), la media cae por debajo de la mediana y la moda:

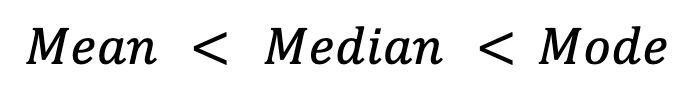
Las distribuciones simétricas, comola distribución normal,muestran idealmente la igualdad entre las tres medidas:

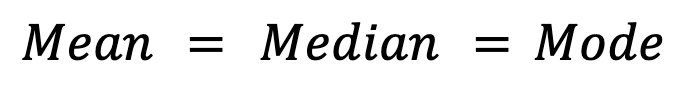
Sin embargo, en la práctica pueden producirse pequeñas desviaciones en las distribuciones simétricas debidoa la variabilidad del muestreo.

Relaciones entre la media, la mediana y la moda

En la sección anterior, ya hemos visto las relaciones generales entre la media, la mediana y la moda en distribuciones normales y sesgadas. En general, las relaciones entre las tres medidas sirven como herramienta de diagnóstico para la asimetría. En estudios empíricos, los estadísticos suelen aplicar el segundo coeficiente de asimetría de Pearson:

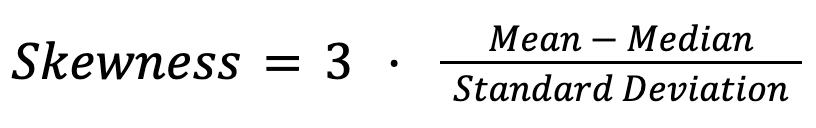
Por ejemplo, en la distribución salarial, una diferencia significativa entre la media y la mediana indica que existe desigualdad de ingresos. Del mismo modo, en los mercados inmobiliarios, el precio medio de la vivienda suele reflejar mejor los costes típicos que la media, que puede verse sesgada por unas pocas propiedades extremadamente caras.

Aplicabilidad por tipo de datos

Las diferentes medidas de tendencia central se adaptan a diferentes tipos de datos. La tabla siguiente resume los casos de uso óptimos y las limitaciones de cada medida.

Como vemos, es importante alinear la medida estadística con la naturaleza de los datos.

Medidas especializadas de tendencia central

Aparte de las medidas primarias de tendencia central, existen alternativas especializadas que abordan retos específicos relacionados con los datos, como la asimetría, los valores atípicos y la escala de los datos.

Recortado y winsorizado significa

Una media recortada ( ) excluye un porcentaje fijo de valores extremos de ambos extremos del conjunto de datos antes de calcular la media. Por ejemplo, una media recortada del 10 % elimina el 10 % más bajo y el 10 % más alto de los valores.

Una media winsorizada no elimina los valores extremos de forma e, sino que los sustituye por los valores restantes más cercanos. Esta medida es útil en campos como las finanzas, la fabricación y el análisis de encuestas, donde los datos pueden incluir valores extremos poco frecuentes pero influyentes.

Ambas técnicas reducen la influencia de los valores atípicos, logrando un equilibrio entre la solidez y la retención de datos al combinar la sensibilidad de la media con la resiliencia de la mediana.

Medias geométricas y armónicas

La media geométrica multiplica todos los puntos de datos y toma la raíz n-ésima (donde n es el número de puntos de datos). Es especialmente útil en procesos multiplicativos, como tasas de crecimiento, rentabilidad de inversiones y mediciones biológicas. La fórmula para calcular las medias geométricas es la siguiente:

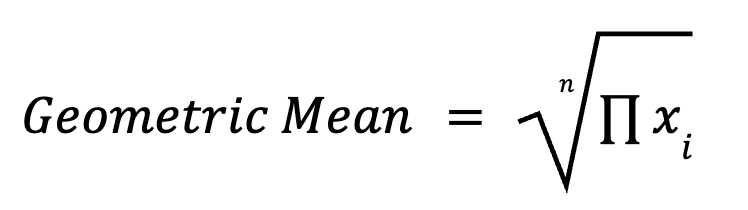
Por ejemplo, el crecimiento medio durante varios años se resume mejor con una media geométrica que con una media aritmética.

La media armónica secalcula de la siguiente manera:

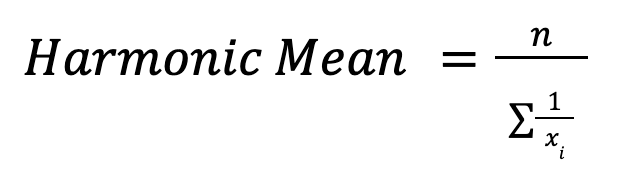
Es útil cuando se calcula el promedio de tasas, como la velocidad o los ratios financieros. Por ejemplo, al calcular la velocidad media en diferentes distancias, la media armónica da la velocidad global correcta.

Medidas ponderadas y trimedias

Una media ponderada asigna una importancia variable a los puntos de datos. Por ejemplo, la nota final de un estudiante puede combinar las calificaciones de los exámenes y los trabajos del curso con diferentes ponderaciones. Esta medida corrige los sesgos y garantiza que las observaciones más significativas tengan mayor influencia.

El trimeana combina la mediana y los cuartiles:

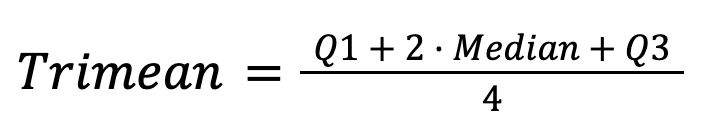
Ofrece una estimación de la tendencia central estable y reveladora al combinar la solidez de la mediana con información sobre la dispersión de los datos.

Para dominar tus habilidades de pensamiento estadístico, inscríbeteen los siguientes cursos: 

• Pensamiento estadístico en Python (Parte 1)
• Pensamiento estadístico en Python (Parte 2)
• Casos prácticos de pensamiento estadístico

Robustez en las medidas de tendencia central

La robustez describe la resistencia de una medida de tendencia central a la distorsión provocada por valores atípicos o distribuciones no normales. En este capítulo, profundizaremos en este concepto.

Análisis del punto de ruptura

El punto de ruptura indica la cantidad de contaminación que puede soportar una estadística antes de empezar a dar resultados extremadamente inexactos. Por ejemplo:

• La media tiene un punto de ruptura del 0 % porque un valor atípico extremo puede sesgarla.
• La mediana tiene un punto de ruptura del 50 %, lo que significa que hasta la mitad de los datos pueden distorsionarse antes de que la mediana falle por completo.
• Los medios recortados tienen puntos de ruptura intermedios, ya que mejoran la solidez al tiempo que preservan la eficiencia de los datos.

Comprender los puntos de ruptura ayuda a los analistas de datos a elegir las estadísticas adecuadas cuando se enfrentan a una posible contaminación de los datos.

Compromiso entre robustez y sensibilidad

Las medidas robustas, como la mediana, sacrifican cierta eficiencia estadística, lo que significa que pueden requerir muestras más grandes para lograr la misma precisión que medidas menos robustas, como la media.

Por ejemplo, aunque la mediana es robusta, es menos eficiente para distribuciones normales. Por el contrario, la media es eficaz para distribuciones normales, pero sensible a datos sesgados. Los analistas de datos deben equilibrar la solidez y la eficiencia, dependiendo de las características de los datos.

En situaciones prácticas, se prefiere la solidez a la eficiencia en ámbitos como las finanzas o la investigación biomédica, donde las anomalías en los datos son habituales y los riesgos son considerables.

Consideraciones avanzadas

Los retos que plantean los datos modernos llevan el análisis de la tendencia central más allá de sus métodos tradicionales. Veamos más detenidamente algunos temas avanzados.

Interacciones de sesgo

La asimetría afecta fundamentalmente a la interpretación de las medidas de tendencia central. Informar solo la media en un conjunto de datos sesgado puede ser engañoso. Para reflejar mejor la asimetría de los datos, las mejores prácticas recomiendan informar tanto la media como la mediana. Por ejemplo, en los estudios sobre ingresos, la mediana suele ofrecer una imagen más clara de los ingresos «típicos» que la media.

Distribuciones multimodales

Las distribuciones multimodales contienen múltiples picos, cada uno de los cuales puede representar un subgrupo diferente. Basarse únicamente en una única medida, como la media, puede ocultar información fundamental.

Por ejemplo, en las calificaciones de un examen universitario, dos modos podrían indicar dos grupos de estudiantes: los que entendieron bien el material y los que tuvieron dificultades. En tales casos, informar sobre múltiples modos o medianas específicas de grupos ayuda a revelar estos patrones.

Enfoques de datos categóricos

Los datos nominales y ordinales suelen dificultar la síntesis numérica tradicional. Para los datos nominales, la moda sigue siendo la herramienta principal. Sin embargo, métodos avanzados como la entropía de categorías modales evalúan la diversidad y la certeza en datos categóricos, cuantificando cuán concentradas o dispersas son las respuestas entre categorías.

Para datos ordinales, técnicas como los porcentajes acumulativos o las medias rangos ofrecen una visión más profunda de la tendencia central, conservando el orden sin suponer intervalos iguales.

Conclusión

Los nuevos métodos computacionales y las técnicas de ciencia de datos continúan perfeccionando nuestra comprensión de la tendencia central. Los nuevos enfoques permiten realizar análisis más matizados, incluso en conjuntos de datos complejos y de alta dimensión. Las futuras investigaciones y desarrollos en el campo de la tendencia central podrían centrarse en medidas adaptativas que se ajusten automáticamente a la asimetría o la contaminación de los datos, garantizando una mayor solidez e interpretabilidad.

Si te interesa mejorar tus habilidades con los datos y deseas adquirir una base más sólida en los fundamentos de la estadística en Python y R, te recomiendo encarecidamente que consideres la posibilidad de participar en nuestros programas de capacitación:

• Fundamentos de estadística en Python
• Fundamentos de estadística en R