Medidas de tendência central: Uma visão geral completa

A tendência central é um dos conceitos mais importantes da estatística, que mostra o valor típico em torno do qual os dados costumam se agrupar. Ele dá um número único e representativo que resume todo um conjunto de dados, tornando grandes quantidades de informação fáceis de entender e comparar.

Olha só, a ideia de um “valor central” já existe há séculos. Os estudiosos antigos, como os gregos, consideravam médias simples, enquanto os matemáticos dos séculos XVII e XVIII formalizaram a média, a mediana e a moda como ferramentas estatísticas. O século XX trouxe mais sofisticação, com medidas específicas pra lidar com dados distorcidos ou com muitos valores atípicos. Hoje, a tendência central continua sendo super importante em várias áreas, desde ciências sociais e economia até engenharia e machine learning.

Noções básicas sobre tendência central

Antes de falar sobre as variantes, vamos dar uma olhada em alguns termos. Para saber mais sobre isso e muito mais, inscreva-se no nosso curso Introdução à Estatística.

Definição e objetivo

A tendência central é uma medida estatística que mostra o ponto central de um conjunto de dados. Funciona como uma estatística resumida, mostrando onde a maioria dos valores na distribuição costuma se juntar. Ao oferecer um valor único e representativo, simplifica a complexa variabilidade inerente aos dados brutos.

Um dos principais objetivos da tendência central é permitir comparações entre conjuntos de dados. Por exemplo, usando medidas centrais, dá pra comparar a renda média entre cidades e descobrir padrões socioeconômicos rapidinho. É importante notar que a tendência central é diferente das medidas de dispersão, que mostram como os dados se espalham em torno do centro. Enquanto a média ou mediana mostra onde o centro dos dados está, medidas como a variância e o desvio padrão mostram como os dados estão distribuídos em torno desse centro.

Papel na estatística descritiva

Em estatística descritiva, a tendência central é usada para resumir de forma eficaz grandes conjuntos de dados. Seja analisando notas de exames, tempos de produção ou avaliações de clientes, saber o valor típico é super importante pra entender as tendências.

A tendência central interage muito com as medidas de variabilidade. Por exemplo, dois conjuntos de dados podem ter a mesma média, mas diferir drasticamente na dispersão, influenciando a confiabilidade dessa média como estatística resumida. 

Em situações reais, a tendência central ajuda os políticos, os líderes empresariais e os pesquisadores a tomar decisões com base em valores representativos. Um varejista pode analisar as vendas médias para criar estratégias de estoque, enquanto um pesquisador da área de saúde pode examinar os tempos médios de sobrevivência para avaliar a eficácia de um tratamento.

Tipos de dados e tendência central

Escolher uma medida de tendência central que seja boa depende muito do tipo de dados. Os dados podem ser divididos em quatro grandes categorias:

• Dados nominais representam categorias sem ordem inerente (por exemplo, tipos sanguíneos, cores).
• Dados ordinais mostram uma ordem de classificação, mas sem intervalos consistentes (por exemplo, avaliações de pesquisas como ruim, regular, bom).
• Dados de intervalo têm valores ordenados com intervalos iguais, mas sem zero verdadeiro (por exemplo, temperaturas em graus Celsius).
• Os dados de razão apresentam intervalos iguais e um zero absoluto (por exemplo, peso, altura, renda).

Aqui estão as medidas de tendência central mais adequadas para cada tipo de dados:

• Para dados nominais, a moda é a melhor, porque fazer a média de categorias como “vermelho”, “azul” e “verde” não faz sentido.
• Para dados ordinais, a mediana é geralmente a melhor escolha, respeitando a classificação sem assumir diferenças iguais entre as classificações.
• Para dados de intervalo e proporção, a média, a mediana ou a moda podem ser boas, dependendo da distribuição dos dados e da presença de valores atípicos.

Por exemplo, a renda média das famílias é frequentemente divulgada porque os dados sobre renda são distorcidos por pessoas com rendimentos extremamente altos, enquanto a altura média é razoável para alturas humanas normalmente distribuídas.

Medidas primárias de tendência central

Existem três medidas principais de tendência central: a média aritmética, a mediana e a moda. Vamos ver cada um deles, prestando atenção especial nos pontos fortes e fracos.

Média aritmética

A média aritmética, muitas vezes chamada simplesmentede média, é calculada somando todos os valores de um conjunto de dados e dividindo pelo número de observações:

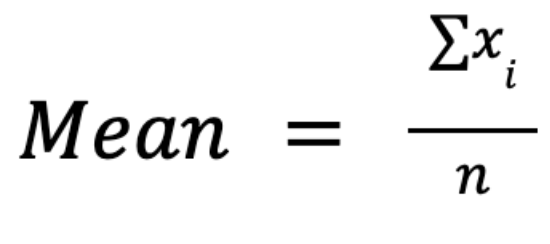
A principal vantagem dessa medida está nas suas propriedades matemáticas: ela é manipulável algebricamente, permitindo formulações elegantes em estatística inferencial, testes de hipóteses e análise de regressão. Por exemplo, ele se encaixa direitinho nos cálculos de variação e desvio padrão.

Mas, a média é super sensível a valores fora do normal: alguns valores extremos podem distorcer bastante, fazendo com que ela não represente bem distribuições distorcidas. Por exemplo, nos dados de renda, vários bilionários podem elevar a média muito acima do que a maioria das pessoas ganha.

Falando sobre a média, é super importante diferenciar entre a média da população (μ) ea média amostral me e (x̄). O primeiro deles fala sobre toda a população, enquanto o segundo dá uma estimativa a partir de um subconjunto. Para tirar conclusões sobre toda a população a partir de uma amostra de dados, usamos um processo chamado inferência estatística.

Os cenários em que a média não deve ser usada incluem distribuições muito distorcidas, dados com valores atípicos significativos ou dados ordinais, em que a média das classificações não tem significado prático.

Média

A mediana é o valor do meio de um conjunto de dados que estão em ordem. Para um número ímpar de valores, é o valor central único. Para um conjunto de dados com um número par, é a média dos dois valores do meio.

Para calcular a mediana, precisamos de:

1. Para ordenar os dados do menor para o maior.
2. Para achar o valor do meio.

A principal vantagem da mediana é que ela é super resistente a valores fora do normal: os valores extremos em cada ponta da distribuição não afetam o valor dela, o que a torna ideal para dados distorcidos, como renda ou preços de imóveis.

Mas, a mediana é mais complicada de lidar do que a média. É menos útil em fórmulas estatísticas complexas ou modelagem e não se integra facilmente em manipulações algébricas.

Modo

A moda é o valor que aparece mais vezes num conjunto de dados. Ao contrário da média e da mediana, otambém pode serusado com dados nominais, o que o torna aplicável a diferentes tipos de dados.

Esse modo ajuda a identificar categorias de alta frequência, como a cor mais popular de um produto ou a reclamação mais comum dos clientes. Mas tem algumas limitações:

• Em distribuições uniformes, pode não haver moda.
• Nas distribuições multimodais, pode haver vários modos, o que complica a interpretação.
• Para dados numéricos, a moda pode ser menos informativa, podendo até mesmo ser sem sentido se todos os valores forem únicos.

Uma tabela de distribuição de frequências geralmente ajuda a determinar o modo. Por exemplo, na tabela de distribuição de frequência das cores das maçãs abaixo, “verde” é a m:

Análise comparativa das medidas primárias

Entender como a média, a mediana e a moda diferem em desempenho e adequação é super importante em estatística. Vamos comparar:

Sensibilidade a valores atípicos e assimetria

Entre as três medidas, a média é a mais sensível a valores atípicos: um único valor extremo pode distorcer significativamente a média. Já a mediana fica estável, a menos que apareçam muitos valores extremos que mudem o ponto do meio. O modo é totalmente insensível a valores atípicos, porque depende só da frequência.

A assimetria também afeta essas medidas. Em distribuições assimétricas para a direita (por exemplo, dados de renda), a média é normalmente maior do que a mediana, que por sua vez é maior do que a moda.(Por moda, quero dizer a moda em uma distribuição contínua, onde a moda é o pico da curva de densidade de probabilidade, supondo que exista uma.)

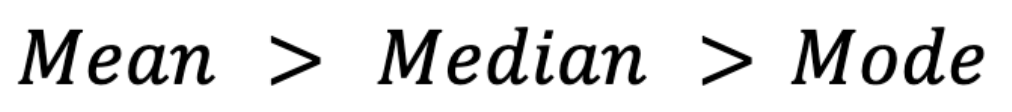
Por outro lado, em distribuições assimétricas para a esquerda (por exemplo, notas de testes em que a maioria dos alunos tem notas altas), a média fica abaixo da mediana e da moda:

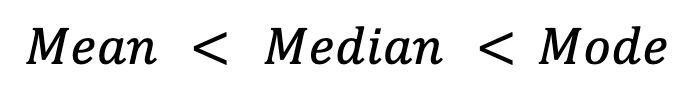
Distribuições simétricas, comoa distribuição normal,mostram, idealmente, igualdade entre as três medidas:

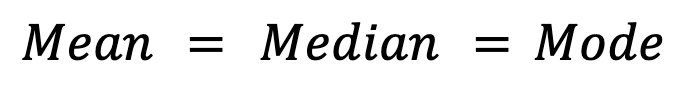
Na prática, porém, podem ocorrer pequenos desvios nas distribuições simétricas devidoà variabilidade da amostragem.

Relações entre média, mediana e moda

Na seção anterior, já vimos as relações gerais entre média, mediana e moda em distribuições normais e assimétricas. Em geral, as relações entre as três medidas servem como uma ferramenta de diagnóstico para a assimetria. Em estudos empíricos, os estatísticos costumam usar o segundo coeficiente de assimetria de Pearson:

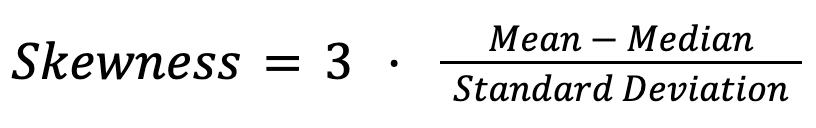
Por exemplo, na distribuição salarial, uma diferença grande entre a média e a mediana mostra que tem desigualdade de renda. Da mesma forma, nos mercados imobiliários, o preço médio das casas geralmente reflete melhor os custos típicos do que a média, que pode ser distorcida por algumas propriedades super caras.

Aplicabilidade por tipo de dados

Diferentes medidas de tendência central se encaixam em diferentes tipos de dados. A tabela abaixo mostra os casos de uso ideal e as limitações de cada medida.

Como a gente vê, é importante combinar a medida estatística com o tipo de dados.

Medidas especializadas de tendência central

Além das principais medidas de tendência central, existem alternativas especializadas que lidam com desafios específicos dos dados, como assimetria, valores atípicos e escala de dados.

Cortado e winsorizado significa

Uma média aparada ( ) exclui uma porcentagem fixa de valores extremos de ambos os extremos do conjunto de dados antes de calcular a média. Por exemplo, uma média aparada de 10% tira os 10% mais baixos e os 10% mais altos dos valores.

Uma média winsorizada não elimina valores extremos, mas substitui-os pelos valores mais próximos restantes. Essa medida é útil em áreas como finanças, manufatura e análise de pesquisas, onde os dados podem incluir extremos raros, mas influentes.

As duas técnicas diminuem a influência dos valores atípicos, conseguindo um equilíbrio entre robustez e retenção de dados, combinando a sensibilidade da média com a resiliência da mediana.

Médias geométricas e harmônicas

A média geométrica multiplica todos os pontos de dados e tira a raiz n-ésima (onde n é o número de pontos de dados). É super útil em processos multiplicativos, tipo taxas de crescimento, retorno de investimentos e medições biológicas. A fórmula pra calcular as médias geométricas é assim:

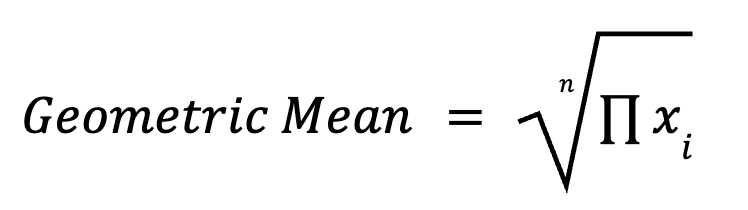
Por exemplo, o crescimento médio ao longo de vários anos é melhor resumido com uma média geométrica do que com uma média aritmética.

A média harmônica écalculada assim:

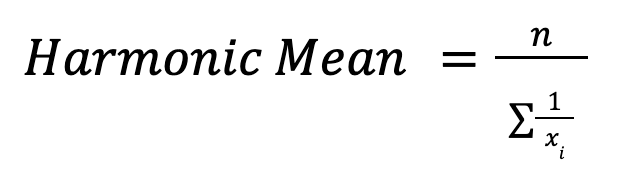
É útil quando você quer calcular médias, tipo velocidade ou índices financeiros. Por exemplo, ao calcular a velocidade média em diferentes distâncias, a média harmônica dá a taxa geral correta.

Medidas ponderadas e trimedia

Uma média ponderada dá uma importância diferente para os pontos de dados. Por exemplo, a nota final de um aluno pode juntar as notas dos exames e dos trabalhos com pesos diferentes. Essa medida ajusta os vieses e garante que as observações mais significativas tenham mais influência.

A trimeano combina a mediana e os quartis:

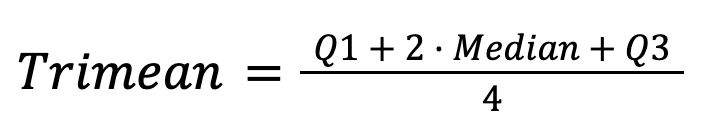
Oferece uma estimativa da tendência central estável e perspicaz, combinando a robustez da mediana com informações sobre a dispersão dos dados.

Para dominar suas habilidades de raciocínio estatístico, inscreva-senos seguintes cursos: 

• Pensamento estatístico em Python (Parte 1)
• Pensamento estatístico em Python (Parte 2)
• Estudos de caso em pensamento estatístico

Robustez nas medidas de tendência central

Robustez é quando uma medida de tendência central é resistente a distorções causadas por valores atípicos ou distribuições não normais. Neste capítulo, vamos dar uma olhada mais de perto nesse conceito.

Análise do ponto de ruptura

O ponto de ruptura mostra o quanto de contaminação uma estatística aguenta antes de começar a dar resultados super imprecisos. Por exemplo:

• A média tem um ponto de ruptura de 0% porque um valor extremo pode distorcer o resultado.
• A mediana tem um ponto de ruptura de 50%, o que significa que até metade dos dados podem ser distorcidos antes que a mediana falhe completamente.
• Os meios aparados têm pontos de divisão intermediários, pois melhoram a robustez e, ao mesmo tempo, mantêm a eficiência dos dados.

Entender os pontos de falha ajuda os analistas de dados a escolher as estatísticas certas quando estão lidando com uma possível contaminação dos dados.

Equilíbrio entre robustez e sensibilidade

Medidas robustas, como a mediana, sacrificam um pouco a eficiência estatística, o que significa que podem precisar de amostras maiores para ter a mesma precisão que medidas menos robustas, como a média.

Por exemplo, embora a mediana seja robusta, ela é menos eficiente para distribuições normais. Por outro lado, a média é boa para distribuições normais, mas não é muito legal para dados que não estão bem alinhados. Os analistas de dados precisam equilibrar robustez e eficiência, dependendo das características dos dados.

Na prática, a robustez é mais importante do que a eficiência em áreas como finanças ou pesquisa biomédica, onde é comum ter dados estranhos e os riscos são grandes.

Considerações avançadas

Os desafios dos dados modernos levam a análise da tendência central além dos métodos tradicionais. Vamos dar uma olhada em alguns tópicos mais avançados.

Interações de assimetria

A assimetria afeta muito a interpretação das medidas de tendência central. Relatar só a média em um conjunto de dados distorcido pode ser meio confuso. Para mostrar melhor a assimetria dos dados, é melhor usar tanto a média quanto a mediana. Por exemplo, em estudos sobre renda, a mediana geralmente dá uma ideia mais clara do que é um salário “típico” do que a média.

Distribuições multimodais

As distribuições multimodais têm vários picos, cada um deles podendo representar um subgrupo diferente. Confiar só numa única medida, como a média, pode esconder informações importantes.

Por exemplo, nas notas de um exame da universidade, dois modos podem indicar dois grupos de alunos: aqueles que entenderam bem o material e aqueles que tiveram dificuldades. Nesses casos, relatar vários modos ou medianas específicas do cluster ajuda a revelar esses padrões.

Abordagens de dados categóricos

Os dados nominais e ordinais muitas vezes dificultam a síntese numérica tradicional. Para dados nominais, a moda continua sendo a principal ferramenta. Mas, métodos mais avançados, como a entropia de categoria modal, avaliam a diversidade e a certeza dentro de dados categóricos, mostrando o quanto as respostas estão concentradas ou espalhadas pelas categorias.

Para dados ordinais, técnicas como porcentagens cumulativas ou classificações medianas oferecem insights mais profundos sobre a tendência central, mantendo a ordem sem assumir intervalos iguais.

Conclusão

Os novos métodos computacionais e as técnicas de ciência de dados continuam a melhorar nossa compreensão da tendência central. Novas abordagens permitem análises mais detalhadas, mesmo em conjuntos de dados complexos e com muitas dimensões. Pesquisas e desenvolvimentos futuros na área de tendência central podem se concentrar em medidas adaptativas que se ajustam automaticamente à assimetria ou contaminação de dados, garantindo ainda mais robustez e interpretabilidade.

Se você está interessado em melhorar suas habilidades com dados e quer uma base mais sólida nos fundamentos de estatística em Python e R, considere fazer nossos programas de habilidades, que eu recomendo muito:

• Fundamentos de estatística em Python
• Fundamentos de estatística em R