Cours
Analyse exploratoire des données en R
4 h
115.1K
Lors de l'interprétation des données, le choix de la bonne mesure de tendance centrale peut être déterminant pour la réussite de votre analyse. Parmi les mesures les plus courantes figurent lamoyenne et la médiane , deux concepts apparemment simples qui ont des implications profondes dans l'interprétation des données. Alors que la moyenne nous donne la moyenne arithmétique, la médiane est le point central d'un ensemble de valeurs triées, de sorte que la moitié des observations se trouvent de chaque côté. Cependant, lequel est le plus fiable ? La réponse dépend souvent de la distribution de vos données, de la présence de valeurs aberrantes et du message que vous souhaitez faire passer.
Dans cet article, je vais vous expliquer les différences entre la moyenne et la médiane, leurs avantages et leurs inconvénients, ainsi que la manière de choisir la plus appropriée selon les situations. J'examinerai également comment les distributions asymétriques et les valeurs aberrantes influencent ces mesures, en fournissant des exemples concrets et des illustrations pour vous aider à comprendre ces concepts fondamentaux. Nous aborderons également des concepts plus avancés.
Définitions de la moyenne et de la médiane
Afin de bien comprendre les différences entre la moyenne et la médiane, examinons chacune de ces mesures et soulignons leurs principales propriétés.
Quelle est la moyenne ?
La moyenne peut être considérée comme le « point d'équilibre » (ou centre de gravité) des données. Il prend en compte tous les points de données d'un ensemble de données et fournit une valeur unique qui représente la moyenne. Plus précisément, l'qu'il désigne est calculée en additionnant toutes les valeurs d'un ensemble de données, puis en divisant le résultat par le nombre de valeurs.
Quelle est la médiane ?
La médiane est la valeur centrale lorsque les données sont triées. Contrairement à la moyenne, elle est plus résistante aux valeurs aberrantes, ce qui permet de mieux mesurer la tendance centrale des données asymétriques.
Quel est le mode ?
Le mode est une autre mesure de tendance centrale, représentant la valeur la plus fréquente dans un ensemble de données. Examinons un exemple :
3, 3, 6, 8, 9Ici, le mode est 3 car il apparaît deux fois, tandis que toutes les autres valeurs n'apparaissent qu'une seule fois.
Comment calculer la moyenne et la médiane
Lire une définition est une chose, mais calculer en est une autre. Dans cette section, je vais détailler les étapes de calcul de chaque mesure et mettre en évidence leurs différences computationnelles.
Comment calculer la moyenne
La moyenne est la moyenne arithmétique d'un ensemble de données et se calcule comme suit :
- Veuillez additionner les valeurs : Veuillez additionner tous les nombres de votre ensemble de données.
- Divisez par le nombre total de valeurs : Veuillez prendre la somme totale et la diviser par le nombre de valeurs.
Voici le processus représenté sous forme d'équation générale :
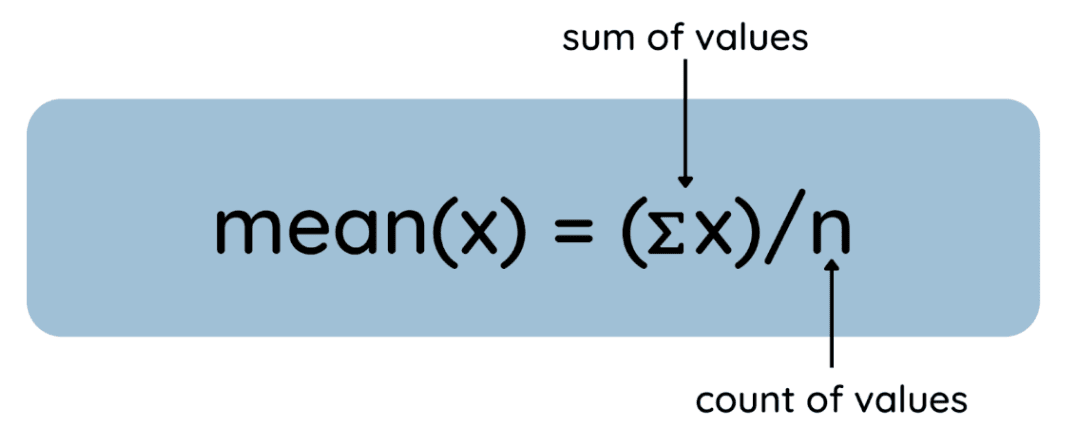
Comment calculer la moyenne. Image par l'auteur
Prenons l'exemple d'un ensemble de données contenant les notes d'examens :
78, 85, 92, 88, 70- Étape 1 (Somme) : 78 + 85 + 92 + 88 + 70 = 413
- Étape 2 (Diviser) : 413 ÷ 5 = 82.6
La note moyenne est de 82,6.
Comment déterminer la médiane
La médiane est la valeur centrale d'un ensemble de données classées par ordre croissant. Voici comment le localiser :
- Trier les données : Veuillez classer les valeurs de la plus petite à la plus grande.
- Identifier la valeur moyenne : Si l'ensemble de données contient un nombre impair de valeurs, la médiane est la valeur du milieu ; si l'ensemble de données contient un nombre pair de valeurs, la médiane est la moyenne des deux valeurs du milieu.
Voici ces étapes représentées sous forme d'équations :
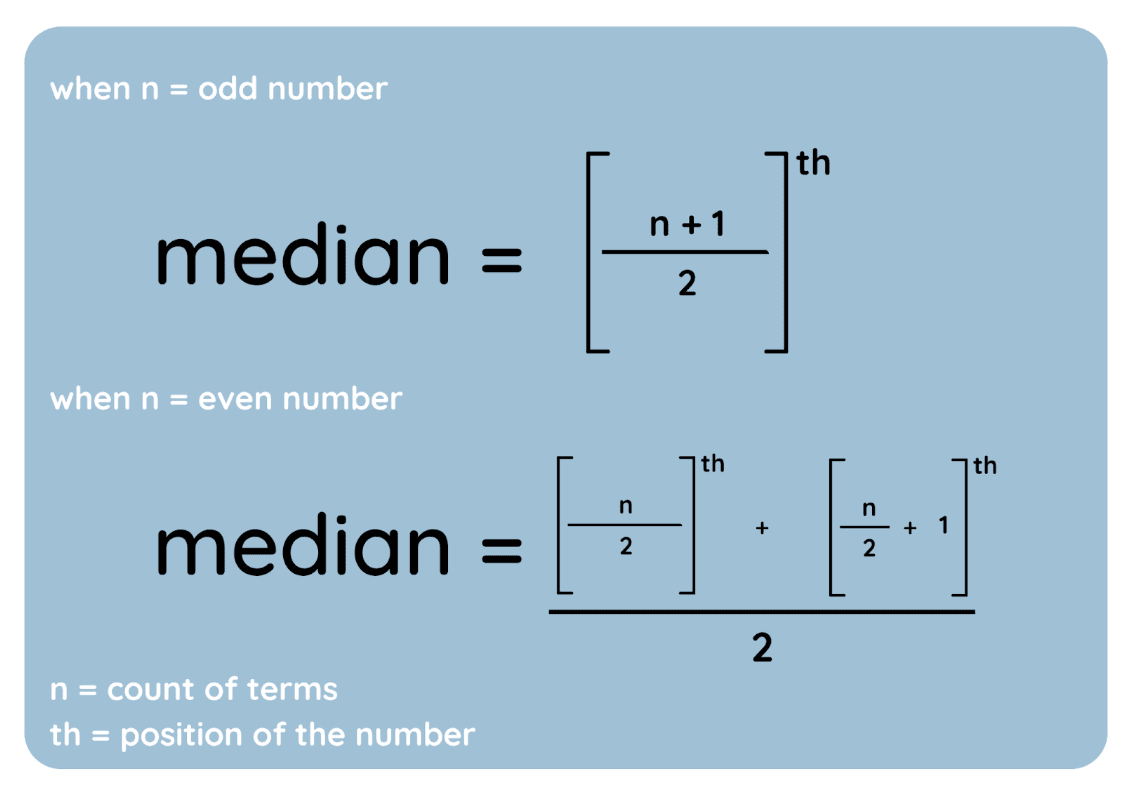
Formule médiane. Image par l'auteur
J'ai également créé un visuel pour illustrer le processus.
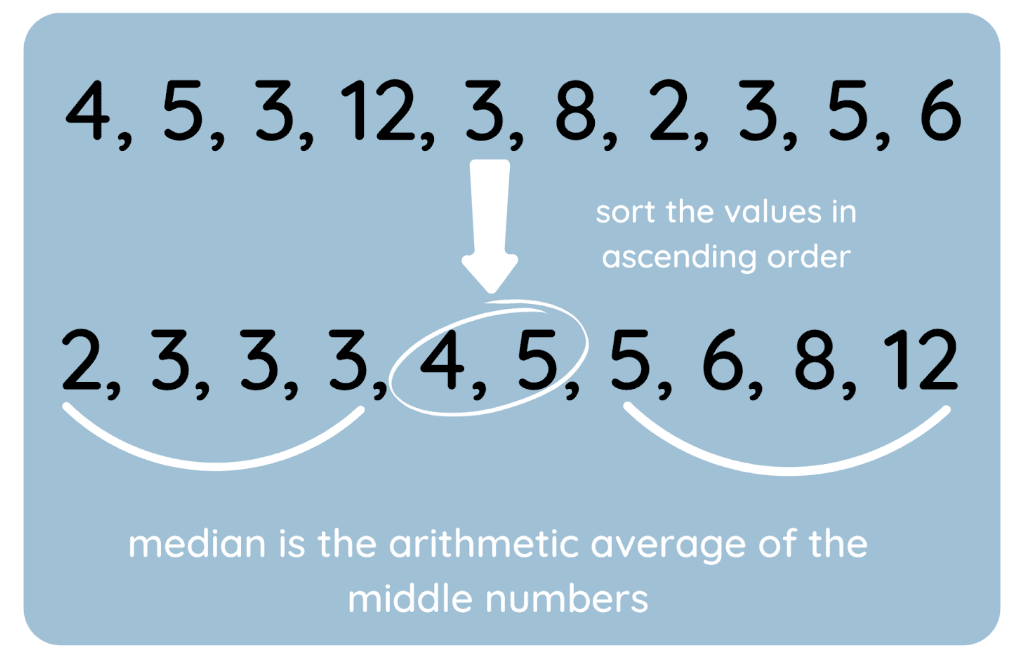
Comment déterminer la médiane. Image par l'auteur
Voici un exemple d'ensemble de données comportant un nombre impair de valeurs :
70, 78, 85, 88, 92- Étape 1 (Trier) : Déjà réglé.
- Étape 2 (valeur moyenne) : La troisième valeur est 85.
La médiane est de 85.
Voici un autre exemple, mais avec un nombre pair de valeurs :
70, 78, 85, 88- Étape 1 (Trier) : Déjà réglé.
- Étape 2 (Moyenne des valeurs intermédiaires) : (78 + 85) ÷ 2 = 81,5
La médiane est de 81,5.
Pourquoi cette différence est-elle importante ? Valeurs aberrantes et asymétrie
Bien que la moyenne et la médiane décrivent toutes deux le centre d'un ensemble de données, leur comportement diverge considérablement en présence de valeurs aberrantes et de distributions asymétriques. Il est essentiel de bien comprendre cette distinction afin d'interpréter correctement les données et d'éviter de tirer des conclusions trompeuses.
Impact des valeurs aberrantes
Les valeurs aberrantes sont des valeurs qui sont significativement plus élevées ou plus basses que le reste des données. Ils peuvent fortement influencer la moyenne, mais ont peu ou pas d'effet sur la médiane.
Examinons un ensemble de données sur les revenus mensuels (en milliers) :
3, 3.5, 4, 4.5, 5, 6, 50Le revenu moyen ici est de 10,85 k, ce qui est fortement influencé par la valeur extrême de 50 000.
D'autre part, la valeur médiane est de 4,5 k, ce qui, selon moi, représente beaucoup mieux le revenu de ce groupe.
Distributions asymétriques
La moyenne et la médiane diffèrent également dans leur représentation des données dans les distributions asymétriques (ensembles de données qui ne sont pas symétriques).
Par exemple, dans les distributions asymétriques à droite (par exemple, les revenus ou les prix de l'immobilier), la plupart des valeurs sontdans les distributions asymétriques à droite (par exemple, les revenus ou les prix de l'immobilier), la plupart des valeurs sont regroupées dans la partie inférieure, avec quelques valeurs extrêmes tirant la queue vers la droite.
- Moyenne : Décalage vers la queue, entraînant une valeur supérieure à la médiane.
- Médiane : Reste plus proche du groupe de valeurs typiques, reflétant mieux le cas « typique ».
Veuillez considérer les revenus :
30k, 35k, 40k, 45k, 50k, 100k, 200k- Moyenne : 71,4 k (augmentation de 100 k et 200 k).
- Médiane : 45 000 (plus proche de la majorité des revenus).
Pourquoi est-ce important ?
- Dans les données asymétriques : La médiane est souvent plus représentative d'un point de données « typique » car elle n'est pas influencée par les valeurs extrêmes.
- Dans les données symétriques : La moyenne et la médiane seront pratiquement identiques, donc l'une ou l'autre peut être utilisée comme mesure de tendance centrale.
Il est essentiel de toujours examiner la distribution de vos données avant de décider d'utiliser la moyenne ou la médiane. Des outils tels que les histogrammes et les graphiques à boîtes à moustaches peuvent aider à visualiser l'asymétrie et à identifier les valeurs aberrantes. Nous aborderons ces points ultérieurement. Je tiens également à souligner que l'examen de la différence entre la moyenne et la médiane constitue une méthode d'évaluation de l'asymétrie.
Quand utiliser la moyenne ou la médiane
Lors de l'analyse des données, le choix entre la moyenne et la médiane dépend des caractéristiques de votre ensemble de données et des informations que vous souhaitez en tirer. Vous trouverez ci-dessous un tableau de référence rapide pour vous aider dans votre choix :
| Utilisez la moyenne lorsque | Utilisez la médiane lorsque |
|---|---|
| La distribution des données est approximativement normale (symétrique). | Les données sont fortement asymétriques (par exemple, revenus, valeur des biens immobiliers). |
| Les valeurs aberrantes sont minimes ou sans importance pour l'analyse. | Des valeurs aberrantes sont présentes et pourraient fausser les résultats si elles étaient incluses. |
| Il est nécessaire de disposer d'une mesure sensible à chaque point de données, par exemple dans la modélisation prédictive ou lors du calcul de totaux. | Vous souhaitez refléter la valeur « typique » plutôt que le « centre mathématique » de l'ensemble de données. |
Voici un conseil pratique qui vous sera très utile : Commencez toujours par une analyse visuelle de vos données (par exemple, un histogramme ou un graphique en boîte) afin de vérifier la symétrie, l'asymétrie et la présence de valeurs aberrantes. Cela vous aidera à déterminer si la moyenne ou la médiane convient le mieux à votre situation.
Visualisation de la moyenne par rapport à la médiane
Les visualisations constituent des outils efficaces pour appréhender le comportement de la moyenne et de la médiane dans différents ensembles de données. Ils peuvent clairement démontrer comment ces mesures répondent aux valeurs aberrantes et aux distributions asymétriques, contribuant ainsi à éclairer la prise de décisions fondées sur les données.
exemple de graphique à barres
Veuillez considérer un petit ensemble de données sur les revenus en milliers :
30, 35, 40, 45, 50, 55, 1000Le graphique à barres suivant montre comment une seule valeur extrême peut considérablement influencer la moyenne, tout en laissant la médiane relativement stable. Dans ce cas, la plupart des points de données se situent entre 30 et 55, mais la présence d'une valeur aberrante (1000) tire la moyenne vers le haut.
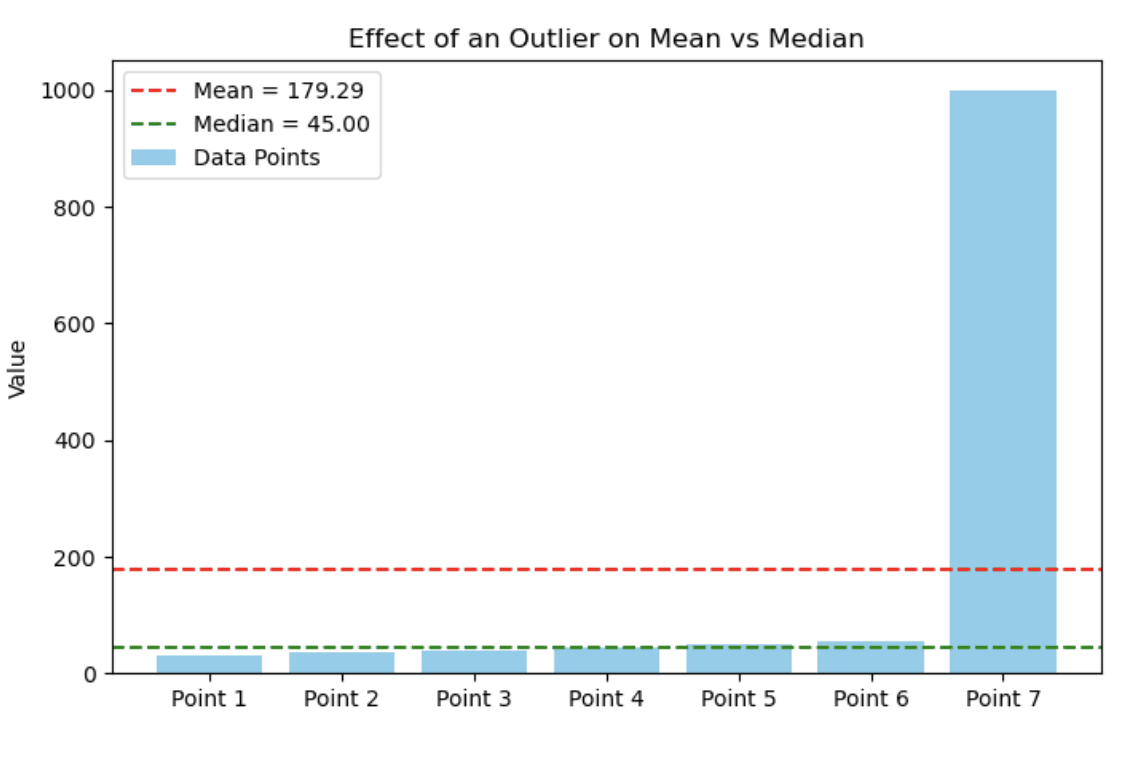
Graphique à barres illustrant l'impact d'une valeur aberrante sur la moyenne par rapport à la médiane. Image par l'auteur
Exemple d'histogramme
Dans une distribution asymétrique à droite (comme les revenus ou les prix de l'immobilier), la moyenne est souvent tirée vers la longue queue des valeurs élevées, tandis que la médiane reste plus proche du point de données « typique ». Dans de tels cas, la médiane constitue donc une meilleure mesure de la tendance centrale.
L'histogramme ci-dessous présente une distribution simulée des revenus où la moyenne (ligne pointillée rouge) est nettement supérieure à la médiane (ligne pointillée verte) en raison de l'asymétrie.
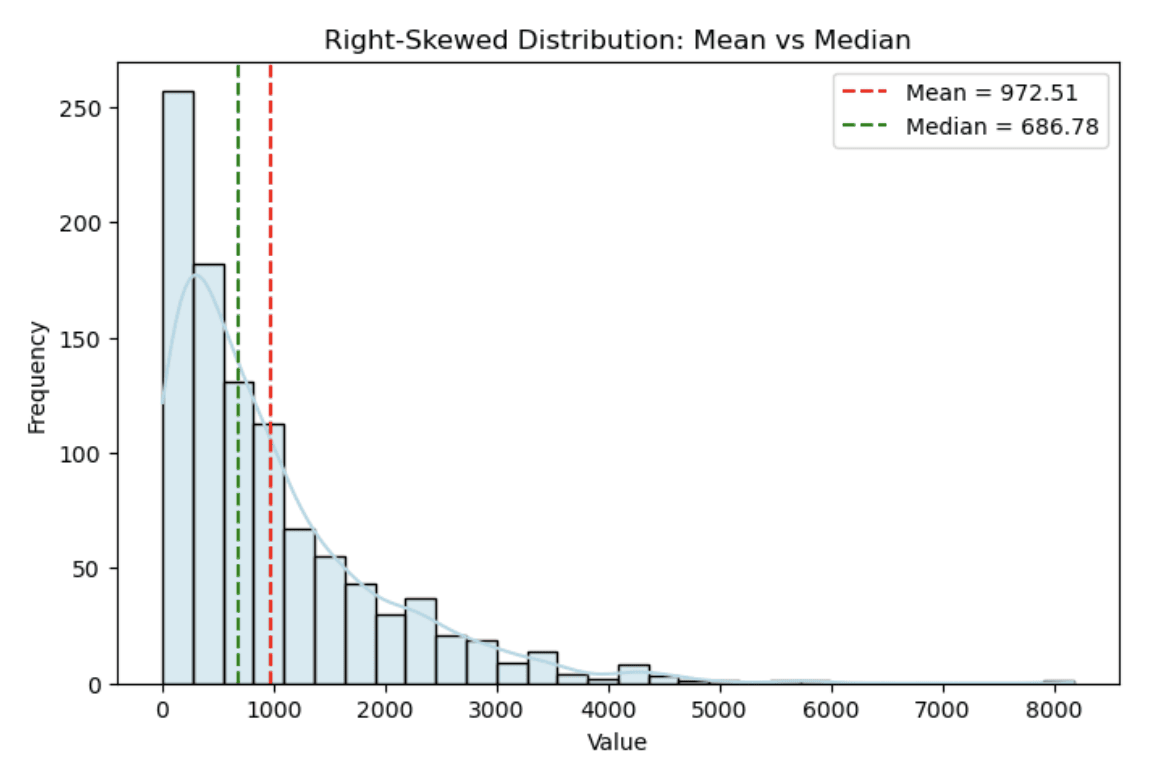
Histogramme illustrant une distribution asymétrique à droite. Image par l'auteur
Vous pouvez observer comment l'asymétrie à droite étire la queue, créant une différence nette entre la moyenne et la médiane.
Exemple de graphique en boîte
Un graphique en boîte est un excellent moyen de visualiser l'impact des valeurs aberrantes sur la médiane. Ci-dessous, nous comparons deux groupes : l'un avec des valeurs aberrantes et l'autre sans. La médiane (ligne verticale à l'intérieur de la boîte) reste stable même en présence de valeurs extrêmes, mais la plage globale des données est fortement influencée par la valeur aberrante.
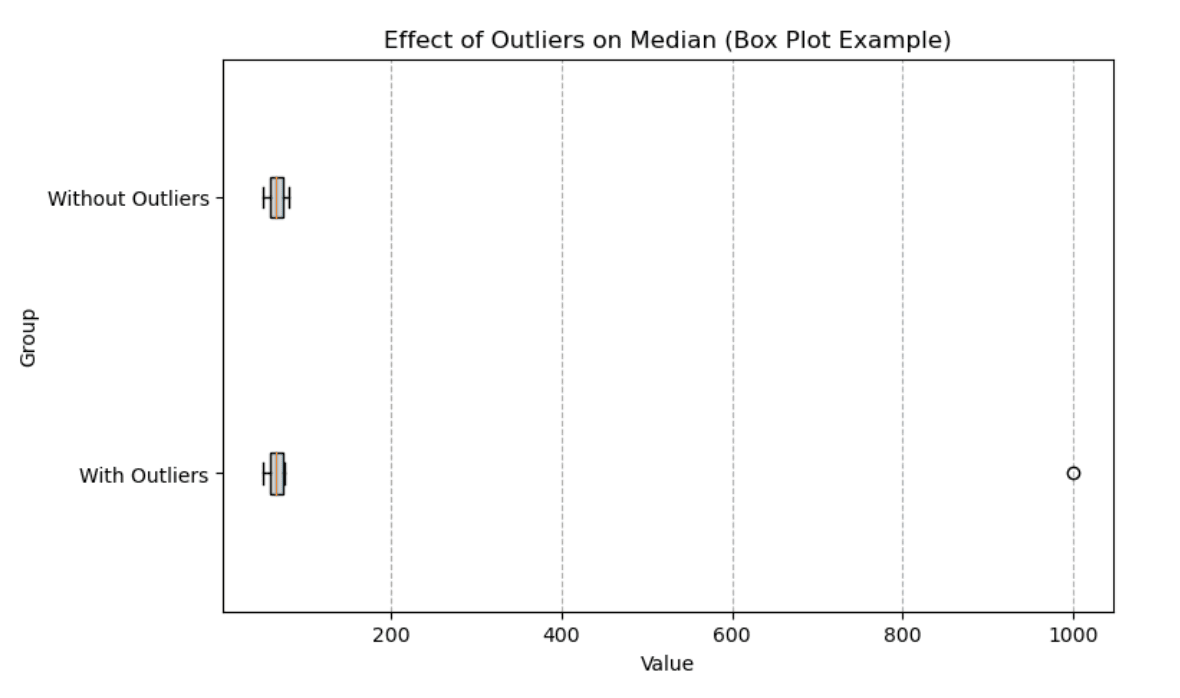
Graphique en boîte illustrant l'impact des valeurs aberrantes sur la médiane. Image par l'auteur
Ces visualisations mettent en évidence la manière dont la moyenne et la médiane réagissent à différentes caractéristiques des données, ce qui permet de mieux comprendre quand utiliser chacune de ces mesures. Qu'il s'agisse d'analyser des données asymétriques, des ensembles de données sujets aux valeurs aberrantes ou de comparer des groupes, ces aides visuelles peuvent faciliter la compréhension de relations complexes.
Sujets avancés et meilleures pratiques modernes
Si vous souhaitez approfondir vos connaissances, nous allons maintenant examiner quelques concepts plus avancés.
Imputation de la moyenne et de la médiane
Si vous êtes data scientist et que vous devez combler des lacunes dans vos données, vous devrez peut-être choisir une méthode d'imputation. Vous vous demandez peut-être quelle est la différence pratique entre l'imputation par la moyenne et l'imputation par la médiane.
Comme vous pouvez le deviner, l'imputation de la moyenne remplace les valeurs manquantes par la moyenne des données disponibles, qui, comme nous l'avons mentionné, peut être faussée par des valeurs extrêmes. L'imputation médiane, quant à elle, remplace les valeurs manquantes par la valeur médiane de l'ensemble de données.
Une règle empirique utile consiste à examiner la distribution de vos données. Si votre distribution de données était asymétrique avec de nombreuses valeurs manquantes et que vous aviez utilisé l'imputation de la moyenne, vous auriez pu modifier la distribution de vos données.
, mais il convient également de garder à l'esprit que l'imputation à valeur unique (moyenne ou médiane) peut réduire la variance et affaiblir les relations entre les variables. Si les données manquantes sont importantes, envisagez l'imputation multiple ou l'imputation basée sur un modèle afin de mieux préserver l'incertitude et la structure.
Méthodes paramétriques et basées sur le classement
Dans de nombreuses méthodes paramétriques, la moyenne (et la variance) sont des paramètres centraux. Par exemple, un modèle de régression linéaire simple suppose que les erreurs sont normalement distribuées autour d'une moyenne. Lorsque vos données satisfont à l'hypothèse de normalité, la moyenne de l'échantillon constitue un estimateur naturel et s'intègre bien dans les cadres paramétriques.
Aujourd'hui, la médiane est fréquemment utilisée dans des contextes robustes et non paramétriques, et constitue un choix courant lorsque les données sont asymétriques ou contiennent des valeurs aberrantes. De nombreux tests, comme le test de Mann-Whitney, sont basés sur les rangs et comparent les distributions (souvent interprétées comme un déplacement de localisation sous certaines hypothèses) plutôt que les moyennes, et ils ne testent pas toujours la différence entre les médianes.
Tout cela pour dire que comprendre la distinction entre la moyenne et la médiane ne sert pas seulement à décrire correctement les données, mais est également important dans le cadre des tests d'hypothèses.
Stabilité bootstrap pour la moyenne et la médiane
Lorsqu'il s'agit de déterminer s'il convient d'utiliser la moyenne ou la médiane, une question essentielle est de savoir dans quelle mesure nos statistiques sont stables pour un ensemble de données donné. Le bootstrapping est une option qui nous permettrait d'estimer empiriquement la distribution d'échantillonnage de la moyenne et de la médiane en rééchantillonnant de manière répétée (avec remplacement) à partir des données originales.
Vous pourriez mettre en évidence les différences de stabilité moyenne et médiane de manière empirique. Il serait possible d'introduire quelques valeurs aberrantes dans un ensemble de données, puis de relancer une procédure de bootstrap, ce qui permettrait de montrer visuellement comment la distribution de la moyenne varie de manière plus spectaculaire que celle de la médiane. De plus, le bootstrapping peut rendre cela concret en montrant l'ampleur potentielle de vos intervalles de confiance dans des scénarios réalistes. Veuillez consulter notre tutoriel sur l'application des méthodes bootstrap pour en savoir plus.
Perte au carré et perte absolue
Permettez-moi de vous proposer une autre définition, tout aussi valable : La moyenne est la valeur qui minimise la somme des écarts quadratiques par rapport aux données, tandis que la médiane est la valeur qui minimise la somme des écarts absolus.
Veuillez examiner cette équation :
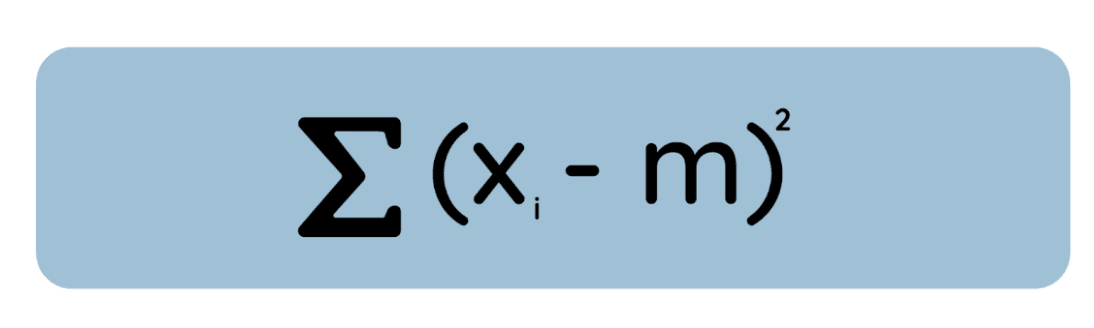
Si vous dérivez cette équation par rapport à , que vous la mettez à zéro et que vous la résolvez, vous constaterez que la valeur minimale est simplement la moyenne arithmétique. Ceci est important car dans de nombreuses méthodes statistiques, telles que la régression OLS, nous minimisons les erreurs quadratiques pour des raisons de commodité mathématique et afin de nous conformer aux hypothèses d'erreurs normalement distribuées.
Maintenant, envisagez une autre perspective : Au lieu de calculer le carré de chaque écart, nous mesurons l'erreurabsolue d' e entre m et chaque point de données :
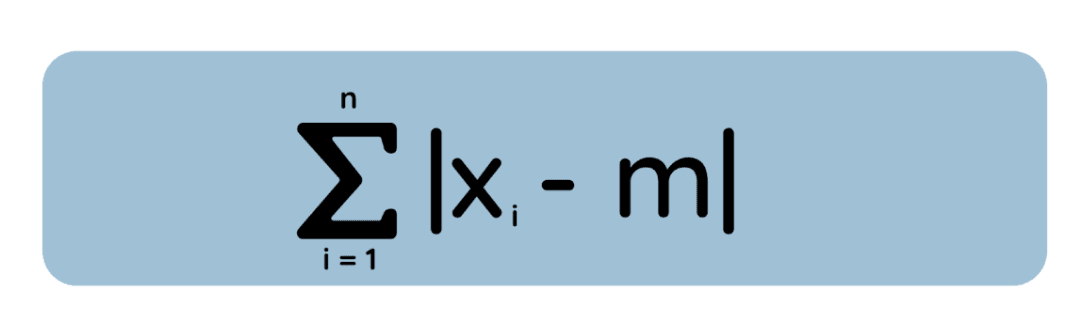
Nous souhaitons déterminer la valeur de m qui minimise cet écart absolu total. Il s'avère (en analysant la dérivée de la perte absolue ou par un argument géométrique) que la solution est lamédiane d' de l'ensemble de données. (Et lorsque vous disposez d'un nombre pair d'observations, toute valeur comprise entre les deux points centraux minimise l'écart absolu total. Par conséquent, le minimiseur peut ne pas être unique.)
Intuitivement, si se trouve à gauche de la médiane, il y a plus de points de données à droite, ce qui l'entraîne à se déplacer. Seule la médiane est le point où les forces exercées à gauche et à droite s'équilibrent, minimisant ainsi la distance absolue totale.
Moyenne et médiane à l'échelle
Enfin, je dirais que la moyenne est plus simple à calculer à grande échelle. Cela signifie que vous pouvez effectuer le calcul de manière incrémentielle à mesure que les données arrivent, sans avoir besoin de les trier.
La médiane est souvent calculée par tri dans la pratique, ce qui peut s'avérer coûteux à grande échelle. Cependant, la médiane ne nécessite pas intrinsèquement un tri complet (il existe des algorithmes de sélection) et, pour les ensembles de données très volumineux ou en continu, des algorithmes d'approximation quantile sont couramment utilisés pour estimer efficacement la médiane. Notre cours « Concepts en informatique » constitue une excellente ressource pour approfondir ces questions.
Étapes suivantes
Comme vous l'avez observé, la moyenne est la moyenne arithmétique d'un ensemble de données, ce qui la rend sensible aux valeurs extrêmes, tandis que la médiane représente la valeur médiane dans un ensemble de données ordonné. Le choix approprié peut faire toute la différence, mais cela dit, dans les analyses du monde réel, il est souvent préférable de rapporter à la fois la moyenne et la médiane, ainsi que des statistiques supplémentaires telles que le mode, l'écart type et les centiles. C'est la meilleure approche car elle offre une vision globale.
Si vous souhaitez approfondir vos connaissances en matière de concepts statistiques, plusieurs domaines méritent votre attention. Commencez par vous informer sur les variantes plus avancées de la moyenne, telles que la moyenne tronquée, la moyenne géométrique et la moyenne pondérée, qui ont chacune leur utilité. Je recommanderais également notre cours d'introduction aux statistiques, qui est indépendant de toute technologie particulière.
Ensuite, pour approfondir vos connaissances, il est recommandé de sélectionner et de maîtriser un outil. Notre cours « Introduction aux statistiques dans R » et notre cursus professionnel « Statisticien dans R » constituent tous deux d'excellents points de départ si vous souhaitez utiliser R, un langage très répandu dans le domaine de la science des données et des statistiques. Si vous préférez travailler avec des feuilles de calcul et un langage de programmation tel que Python, nos cours « Introduction aux statistiques dans Google Sheets » et « Introduction aux statistiques dans Python » offrent une approche pratique de l'analyse statistique à l'aide de formules et de bibliothèques performantes.