Coeficiente de determinação: O que o R-Quadrado nos diz

Imagina que você está tentando prever a nota de alguém em uma prova com base em quantas horas ele estudou. E aí, como tá a sua previsão em relação aos resultados reais? É isso que o coeficiente de determinação, também conhecido como^R² (R-quadrado), nos diz.

Isso mostra quanto da mudança em uma coisa (como notas em provas) pode ser explicada por mudanças em outra (como horas de estudo). Assim, você consegue entender como o seu modelo “se encaixa” nos dados.

Neste artigo, vamos te ajudar a entender o que é^R², por que é importante e como calcular e interpretar, mesmo que você seja novo no mundo da estatística. 

O que é o coeficiente de determinação?

O coeficiente de determinação, geralmente escrito como^R² (R-quadrado), é um número que nos diz o quão bem um modelo de regressão explica o que está acontecendo nos dados. Isso mostra o quanto da mudança no resultado (variável dependente) pode ser explicada pelas coisas que estamos usando para prever isso (variável(is) independente(s)). 

Imagina que você quer adivinhar o peso de alguém com base na altura dele. Se^R² estiver perto de 1, sua previsão está indo muito bem. A maioria das diferenças de peso pode ser por causa das diferenças de altura. Se^R² estiver perto de 0, então sua previsão é basicamente um palpite, porque, nesse caso, a altura não explica muito da mudança no peso.

A gente espera valores^{de R²} entre 0 e 1:

• 0 quer dizer que o modelo não explica nada da variação nos dados.

• 1 significa que o modelo explica toda a variabilidade.

• Valores mais próximos de 1 significam um ajuste melhor, o que mostra que seu modelo está capturando mais do padrão nos dados.

Regressão linear simples

Quando você tá trabalhando só com uma variável independente, o modelo é chamado de regressão linear simples. Nesse caso,^R² tem uma relação direta com o coeficiente de correlação de Pearson (r): R^² = r^²

Isso quer dizer que, se tiver uma forte correlação positiva ou negativa entre o seu preditor e o resultado,^{o R²} vai ser alto.

Observação: Em modelos com mais de um preditor (chamados de regressão múltipla),^R² ainda mostra a variação explicada, mas não é mais só^r², porque agora você está juntando os efeitos de várias variáveis.

O coeficiente de determinação pode ser negativo?

^R² geralmente varia de 0 a 1. Mas, às vezes, você pode ver um R^² negativo^. Isso pode acontecer se:

• Seu modelo não tem uma interceptação (um valor inicial constante).
• Você tá usando o tipo errado de modelo pros dados.

Um^R² negativo quer dizer que seu modelo tá indo pior do que adivinhar a média. Em outras palavras, não combina com os dados de jeito nenhum, o que acaba sendo meio enganador.

Como calcular o coeficiente de determinação

Tem duas maneiras comuns de calcular^{o R²}:

1. Usando a soma dos quadrados
2. Usando o coeficiente de correlação (r)

Vamos ver os dois.

Usando a soma dos quadrados

A fórmula mais comum para^R² é:

Aqui, a soma residual dos quadrados (a parte que não foi explicada) mostra o quanto os valores reais estão longe dos valores previstos pelo seu modelo. É o erro que o seu modelo faz.

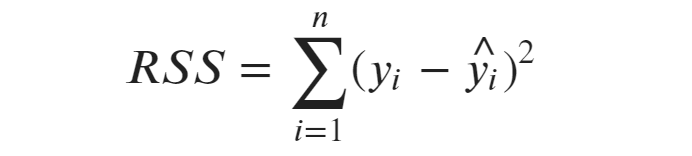
A soma total dos quadrados é a variação total nos dados observados. Isso mostra o quanto os valores reais estão longe da média da variável dependente.

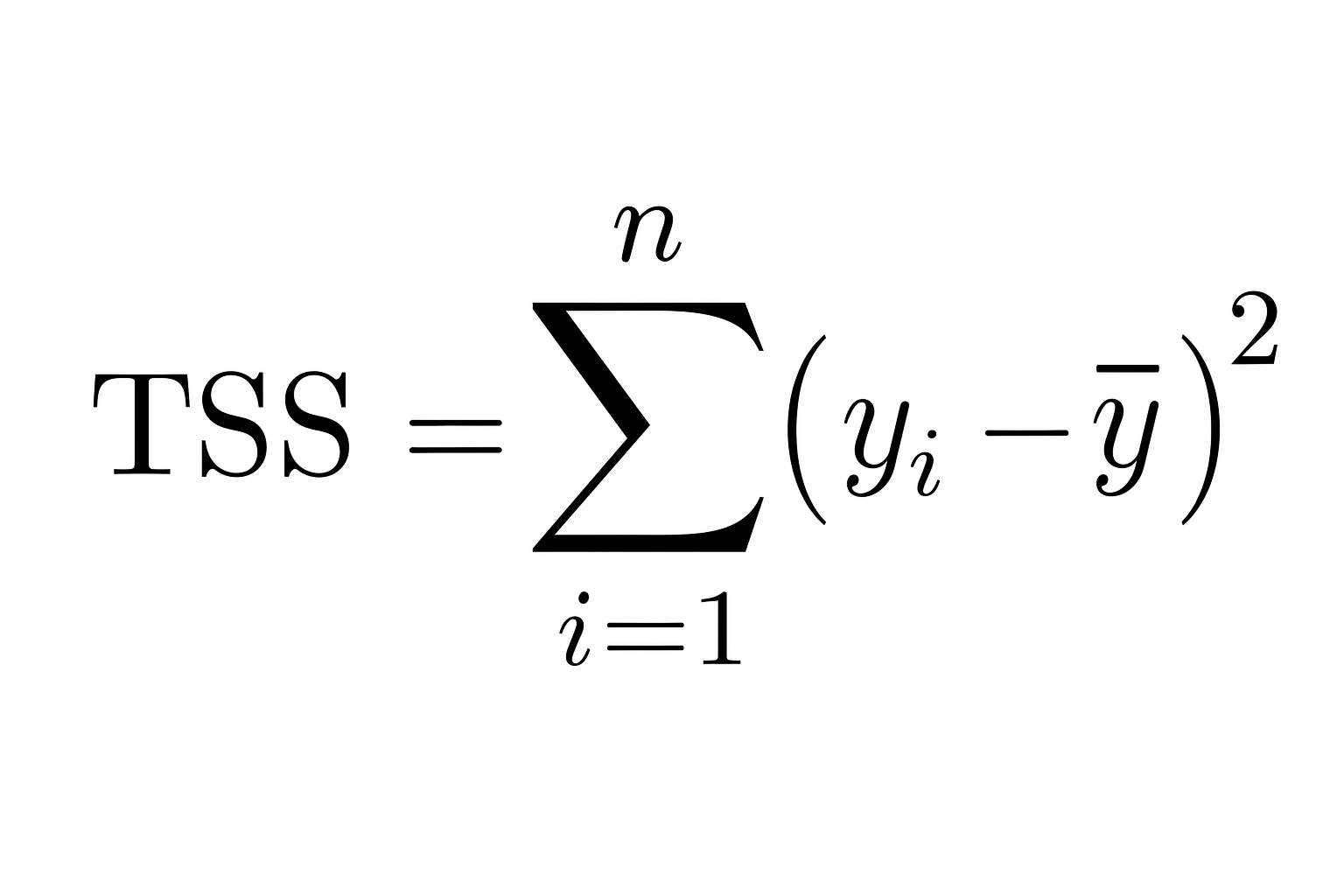
Então, quanto menor a soma dos quadrados residuais em relação à soma dos quadrados totais, melhor o seu modelo se encaixa nos dados e mais próximo de 1 fica^{o R} ².

Vamos entender isso com um exemplo: 

Imagina que você tem um pequeno conjunto de dados com os seguintes valores:

Primeiro, calcula a média dos valores reais:

• y = (10+12+14)/3 = 12

Depois, soma a soma dos quadrados (a distância dos valores reais da média):

• soma dos quadrados total = (10 − 12)² + (12 − 12)² + (14 − 12)² = 4 + 0 + 4 = 8

Depois, calcula a soma dos quadrados residuais (a diferença entre os valores reais e os valores previstos):

• soma residual dos quadrados = (10 − 12)² + (12 − 11)² + (14 − 13)² = 4 + 1 + 1 = 6

Agora, junta isso à fórmula:

• ^R² = 1 − ( soma dos quadrados residuais / soma total dos quadrados) = 1 − (6/8) = 1 − 0,75 = 0,25

Então,^R² = 0,25, o que quer dizer que o modelo explica 25% da variação nos dados.

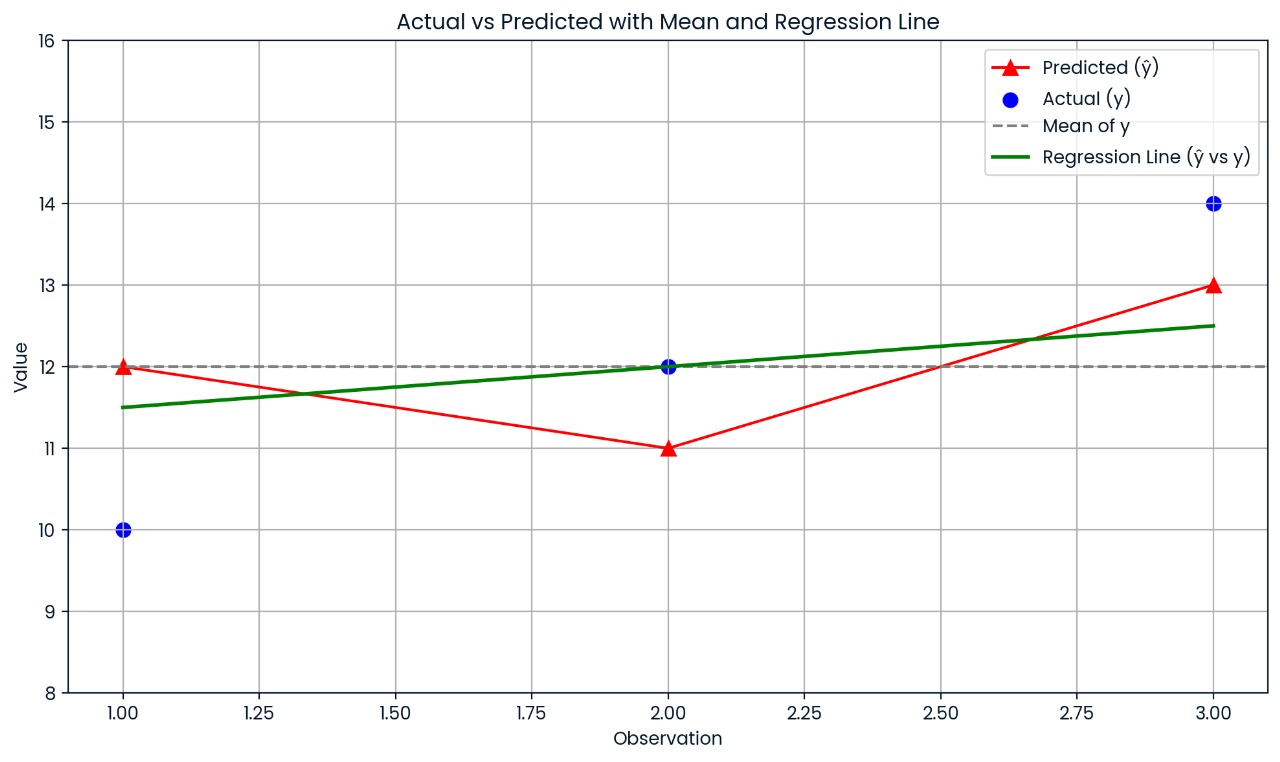
Esse gráfico mostra a distância entre cada valor real e o valor previsto. As previsões do modelo estão bem erradas, e é por isso que o R² é só 0,25; só 25% da variação é explicada.

Usando o coeficiente de correlação

Se você estiver usando regressão linear simples (apenas uma variável independente), use esta fórmula:

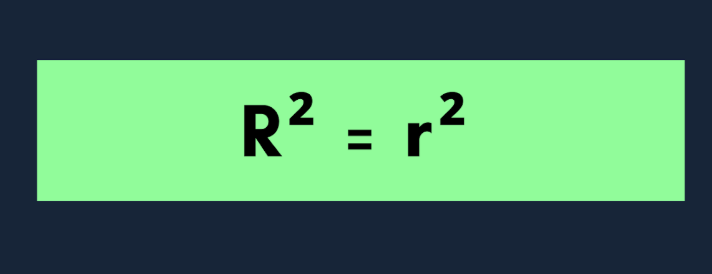
Aqui, r é o coeficiente de correlação de Pearson entre os valores reais e os valores previstos. Esse atalho só funciona quando tem um único preditor.

Digamos que a correlação entre X e Y seja: r = −0,8

Mesmo que a correlação seja negativa (o que significa que as variáveis se movem em direções opostas),^R² é positivo: ^R² = (−0,8)^² = 0,64

Então, 64% da variação no resultado ainda pode ser explicada pelo preditor, mesmo que a relação seja negativa. É por isso que^R² é sempre positivo ou zero; representa a quantidade de variação explicada, não a direção.

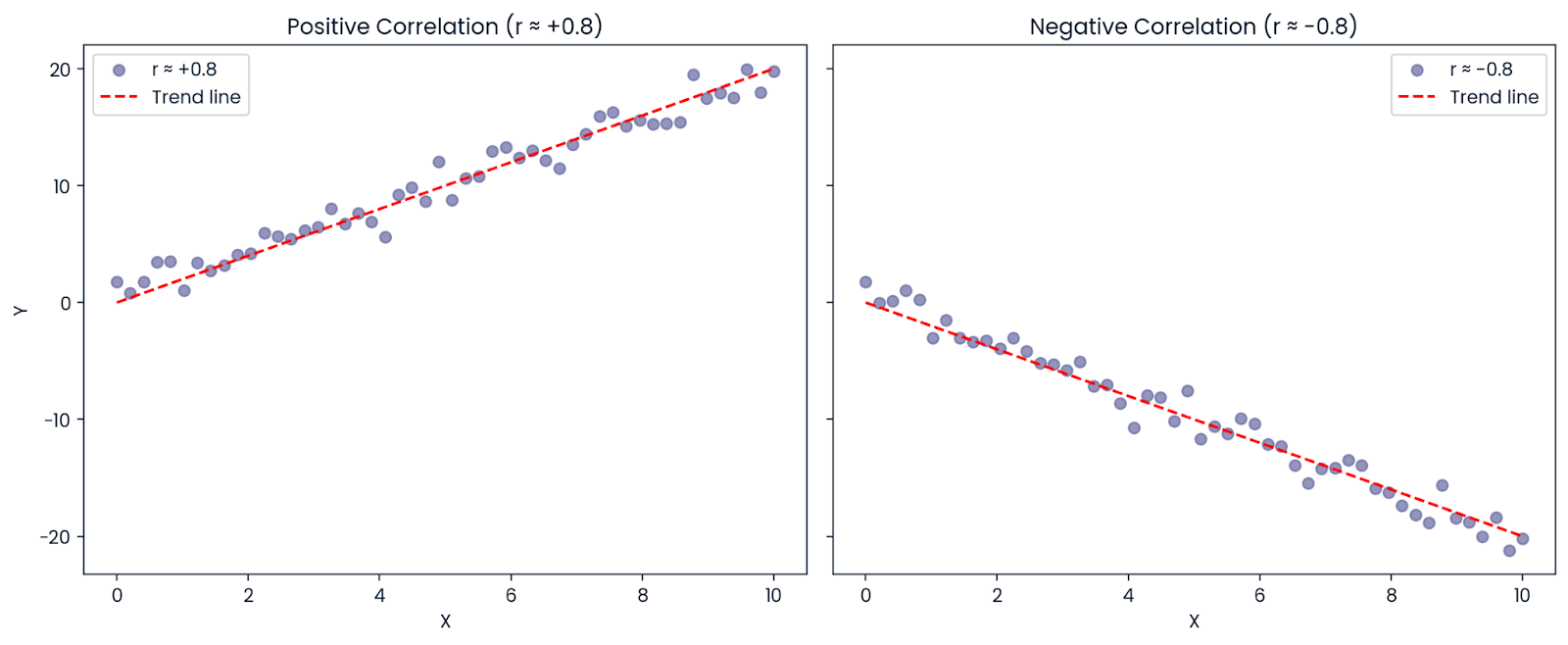
Correlação positiva e negativa. Imagem do autor.

Como interpretar o coeficiente de determinação

O coeficiente de determinação mostra quanto da variação no resultado (variável dependente) é explicada pelo nosso modelo. Em termos simples, é como perguntar: “Quanto das mudanças que estou tentando prever podem ser explicadas pelos dados que estou usando?”

Digamos que você está criando um modelo pra prever as notas dos alunos nos exames com base em quantas horas eles estudam. Se o seu modelo te der: ^R² = 0,90

Isso quer dizer que 90% das diferenças nas notas dos exames podem ser explicadas pelas diferenças no tempo de estudo. Os outros 10% vêm de outros fatores que seu modelo não incluiu, como sono, habilidade natural, conhecimento prévio ou dificuldade do teste.

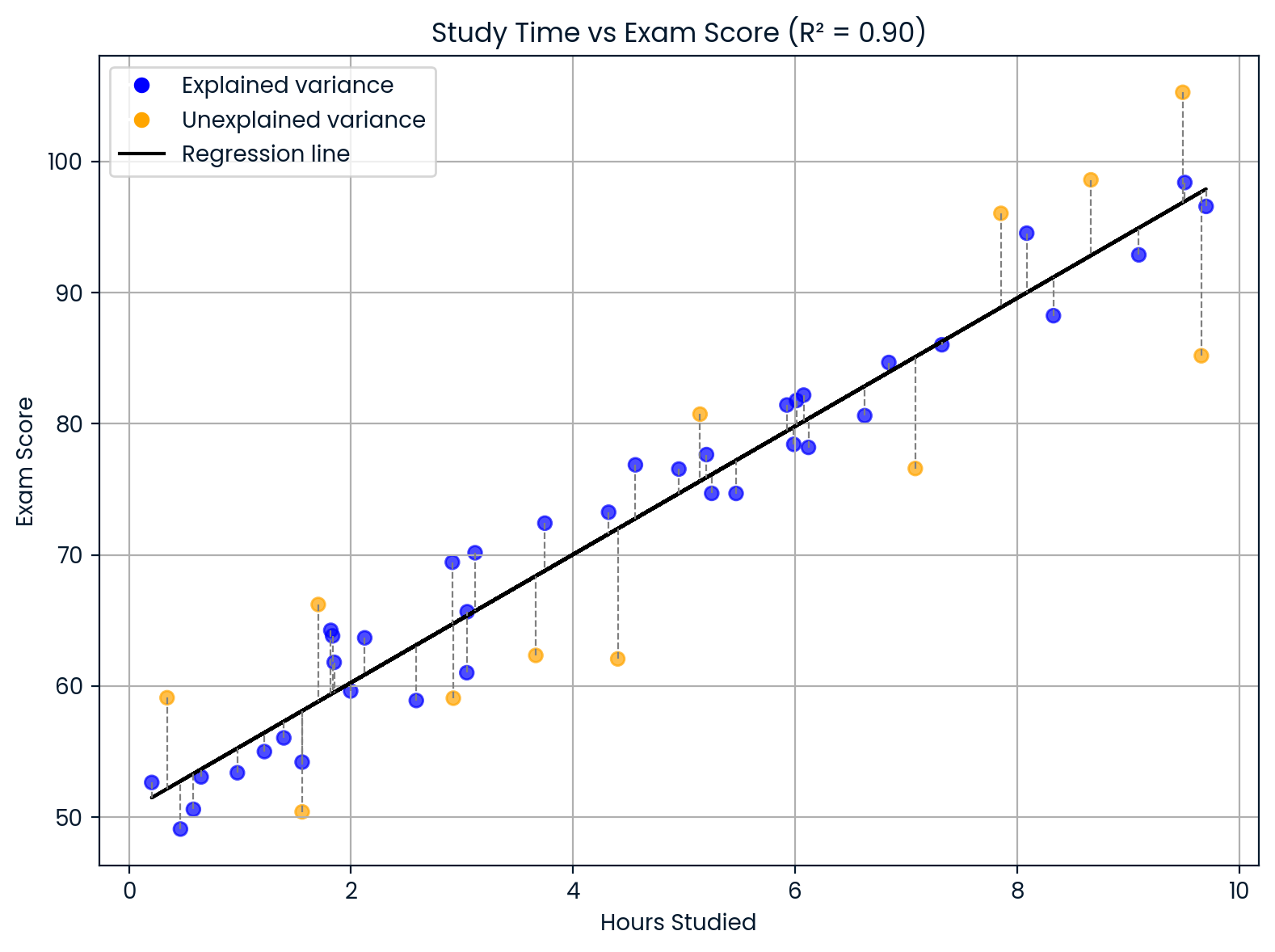
Interpretando o coeficiente de determinação. Imagem do autor.

Esse gráfico mostra como o tempo de estudo afeta as notas dos exames. 

• A linha preta é o que o modelo acha que vai acontecer. 
• Os pontos azuis são as pontuações que o modelo explicou bem usando o tempo de estudo. 
• Os pontos laranja são notas que não batem certo, provavelmente por causa de outros fatores, como sono, dificuldade da prova ou o que o aluno já sabia antes. Como^R² = 0,90, a maioria das pontuações segue o padrão, mas nem todas.

Diretrizes de Cohen

Jacob Cohen criou um guia super útil pra ajudar a entender o que os diferentes valores^{de R²} podem significar quando a gente tá interpretando a força de uma relação.

Aqui estão os parâmetros de referência aproximados de Cohen para^R²:

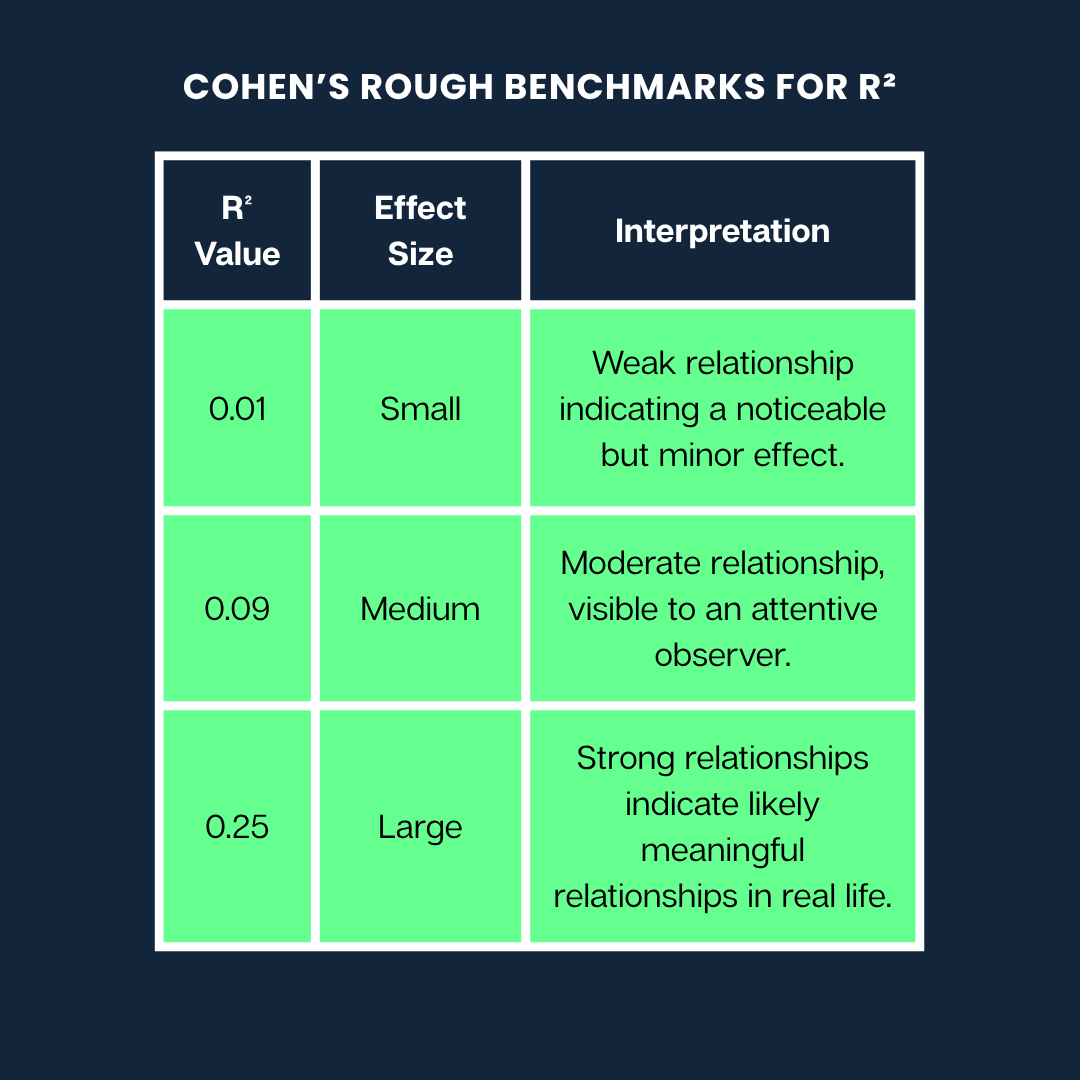
Os parâmetros aproximados de Cohen. Imagem do autor

Observação: Essas são só algumas dicas gerais. O que é considerado um efeito “grande” ou “pequeno” pode variar bastante dependendo da área (por exemplo, psicologia versus engenharia) e do contexto da pesquisa.

Limitações e equívocos comuns

Embora^{o R²} seja útil, é importante entender o que ele pode e não pode dizer. Aqui estão alguns equívocos e limitações comuns a serem observados:

Mito 1: Um coeficiente de determinação alto quer dizer que o modelo é melhor.

Pode parecer que um^R² mais alto sempre significa um modelo melhor, mas isso não é necessariamente verdade. ^{O R²} sempre aumenta ou fica igual quando você adiciona mais variáveis a um modelo, mesmo que essas variáveis não tenham nada a ver com ele. 

Por quê? 

Porque o modelo tem mais flexibilidade para se ajustar aos dados de treinamento, mesmo que seja apenas ajustando ruídos aleatórios. Isso pode fazer com que o modelo fique superajustado, ou seja, ele vai parecer ótimo nos dados que usou pra treinar, mas vai funcionar mal com dados novos.

Dica: Ue o R² ajustado ao comparar modelos com diferentes números de preditores. Isso penaliza a complexidade desnecessária e pode ajudar a detectar o sobreajuste. 

Mito 2: Um coeficiente de determinação alto significa previsões precisas sobre novos dados ou causalidade.

^R² só mede o quão bem o modelo descreve os dados que você já tem. Não diz:

• Se o modelo vai fazer boas previsões com novos dados
• Se uma variável causa a outra

Um^R² alto pode até acontecer por acaso se você estiver usando muitos preditores. Portanto, sempre dê uma olhada em outras métricas de avaliação de modelos (como RMSE ou MAE para qualidade de previsão) e lembre-se: correlação não é causalidade.

Mito 3: Um R-quadrado baixo quer dizer que o modelo não serve pra nada.

Às vezes, em sistemas complexos (como prever o comportamento humano ou os mercados financeiros), é normal ter um^R² baixo.

Por exemplo, se você estiver modelando algo influenciado por muitos fatores imprevisíveis ou não mensuráveis, seu modelo ainda pode ser útil, mesmo com um^R² baixo^. Pode capturar uma tendência importante ou dar uma ideia, mesmo que não explique grande parte da variação.

Em pesquisas médicas ou psicológicas, é comum ver valores baixos^{de R²}, porque os resultados das pessoas dependem de muitas variáveis que interagem entre si.

Outras variantes: R-quadrado parcial e generalizações

Embora^R² ajude a entender como o modelo se encaixa na regressão linear, existem outras variantes e generalizações que ajudam em diferentes contextos de modelagem.

R-quadrado ajustado

Assim como o^R² normal,^{o R²} ajustado mostra quanto da variação na variável dependente é explicada pelo modelo. Mas vai além, penalizando a complexidade desnecessária. Em outras palavras, isso evita que você encha seu modelo com preditores extras que não ajudam em nada.

A fórmula é:

Adjusted R² = 1 - [ (1 - R²) × (n - 1) / (n - p - 1) ]

Aqui:

• n é o número de observações (pontos de dados)

• p é o número de preditores (variáveis independentes)

A fórmula ajusta^{o R²} pra baixo se uma nova variável não melhorar o modelo. Essa penalidade fica mais forte conforme você adiciona mais preditores.

Por exemplo, se você adicionar uma nova variável que melhora a precisão do seu modelo,^{o R²} ajustado vai subir. Mas se essa variável não mudar quase nada ou só ajudar por acaso,^{o R²} ajustado vai cair, te alertando sobre um possível sobreajuste.

Isso torna^{o R²} ajustado útil para comparar modelos.

Digamos que você queira escolher entre um modelo mais simples com três preditores e um mais complexo com seis. Mesmo que o modelo complexo tenha um^R² um pouco maior, o^R² ajustado pode ser menor, o que mostra que não vale a pena ter mais complexidade.

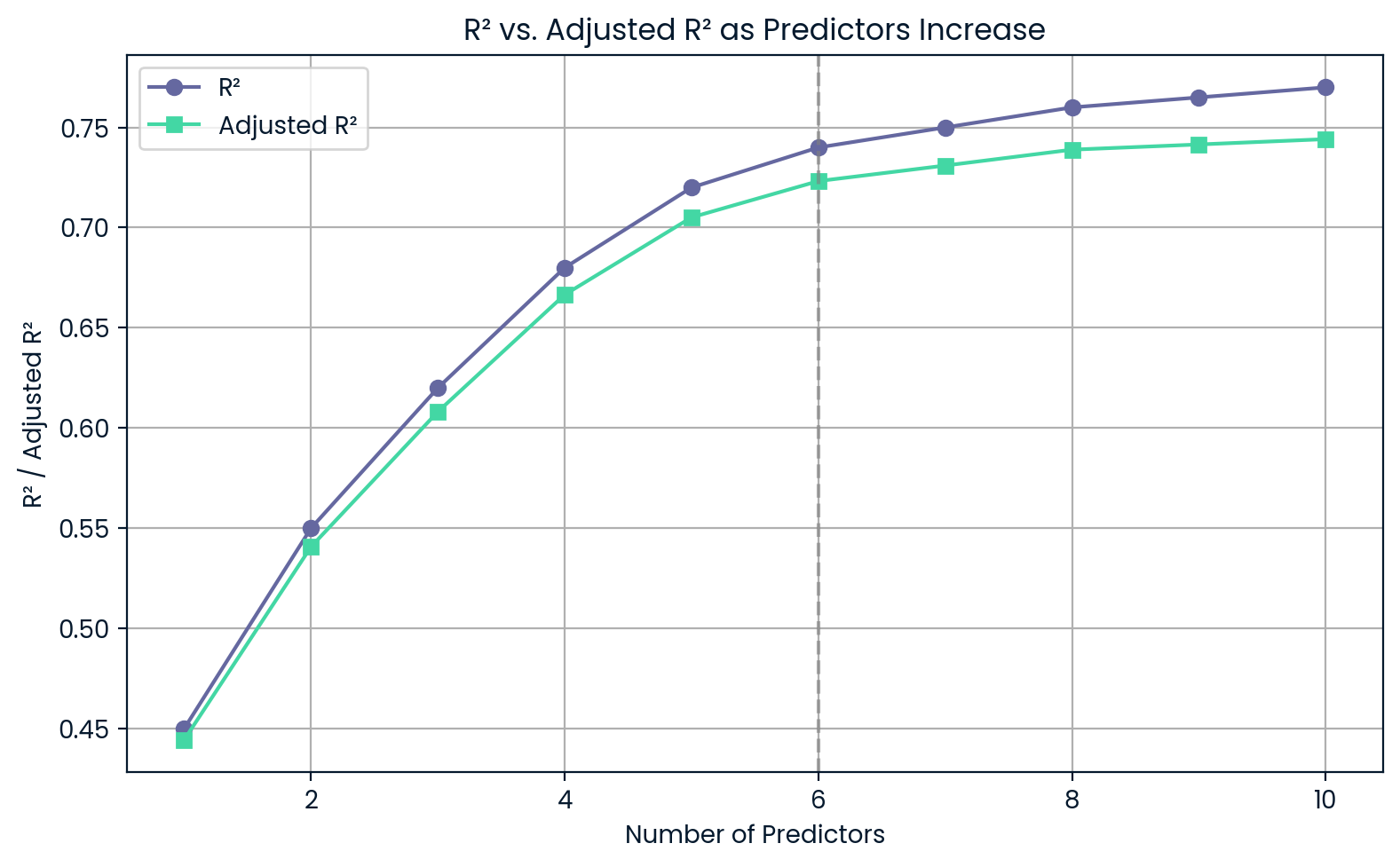
R² versus R² ajustado à medida que os preditores aumentam. Imagem do autor.

Esse gráfico mostra que, conforme você adiciona mais preditores,^{o R²} continua subindo, mesmo que esses preditores não sejam muito úteis. Por outro lado,^{o R²} ajustado cai se você adicionar demais, alertando você sobre o excesso de ajuste.

Coeficiente de determinação parcial

^{O R²} parcial (ou coeficiente de determinação parcial) mostra quanto da variação adicional na variável dependente é explicada ao adicionar um preditor específico a um modelo que já inclui outros.

Para calcular^{o R²} parcial, a gente compara dois modelos:

• O modelo reduzido, que tira o indicador que estamos falando.
• O modelo completo, que inclui todos os indicadores

A fórmula para^{o R²} parcial é baseada na redução da Soma dos Erros Quadrados (SSE) quando a nova variável é adicionada. Uma forma comum é:

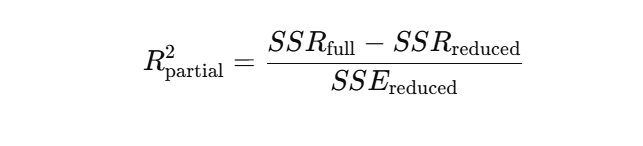
Ou em termos de somas dos quadrados da regressão:

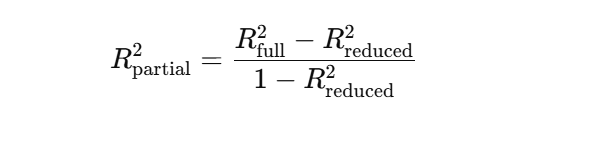
Imagina que você tá criando um modelo pra prever as vendas de um produto. 

Você já tem “preço do produto” e “temporada” no modelo. Agora, você quer ver se adicionar “gastos com marketing” melhora as previsões. O R² parcial mostra quanto mais da variação nas vendas pode ser explicada incluindo os “gastos com marketing”.

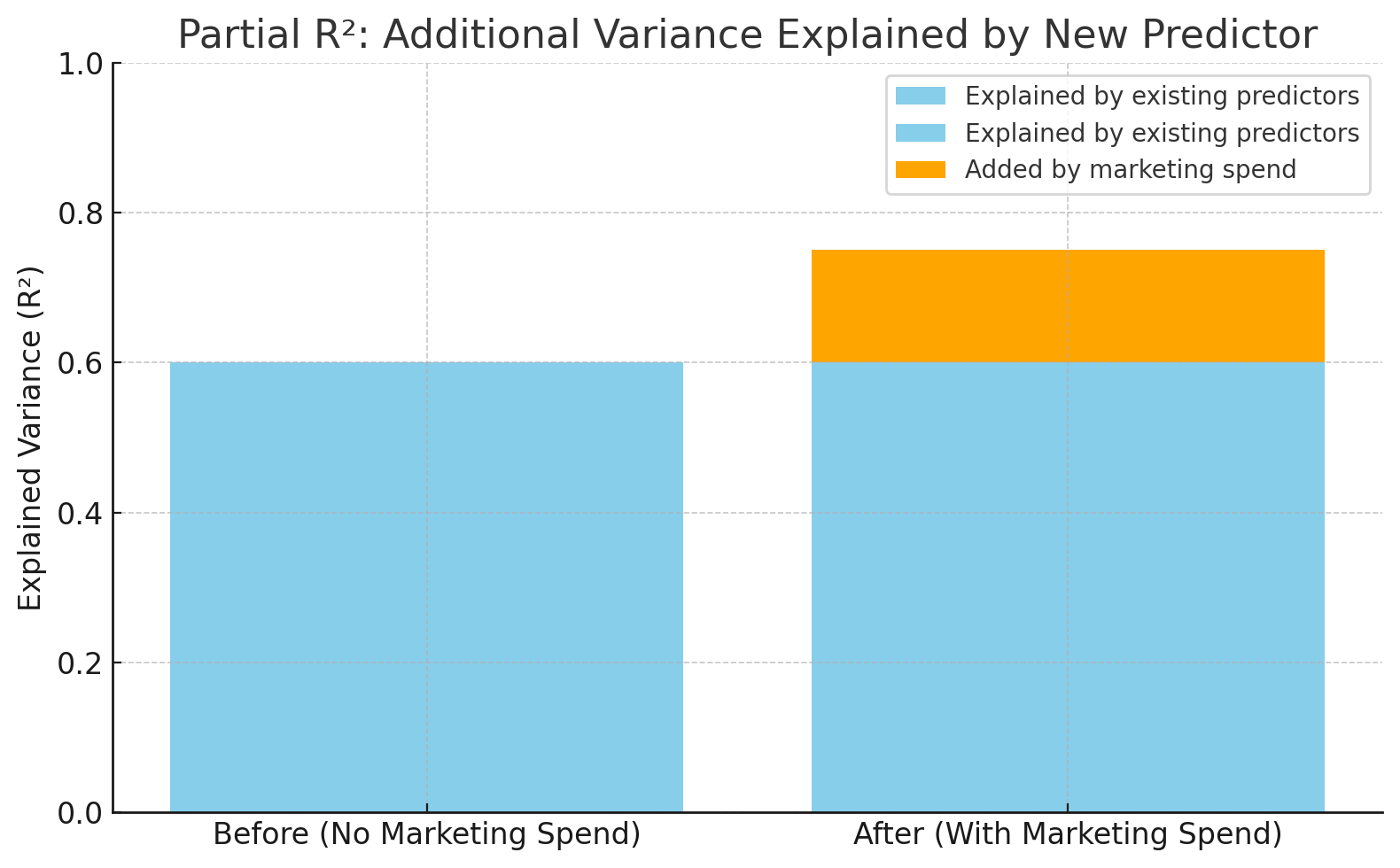
^{O R²} aumentou de 0,60 para 0,75 depois de adicionar os gastos com marketing. Imagem do autor.

Esse gráfico mostra como o modelo fica mais preciso quando a gente adiciona os “gastos com marketing”. ^R² vai de 0,60 para 0,75, o que significa que a nova variável explica 15% a mais da variação nas vendas — isso é o R² parcial^.

Coeficiente de determinação na regressão logística

Na regressão logística, a variável de resultado é categórica, tipo sim/não, aprovado/reprovado, então^{o R²} tradicional não rola. Em vez disso, usamos métricas^pseudo-R², que têm uma função parecida: estimar o quão bem o modelo explica a variação nos resultados.

Dois valores^pseudo-R² comuns são:

• Cox & Snell^R²: As estimativas explicaram a variância, mas o valor máximo é menor que 1, mesmo para um modelo perfeito.
• Nagelkerke R^²: Uma versão corrigida do Cox & Snell^R² que vai até 1, facilitando a interpretação como o R^² tradicional^.

Imagina que você tá tentando descobrir se um cliente vai clicar num anúncio (sim/não). Como o resultado é binário, você não pode usar o R² normal^. Mas valores^pseudo-R², como o de Nagelkerke, ajudam a comparar modelos logísticos e avaliar seu poder preditivo, mesmo que não sejam diretamente equivalentes ao^R² na regressão linear.

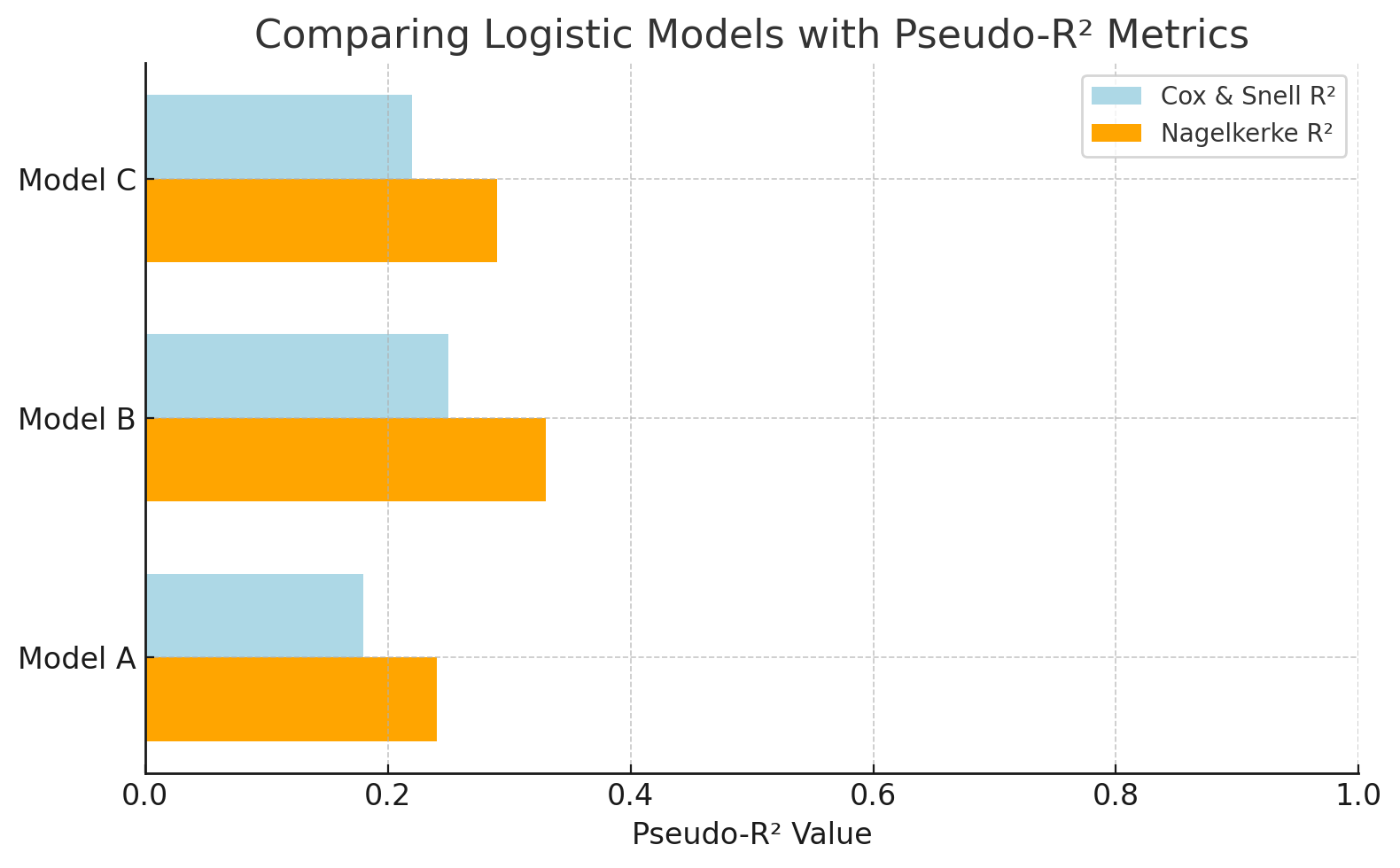
Compare modelos de logística com métricas^pseudo-R ². Imagem do autor.

Este gráfico compara modelos de regressão logística usando valores^pseudo-R ². ^{O R²} de Nagelkerke é uma escala mais fácil de entender do que a de Cox e Snell. Isso facilita a avaliação do desempenho de cada modelo na explicação do resultado (por exemplo, previsão de cliques em anúncios).

Coeficiente de determinação vs. outras métricas de ajuste do modelo

Embora^R² seja útil para entender quanta variação é explicada, ele não mede o quão distantes estão suas previsões. É aí que entram métricas baseadas em erros, como RMSE, MAE e MAPE.

Aqui vai uma comparação rápida:

Aplicações práticas em várias áreas

Agora, vamos dar uma olhada em alguns dos muitos casos em que o coeficiente de determinação foi usado. 

Economia: Explicando as flutuações do PIB

Em economia,^{o R²} é usado pra explicar mudanças em indicadores gerais, tipo o Produto Interno Bruto (PIB). Por exemplo, um modelo pode incluir variáveis como taxas de juros, gastos do consumidor e balanças comerciais para prever o PIB.

Se esse modelo der um^R² de 0.83, quer dizer que 83% da variação no PIB pode ser explicada por esses fatores econômicos. Isso ajuda os economistas a entender quanto das altas e baixas do PIB pode ser atribuído a fatores conhecidos.

Um estudo da Associação Nacional de Centros de Recursos para a Saúde ( ) usou dados do U.S. e do PIB como variável independente para prever o índice S&P 500 e encontrou um^R² de 0.83. Isso mostrou uma forte relação entre a atividade econômica e as tendências do mercado de ações.

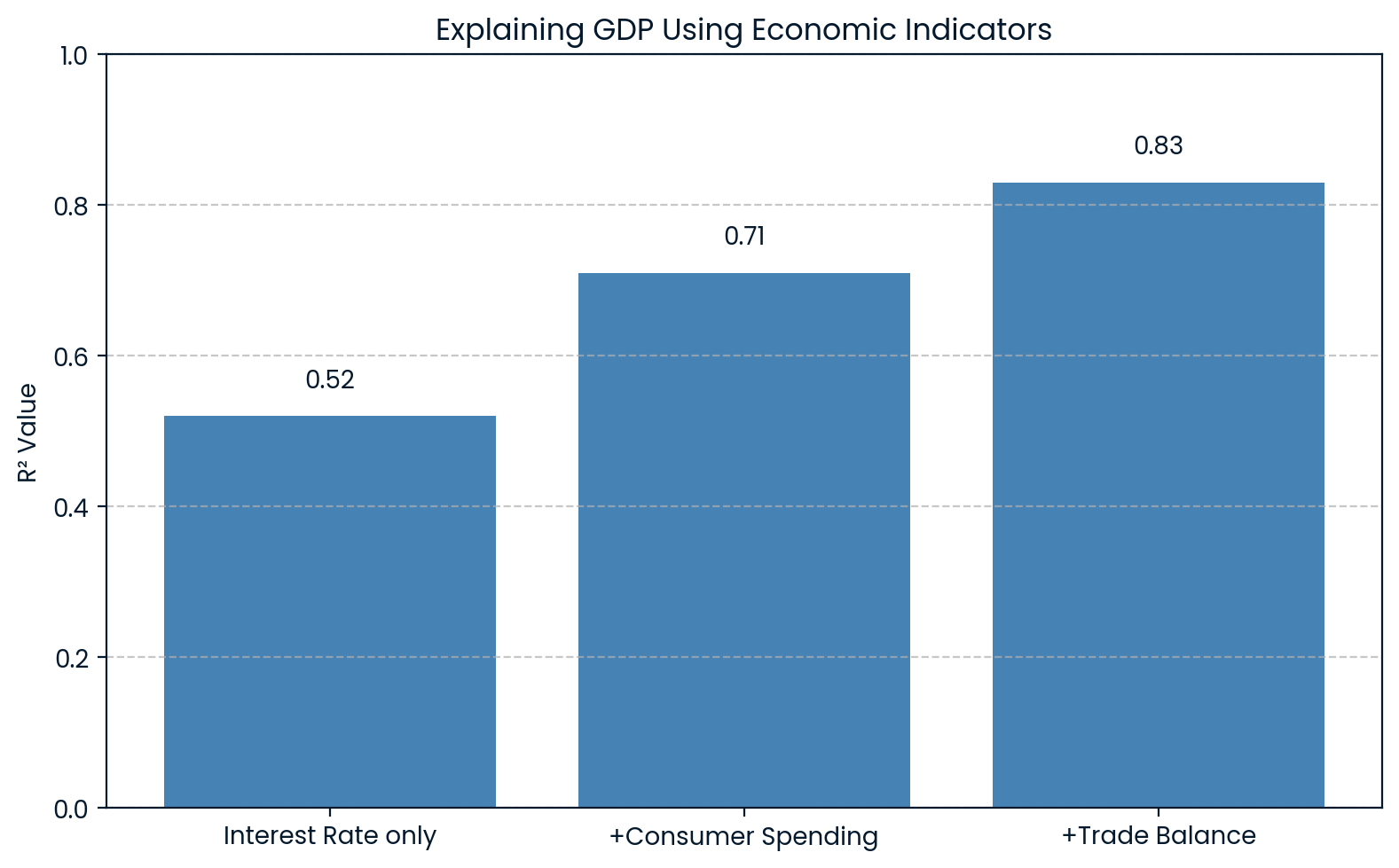
^R² explicando a economia do PIB. Imagem do autor.

O gráfico mostra que, à medida que mais indicadores econômicos são adicionados ao modelo, o^R² aumenta, de 0.52 para 0.83 com todas as três variáveis. Isso deixa claro que cada fator adicionado explica melhor as flutuações no PIB.

Finanças: Movimentação do preço das ações em relação ao índice do mercado

Em finanças,^R² é usado pra medir o quanto os retornos de uma ação são explicados pelos movimentos gerais do mercado. Isso é feito comparando o retorno de uma ação com um índice de mercado, tipo o S&P 500.

Por exemplo, se você comparar os retornos da Apple (AAPL) com o S&P 500 e chegar^{a R²} = 0, 0.82, isso quer dizer que 85% dos movimentos dos retornos da Apple são explicados pelo mercado em geral.

• Um^R² alto mostra que a ação está bem ligada ao mercado.
• Um^R² baixo quer dizer que o estoque é mais independente.

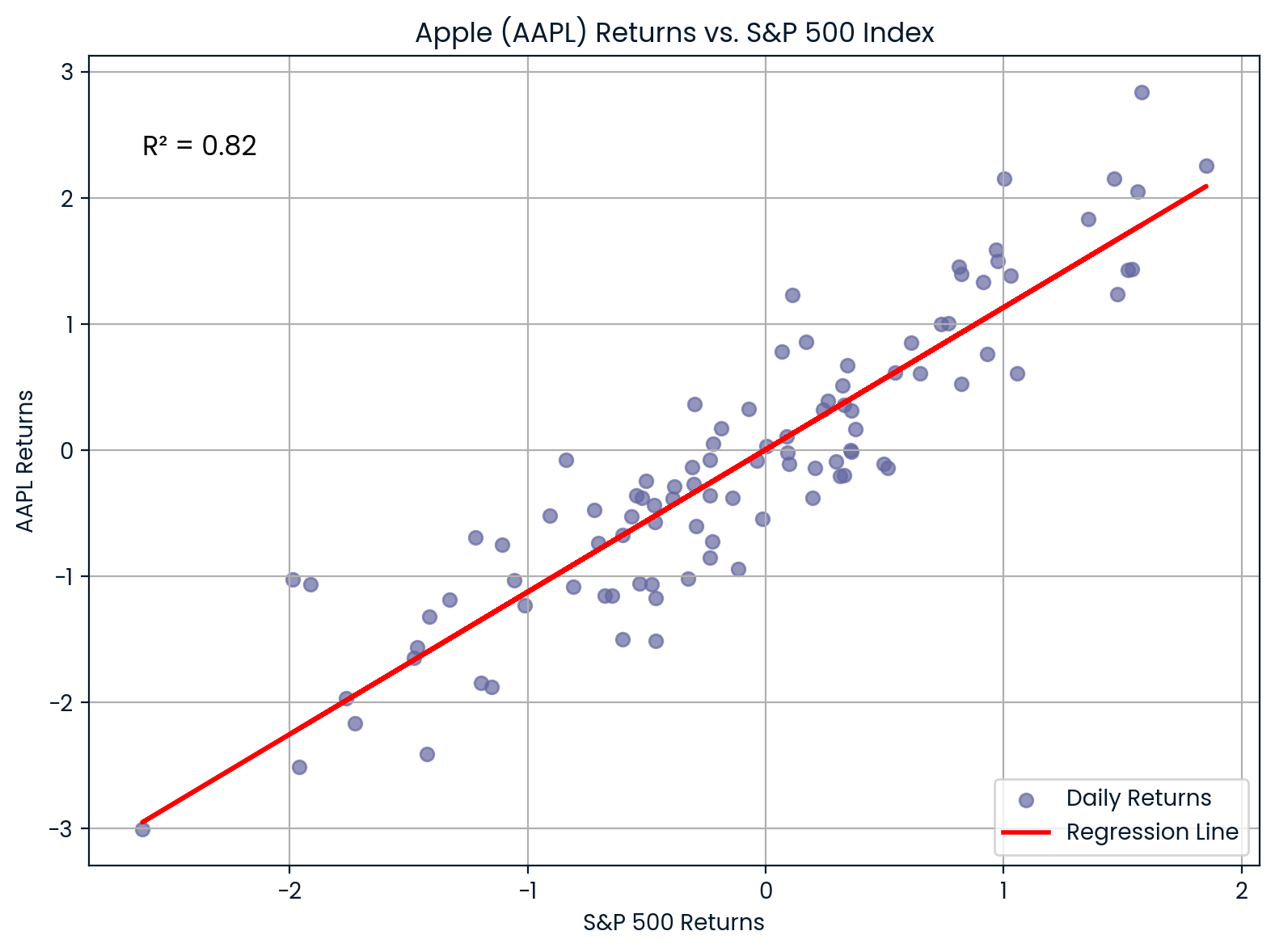
Correlação entre AAPL e S&P 500. Imagem do autor.

O gráfico mostra a forte correlação entre a Apple (AAPL) e o S&P 500. Com um^R² de 0.82, a maioria dos movimentos de preço da Apple está bem alinhada com as tendências do mercado, mostrando uma alta sensibilidade ao mercado.

Marketing: Gastos com publicidade e conversões

No marketing,^R² mostra como os gastos com publicidade explicam as taxas de conversão dos clientes.

Imagina que você trabalha numa empresa de comércio eletrônico e quer saber se aumentar os gastos mensais com publicidade melhora as taxas de conversão. Você faz uma regressão linear e descobre que^R² = 0,98. Isso quer dizer que 98% da variação na taxa de conversão é explicada pelo seu gasto com anúncios, o que mostra uma relação bem forte.

Essas informações ajudam os profissionais de marketing a:

• Previsão dos resultados da conversão
• Justificar orçamentos de publicidade
• Preveja o retorno sobre o investimento (ROI)

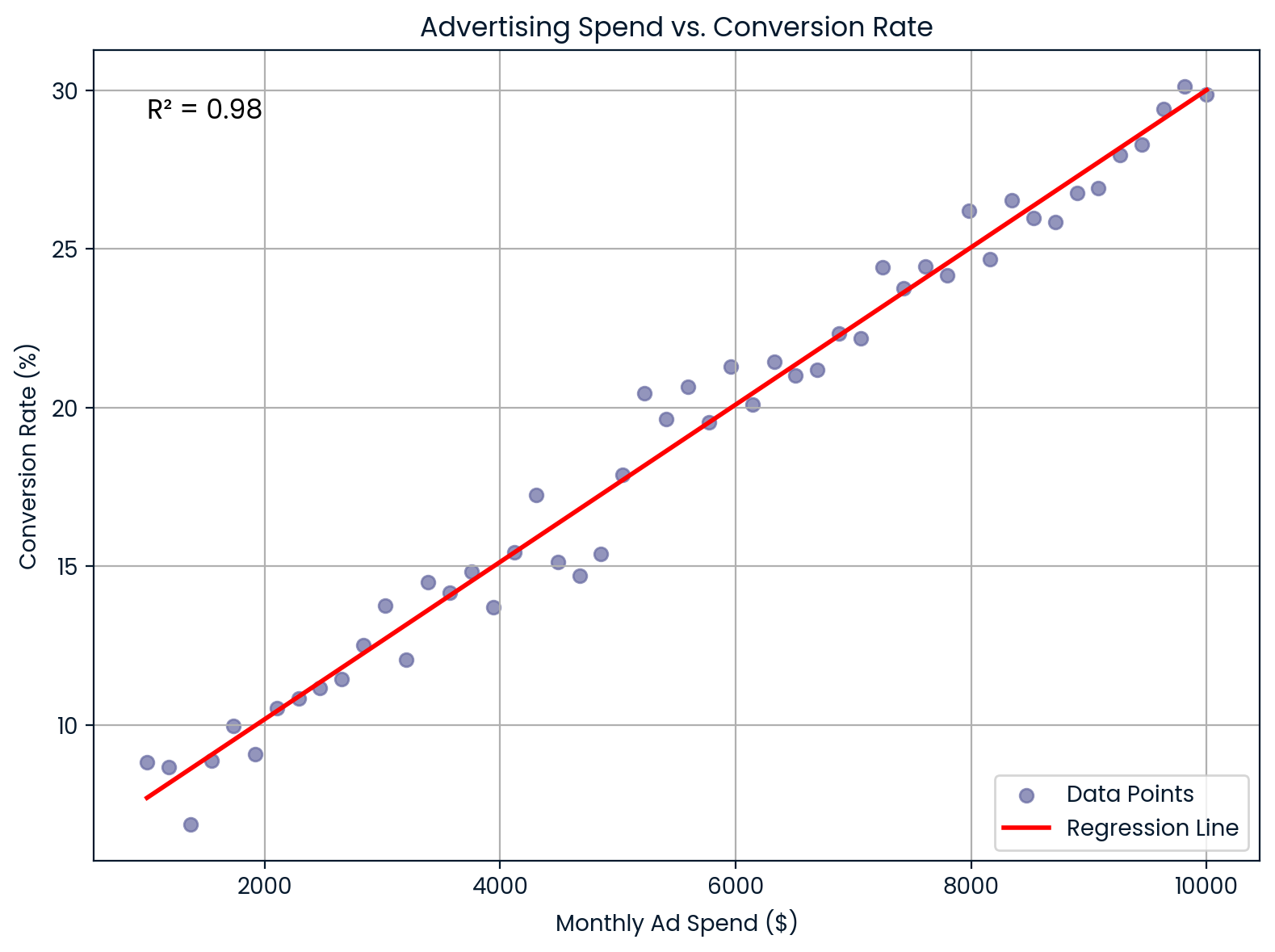
Gastos mensais com publicidade versus taxa de conversão. Imagem do autor.

Esse gráfico mostra uma relação quase perfeita entre os gastos mensais com publicidade e a taxa de conversão. Ele ajuda a prever o retorno do investimento e a planejar o orçamento.

Machine learning: Modelos de regressão de pontuação

No machine learning,^R² é usado como uma métrica de desempenho para tarefas de regressão. Bibliotecas como scikit-learn têm a função r2_score() pra calcular isso.

Isso mostra como o seu modelo explica a variação nos dados:

• ^R² perto de 1 significa um bom ajuste e baixo erro.

• ^R² perto de 0, 0 significa que o ajuste é ruim.

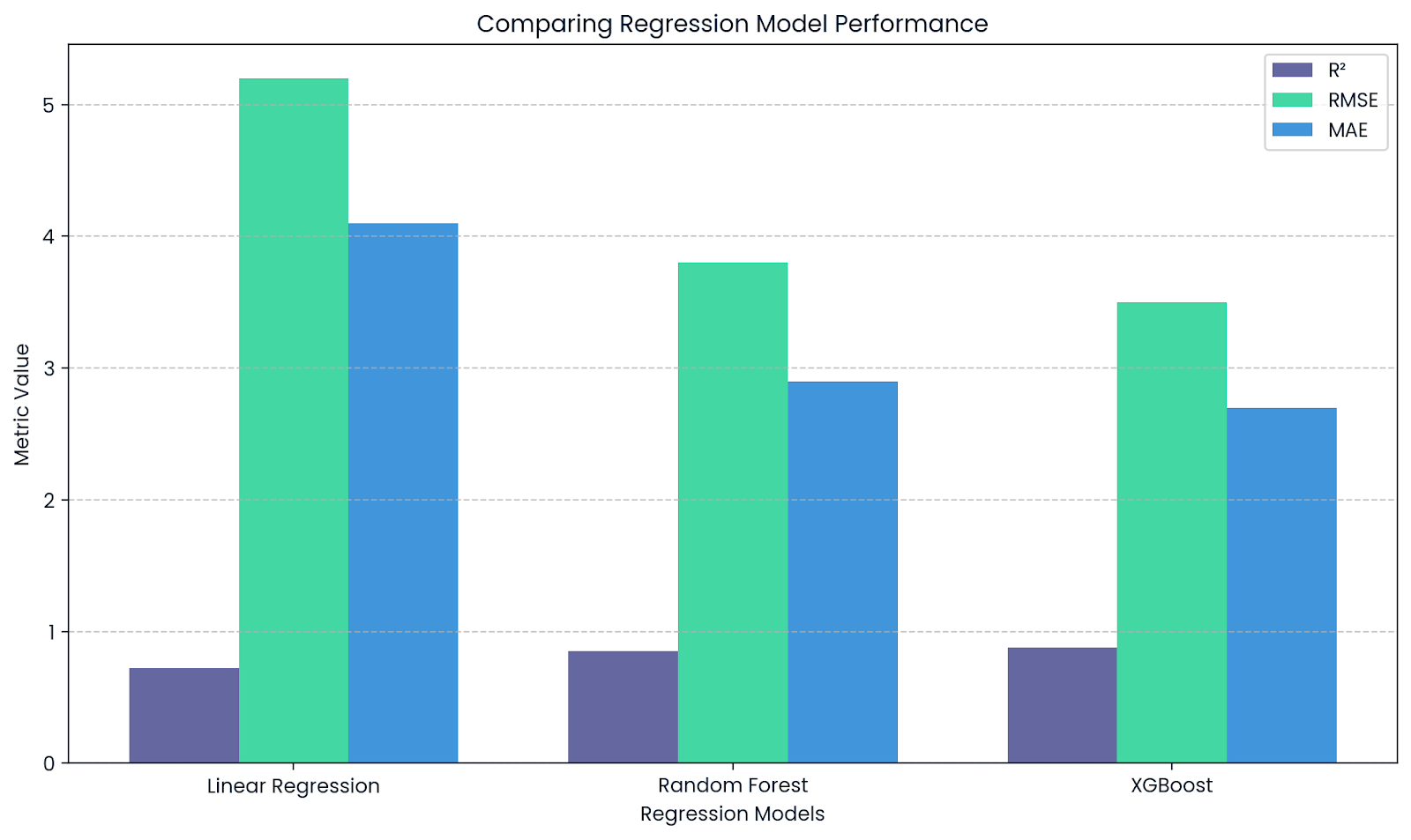
^R² complementa RMSE e MAE. Imagem do autor.

Este gráfico mostra como o R² complementa outras métricas, como RMSE e MAE, na hora de avaliar modelos de regressão. Enquanto^R² mostra o poder explicativo, RMSE e MAE dão uma ideia do tamanho real dos erros de previsão.

Relatando o coeficiente de determinação em pesquisas

Se você estiver incluindo^R² em um artigo científico ou projeto, tem algumas regras de formatação que é bom lembrar:

• Não esquece de colocar^R² em itálico e sim, deve ser um R maiúsculo, não minúsculo. 
• Não coloque um zero antes da vírgula decimal. Então, em vez de escrever^R² = 0,73, escreva^R² = 0,73. E, a menos que você realmente precise de mais detalhes, arredonde para duas casas decimais.

Se você está usando^R² como parte de uma análise de regressão ou ANOVA e quer saber se seu modelo é significativo, inclua mais algumas coisas: a estatística F, os graus de liberdade e o valor p. Isso mostra ao leitor o quanto a gente pode confiar que o seu modelo explica algo importante.

Então, quando você estiver relatando os resultados, pode ficar mais ou menos assim:

“O modelo explicou uma parte significativa da variação nas vendas,^R² = 0,73, F(2, 97) = 25,42, p < 0,001.”

Mas, se você não estiver fazendo um teste de hipótese, tipo, se estiver fazendo uma análise exploratória ou avaliando o desempenho de um modelo com validação cruzada, então tá tudo certo em só reportar o valor R².

O Coeficiente de Determinação em Python, R e Excel

Vamos ver como calcular^R² de três maneiras diferentes: Python, R e Excel através de um mini-projeto onde a gente tenta adivinhar as notas dos alunos com base no tempo que eles estudam.

Vamos usar o seguinte conjunto de dados para todos os três exemplos:

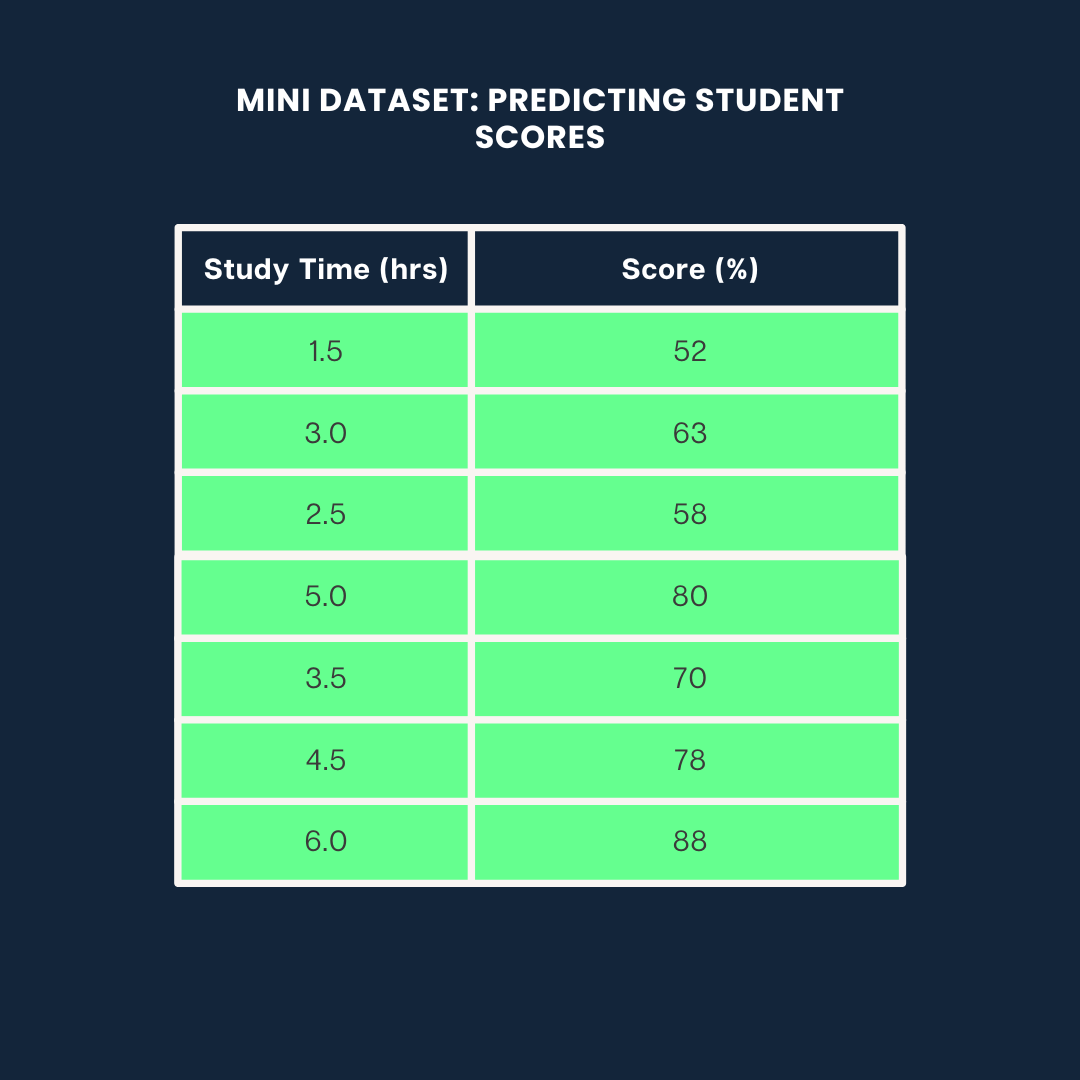
Conjunto de dados de exemplo. Imagem do autor

Coeficiente de determinação em Python

Veja como calcular^R² em Python usando scikit-learn:

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np

# Data
study_time = np.array([1.5, 3.0, 2.5, 5.0, 3.5, 4.5, 6.0]).reshape(-1, 1)
scores = np.array([52, 63, 58, 80, 70, 78, 88])

# Model
model = LinearRegression()
model.fit(study_time, scores)
predicted_scores = model.predict(study_time)

# R² score
r2 = r2_score(scores, predicted_scores)
print(f"R² = {r2:.2f}")

0.99

Isso quer dizer que 99% da diferença nas notas é por causa do tempo que a galera estudou.

Se você quiser saber mais sobre regressão e modelos estatísticos, dá uma olhada no nosso guia Introdução à regressão com statsmodels em Python. 

Coeficiente de determinação em R

No R, você pode calcular R² com algumas linhas usando a função lm():

# Data
study_time <- c(1.5, 3.0, 2.5, 5.0, 3.5, 4.5, 6.0)
scores <- c(52, 63, 58, 80, 70, 78, 88)

# Linear model
model <- lm(scores ~ study_time)

# R-squared
summary(model)$r.squared

0.9884718

Cerca de 98% da variação nas notas é explicada pelo tempo de estudo. Se você quiser saber mais sobre regressão no R, dá uma olhada no nosso curso Introdução à regressão no R.

Coeficiente de determinação no Excel

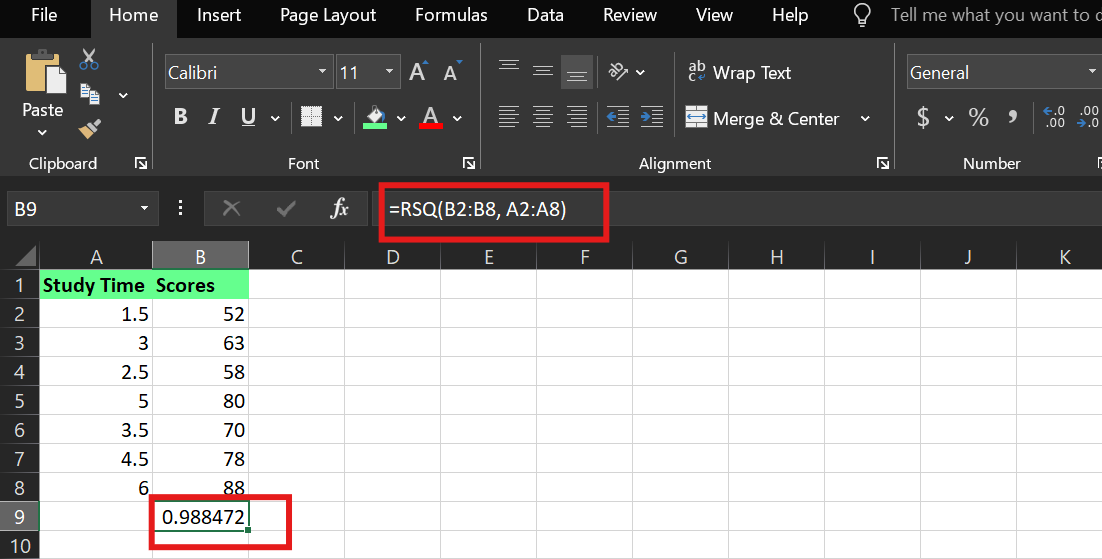
No Excel, você pode calcular o R² usando a função embutida “ RSQ() ”. Supondo que:

• A hora de estudar está nas células A2:A8

• As pontuações estão nas células B2:B8

A sintaxe é:

RSQ(known_y's,known_x's)

Usei a seguinte fórmula:

=RSQ(B2:B8,A2:A8)

Isso diz ao Excel para calcular o valor^R² entre a variável dependente (notas) e a variável independente (tempo de estudo).

Exemplo de^R² no Excel. Imagem do autor.  

Pontos principais

Se você está prevendo notas de alunos, retornos de ações ou comportamento de clientes, o coeficiente de determinação mostra o quanto do resultado seu modelo realmente entende. 

Um coeficiente de determinação alto pode parecer incrível, mas não se deixe enganar achando que o modelo é perfeito ou que prova causa e efeito. E um coeficiente de determinação baixo nem sempre significa que deu errado; pode ser que seu sistema seja complexo ou que suas variáveis estejam incompletas.

Então, se você está criando ou analisando modelos, pergunte a si mesmo:

• O que estou explicando bem?
• O que estou esquecendo?
• E o meu modelo é útil, não só preciso?

Comece com essa mentalidade e você vai usar o coeficiente de determinação como uma lente para tomar melhores decisões.