Cursus
Les fonctions de coût agissent comme le « marqueur » des décisions. Ils mesurent l'écart entre les prévisions et les valeurs réelles d'un ensemble de données par rapport aux valeurs prévues. Dans le domaine de l'apprentissage automatique, ils orientent les algorithmes d'optimisation afin de minimiser les erreurs et d'améliorer la précision des modèles.
Dans cet article, nous développons l'intuition étape par étape. Nous commençons par les applications économiques, où les fonctions de coût décrivent le compromis entre production et efficacité. Nous nous tournons ensuite vers l'apprentissage automatique, où ils pilotent la formation des modèles. Ensuite, nous examinerons l'optimisation en tant que lien entre les deux. Enfin, nous examinons des exemples concrets.
Concepts fondamentaux de la fonction de coût
Les fonctions de coût sont essentielles à l'optimisation et à l'évaluation. Définissons mathématiquement les fonctions de coût et examinons leurs propriétés clés.
Définition de base et expression mathématique des fonctions de coût
Une fonction de coût (également appelée « fonction d'erreur ») associe une ou plusieurs variables d'entrée à une seule valeur numérique qui représente le « coût » d'une décision ou d'une prédiction. En apprentissage automatique, elle est généralement définie comme la moyenne de la fonction de perte sur l'ensemble des échantillons du jeu de données.
La fonction de coût remplit deux rôles : elle sert d'objectif à minimiser par un algorithme d'optimisation et de métrique d'évaluation pour mesurer les performances d'un modèle.
Considérons une fonction de coût comme objectif. Pour chaque maison, la fonction de perte pénalise la différence entre le prix de vente réel et le prix prévu. La fonction de coût agrège ces pénalités pour l'ensemble des logements :
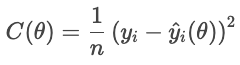
- Yi représente le prix réel,
- Ŷi(θ) est le prix prévu, qui dépend des paramètres θ,
- n est le nombre d'échantillons.
Un coût plus faible indique une meilleure adéquation globale, tandis qu'un coût plus élevé indique une erreur moyenne plus importante. L'optimiseur ajuste les paramètres afin de minimiser ce coût.
En tant que mesure d'évaluation, les fonctions de coût évaluent la performance. Par exemple, un classificateur peut être évalué en fonction de sa précision, de son rappel ou de tout autre indicateur approprié à l'application. De cette manière, les fonctions de coût permettent d'évaluer le succès.
Propriétés des fonctions de coût
Trois propriétés mathématiques sont particulièrement pertinentes.
- Convexité : Une fonction convexe a la forme d'un bol, sans aucune vallée. Cela garantit que l'optimiseur atteint le minimum global plutôt que de rester bloqué dans un creux local.
- Différenciabilité : Une fonction de coût différentiable présente une pente bien définie. Cela permet aux méthodes basées sur les gradients d'ajuster efficacement les paramètres.
- Continuité : Une fonction continue évolue de manière régulière en fonction de ses entrées. L'absence de fluctuations soudaines garantit une optimisation stable.
Ensemble, ces propriétés déterminent dans quelle mesure une fonction de coût est facile à optimiser. Lorsque l'une de ces propriétés fait défaut, des techniques spéciales peuvent être nécessaires pour compenser.
Économie et applications commerciales des fonctions de coût
Les fonctions de coût décrivent la relation entre la quantité produite et le coût total des produits. Ils constituent un outil essentiel pour appréhender le comportement des entreprises, les stratégies de tarification et l'analyse des bénéfices.
Types de coûts économiques
- Coûts fixes. Les dépenses qui ne varient pas en fonction de la production, telles que le loyer ou les frais de services publics.
- Coûts variables. Les dépenses qui augmentent ou diminuent en fonction du volume produit, telles que la main-d'œuvre horaire ou les commissions sur les ventes.
- Coût total (CT). La somme des coûts fixes et des coûts variables.
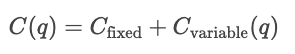
- Coût moyen. Le coût par unité.
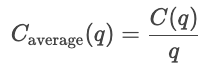
- Coût marginal (CM). Le coût de production d'une unité supplémentaire, qui est donné par la dérivée du coût par rapport à la quantité.
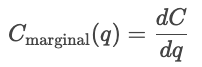
- Revenu marginal (MR). Le revenu total supplémentaire généré par l'augmentation des ventes de produits d'une unité.
Courbes de coûts
Les courbes de coûts illustrent la variation des coûts en fonction de la quantité totale produite. Les coûts fixes sont constants, ils sont donc représentés par une ligne horizontale, tandis que les coûts variables augmentent en fonction des unités produites.
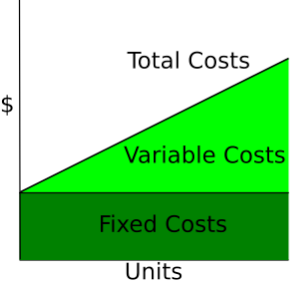
Wikipédia : Courbe des coûts
Coûts à court terme par rapport aux coûts à long terme
À court terme, au moins un facteur de production, tel que le capital ou la taille de l'usine, est maintenu constant, tandis que les autres facteurs varient. Les coûts à court terme évaluent l'efficacité avec laquelle une entreprise fonctionne dans sa configuration actuelle. Ainsi, pour une quantité q donnée, le coût à court terme correspond à la somme des coûts fixes et des coûts variables dépendant de la quantité.
![]()
À court terme, optimiser dans les limites des capacités actuelles.
À long terme, tous les intrants sont variables. L'entreprise pourrait envisager d'augmenter ses processus de production. Les coûts à long terme mesurent l'efficacité lorsque la capacité elle-même peut varier, indiquant le coût minimal réalisable pour tout niveau de production.
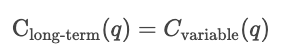
À long terme, optimisez en sélectionnant la capacité optimale elle-même.
Analyse de la production et des bénéfices
Les fonctions de coût sont utilisées pour analyser le comportement en matière de tarification. Les entreprises comparent les courbes de coûts avec les prix du marché afin de déterminer s'il convient d'augmenter ou de réduire leur production. Si le coût marginal est inférieur au prix du marché, produire davantage augmente les bénéfices ; si le coût marginal est supérieur au prix du marché, produire davantage coûte de l'argent.
Les fonctions de coût sont également utilisées dans les stratégies de tarification. Ils déterminent le prix minimum viable qu'une entreprise peut pratiquer. Les entreprises peuvent modifier leur prix au-dessus du coût marginal afin de maximiser leurs profits, ou se rapprocher du CM dans les secteurs hautement concurrentiels. Ainsi, l'analyse des coûts permet de déterminer le prix d'équilibre, le prix de revient majoré et les stratégies de tarification dynamique.
Le seuil de rentabilité est atteint lorsque le revenu total est égal au coût total.![]()
À ce stade, l'entreprise prend en charge tous les coûts, mais ne réalise aucun bénéfice. Produire moins entraîne une perte, tandis que produire davantage génère des bénéfices.
Le bénéfice correspond à la différence entre le chiffre d'affaires total et le coût total.
![]()
Si le revenu marginal dépasse le coût marginal (MR > MC), l'entreprise augmentera sa production afin de générer davantage de bénéfices. Si le revenu marginal est inférieur au coût marginal (MR < MC), l'entreprise réduira sa production afin de réaliser des bénéfices supplémentaires. L'entreprise maximise ses profits en produisant la quantité pour laquelle MR = MC.
Pour plus d'informations sur la finance, je vous recommande de consulter ces ressources DataCamp.
- Modélisation financière dans ExcelPMT().
- Évaluation des actions dans R.
- Évaluation et analyse des obligations dans R.
- Excel : Calculez les remboursements de prêt, les économies et plus encore.
- Formule Excel pour le TCAC : Guide complet.
- Prévision des prix alimentaires à l'aide de fonctions.
Applications de l'apprentissage automatique aux fonctions de coût
Dans les applications ML, les fonctions de coût quantifient les résidus (la différence entre les valeurs prédites et les valeurs réelles) sur l'ensemble du jeu de données. Cette section examine les principales familles de fonctions de coût et leur influence sur le comportement des modèles.
Pertes de régression
Dans le contexte de l'apprentissage automatique, l'objectif de la régression (pas nécessairement linéaire est de prédire une valeur continue.) est de prédire une valeur continue. Une fonction de perte de régression quantifie l'écart entre les valeurs réelles et les valeurs prédites pour un échantillon particulier ; les fonctions de coût regroupent les fonctions de perte en une quantité globale. Les processus d'optimisation utilisent des fonctions de coût pour minimiser l'erreur globale.
Nous nous concentrons sur les quatre principales familles de fonctions de coût : l'erreur absolue moyenne (MAE), l'erreur quadratique moyenne (MSE), l'erreur quadratique moyenne racine (RMSE) et la perte de Huber.
Les différentes fonctions de coût gèrent les erreurs de manière différente. En effet, ils déterminent le degré de sévérité avec lequel les écarts entre les valeurs prévues et les valeurs réelles doivent être sanctionnés. Le MAE applique une pénalité uniforme, représentant le comportement médian et la robustesse face aux valeurs aberrantes. Le MSE élève chaque résidu au carré, ce qui fait ressortir les erreurs importantes et les pénalise plus sévèrement. La perte de Huber combine ces deux approches, en utilisant une pénalité quadratique pour les petites erreurs et une pénalité linéaire pour les grandes erreurs (au-delà d'un seuil δ).
Erreur absolue moyenne (EAM)
L'erreur absolue moyenne est définie comme la moyenne de la valeur absolue des résidus.
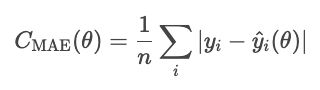
La MAE traite tous les écarts de manière égale, elle est donc moins sensible aux valeurs aberrantes que d'autres méthodes que nous verrons, telles que la MSE. Cependant, l'erreur absolue est mathématiquement complexe et rend l'optimisation basée sur le gradient plus difficile.
Remarque concernant le paramètre de fonction. θ représente les paramètres du modèle. L'optimiseur contrôle les coûts en fonction de ces paramètres, et non directement en fonction des valeurs prédites qui en découlent. Par conséquent, nous exprimons le coût comme une fonction de la θ, et non de Ŷi.
MSE
L'erreur quadratique moyenne (MSE) est calculée à l'aide de la formule suivante.
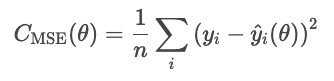
La mise au carré des résidus amplifie les erreurs importantes, ce qui rend la MSE sensible aux valeurs aberrantes. Cependant, cette forme d'erreur est différentiable et convexe, ce qui la rend favorable à l'optimisation.
RMSE
Un inconvénient de l'erreur quadratique moyenne est que ses unités sont au carré. Par exemple, dans un modèle de régression des prix immobiliers, la perte est exprimée en dollars au carré, ce qui manque de sens intuitif. Le RMSE corrige ce problème en calculant la racine carrée du MSE.
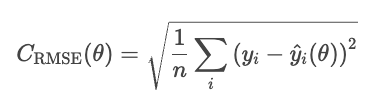
Le RMSE se comporte de manière similaire au MSE, mais les unités sont les mêmes que celles du problème (dollars, et non dollars au carré).
Huber
La perte de Huber est moins sensible aux valeurs aberrantes dans les données que la MSE (ou RMSE). Il combine MAE et MSE, et contrôle la transition à l'aide d'un paramètre. δ.
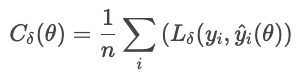
où
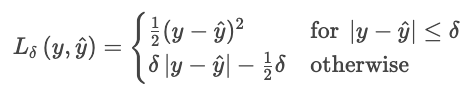
Cette formule empêche quelques résidus importants de dominer la perte. La perte de Huber constitue un choix judicieux pour les données réelles bruitées où l'on peut s'attendre à des observations extrêmes occasionnelles.
Pertes de classification
La classification prédit des catégories distinctes. Ces fonctions de coût comparent les distributions de probabilité aux étiquettes réelles, en pénalisant les prédictions incorrectes ou trop confiantes.
Perte de cross-entropie
La perte de cross-entropie (perte logarithmique) récompense un modèle lorsqu'il est correct avec un haut degré de confiance et le pénalise lorsqu'il est incorrect avec un haut degré de confiance.
Pour un classificateur qui génère des probabilités pures Ŷ, la probabilité que l'étiquette observée Y est
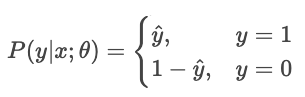
Estimation du maximum de vraisemblance (EMV) maximise cette vraisemblance sur l'ensemble des échantillons.
Transformons cette idée en une réduction des coûts d'. Minimiser revient à maximiser le négatif, alors inversons le signe. Veuillez également prélever des échantillons de bois.
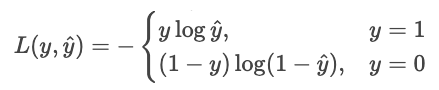
Nous pouvons exprimer cela de manière plus concise sous la forme d'une somme unique.
![]()
Pourquoi le journal ? Le journal présente plusieurs avantages.
- Cela transforme le produit en une somme. Au lieu de multiplier de petits nombres et de risquer un dépassement de capacité, nous additionnons les probabilités.
- Cela rend la fonction concave. Le logarithme transforme la vraisemblance en une fonction concave avec un seul maximum global.
- Il fournit une courbe de pénalité significative.
- p = 1,0 entraîne une perte de 0,
- p = 0,9 entraîne une perte de 0,1 (faible)
- p = 0,2 entraîne une perte de 2,3 (importante)
- p = 0,01 entraîne une perte de 4,6 (considérable)
- Cela évite les exposants imbriqués. Dans la régression logistique et les réseaux neuronaux, le logarithme « décompresse » les exponentielles imbriquées, rendant les dérivées simples et stables.
Supposons qu'un modèle prédise les probabilités pour deux choix : « chien » (choix 0) ou « chat » (choix 1). Si la réponse réelle est 1 (« chat ») et que le modèle est sûr à 90 % qu'il s'agit d'un chat, la perte est faible car le modèle était sûr de lui et correct. Si le modèle indique qu'il y a 10 % de certitude qu'il s'agit d'un chat, la perte est importante, car le modèle était confiant mais erroné.
Entropie croisée pour la classification multi-classes
Lorsqu'il y a plus de deux classes (« chat », « chien », « oiseau »), le modèle produit un score brut (« logit ») pour chaque classe, noté Zi. Les logits peuvent être n'importe quel nombre réel, ils sont donc convertis en probabilités dont la somme est égale à un via la fonction softmax.
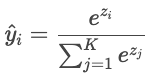
Les prédictions du modèle sont ensuite comparées aux étiquettes réelles à l'aide de l'entropie croisée.
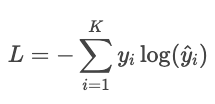
Exemple
Supposons que l'étiquette réelle soit « chat » et que le modèle prédise les probabilités : chat : 80 %, chien : 15 %, oiseau : 5 %. La perte est
![]()
Si la probabilité prévue pour « chat » n'était que de 30 %, la perte serait alors beaucoup plus importante :
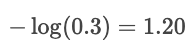
Le journal sanctionne les erreurs commises avec assurance et récompense les prédictions faites avec une grande assurance.
Perte de charnière
La perte de charnière est principalement utilisée pour la classification à marge maximale, comme dans les machines à vecteurs de support (SVM). L'objectif est de classer avec certitude en maintenant les prédictions loin de la limite de décision.
Pour la classification binaire, la perte de charnière est donnée par la formule suivante.
![]()
où
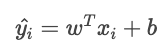
La fonction de coût total est la suivante :
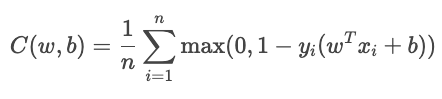
Le terme YiŶi mesure la qualité du classement de l'échantillon.
- Lorsque cette valeur est supérieure à 1, l'échantillon se trouve du bon côté de la limite sans perte.
- Lorsque la valeur est comprise entre 0 et 1, le point se trouve dans la marge, et une petite pénalité est appliquée.
- Lorsque cette valeur est inférieure à 0, le modèle a effectué une classification erronée. La perte augmente de manière linéaire avec la distance par rapport à la frontière.
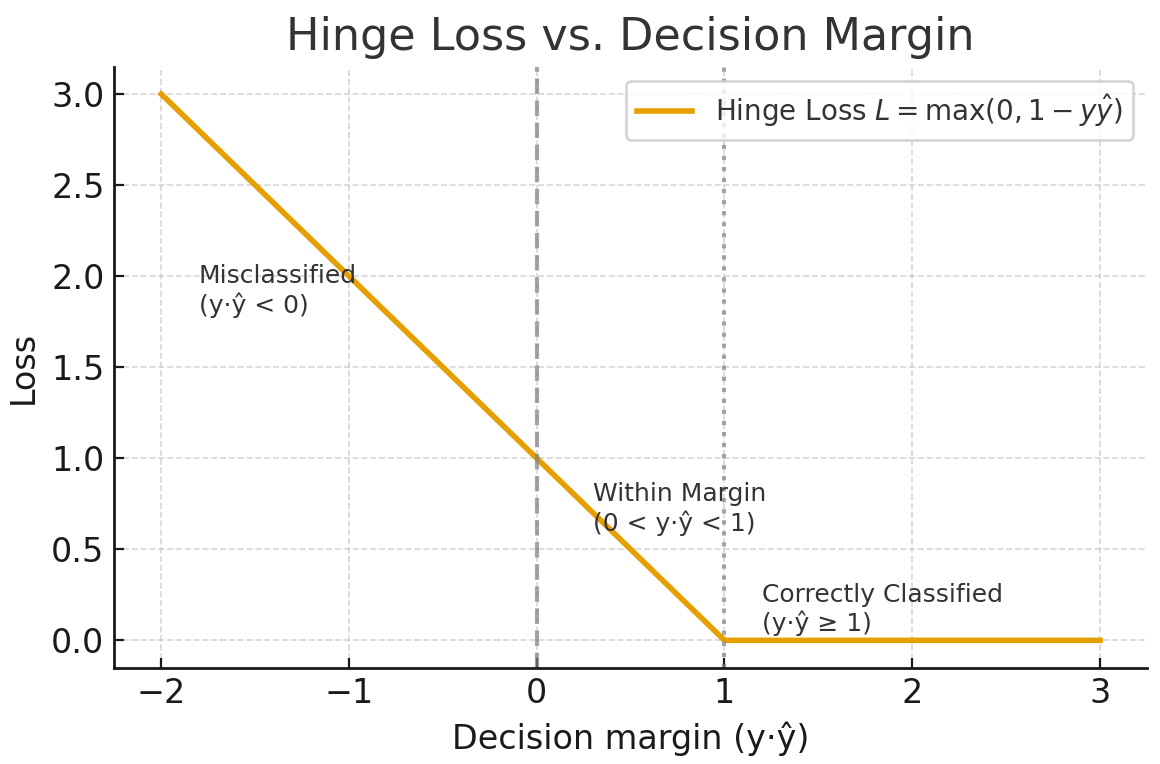
Généré par chatGPT 5
Kullback-Leibler (KL)
La divergence de Kullback-Leibler (KL) est une mesure de la différence entre une distribution de probabilité approximative Q et une distribution de probabilité donnée P. Elle est définie comme suit :
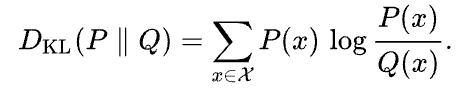
Wikipédia
La divergence KL peut être interprétée comme la différence moyenne du nombre de bits nécessaires pour coder les échantillons de P à l'aide d'un code optimisé pour Q.
Régularisation
Les techniques de régularisation empêchent les modèles d'ajuster le bruit dans les données d'apprentissage en ajoutant un terme à la fonction de coût qui pénalise les solutions trop complexes.
Sans régularisation, le modèle minimise la perte :
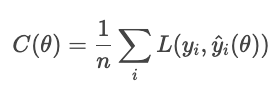
Avec la régularisation, le modèle ajoute un terme de pénalité.
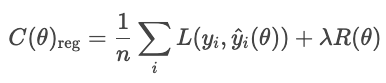
où
- L représente la perte habituelle (par exemple, RMSE, entropie croisée).
- R(θ) mesure la complexité du modèle.
- λ contrôle le compromis entre ajustement et simplicité
Les types courants de régularisation sont L1, L2 et elastic net.
La régularisation L1 (également appelée lasso) ajoute la valeur absolue de chaque poids du modèle à la fonction de coût.
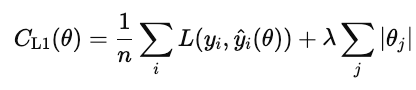
Lorsque ce coût est minimisé, de nombreux poids sont ramenés à zéro. Cela fait de L1 une forme de sélection automatique des caractéristiques. Les fonctionnalités qui n'apportent pas de valeur ajoutée sont supprimées.
La régularisation L2 (également appelée régression ridge) pénalise le carré de chaque poids du modèle.
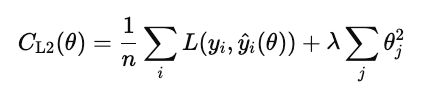
Contrairement à L1, il ne fixe pas les poids exactement à zéro, mais les réduit progressivement. Cela permet de conserver toutes les caractéristiques du modèle tout en réduisant leur influence afin de stabiliser les prédictions.
Le réseau élastique combine les couches L1 et L2.
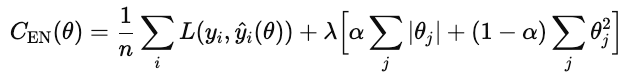
λ contrôle l'intensité de la régularisation globale. α est un nombre compris entre 0 et 1 qui contrôle les pourcentages de L1 par rapport à L2, où 1 correspond à un L1 pur et 0 à un ridge pur.
Compromis
Les différentes stratégies de perte de classification présentent des avantages et des inconvénients.
L'entropie croisée maximise la probabilité correcte en pénalisant les réponses erronées sûres. Les inconvénients sont qu'il est sensible aux valeurs aberrantes et aux données mal étiquetées. Il est particulièrement efficace lorsque la qualité de la confiance est importante (par exemple, les modèles de risque).
La perte de charnière impose une marge afin que les classifications correctes ne soient pas seulement correctes, mais également fiables. Il ignore les échantillons de valeurs qui se situent largement au-delà de la marge et applique une pénalité linéaire en cas de dépassement. Elle est moins sensible aux valeurs aberrantes que l'entropie croisée, mais plus difficile à optimiser de manière fluide, car elle n'est pas différentiable au niveau de la charnière.
La divergence de Kullback-Leibler (KL) permet de comparer deux distributions de probabilités. Cela équivaut à l'entropie croisée moins l'entropie de la distribution réelle.
Pour plus d'informations, veuillez consulter les liens suivants.
- Fonction de perte d'entropie croisée dans l'apprentissage automatique : Amélioration de la précision des modèles
- Des données aux dollars - Prévision des frais d'assurance
- Optimisez les prévisions de prix grâce à l'ingénierie des fonctionnalités
- Fiche récapitulative sur les dimensions de la qualité des données
- Tutoriel sur la corrélation R
Mise en œuvre et pratique de la fonction de coût dans l'apprentissage automatique
Jusqu'à présent, nous avons abordé les fonctions de coût d'un point de vue théorique. En pratique, le succès d'un modèle d'apprentissage automatique dépend de son efficacité à minimiser ces fonctions. Dans cette section, nous présentons les détails pratiques des algorithmes d'optimisation de base et des stratégies de réglage.
Algorithmes d'optimisation et réglage des paramètres
L'optimisation est le processus qui consiste à déterminer les valeurs optimales des paramètres d'un modèle qui minimisent une fonction de coût. En ML, cela implique de déterminer les paramètres qui permettent d'obtenir des prédictions aussi proches que possible des valeurs réelles.
Descente de gradient
L'e de descente de gradient est l'algorithme standard utilisé pour optimiser les fonctions de coût. Il met à jour de manière itérative les paramètres du modèle dans la direction qui réduit le plus le coût, le gradient négatif. Conceptuellement, il mesure la pente multivariable de la fonction de coût et descend la pente.
La règle de mise à jour est la suivante :
![]()
où θ sont les paramètres du modèle, n est le taux d'apprentissage, et ![]() est le gradient de la fonction de coût par rapport aux paramètres.
est le gradient de la fonction de coût par rapport aux paramètres.
Le choix du taux d'apprentissage est essentiel. Si elle est trop grande, les mises à jour dépassent le minimum et oscillent ou divergent. Si elle est trop petite, la convergence devient lente et peut stagner dans des minima locaux.
Les principales variantes sont le traitement par lots, le traitement stochastique et le traitement par mini-lots.
- . Calcule le gradient en utilisant l'ensemble complet de données d'apprentissage. Il est stable mais lent et nécessite beaucoup de mémoire pour les grands ensembles de données ou l'apprentissage en ligne.
- Stochastic gradient descent (SGD). Mise à jour des paramètres après chaque exemple d'apprentissage. Il est rapide et efficace en termes de mémoire, mais peut être perturbant dans le sens où chaque étape peut s'écarter légèrement de la trajectoire optimale. Cependant, le caractère aléatoire peut contribuer à éviter les minima locaux.
- s de la descente de gradient par mini-lots. Un compromis pratique. Il calcule les gradients sur de petits lots afin d'équilibrer vitesse et stabilité. Il permet également le parallélisme GPU.
Optimiseurs adaptatifs
La descente de gradient standard applique un taux d'apprentissage fixe à tous les paramètres. Dans les modèles complexes, différents paramètres peuvent nécessiter différentes tailles de pas. Les optimiseurs adaptatifs ajustent les taux d'apprentissage en fonction de l'historique des amplitudes des gradients.
- RMSProp utilise une moyenne exponentiellement décroissante des gradients carrés récents.
![]()
L'apprentissage de chaque paramètre est inversement proportionnel à cette moyenne. Cela empêche les oscillations et permet une progression stable, même lorsque certains paramètres présentent des gradients importants. RMSProp est largement utilisé pour les réseaux récurrents et les données bruitées.
- Estimation adaptative du moment (Adam) suit à la fois la moyenne et la variance des gradients passés et adapte dynamiquement la taille des pas.
![]()
Il converge rapidement, est robuste face aux données bruitées et constitue l'optimiseur par défaut pour les frameworks de réseaux profonds.
Mise à l'échelle et initialisation des fonctionnalités
Avant d'optimiser avec la descente de gradient, veuillez mettre à l'échelle les caractéristiques afin qu'elles fonctionnent sur des plages comparables. Une mise à l'échelle adéquate améliore la stabilité et l'efficacité de l'optimisation.
Sans mise à l'échelle, les caractéristiques présentant de grandes plages numériques dominent le gradient. La descente de gradient procède alors par zigzags au lieu de suivre un chemin direct vers le minimum.
Il existe deux approches courantes.
- Normalisation. Centres chacun à zéro et recalibre à la variance unitaire.
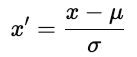
où u est la moyenne et ơ est l'écart type. La normalisation préserve la structure des données.
- Normalisation. Redimensionnez chaque caractéristique à une plage fixe, généralement comprise entre [0, 1].
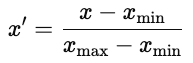
La normalisation est courante dans les réseaux neuronaux, où les fonctions d'activation fonctionnent mieux avec des entrées limitées.
Stratégies d'initialisation des paramètres
L'initialisation des paramètres a une forte influence sur l'entraînement du modèle. Une mauvaise initialisation peut entraîner une convergence lente, une explosion ou une disparition des gradients, ou encore des modèles qui ne parviennent pas à apprendre. Une bonne initialisation place les paramètres dans une région de la surface de coût où les gradients sont stables.
- Initialisation aléatoire. Attribue de petites valeurs aléatoires, généralement tirées d'une distribution uniforme ou normale. La randomisation rompt la symétrie afin que les paramètres apprennent des caractéristiques distinctes. Cependant, si la variance est trop élevée ou trop faible, les gradients peuvent s'intensifier ou disparaître.
- Xavier (Glorot) initialisation. Conçu pour les fonctions d'activation non linéaires telles que tanh ou sigmoid, Xavier ajuste la variance des poids en fonction du nombre de connexions d'entrée et de sortie.
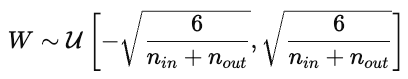
Cela permet de maintenir les activations et les gradients à un niveau approximativement constant d'une couche à l'autre.
- Il a initialisé l'. Ajuste la variance pour les activations ReLU, qui remettent à zéro les valeurs négatives. Les poids sont tirés d'une distribution normale avec une variance spécifiée :
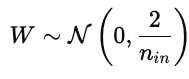
Cela empêche les gradients de disparaître trop rapidement pendant la rétropropagation.
Surveillance, diagnostic et visualisation
Une courbe de perte d'entraînement affiche un graphique de l'erreur du modèle sur l'ensemble de données d'entraînement au fil du temps. Il démontre l'efficacité avec laquelle le modèle actualise ses paramètres afin de minimiser l'erreur. Une courbe en baisse constante indique que le modèle apprend des modèles à partir des données.
La courbe de perte de validation illustre la capacité du modèle à généraliser sur des données non observées, telles qu'un ensemble de validation ou de test. Il indique la capacité du modèle à prédire des données non observées auparavant.
Idéalement, les deux courbes diminuent au début, puis se stabilisent. Cela démontre que le modèle apprend efficacement et généralise efficacement.
Le surapprentissage se produit lorsque le modèle interprète le bruit comme s'il s'agissait d'un signal et ne généralise pas correctement. Ceci apparaît dans un graphique illustrant les courbes d'apprentissage et de validation lorsque la perte d'apprentissage diminue mais que la perte de validation augmente. Les solutions consistent notamment à utiliser un ensemble de données plus important ou à appliquer une régularisation dans le modèle.
Le sous-ajustement ( ) se produit lorsque le modèle ne parvient pas à saisir les modèles sous-jacents dans les données. Les courbes d'apprentissage et de validation restent élevées. Dans ce cas, veuillez envisager d'utiliser davantage de données, un modèle plus complexe ou de réduire la régularisation.
La convergence est le point où la courbe s'aplatit et où l'enrichissement du minerai n'apporte que peu d'amélioration. Il s'agit du juste milieu entre le surajustement et le sous-ajustement.
Optimisation de la fonction de coût et théorie de la décision
Nous avons observé comment l'économie et l'apprentissage automatique s'appuient sur l'optimisation pour orienter la prise de décision et la formation. Les deux domaines s'efforcent de prendre les meilleures décisions possibles en se basant sur des indicateurs de coût ou de perte. Approfondissons la théorie de l'optimisation de manière plus générale.
Fonctions objectives
Une fonction objectif est une fonction mathématique qui définit ce que nous souhaitons minimiser ou maximiser. Dans les cas que nous avons examinés jusqu'à présent, nous avons réduit au minimum les coûts ou les erreurs. En économie, nous avons examiné les courbes de coûts, et en apprentissage automatique, nous avons examiné les pertes de régression (MAE, RMSE, Huber) et les pertes de classification (entropie croisée, perte de charnière, perte KL). Ce sont deux exemples d'optimisation d'une fonction objectif.
Optimisation multi-objectifs
Souvent, nous cherchons à optimiser plusieurs objectifs, qui sont fréquemment contradictoires. Une entreprise pourrait souhaiter maximiser ses profits tout en minimisant les risques. Un scientifique des données pourrait souhaiter améliorer la précision d'un modèle sans compromettre son interprétabilité ou son équité. Ces objectifs concurrents définissent un problème d'optimisation multi-objectifs dans lequel l'amélioration d'un objectif peut entraîner la détérioration d'un autre.
frontière de Pareto
Une solution est optimale au sens de Pareto si aucun objectif ne peut être amélioré sans détériorer au moins un autre objectif. L'ensemble des solutions pareto-optimales forme lafrontière de Pareto d' , une courbe qui représente les meilleurs compromis possibles. Chaque point sur cette courbe représente un équilibre différent entre les priorités.
Par exemple, augmenter la complexité d'un modèle peut améliorer sa précision, mais réduire son interprétabilité. Les modèles plus simples sont plus faciles à expliquer, mais peuvent être moins performants. La frontière de Pareto inclut les « meilleurs compromis » et exclut les solutions dominées par d'autres variables.
Le choix du point approprié dépend du contexte et du jugement. Vous pouvez attribuer des pondérations à chaque objectif ou utiliser des contraintes politiques.
Perte attendue
Lorsque les résultats sont incertains, l'optimisation minimise la perte attendue, c'est-à-dire la perte moyenne sur tous les scénarios possibles. En ML, cette notion apparaît dans la fonction de risque.
![]()
où L(Y,f(x)) représente la perte pour une prédiction donnée, et l'espérance est calculée en moyenne sur la distribution des données. L'objectif est de déterminer le modèle f qui minimise cette perte attendue. Ce modèle offre les meilleures performances en moyenne, et pas seulement sur des échantillons individuels.
risque bayésien
L' e de risque de Bayes représente la limite inférieure théorique de la perte attendue. Formellement, elle est donnée par la formule suivante.
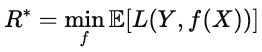
Intuitivement, il s'agit du « score parfait », c'est-à-dire la plus petite valeur possible lorsque l'on dispose d'informations complètes sur la distribution des données. Plus la performance d'un modèle est proche du risque bayésien, plus il est optimal.
Applications interdisciplinaires
Les fonctions de coût sont utilisées dans tous les secteurs qui prennent des décisions basées sur des données. Ils contribuent à équilibrer les objectifs concurrents et à définir ce que signifie « mieux ». Ces fonctions permettent d'équilibrer des objectifs concurrents et orientent l'optimisation. La même logique utilisée pour former les modèles d'apprentissage automatique est appliquée pour optimiser les processus dans le monde réel.
Applications industrielles et cas d'utilisation dans différents domaines
Dans le secteur manufacturier, par exemple, les fonctions de coût permettent de quantifier les pertes, telles que les pertes de stock. Une fonction de coût des stocks permet d'équilibrer les dépenses liées aux excédents de stock et les pénalités liées aux pénuries. Des cadres similaires sont utilisés pour la planification de la production ou la consommation d'énergie afin de minimiser le coût total prévu dans un contexte d'incertitude.
Dans le domaine des soins de santé, les modèles prédictifs utilisent des fonctions de coût pour équilibrer la précision et l'allocation des ressources. Par exemple, un modèle de risque de réadmission permet d'identifier rapidement les patients à haut risque afin que les cliniciens puissent intervenir en effectuant des appels de suivi ou des visites à domicile. Oublier un patient à haut risque est plus coûteux que signaler un patient à faible risque, c'est pourquoi la fonction pénalise ces erreurs différemment.
La finance utilise également des fonctions objectives. Par exemple, les modèles de notation de crédit prédisent la probabilité qu'un emprunteur se trouve en défaut de paiement sur un prêt au cours d'une période donnée, par exemple douze mois. L'acceptation d'un emprunteur à risque peut entraîner des pertes financières potentielles, tandis que le refus d'un emprunteur sûr peut entraîner une perte de revenus. Le modèle minimise les coûts prévus.
Dans tous ces domaines, les fonctions de coût équilibrent les compromis en quantités mesurables que les décideurs peuvent utiliser et analyser.
Conclusion
Les fonctions de coût constituent une méthode d'évaluation des décisions. En économie, ils modélisent le compromis entre production et efficacité. Dans le domaine de l'apprentissage automatique, ils mesurent l'écart entre les prédictions et la réalité.
En apprentissage automatique, les fonctions de coût constituent la base de la conception des modèles. Le choix des fonctions de perte détermine ce que le modèle considère comme un « succès ». L'erreur quadratique moyenne récompense la précision globale, l'entropie croisée récompense les probabilités calibrées et la perte de charnière récompense la séparation fiable.
Dans tous les domaines et toutes les industries, la logique sous-jacente est la même : définir un objectif et l'optimiser. Les fonctions de coût transforment des objectifs vagues en chiffres concrets qui guident l'optimisation.
Les fonctions de coût sont utiles en économie, en apprentissage automatique, dans le secteur manufacturier, en finance, dans le domaine de la santé et dans tous les autres domaines où l'on souhaite quantifier les compromis.
Pour plus d'informations, je vous recommande ces ressources DataCamp.
Foire aux questions sur la fonction de coût
Qu'est-ce qu'une fonction de coût ?
Une fonction de coût détermine dans quelle mesure les prédictions d'un modèle correspondent aux données. Il agrège l'erreur en une seule valeur. Les algorithmes d'optimisation minimisent ensuite cette valeur afin d'améliorer les performances.
En quoi les fonctions de coût diffèrent-elles entre les tâches de régression et de classification ?
Les modèles de régression prédisent des valeurs continues, de sorte que leur perte (par exemple, MSE, MAE) mesure la distance numérique par rapport à la cible.
Les modèles de classification prédisent les probabilités de classe ; les pertes telles que l'entropie croisée comparent la distribution de probabilité prédite à la classe réelle et pénalisent fortement les erreurs de confiance.
Quelles sont les applications concrètes des fonctions de coût dans le monde des affaires ?
Les fonctions de coût sont utiles dans tout processus commercial impliquant des compromis ou une optimisation. Parmi les exemples, citons l'optimisation des prix et des revenus, la gestion des stocks, la modélisation du crédit et des risques, la fidélisation de la clientèle ou la logistique.
Comment la fonction de perte de Huber traite-t-elle les valeurs aberrantes dans les données ?
La fonction de perte de Huber traite les petites erreurs comme le MSE et les grandes erreurs comme le MAE, ce qui la rend moins sensible aux valeurs aberrantes.
Quelle est la relation entre le coût marginal et le coût moyen ?
Le coût marginal (CM) évalue le coût de production d'une unité supplémentaire. Le coût moyen (CM) correspond au coût total divisé par le nombre d'unités. Lorsque MC < AC, augmenter la production réduit le coût moyen, lorsque MC > AC, augmenter la production augmente le coût moyen, et lorsque MC = AC, le coût moyen est à son minimum.

Mark Pedigo, PhD, est un éminent scientifique des données, spécialisé dans la science des données de santé, la programmation et l'éducation. Titulaire d'un doctorat en mathématiques, d'une licence en informatique et d'un certificat professionnel en intelligence artificielle, Mark allie connaissances techniques et résolution de problèmes pratiques. Au cours de sa carrière, il a joué un rôle dans la détection des fraudes, la prédiction de la mortalité infantile et les prévisions financières, et a contribué au logiciel d'estimation des coûts de la NASA. En tant qu'éducateur, il a enseigné à DataCamp et à l'université Washington de St. Louis et a encadré des programmeurs juniors. Pendant son temps libre, Mark profite de la nature du Minnesota avec sa femme Mandy et son chien Harley, et joue du piano jazz.
