programa
Las funciones de coste actúan como «marcador» de las decisiones. Miden cuánto se desvían las predicciones de los valores reales de un conjunto de datos en comparación con los valores previstos. En machine learning, guían los algoritmos de optimización para minimizar los errores y mejorar la precisión de los modelos.
En este artículo, desarrollamos la intuición paso a paso. Comenzamos con las aplicaciones económicas, donde las funciones de coste describen el equilibrio entre producción y eficiencia. A continuación, pasamos a machine learning, donde impulsan el entrenamiento de modelos. A continuación, examinamos la optimización como puente entre ambos. Por último, exploramos ejemplos del mundo real.
Conceptos básicos de la función de coste
Las funciones de coste son fundamentales para la optimización y la evaluación. Definamos matemáticamente las funciones de coste y examinemos sus propiedades clave.
Definición básica y expresión matemática de las funciones de coste.
Una función de coste (también denominada «función de error») asigna una o varias variables de entrada a un único valor numérico que representa el «coste» de una decisión o predicción. En machine learning, se suele definir como la media de la función de pérdida sobre todas las muestras del conjunto de datos.
La función de coste desempeña dos funciones: sirve como objetivo que minimiza un algoritmo de optimización y como métrica de evaluación para medir el rendimiento de un modelo.
Veamos una función de coste como objetivo. Para cada vivienda, la función de pérdida penaliza la diferencia entre el precio de venta real y el precio previsto. La función de coste agrega estas penalizaciones en todas las viviendas:
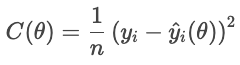
- Yi es el precio real,
- Ŷi(θ) es el precio previsto, que depende de los parámetros θ,
- n es el número de muestras.
Un coste menor indica un mejor ajuste general, mientras que un coste mayor indica un error medio mayor. El optimizador ajusta los parámetros para minimizar este coste.
Como métrica de evaluación, las funciones de coste miden el rendimiento. Por ejemplo, un clasificador puede evaluarse con precisión, recuperación o cualquier otra métrica que sea adecuada para la aplicación. De esta manera, las funciones de coste proporcionan una forma de evaluar el éxito.
Propiedades de las funciones de coste
Hay tres propiedades matemáticas que son especialmente relevantes.
- Convexidad: Una función convexa tiene forma de cuenco, sin ningún valle. Esto garantiza que el optimizador alcance el mínimo global en lugar de quedarse atascado en un mínimo local.
- Diferenciabilidad: Una función de coste diferenciable tiene una pendiente bien definida. Esto permite que los métodos basados en gradientes ajusten los parámetros de manera eficiente.
- Continuidad: Una función continua cambia suavemente con sus entradas. Sin saltos repentinos, la optimización es estable.
En conjunto, estas propiedades determinan la facilidad con la que se puede optimizar una función de coste. Cuando falta una de estas propiedades, es posible que se requieran técnicas especiales para compensarlo.
Aplicaciones económicas y empresariales de las funciones de coste
Las funciones de coste describen la relación entre la cantidad de producción y el coste total de los productos. Son una herramienta esencial para comprender el comportamiento de las empresas, las estrategias de fijación de precios y el análisis de beneficios.
Tipos de costes económicos
- Costes fijos. Gastos que no varían en función de la producción, como el alquiler o los gastos de suministros.
- Costes variables. Gastos que aumentan o disminuyen en función de la cantidad producida, como la mano de obra por hora o las comisiones por ventas.
- Coste total (CT). La suma de los costes fijos y los costes variables.
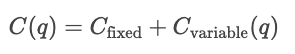
- Coste medio. El costo por unidad.
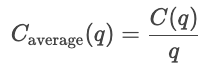
- Coste marginal (CM). El costo de producir una unidad más, que viene dado por la derivada del costo con respecto a la cantidad.
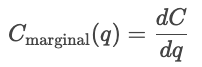
- Ingresos marginales (IM). Los ingresos totales adicionales generados por el aumento de las ventas de productos en una unidad.
Curvas de costes
Las curvas de costos muestran cómo varían los costos en función de la cantidad total producida. Los costes fijos son constantes, por lo que se muestran como una línea horizontal, mientras que los costes variables aumentan en función de las unidades producidas.
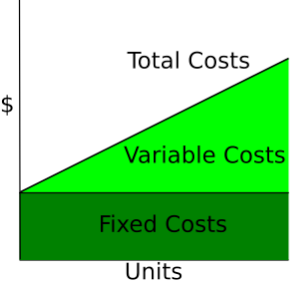
Wikipedia: Curva de costes
Costes a corto plazo frente a costes a largo plazo
A corto plazo, al menos uno de los insumos, como el capital o el tamaño de la planta, se mantiene constante, y los demás insumos varían. Los costes a corto plazo miden la eficiencia con la que opera una empresa con su configuración actual. Por lo tanto, para una cantidad q determinada, el costo a corto plazo es la suma de los costos fijos y los costos variables que dependen de la cantidad.
![]()
A corto plazo, optimizar dentro de la capacidad actual.
A largo plazo, todos los insumos son variables. La empresa podría ampliar tus procesos de producción. Los costes a largo plazo miden la eficiencia cuando la capacidad en sí misma puede variar, mostrando el coste mínimo alcanzable para cualquier nivel de producción.
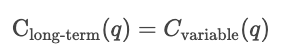
A largo plazo, optimiza eligiendo la capacidad óptima.
Análisis de producción y beneficios
Las funciones de coste se utilizan para analizar el comportamiento de los precios. Las empresas comparan las curvas de costes con los precios de mercado para decidir si ampliar o reducir la producción. Si el costo marginal es inferior al precio de mercado, producir más aumenta los beneficios; si el costo marginal es inferior al precio de mercado, producir más unidades cuesta dinero.
Las funciones de coste también se utilizan en las estrategias de fijación de precios. Determinan el precio mínimo viable que una empresa puede cobrar. Las empresas pueden cambiar por encima del coste marginal para maximizar los beneficios, o acercarse más al CM en sectores altamente competitivos. Por lo tanto, el análisis de costes sirve de base para las estrategias de precios de equilibrio, precios de coste incrementado y precios dinámicos.
El punto de equilibrio se alcanza cuando los ingresos totales igualan los costos totales.![]()
En este momento, la empresa cubre todos los gastos, pero no obtiene beneficios. Producir menos da lugar a pérdidas, mientras que producir más genera beneficios.
El beneficio es la diferencia entre los ingresos totales y los costes totales.
![]()
Si los ingresos marginales superan los costes marginales (MR > MC), la empresa aumentará la producción para generar más beneficios. Si los ingresos marginales son inferiores a los costes marginales (MR < MC), la empresa reducirá la producción para obtener beneficios adicionales. La empresa maximiza sus beneficios produciendo la cantidad en la que MR = MC.
Para obtener más información sobre finanzas, te recomiendo que consultes estos recursos de DataCamp.
- Modelización financiera en ExcelPMT().
- Valoración de acciones en R.
- Valoración y análisis de bonos en R.
- Excel: Calcula los pagos de préstamos, ahorros y mucho más.
- CAGR Excel Formula: Guía completa.
- Previsión de los precios de los alimentos con funciones.
Función de coste Aplicaciones de machine learning
En las aplicaciones de ML, las funciones de coste cuantifican los residuos (la diferencia entre los valores previstos y los valores reales) en todo el conjunto de datos. En esta sección se analizan las principales familias de funciones de coste y cómo influyen en el comportamiento del modelo.
Pérdidas por regresión
En el contexto del machine learning, el objetivo de la regresión (no necesariamente lineal lineal) es predecir un valor continuo. Una función de pérdida de regresión cuantifica el error entre los valores reales y los valores previstos para una muestra concreta; las funciones de coste agregan las funciones de pérdida en una cantidad global. Los procesos de optimización utilizan funciones de coste para minimizar el error global.
Nos centramos en las cuatro familias principales de funciones de coste: error absoluto medio (MAE), error cuadrático medio (MSE), error cuadrático medio raíz (RMSE) y pérdida de Huber.
Las diferentes funciones de coste gestionan los errores de forma diferente. En efecto, definen la severidad con la que se castigan las desviaciones entre los valores previstos y los valores reales. El MAE aplica una penalización uniforme, que representa el comportamiento mediano y la robustez frente a los valores atípicos. El MSE eleva al cuadrado cada residuo, lo que hace que los errores grandes predominen y se castiguen con mayor severidad. La pérdida de Huber combina estas dos, utilizando una penalización cuadrática para los errores pequeños y una lineal para los grandes (más allá de un umbral δ).
Error absoluto medio (MAE)
El error absoluto medio se define como la media del valor absoluto de los residuos.
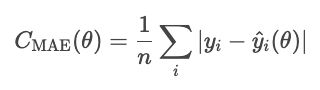
El MAE trata todas las desviaciones por igual, por lo que no se ve tan afectado por los valores atípicos como otros métodos que veremos, como el MSE. Sin embargo, el error absoluto es matemáticamente complicado y dificulta la optimización basada en gradientes.
Una nota sobre el parámetro de la función. θ representa los parámetros del modelo. El optimizador controla el costo basándose en estos parámetros, no directamente en los valores previstos que se derivan de ellos. Por lo tanto, escribimos el costo como una función de la θ, no de Ŷi.
MSE
El error cuadrático medio (MSE) se calcula mediante la siguiente fórmula.
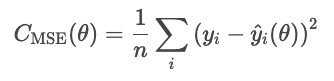
La cuadratura de los residuos exagera los errores grandes, lo que hace que el MSE sea sensible a los valores atípicos. Sin embargo, esta forma de error es diferenciable y convexa, lo que la hace fácil de optimizar.
RMSE
Un inconveniente del MSE es que sus unidades están al cuadrado. Por ejemplo, en un modelo de regresión de los precios de la vivienda, la pérdida se expresa en dólares al cuadrado, lo que carece de significado intuitivo. El RMSE corrige este problema tomando la raíz cuadrada del MSE.
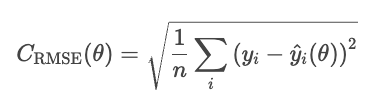
El RMSE se comporta de manera similar al MSE, pero las unidades son las mismas que las del problema (dólares, no dólares al cuadrado).
Huber
La pérdida de Huber es menos sensible a los valores atípicos en los datos que el MSE (o RMSE). Combina MAE y MSE, y controla la transición con un parámetro δ.
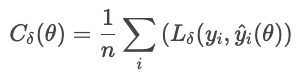
dónde
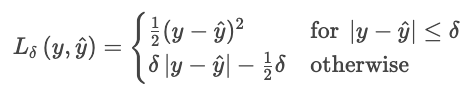
Esta fórmula evita que unos pocos residuos grandes dominen la pérdida. La pérdida de Huber es una buena opción para datos reales ruidosos en los que se esperan observaciones extremas ocasionales.
Pérdidas por clasificación
La clasificación predice categorías discretas. Estas funciones de coste comparan las distribuciones de probabilidad con las etiquetas reales, penalizando las predicciones incorrectas o excesivamente seguras.
Pérdida por entropía cruzada
La pérdida de entropía cruzada (pérdida logarítmica) recompensa a un modelo cuando es correctamente seguro y lo castiga cuando es erróneamente seguro.
Para un clasificador que genera probabilidades puras Ŷ, la probabilidad de la etiqueta observada Y es
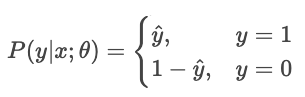
Estimación de máxima verosimilitud (MLE) maximiza esta verosimilitud en todas las muestras.
Convirtamos esta idea en minimizar un cost. Minimizar es lo mismo que maximizar lo negativo, así que cambiemos el signo. Tomemos también los registros.
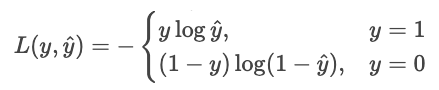
Podemos escribir esto de forma más sucinta como una sola suma.
![]()
¿Por qué el registro? El registro tiene varias ventajas
- Convierte el producto en una suma. En lugar de multiplicar números pequeños y arriesgarnos a un desbordamiento por debajo del rango, sumamos probabilidades.
- Hace que la función sea cóncava. El logaritmo transforma la probabilidad en una función cóncava con un único máximo global.
- Proporciona una curva de penalización significativa.
- p = 1,0 da como resultado una pérdida de 0.
- p = 0,9 da como resultado una pérdida de 0,1 (pequeña).
- p = 0,2 da como resultado una pérdida de 2,3 (grande).
- p = 0,01 da como resultado una pérdida de 4,6 (enorme).
- Evita los exponentes anidados. En la regresión logística y las redes neuronales, el logaritmo «desenvuelve» las exponenciales anidadas, lo que hace que las derivadas sean simples y estables.
Supongamos que un modelo predice las probabilidades de dos opciones: «perro» (opción 0) o «gato» (opción 1). Si la respuesta real es 1 («gato») y el modelo tiene un 90 % de certeza de que se trata de un gato, la pérdida es pequeña porque el modelo estaba seguro y acertó. Si el modelo dice que hay un 10 % de certeza de que es un gato, la pérdida es grande, porque el modelo estaba seguro pero se equivocó.
Entropía cruzada para la clasificación multiclase
Cuando hay más de dos clases («gato», «perro», «pájaro»), el modelo produce una puntuación bruta («logit») para cada clase, denotada Zi. Los logits pueden ser cualquier número real, por lo que se convierten en probabilidades que suman uno mediante la función softmax.
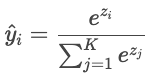
A continuación, las predicciones del modelo se comparan con las etiquetas reales utilizando la entropía cruzada.
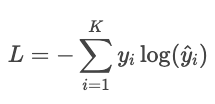
Ejemplo
Supongamos que la etiqueta verdadera es «gato» y que el modelo predice probabilidades: gato: 80 %, perro: 15 %, pájaro: 5 %. La pérdida es
![]()
Si la probabilidad prevista para «gato» fuera solo del 30 %, la pérdida sería mucho mayor:
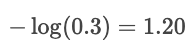
El registro castiga los errores cometidos con confianza y recompensa las predicciones realizadas con gran confianza.
Pérdida de bisagra
La pérdida de bisagra se utiliza principalmente para la clasificación de margen máximo, como en las máquinas de vectores de soporte (SVM). El objetivo es clasificar con seguridad manteniendo las predicciones lejos del límite de decisión.
Para la clasificación binaria, la pérdida de bisagra viene dada por la siguiente fórmula.
![]()
dónde
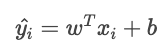
La función de coste total es
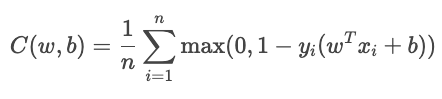
El término YiŶi mide lo bien que está clasificada la muestra.
- Cuando es mayor que 1, la muestra se encuentra en el lado correcto del límite sin pérdida.
- Cuando está entre 0 y 1, el punto está dentro del margen, por lo que se aplica una pequeña penalización.
- Cuando es inferior a 0, el modelo ha clasificado erróneamente. La pérdida crece linealmente con la distancia desde el límite.
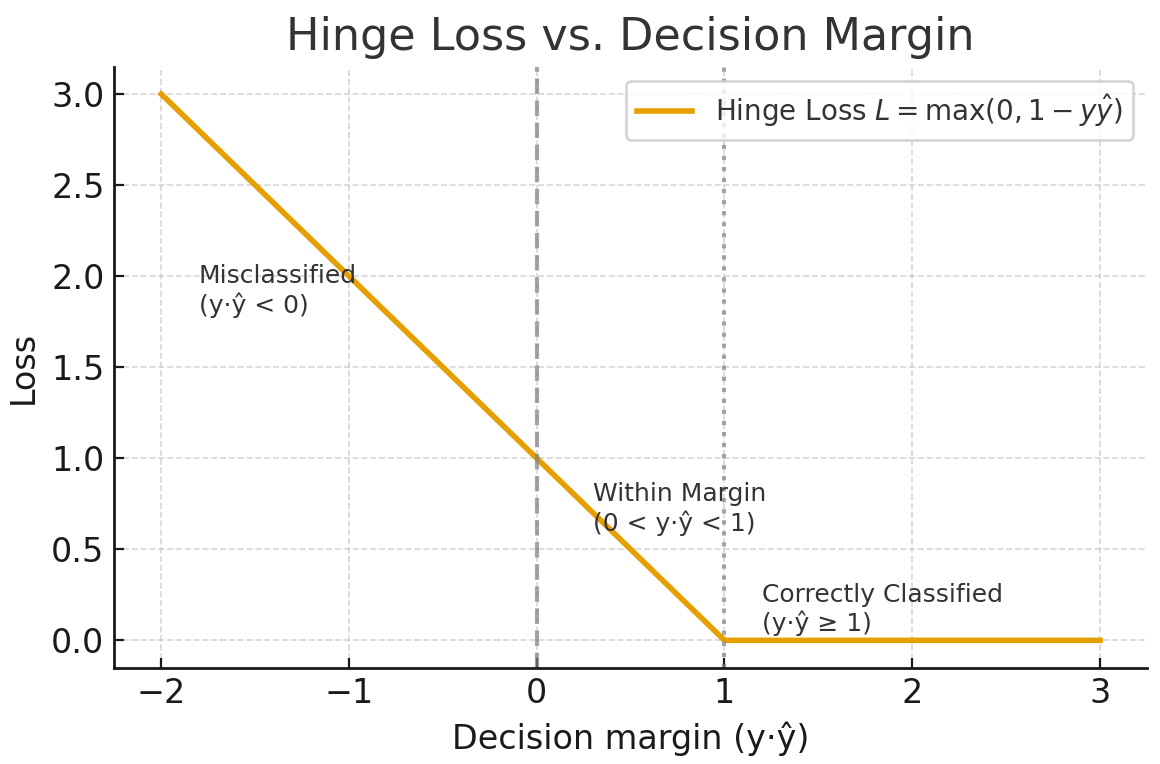
Generado por chatGPT 5
Kullback-Leibler (KL)
La divergencia de Kullback-Leibler (KL) es una medida de cuánto difiere una distribución de probabilidad aproximada Q de una distribución de probabilidad dada P. Se define como
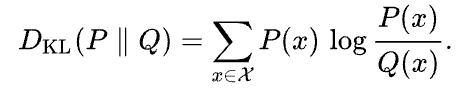
Wikipedia
La divergencia KL puede interpretarse como la diferencia media del número de bits para codificar muestras de P utilizando un código optimizado para Q.
Regularización
Las técnicas de regularización evitan que los modelos se ajusten al ruido en los datos de entrenamiento añadiendo un término a la función de coste que penaliza las soluciones excesivamente complejas.
Sin regularización, el modelo minimiza la pérdida:
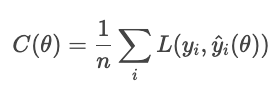
Con la regularización, el modelo añade un término de penalización.
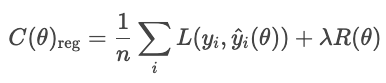
dónde
- L es la pérdida habitual (por ejemplo, RMSE, entropía cruzada).
- R(θ) mide la complejidad del modelo.
- λ controla el equilibrio entre ajuste y simplicidad
Los tipos comunes de regularización son L1, L2 y red elástica.
La regularización L1 (también conocida como lasso) añade el valor absoluto de cada peso del modelo a la función de coste.
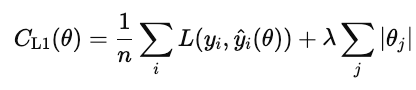
Cuando este coste se minimiza, muchos pesos se reducen a cero. Esto convierte a L1 en una forma de selección automática de características. Las características que no contribuyen se reducen a cero.
La regularización L2 (también conocida como regresión ridge) penaliza el cuadrado de cada peso del modelo.
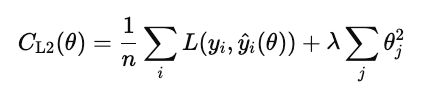
A diferencia de L1, no establece los pesos exactamente en cero, sino que los reduce gradualmente. Esto mantiene todas las características del modelo, pero reduce su influencia para estabilizar las predicciones.
La red elástica añade tanto L1 como L2.
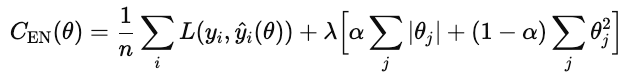
λ controla la intensidad de la regularización general. α es un número entre 0 y 1 que controla los porcentajes de L1 frente a L2, donde 1 es L1 puro y 0 es ridge puro.
Compromisos
Las diferentes estrategias de pérdida de clasificación tienen ventajas e inconvenientes.
La entropía cruzada maximiza la probabilidad correcta penalizando las respuestas erróneas seguras. Las desventajas son que es sensible a los valores atípicos y a los datos mal etiquetados. Funciona mejor cuando te preocupas por la calidad de la confianza (por ejemplo, modelos de riesgo).
La pérdida de bisagra impone un margen para que las clasificaciones correctas no solo sean correctas, sino también seguras. Ignora las muestras de valores que están claramente fuera del margen y aplica una penalización lineal por las infracciones. Es menos sensible a los valores atípicos que la entropía cruzada, pero más difícil de optimizar de forma fluida, ya que no es diferenciable en el punto de inflexión.
La divergencia de Kullback-Leibler (KL) compara una distribución de probabilidad con otra. Es equivalente a la entropía cruzada menos la entropía de la distribución real.
Para obtener más información, consulta estos enlaces.
- Función de pérdida de entropía cruzada en machine learning: Mejora de la precisión del modelo
- De los datos al dinero: predicción de los costes de los seguros
- Optimiza las predicciones de precios con ingeniería de características
- Hoja de referencia sobre las dimensiones de la calidad de los datos
- Tutorial sobre correlación R
Implementación y práctica de la función de coste en machine learning
Hasta ahora, hemos hablado de las funciones de coste en teoría. En la práctica, el éxito de un modelo de aprendizaje automático depende de la eficiencia con la que minimice esas funciones. En esta sección, presentamos detalles prácticos sobre los algoritmos de optimización básicos y las estrategias de ajuste.
Algoritmos de optimización y ajuste de parámetros
La optimización es el proceso de encontrar los valores óptimos de los parámetros del modelo que minimizan una función de coste. En ML, esto significa descubrir los parámetros que hacen que las predicciones sean lo más cercanas posible a los valores reales.
Descenso por gradiente
El descenso por gradiente es el algoritmo estándar para optimizar funciones de coste. Actualiza iterativamente los parámetros del modelo en la dirección que más reduce el coste, el gradiente negativo. Conceptualmente, mide la pendiente multivariable de la función de coste y desciende por ella.
La regla de actualización es
![]()
donde θ son los parámetros del modelo, n es la tasa de aprendizaje y ![]() es el gradiente de la función de coste con respecto a los parámetros.
es el gradiente de la función de coste con respecto a los parámetros.
La elección de la tasa de aprendizaje es fundamental. Si es demasiado grande, las actualizaciones superan el mínimo y oscilan o divergen. Si es demasiado pequeño, la convergencia se vuelve lenta y puede estancarse en mínimos locales.
Las principales variantes son por lotes, estocásticas y minilotes.
- Descenso por gradiente por lotes. Calcula el gradiente utilizando todo el conjunto de entrenamiento. Es estable, pero lento y consume mucha memoria para conjuntos de datos grandes o aprendizaje en línea.
- Descenso estocástico por gradiente (SGD). Actualiza los parámetros después de cada ejemplo de entrenamiento. Es rápido y eficiente en cuanto a memoria, pero ruidoso en el sentido de que cada paso puede desviarse ligeramente de la ruta óptima. Sin embargo, la aleatoriedad puede ayudar a escapar de los mínimos locales.
- Descenso de gradiente por minilotes. Un compromiso práctico. Calcula gradientes en lotes pequeños para equilibrar velocidad y estabilidad. También permite el paralelismo de la GPU.
Optimizadores adaptativos
El descenso de gradiente estándar aplica una tasa de aprendizaje fija a todos los parámetros. En modelos complejos, es posible que diferentes parámetros requieran diferentes tamaños de paso. Los optimizadores adaptativos ajustan las tasas de aprendizaje basándose en el historial de magnitudes de gradiente.
- RMSProp emplea un promedio exponencialmente decreciente de los gradientes cuadrados recientes.
![]()
El aprendizaje de cada parámetro se escala de forma inversa a este promedio. Esto evita la oscilación y permite un progreso estable incluso cuando algunos parámetros tienen gradientes pronunciados. RMSProp se utiliza ampliamente para redes recurrentes y datos ruidosos.
- Estimación adaptativa del momento (Adam) programa tanto la media como la varianza de los gradientes pasados y adapta dinámicamente los tamaños de los pasos.
![]()
Converge rápidamente, es resistente a los datos ruidosos y es el optimizador predeterminado para los marcos de redes profundas.
Escalado e inicialización de características
Antes de optimizar con descenso de gradiente, escala las características para que funcionen en rangos comparables. Un escalado adecuado mejora la estabilidad y la eficiencia de la optimización.
Sin escalado, las características con grandes rangos numéricos dominan el gradiente. El descenso por gradiente entonces zigzaguea en lugar de dar pasos directos hacia el mínimo.
Hay dos enfoques comunes.
- Estandarización. Centros cada característica en cero y reescala a la varianza unitaria.
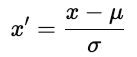
donde u es la media y ơ es la desviación estándar. La estandarización preserva la estructura de los datos.
- Normalización. Reescala cada característica a un rango fijo, normalmente [0, 1].
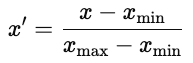
La normalización es habitual en las redes neuronales, donde las funciones de activación funcionan mejor con entradas limitadas.
Estrategias de inicialización de parámetros
La inicialización de los parámetros influye considerablemente en el entrenamiento del modelo. Una inicialización deficiente puede provocar una convergencia lenta, gradientes explosivos o desaparecidos, o modelos que no aprenden. Una buena inicialización coloca los parámetros en una región de la superficie de coste donde los gradientes son estables.
- Inicialización aleatoria. Asigna pequeños valores aleatorios, normalmente extraídos de una distribución uniforme o normal. La aleatorización rompe la simetría para que los parámetros aprendan características distintas. Sin embargo, si la varianza es demasiado alta o baja, los gradientes pueden explotar o desaparecer.
- Inicialización de Xavier (Glorot). Diseñado para funciones de activación no lineales como tanh o sigmoide, Xavier escala la varianza de los pesos según el número de conexiones de entrada y salida.
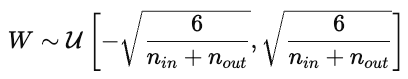
Esto mantiene las activaciones y los gradientes más o menos constantes en todas las capas.
- Inicialización. Ajusta la varianza para las activaciones ReLU, que ponen a cero los valores negativos. Los pesos se obtienen a partir de una distribución normal con una varianza especificada:
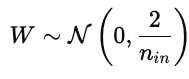
Esto evita que los gradientes desaparezcan demasiado rápido durante la retropropagación.
Monitorización, diagnóstico y visualización
Una curva de pérdida de entrenamiento gráficando el error del modelo en el conjunto de datos de entrenamiento a lo largo del tiempo. Muestra lo bien que el modelo actualiza sus parámetros para minimizar el error. Una curva que disminuye de manera constante indica que el modelo está aprendiendo patrones a partir de los datos.
La curva de pérdida de validación muestra la capacidad del modelo para generalizar datos no vistos, como un conjunto de retención o validación. Indica la capacidad del modelo para predecir datos no vistos anteriormente.
Lo ideal es que ambas curvas disminuyan al principio y luego se estabilicen. Esto demuestra que el modelo está aprendiendo y generalizando de manera eficaz.
El sobreajuste ( ) se produce cuando el modelo aprende el ruido como si fuera señal y no generaliza bien. Esto aparece en un gráfico que muestra las curvas de entrenamiento y validación cuando la pérdida de entrenamiento disminuye, pero la pérdida de validación aumenta. Las soluciones incluyen el uso de un conjunto de datos más grande o la aplicación de regularización en el modelo.
El subajuste se produce cuando el modelo no logra captar los patrones subyacentes en los datos. Tanto las curvas de entrenamiento como las de validación se mantienen altas. En este caso, prueba con más datos, un modelo más complejo o reduce la regularización.
La convergencia es el punto en el que la curva se aplana y la formación del mineral ofrece pocas mejoras. Este es el punto óptimo entre el sobreajuste y el subajuste.
Optimización de la función de coste y teoría de la decisión
Hemos visto cómo la economía y el machine learning se basan en la optimización para orientar la toma de decisiones y la formación. Ambos campos se esfuerzan por tomar las mejores decisiones basándose en una métrica de coste o pérdida. Profundicemos en la teoría de la optimización de una manera más general.
Funciones objetivas
Una función objetivo es una función matemática que define lo que queremos minimizar o maximizar. En los casos que hemos visto hasta ahora, hemos minimizado el costo o el error. Para econ, analizamos las curvas de costes, y con ML, analizamos las pérdidas de regresión (MAE, RMSE, Huber) y las pérdidas de clasificación (entropía cruzada, pérdida de bisagra, pérdida KL). Ambos son ejemplos de optimización de una función objetivo.
Optimización multiobjetivo
A menudo, queremos optimizar múltiples objetivos, que a menudo son contradictorios. Una empresa puede querer maximizar los beneficios y minimizar los riesgos. Un científico de datos puede querer mejorar la precisión del modelo sin sacrificar la interpretabilidad o la equidad. Estos objetivos contrapuestos definen un problema de optimización multiobjetivo en el que mejorar un objetivo puede empeorar otro.
frontera de Pareto
Una solución es óptima según Pareto si no se puede mejorar ningún objetivo sin empeorar al menos otro objetivo. El conjunto de soluciones óptimas de Pareto forma lafrontera de Pareto e e, una curva que consiste en las mejores compensaciones posibles. Cada punto de esta curva representa un equilibrio diferente de prioridades.
Por ejemplo, aumentar la complejidad de un modelo puede mejorar la precisión, pero reducir la interpretabilidad. Los modelos más simples son más fáciles de explicar, pero pueden tener un rendimiento inferior. La frontera de Pareto incluye las «mejores compensaciones» y excluye las soluciones que están dominadas por otras variables.
Elegir el punto adecuado depende del contexto y del criterio personal. Puedes asignar ponderaciones a cada objetivo o utilizar restricciones normativas.
Pérdida esperada
Cuando los resultados son inciertos, la optimización minimiza la pérdida esperada, es decir, la pérdida media en todos los escenarios posibles. En ML, esta idea aparece en la función de riesgo.
![]()
donde L(Y,f(x)) es la pérdida para una predicción dada, y la esperanza se promedia sobre la distribución de datos. El objetivo es encontrar el modelo f que minimice esta pérdida esperada. Este modelo ofrece el mejor rendimiento en promedio, no solo en muestras individuales.
Riesgo bayesiano
El riesgo bayesiano es el límite inferior teórico de la pérdida esperada. Formalmente, se expresa mediante la siguiente fórmula.
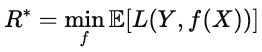
Intuitivamente, es la «puntuación perfecta», es decir, el valor más pequeño que se puede alcanzar con información perfecta sobre la distribución de los datos. Cuanto más se acerque el rendimiento de un modelo al riesgo bayesiano, más óptimo será.
Aplicaciones interdisciplinarias
Las funciones de coste se utilizan en cualquier sector que tome decisiones basadas en datos. Ayudan a equilibrar objetivos contrapuestos y a formalizar lo que significa «mejor». Estas funciones equilibran objetivos contrapuestos y guían la optimización. La misma lógica que se utiliza para entrenar modelos de ML se utiliza para optimizar procesos del mundo real.
Aplicaciones industriales y casos de uso en distintos ámbitos
En la industria manufacturera, por ejemplo, las funciones de coste cuantifican pérdidas, como la pérdida de inventario. Una función de coste de inventario equilibra el gasto del exceso de existencias con las sanciones por escasez. Se utilizan marcos similares para la programación de la producción o el uso de energía con el fin de minimizar el costo total previsto en condiciones de incertidumbre.
En el ámbito sanitario, los modelos predictivos utilizan funciones de coste para equilibrar la precisión y la asignación de recursos. Por ejemplo, un modelo de riesgo de reingreso identifica tempranamente a los pacientes de alto riesgo para que los médicos puedan intervenir con llamadas de seguimiento o visitas domiciliarias. Pasar por alto a un paciente de alto riesgo es más costoso que señalar a uno de bajo riesgo, por lo que la función penaliza esos errores de manera diferente.
Las finanzas también utilizan funciones objetivas. Por ejemplo, los modelos de puntuación crediticia predicen la probabilidad de que un prestatario incumpla el pago de un préstamo en un periodo de tiempo determinado, por ejemplo, doce meses. Aprobar a un prestatario arriesgado conlleva una posible pérdida financiera, mientras que rechazar a un prestatario seguro conlleva una posible pérdida de ingresos. El modelo minimiza el costo esperado.
En todos estos ámbitos, las funciones de coste equilibran las compensaciones en cantidades medibles que los responsables de la toma de decisiones pueden utilizar y razonar.
Conclusión
Las funciones de coste proporcionan un método para evaluar las decisiones. En economía, modelan la relación entre producción y eficiencia. En machine learning, miden la diferencia entre las predicciones y la realidad.
En el aprendizaje automático, las funciones de coste son la base del diseño de modelos. La elección de las funciones de pérdida determina lo que el modelo considera «éxito». El error cuadrático medio recompensa la precisión general, la entropía cruzada recompensa las probabilidades calibradas y la pérdida de bisagra recompensa la separación segura.
En todos los ámbitos y sectores, la lógica subyacente es la misma: definir un objetivo y optimizarlo. Las funciones de coste traducen objetivos vagos en cifras concretas que guían la optimización.
Las funciones de coste son útiles en economía, machine learning, fabricación, finanzas, sanidad y cualquier otro ámbito en el que se desee cuantificar las compensaciones.
Para obtener más información, recomiendo estos recursos de DataCamp.
Preguntas frecuentes sobre la función de coste
¿Qué es una función de coste?
Una función de coste determina en qué medida las predicciones de un modelo coinciden con los datos. Agrega el error a un único valor. Los algoritmos de optimización minimizan este valor para mejorar el rendimiento.
¿En qué se diferencian las funciones de coste entre las tareas de regresión y clasificación?
Los modelos de regresión predicen valores continuos, por lo que su pérdida (por ejemplo, MSE, MAE) mide la distancia numérica con respecto al objetivo.
Los modelos de clasificación predicen probabilidades de clase; las pérdidas, como la entropía cruzada, comparan la distribución de probabilidad prevista con la clase real y penalizan severamente los errores seguros.
¿Cuáles son algunas aplicaciones reales de las funciones de coste en los negocios?
Las funciones de coste son útiles en cualquier proceso empresarial que implique compensaciones u optimización. Algunos ejemplos son la optimización de precios e ingresos, la gestión de inventarios, los modelos de crédito y riesgo, la retención de clientes o la logística.
¿Cómo maneja la función de pérdida de Huber los valores atípicos en los datos?
La función de pérdida de Huber trata los errores pequeños como MSE y los errores grandes como MAE, lo que la hace menos sensible a los valores atípicos.
¿Cuál es la relación entre el costo marginal y el costo promedio?
El costo marginal (CM) mide el costo de producir una unidad adicional. El costo promedio (AC) es el costo total dividido por el número de unidades. Cuando MC < AC, producir más reduce el coste medio; cuando MC > AC, producir más aumenta el coste medio, y cuando MC = AC, el coste medio se encuentra en su mínimo.

Mark Pedigo, PhD, es un distinguido científico de datos con experiencia en ciencia de datos sanitarios, programación y educación. Doctor en Matemáticas, Licenciado en Informática y Certificado Profesional en Inteligencia Artificial, Mark combina los conocimientos técnicos con la resolución práctica de problemas. Su carrera incluye funciones en la detección del fraude, la predicción de la mortalidad infantil y la previsión financiera, junto con contribuciones al software de estimación de costes de la NASA. Como educador, ha impartido clases en DataCamp y en la Universidad Washington de San Luis, y ha sido mentor de programadores noveles. En su tiempo libre, Mark disfruta de la naturaleza de Minnesota con su esposa Mandy y su perro Harley, y toca el piano de jazz.

