Programa
As funções de custo são tipo o “marcador” das decisões. Eles medem o quanto as previsões se desviam dos valores reais de um conjunto de dados em comparação com os valores previstos. No machine learning, eles orientam os algoritmos de otimização para minimizar erros e melhorar a precisão do modelo.
Neste artigo, vamos desenvolver a intuição passo a passo. Começamos com aplicações econômicas, onde as funções de custo mostram o equilíbrio entre produção e eficiência. Depois, a gente passa para o machine learning, onde eles orientam o treinamento de modelos. Depois, vamos ver a otimização como a ponte entre os dois. Por fim, vamos ver alguns exemplos reais.
Conceitos básicos da função de custo
As funções de custo são essenciais para otimizar e avaliar. Vamos definir as funções de custo matematicamente e examinar suas principais propriedades.
Definição básica e expressão matemática das funções de custo
Uma função de custo (também chamada de “função de erro”) transforma uma ou mais variáveis de entrada em um único valor numérico que representa o “custo” de uma decisão ou previsão. No machine learning, geralmente é definido como a média da função de perda em todas as amostras do conjunto de dados.
A função de custo tem duas funções: ela serve como um objetivo que um algoritmo de otimização tenta minimizar e como uma métrica de avaliação para ver como o modelo está se saindo.
Vamos analisar uma função de custo como objetivo. Para cada casa, a função de perda penaliza a diferença entre o preço de venda real e o preço previsto. A função de custo soma essas multas em todas as casas:
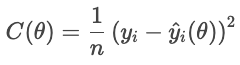
- Yi é o preço real,
- Ŷi(θ) é o preço previsto, dependente dos parâmetros θ,
- n é o número de amostras.
Um custo menor mostra que o ajuste geral é melhor, enquanto um custo maior indica um erro médio maior. O otimizador ajusta os parâmetros para minimizar esse custo.
Como métrica de avaliação, as funções de custo medem o desempenho. Por exemplo, um classificador pode ser avaliado com precisão, ou recall, ou qualquer métrica que seja apropriada para a aplicação. Assim, as funções de custo são uma forma de avaliar o sucesso.
Propriedades das funções de custo
Três propriedades matemáticas são especialmente relevantes.
- Convexidade: Uma função convexa tem a forma de uma tigela, sem apenas um vale. Isso garante que o otimizador chegue ao mínimo global, em vez de ficar preso em um vale local.
- Diferenciabilidade: Uma função de custo diferenciável tem uma inclinação bem comportada. Isso permite que os métodos baseados em gradiente ajustem os parâmetros de forma eficiente.
- Continuidade: Uma função contínua muda suavemente com suas entradas. Sem saltos repentinos significa otimização estável.
Juntas, essas propriedades determinam o quão maleável é uma função de custo para otimização. Quando uma dessas propriedades está faltando, podem ser necessárias técnicas especiais para compensar.
Economia e aplicações comerciais das funções de custo
As funções de custo mostram a relação entre a quantidade produzida e o custo total dos produtos. São uma ferramenta essencial para entender o comportamento das empresas, as estratégias de preços e a análise de lucros.
Tipos de custos econômicos
- Custos fixos. Despesas que não mudam com a produção, como aluguel ou custos de serviços públicos.
- Custos variáveis. Despesas que aumentam ou diminuem com a quantidade produzida, como mão de obra por hora ou comissão de vendas.
- Custo total (CT). A soma dos custos fixos e dos custos variáveis.
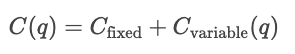
- Custo médio. O custo por unidade.
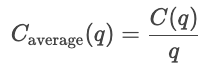
- Custo marginal (CM). O custo de produzir mais uma unidade, que é dado pela derivada do custo em relação à quantidade.
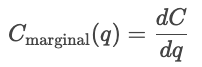
- Receita marginal (RM). A receita total extra que rolou por aumentar as vendas do produto em uma unidade.
Curvas de custos
As curvas de custo mostram como os custos mudam dependendo da quantidade total produzida. Os custos fixos são constantes, por isso são mostrados como uma linha horizontal, enquanto os custos variáveis aumentam de acordo com as unidades produzidas.
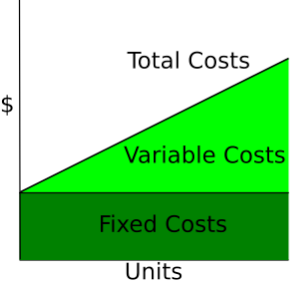
Wikipedia: Curva de custos
Custos de curto prazo versus custos de longo prazo
No curto prazo, pelo menos um insumo, como capital ou tamanho da fábrica, é mantido constante, e outros insumos variam. Os custos de curto prazo medem a eficiência com que uma empresa opera com sua estrutura atual. Então, para uma determinada quantidade q, o custo no curto prazo é a soma dos custos fixos e dos custos variáveis que dependem da quantidade.
![]()
No curto prazo, otimize dentro da capacidade atual.
No longo prazo, todos os insumos são variáveis. A empresa pode aumentar seus processos de produção. Os custos de longo prazo medem a eficiência quando a própria capacidade pode mudar, mostrando o custo mínimo alcançável para qualquer nível de produção.
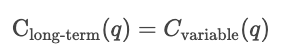
No longo prazo, otimize escolhendo a capacidade ideal.
Análise da produção e dos lucros
As funções de custo são usadas para analisar o comportamento dos preços. As empresas comparam as curvas de custo com os preços de mercado para ajudar a decidir se devem expandir ou reduzir a produção. Se o custo marginal for menor que o preço de mercado, produzir mais aumenta o lucro; se o custo marginal for maior que o preço de mercado, produzir mais unidades custa dinheiro.
As funções de custo também são usadas em estratégias de precificação. Eles decidem o preço mínimo que uma empresa pode cobrar. As empresas podem mudar acima do custo marginal para maximizar o lucro, ou mais perto do CM em setores altamente competitivos. Então, a análise de custos ajuda a definir o preço de equilíbrio, o preço com margem de lucro e as estratégias de preços dinâmicos.
O ponto de equilíbrio é quando a receita total é igual ao custo total.![]()
Neste momento, a empresa cobre todos os custos, mas não tem lucro. Produzir menos resulta em prejuízo, enquanto produzir mais gera lucro.
Lucro é a diferença entre a receita total e o custo total.
![]()
Se a receita marginal for maior que o custo marginal (MR > MC), a empresa vai aumentar a produção pra gerar mais lucro. Se a receita marginal for menor que o custo marginal (RM < CM), a empresa vai diminuir a produção pra ter mais lucro. A empresa maximiza o lucro produzindo a quantidade em que MR = MC.
Pra saber mais sobre finanças, recomendo dar uma olhada nesses recursos do DataCamp.
- Modelagem financeira no ExcelPMT().
- Avaliação patrimonial em R.
- Avaliação e análise de títulos no R.
- Excel: Calcule pagamentos de empréstimos, poupanças e muito mais.
- Fórmula do Excel para CAGR: Um guia completo.
- Previsão dos preços dos alimentos com funções.
Aplicações de machine learning com função de custo
Em aplicações de ML, as funções de custo medem os resíduos (a diferença entre os valores previstos e os valores reais) em todo o conjunto de dados. Essa seção fala sobre as principais famílias de funções de custo e como elas moldam o comportamento do modelo.
Perdas de regressão
No contexto do machine learning, o objetivo da regressão (não necessariamente linear regressão) é prever um valor contínuo. Uma função de perda de regressão mostra o erro entre os valores reais e os previstos para uma amostra específica; as funções de custo juntam as funções de perda em uma quantidade geral. Os processos de otimização usam funções de custo para minimizar o erro geral.
A gente foca nas quatro principais famílias de funções de custo: erro absoluto médio (MAE), erro quadrático médio (MSE), erro quadrático médio (RMSE) e perda de Huber.
Funções de custo diferentes lidam com erros de maneiras diferentes. Na verdade, eles definem o quanto punir os desvios entre os valores previstos e os reais. O MAE usa uma penalidade uniforme, que mostra o comportamento médio e a resistência a valores atípicos. O MSE eleva ao quadrado cada resíduo, fazendo com que os erros grandes se destaquem e sejam mais severamente penalizados. A perda de Huber mistura essas duas, usando uma penalidade quadrática para pequenos erros e uma linear para grandes erros (além de um limite δ).
Erro absoluto médio (MAE)
O erro absoluto médio é o valor médio do valor absoluto dos resíduos.
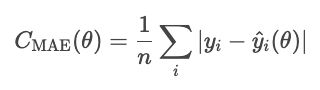
O MAE trata todos os desvios da mesma forma, então não é tão afetado por valores atípicos como outros métodos que veremos, como o MSE. Mas, o erro absoluto é meio complicado matematicamente e deixa a otimização baseada em gradiente mais difícil.
Uma observação sobre o parâmetro da função. θ representa os parâmetros do modelo. O otimizador controla o custo com base nesses parâmetros, e não diretamente nos valores previstos que deles decorrem. Então, a gente escreve o custo como uma função do θ, e não Ŷi.
MSE
O erro quadrático médio (MSE) é dado pela seguinte fórmula.
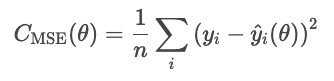
A quadratura dos resíduos exagera os erros grandes, o que torna o MSE sensível a valores atípicos. Mas esse tipo de erro é diferenciável e convexo, o que o torna fácil de otimizar.
RMSE
Uma desvantagem do MSE é que suas unidades são elevadas ao quadrado. Por exemplo, num modelo de regressão dos preços das casas, a perda é expressa em dólares ao quadrado, o que não tem um significado intuitivo. O RMSE resolve esse problema tirando a raiz quadrada do MSE.
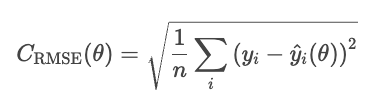
O RMSE funciona de forma parecida com o MSE, mas as unidades são as mesmas do problema (dólares, não dólares ao quadrado).
Huber
A perda de Huber é menos sensível a valores atípicos nos dados do que o MSE (ou RMSE). Combina MAE e MSE e controla a transição com um parâmetro δ.
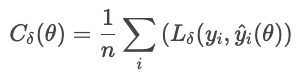
onde
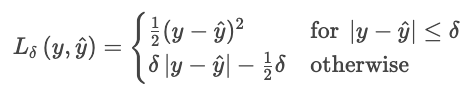
Essa fórmula evita que alguns resíduos grandes dominem a perda. A perda de Huber é uma boa escolha para dados reais barulhentos, onde você espera observações extremas ocasionais.
Perdas de classificação
A classificação prevê categorias distintas. Essas funções de custo comparam distribuições de probabilidade com rótulos verdadeiros, penalizando previsões incorretas ou excessivamente confiantes.
Perda de entropia cruzada
A perda de entropia cruzada (perda logarítmica) recompensa um modelo quando ele está certo com confiança e o penaliza quando está errado com confiança.
Para um classificador que gera probabilidades puras Ŷ, a probabilidade de o rótulo observado Y é
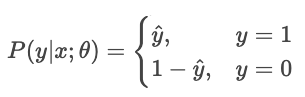
Estimativa de máxima verossimilhança (MLE) maximiza essa verossimilhança em todas as amostras.
Vamos transformar essa ideia em minimizar o custo. Minimizar é o mesmo que maximizar o negativo, então vamos inverter o sinal. Vamos também pegar lenha.
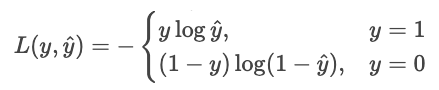
Podemos escrever isso de forma mais sucinta como uma única soma.
![]()
Por que o registro? O registro tem várias vantagens
- Transforma o produto em uma soma. Em vez de multiplicar números pequenos e arriscar um subfluxo, somamos probabilidades.
- Isso torna a função côncava. O log transforma a probabilidade numa função côncava com um único máximo global.
- Isso dá uma curva de penalidade significativa.
- p = 1,0 resulta em uma perda de 0,
- p = 0,9 resulta em uma perda de 0,1 (pequena)
- p = 0,2 resulta numa perda de 2,3 (grande)
- p = 0,01 resulta em uma perda de 4,6 (enorme)
- Evita expoentes aninhados. Na regressão logística e nas redes neurais, o log “desembrulha” exponenciais aninhados, tornando as derivadas simples e estáveis.
Digamos que um modelo prevê as chances para duas opções: “cão” (opção 0) ou “gato” (opção 1). Se a resposta certa for 1 (“gato”) e o modelo tiver 90% de certeza de que é um gato, a perda é pequena porque o modelo estava confiante e correto. Se o modelo diz que tem 10% de certeza de que é um gato, a perda é grande, porque o modelo estava confiante, mas errado.
Entropia cruzada para classificação multiclasse
Quando há mais de duas classes (“gato”, “cão”, “pássaro”), o modelo gera uma pontuação bruta (“logit”) para cada classe, indicada por Zi. Os logits podem ser qualquer número real, então eles são convertidos em probabilidades que somam um através da função softmax.
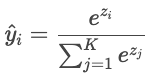
As previsões do modelo são então comparadas com os rótulos reais usando a entropia cruzada.
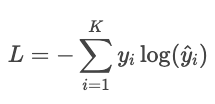
Exemplo
Digamos que o rótulo verdadeiro seja “gato” e o modelo preveja probabilidades: gato: 80%, cachorro: 15%, pássaro: 5%. A perda é
![]()
Se a probabilidade prevista para “gato” fosse de apenas 30%, a perda seria bem maior:
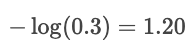
O registro pune erros confiantes e recompensa previsões altamente confiáveis.
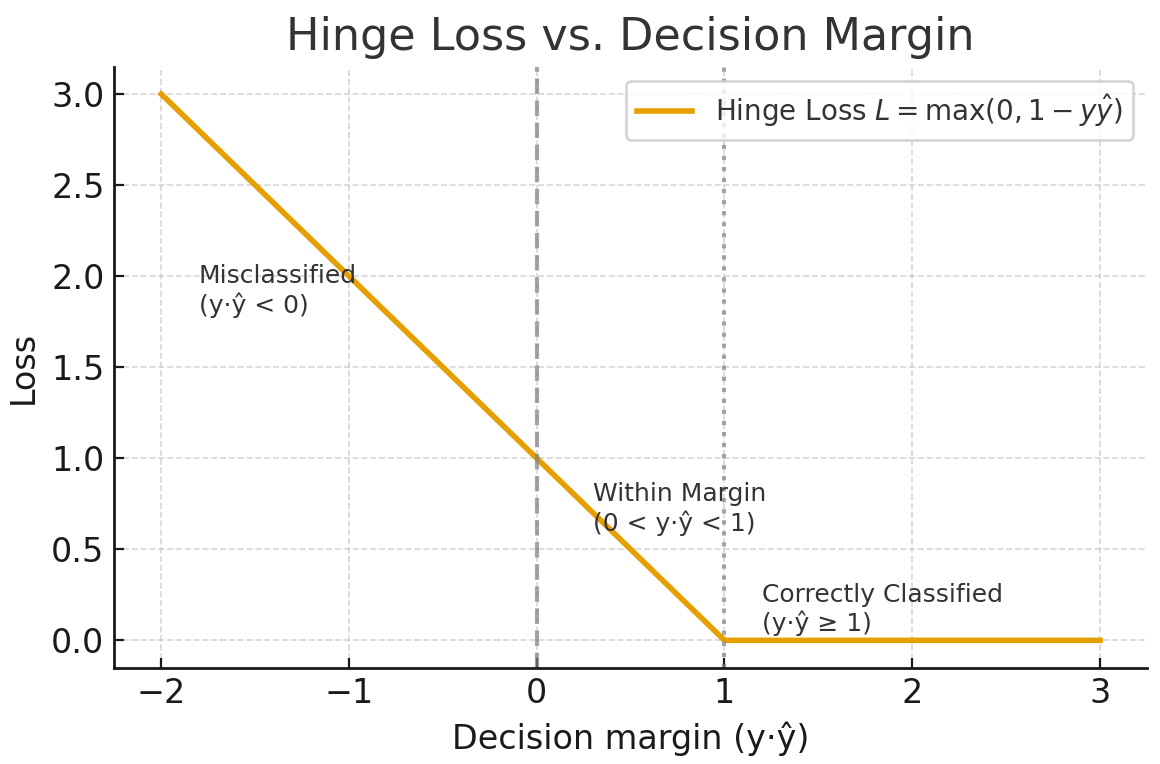
Perda da dobradiça
A perda de articulação é usada principalmente para classificação de margem máxima, como em máquinas de vetor de suporte (SVMs). O objetivo é classificar com segurança, mantendo as previsões longe da fronteira de decisão.
Para classificação binária, a perda de articulação é dada pela seguinte fórmula.
![]()
onde
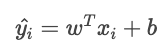
A função de custo total é
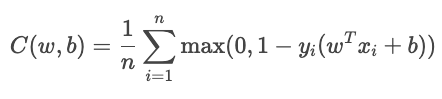
O termo YiŶi mexe como a amostra está bem classificada.
- Quando é maior que 1, a amostra fica do lado certo da fronteira, sem perda.
- Quando está entre 0 e 1, o ponto está dentro da margem, então uma pequena penalidade é aplicada.
- Quando é menor que 0, o modelo classificou errado. A perda aumenta linearmente com a distância da fronteira.
Gerado pelo chatGPT 5
Kullback-Leibler (KL)
A divergência de Kullback-Leibler (KL) é uma medida de quanto uma distribuição de probabilidade aproximada Q difere de uma determinada distribuição de probabilidade P. Ela é definida como
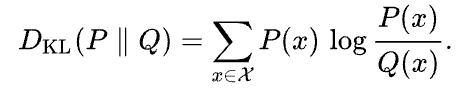
Wikipedia
A divergência KL pode ser interpretada como a diferença média do número de bits para codificar amostras de P usando um código otimizado para Q.
Regularização
As técnicas de regularização evitam que os modelos se ajustem ao ruído nos dados de treinamento, adicionando um termo à função de custo que penaliza soluções muito complexas.
Sem regularização, o modelo minimiza a perda:
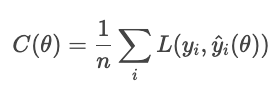
Com a regularização, o modelo adiciona um termo de penalidade.
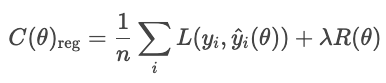
onde
- L é a perda normal (por exemplo, RMSE, entropia cruzada)
- R(θ) mede a complexidade do modelo
- λ controla o equilíbrio entre ajuste e simplicidade
Os tipos comuns de regularização são L1, L2 e elastic net.
A regularização L1 (também conhecida como lasso) adiciona o valor absoluto de cada peso do modelo à função de custo.
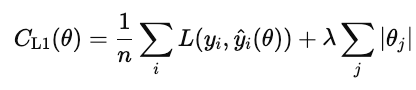
Quando esse custo é minimizado, muitos pesos são reduzidos a zero. Isso faz do L1 uma forma de seleção automática de características. Os recursos que não contribuem são colocados em zero.
A regularização L2 (também conhecida como regressão ridge) penaliza o quadrado de cada peso do modelo.
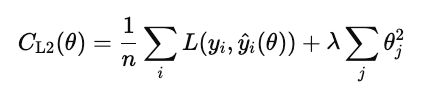
Diferente do L1, ele não zera os pesos, mas os reduz de forma suave. Isso mantém todas as características do modelo, mas reduz a influência delas para estabilizar as previsões.
A rede elástica adiciona tanto L1 quanto L2.
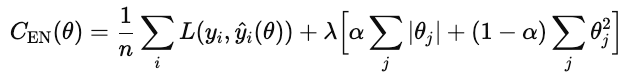
λ controla a intensidade da regularização geral. α é um número entre 0 e 1 que controla as porcentagens de L1 versus L2, onde 1 é L1 puro e 0 é ridge puro.
Compromissos
As diferentes estratégias de perda de classificação têm vantagens e desvantagens.
A entropia cruzada maximiza a probabilidade correta, penalizando respostas erradas dadas com confiança. As desvantagens são que ele é sensível a valores atípicos e dados mal rotulados. Funciona melhor quando você se preocupa com a qualidade da confiança (por exemplo, modelos de risco).
A perda de articulação reforça uma margem para que as classificações corretas não sejam apenas corretas, mas também confiáveis. Ele ignora amostras de valores que estão bem além da margem e aplica uma penalidade linear para violações. É menos sensível a valores atípicos do que a entropia cruzada, mas mais difícil de otimizar suavemente, pois não é diferenciável na articulação.
A divergência de Kullback-Leibler (KL) compara uma distribuição de probabilidade com outra. É igual à entropia cruzada menos a entropia da distribuição real.
Para mais informações, confira estes links.
- Função de perda de entropia cruzada em machine learning: Aumentando a precisão do modelo
- De dados a dinheiro - Prevendo os custos dos seguros
- Otimize as previsões de preços com engenharia de recursos
- Folha de referência sobre dimensões da qualidade dos dados
- Tutorial sobre correlação R
Implementação e prática da função de custo no machine learning
Até agora, falamos sobre funções de custo na teoria. Na prática, o sucesso de um modelo de ML depende de como ele consegue minimizar essas funções de forma eficiente. Nesta seção, vamos falar sobre os detalhes práticos dos principais algoritmos de otimização e estratégias de ajuste.
Algoritmos de otimização e ajuste de parâmetros
Otimização é o processo de achar os valores ideais dos parâmetros do modelo que minimizam uma função de custo. Em ML, isso significa descobrir os parâmetros que tornam as previsões o mais próximas possível dos valores reais.
Descida gradiente
O gradiente descendente é o algoritmo padrão para otimizar funções de custo. Ele atualiza os parâmetros do modelo de forma iterativa na direção que mais reduz o custo, o gradiente negativo. Basicamente, ele mede a inclinação multivariável da função de custo e desce a ladeira.
A regra de atualização é
![]()
onde θ são os parâmetros do modelo, n é a taxa de aprendizagem e ![]() é o gradiente da função de custo em relação aos parâmetros.
é o gradiente da função de custo em relação aos parâmetros.
A escolha da taxa de aprendizagem é super importante. Se for muito grande, as atualizações ultrapassam o mínimo e oscilam ou divergem. Se for muito pequeno, a convergência fica lenta e pode parar nos mínimos locais.
As principais variantes são batch, estocástico e mini-batch.
- Descida de gradiente em lote. Calcula o gradiente usando todo o conjunto de treinamento. É estável, mas lento e consome muita memória para grandes conjuntos de dados ou aprendizagem online.
- Descida de gradiente estocástico (SGD). Atualiza os parâmetros depois de cada exemplo de treinamento. É rápido e eficiente em termos de memória, mas barulhento no sentido de que cada etapa pode se desviar ligeiramente do caminho ideal. Mas, a aleatoriedade pode ajudar a escapar dos mínimos locais.
- Descida de gradiente em mini-lotes. Um acordo prático. Ele calcula gradientes em pequenos lotes para equilibrar velocidade e estabilidade. Também permite o paralelismo da GPU.
Otimizadores adaptativos
O gradiente descendente padrão usa uma taxa de aprendizagem fixa para todos os parâmetros. Em modelos complexos, diferentes parâmetros podem precisar de diferentes tamanhos de passo. Os otimizadores adaptativos ajustam as taxas de aprendizagem com base no histórico das magnitudes dos gradientes.
- RMSProp usa uma média exponencialmente decrescente dos gradientes quadrados recentes.
![]()
O aprendizado de cada parâmetro é dimensionado inversamente a essa média. Isso evita oscilações e permite um progresso estável, mesmo quando alguns parâmetros têm gradientes acentuados. O RMSProp é muito usado para redes recorrentes e dados ruidosos.
- Estimativa Adaptativa do Momento (Adam) programa tanto a média quanto a variação dos gradientes anteriores e adapta os tamanhos dos passos de forma dinâmica.
![]()
Ele converge rápido, é resistente a dados ruidosos e é o otimizador padrão para estruturas de redes profundas.
Escalonamento e inicialização de recursos
Antes de otimizar com o método de descida de gradiente, ajuste as características para que funcionem em intervalos comparáveis. O dimensionamento adequado melhora a estabilidade e a eficiência da otimização.
Sem escalonamento, os recursos com grandes intervalos numéricos dominam o gradiente. O gradiente descendente então ziguezagueia em vez de dar passos diretos em direção ao mínimo.
Existem duas abordagens comuns.
- Padronização. Cada centro apresenta zero e redimensiona para a variância unitária.
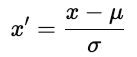
onde u é a média e ơ é o desvio padrão. A padronização mantém a estrutura dos dados.
- Normalization. Redimensione cada recurso para um intervalo fixo, normalmente [0, 1].
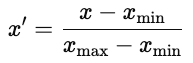
A normalização é comum em redes neurais, onde as funções de ativação funcionam melhor com entradas limitadas.
Estratégias de inicialização de parâmetros
A inicialização dos parâmetros influencia fortemente o treinamento do modelo. Uma inicialização ruim pode fazer com que a convergência demore, os gradientes explodam ou sumam, ou os modelos não aprendam. Uma boa inicialização coloca os parâmetros numa região da superfície de custo onde os gradientes são estáveis.
- Inicialização aleatória. Atribui pequenos valores aleatórios, normalmente extraídos de uma distribuição uniforme ou normal. A aleatoriedade quebra a simetria para que os parâmetros aprendam características distintas. Mas, se a variação for muito alta ou baixa, os gradientes podem explodir ou sumir.
- Inicialização do Xavier (Glorot). Feito pra funções de ativação não lineares, tipo tanh ou sigmoid, o Xavier ajusta a variância dos pesos de acordo com o número de conexões de entrada e saída.
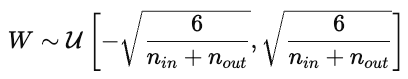
Isso mantém as ativações e os gradientes mais ou menos constantes entre as camadas.
- Ele inicializou. Ajusta a variação para ativações ReLU, que zera valores negativos. Os pesos são tirados de uma distribuição normal com uma variância específica:
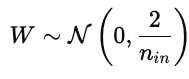
Isso evita que os gradientes desapareçam muito rápido durante a retropropagação.
Monitoramento, diagnóstico e visualização
Uma curva de perda de treinamento mostra o erro do modelo no conjunto de dados de treinamento ao longo do tempo. Isso mostra como o modelo atualiza seus parâmetros pra minimizar o erro. Uma curva que vai diminuindo mostra que o modelo está aprendendo padrões a partir dos dados.
A curva de perda de validação mostra como o modelo consegue generalizar em dados que não foram vistos, tipo um conjunto de retenção ou validação. Isso mostra como o modelo consegue prever dados que nunca foram vistos antes.
O ideal é que as duas curvas diminuam no começo e depois fiquem mais planas. Isso mostra que o modelo está aprendendo e generalizando de forma eficaz.
O sobreajuste ( ) rola quando o modelo aprende o ruído como se fosse sinal e não generaliza bem. Isso aparece em um gráfico que mostra as curvas de treinamento e validação quando a perda de treinamento diminui, mas a perda de validação aumenta. As correções incluem usar um conjunto de dados maior ou aplicar regularização no modelo.
O subajuste acontece quando o modelo não consegue captar os padrões subjacentes nos dados. Tanto as curvas de treinamento quanto as de validação continuam altas. Nesse caso, tente usar mais dados, um modelo mais complexo ou diminua a regularização.
A convergência é o ponto em que a curva se estabiliza e a formação de minério oferece pouca melhoria. Esse é o ponto ideal entre o sobreajuste e o subajuste.
Otimização da função de custo e teoria da decisão
Vimos como a economia e o machine learning dependem da otimização para orientar a tomada de decisões e o treinamento. Ambos os campos se esforçam para tomar as melhores decisões com base em uma métrica de custo ou perda. Vamos nos aprofundar na teoria da otimização de forma mais geral.
Funções objetivas
Uma função objetivo é uma função matemática que define o que queremos minimizar ou maximizar. Nos casos que vimos até agora, a gente minimizou o custo ou o erro. Para a economia, analisamos as curvas de custo e, com o aprendizado de máquina, analisamos as perdas de regressão (MAE, RMSE, Huber) e as perdas de classificação (entropia cruzada, perda de dobradiça, perda KL). Esses são dois exemplos de como otimizar uma função objetivo.
Otimização multiobjetiva
Muitas vezes, a gente quer otimizar vários objetivos, que muitas vezes são conflitantes. Uma empresa pode querer aumentar o lucro e, ao mesmo tempo, diminuir o risco. Um cientista de dados pode querer melhorar a precisão do modelo sem perder a capacidade de interpretação ou a imparcialidade. Esses objetivos concorrentes definem um problema de otimização multiobjetivo, no qual melhorar um objetivo pode piorar outro.
fronteira de Pareto
Uma solução é ótima no sentido de Pareto se nenhum objetivo puder ser melhorado sem piorar pelo menos um outro objetivo. O conjunto de soluções ótimas de Pareto forma afronteira de Pareto , uma curva que consiste nas melhores combinações possíveis. Cada ponto nessa curva mostra um equilíbrio diferente de prioridades.
Por exemplo, aumentar a complexidade de um modelo pode melhorar a precisão, mas reduzir a interpretabilidade. Modelos mais simples são mais fáceis de explicar, mas podem ter um desempenho pior. A fronteira de Pareto inclui as “melhores combinações” e exclui as soluções que são dominadas por outras variáveis.
Escolher o ponto certo depende do contexto e do bom senso. Você pode atribuir pesos a cada meta ou usar restrições de política.
Prejuízo esperado
Quando os resultados são incertos, a otimização minimiza a perda esperada (), que é a perda média em todos os cenários possíveis. Em ML, essa ideia aparece na função de risco.
![]()
onde L(Y,f(x)) é a perda para uma determinada previsão, e a expectativa é calculada com base na distribuição dos dados. O objetivo é achar o modelo f que minimiza essa perda esperada. Esse modelo tem o melhor desempenho em média, não só em amostras individuais.
Risco bayesiano
O risco de Bayes é o limite inferior teórico da perda esperada. Formalmente, é dada pela seguinte fórmula.
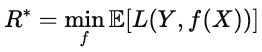
Intuitivamente, é a “pontuação perfeita”, ou seja, o menor valor possível com informações perfeitas sobre a distribuição dos dados. Quanto mais próximo o desempenho de um modelo estiver do risco de Bayes, mais ideal ele será.
Aplicações interdisciplinares
As funções de custo são usadas em qualquer setor que toma decisões com base em dados. Elas ajudam a equilibrar objetivos concorrentes e a formalizar o que significa “melhor”. Essas funções equilibram objetivos concorrentes e orientam a otimização. A mesma lógica usada para treinar modelos de ML é usada para otimizar processos do mundo real.
Aplicações industriais e casos de uso do domínio
Na fabricação, por exemplo, as funções de custo medem as perdas, como a perda de estoque. Uma função de custo de estoque equilibra o gasto com excesso de estoque e as multas por falta de estoque. Estruturas parecidas são usadas para planejar a produção ou o uso de energia, pra minimizar o custo total esperado em situações de incerteza.
Na área da saúde, os modelos preditivos usam funções de custo para equilibrar a precisão e a alocação de recursos. Por exemplo, um modelo de risco de readmissão identifica pacientes de alto risco logo de cara, para que os médicos possam intervir com ligações de acompanhamento ou visitas domiciliares. Deixar passar um paciente de alto risco custa mais caro do que sinalizar um de baixo risco, então a função penaliza esses erros de forma diferente.
As finanças também usam funções objetivas. Por exemplo, os modelos de pontuação de crédito prevêem a probabilidade de um mutuário entrar em incumprimento num empréstimo dentro de um determinado período de tempo, digamos, doze meses. Aprovar um tomador de empréstimo arriscado pode trazer prejuízo financeiro, enquanto rejeitar um tomador seguro pode fazer você perder receita. O modelo minimiza o custo esperado.
Em todos esses domínios, as funções de custo equilibram as compensações em quantidades mensuráveis que os tomadores de decisão podem usar e analisar.
Conclusão
As funções de custo são um jeito de avaliar as decisões. Na economia, eles modelam o equilíbrio entre produção e eficiência. No machine learning, eles medem a diferença entre as previsões e a realidade.
No aprendizado de máquina, as funções de custo são a base do design do modelo. A escolha das funções de perda determina o que o modelo considera “sucesso”. O erro quadrático médio recompensa a precisão geral, a entropia cruzada recompensa as probabilidades calibradas e a perda de dobradiça recompensa a separação confiável.
Em todos os domínios e setores, a lógica por trás disso é a mesma: definir um objetivo e otimizá-lo. As funções de custo transformam metas vagas em números concretos que orientam a otimização.
As funções de custo são úteis em economia, machine learning, manufatura, finanças, saúde e em qualquer outro lugar onde se queira quantificar as compensações.
Pra saber mais, recomendo esses recursos do DataCamp.
Perguntas frequentes sobre a função de custo
O que é uma função de custo?
Uma função de custo mostra como as previsões de um modelo se encaixam nos dados. Ele junta o erro em um único valor. Os algoritmos de otimização minimizam esse valor para melhorar o desempenho.
Como as funções de custo diferem entre tarefas de regressão e classificação?
Os modelos de regressão prevêem valores contínuos, então a perda deles (por exemplo, MSE, MAE) mede a distância numérica do alvo.
Os modelos de classificação prevêem as probabilidades das classes; perdas como a entropia cruzada comparam a distribuição de probabilidade prevista com a classe real e penalizam fortemente os erros confiantes.
Quais são algumas aplicações reais das funções de custo nos negócios?
As funções de custo são úteis em qualquer processo de negócios que envolva compromissos ou otimização. Exemplos incluem otimização de preços e receitas, gestão de estoque, modelagem de crédito e risco, retenção de clientes ou logística.
Como a função de perda de Huber lida com valores atípicos nos dados?
A função de perda de Huber trata pequenos erros como MSE e grandes erros como MAE, o que a torna menos sensível a valores atípicos.
Qual é a relação entre custo marginal e custo médio?
O custo marginal (CM) mede o custo de produzir uma unidade a mais. O custo médio (CM) é o custo total dividido pelo número de unidades. Quando MC < AC, produzir mais diminui o custo médio; quando MC > AC, produzir mais aumenta o custo médio; e quando MC = AC, o custo médio está no seu mínimo.

Mark Pedigo, PhD, é um ilustre cientista de dados com experiência em ciência de dados de saúde, programação e educação. Com doutorado em matemática, bacharelado em ciência da computação e certificado profissional em IA, Mark combina conhecimento técnico com solução prática de problemas. Sua carreira inclui funções em detecção de fraudes, previsão de mortalidade infantil e previsão financeira, além de contribuições para o software de estimativa de custos da NASA. Como educador, ele lecionou no DataCamp e na Washington University em St. Louis e foi mentor de programadores juniores. Em seu tempo livre, Mark curte o ar livre de Minnesota com sua esposa Mandy e seu cachorro Harley e toca piano jazz.


