Lernpfad
Kostenfunktionen sind sozusagen die „Punktezähler“ von Entscheidungen. Sie messen, wie stark die Vorhersagen von den tatsächlichen Werten eines Datensatzes im Vergleich zu den vorhergesagten Werten abweichen. Beim maschinellen Lernen helfen sie dabei, Optimierungsalgorithmen so zu steuern, dass Fehler minimiert werden und die Genauigkeit der Modelle verbessert wird.
In diesem Artikel entwickeln wir Schritt für Schritt ein Gefühl dafür. Wir fangen mit wirtschaftlichen Anwendungen an, wo Kostenfunktionen den Kompromiss zwischen Produktion und Effizienz beschreiben. Dann reden wir über maschinelles Lernen, wo sie das Training von Modellen vorantreiben. Als Nächstes schauen wir uns die Optimierung als Brücke zwischen den beiden an. Zum Schluss schauen wir uns ein paar Beispiele aus der Praxis an.
Kernkonzepte der Kostenfunktion
Kostenfunktionen sind echt wichtig für die Optimierung und Bewertung. Lass uns Kostenfunktionen mathematisch definieren und ihre wichtigsten Eigenschaften anschauen.
Grundlegende Definition und mathematischer Ausdruck von Kostenfunktionen
Eine Kostenfunktion (auch „Fehlerfunktion” genannt) ordnet eine oder mehrere Eingabevariablen einem einzigen numerischen Wert zu, der die „Kosten” einer Entscheidung oder Vorhersage darstellt. Beim maschinellen Lernen wird es normalerweise als der Durchschnitt der Verlustfunktion über alle Beispiele im Datensatz.
Die Kostenfunktion hat zwei Aufgaben: Sie ist das Ziel, das ein Optimierungsalgorithmus minimiert, und sie ist ein Maßstab, um zu sehen, wie gut ein Modell funktioniert.
Schauen wir uns mal eine Kostenfunktion als Ziel an. Für jedes Haus wird die Differenz zwischen dem tatsächlichen Verkaufspreis und dem vorhergesagten Preis in der Verlustfunktion als Minuspunkt gewertet. Die Kostenfunktion summiert diese Strafen für alle Häuser:
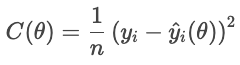
- Yi ist der tatsächliche Preis,
- Ŷi(θ) ist der vorhergesagte Preis, der von den Parametern θ,
- n ist die Anzahl der Proben.
Niedrigere Kosten bedeuten, dass es insgesamt besser passt, während höhere Kosten auf einen größeren durchschnittlichen Fehler hindeuten. Der Optimierer passt die Einstellungen an, um diese Kosten zu senken.
Als Bewertungsmaßstab messen Kostenfunktionen die Leistung. Ein Klassifikator kann zum Beispiel anhand der Genauigkeit, der Wiederauffindbarkeit oder einer anderen für die Anwendung passenden Metrik bewertet werden. So kann man mit Kostenfunktionen den Erfolg einschätzen.
Eigenschaften von Kostenfunktionen
Drei mathematische Eigenschaften sind besonders wichtig.
- Konvexität: Eine konvexe Funktion sieht aus wie eine Schüssel, nur ohne ein einziges Tal. Das stellt sicher, dass der Optimierer das globale Minimum findet und nicht in einem lokalen Tief hängen bleibt.
- Differenzierbarkeit: Eine differenzierbare Kostenfunktion hat eine gut verhaltensweise Steigung. Dadurch können gradientenbasierte Methoden Parameter effizient anpassen.
- Kontinuität: Eine stetige Funktion ändert sich gleichmäßig mit ihren Eingaben. Keine plötzlichen Sprünge bedeutet eine stabile Optimierung.
Zusammen bestimmen diese Eigenschaften, wie gut sich eine Kostenfunktion für die Optimierung eignet. Wenn eine dieser Eigenschaften fehlt, braucht man vielleicht spezielle Techniken, um das auszugleichen.
Wirtschaft und Geschäftsanwendungen von Kostenfunktionen
Kostenfunktionen zeigen, wie die Menge der Produktion und die Gesamtkosten der Produkte zusammenhängen. Sie sind echt wichtig, um das Verhalten von Unternehmen, Preisstrategien und Gewinnanalysen zu verstehen.
Arten von wirtschaftlichen Kosten
- Fixkosten. Kosten, die sich nicht mit der Produktion ändern, wie Miete oder Nebenkosten.
- Variable Kosten. Kosten, die mit der produzierten Menge steigen oder fallen, wie zum Beispiel Stundenlohn oder Verkaufsprovisionen.
- Gesamtkosten (TC). Die Summe aus Fixkosten und variablen Kosten.
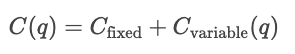
- Durchschnittliche Kosten. Die Kosten pro Einheit.
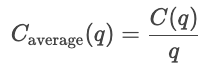
- Grenzkosten (MC). Die Kosten für die Produktion einer weiteren Einheit, die man durch die Ableitung der Kosten nach der Menge berechnet.
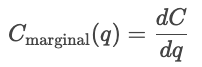
- Grenzertrag (MR). Der zusätzliche Gesamtumsatz, der durch den Verkauf einer zusätzlichen Produkteinheit erzielt wird.
Kostenkurven
Kostenkurven zeigen, wie sich die Kosten je nach Gesamtproduktionsmenge ändern. Fixkosten sind immer gleich, deshalb werden sie als gerade Linie gezeigt, während variable Kosten mit der Anzahl der produzierten Einheiten steigen.
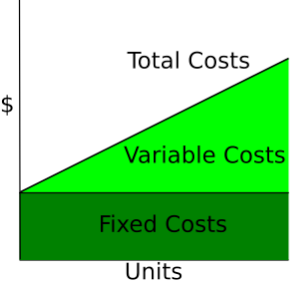
Wikipedia: Kostenkurve
Kurzfristige versus langfristige Kosten
Kurzfristig bleibt mindestens ein Input, wie Kapital oder Anlagengröße, gleich, während andere Inputs variieren. Kurzfristige Kosten zeigen, wie gut ein Unternehmen mit seiner aktuellen Struktur läuft. Also, für eine bestimmte Menge q sind die kurzfristigen Kosten die Summe aus den Fixkosten und den von der Menge abhängigen variablen Kosten.
![]()
Kurzfristig solltest du innerhalb der aktuellen Kapazitäten optimieren.
Auf lange Sicht sind alle Inputs variabel. Die Firma könnte ihre Produktionsprozesse ausbauen. Langfristige Kosten zeigen, wie effizient es ist, wenn sich die Kapazität ändern kann, und zeigen die niedrigsten Kosten, die man für jedes Produktionsniveau erreichen kann.
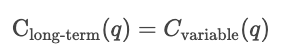
Auf lange Sicht solltest du die Optimierung machen, indem du die beste Kapazität auswählst.
Produktions- und Gewinnanalyse
Kostenfunktionen werden benutzt, um das Preisverhalten zu analysieren. Firmen schauen sich die Kostenkurven und die Marktpreise an, um zu entscheiden, ob sie die Produktion hochfahren oder runterfahren sollen. Wenn die Grenzkosten unter dem Marktpreis liegen, bringt mehr Produktion mehr Gewinn; wenn die Grenzkosten über dem Marktpreis liegen, kostet mehr Produktion Geld.
Kostenfunktionen werden auch bei Preisstrategien genutzt. Sie legen den niedrigsten Preis fest, den ein Unternehmen verlangen kann. Firmen können ihre Preise über die Grenzkosten hinaus anheben, um ihren Gewinn zu maximieren, oder sich in Branchen mit starkem Wettbewerb näher an die Grenzkosten halten. Die Kostenanalyse hilft also bei der Break-even-Preisgestaltung, der Kosten-Plus-Preisgestaltung und dynamischen Preisstrategien.
Die Gewinnschwelle ist erreicht, wenn die Gesamteinnahmen den Gesamtkosten entsprechen.![]()
Im Moment übernimmt die Firma alle Kosten, macht aber keinen Gewinn. Weniger zu machen führt zu Verlusten, während mehr machen Gewinn bringt.
Der Gewinn ist die Differenz zwischen dem Gesamtumsatz und den Gesamtkosten.
![]()
Wenn der Grenzerlös die Grenzkosten übersteigt (MR > MC), wird das Unternehmen die Produktion erhöhen, um mehr Gewinn zu machen. Wenn der Grenzerlös unter den Grenzkosten liegt (MR < MC), wird das Unternehmen die Produktion runterfahren, um mehr Gewinn zu machen. Die Firma macht den größten Gewinn, indem sie so viel produziert, dass der Grenzerlös gleich den Grenzkosten ist.
Für mehr Infos zum Thema Finanzen schau dir doch mal diese DataCamp-Ressourcen an.
- Finanzmodellierung in ExcelPMT().
- Aktienbewertung in R.
- Anleihebewertung und -analyse in R.
- Excel: Berechne Kreditraten, Ersparnisse und mehr.
- Excel-Formel für CAGR: Ein umfassender Leitfaden.
- Prognose der Lebensmittelpreise mit Funktionen.
Kostenfunktion Anwendungen des maschinellen Lernens
In ML-Anwendungen messen Kostenfunktionen die Residuen (also die Differenz zwischen vorhergesagten und tatsächlichen Werten) über den ganzen Datensatz. Hier geht's um die wichtigsten Arten von Kostenfunktionen und wie sie das Verhalten von Modellen beeinflussen.
Regressionsverluste
Im Zusammenhang mit maschinellem Lernen ist das Ziel der Regression (nicht unbedingt lineare Regression) ist es, einen kontinuierlichen Wert vorherzusagen. Eine Regressionsverlustfunktion misst den Fehler zwischen den tatsächlichen und den vorhergesagten Werten für eine bestimmte Stichprobe; Kostenfunktionen fassen Verlustfunktionen zu einer Gesamtgröße zusammen. Optimierungsprozesse nutzen Kostenfunktionen, um den Gesamtfehler zu minimieren.
Wir konzentrieren uns auf die vier Hauptfamilien von Kostenfunktionen: mittlerer absoluter Fehler (MAE), mittlerer quadratischer Fehler (MSE), mittlere quadratische Fehlerwurzel (RMSE) und Huber-Verlust.
Verschiedene Kostenfunktionen gehen unterschiedlich mit Fehlern um. Im Grunde legen sie fest, wie streng Abweichungen zwischen den vorhergesagten und den tatsächlichen Werten bestraft werden sollen. Der MAE nutzt eine einheitliche Strafe, die das mittlere Verhalten und die Robustheit gegenüber Ausreißern zeigt. MSE quadriert jeden Restwert, sodass große Fehler dominieren und stärker bestraft werden. Der Huber-Verlust mischt diese beiden, indem er eine quadratische Strafe für kleine Fehler und eine lineare für große Fehler (über einem Schwellenwert δ) verwendet.
Mittlerer absoluter Fehler (MAE)
Der mittlere absolute Fehler ist der Durchschnitt vom absoluten Wert der Residuen.
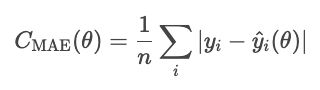
Der MAE behandelt alle Abweichungen gleich, sodass er nicht so stark von Ausreißern beeinflusst wird wie andere Methoden, die wir noch sehen werden, wie zum Beispiel der MSE. Der absolute Fehler ist aber mathematisch kompliziert und macht die gradientenbasierte Optimierung schwieriger.
Ein Hinweis zum Funktionsparameter. θ steht für die Modellparameter. Der Optimierer regelt die Kosten anhand dieser Parameter und nicht direkt anhand der daraus abgeleiteten Vorhersagewerte. Deshalb schreiben wir die Kosten als Funktion von θ, nicht als Funktion von Ŷi.
MSE
Der mittlere quadratische Fehler (MSE) wird durch die folgende Formel berechnet.
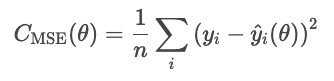
Die Quadrierung der Residuen übertreibt große Fehler, was die MSE empfindlich gegenüber Ausreißern macht. Diese Art von Fehler ist aber differenzierbar und konvex, was die Optimierung einfacher macht.
RMSE
Ein Problem beim MSE ist, dass die Werte quadriert sind. In einem Regressionsmodell für Immobilienpreise ist der Verlust zum Beispiel in Dollar zum Quadrat angegeben, was nicht wirklich einleuchtend ist. Der RMSE macht das wieder gut, indem er die Quadratwurzel aus dem MSE zieht.
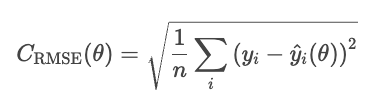
RMSE ist ähnlich wie MSE, aber die Einheiten sind die gleichen wie im Problem (Dollar, nicht quadrierte Dollar).
Huber
Der Huber-Verlust reagiert weniger empfindlich auf Ausreißer in den Daten als der MSE (oder RMSE). Es kombiniert MAE und MSE und steuert den Übergang mit einem Parameter δ.
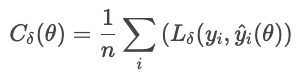
wo
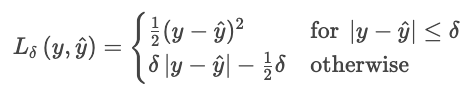
Diese Formel verhindert, dass ein paar große Restwerte den Verlust dominieren. Der Huber-Verlust ist eine gute Wahl für verrauschte Daten aus der Praxis, bei denen man gelegentlich extreme Beobachtungen erwarten kann.
Klassifizierungsverluste
Die Klassifizierung sagt einzelne Kategorien voraus. Diese Kostenfunktionen vergleichen Wahrscheinlichkeitsverteilungen mit echten Labels und bestrafen falsche oder zu selbstsichere Vorhersagen.
Kreuzentropieverlust
Der Kreuzentropieverlust (logarithmischer Verlust) belohnt ein Modell, wenn es sicher richtig liegt, und bestraft es, wenn es sicher falsch liegt.
Für einen Klassifikator, der reine Wahrscheinlichkeiten ausgibt Ŷ, ist die Wahrscheinlichkeit, dass das beobachtete Label Y ist
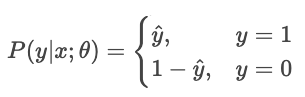
Maximalwahrscheinlichkeitsschätzung (MLE) maximiert diese Wahrscheinlichkeit über alle Stichproben.
Lass uns diese Idee nutzen, um die Kosten für zu senken. Minimieren ist dasselbe wie das Negative maximieren, also drehen wir das Vorzeichen um. Lasst uns auch Protokolle erstellen.
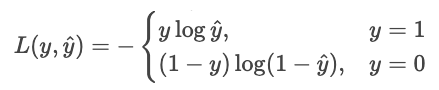
Wir können das kürzer als eine einzige Summe schreiben.
![]()
Wieso das Protokoll? Das Protokoll hat ein paar Vorteile.
- Es macht das Produkt zu einer Summe. Anstatt kleine Zahlen zu multiplizieren und einen Unterlauf zu riskieren, addieren wir Wahrscheinlichkeiten.
- Das macht die Funktion konkav. Das Protokoll macht aus der Wahrscheinlichkeit eine konkave Funktion mit einem einzigen globalen Maximum.
- Es gibt eine sinnvolle Strafkurve.
- p = 1,0 führt zu einem Verlust von 0,
- p = 0,9 führt zu einem Verlust von 0,1 (gering)
- p = 0,2 führt zu einem Verlust von 2,3 (groß)
- p = 0,01 führt zu einem Verlust von 4,6 (riesig)
- Es vermeidet verschachtelte Exponenten. Bei der logistischen Regression und in neuronalen Netzen „entpackt“ der Logarithmus verschachtelte Exponentialfunktionen, wodurch Ableitungen einfach und stabil werden.
Angenommen, ein Modell sagt die Wahrscheinlichkeiten für zwei Optionen voraus: „Hund“ (Option 0) oder „Katze“ (Option 1). Wenn die richtige Antwort 1 („Katze“) ist und das Modell zu 90 % sicher ist, dass es sich um eine Katze handelt, ist der Verlust gering, weil das Modell zuversichtlich und richtig lag. Wenn das Modell sagt, dass es zu 10 % sicher ist, dass es sich um eine Katze handelt, ist der Verlust groß, weil das Modell zuversichtlich war, aber falsch lag.
Kreuzentropie für die Mehrklassenklassifizierung
Wenn es mehr als zwei Klassen gibt („Katze“, „Hund“, „Vogel“), gibt das Modell für jede Klasse einen Rohwert („Logit“) aus, der mit Zi bezeichnet wird. Logits können beliebige reelle Zahlen sein, deshalb werden sie über die Softmax-Funktion in Wahrscheinlichkeiten umgewandelt, die sich zu eins addieren.
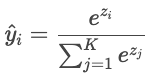
Die Vorhersagen des Modells werden dann mit den tatsächlichen Labels mithilfe der Kreuzentropie verglichen.
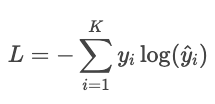
Beispiel
Angenommen, die richtige Bezeichnung ist „Katze“ und das Modell sagt Wahrscheinlichkeiten voraus: Katze: 80 %, Hund: 15 %, Vogel: 5 %. Der Verlust ist
![]()
Wenn die Wahrscheinlichkeit für „Katze“ nur 30 % wäre, wäre der Verlust viel größer:
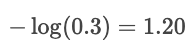
Das Protokoll bestraft selbstbewusste Fehler und belohnt Vorhersagen mit hohem Selbstvertrauen.
Gelenkverlust
Der Scharnierverlust wird meistens für die Max-Margin-Klassifizierung verwendet, wie bei Support-Vektor-Maschinen (SVMs). Das Ziel ist, zuverlässig zu klassifizieren, indem man die Vorhersagen weit weg von der Entscheidungsgrenze hält.
Für die binäre Klassifizierung wird der Scharnierverlust durch die folgende Formel berechnet.
![]()
wo
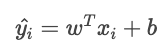
Die Gesamtkostenfunktion lautet
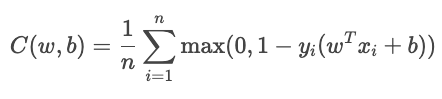
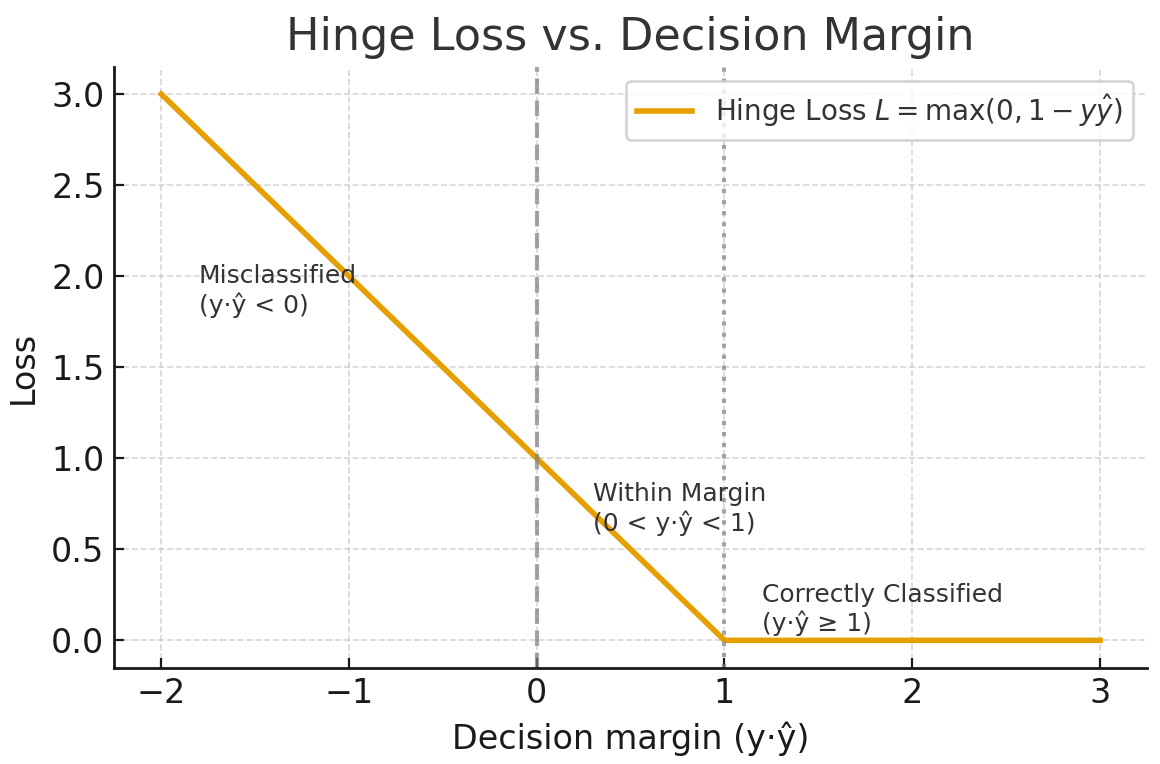
Der Begriff YiŶi zeigt, wie gut die Stichprobe klassifiziert ist.
- Wenn der Wert größer als 1 ist, liegt die Probe ohne Verlust auf der richtigen Seite der Grenze.
- Wenn der Wert zwischen 0 und 1 liegt, ist der Punkt innerhalb der Toleranzgrenze, sodass eine kleine Strafe verhängt wird.
- Wenn der Wert unter 0 liegt, hat das Modell eine falsche Klassifizierung vorgenommen. Der Verlust nimmt linear mit der Entfernung von der Grenze zu.
Erstellt von chatGPT 5
Kullback-Leibler (KL)
Die Kullback-Leibler-Divergenz (KL-Divergenz) zeigt, wie sehr eine angenäherte Wahrscheinlichkeitsverteilung Q von einer bestimmten Wahrscheinlichkeitsverteilung P abweicht. Sie wird so definiert:
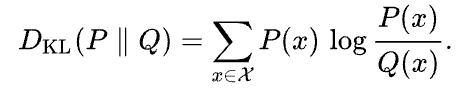
Wikipedia
Die KL-Divergenz kann man sich als den durchschnittlichen Unterschied in der Anzahl der Bits vorstellen, die man braucht, um Proben von P mit einem für Q optimierten Code zu kodieren.
Regulierung
Regularisierungstechniken verhindern, dass Modelle sich an Rauschen in den Trainingsdaten anpassen, indem sie einen Term zur Kostenfunktion hinzufügen, der zu komplexe Lösungen bestraft.
Ohne Regularisierung minimiert das Modell den Verlust:
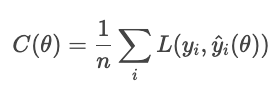
Mit der Regularisierung fügt das Modell einen Strafterm hinzu.
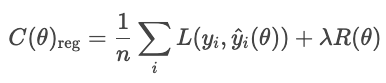
wo
- L ist der übliche Verlust (z. B. RMSE, Kreuzentropie).
- R(θ) misst die Komplexität des Modells.
- λ gibt's die Balance zwischen Passform und Einfachheit
Gängige Arten der Regularisierung sind L1, L2 und Elastic Net.
Die L1-Regularisierung (auch bekannt als Lasso) fügt den absoluten Wert jedes Modellgewichts zur Kostenfunktion hinzu.
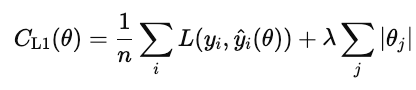
Wenn diese Kosten runtergehen, werden viele Gewichte auf Null gesetzt. Damit ist L1 eine Art automatische Merkmalsauswahl. Funktionen, die nichts beitragen, werden auf Null gesetzt.
Die L2-Regularisierung (auch bekannt als Ridge-Regression) bestraft das Quadrat jedes Modellgewichts.
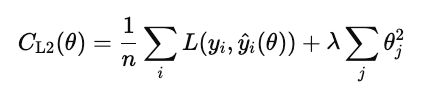
Anders als L1 setzt es die Gewichte nicht genau auf Null, sondern verringert sie sanft. Dadurch bleiben alle Funktionen im Modell erhalten, aber ihr Einfluss wird reduziert, um die Vorhersagen zu stabilisieren.
Elastic Net kombiniert sowohl L1 als auch L2.
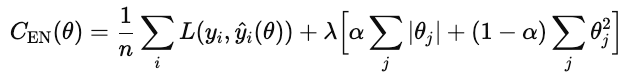
λ bestimmt, wie stark die Regularisierung insgesamt ist. α ist eine Zahl zwischen 0 und 1, die den Prozentsatz von L1 gegenüber L2 regelt, wobei 1 reines L1 und 0 reines Ridge ist.
Trade-offs
Die verschiedenen Strategien zur Klassifizierungsverlustbehandlung haben ihre Vor- und Nachteile.
Die Kreuzentropie macht die richtige Wahrscheinlichkeit größer, indem sie sichere falsche Antworten bestraft. Der Nachteil ist, dass es empfindlich auf Ausreißer und falsch beschriftete Daten reagiert. Es funktioniert am besten, wenn dir die Qualität der Zuverlässigkeit wichtig ist (z. B. bei Risikomodellen).
Der Hinge-Verlust sorgt für eine Marge, damit richtige Klassifizierungen nicht nur richtig, sondern auch sicher richtig sind. Es ignoriert Werte, die weit außerhalb der Toleranz liegen, und gibt eine lineare Strafe für Verstöße. Es reagiert weniger empfindlich auf Ausreißer als die Kreuzentropie, ist aber schwieriger reibungslos zu optimieren, da es am Gelenk nicht differenzierbar ist.
Die Kullback-Leibler-Divergenz vergleicht eine Wahrscheinlichkeitsverteilung mit einer anderen. Es ist wie die Kreuzentropie minus der Entropie der echten Verteilung.
Mehr Infos findest du unter diesen Links.
- Kreuzentropie-Verlustfunktion beim maschinellen Lernen: Verbesserung der Modellgenauigkeit
- Von Daten zu Dollars – Vorhersage von Versicherungsgebühren
- Optimiere Preisprognosen mit Feature Engineering
- Spickzettel zu den Dimensionen der Datenqualität
- R Correlation Tutorial
Implementierung und Anwendung der Kostenfunktion im maschinellen Lernen
Bisher haben wir uns mit Kostenfunktionen in der Theorie beschäftigt. In der Praxis hängt der Erfolg eines ML-Modells davon ab, wie gut es diese Funktionen minimiert. Hier zeigen wir dir die praktischen Details der wichtigsten Optimierungsalgorithmen und Tuning-Strategien.
Optimierungsalgorithmen und Parameteroptimierung
Optimierung ist der Prozess, bei dem man die besten Werte für Modellparameter findet, die eine Kostenfunktion minimieren. Im ML heißt das, die Parameter zu finden, die Vorhersagen machen, die so nah wie möglich an den tatsächlichen Werten sind.
Gradientenabstieg
Der Gradientenabstiegs us ist der Standardalgorithmus zur Optimierung von Kostenfunktionen. Es aktualisiert die Modellparameter immer wieder in der Richtung, die die Kosten am meisten senkt, also dem negativen Gradienten. Im Grunde misst es die Steigung der Kostenfunktion mit mehreren Variablen und geht bergab.
Die Aktualisierungsregel lautet
![]()
wo θ sind die Modellparameter, n die Lernrate ist und ![]() der Gradient der Kostenfunktion in Bezug auf die Parameter ist.
der Gradient der Kostenfunktion in Bezug auf die Parameter ist.
Die Wahl der Lernrate ist echt wichtig. Wenn es zu groß ist, gehen die Aktualisierungen über das Minimum hinaus und schwanken oder weichen ab. Wenn es zu klein ist, wird die Konvergenz langsam und kann in lokalen Minima hängen bleiben.
Die wichtigsten Varianten sind Batch, Stochastic und Mini-Batch.
- Batch-Gradientenabstiegs. Berechnet den Gradienten mit dem ganzen Trainingssatz. Es ist stabil, aber langsam und braucht viel Speicherplatz für große Datensätze oder Online-Lernen.
- Stochastische Gradientenabstiegsmethode (SGD). Aktualisiert die Parameter nach jedem Trainingsbeispiel. Es ist schnell und speichereffizient, aber auch ungenau, weil jeder Schritt ein bisschen vom optimalen Weg abweichen kann. Die Zufälligkeit kann aber dabei helfen, lokale Minima zu umgehen.
- Mini-Batch-Gradientenabstiegs. Ein praktischer Kompromiss. Es berechnet Gradienten in kleinen Chargen, um Geschwindigkeit und Stabilität unter einen Hut zu bringen. Es macht auch GPU-Parallelität möglich.
Adaptive Optimierer
Beim Standard-Gradientenabstieg wird für alle Parameter eine feste Lernrate benutzt. Bei komplizierten Modellen brauchen verschiedene Parameter vielleicht unterschiedliche Schrittweiten. Adaptive Optimierer passen die Lernraten anhand der bisherigen Gradientenwerte an.
- RMSProp benutzt einen exponentiell abklingenden Durchschnitt der letzten quadrierten Gradienten.
![]()
Das Lernen jedes Parameters wird umgekehrt zu diesem Durchschnitt skaliert. Das verhindert Schwingungen und sorgt für einen stabilen Fortschritt, auch wenn manche Parameter steile Gradienten haben. RMSProp wird oft für rekurrenten Netzwerke und verrauschte Daten benutzt.
- Adaptive Momentenschätzung (Adam) verfolgt sowohl den Mittelwert als auch die Varianz vergangener Gradienten und passt die Schrittgrößen dynamisch an.
![]()
Es läuft schnell zusammen, ist robust gegenüber verrauschten Daten und ist der Standardoptimierer für Deep-Network-Frameworks.
Skalierung und Initialisierung von Funktionen
Bevor du mit Gradientenabstieg optimierst, skalierst du die Merkmale, damit sie in vergleichbaren Bereichen funktionieren. Die richtige Skalierung macht die Optimierung stabiler und effizienter.
Ohne Skalierung dominieren Merkmale mit großen Zahlenbereichen den Gradienten. Der Gradientenabstieg geht dann im Zickzack vor, anstatt direkt auf das Minimum zuzugehen.
Es gibt zwei gängige Ansätze.
- Standardisierung. Jedes Zentrum ist bei Null zentriert und wird auf die Varianz der Einheit skaliert.
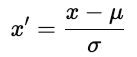
wobei u der Mittelwert und ơ die Standardabweichungist. Durch Standardisierung bleibt die Struktur der Daten erhalten.
- Normalisierung. Skalier jedes Merkmal auf einen festen Bereich, normalerweise [0, 1].
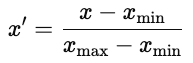
Normalisierung ist in neuronalen Netzen üblich, wo Aktivierungsfunktionen bei begrenzten Eingaben am besten funktionieren.
Strategien zur Initialisierung von Parametern
Die Initialisierung der Parameter hat einen großen Einfluss auf das Training des Modells. Eine schlechte Initialisierung kann zu langsamer Konvergenz, explodierenden oder verschwindenden Gradienten oder zu Modellen führen, die nicht lernen können. Eine gute Initialisierung platziert die Parameter in einem Bereich der Kostenoberfläche, wo die Gradienten stabil sind.
- Zufällige Initialisierung. Weist kleine Zufallswerte zu, die normalerweise aus einer gleichmäßigen oder normalen Verteilung kommen. Die Randomisierung bricht die Symmetrie, sodass die Parameter unterschiedliche Merkmale lernen. Wenn die Varianz aber zu hoch oder zu niedrig ist, können Gradienten explodieren oder verschwinden.
- Xavier (Glorot) Initialisierungs. Xavier ist für nichtlineare Aktivierungsfunktionen wie tanh oder Sigmoid gemacht und passt die Streuung der Gewichte je nach Anzahl der Eingangs- und Ausgangsanbindungen an.
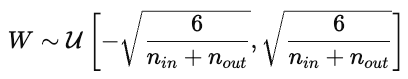
Dadurch bleiben die Aktivierungen und Gradienten über die Schichten hinweg ungefähr gleich.
- Er hat die Initialisierungs. Passt die Varianz für ReLU-Aktivierungen an, die negative Werte auf Null setzen. Die Gewichte werden aus einer Normalverteilung mit einer bestimmten Varianz gezogen:
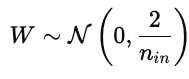
Das verhindert, dass die Gradienten während der Rückpropagation zu schnell verschwinden.
Überwachung, Diagnose und Visualisierung
Eine Trainingsverlustkurve zeigt, wie sich der Fehler des Modells im Trainingsdatensatz mit der Zeit entwickelt. Es zeigt, wie gut das Modell seine Parameter aktualisiert, um den Fehler zu minimieren. Eine stetig abfallende Kurve zeigt, dass das Modell Muster aus den Daten lernt.
Die Validierungsverlustkurve zeigt, wie gut das Modell unbekannte Daten, wie zum Beispiel einen Hold-out- oder Validierungssatz, verallgemeinern kann. Es zeigt, wie gut das Modell Daten vorhersagen kann, die es vorher noch nicht gesehen hat.
Im Idealfall fallen beide Kurven am Anfang ab und werden dann flacher. Das zeigt, dass das Modell sowohl effektiv lernt als auch effektiv verallgemeinert.
Überanpassung passiert, wenn das Modell Rauschen wie ein Signal lernt und nicht gut verallgemeinert. Das sieht man in einem Diagramm, das Trainings- und Validierungskurven zeigt, wenn der Trainingsverlust abnimmt, der Validierungsverlust aber zunimmt. Zu den Korrekturen gehören die Verwendung eines größeren Datensatzes oder die Anwendung von Regularisierung im Modell.
Unteranpassung passiert, wenn das Modell die zugrunde liegenden Muster in den Daten nicht richtig erfasst. Sowohl die Trainings- als auch die Validierungskurven bleiben auf hohem Niveau. Probier's in diesem Fall mit mehr Daten, einem komplexeren Modell oder weniger Regularisierung.
Die Konvergenz ist der Punkt, an dem die Kurve abflacht und die Erzausbildung kaum noch besser wird. Das ist der perfekte Mittelweg zwischen Überanpassung und Unteranpassung.
Kostenfunktionsoptimierung und Entscheidungstheorie
Wir haben gesehen, wie Wirtschaft und maschinelles Lernen auf Optimierung setzen, um Entscheidungen zu treffen und zu trainieren. Beide Bereiche versuchen, die besten Entscheidungen zu treffen, indem sie Kosten oder Verluste als Maßstab nehmen. Lass uns mal genauer über die Optimierungstheorie reden.
Zielfunktionen
Eine Zielfunktion ist eine mathematische Funktion, die festlegt, was wir minimieren oder maximieren wollen. In den Fällen, die wir bisher gesehen haben, haben wir die Kosten oder Fehler minimiert. Für die Wirtschaftswissenschaften haben wir uns die Kostenkurven angeschaut, und bei ML haben wir uns die Regressionsverluste (MAE, RMSE, Huber) und Klassifizierungsverluste (Kreuzentropie, Hinge-Verlust, KL-Verlust) angesehen. Das sind beides Beispiele für die Optimierung einer Zielfunktion.
Mehrzieloptimierung
Oft wollen wir mehrere, oft widersprüchliche Ziele optimieren. Ein Unternehmen könnte versuchen, den Gewinn zu maximieren und gleichzeitig das Risiko zu minimieren. Ein Datenwissenschaftler könnte die Genauigkeit eines Modells verbessern wollen, ohne dabei die Interpretierbarkeit oder Fairness zu beeinträchtigen. Solche konkurrierenden Ziele machen ein Problem der Mehrzieloptimierung aus, bei dem die Verbesserung eines Ziels ein anderes verschlechtern kann.
Pareto-Grenze
Eine Lösung ist Pareto-optimal, wenn man kein Ziel verbessern kann, ohne mindestens ein anderes Ziel schlechter zu machen. Die Menge der Pareto-optimalen Lösungen bildet diePareto-Frontier „ “ ( ), eine Kurve, die aus den bestmöglichen Kompromissen besteht. Jeder Punkt auf dieser Kurve steht für eine andere Balance der Prioritäten.
Zum Beispiel kann eine höhere Komplexität eines Modells die Genauigkeit verbessern, aber die Interpretierbarkeit verringern. Einfachere Modelle sind leichter zu erklären, können aber schlechter funktionieren. Die Pareto-Grenze zeigt die „besten Kompromisse“ und lässt Lösungen weg, die von anderen Variablen dominiert werden.
Die richtige Stelle zu finden, hängt vom Kontext und deinem eigenen Urteilsvermögen ab. Du kannst jedem Ziel Gewichte zuweisen oder Richtlinienbeschränkungen verwenden.
Erwarteter Verlust
Wenn die Ergebnisse ungewiss sind, minimiert die Optimierung den erwarteten Verlust, also den durchschnittlichen Verlust über alle möglichen Szenarien. In ML taucht diese Idee in der Risikofunktion auf.
![]()
wobei L(Y,f(x)) der Verlust für eine bestimmte Vorhersage ist und der Erwartungswert über die Datenverteilung gemittelt wird. Das Ziel ist, das Modell f zu finden, das diesen erwarteten Verlust so gering wie möglich macht. Dieses Modell schneidet im Durchschnitt am besten ab, nicht nur bei einzelnen Beispielen.
Bayes-Risiko
Der Bayes-Risiko us ist die theoretische Untergrenze des erwarteten Verlusts. Formell wird es durch die folgende Formel ausgedrückt.
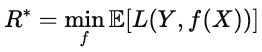
Einfach gesagt ist es die „perfekte Punktzahl“, also der niedrigste Wert, den man erreichen kann, wenn man alle Infos über die Datenverteilung hat. Je näher die Leistung eines Modells am Bayes-Risiko liegt, desto besser ist es.
Interdisziplinäre Anwendungen
Kostenfunktionen werden in jeder Branche genutzt, die Entscheidungen auf Basis von Daten trifft. Sie helfen dabei, konkurrierende Ziele auszugleichen und zu definieren, was „besser” eigentlich bedeutet. Diese Funktionen bringen konkurrierende Ziele in Einklang und helfen bei der Optimierung. Die gleiche Logik, die beim Training von ML-Modellen angewendet wird, wird auch zur Optimierung realer Prozesse genutzt.
Anwendungen in der Industrie und Anwendungsfälle in verschiedenen Bereichen
In der Fertigung messen Kostenfunktionen zum Beispiel Verluste, wie zum Beispiel Lagerverluste. Eine Funktion zur Berechnung der Lagerkosten gleicht die Kosten für Überbestände gegen die Strafen für Fehlbestände aus. Ähnliche Rahmenbedingungen werden für die Produktionsplanung oder den Energieverbrauch genutzt, um die erwarteten Gesamtkosten unter Unsicherheit zu minimieren.
Im Gesundheitswesen nutzen Vorhersagemodelle Kostenfunktionen, um Genauigkeit und Ressourcenzuteilung unter einen Hut zu bringen. Ein Modell zur Vorhersage des Wiederaufnahmerisikos findet zum Beispiel frühzeitig Patienten mit hohem Risiko, damit Ärzte mit Nachfassanrufen oder Hausbesuchen eingreifen können. Einen Risikopatienten zu übersehen ist teurer als einen Patienten mit geringem Risiko zu markieren, deshalb werden diese Fehler unterschiedlich bewertet.
Auch die Finanzwelt nutzt Zielfunktionen. Kreditbewertungsmodelle sagen zum Beispiel voraus, wie wahrscheinlich es ist, dass jemand einen Kredit innerhalb einer bestimmten Zeit, zum Beispiel zwölf Monaten, nicht zurückzahlt. Wenn man einen riskanten Kreditnehmer akzeptiert, kann das zu finanziellen Verlusten führen, während man bei der Ablehnung eines sicheren Kreditnehmers möglicherweise Einnahmen verliert. Das Modell hält die Kosten niedrig.
In all diesen Bereichen bringen Kostenfunktionen die Vor- und Nachteile in messbare Werte, die Entscheidungsträger nutzen und mit denen sie arbeiten können.
Fazit
Kostenfunktionen bieten eine Methode, um Entscheidungen zu bewerten. In der Wirtschaft modellieren sie den Kompromiss zwischen Output und Effizienz. Beim maschinellen Lernen messen sie den Unterschied zwischen Vorhersagen und der Realität.
In ML sind Kostenfunktionen die Basis für das Modelldesign. Die Wahl der Verlustfunktionen entscheidet darüber, was das Modell als „Erfolg“ sieht. Der mittlere quadratische Fehler belohnt die Gesamtgenauigkeit, die Kreuzentropie belohnt kalibrierte Wahrscheinlichkeiten und der Hinge-Verlust belohnt eine zuverlässige Trennung.
In allen Bereichen und Branchen läuft es im Grunde so: Man setzt sich ein Ziel und versucht, es zu verbessern. Kostenfunktionen machen vage Ziele zu konkreten Zahlen, die bei der Optimierung helfen.
Kostenfunktionen sind super nützlich in der Wirtschaft, beim maschinellen Lernen, in der Fertigung, im Finanzwesen, im Gesundheitswesen und überall sonst, wo man Kompromisse irgendwie quantifizieren will.
Für mehr Infos empfehle ich diese DataCamp-Ressourcen.
Häufig gestellte Fragen zur Kostenfunktion
Was ist eine Kostenfunktion?
Eine Kostenfunktion zeigt, wie gut die Vorhersagen eines Modells mit den Daten übereinstimmen. Es fasst den Fehler zu einem einzigen Wert zusammen. Optimierungsalgorithmen versuchen dann, diesen Wert zu minimieren, um die Leistung zu verbessern.
Wie unterscheiden sich die Kostenfunktionen bei Regressions- und Klassifizierungsaufgaben?
Regressionsmodelle sagen kontinuierliche Werte voraus, also messen ihre Verluste (z. B. MSE, MAE) den numerischen Abstand vom Ziel.
Klassifizierungsmodelle sagen die Wahrscheinlichkeit von Klassen voraus; Verluste wie die Kreuzentropie vergleichen die vorhergesagte Wahrscheinlichkeitsverteilung mit der echten Klasse und bestrafen sichere Fehler ziemlich hart.
Was sind ein paar praktische Anwendungen von Kostenfunktionen in der Wirtschaft?
Kostenfunktionen sind in jedem Geschäftsprozess nützlich, bei dem es um Kompromisse oder Optimierungen geht. Beispiele sind Preisgestaltung und Umsatzoptimierung, Bestandsverwaltung, Kredit- und Risikomodellierung, Kundenbindung oder Logistik.
Wie geht die Huber-Verlustfunktion mit Ausreißern in den Daten um?
Die Huber-Verlustfunktion behandelt kleine Fehler wie MSE und große Fehler wie MAE, wodurch sie weniger empfindlich gegenüber Ausreißern ist.
Was ist der Zusammenhang zwischen Grenzkosten und Durchschnittskosten?
Die Grenzkosten (MC) zeigen, wie viel es kostet, eine weitere Einheit zu produzieren. Die Durchschnittskosten (AC) sind die Gesamtkosten geteilt durch die Anzahl der Einheiten. Wenn die Grenzkosten (MC) unter den Gesamtkosten (AC) liegen, sinken die Durchschnittskosten, wenn die Grenzkosten über den Gesamtkosten liegen, steigen die Durchschnittskosten, und wenn die Grenzkosten den Gesamtkosten entsprechen, sind die Durchschnittskosten am niedrigsten.

Mark Pedigo, PhD, ist ein angesehener Datenwissenschaftler mit Fachwissen in den Bereichen Datenwissenschaft im Gesundheitswesen, Programmierung und Bildung. Mit einem Doktortitel in Mathematik, einem B.S. in Informatik und einem Professional Certificate in KI verbindet Mark technisches Wissen mit praktischer Problemlösungskompetenz. In seiner beruflichen Laufbahn war er unter anderem an der Aufdeckung von Betrug, der Vorhersage von Kindersterblichkeit und Finanzprognosen beteiligt und hat an der Kostenschätzungssoftware der NASA mitgearbeitet. Als Pädagoge hat er auf dem DataCamp und an der Washington University in St. Louis unterrichtet und junge Programmierer angeleitet. In seiner Freizeit genießt Mark mit seiner Frau Mandy und seinem Hund Harley die Natur in Minnesota und spielt Jazz-Piano.
