Cours
Les modèles de régression linéaire sont largement utilisés dans les statistiques et l'apprentissage automatique pour prédire des valeurs numériques sur la base de caractéristiques d'entrée, ainsi que pour comprendre la relation entre les variables. Cependant, ce n'est pas parce que vous pouvez tracer une ligne sur vos données que vous devez le faire. Nous devons également diagnostiquer la qualité de l'ajustement pour déterminer si le modèle est approprié aux données ou s'il doit être affiné.
Il existe plusieurs façons de tester un modèle, notamment en l'évaluant à l'aide d'un flux de travail train/test et en examinant les statistiques du modèle telles que le r-carré ajusté. Dans cet article, je me concentrerai sur la manière de créer et d'interpréter un graphique de diagnostic spécifique appelé graphique Q-Q, et je vous montrerai quelques méthodes différentes pour créer ce graphique Q-Q dans le langage de programmation R. Pour vraiment continuer à maîtriser les techniques de régression, prenez Introduction à la régression en R ou Régression intermédiaire en R ou, pour Python, prenez Introduction à la régression en Python ou Régression intermédiaire en Python, en fonction de votre niveau d'aisance.
Qu'est-ce qu'un graphe Q-Q ?
Un graphique Q-Q (Quantile-Quantile) est utilisé pour vérifier si un ensemble de données suit une distribution théorique particulière. Le graphique Q-Q compare les quantiles des données observées aux quantiles de notre autre distribution théorique. Je parle de "distribution théorique" pour être exact, mais souvent, lorsque nous créons un graphique Q-Q, nous pensons en fait à la distribution normale ou gaussienne. distribution normale ou gaussienne gaussienne, et nous l'appelons "graphique Q-Q normal". Cependant, les diagrammes Q-Q peuvent également être utilisés pour comparer les données à d'autres distributions, telles que la distribution exponentielle, la distribution uniforme, la distribution chi-carré, la distribution t, distribution de Poissonou d'autres, selon le contexte de l'analyse.
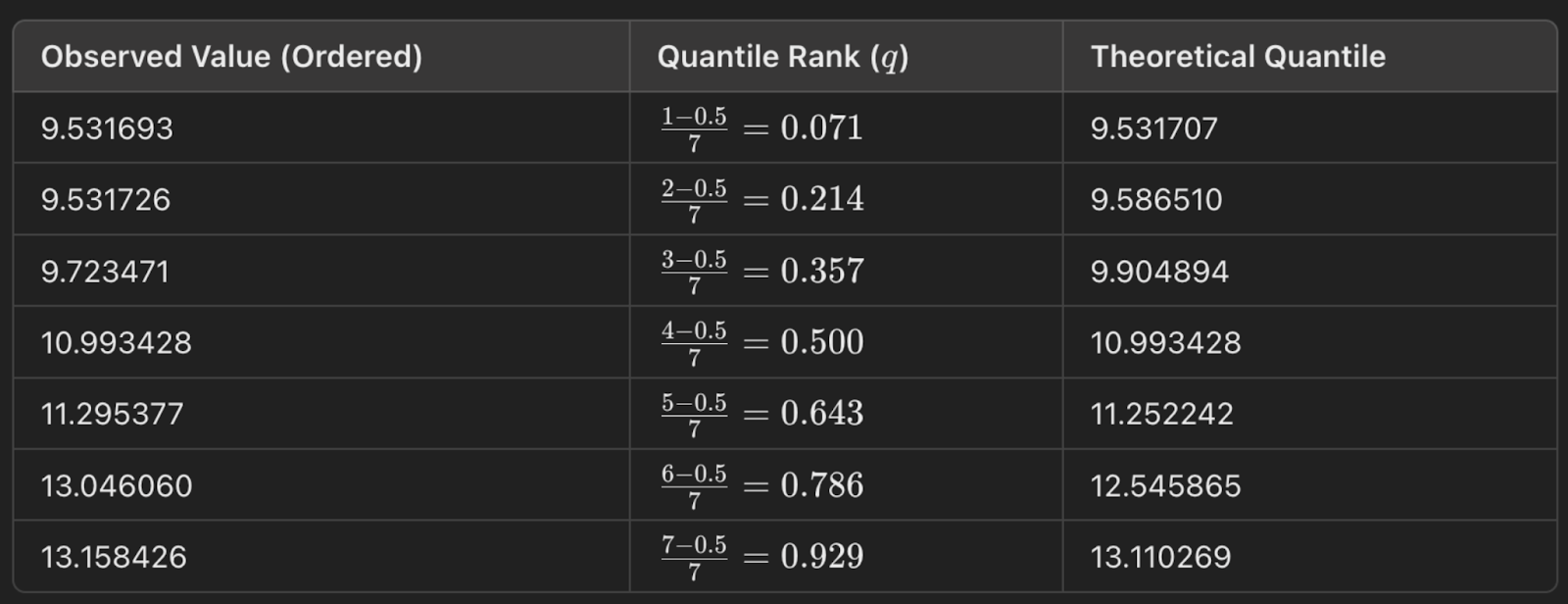
Il est utile de comprendre en montrant un exemple. Ici, j'ai une distribution de nombres. Pour construire un graphique Q-Q normal, je commence par mettre les chiffres dans l'ordre. Je calcule ensuite le rang quantile à l'aide de l'équation suivante : q = (i- 0,5)/n. Ensuite, je pourrais utiliser la fonction de point de pourcentage (PPF) de la distribution normale standard pour trouver la valeur correspondante pour le rang quantile. (Vous êtes peut-être plus familier avec la fonction de distribution cumulative (FDC), qui nous indique la probabilité jusqu'à une valeur x.) Le PPF, c'est un peu le contraire : Il nous donne la valeur x pour une probabilité donnée). Pour créer le graphique, nous tracerons alors les valeurs du rang quantile par rapport aux quantiles théoriques (d'où les deux Q dans le graphique Q-Q).
Pourquoi utiliser un graphique Q-Q ?
Un graphique Q-Q est un bon moyen visuel de vérifier les hypothèses de distribution. Il existe d'autres moyens de vérifier si les données suivent une distribution normale, comme le test de Shapiro-Wilk, par exemple, mais rien, à mon avis, n'est vraiment aussi visuel et ne rend l'histoire aussi évidente que le graphique Q-Q.
Connaître la distribution d'un produit est important à plusieurs égards. D'une part, nous voudrons probablement connaître les meilleures mesures pour le centre et l'étalement. De même, lors de la création d'une régression linéaire, nous voulons savoir si notre variable dépendante, en particulier, suit une distribution normale, et nous voulons également voir si les résidus de notre modèle sont normalement distribués afin d'avoir une meilleure confiance dans nos estimations. En résumé, je pense que les diagrammes Q-Q sont utiles pour deux raisons générales : comparer nos données à des distributions d'échantillons et tester la normalité.
Comment créer un graphique Q-Q dans R
Voyons maintenant comment créer un graphique Q-Q dans R. Pour cette section, je vais passer en revue trois méthodes différentes : R de base, le paquet car et les méthodes tidyverse. Je pense que vous verrez que je préfère les méthodes tidyverse parce qu'elles vous donnent plus de flexibilité pour rendre le graphique plus joli et qu'elles sont plus extensibles avec d'autres paquets.
Pour chaque méthode, je créerai un graphique Q-Q sur les résidus d'une régression linéaire simple, ce qui est l'une des utilisations les plus courantes - si ce n'est la plus courante - de ce graphique. Cependant, vous pouvez également créer un graphique Q-Q pour vérifier la distribution des variables avant de créer une régression linéaire. Tout ce dont vous avez besoin, c'est de la distribution d'une variable et d'une distribution théorique à laquelle la comparer.
Si vous voulez suivre, vous pouvez télécharger l'ensemble de données Kaggle que j'utilise : Prix des voitures en Jordanie en 2023.
Création d'un graphique Q-Q dans la base R
Commençons par créer un graphique Q-Q dans le R de base, ce qui signifie que nous n'installerons aucun paquet supplémentaire et que nous n'utiliserons que les fonctions intégrées.
# importing data (in my case, saved on my desktop)
car_prices_jordan <- read.csv('~/Desktop/car_prices_jordan.csv')
# Create a linear model
car_linear_model <- lm(Price ~ sqrt(Price), filtered_car_prices)
# Extract the residuals
residuals <- resid(car_linear_model)
# Q-Q plot of residuals
qqnorm(residuals, main = "Q-Q Plot of Residuals from Linear Regression")
qqline(residuals, col = "red")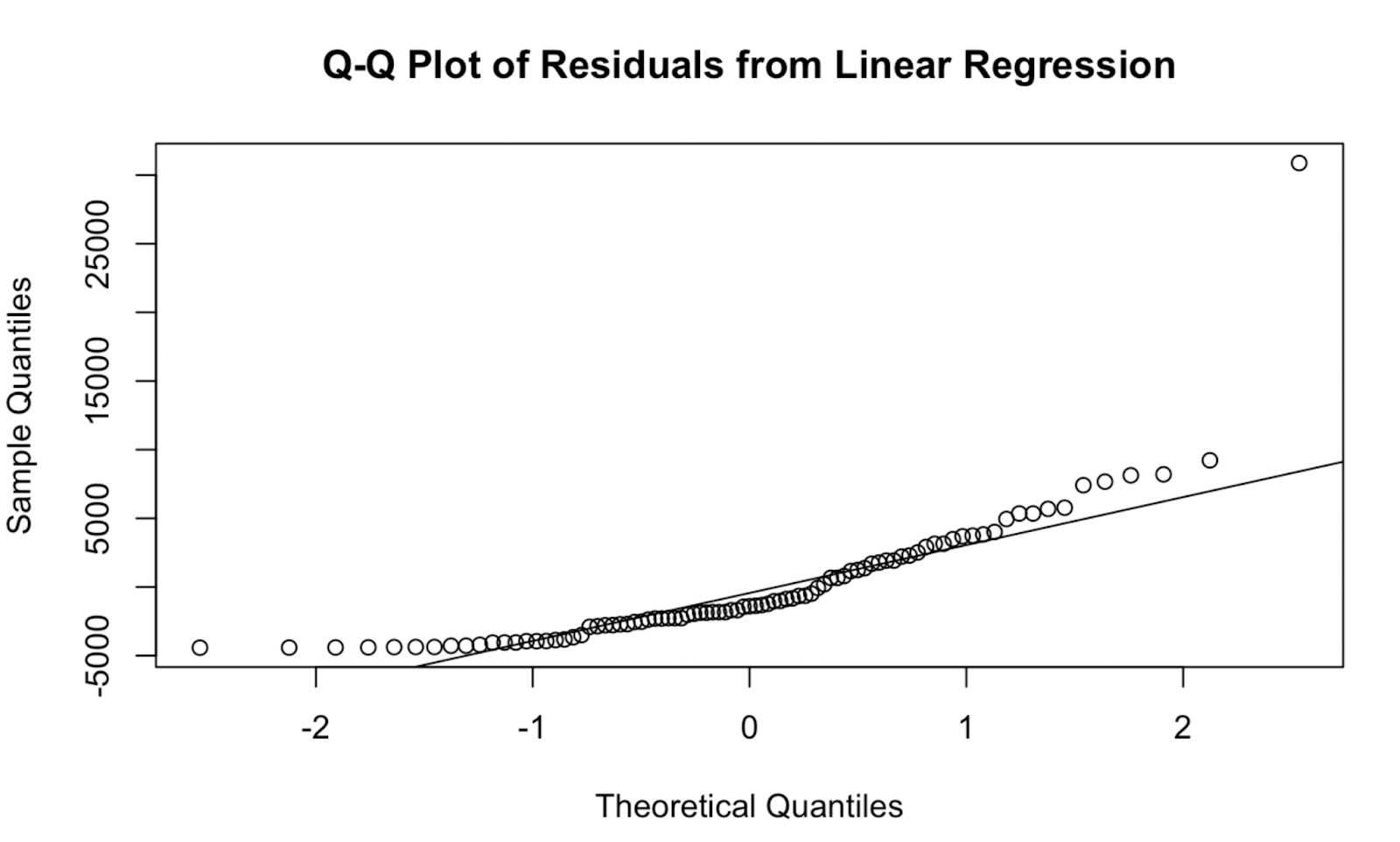 Graphique Q-Q créé dans la base R. Image de l'auteur
Graphique Q-Q créé dans la base R. Image de l'auteur
Création d'un graphique Q-Q à l'aide du paquet "voiture
Essayons maintenant de créer un graphique Q-Q à l'aide du logiciel car. À mon avis, la qualité de la visualisation n'est pas très différente, mais ce graphique Q-Q présente l'avantage de montrer une enveloppe de confiance qui définit la zone dans laquelle nos points de données devraient se trouver si l'hypothèse de normalité du modèle se vérifiait.
# Install the car package if not already installed
# install.packages("car")
library(car)
# Q-Q plot of residuals using car package
car::qqPlot(car_linear_model, main = "Q-Q Plot of Residuals from Linear Regression")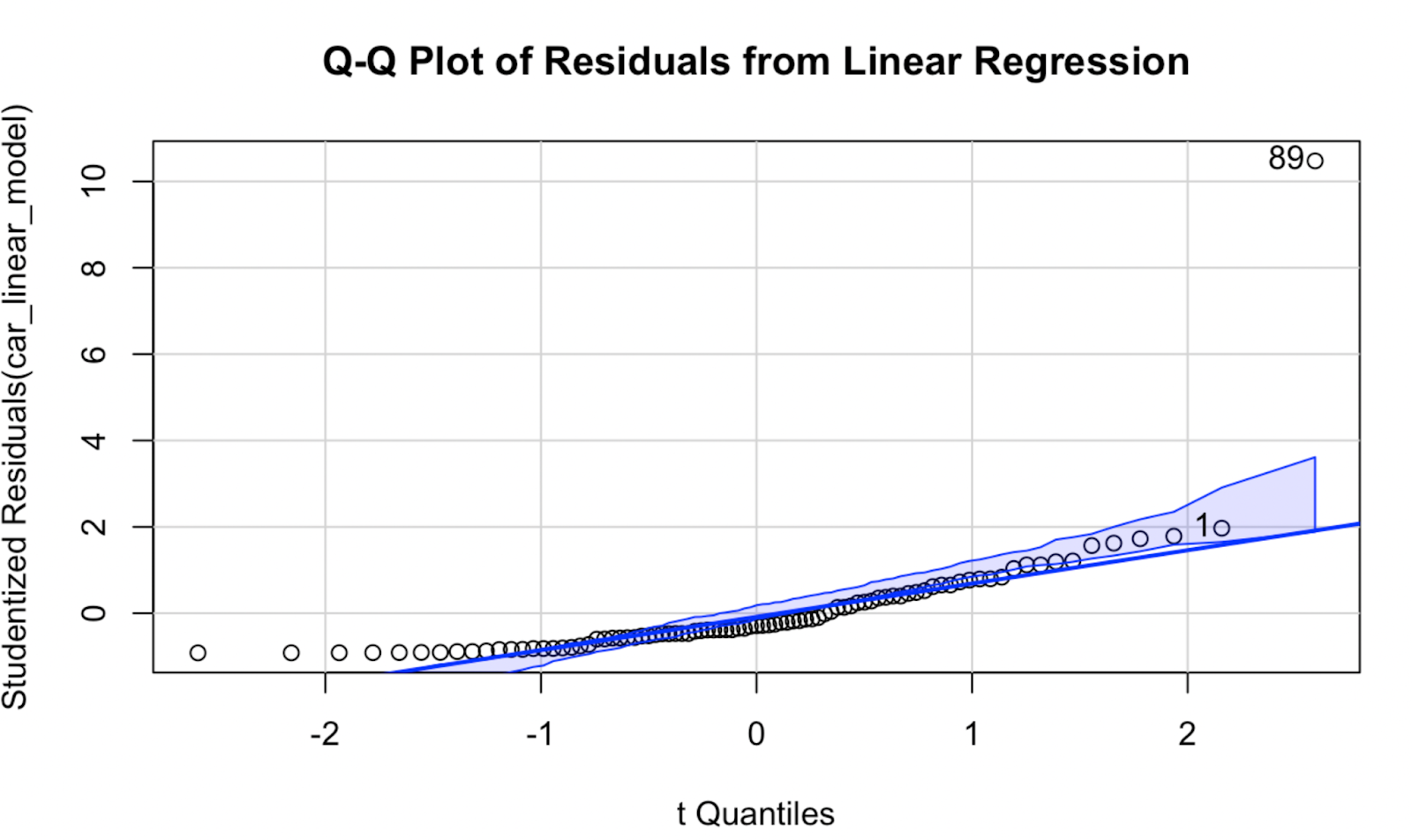 Graphique Q-Q créé à l'aide du package car dans R. Image par l'auteur
Graphique Q-Q créé à l'aide du package car dans R. Image par l'auteur
Création d'un graphique Q-Q à l'aide de ggplot2
Voyons maintenant comment créer un graphique Q-Q à l'aide des méthodes tidyverse pour plus de flexibilité et pour qu'il soit plus joli. Cette fois-ci, je vais placer le graphique Q-Q dans un panneau à côté de mon nuage de points original.
library(tidyverse)
library(metBrewer)
car_prices_jordan$Power <- as.numeric(gsub("[^0-9]", "", car_prices_jordan$Power))
car_prices_jordan$Price <- as.numeric(gsub("[^0-9]", "", car_prices_jordan$Price))
slope <- (cor(car_prices_jordan$Power, car_prices_jordan$Price) * (sd(car_prices_jordan$Price)) / sd(car_prices_jordan$Power))
intercept <- (mean(car_prices_jordan$Price) - slope * mean(car_prices_jordan$Power))
car_prices_graph <- ggplot(car_prices_jordan, aes(x = Power, y = Price)) +
geom_point() +
ggtitle("Car Prices in Jordan") +
geom_abline(slope = slope, intercept = intercept, color = '#376795', size = 1)
car_linear_model <- lm(Price ~ Price, car_prices_jordan)
qq_plot <- ggplot(data = car_linear_model, aes(sample = .resid)) +
stat_qq() +
stat_qq_line(linetype = 'dashed', color = '#ef8a47', size = 1) +
labs(title = "Car Prices in Jordan") +
labs(subtitle = "Residual QQ Plot")
library(patchwork)
car_prices_graph + qq_plot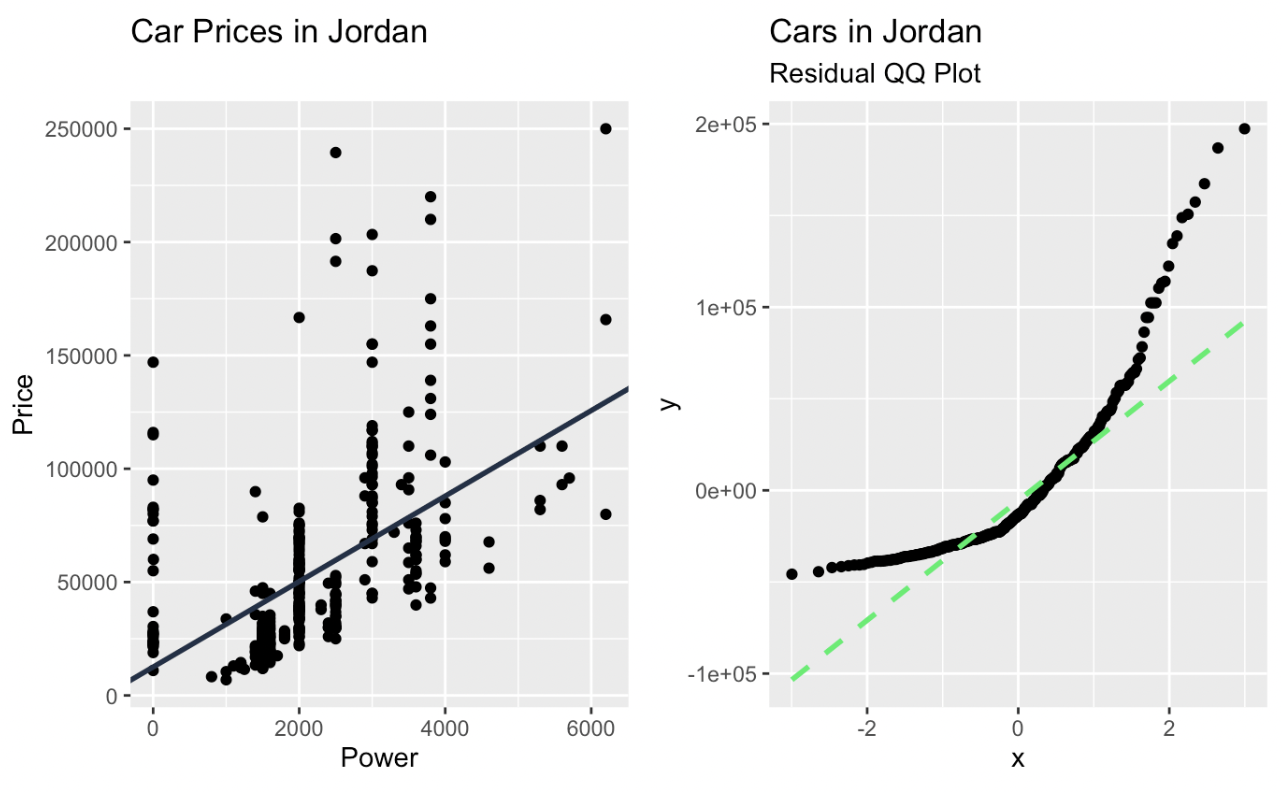
Régression linéaire et graphique Q-Q des résidus créés dans ggplot2. Image par l'auteur
Ce qu'un graphique Q-Q peut nous apprendre
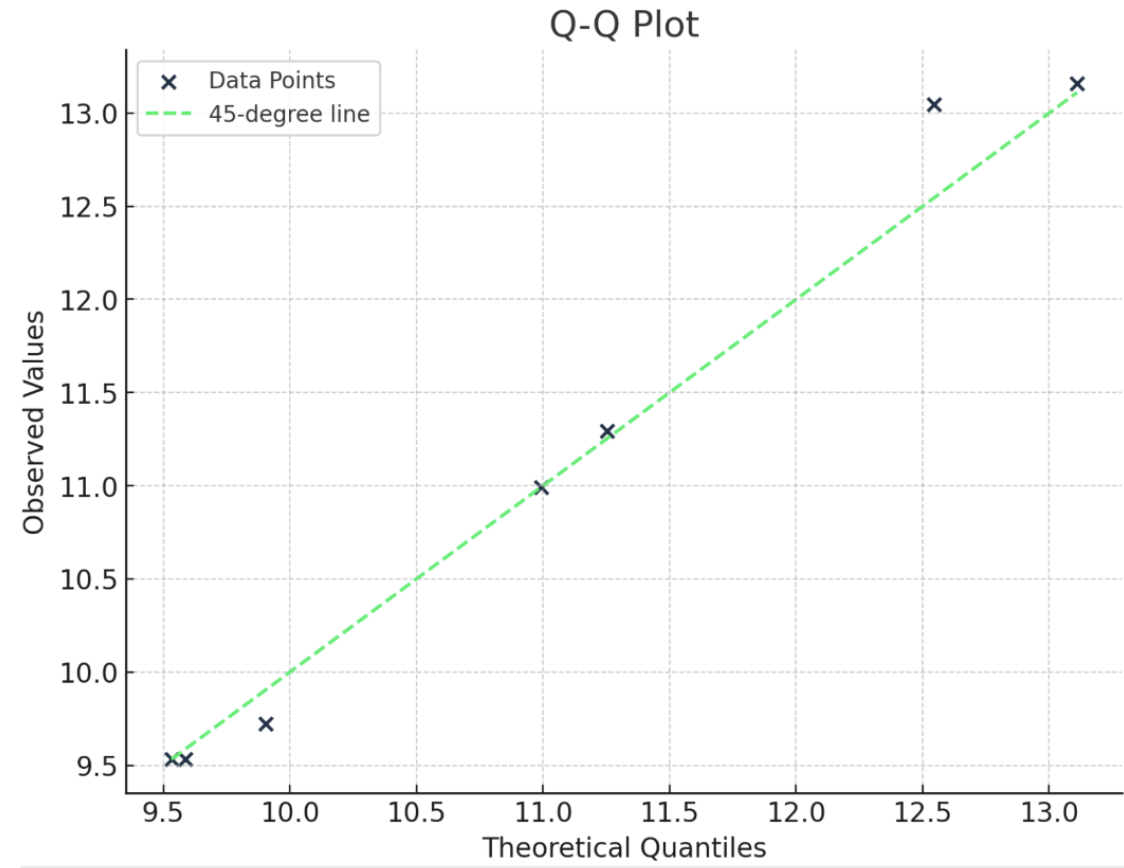
Avec un graphique Q-Q, les quantiles des données observées sont représentés par rapport aux quantiles théoriques. Si les données suivent de près la distribution théorique, les points du graphique Q-Q se déplacent sur une ligne diagonale. Les écarts par rapport à cette ligne indiquent des écarts par rapport à la distribution attendue. Les points situés au-dessus ou au-dessous de la ligne indiquent une asymétrie ou des valeurs aberrantes, et les motifs tels que les courbes ou les écarts en forme de S indiquent des différences systématiques, comme des queues plus lourdes ou plus légères.
Il y a environ trois choses que nous recherchons.
- Ligne droite: Les données correspondent bien à la distribution théorique.
- Motifs courbes: Indique des données asymétriques ou des distributions non normales.
- Queues lourdes ou légères: Si les points s'écartent aux extrémités, les données peuvent avoir des queues plus lourdes ou plus légères que prévu.
Nous allons vous présenter un exemple pour chacun d'entre eux :
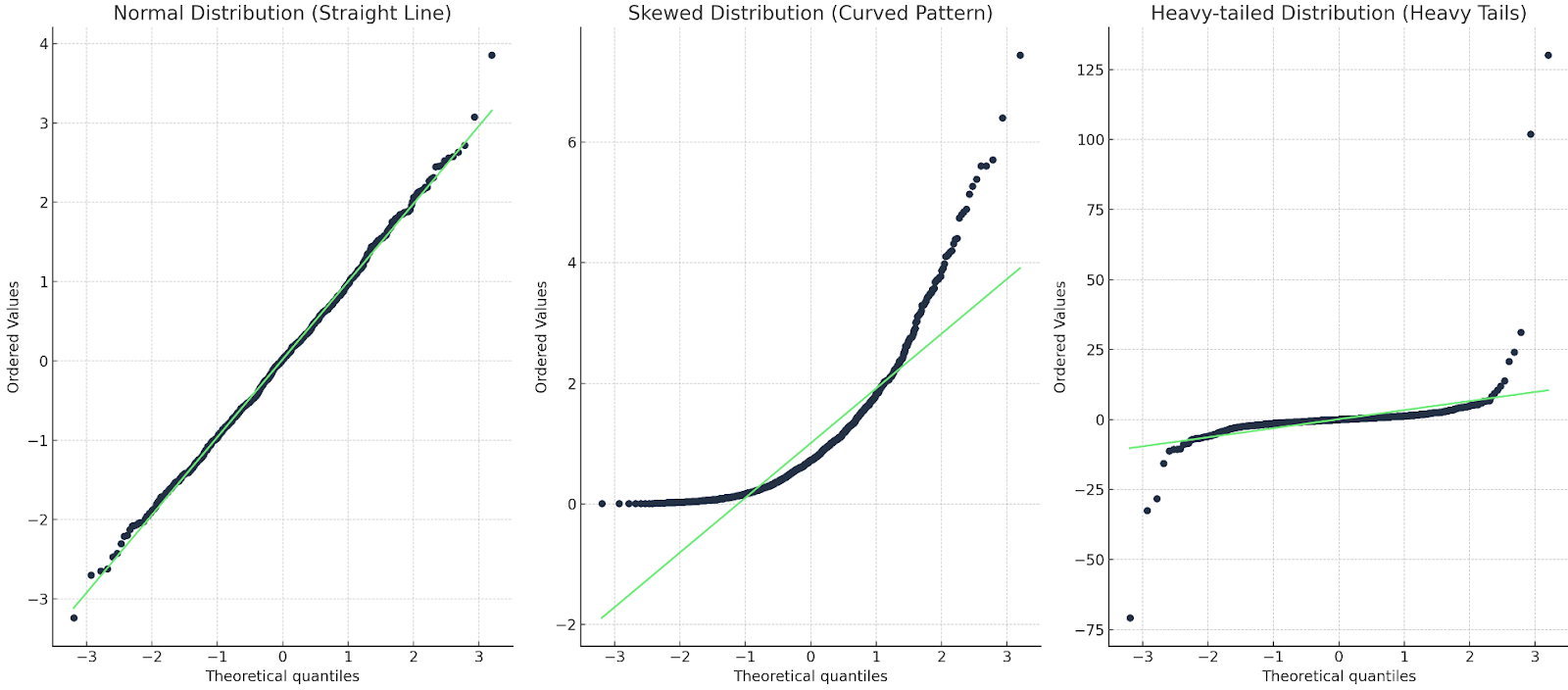
Trois tracés Q-Q : l'un avec une ligne droite, l'autre avec une courbe, l'autre avec une queue épaisse. Image par l'auteur
Dans le premier cas, la ligne Q-Q correspond aux points de données, la distribution est donc bien normale. Dans le second cas, nous observons une courbe, ce qui signifie que les données ne sont pas normales ou qu'elles sont faussées. Dans le dernier cas, on observe une sorte de forme en "s", ce qui signifie que la distribution présente des queues lourdes ou des valeurs plus extrêmes.
Graphiques Q-Q dans la régression linéaire
Il existe plusieurs hypothèses pour les modèles linéaires, notamment la linéarité (la relation entre les variables est linéaire), l'indépendance des erreurs (les erreurs ne sont pas corrélées entre elles), l'homoscédasticité (les résidus doivent avoir une variance constante) et l 'indépendance des erreurs (les erreurs ne sont pas corrélées entre elles). les résidus doivent avoir une variance constante)et la normalité des résidus (les résidus suivent une distribution normale). Le graphique Q-Q permet notamment de vérifier la quatrième hypothèse du modèle linéaire, à savoir la normalité des résidus.
Voici comment les différents modèles affectent l'interprétation et la fiabilité de notre modèle :
Alignement en ligne droite
- Ce que cela signifie: Les résidus sont approximativement normaux, ce qui indique que le modèle correspond bien aux données en termes d'hypothèse de normalité.
- Implication dans la pratique: Les intervalles de confiance, les valeurs p et les tests d'hypothèse dérivés du modèle sont susceptibles d'être fiables, car ils supposent que les résidus sont normalement distribués.
Modèles courbes
- Ce que cela signifie: Un graphique Q-Q courbe est souvent le signe d'une non-normalité, telle qu'une asymétrie dans les résidus. La courbe peut être ascendante ou descendante. (C'est cette courbe que nous voyons dans l'exemple ci-dessus).
- Implication dans la pratique: Les résidus non normaux peuvent fausser les valeurs p ou les intervalles de confiance, en particulier pour les petits ensembles de données. Nous devrions envisager de transformer la variable dépendante ou de revoir la structure du modèle.
Queues lourdes ou légères
- Ce que cela signifie: S'il y a des queues lourdes, les résidus ont plus de valeurs extrêmes que ce que l'on attend de la normalité, ce qui peut être dû à des valeurs aberrantes, ou à une spécification incorrecte du modèle. Si les queues sont légères, cela signifie qu'il y a moins de résidus extrêmes que prévu, ce qui peut indiquer une troncature des données.
- Implication dans la pratique: Lorsque les queues sont lourdes, les valeurs aberrantes peuvent affecter de manière disproportionnée la ligne de régression, ce qui conduit à des résultats trompeurs. Nous devrions envisager de supprimer ou de réduire la pondération des valeurs aberrantes. Je pense que les queues légères n'ont pas tellement d'impact sur le modèle, mais qu'elles peuvent être un indice que les données sont incomplètes.
Diagrammes Q-Q et autres diagrammes de diagnostic
Si vous connaissez les diagrammes de diagnostic des modèles linéaires, vous savez peut-être aussi qu'il existe un certain nombre d'options pour évaluer l'adéquation d'un modèle. Afin de comprendre exactement ce que montre le graphique Q-Q, examinons quelques autres diagnostics. Cela nous aidera à mieux comprendre ce que fait le graphique Q-Q et quels autres graphiques pourraient le compléter.
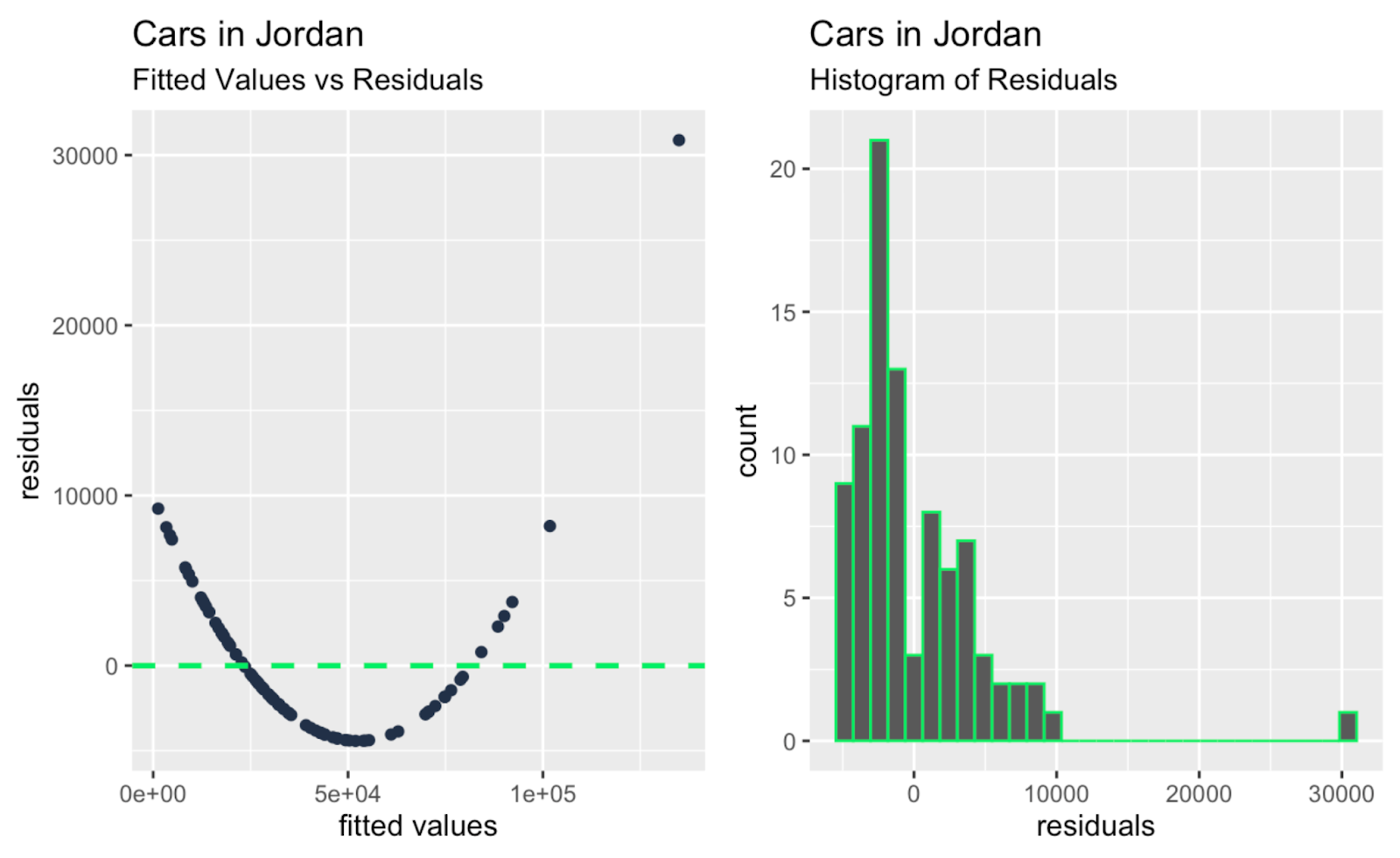
- Valeurs ajustées et résidus: Ce graphique montre la relation entre les valeurs prédites (valeurs ajustées) et les résidus, qui sont les différences entre les valeurs observées et prédites.
- Histogramme des résidus: Ce graphique montre la distribution des résidus.
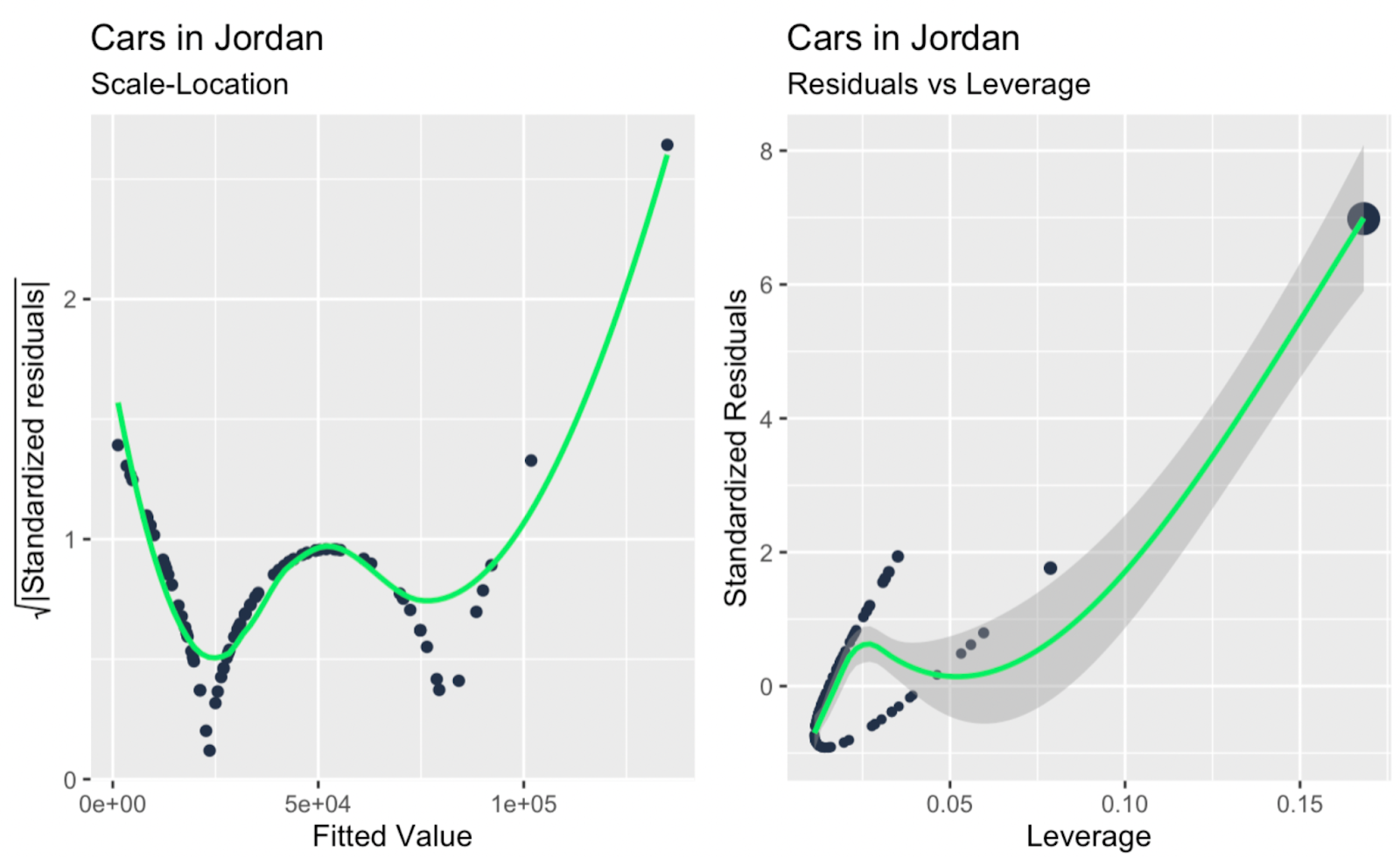
- Tracé de l'échelle et de la localisation: Ce graphique montre la relation entre les résidus et les valeurs ajustées.
- Effet de levier ou résidus standardisés: Ce graphique met en évidence la position d'un point de données dans l'espace prédicteur et indique si le modèle s'y adapte bien ou mal. Nous normalisons les résidus afin d'évaluer leur relation avec l'effet de levier sur une échelle cohérente.
- Nombre d'observations par rapport à la distance de Cook: Ce graphique identifie les points de données spécifiques ayant l'influence globale la plus élevée sur le modèle en combinant l'effet de levier et la taille résiduelle. Le numéro de l'observation sur l'axe des x sert d'identifiant pour chaque point de données.
- Effet de levier et distance de Cook: Ce graphique compare le potentiel d'un point à influencer le modèle avec son impact global réel sur les prédictions du modèle.
Je vais vous montrer rapidement comment créer chaque graphique à l'aide des méthodes tidyverse. L'objectif ici n'est pas d'interpréter le modèle linéaire de notre ensemble de données "Cars in Jordan" pour chaque diagnostic de modèle linéaire de cette liste. Je souhaite plutôt montrer les autres tracés de diagnostic afin que vous puissiez les reconnaître, utiliser le code s'il s'avère utile et, dans le cadre de cet article, afin que vous puissiez mieux situer le tracé Q-Q parmi les autres tracés de diagnostic. De cette façon, vous comprendrez mieux ce que le graphique Q-Q montre et ne montre pas, en quoi il est utile et ce qu'il manque.
fitted_values_vs_residuals <- ggplot(data = car_linear_model, aes(x = .fitted, y = .resid)) +
geom_point(color = '#203147') +
geom_hline(yintercept = 0, linetype = "dashed", color = '#01ef63', size = 1) +
xlab("fitted values") +
ylab("residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Fitted Values vs Residuals")
histogram_of_residuals <- ggplot(data = car_linear_model, aes(x = .resid)) +
geom_histogram(color = '#01ef63') +
xlab("residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Histogram of Residuals")
scale_location <- ggplot(car_linear_model, aes(.fitted, sqrt(abs(.stdresid)))) +
geom_point(color = '#203147', na.rm=TRUE) +
stat_smooth(method="loess", na.rm = TRUE, color = '#01ef63', size = 1, se = FALSE) +
xlab("Fitted Value") +
ylab(expression(sqrt("|Standardized residuals|"))) +
labs(title = "Cars in Jordan") +
labs(subtitle = "Scale-Location")
leverage_vs_standardized_residuals <- ggplot(data = car_linear_model, aes(.hat, .stdresid)) +
geom_point(aes(size = .cooksd), color = '#203147') +
stat_smooth(method="loess", na.rm=TRUE, color = '#01ef63', size = 1) +
xlab("Leverage") +
ylab("Standardized Residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Residuals vs Leverage") +
scale_size_continuous("Cook's Distance", range=c(1,5)) +
theme(legend.title = element_blank()) +
theme(legend.position= "none")
observation_number_vs_cooks_distance <- ggplot(car_linear_model, aes(seq_along(.cooksd), .cooksd)) +
geom_bar(stat="identity", position="identity", color = '#01ef63', size = 1) +
xlab("Obs. Number") +
ylab("Cook's distance") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Cook's distance")
leverage_vs_cooks_distance <- ggplot(car_linear_model, aes(.hat, .cooksd))+geom_point(na.rm=TRUE) +
stat_smooth(method="loess", na.rm=TRUE, color = '#01ef63', size = 1) +
xlab("Leverage hii")+
ylab("Cook's Distance") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Cook's dist vs Leverage hii/(1-hii)") +
geom_abline(slope=seq(0,3,0.5), color = "gray", linetype = "dotdash")
library(patchwork)
fitted_values_vs_residuals + histogram_of_residuals
library(patchwork)
scale_location + leverage_vs_standardized_residuals
library(patchwork)
observation_number_vs_cooks_distance + leverage_vs_cooks_distanceValeurs ajustées en fonction des résidus ; histogramme des résidus. Image par l'auteur
Diagramme échelle-localisation ; effet de levier par rapport aux résidus standardisés. Image par l'auteur
Nombre d'observations en fonction de la distance de Cook ; distance de Cook en fonction de l'effet de levier. Image par l'auteur
La principale conclusion à tirer de l'examen de tous les diagrammes de diagnostic supplémentaires ci-dessus est peut-être qu'il existe une ou deux grandes valeurs aberrantes qui ont un impact important sur la pente de la ligne de régression, et que ces valeurs aberrantes ne sont pas aussi évidentes lorsque l'on examine uniquement le diagramme Q-Q. Le graphique Q-Q de notre exemple remplit donc sa fonction - tester la normalité des résidus - et révèle également une limite, à savoir qu'il ne tient pas compte de l'indépendance, de l'homoscédasticité ou des valeurs aberrantes.
À titre de référence supplémentaire, j'inclus ici un tableau de haut niveau montrant quelle hypothèse de modèle linéaire est testée avec chaque graphique de diagnostic, et je suggère également comment d'autres graphiques de diagnostic pourraient fonctionner en tandem avec le graphique Q-Q. Gardez à l'esprit que, en fonction des données, différents types de modèles peuvent être révélés avec différents diagrammes de diagnostic, et que certains autres éléments peuvent être révélés en combinaison. Par exemple, un graphique Q-Q peut confirmer la normalité, tandis qu'un graphique échelle-emplacement peut identifier l'hétéroscédasticité, et vous ne verrez la normalité et l'hétéroscédasticité qu'en utilisant les deux graphiques.
| Type de graphe de diagnostic | Aide à | Comment cela fonctionne-t-il avec le graphe Q-Q ? |
|---|---|---|
| Plot Q-Q | Normalité des résidus | |
| Histogramme des résidus | Normalité des résidus | Permet une visualisation rapide et un sens général de la symétrie et de l'étendue. |
| Valeurs ajustées et résidus | Linéarité, indépendance des erreurs | Révèle les schémas et la non-linéarité, en complément du contrôle de normalité du graphique Q-Q. |
| Tracé de l'échelle et de la localisation | Homoscédasticité | Met en évidence la cohérence des écarts résiduels, en complément des graphiques Q-Q pour les contrôles de normalité. |
| Graphique de l'effet de levier par rapport aux résidus | Indépendance des erreurs | Se concentre sur les points à fort effet de levier, que les diagrammes Q-Q n'abordent pas. |
| Nombre d'observations en fonction de la distance de Cook | Identifier les points d'influence | Complète les graphiques Q-Q en localisant les valeurs aberrantes ayant une grande influence. |
| Effet de levier et graphique de la distance de Cook | Identifier les points à fort effet de levier | met en évidence les observations influentes, tandis que les graphiques Q-Q valident la normalité. |
Réflexions finales
J'espère que vous appréciez désormais les graphiques Q-Q en tant qu'outil utile pour évaluer la normalité et que vous comprenez mieux leur utilisation courante pour évaluer la normalité des résidus d'une régression linéaire. J'espère également que vous aurez une nouvelle appréciation de l'idée et de l'importance des diagnostics de modèles linéaires de manière plus générale.
Poursuivez votre apprentissage de la régression linéaire avec notre site Multiple Linear Regression in R : Tutoriel avec exemples qui couvre des modèles plus complexes impliquant des prédicteurs multiples, y compris les idées de multicolinéarité dans la régression. Je vous conseille vivement de vous inscrire à notre parcours professionnel complet, Machine Learning Scientist in Python, pour tout savoir sur le flux de travail de construction de modèles, y compris l'apprentissage supervisé et non supervisé.
Devenez un scientifique ML

Je suis rédacteur et éditeur dans le domaine de la science des données. Je suis particulièrement intéressé par l'algèbre linéaire, les statistiques, R, etc. Je joue également beaucoup aux échecs !
FAQ sur l'intrigue Q-Q
Qu'est-ce qu'un graphique Q-Q ?
Un graphique Q-Q, ou graphique Quantile-Quantile, est un outil visuel utilisé pour comparer la distribution d'un ensemble de données à une distribution théorique, telle que la distribution normale.
Un graphique Q-Q est-il identique à un graphique Q-Q normal ?
Un graphique Q-Q normal est un type de graphique Q-Q dans lequel un ensemble de données est comparé à une distribution normale avec des paramètres spécifiés. Il est utilisé pour évaluer si un ensemble de données suit une distribution normale. Ainsi, tous les tracés Q-Q normaux sont des tracés Q-Q, mais tous les tracés Q-Q ne sont pas des tracés Q-Q normaux.