Kurs
Lineare Regressionsmodelle werden in der Statistik und beim maschinellen Lernen häufig verwendet, um numerische Werte auf der Grundlage von Eingabemerkmalen vorherzusagen und um die Beziehung zwischen Variablen zu verstehen. Aber nur weil du eine Linie durch deine Daten ziehen kannst, heißt das nicht, dass du das auch tun solltest. Wir müssen auch die Qualität der Anpassung diagnostizieren, um festzustellen, ob das Modell für die Daten geeignet ist oder ob es verfeinert werden muss.
Es gibt verschiedene Möglichkeiten, ein Modell zu testen, z. B. die Bewertung des Modells mithilfe eines Train/Test-Workflows oder die Betrachtung von Modellstatistiken wie dem bereinigten r-Quadrat. In diesem Artikel werde ich mich darauf konzentrieren, wie man eine bestimmte diagnostische Darstellung, die sogenannte Q-Q-Darstellung, erstellt und interpretiert, und ich zeige dir ein paar verschiedene Methoden, um diese Q-Q-Darstellung in der Programmiersprache R zu erstellen. Um die Regressionstechniken wirklich zu beherrschen, nimmst du an Introduction to Regression in R oder Intermediate Regression in R teil oder für Python an Introduction to Regression in Python oder Intermediate Regression in Python, je nachdem, wie gut du dich auskennst.
Was ist ein Q-Q-Plot?
Eine Q-Q-Darstellung (Quantil-Quantil) wird verwendet, um zu sehen, ob ein Datensatz einer bestimmten theoretischen Verteilung folgt. Eine Q-Q-Darstellung funktioniert, indem die Quantile der beobachteten Daten mit den Quantilen unserer anderen theoretischen Verteilung verglichen werden. Ich sage "theoretische Verteilung", um genau zu sein, aber wenn wir ein Q-Q-Diagramm erstellen, denken wir oft an die Normal- oder Gauß-Verteilung und bezeichnen sie als normale Q-Q-Darstellung. Q-Q-Diagramme können aber auch verwendet werden, um Daten mit anderen Verteilungen zu vergleichen, z. B. mit der Exponential-, Uniform-, Chi-Quadrat- oder t-Verteilung, Poisson-Verteilungoder andere, je nach Kontext der Analyse.
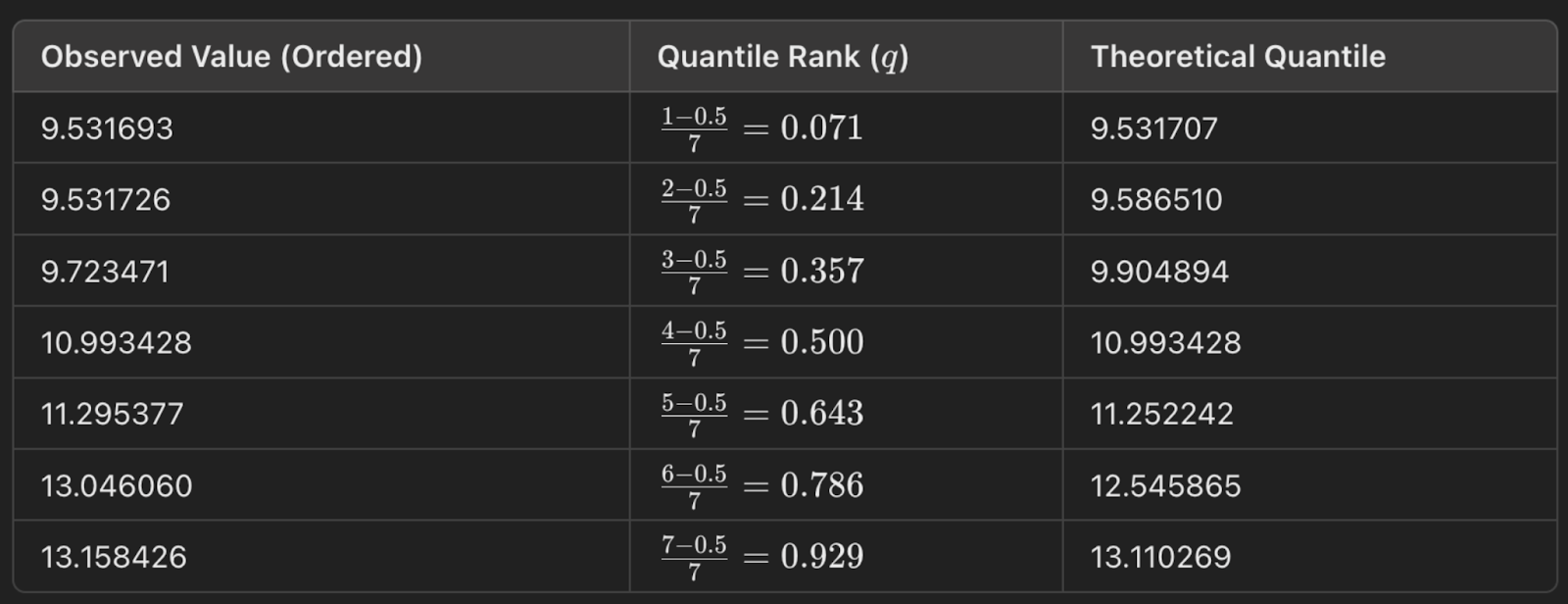
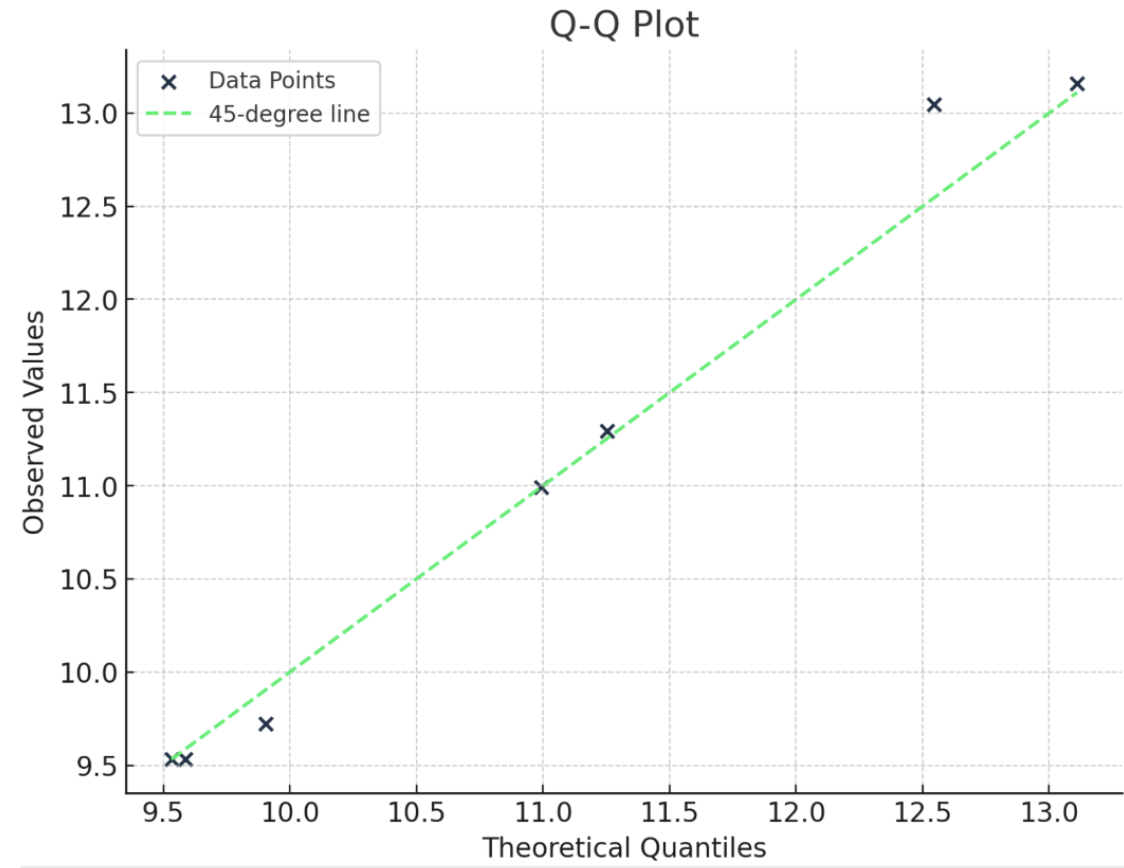
Es ist hilfreich, das anhand eines Beispiels zu verstehen. Hier habe ich eine Verteilung von Zahlen. Um ein normales Q-Q-Diagramm zu erstellen, bringe ich zuerst die Zahlen in die richtige Reihenfolge. Dann berechne ich den Quantilsrang mit dieser Gleichung: q = (i- 0,5)/n. Dann könnte ich die Prozentpunktfunktion (PPF) der Standardnormalverteilung verwenden, um den entsprechenden Wert für den Quantilsrang zu finden. (Du bist vielleicht mit der kumulativen Verteilungsfunktion (CDF) vertrauter, die uns die Wahrscheinlichkeit bis zu einem Wert x angibt. Nun, der PPF ist das Gegenteil davon: Sie gibt uns den x-Wert für eine bestimmte Wahrscheinlichkeit). Um das Diagramm zu erstellen, würden wir die Quantilsrangwerte gegen die theoretischen Quantile auftragen (daher die beiden Qs in Q-Q-Plot).
Warum ein Q-Q-Diagramm verwenden?
Ein Q-Q-Diagramm ist eine schöne visuelle Methode, um die Verteilungsannahmen zu überprüfen. Es gibt noch andere Methoden, um zu prüfen, ob die Daten einer Normalverteilung folgen, wie z.B. den Shapiro-Wilk-Test, aber nichts ist meiner Meinung nach so anschaulich und macht die Geschichte so deutlich wie der Q-Q-Plot.
Die Verteilung von etwas zu kennen, ist in vielerlei Hinsicht wichtig. Zum einen wollen wir wahrscheinlich die besten Maße für die Mitte und die Streuung wissen. Wenn wir eine lineare Regression erstellen, wollen wir auch wissen, ob unsere abhängige Variable einer Normalverteilung folgt und ob die Residuen unseres Modells normalverteilt sind, damit wir mehr Vertrauen in unsere Schätzungen haben. Ich denke also, dass Q-Q-Diagramme aus zwei allgemeinen Gründen nützlich sind: um unsere Daten mit Stichprobenverteilungen zu vergleichen und um die Normalität zu prüfen.
Wie man ein Q-Q-Diagramm in R erstellt
Schauen wir uns nun an, wie man ein Q-Q-Diagramm in R erstellt. In diesem Abschnitt gehe ich auf drei verschiedene Methoden ein: Base R, das Paket car und die Tidyverse-Methode. Ich denke, du wirst sehen, dass ich die tidyverse-Methoden bevorzuge, weil sie dir mehr Flexibilität bieten, um den Graphen schöner aussehen zu lassen, und weil sie mit anderen Paketen besser erweiterbar sind.
Für jede Methode werde ich ein Q-Q-Diagramm für die Residuen einer einfachen linearen Regression erstellen, was eine der häufigsten Anwendungen - wenn nicht sogar die häufigste - des Q-Q-Diagramms ist. Du könntest aber auch ein Q-Q-Diagramm erstellen, um die Verteilung der Variablen zu überprüfen, bevor du überhaupt eine lineare Regression erstellst. Alles, was du brauchst, ist die Verteilung einer Variablen und eine theoretische Verteilung, mit der du sie vergleichen kannst.
Wenn du mitmachen willst, kannst du den Kaggle-Datensatz herunterladen, den ich verwende: Autopreise Jordanien 2023.
Erstellen eines Q-Q-Plots in Base R
Erstellen wir zunächst einen Q-Q-Plot in Basis-R, d.h. wir installieren keine zusätzlichen Pakete, sondern verwenden nur die eingebauten Funktionen.
# importing data (in my case, saved on my desktop)
car_prices_jordan <- read.csv('~/Desktop/car_prices_jordan.csv')
# Create a linear model
car_linear_model <- lm(Price ~ sqrt(Price), filtered_car_prices)
# Extract the residuals
residuals <- resid(car_linear_model)
# Q-Q plot of residuals
qqnorm(residuals, main = "Q-Q Plot of Residuals from Linear Regression")
qqline(residuals, col = "red")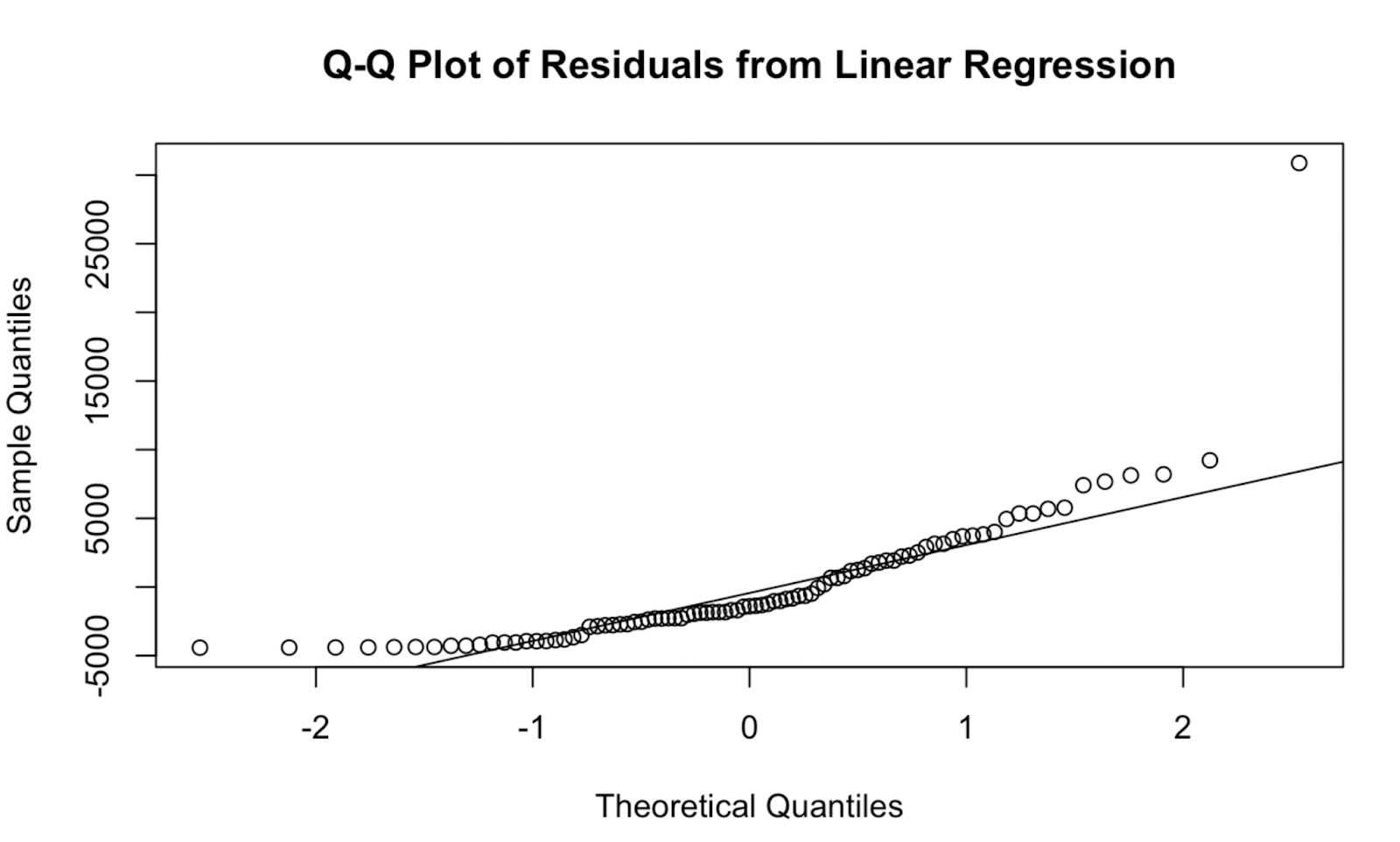 Q-Q-Plot erstellt in Base R. Bild vom Autor
Q-Q-Plot erstellt in Base R. Bild vom Autor
Erstellen eines Q-Q-Plots mit dem Auto-Paket
Versuchen wir nun, mit dem Paket car ein Q-Q-Diagramm zu erstellen. Meiner Meinung nach unterscheidet sich die Qualität der Visualisierung nicht allzu sehr, aber diese Q-Q-Darstellung hat den Vorteil, dass sie eine Konfidenzhüllkurve anzeigt, die den Bereich definiert, in dem unsere Datenpunkte voraussichtlich liegen werden, wenn die Modellannahme der Normalität zutreffen würde.
# Install the car package if not already installed
# install.packages("car")
library(car)
# Q-Q plot of residuals using car package
car::qqPlot(car_linear_model, main = "Q-Q Plot of Residuals from Linear Regression")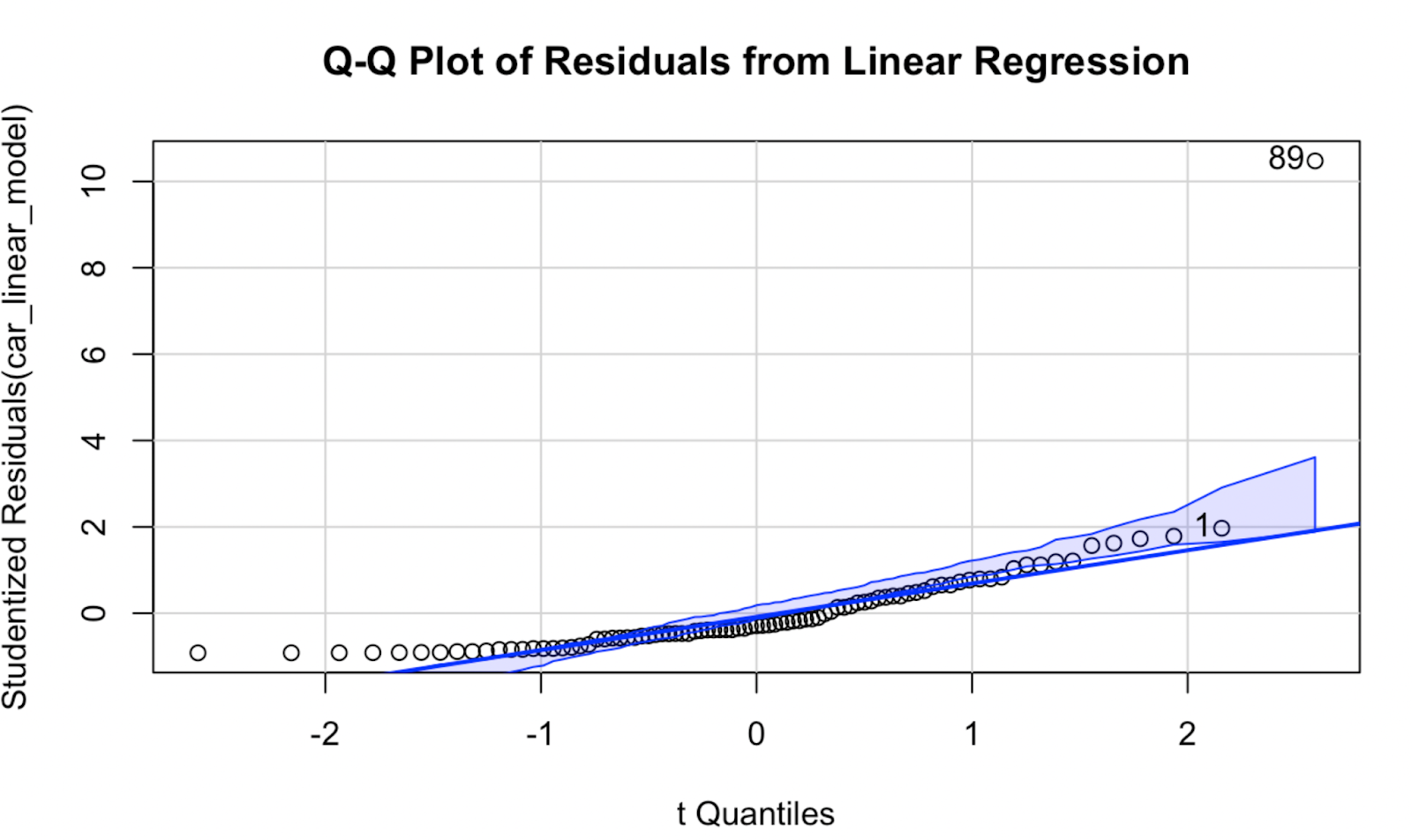 Q-Q-Plot erstellt mit dem car-Paket in R. Bild vom Autor
Q-Q-Plot erstellt mit dem car-Paket in R. Bild vom Autor
Erstellen eines Q-Q-Plots mit ggplot2
Jetzt schauen wir uns an, wie man ein Q-Q-Diagramm mit Tidyverse-Methoden erstellt, um flexibler zu sein und es schöner aussehen zu lassen. Dieses Mal werde ich das Q-Q-Diagramm als Panel neben meinem ursprünglichen Scatterplot einfügen.
library(tidyverse)
library(metBrewer)
car_prices_jordan$Power <- as.numeric(gsub("[^0-9]", "", car_prices_jordan$Power))
car_prices_jordan$Price <- as.numeric(gsub("[^0-9]", "", car_prices_jordan$Price))
slope <- (cor(car_prices_jordan$Power, car_prices_jordan$Price) * (sd(car_prices_jordan$Price)) / sd(car_prices_jordan$Power))
intercept <- (mean(car_prices_jordan$Price) - slope * mean(car_prices_jordan$Power))
car_prices_graph <- ggplot(car_prices_jordan, aes(x = Power, y = Price)) +
geom_point() +
ggtitle("Car Prices in Jordan") +
geom_abline(slope = slope, intercept = intercept, color = '#376795', size = 1)
car_linear_model <- lm(Price ~ Price, car_prices_jordan)
qq_plot <- ggplot(data = car_linear_model, aes(sample = .resid)) +
stat_qq() +
stat_qq_line(linetype = 'dashed', color = '#ef8a47', size = 1) +
labs(title = "Car Prices in Jordan") +
labs(subtitle = "Residual QQ Plot")
library(patchwork)
car_prices_graph + qq_plot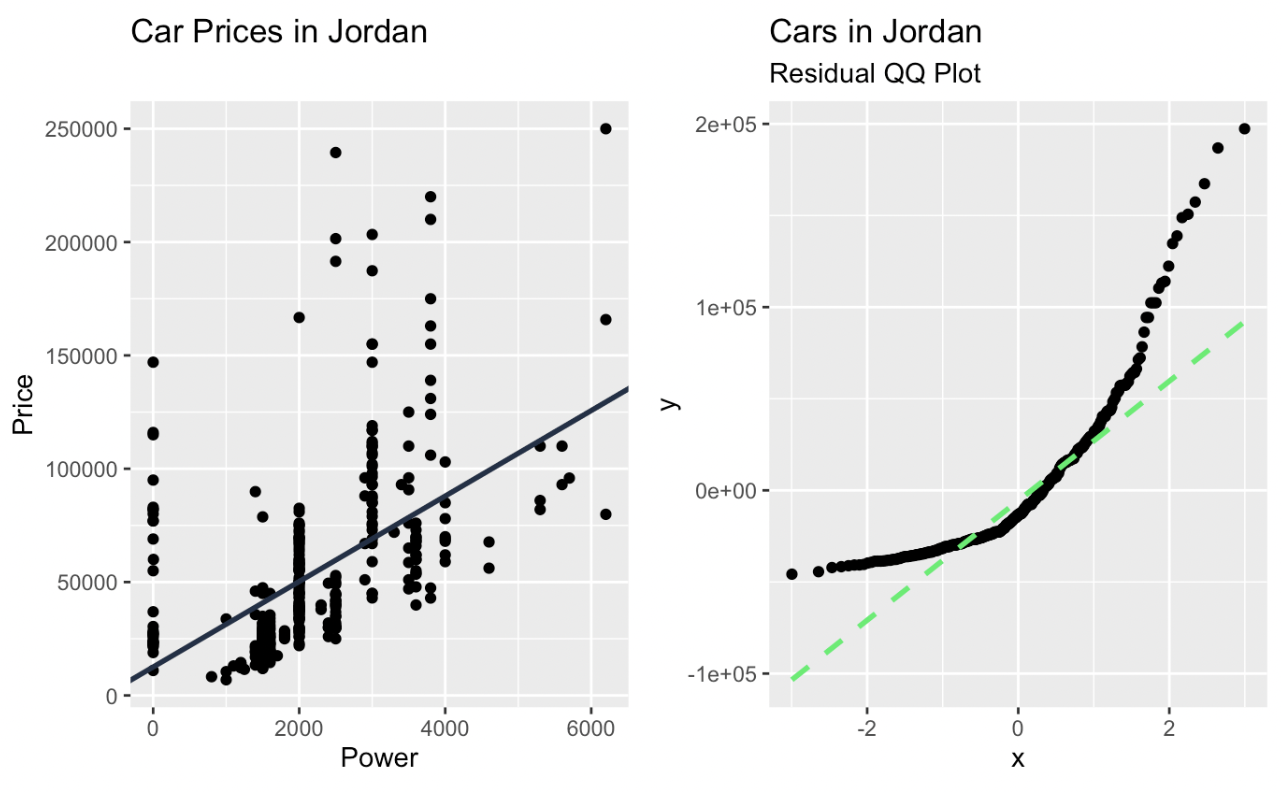
Lineare Regression und ein Q-Q-Diagramm der Residuen, erstellt in ggplot2. Bild vom Autor
Was uns ein Q-Q-Plot sagen kann
In einem Q-Q-Diagramm werden die Quantile der beobachteten Daten gegen die theoretischen Quantile aufgetragen. Wenn die Daten der theoretischen Verteilung genau entsprechen, bewegen sich die Punkte auf dem Q-Q-Diagramm auf einer diagonalen Linie. Abweichungen von dieser Linie zeigen Abweichungen von der erwarteten Verteilung an. Punkte, die über oder unter die Linie fallen, deuten auf Schiefe oder Ausreißer hin, und Muster wie Kurven oder s-förmige Abweichungen weisen auf systematische Unterschiede hin, wie z. B. schwerere oder leichtere Schwänze.
Es gibt ungefähr drei Dinge, auf die wir achten.
- Gerade Linie: Die Daten stimmen gut mit der theoretischen Verteilung überein.
- Gebogene Muster: Kennzeichne schiefe Daten oder nicht-normale Verteilungen.
- Schwere oder leichte Schwänze: Wenn die Punkte an den Enden abweichen, haben die Daten möglicherweise schwerere oder leichtere Schwänze als erwartet.
Das wollen wir an einem Beispiel zeigen:
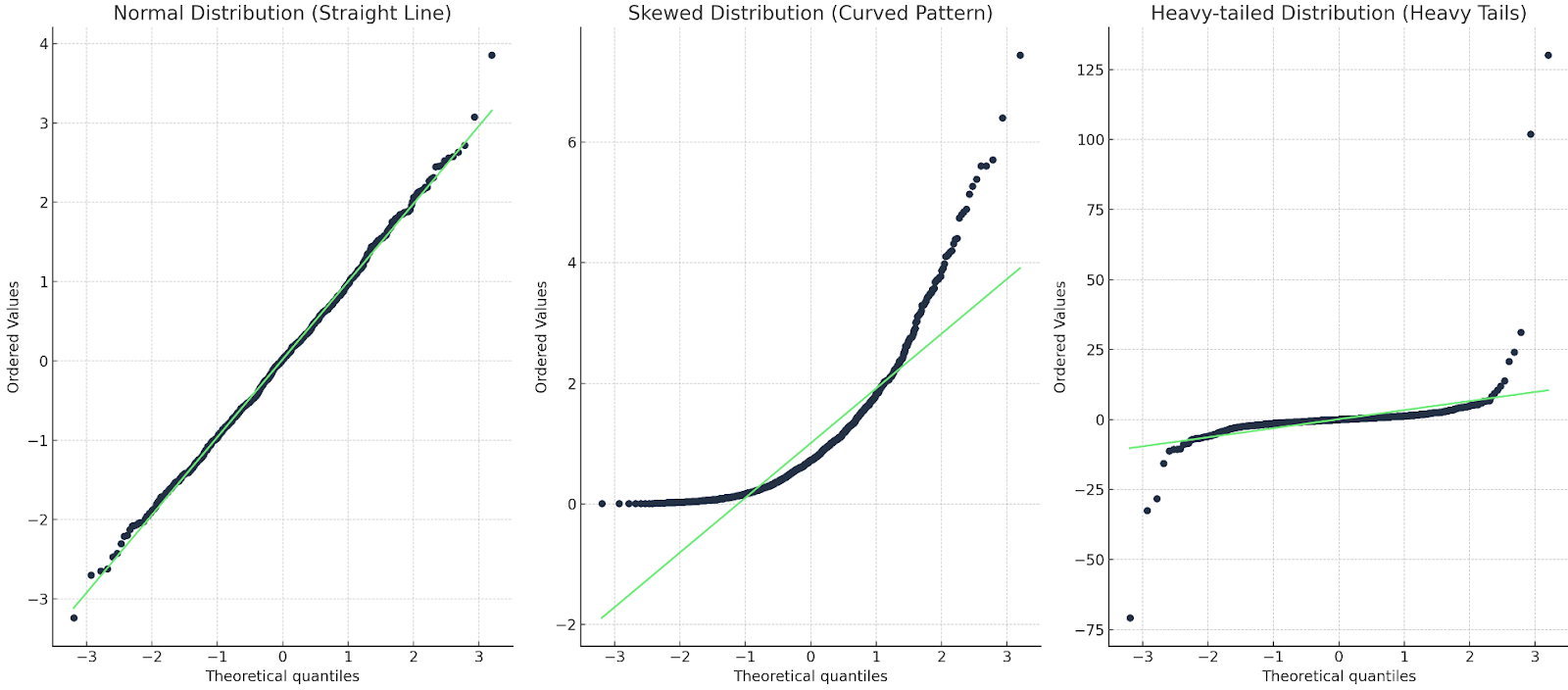
Drei Q-Q-Diagramme: eines mit einer geraden Linie, eines mit einer Kurve, eines mit einem starken Ausläufer. Bild vom Autor
Im ersten Fall stimmt die Q-Q-Linie mit den Datenpunkten überein, also ist die Verteilung tatsächlich normal. Im zweiten Fall sehen wir ein gekrümmtes Muster, d.h. die Daten sind entweder nicht normal oder sie sind schief. Im letzten Fall sehen wir eine Art "S"-Form, d.h. die Verteilung hat starke Schwänze oder mehr Extremwerte.
Q-Q-Diagramme in der linearen Regression
Es gibt verschiedene Annahmen für lineare Modelle, darunter die Linearität (dass die Beziehung zwischen den Variablen linear ist), die Unabhängigkeit der Fehler (dass die Fehler nicht miteinander korreliert sind), die Homoskedastizität (dass diedass die Residuen eine konstante Varianz haben sollten)und Normalität der Residuen (dass die Residuen einer Normalverteilung folgen). Das Q-Q-Diagramm hilft vor allem bei der vierten Annahme des linearen Modells, der Normalität der Residuen.
Hier siehst du, wie verschiedene Muster die Interpretation und Zuverlässigkeit unseres Modells beeinflussen:
Geradliniges Ausrichten
- Was es bedeutet: Die Residuen sind annähernd normal, was darauf hindeutet, dass das Modell im Hinblick auf die Normalitätsannahme gut zu den Daten passt.
- Auswirkungen auf die Praxis: Konfidenzintervalle, p-Werte und Hypothesentests, die aus dem Modell abgeleitet werden, sind wahrscheinlich zuverlässig, da sie von normalverteilten Residuen ausgehen.
Gekrümmte Muster
- Was es bedeutet: Ein gekrümmtes Q-Q-Diagramm deutet oft auf eine Nicht-Normalität hin, wie z. B. eine Schiefe in den Residuen. Die Kurve kann eine Aufwärts- oder Abwärtskurve sein. (Dieses gekrümmte Muster ist das, was wir in unserem Beispiel oben sehen).
- Auswirkungen auf die Praxis: Nicht-normale Residuen können zu verzerrten p-Werten oder Konfidenzintervallen führen, insbesondere bei kleineren Datensätzen. Wir sollten in Betracht ziehen, die abhängige Variable zu transformieren oder die Modellstruktur zu überarbeiten.
Schwere oder leichte Schwänze
- Was es bedeutet: Wenn es starke Schwänze gibt, haben die Residuen mehr Extremwerte als unter Normalität erwartet, möglicherweise aufgrund von Ausreißern, oder es liegt eine falsche Modellspezifikation vor. Wenn es leichte Schwänze gibt, bedeutet das, dass es weniger extreme Residuen gibt als erwartet, was auf eine Datenbeschneidung hindeuten kann.
- Auswirkungen auf die Praxis: Bei starken Schwänzen können Ausreißer die Regressionslinie unverhältnismäßig stark beeinflussen, was zu irreführenden Ergebnissen führt. Wir sollten in Betracht ziehen, Ausreißer zu entfernen oder herunterzugewichten. Ich denke, dass leichte Schwänze das Modell nicht so sehr beeinflussen, aber es könnte ein Hinweis darauf sein, dass die Daten irgendwie unvollständig sind.
Q-Q-Diagramme und andere diagnostische Diagramme
Wenn du dich mit den Diagnoseplots für lineare Modelle auskennst, weißt du vielleicht auch, dass es eine ganze Reihe von Optionen gibt, um die Modellanpassung zu bewerten. Um genau zu verstehen, was das Q-Q-Diagramm anzeigt, sollten wir uns ein paar andere Diagnosen ansehen. So können wir besser verstehen, was der Q-Q-Plot bewirkt und welche anderen Plots ihn ergänzen könnten.
- Angepasste Werte versus Residuen: Diese Grafik zeigt das Verhältnis zwischen den vorhergesagten Werten (angepassten Werten) und den Residuen, also den Differenzen zwischen den beobachteten und vorhergesagten Werten.
- Histogramm der Residuen: Diese Grafik zeigt die Verteilung der Residuen.
- Scale-Location Plot: Diese Grafik zeigt das Verhältnis zwischen den Residuen und den angepassten Werten.
- Hebelwirkung versus standardisierte Residualwerte: Diese Darstellung zeigt, wie weit ein Datenpunkt im Prädiktorenraum liegt und ob das Modell gut oder schlecht passt. Wir standardisieren die Residuen, um ihre Beziehung zur Verschuldung auf einer einheitlichen Skala zu bewerten.
- Anzahl der Beobachtungen im Vergleich zur Cook'schen Entfernung: Dieses Diagramm zeigt die Datenpunkte mit dem größten Einfluss auf das Modell, indem es die Hebelwirkung und die Restgröße kombiniert. Die Beobachtungsnummer auf der x-Achse dient als Kennung für jeden Datenpunkt.
- Hebelwirkung versus Cook's Distance: Diese Grafik vergleicht das Potenzial eines Punktes, das Modell zu beeinflussen, mit seinem tatsächlichen Einfluss auf die Modellvorhersagen.
Ich zeige dir, wie du mit den Tidyverse-Methoden schnell ein Diagramm erstellen kannst. Es geht hier nicht darum, das lineare Modell aus unserem "Autos in Jordanien"-Datensatz für jede lineare Modelldiagnose auf dieser Liste zu interpretieren. Vielmehr möchte ich die anderen diagnostischen Darstellungen zeigen, damit du sie erkennen kannst, den Code verwenden kannst, wenn er hilfreich ist, und - und das ist der Sinn dieses Artikels - damit du die Q-Q-Darstellung besser in die anderen diagnostischen Darstellungen einordnen kannst. Auf diese Weise verstehst du besser, was das Q-Q-Diagramm zeigt und was nicht, wie es hilfreich ist und was ihm fehlt.
fitted_values_vs_residuals <- ggplot(data = car_linear_model, aes(x = .fitted, y = .resid)) +
geom_point(color = '#203147') +
geom_hline(yintercept = 0, linetype = "dashed", color = '#01ef63', size = 1) +
xlab("fitted values") +
ylab("residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Fitted Values vs Residuals")
histogram_of_residuals <- ggplot(data = car_linear_model, aes(x = .resid)) +
geom_histogram(color = '#01ef63') +
xlab("residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Histogram of Residuals")
scale_location <- ggplot(car_linear_model, aes(.fitted, sqrt(abs(.stdresid)))) +
geom_point(color = '#203147', na.rm=TRUE) +
stat_smooth(method="loess", na.rm = TRUE, color = '#01ef63', size = 1, se = FALSE) +
xlab("Fitted Value") +
ylab(expression(sqrt("|Standardized residuals|"))) +
labs(title = "Cars in Jordan") +
labs(subtitle = "Scale-Location")
leverage_vs_standardized_residuals <- ggplot(data = car_linear_model, aes(.hat, .stdresid)) +
geom_point(aes(size = .cooksd), color = '#203147') +
stat_smooth(method="loess", na.rm=TRUE, color = '#01ef63', size = 1) +
xlab("Leverage") +
ylab("Standardized Residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Residuals vs Leverage") +
scale_size_continuous("Cook's Distance", range=c(1,5)) +
theme(legend.title = element_blank()) +
theme(legend.position= "none")
observation_number_vs_cooks_distance <- ggplot(car_linear_model, aes(seq_along(.cooksd), .cooksd)) +
geom_bar(stat="identity", position="identity", color = '#01ef63', size = 1) +
xlab("Obs. Number") +
ylab("Cook's distance") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Cook's distance")
leverage_vs_cooks_distance <- ggplot(car_linear_model, aes(.hat, .cooksd))+geom_point(na.rm=TRUE) +
stat_smooth(method="loess", na.rm=TRUE, color = '#01ef63', size = 1) +
xlab("Leverage hii")+
ylab("Cook's Distance") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Cook's dist vs Leverage hii/(1-hii)") +
geom_abline(slope=seq(0,3,0.5), color = "gray", linetype = "dotdash")
library(patchwork)
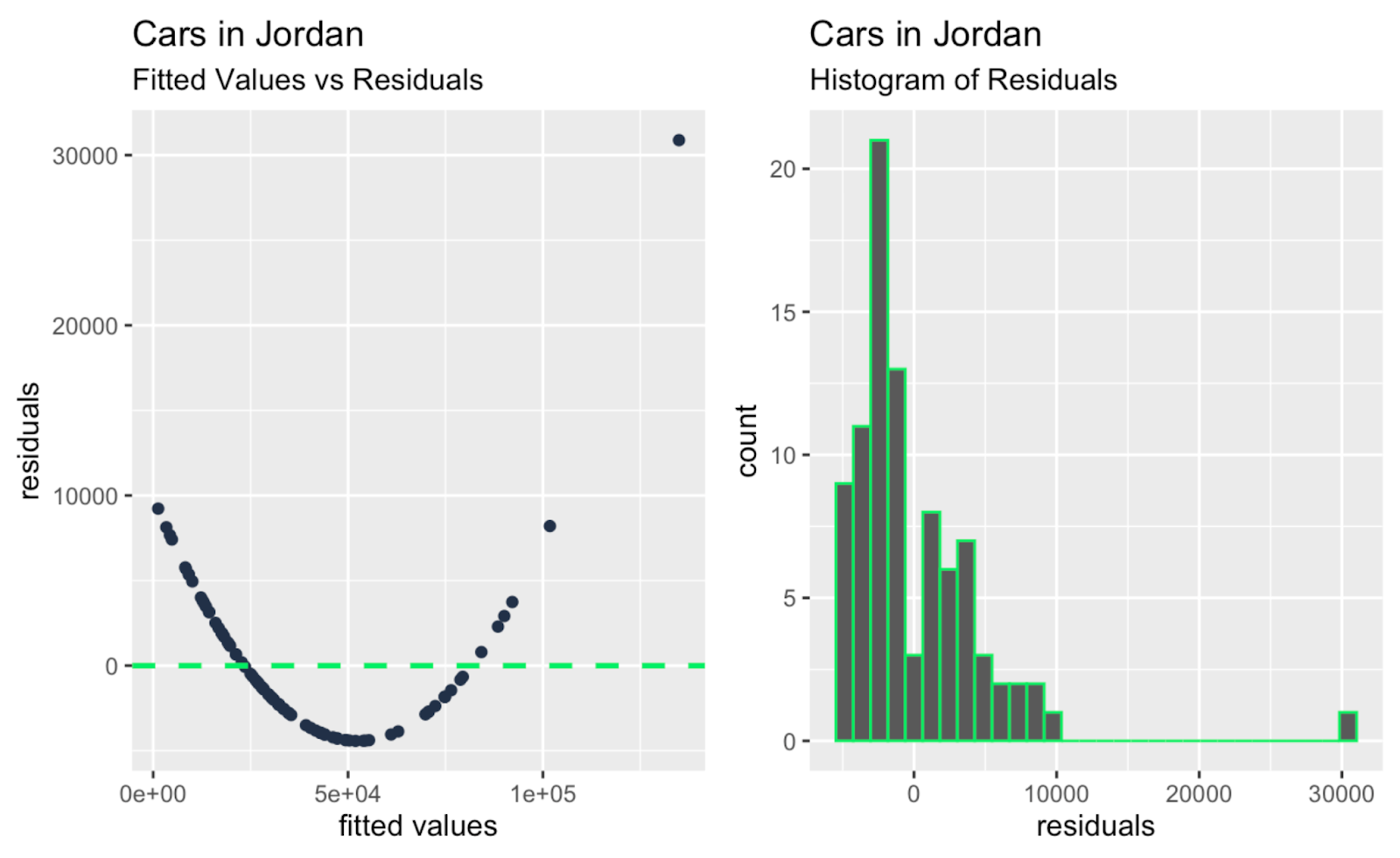
fitted_values_vs_residuals + histogram_of_residuals
library(patchwork)
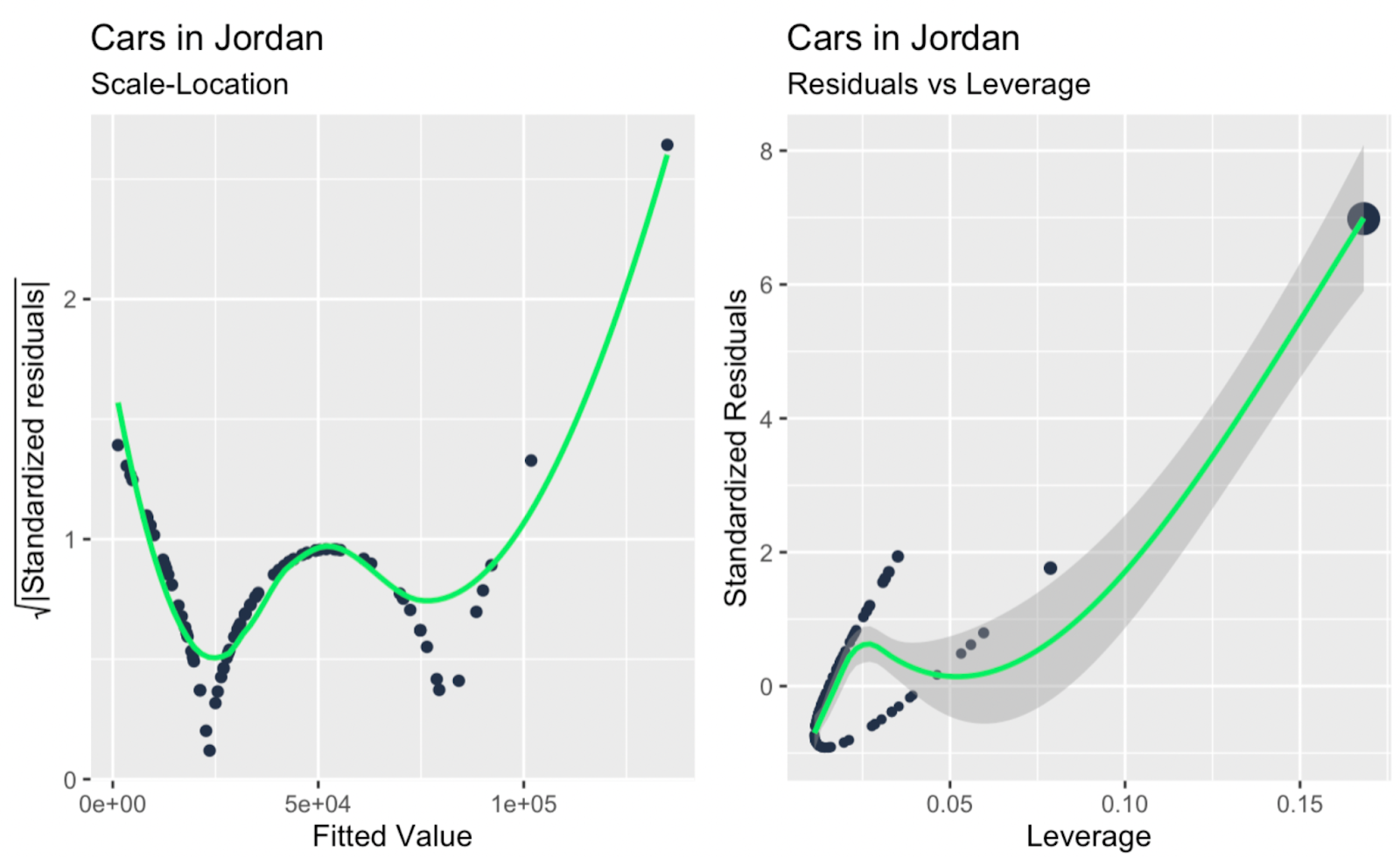
scale_location + leverage_vs_standardized_residuals
library(patchwork)
observation_number_vs_cooks_distance + leverage_vs_cooks_distanceAngepasste Werte gegen Residuen; Histogramm der Residuen. Bild vom Autor
Skala-Lage-Diagramm; Hebelwirkung gegenüber standardisierten Residuen. Bild vom Autor
Anzahl der Beobachtungen gegen Cooks Abstand; Cooks Abstand gegen Hebelwirkung. Bild vom Autor
Die wichtigste Erkenntnis aus der Betrachtung aller zusätzlichen diagnostischen Diagramme oben ist vielleicht, dass es ein oder zwei große Ausreißer gibt, die einen großen Einfluss auf die Steigung der Regressionslinie haben, und diese Ausreißer sind nicht so offensichtlich, wenn man nur das Q-Q-Diagramm betrachtet. Das Q-Q-Diagramm in unserem Beispiel erfüllt also seine Funktion - die Prüfung der Normalität der Residuen - und offenbart auch eine Einschränkung, nämlich dass es weder die Unabhängigkeit noch die Homoskedastizität oder Ausreißer berücksichtigt.
Als zusätzliche Referenz füge ich hier eine übersichtliche Tabelle ein, die zeigt, welche lineare Modellannahme mit jedem Diagnoseplot getestet wird, und ich mache auch Vorschläge, wie andere Diagnoseplots mit dem Q-Q-Plot zusammenarbeiten könnten. Bedenke, dass je nach Datenlage unterschiedliche Muster mit verschiedenen Diagnoseplots aufgedeckt werden können und dass bestimmte andere Dinge in Kombination aufgedeckt werden können. Ein Q-Q-Diagramm könnte zum Beispiel Normalität bestätigen, während ein Skalen-Ort-Diagramm Heteroskedastizität aufzeigen könnte, und du könntest nur Normalität und Heteroskedastizität sehen, wenn du beide Diagramme verwendest.
| Diagnostischer Plot-Typ | Hilft bei | So funktioniert es mit dem Q-Q-Plot |
|---|---|---|
| Q-Q Plot | Normalität der Residuen | |
| Histogramm der Residuen | Normalität der Residuen | Ermöglicht einen schnellen Blick und ein allgemeines Gefühl für Symmetrie und Verbreitung. |
| Angepasste Werte versus Residuen | Linearität, Unabhängigkeit von Fehlern | Zeigt Muster und Nichtlinearität auf und ergänzt die Normalitätsprüfung des Q-Q-Plots. |
| Skala-Lage-Diagramm | Homoskedastizität | Hebt die Konsistenz der Restspanne hervor und ergänzt die Q-Q-Diagramme zur Überprüfung der Normalität. |
| Leverage versus Residuals Diagramm | Unabhängigkeit von Fehlern | Konzentriert sich auf die wichtigsten Punkte, die in den Q-Q-Diagrammen nicht berücksichtigt sind. |
| Anzahl der Beobachtungen im Vergleich zur Cook'schen Distanz | Identifizierung einflussreicher Punkte | Ergänzt Q-Q-Diagramme, indem es Ausreißer mit hohem Einfluss aufspürt. |
| Hebelwirkung versus Cook's Distance Plot | Identifizierung von Punkten mit hoher Hebelwirkung | Hebt einflussreiche Beobachtungen hervor, während Q-Q-Diagramme die Normalität bestätigen. |
Schlussgedanken
Ich hoffe, du hast ein neues Verständnis für Q-Q-Diagramme als nützliches Instrument zur Beurteilung der Normalität entwickelt und weißt nun, wie sie häufig zur Beurteilung der Normalität von Residuen in einer linearen Regression eingesetzt werden. Ich hoffe auch, dass du die Idee und die Bedeutung der linearen Modelldiagnose im Allgemeinen neu schätzen gelernt hast.
Lerne weiter über lineare Regression mit unserem Multiple Linear Regression in R: Tutorium mit Beispielen, das komplexere Modelle mit mehreren Prädiktoren behandelt, einschließlich Ideen zur Multikollinearität in der Regression. Ich empfehle dir dringend, dich für unseren umfassenden Lernpfad " Machine Learning Scientist in Python" anzumelden, um alles über die Modellbildung zu erfahren, einschließlich überwachtem und unüberwachtem Lernen.
Werde ein ML-Wissenschaftler

Q-Q Plot FAQs
Was ist ein Q-Q-Plot?
Ein Q-Q-Diagramm oder Quantil-Quantil-Diagramm ist ein visuelles Hilfsmittel, um die Verteilung eines Datensatzes mit einer theoretischen Verteilung wie der Normalverteilung zu vergleichen.
Ist ein Q-Q-Plot dasselbe wie ein normaler Q-Q-Plot?
Ein normaler Q-Q-Plot ist eine Art Q-Q-Plot, bei dem ein Datensatz mit einer Normalverteilung mit bestimmten Parametern verglichen wird. Sie wird verwendet, um zu beurteilen, ob ein Datensatz einer Normalverteilung folgt. Alle normalen Q-Q-Plots sind also Q-Q-Plots, aber nicht alle Q-Q-Plots sind normale Q-Q-Plots.