Curso
Los modelos de regresión lineal se utilizan mucho en estadística y aprendizaje automático para predecir valores numéricos a partir de características de entrada, y también para comprender la relación entre variables. Sin embargo, que puedas trazar una línea a través de tus datos no significa que debas hacerlo. También tenemos que diagnosticar la calidad del ajuste para determinar si el modelo es adecuado para los datos o si hay que refinarlo.
Hay varias formas de probar un modelo, como evaluar el modelo mediante un flujo de trabajo de entrenamiento/prueba y observar las estadísticas del modelo, como la r-cuadrado ajustada. En este artículo, me centraré en cómo crear e interpretar un gráfico de diagnóstico específico llamado gráfico Q-Q, y te mostraré algunos métodos diferentes para crear este gráfico Q-Q en el lenguaje de programación R. Para seguir dominando realmente las técnicas de regresión, toma Introducción a la regresión en R o Regresión intermedia en R o, para Python, toma Introducción a la regresión en Python o Regresión intermedia en Python, según tu nivel de comodidad.
¿Qué es una Gráfica Q-Q?
Un gráfico Q-Q (Cuantil-Cuantil) se utiliza para ver si un conjunto de datos sigue una determinada distribución teórica. Un gráfico Q-Q funciona comparando los cuantiles de los datos observados con los cuantiles de nuestra otra distribución teórica. Digo "distribución teórica" para ser exactos, pero a menudo cuando creamos un gráfico Q-Q estamos pensando realmente en la distribución normal o gaussiana y nos referimos a ella como diagrama Q-Q normal. Sin embargo, los gráficos Q-Q también pueden utilizarse para comparar datos con otras distribuciones, como la exponencial, la uniforme, la chi-cuadrado o la distribución t, distribución de Poissonu otras, según el contexto del análisis.
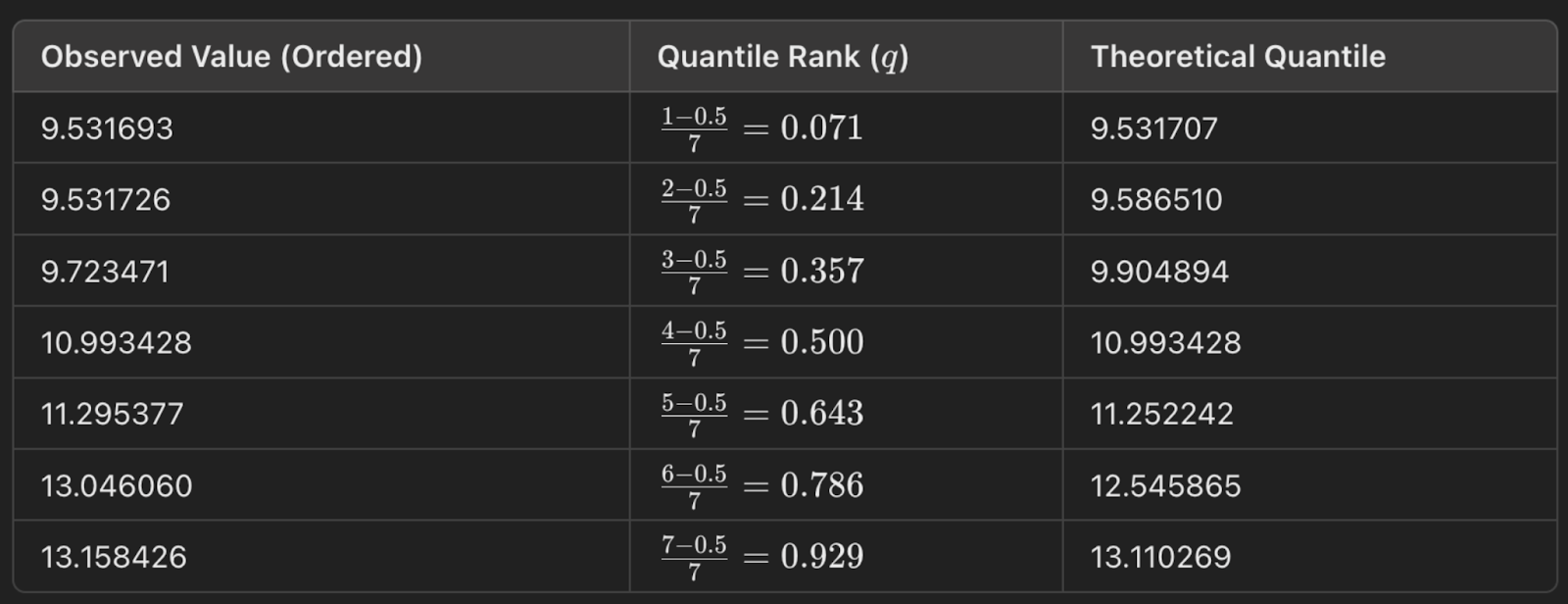
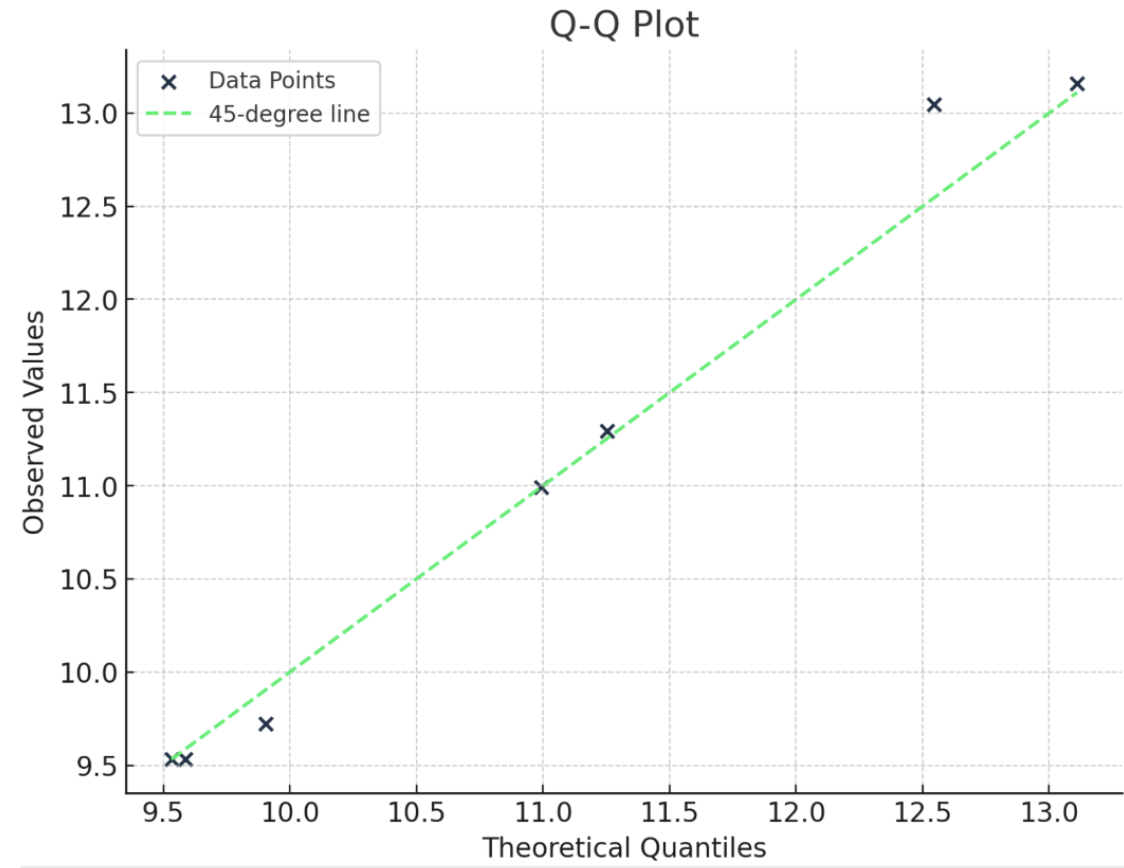
Es útil entenderlo mostrando un ejemplo. Aquí tengo una distribución de números. Para construir un gráfico Q-Q normal, primero pongo los números en orden. A continuación, calculo el rango cuantil con esta ecuación: q = (i- 0,5)/n. Entonces, podría utilizar la función de punto porcentual (PPF) de la distribución normal estándar para hallar el valor correspondiente del rango cuantílico. (Quizá te resulte más familiar la función de distribución acumulativa (FDA), que nos indica la probabilidad hasta un valor x. Pues el PPF es todo lo contrario: Nos da el valor x para una probabilidad dada). Para crear el gráfico, compararíamos los valores de los rangos cuantílicos con los cuantiles teóricos (de ahí las dos Q del gráfico Q-Q).
¿Por qué utilizar un diagrama Q-Q?
Un gráfico Q-Q es una buena forma visual de comprobar los supuestos de distribución. Hay otras formas de comprobar si los datos siguen una distribución normal, como la prueba de Shapiro-Wilk, por ejemplo, pero nada, en mi opinión, es realmente tan visual, y hace la historia tan obvia, como el gráfico Q-Q.
Conocer la distribución de algo es importante de varias maneras. Por un lado, probablemente querremos saber cuáles son las mejores medidas para el centro y la dispersión. Además, al crear una regresión lineal, queremos saber si nuestra variable dependiente, en particular, sigue una distribución normal, y también queremos ver si los residuos de nuestro modelo se distribuyen normalmente para tener una mayor confianza en nuestras estimaciones. Así que, básicamente, creo que los gráficos Q-Q son útiles por dos razones generales: comparar nuestros datos con distribuciones muestrales y comprobar la normalidad.
Cómo crear un gráfico Q-Q en R
Veamos ahora cómo crear un gráfico Q-Q en R. Para esta sección, repasaré tres métodos diferentes: R base, el paquete car y los métodos tidyverse. Creo que verás que prefiero los métodos tidyverse porque te dan más flexibilidad para que el gráfico tenga un aspecto más bonito y tiene más extensibilidad con otros paquetes.
Para cada método, crearé un gráfico Q-Q sobre los residuos de una regresión lineal simple, que es uno de los usos más comunes -si no el más común- del gráfico Q-Q. Sin embargo, también podrías crear un gráfico Q-Q para comprobar la distribución de las variables antes de crear una regresión lineal en primer lugar. Sólo necesitas la distribución de una variable y una distribución teórica con la que compararla.
Si quieres seguirme, puedes descargar el conjunto de datos de Kaggle que estoy utilizando: Precios de los coches Jordania 2023.
Crear un gráfico Q-Q en R base
Primero vamos a crear un gráfico Q-Q en R básico, es decir, no vamos a instalar ningún paquete adicional, sino que vamos a utilizar sólo las funciones incorporadas.
# importing data (in my case, saved on my desktop)
car_prices_jordan <- read.csv('~/Desktop/car_prices_jordan.csv')
# Create a linear model
car_linear_model <- lm(Price ~ sqrt(Price), filtered_car_prices)
# Extract the residuals
residuals <- resid(car_linear_model)
# Q-Q plot of residuals
qqnorm(residuals, main = "Q-Q Plot of Residuals from Linear Regression")
qqline(residuals, col = "red")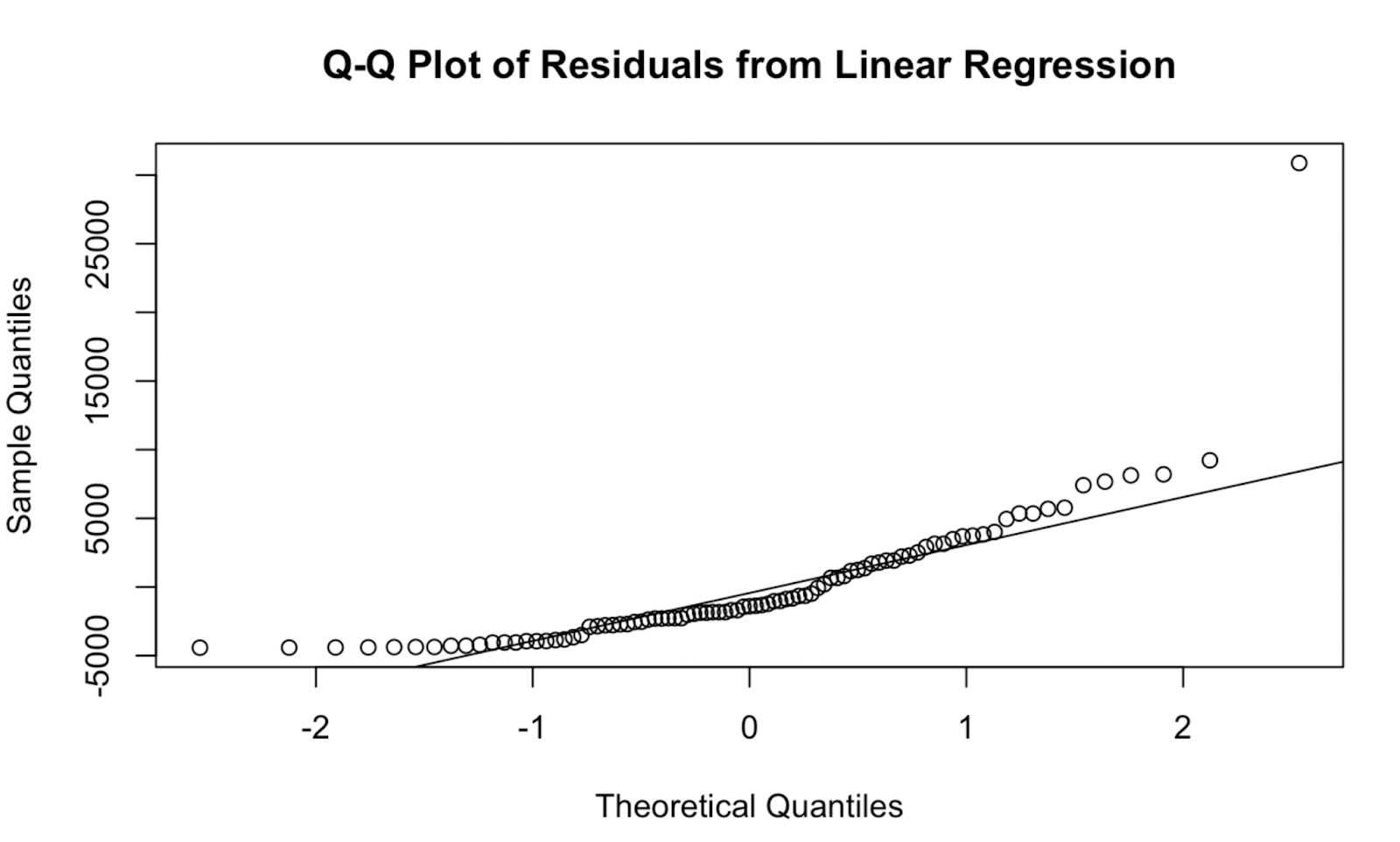 Gráfico Q-Q creado en R base. Imagen del Autor
Gráfico Q-Q creado en R base. Imagen del Autor
Crear un gráfico Q-Q con el paquete coche
Ahora, vamos a intentar crear un gráfico Q-Q utilizando el paquete car. En mi opinión, la calidad de la visualización no es demasiado diferente, pero este gráfico Q-Q tiene la ventaja de que muestra una envolvente de confianza que define el área dentro de la cual se espera que se sitúen nuestros puntos de datos si se cumpliera el supuesto de normalidad del modelo.
# Install the car package if not already installed
# install.packages("car")
library(car)
# Q-Q plot of residuals using car package
car::qqPlot(car_linear_model, main = "Q-Q Plot of Residuals from Linear Regression")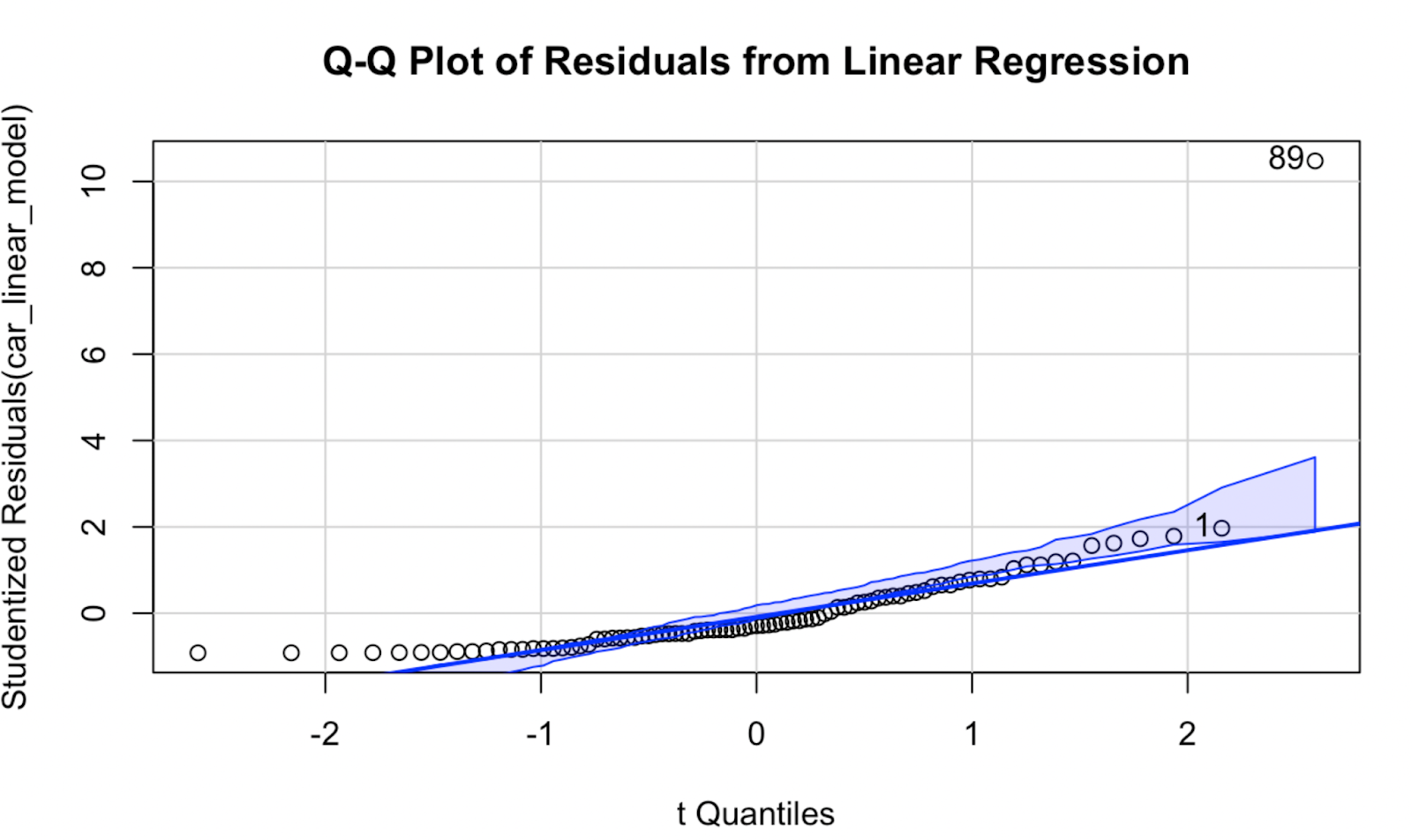 Gráfico Q-Q creado con el paquete car en R. Imagen del autor
Gráfico Q-Q creado con el paquete car en R. Imagen del autor
Crear un gráfico Q-Q con ggplot2
Ahora vamos a ver cómo crear un gráfico Q-Q utilizando métodos tidyverse para tener más flexibilidad y que quede más bonito. Esta vez, voy a colocar el gráfico Q-Q como un panel junto a mi gráfico de dispersión original.
library(tidyverse)
library(metBrewer)
car_prices_jordan$Power <- as.numeric(gsub("[^0-9]", "", car_prices_jordan$Power))
car_prices_jordan$Price <- as.numeric(gsub("[^0-9]", "", car_prices_jordan$Price))
slope <- (cor(car_prices_jordan$Power, car_prices_jordan$Price) * (sd(car_prices_jordan$Price)) / sd(car_prices_jordan$Power))
intercept <- (mean(car_prices_jordan$Price) - slope * mean(car_prices_jordan$Power))
car_prices_graph <- ggplot(car_prices_jordan, aes(x = Power, y = Price)) +
geom_point() +
ggtitle("Car Prices in Jordan") +
geom_abline(slope = slope, intercept = intercept, color = '#376795', size = 1)
car_linear_model <- lm(Price ~ Price, car_prices_jordan)
qq_plot <- ggplot(data = car_linear_model, aes(sample = .resid)) +
stat_qq() +
stat_qq_line(linetype = 'dashed', color = '#ef8a47', size = 1) +
labs(title = "Car Prices in Jordan") +
labs(subtitle = "Residual QQ Plot")
library(patchwork)
car_prices_graph + qq_plot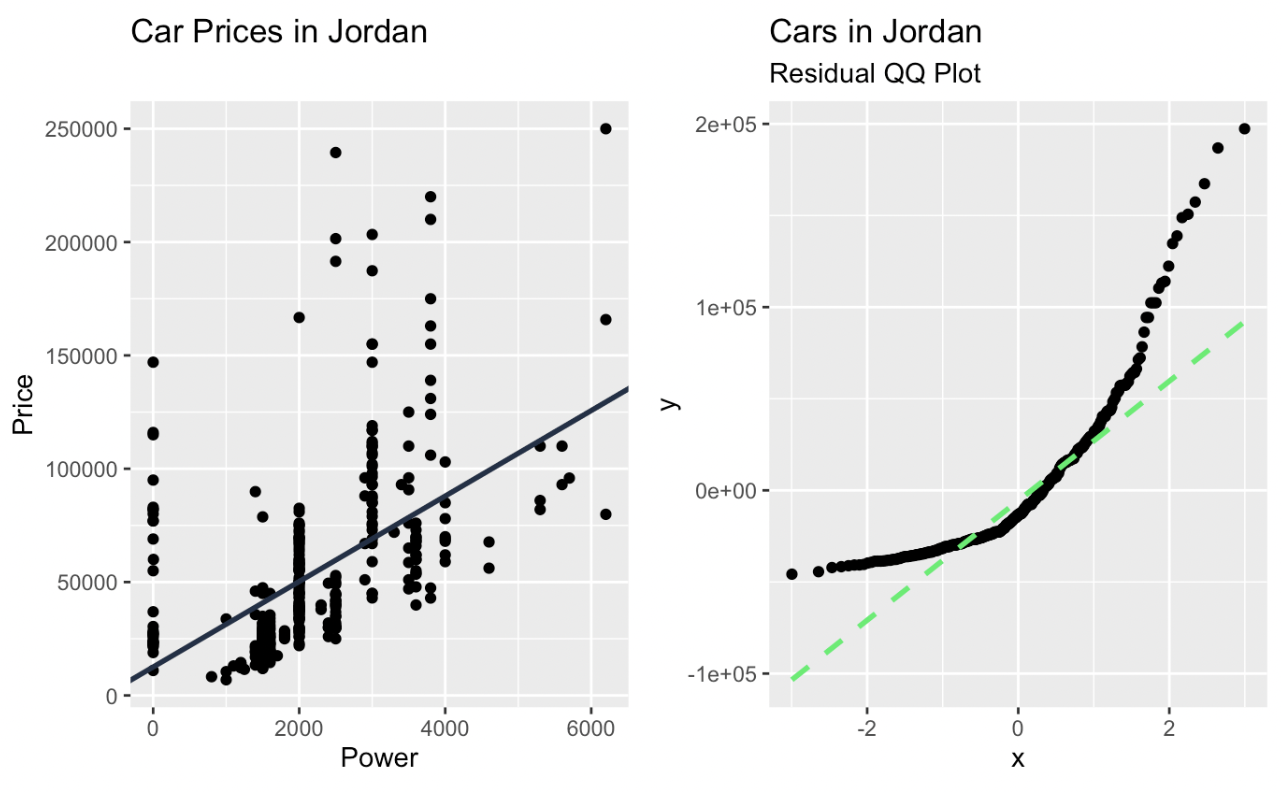
Regresión lineal y un gráfico Q-Q de los residuos creado en ggplot2. Imagen del autor
Lo que puede decirnos una trama Q-Q
Con un gráfico Q-Q, los cuantiles de los datos observados se comparan con los cuantiles teóricos. Si los datos siguen de cerca la distribución teórica, los puntos del gráfico Q-Q se moverán sobre una línea diagonal. Las desviaciones de esta línea indican desviaciones de la distribución esperada. Los puntos que caen por encima o por debajo de la línea sugieren asimetría o valores atípicos, y los patrones como curvas o desviaciones en forma de s indican diferencias sistemáticas, como colas más pesadas o más ligeras.
Hay unas tres cosas que buscamos.
- Línea recta: Los datos se ajustan bien a la distribución teórica.
- Patrones curvos: Indica datos sesgados o distribuciones no normales.
- Colas pesadas o ligeras: Si los puntos se desvían en los extremos, los datos podrían tener colas más pesadas o más ligeras de lo esperado.
Vamos a mostrarlo con un ejemplo para cada uno:
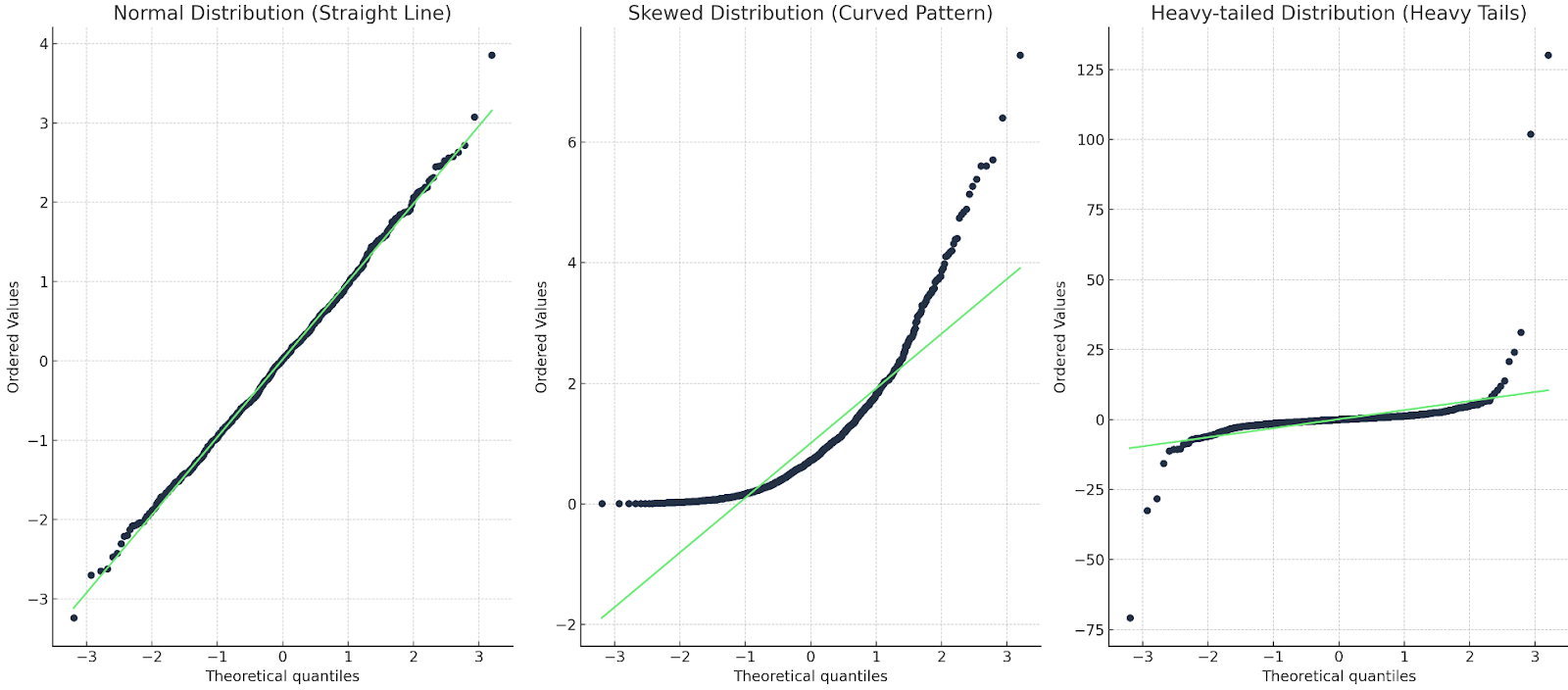 Tres gráficos : uno con una línea recta; uno con una curva; uno con una cola pesada
Tres gráficos : uno con una línea recta; uno con una curva; uno con una cola pesada
Tres gráficos Q-Q: uno con una línea recta; uno con una curva; uno con una cola pesada. Imagen del autor
En el primer caso, la línea Q-Q coincide con los puntos de datos, por lo que la distribución es normal. En el segundo caso, vemos un patrón curvo, por lo que los datos o bien no son normales o bien están sesgados. En el último caso, vemos una especie de forma de "s", por lo que la distribución tiene colas pesadas o valores más extremos.
Gráficos Q-Q en regresión lineal
Existen algunos supuestos diferentes para los modelos lineales, como la linealidad (que la relación entre las variables es lineal), la independencia de los errores (que los errores no están correlacionados entre sí), la homocedasticidad (que los residuos deben tener una varianza constante), y que los errores no están correlacionados entre sí.que los residuos deben tener una varianza constante)y normalidad de los residuos (que los residuos siguen una distribución normal). El gráfico Q-Q ayuda en particular con ese cuarto supuesto del modelo lineal, la normalidad de los residuos.
He aquí cómo afectan los distintos patrones a la interpretación y fiabilidad de nuestro modelo:
Alineación en línea recta
- Qué significa: Los residuos son aproximadamente normales, lo que indica que el modelo se ajusta bien a los datos según el supuesto de normalidad.
- Implicación en la práctica: Es probable que los intervalos de confianza, los valores p y las pruebas de hipótesis derivados del modelo sean fiables, ya que suponen residuos distribuidos normalmente.
Patrones curvos
- Qué significa: Un gráfico Q-Q curvo a menudo indica no normalidad, como asimetría en los residuos. La curva puede ser ascendente o descendente. (Este patrón curvo es lo que vemos en nuestro ejemplo, más arriba).
- Implicación en la práctica: Los residuos no normales pueden dar lugar a valores p o intervalos de confianza sesgados, especialmente con conjuntos de datos pequeños. Deberíamos plantearnos transformar la variable dependiente o revisar la estructura del modelo.
Colas pesadas o ligeras
- Qué significa: Si hay colas pesadas, los residuos tienen más valores extremos de los esperados según la normalidad, posiblemente debido a valores atípicos, o bien puede haber una especificación incorrecta del modelo. Si hay colas ligeras, significa que en realidad hay menos residuos extremos de lo esperado, lo que puede indicar un truncamiento de los datos.
- Implicación en la práctica: Con colas pesadas, los valores atípicos pueden afectar desproporcionadamente a la línea de regresión, dando lugar a resultados engañosos. Deberíamos plantearnos eliminar o ponderar a la baja los valores atípicos. Creo que las colas ligeras podrían no afectar tanto al modelo, pero podrían ser una pista de que los datos podrían estar incompletos de algún modo.
Gráficos Q-Q y otros gráficos de diagnóstico
Si estás familiarizado con los gráficos de diagnóstico de modelos lineales, también sabrás que hay bastantes opciones para evaluar el ajuste del modelo. Para entender exactamente lo que muestra el gráfico Q-Q, veamos otros diagnósticos. Esto nos ayudará a comprender mejor lo que hace la trama Q-Q y qué otras tramas podrían complementarla.
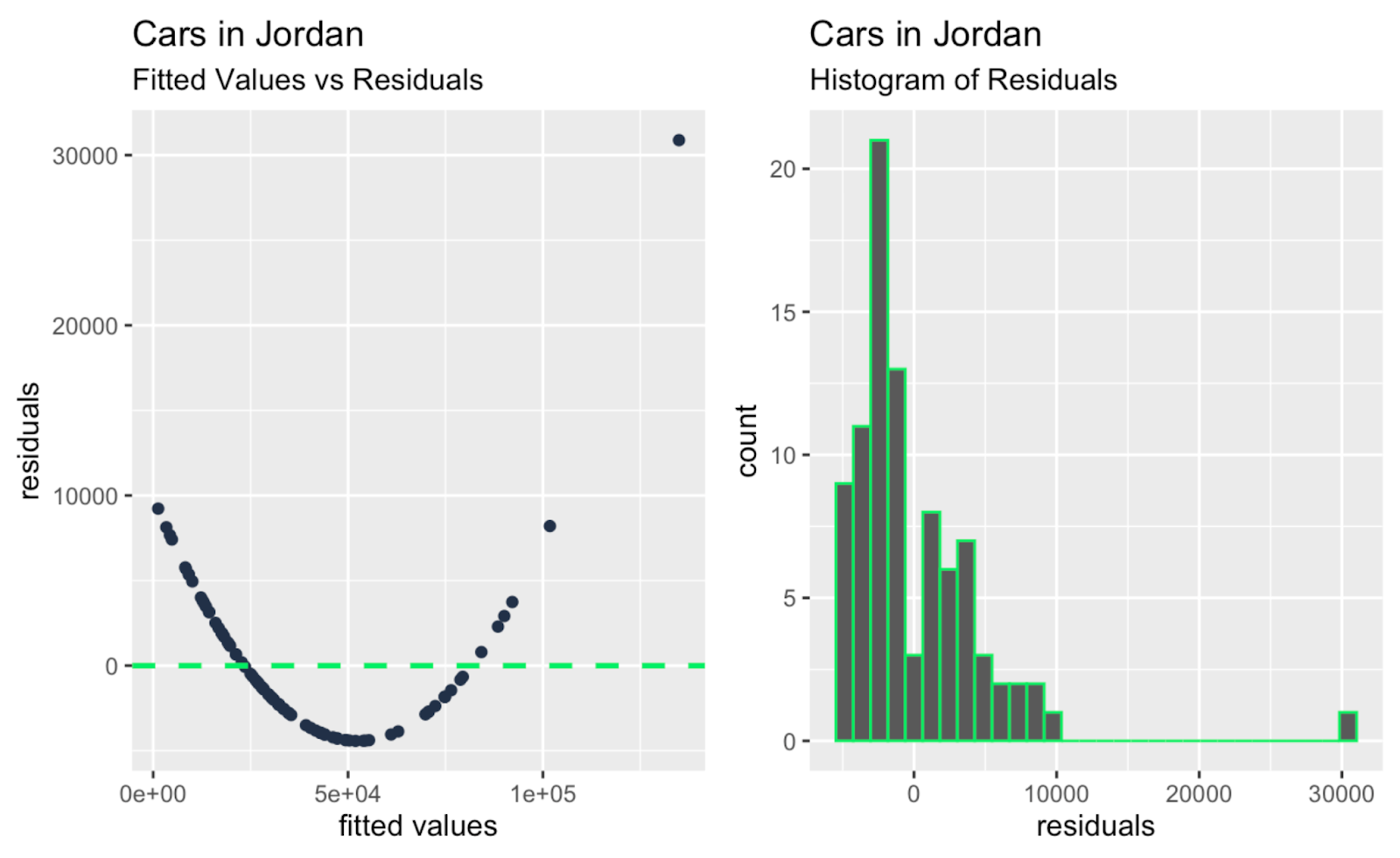
- Valores ajustados frente a residuales: Este gráfico muestra la relación entre los valores predichos (valores ajustados) y los residuos, que son las diferencias entre los valores observados y los predichos.
- Histograma de residuos: Este gráfico muestra la distribución de los residuos.
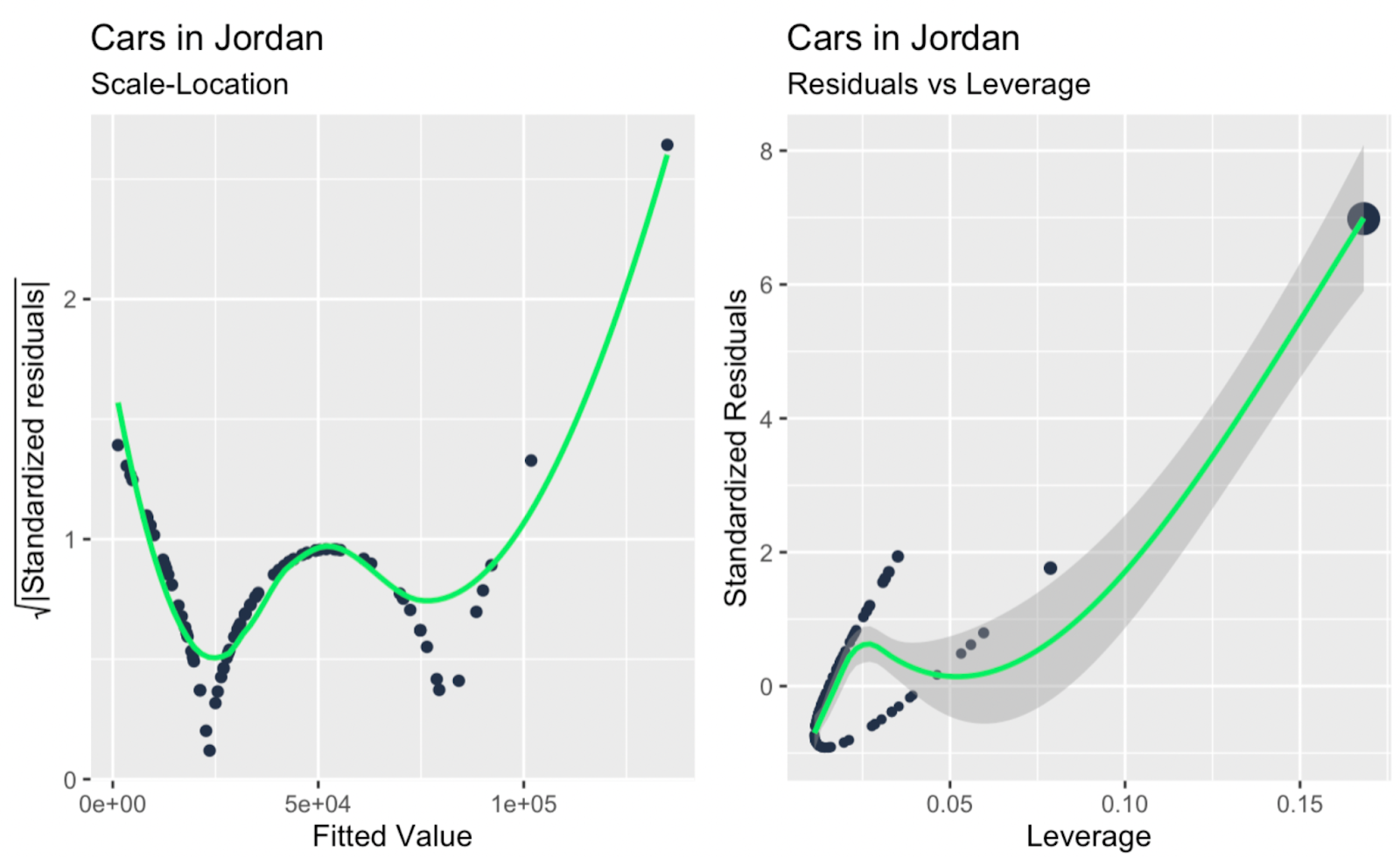
- Gráfico de escala-ubicación: Este gráfico muestra la relación entre los residuos y los valores ajustados.
- Apalancamiento frente a residuos normalizados: Este gráfico pone de manifiesto lo lejos que está un punto de datos en el espacio predictor y si el modelo se ajusta a él bien o mal. Estandarizamos los residuos para evaluar su relación con el apalancamiento en una escala coherente.
- Número de observación frente a la distancia de Cook: Este gráfico identifica los puntos de datos específicos con mayor influencia global en el modelo, combinando el apalancamiento y el tamaño residual. El número de observación en el eje x sirve como identificador de cada punto de datos.
- Apalancamiento frente a Distancia de Cook: Este gráfico compara el potencial de un punto para influir en el modelo con su impacto global real en las predicciones del modelo.
Te mostraré rápidamente cómo crear cada parcela utilizando los métodos tidyverse. El objetivo aquí no es interpretar el modelo lineal de nuestro conjunto de datos "Coches en Jordania" para cada diagnóstico de modelo lineal de esta lista. Más bien, quiero mostrar los otros gráficos de diagnóstico para que puedas reconocerlos, utilizar el código si te resulta útil y, en cuanto al objetivo de este artículo, para que puedas situar mejor el gráfico Q-Q entre los demás gráficos de diagnóstico. De este modo, comprenderás mejor qué muestra y qué no muestra el gráfico Q-Q, en qué es útil y qué le falta.
fitted_values_vs_residuals <- ggplot(data = car_linear_model, aes(x = .fitted, y = .resid)) +
geom_point(color = '#203147') +
geom_hline(yintercept = 0, linetype = "dashed", color = '#01ef63', size = 1) +
xlab("fitted values") +
ylab("residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Fitted Values vs Residuals")
histogram_of_residuals <- ggplot(data = car_linear_model, aes(x = .resid)) +
geom_histogram(color = '#01ef63') +
xlab("residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Histogram of Residuals")
scale_location <- ggplot(car_linear_model, aes(.fitted, sqrt(abs(.stdresid)))) +
geom_point(color = '#203147', na.rm=TRUE) +
stat_smooth(method="loess", na.rm = TRUE, color = '#01ef63', size = 1, se = FALSE) +
xlab("Fitted Value") +
ylab(expression(sqrt("|Standardized residuals|"))) +
labs(title = "Cars in Jordan") +
labs(subtitle = "Scale-Location")
leverage_vs_standardized_residuals <- ggplot(data = car_linear_model, aes(.hat, .stdresid)) +
geom_point(aes(size = .cooksd), color = '#203147') +
stat_smooth(method="loess", na.rm=TRUE, color = '#01ef63', size = 1) +
xlab("Leverage") +
ylab("Standardized Residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Residuals vs Leverage") +
scale_size_continuous("Cook's Distance", range=c(1,5)) +
theme(legend.title = element_blank()) +
theme(legend.position= "none")
observation_number_vs_cooks_distance <- ggplot(car_linear_model, aes(seq_along(.cooksd), .cooksd)) +
geom_bar(stat="identity", position="identity", color = '#01ef63', size = 1) +
xlab("Obs. Number") +
ylab("Cook's distance") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Cook's distance")
leverage_vs_cooks_distance <- ggplot(car_linear_model, aes(.hat, .cooksd))+geom_point(na.rm=TRUE) +
stat_smooth(method="loess", na.rm=TRUE, color = '#01ef63', size = 1) +
xlab("Leverage hii")+
ylab("Cook's Distance") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Cook's dist vs Leverage hii/(1-hii)") +
geom_abline(slope=seq(0,3,0.5), color = "gray", linetype = "dotdash")
library(patchwork)
fitted_values_vs_residuals + histogram_of_residuals
library(patchwork)
scale_location + leverage_vs_standardized_residuals
library(patchwork)
observation_number_vs_cooks_distance + leverage_vs_cooks_distanceValores ajustados frente a residuos; histograma de residuos. Imagen del autor
Gráfico escala-localización; apalancamiento frente a residuos normalizados. Imagen del autor
Número de observaciones frente a distancia de Cook; distancia de Cook frente a palanca. Imagen del autor
Tal vez la principal conclusión, echando un vistazo a todos los gráficos de diagnóstico adicionales anteriores, es que hay uno o dos grandes valores atípicos que están teniendo un gran impacto en la pendiente de la línea de regresión, y estos valores atípicos no son tan obvios cuando se echa un vistazo sólo al gráfico Q-Q. Así que el gráfico Q-Q de nuestro ejemplo cumple su función -comprobar la normalidad de los residuos- y también revela una limitación, y es que no aborda la independencia, la homocedasticidad ni los valores atípicos.
Como referencia adicional, incluyo aquí una tabla de alto nivel que muestra qué supuesto del modelo lineal se comprueba con cada gráfico de diagnóstico, y también sugiero cómo podrían funcionar otros gráficos de diagnóstico junto con el gráfico Q-Q. Ten en cuenta que, dependiendo de los datos, pueden revelarse distintos tipos de patrones con distintos gráficos de diagnóstico, y otras cosas podrían revelarse en combinación. Por ejemplo, un gráfico Q-Q podría confirmar la normalidad, mientras que un gráfico de escala-ubicación podría identificar la heteroscedasticidad, y sólo podrías ver la normalidad y la heteroscedasticidad utilizando ambos gráficos.
| Tipo de parcela de diagnóstico | Ayuda con | Cómo funciona con la Gráfica Q-Q |
|---|---|---|
| Gráfico Q-Q | Normalidad de los residuos | |
| Histograma de residuos | Normalidad de los residuos | Proporciona una visión rápida y una sensación general de simetría y dispersión. |
| Valores ajustados frente a residuales | Linealidad, independencia de los errores | Revela patrones y no linealidad, complementando la comprobación de normalidad del gráfico Q-Q. |
| Gráfico Escala-Localización | Homocedasticidad | Resalta la coherencia de la dispersión residual, complementando los gráficos Q-Q para las comprobaciones de normalidad. |
| Gráfico de apalancamiento frente a residuos | Independencia de los errores | Se centra en los puntos de alto apalancamiento, que los gráficos Q-Q no abordan. |
| Número de observaciones frente a la distancia de Cook | Identificar los puntos de influencia | Complementa los gráficos Q-Q localizando los valores atípicos con gran influencia. |
| Gráfico de apalancamiento frente a distancia de Cook | Identificar los puntos de alto apalancamiento | Destaca las observaciones influyentes, mientras que los gráficos Q-Q validan la normalidad. |
Reflexiones finales
Espero que tengas una nueva apreciación de los gráficos Q-Q como herramienta útil para evaluar la normalidad y que comprendas mejor su uso habitual para evaluar la normalidad de los residuos en una regresión lineal. También espero que tengas una nueva apreciación de la idea y la importancia de los diagnósticos de modelos lineales de forma más general.
Sigue aprendiendo sobre regresión lineal con nuestro Regresión lineal múltiple en R: Tutorial con Ejemplos que cubre modelos más complejos que implican múltiples predictores, incluyendo ideas de multicolinealidad en regresión. Te sugiero encarecidamente que te inscribas en nuestro completo y exhaustivo itinerario profesional, Científico de Aprendizaje Automático en Python, para aprenderlo todo sobre el flujo de trabajo de creación de modelos, incluido el aprendizaje supervisado y no supervisado.
Conviértete en un Científico ML

Preguntas frecuentes sobre la trama Q-Q
¿Qué es un gráfico Q-Q?
Un gráfico Q-Q, o gráfico Cuantil-Cuantil, es una herramienta visual utilizada para comparar la distribución de un conjunto de datos con una distribución teórica, como la distribución normal.
¿Es lo mismo un gráfico Q-Q que un gráfico Q-Q normal?
Un gráfico Q-Q normal es un tipo de gráfico Q-Q en el que un conjunto de datos se compara con una distribución normal con parámetros especificados. Se utiliza para evaluar si un conjunto de datos sigue una distribución normal. Por tanto, todas las gráficas Q-Q normales son gráficas Q-Q, pero no todas las gráficas Q-Q son gráficas Q-Q normales.