Curso
Os modelos de regressão linear são amplamente usados em estatística e aprendizado de máquina para prever valores numéricos com base em recursos de entrada e também para entender a relação entre as variáveis. No entanto, só porque você pode ajustar uma linha aos seus dados, não significa que você deva fazê-lo. Também temos que diagnosticar a qualidade do ajuste para determinar se o modelo é apropriado para os dados ou se precisa ser refinado.
Há algumas maneiras diferentes de testar um modelo, incluindo a avaliação do modelo usando um fluxo de trabalho de treinamento/teste e a análise das estatísticas do modelo, como o r-quadrado ajustado. Neste artigo, vou me concentrar em como criar e interpretar um gráfico de diagnóstico específico chamado gráfico Q-Q, e mostrarei a você alguns métodos diferentes para criar esse gráfico Q-Q na linguagem de programação R. Para realmente continuar a dominar as técnicas de regressão, faça Introdução à regressão em R ou Regressão intermediária em R ou, para Python, faça Introdução à regressão em Python ou Regressão intermediária em Python, dependendo do nível de conforto que você tiver.
O que é um gráfico Q-Q?
Um gráfico Q-Q (Quantile-Quantile) é usado para verificar se um conjunto de dados segue uma distribuição teórica específica. Um gráfico Q-Q funciona comparando os quantis dos dados observados com os quantis de nossa outra distribuição teórica. Estou dizendo "distribuição teórica" para ser exato, mas muitas vezes, quando criamos um gráfico Q-Q, estamos realmente pensando na distribuição normal ou gaussiana e nos referimos a ela como um gráfico Q-Q normal. No entanto, os gráficos Q-Q também podem ser usados para comparar dados com outras distribuições, como exponencial, uniforme, qui-quadrado e distribuição t, distribuição de Poissonou outras, dependendo do contexto da análise.
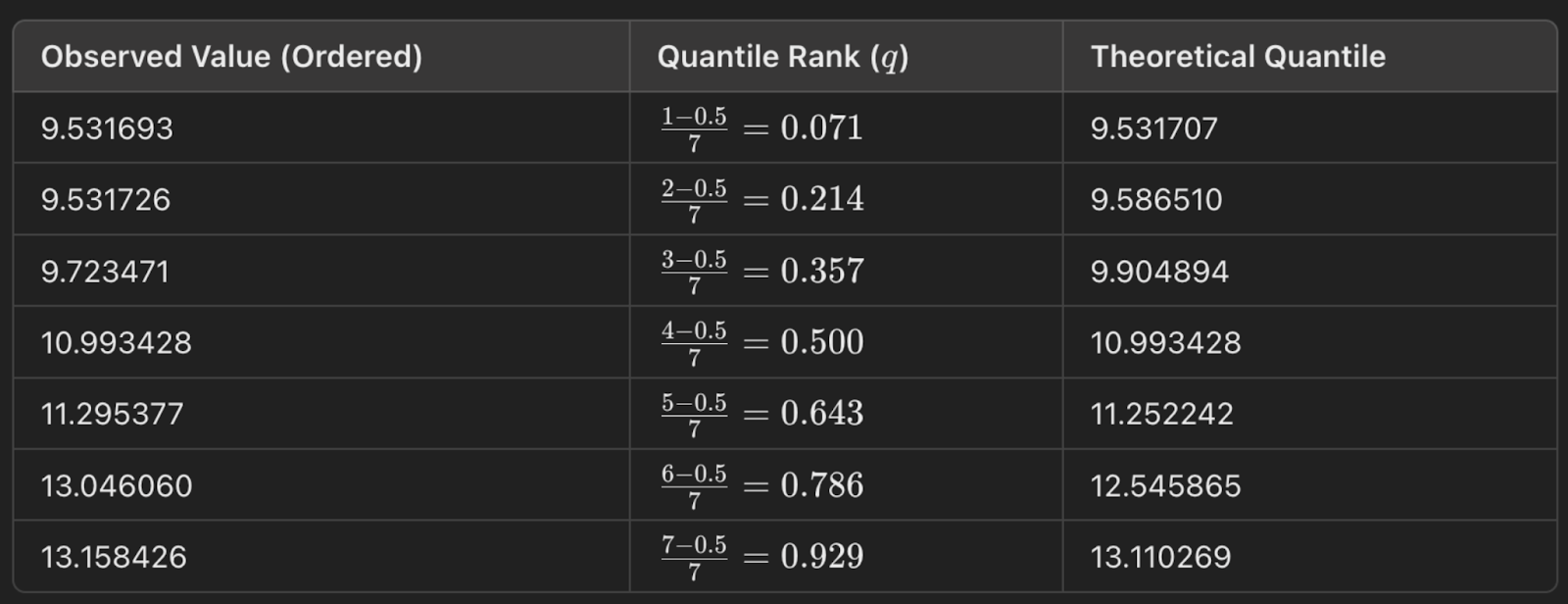
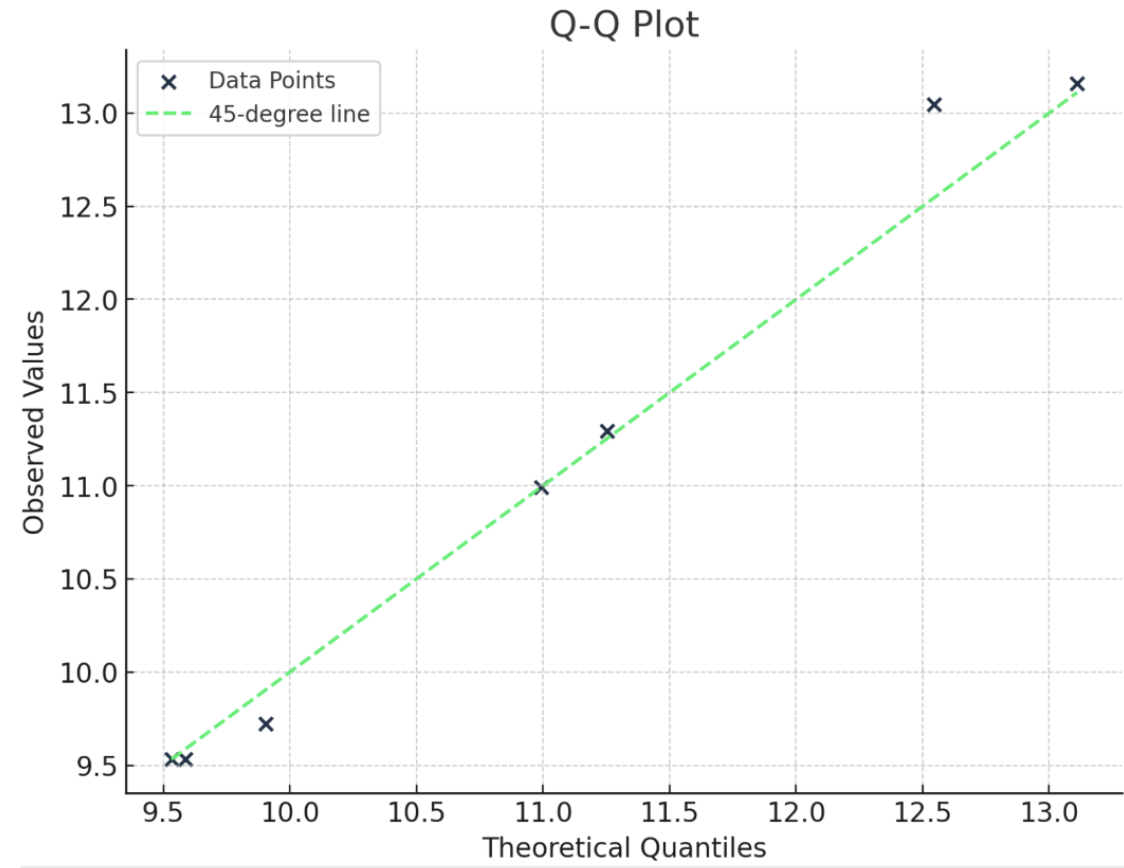
É útil que você entenda mostrando um exemplo. Aqui, tenho uma distribuição de números. Para construir um gráfico Q-Q normal, primeiro coloco os números em ordem. Em seguida, calculo a classificação de quantis com esta equação: q = (i- 0,5)/n. Em seguida, eu poderia usar a função de ponto percentual (PPF) da distribuição normal padrão para encontrar o valor correspondente para a classificação de quantis. (Talvez você esteja mais familiarizado com a função de distribuição cumulativa (CDF), que nos informa a probabilidade até um valor x.) Bem, o PPF é o oposto: Ele nos dá o valor x para uma determinada probabilidade). Para criar o gráfico, você deve plotar os valores de classificação de quantis em relação aos quantis teóricos (daí os dois Qs no gráfico Q-Q).
Por que usar um gráfico Q-Q?
Um gráfico Q-Q é uma boa maneira visual de verificar as suposições de distribuição. Há outras maneiras de testar se os dados seguem uma distribuição normal, como o teste de Shapiro-Wilk, por exemplo, mas, na minha opinião, nada é tão visual e torna a história tão óbvia quanto o gráfico Q-Q. Você pode ver o gráfico Q-Q em qualquer lugar.
Conhecer a distribuição de algo é importante de várias maneiras. Por um lado, provavelmente queremos saber quais são as melhores medidas para centro e propagação. Além disso, ao criar uma regressão linear, queremos saber se nossa variável dependente, em particular, segue uma distribuição normal, e também queremos ver se os resíduos de nosso modelo são distribuídos normalmente para que tenhamos mais confiança em nossas estimativas. Então, basicamente, acho que os gráficos Q-Q são úteis por dois motivos gerais: comparar nossos dados com as distribuições de amostra e testar a normalidade.
Como criar um gráfico Q-Q no R
Vamos ver agora como criar um gráfico Q-Q no R. Nesta seção, examinarei três métodos diferentes: o R básico, o pacote car e os métodos tidyverse. Acho que você verá que prefiro os métodos tidyverse porque eles oferecem mais flexibilidade para deixar o gráfico mais bonito e têm mais extensibilidade com outros pacotes.
Para cada método, criarei um gráfico Q-Q nos resíduos de uma regressão linear simples, que é um dos usos mais comuns - se não o uso mais comum - do gráfico Q-Q. No entanto, você também pode criar um gráfico Q-Q para verificar a distribuição das variáveis antes de criar uma regressão linear. Tudo o que você precisa é a distribuição de uma variável e uma distribuição teórica para compará-la.
Se quiser acompanhar o processo, você pode baixar o conjunto de dados do Kaggle que estou usando: Preços de carros na Jordânia 2023.
Criando um gráfico Q-Q na base R
Primeiro, vamos criar um gráfico Q-Q no R básico, o que significa que não instalaremos nenhum pacote extra, mas usaremos apenas as funções integradas.
# importing data (in my case, saved on my desktop)
car_prices_jordan <- read.csv('~/Desktop/car_prices_jordan.csv')
# Create a linear model
car_linear_model <- lm(Price ~ sqrt(Price), filtered_car_prices)
# Extract the residuals
residuals <- resid(car_linear_model)
# Q-Q plot of residuals
qqnorm(residuals, main = "Q-Q Plot of Residuals from Linear Regression")
qqline(residuals, col = "red")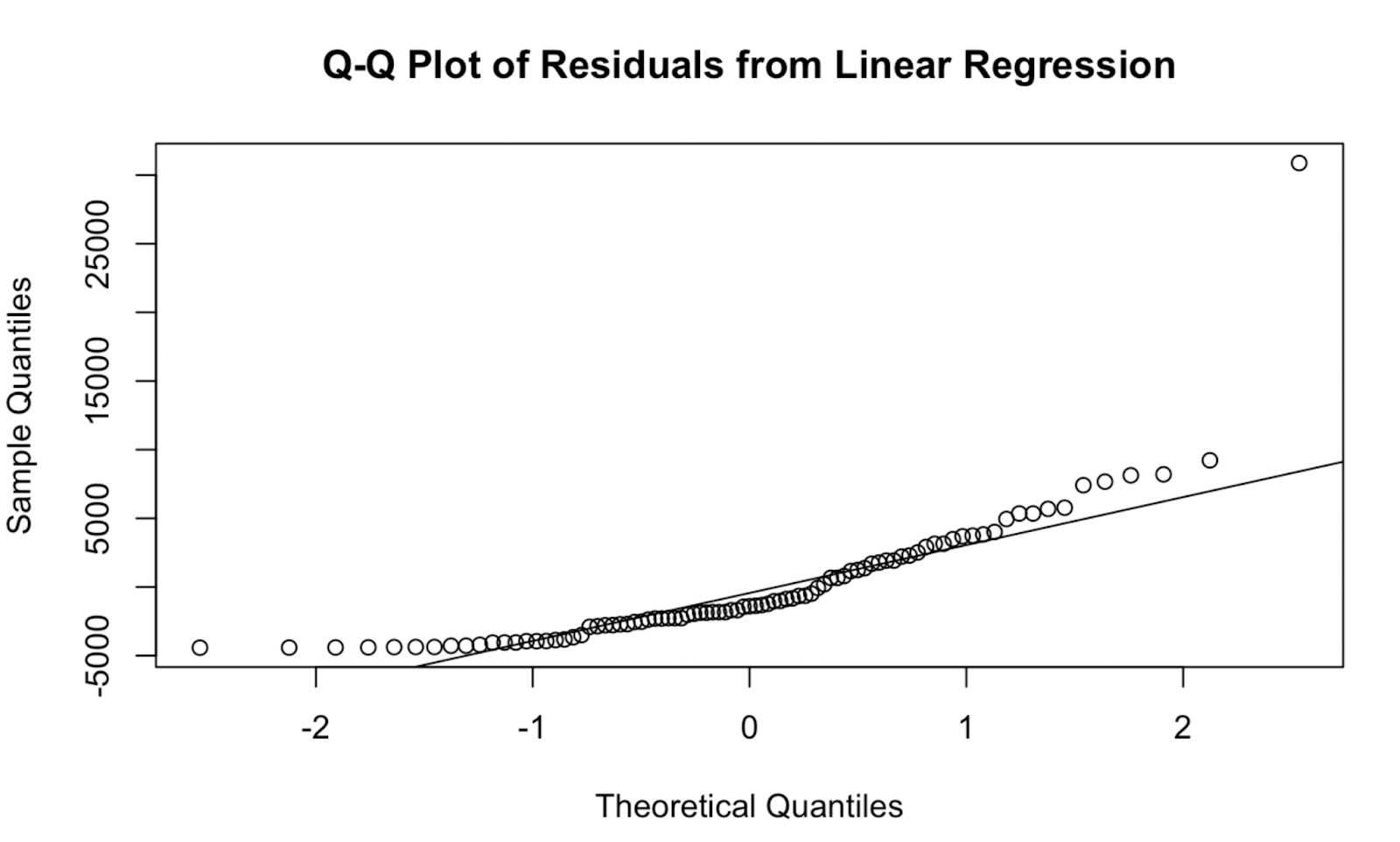 Gráfico Q-Q criado na base R. Imagem do autor
Gráfico Q-Q criado na base R. Imagem do autor
Criando um gráfico Q-Q usando o pacote car
Agora, vamos tentar criar um gráfico Q-Q usando o pacote car. Em minha opinião, a qualidade da visualização não é muito diferente, mas esse gráfico Q-Q tem a vantagem de mostrar um envelope de confiança que define a área dentro da qual se espera que nossos pontos de dados se encontrem se a suposição de normalidade do modelo for verdadeira.
# Install the car package if not already installed
# install.packages("car")
library(car)
# Q-Q plot of residuals using car package
car::qqPlot(car_linear_model, main = "Q-Q Plot of Residuals from Linear Regression")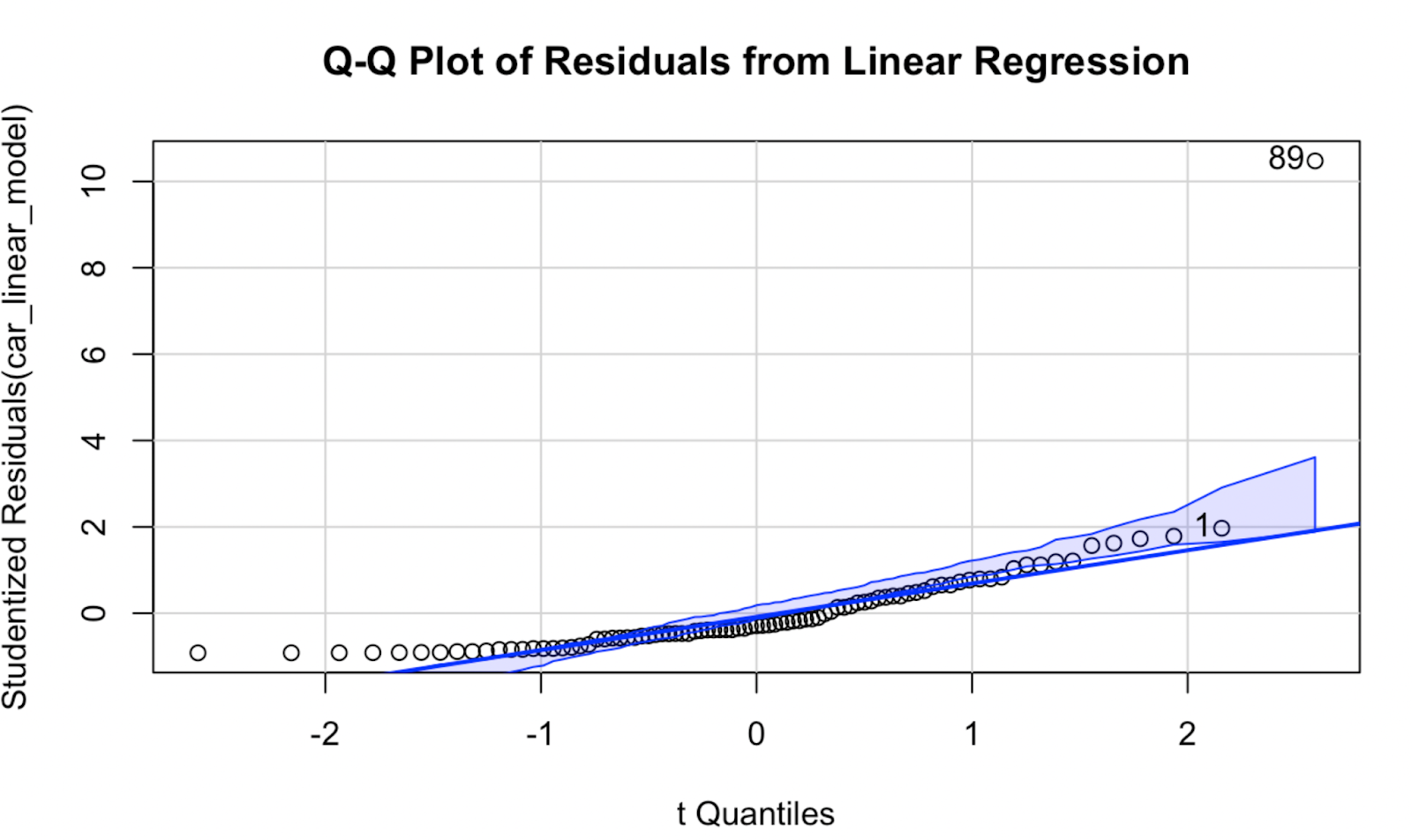 Gráfico Q-Q criado usando o pacote car no R. Imagem do autor
Gráfico Q-Q criado usando o pacote car no R. Imagem do autor
Criando um gráfico Q-Q usando ggplot2
Agora, vamos ver como você pode criar um gráfico Q-Q usando métodos tidyverse para ter mais flexibilidade e torná-lo mais bonito. Desta vez, vou colocar o gráfico Q-Q como um painel ao lado do meu gráfico de dispersão original.
library(tidyverse)
library(metBrewer)
car_prices_jordan$Power <- as.numeric(gsub("[^0-9]", "", car_prices_jordan$Power))
car_prices_jordan$Price <- as.numeric(gsub("[^0-9]", "", car_prices_jordan$Price))
slope <- (cor(car_prices_jordan$Power, car_prices_jordan$Price) * (sd(car_prices_jordan$Price)) / sd(car_prices_jordan$Power))
intercept <- (mean(car_prices_jordan$Price) - slope * mean(car_prices_jordan$Power))
car_prices_graph <- ggplot(car_prices_jordan, aes(x = Power, y = Price)) +
geom_point() +
ggtitle("Car Prices in Jordan") +
geom_abline(slope = slope, intercept = intercept, color = '#376795', size = 1)
car_linear_model <- lm(Price ~ Price, car_prices_jordan)
qq_plot <- ggplot(data = car_linear_model, aes(sample = .resid)) +
stat_qq() +
stat_qq_line(linetype = 'dashed', color = '#ef8a47', size = 1) +
labs(title = "Car Prices in Jordan") +
labs(subtitle = "Residual QQ Plot")
library(patchwork)
car_prices_graph + qq_plot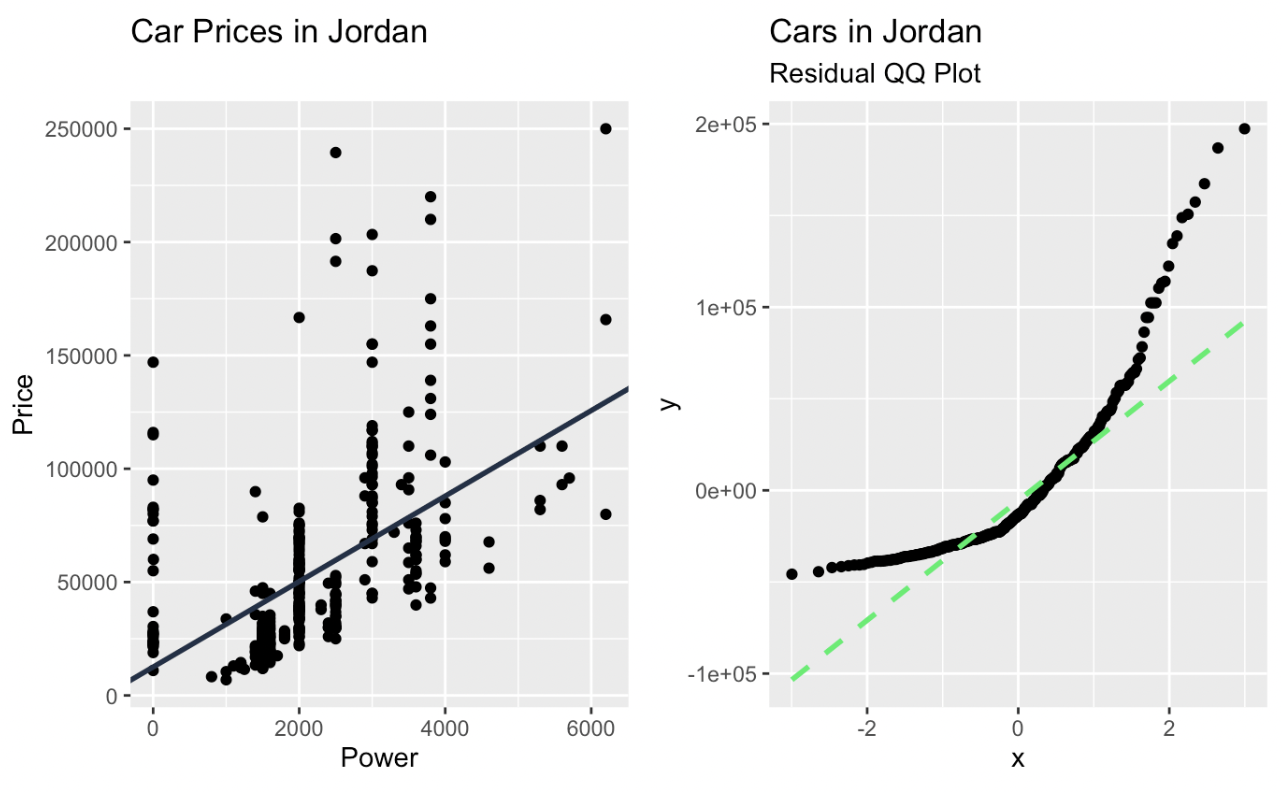
Regressão linear e um gráfico Q-Q dos resíduos criados no ggplot2. Imagem do autor
O que um gráfico Q-Q pode nos dizer
Com um gráfico Q-Q, os quantis dos dados observados são plotados em relação aos quantis teóricos. Se os dados seguirem de perto a distribuição teórica, os pontos no gráfico Q-Q se moverão em uma linha diagonal. Os desvios dessa linha indicam desvios da distribuição esperada. Os pontos que ficam acima ou abaixo da linha sugerem assimetria ou outliers, e padrões como curvas ou desvios em forma de S indicam diferenças sistemáticas, como caudas mais pesadas ou mais leves.
Há cerca de três coisas que procuramos.
- Linha reta: Os dados estão bem alinhados com a distribuição teórica.
- Padrões curvos: Indique dados distorcidos ou distribuições não normais.
- Caudas pesadas ou leves: Se os pontos se desviarem nas extremidades, os dados poderão ter caudas mais pesadas ou mais leves do que o esperado.
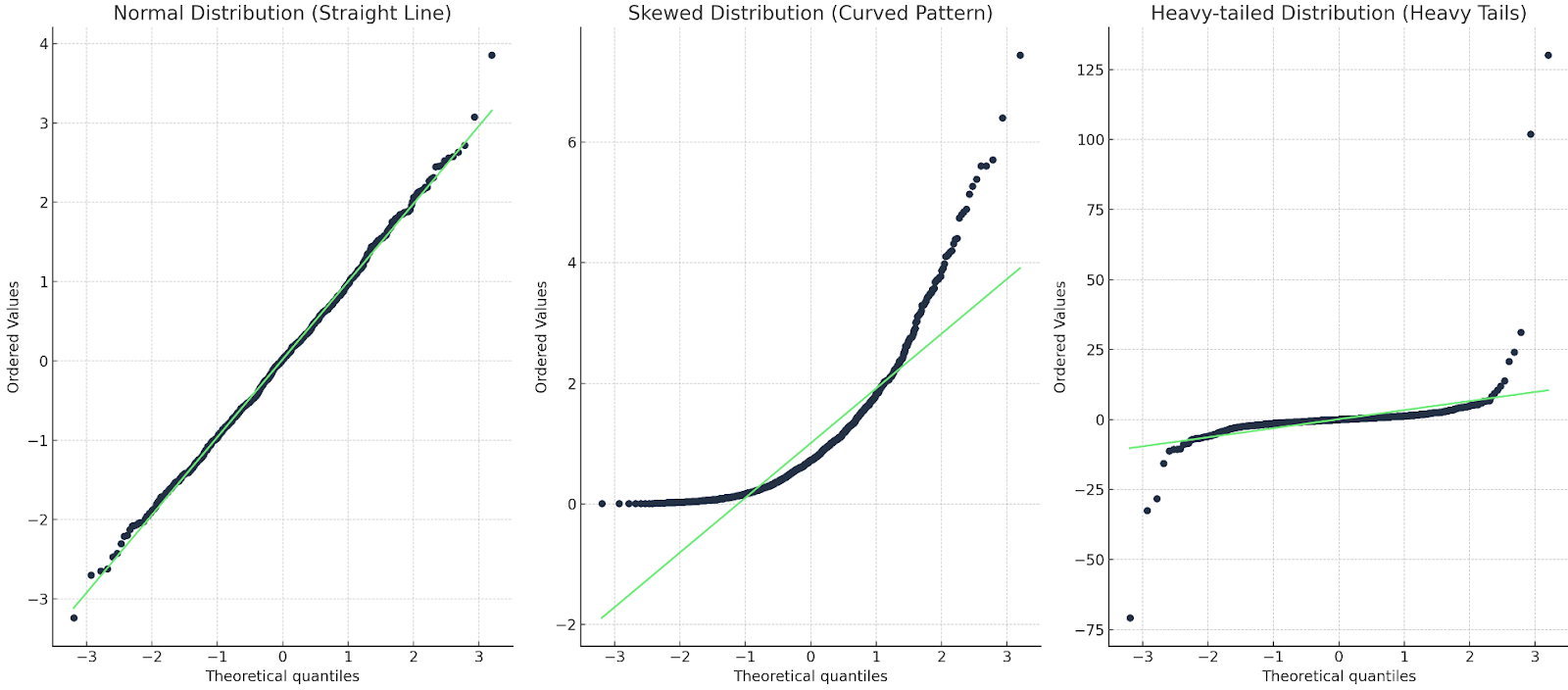
Vamos mostrar um exemplo para cada um deles:
 ada
ada
Três gráficos Q-Q: um com uma linha reta; um com uma curva; um com uma cauda pesada. Imagem do autor
No primeiro caso, a linha Q-Q coincide com os pontos de dados, portanto, a distribuição é de fato normal. No segundo caso, vemos um padrão curvo, portanto, os dados não são normais ou estão distorcidos. No último caso, vemos uma espécie de forma de "s", de modo que a distribuição tem caudas pesadas ou valores mais extremos.
Gráficos Q-Q em regressão linear
Há algumas suposições diferentes de modelos lineares, incluindo linearidade (que a relação entre as variáveis é linear), independência de erros (que os erros não estão correlacionados entre si), homocedasticidade (que os resíduos devem ter variância constante), e a possibilidade de que os resíduos tenham variância constante.que os resíduos devem ter variância constante)e normalidade dos resíduos (que os resíduos sigam uma distribuição normal). O gráfico Q-Q ajuda especialmente com a quarta suposição do modelo linear, a normalidade dos resíduos.
Veja como os diferentes padrões afetam a interpretação e a confiabilidade do nosso modelo:
Alinhamento em linha reta
- O que isso significa: Os resíduos são aproximadamente normais, indicando que o modelo se ajusta bem aos dados em termos da suposição de normalidade.
- Implicações na prática: É provável que os intervalos de confiança, os valores p e os testes de hipótese derivados do modelo sejam confiáveis, pois pressupõem resíduos normalmente distribuídos.
Padrões curvos
- O que isso significa: Um gráfico Q-Q curvo geralmente indica não normalidade, como distorção nos resíduos. A curva pode ser ascendente ou descendente. (Esse padrão curvo é o que estamos vendo em nosso exemplo acima).
- Implicações na prática: Os resíduos não normais podem levar a valores p ou intervalos de confiança tendenciosos, especialmente com conjuntos de dados menores. Devemos considerar a transformação da variável dependente ou a revisão da estrutura do modelo.
Caudas pesadas ou leves
- O que isso significa: Se houver caudas pesadas, os resíduos têm mais valores extremos do que o esperado sob a normalidade, possivelmente devido a outliers, ou então pode haver uma especificação incorreta do modelo. Se houver caudas leves, isso significa que, na verdade, há menos resíduos extremos do que o esperado, o que pode indicar truncamento de dados.
- Implicações na prática: Com caudas pesadas, os outliers podem afetar desproporcionalmente a linha de regressão, levando a resultados enganosos. Devemos considerar a remoção ou a redução da ponderação dos valores discrepantes. Acho que as caudas leves podem não afetar tanto o modelo, mas podem ser um indício de que os dados podem estar incompletos.
Gráficos Q-Q e outros gráficos de diagnóstico
Se você está familiarizado com os gráficos de diagnóstico de modelos lineares, também deve saber que há várias opções para avaliar o ajuste do modelo. Para que você entenda exatamente o que o gráfico Q-Q está mostrando, vamos analisar alguns outros diagnósticos. Isso nos ajudará a entender melhor o que o gráfico Q-Q está fazendo e quais outros gráficos podem complementá-lo.
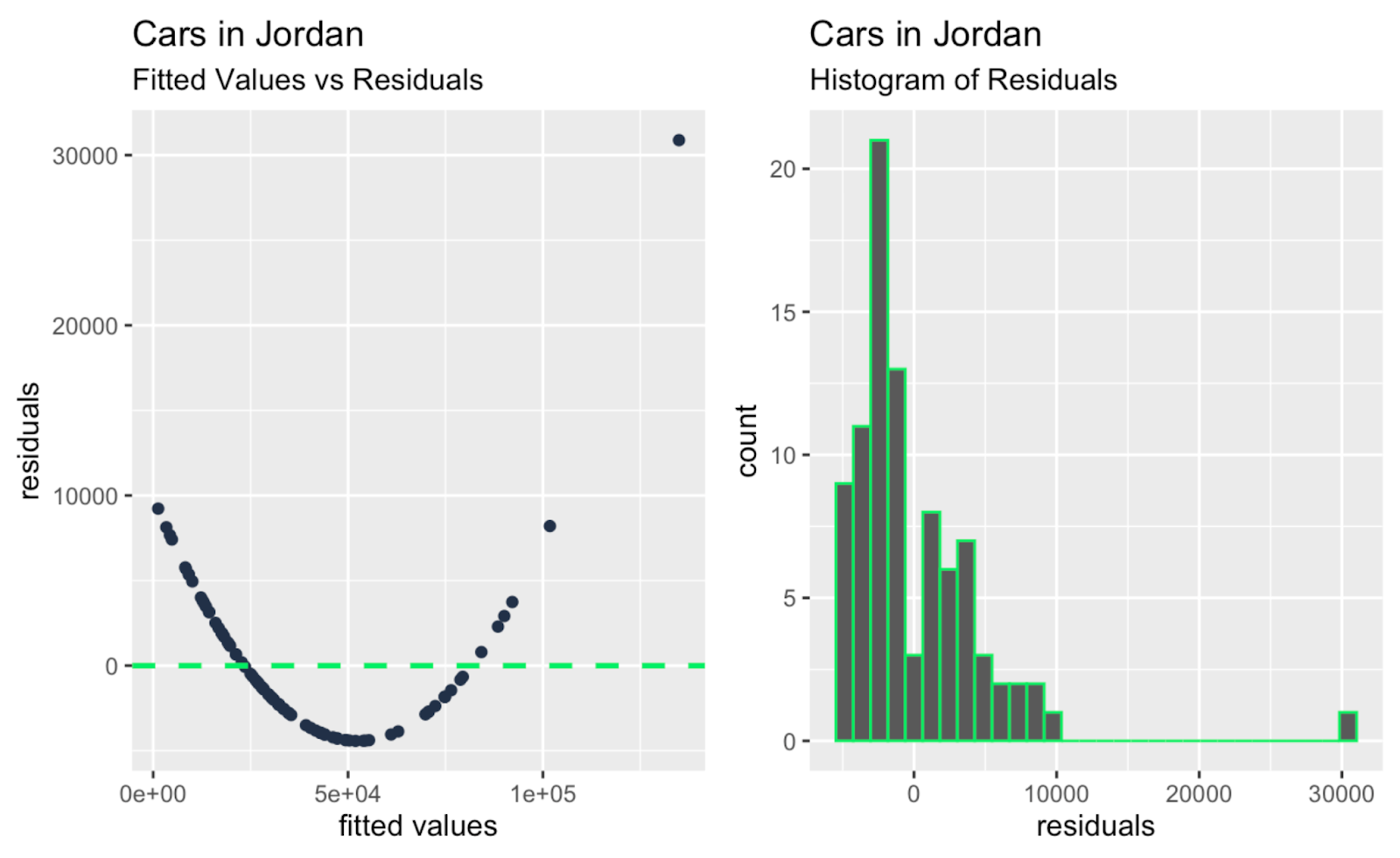
- Valores ajustados versus residuais: Esse gráfico mostra a relação entre os valores previstos (valores ajustados) e os resíduos, que são as diferenças entre os valores observados e previstos.
- Histograma de resíduos: Esse gráfico mostra a distribuição dos resíduos.
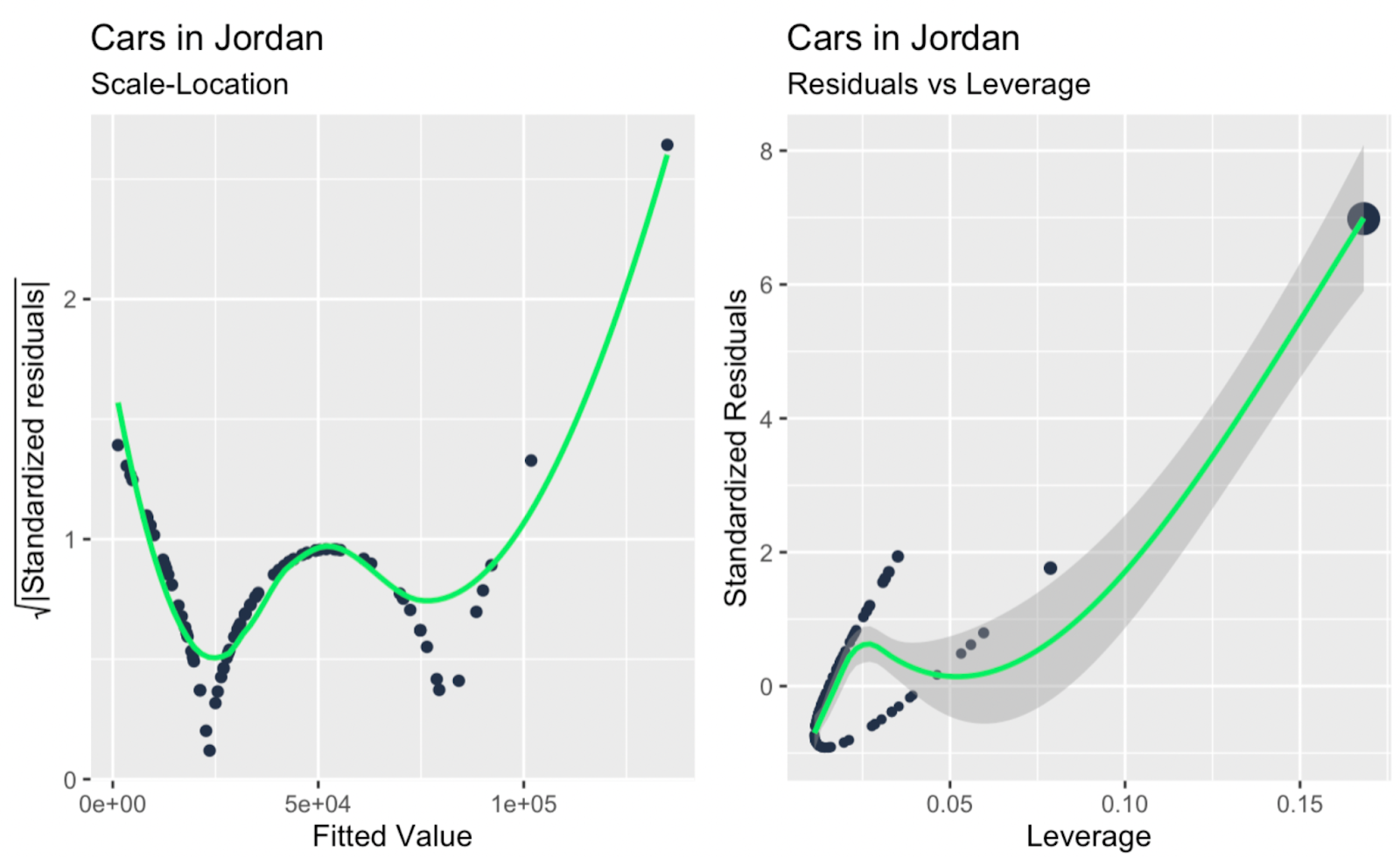
- Scale-Location Plot: Esse gráfico mostra a relação entre os resíduos e os valores ajustados.
- Alavancagem versus resíduos padronizados: Esse gráfico destaca até que ponto um ponto de dados está no espaço do preditor e se o modelo se ajusta bem ou mal a ele. Padronizamos os resíduos para avaliar sua relação com a alavancagem em uma escala consistente.
- Número de observação versus distância de Cook: Esse gráfico identifica pontos de dados específicos com a maior influência geral no modelo, combinando alavancagem e tamanho residual. A observação número no eixo x serve como um identificador para cada ponto de dados.
- Alavancagem versus distância de Cook: Esse gráfico compara o potencial de um ponto para influenciar o modelo com seu impacto geral real nas previsões do modelo.
Mostrarei a você rapidamente como criar cada gráfico usando os métodos tidyverse. O objetivo aqui não é interpretar o modelo linear do nosso conjunto de dados "Cars in Jordan" para cada diagnóstico de modelo linear dessa lista. Em vez disso, quero mostrar os outros gráficos de diagnóstico para que você possa reconhecê-los, usar o código se for útil e, para o objetivo deste artigo, para que você possa situar melhor o gráfico Q-Q entre os outros gráficos de diagnóstico. Dessa forma, você entenderá melhor o que o gráfico Q-Q está mostrando e não está mostrando, como ele é útil e o que está faltando.
fitted_values_vs_residuals <- ggplot(data = car_linear_model, aes(x = .fitted, y = .resid)) +
geom_point(color = '#203147') +
geom_hline(yintercept = 0, linetype = "dashed", color = '#01ef63', size = 1) +
xlab("fitted values") +
ylab("residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Fitted Values vs Residuals")
histogram_of_residuals <- ggplot(data = car_linear_model, aes(x = .resid)) +
geom_histogram(color = '#01ef63') +
xlab("residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Histogram of Residuals")
scale_location <- ggplot(car_linear_model, aes(.fitted, sqrt(abs(.stdresid)))) +
geom_point(color = '#203147', na.rm=TRUE) +
stat_smooth(method="loess", na.rm = TRUE, color = '#01ef63', size = 1, se = FALSE) +
xlab("Fitted Value") +
ylab(expression(sqrt("|Standardized residuals|"))) +
labs(title = "Cars in Jordan") +
labs(subtitle = "Scale-Location")
leverage_vs_standardized_residuals <- ggplot(data = car_linear_model, aes(.hat, .stdresid)) +
geom_point(aes(size = .cooksd), color = '#203147') +
stat_smooth(method="loess", na.rm=TRUE, color = '#01ef63', size = 1) +
xlab("Leverage") +
ylab("Standardized Residuals") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Residuals vs Leverage") +
scale_size_continuous("Cook's Distance", range=c(1,5)) +
theme(legend.title = element_blank()) +
theme(legend.position= "none")
observation_number_vs_cooks_distance <- ggplot(car_linear_model, aes(seq_along(.cooksd), .cooksd)) +
geom_bar(stat="identity", position="identity", color = '#01ef63', size = 1) +
xlab("Obs. Number") +
ylab("Cook's distance") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Cook's distance")
leverage_vs_cooks_distance <- ggplot(car_linear_model, aes(.hat, .cooksd))+geom_point(na.rm=TRUE) +
stat_smooth(method="loess", na.rm=TRUE, color = '#01ef63', size = 1) +
xlab("Leverage hii")+
ylab("Cook's Distance") +
labs(title = "Cars in Jordan") +
labs(subtitle = "Cook's dist vs Leverage hii/(1-hii)") +
geom_abline(slope=seq(0,3,0.5), color = "gray", linetype = "dotdash")
library(patchwork)
fitted_values_vs_residuals + histogram_of_residuals
library(patchwork)
scale_location + leverage_vs_standardized_residuals
library(patchwork)
observation_number_vs_cooks_distance + leverage_vs_cooks_distanceValores ajustados versus resíduos; histograma de resíduos. Imagem do autor
Gráfico de localização de escala; alavancagem versus resíduos padronizados. Imagem do autor
Número de observações versus distância de Cook; distância de Cook versus alavancagem. Imagem do autor
Talvez a principal conclusão, observando todos os gráficos de diagnóstico adicionais acima, seja que há um ou dois valores discrepantes grandes que estão causando um grande impacto na inclinação da linha de regressão, e esses valores discrepantes não são tão óbvios quando você observa apenas o gráfico Q-Q. Portanto, o gráfico Q-Q em nosso exemplo cumpre sua função - testar a normalidade dos resíduos - e também revela uma limitação, que é o fato de não abordar a independência, a homocedasticidade ou os outliers.
Para referência adicional, incluo aqui uma tabela de alto nível que mostra qual suposição de modelo linear é testada com cada gráfico de diagnóstico e também sugiro como outros gráficos de diagnóstico podem funcionar em conjunto com o gráfico Q-Q. Lembre-se de que, dependendo dos dados, diferentes tipos de padrões podem ser revelados com diferentes gráficos de diagnóstico, e algumas outras coisas podem ser reveladas em combinação. Por exemplo, um gráfico Q-Q pode confirmar a normalidade, enquanto um gráfico de localização de escala pode identificar a heterocedasticidade, e você só poderá ver a normalidade e a heterocedasticidade se usar os dois gráficos.
| Tipo de plotagem de diagnóstico | Ajuda com | Como funciona com o gráfico Q-Q |
|---|---|---|
| Gráfico Q-Q | Normalidade dos resíduos | |
| Histograma de resíduos | Normalidade dos resíduos | Fornece um visual rápido e um senso geral de simetria e distribuição. |
| Valores ajustados versus residuais | Linearidade, independência de erros | Revela padrões e não linearidade, complementando a verificação de normalidade do gráfico Q-Q. |
| Gráfico de escala-localização | Homocedasticidade | Destaca a consistência do spread residual, complementando os gráficos Q-Q para verificações de normalidade. |
| Gráfico de alavancagem versus resíduos | Independência de erros | Concentra-se em pontos de alta alavancagem, que os gráficos Q-Q não abordam. |
| Número de observações versus distância de Cook | Identificação de pontos de influência | Complementa os gráficos Q-Q, localizando outliers com alta influência. |
| Alavancagem versus gráfico de distância de Cook | Identificação de pontos de alta alavancagem | Destaca observações influentes, enquanto os gráficos Q-Q validam a normalidade. |
Considerações finais
Espero que você tenha uma nova apreciação dos gráficos Q-Q como uma ferramenta útil para avaliar a normalidade e tenha uma melhor compreensão de seu uso comum para avaliar a normalidade dos resíduos em uma regressão linear. Espero também que você tenha uma nova apreciação da ideia e da importância dos diagnósticos de modelos lineares em geral.
Continue aprendendo sobre regressão linear com nosso site Multiple Linear Regression in R: Tutorial With Examples que aborda modelos mais complexos envolvendo vários preditores, incluindo ideias de multicolinearidade em regressão. Sugiro enfaticamente que você se inscreva em nosso curso de carreira completo e abrangente, Machine Learning Scientist in Python, para aprender tudo sobre o fluxo de trabalho de criação de modelos, incluindo aprendizado supervisionado e não supervisionado.
Torne-se um cientista de ML

Perguntas frequentes sobre o gráfico Q-Q
O que é um gráfico Q-Q?
Um gráfico Q-Q, ou gráfico Quantil-Quantil, é uma ferramenta visual usada para comparar a distribuição de um conjunto de dados com uma distribuição teórica, como a distribuição normal.
Um gráfico Q-Q é igual a um gráfico Q-Q normal?
Um gráfico Q-Q normal é um tipo de gráfico Q-Q em que um conjunto de dados é comparado a uma distribuição normal com parâmetros especificados. É usado para avaliar se um conjunto de dados segue uma distribuição normal. Portanto, todos os gráficos Q-Q normais são gráficos Q-Q, mas nem todos os gráficos Q-Q são gráficos Q-Q normais.