Méthode des moindres carrés : Comment trouver la ligne de démarcation la plus adaptée

Imaginez que vous essayez de prédire les prix des logements en fonction de la superficie. Vous disposez de données sur les ventes récentes, mais elles ne forment pas un modèle parfait. Certains logements se vendent plus cher que prévu, d'autres moins. Comment trouver la meilleure ligne de tendance qui reflète la relation globale entre la taille et le prix sans laisser des maisons individuelles fausser vos prévisions ?

La méthode des moindres carrés peut être la solution dont vous avez besoin. Dans cet article, nous allons explorer les concepts fondamentaux de la méthode des moindres carrés, ses variations et ses applications. À la fin, vous aurez une solide compréhension de la manière d'utiliser cette méthode et de l'appliquer à des problèmes réels.

Qu'est-ce que la méthode des moindres carrés ?

La méthode des moindres carrés est une technique statistique utilisée pour déterminer la ligne ou la courbe la mieux adaptée à un ensemble de points de données. Il minimise les différences au carré entre les valeurs observées et les valeurs prédites dans un ensemble de données. La différence entre les points de données réels et les valeurs prédites par le modèle est appelée résidus. L'objectif est de trouver un modèle qui minimise la somme de ces résidus au carré, ce qui permet d'obtenir les prévisions les plus précises possibles.

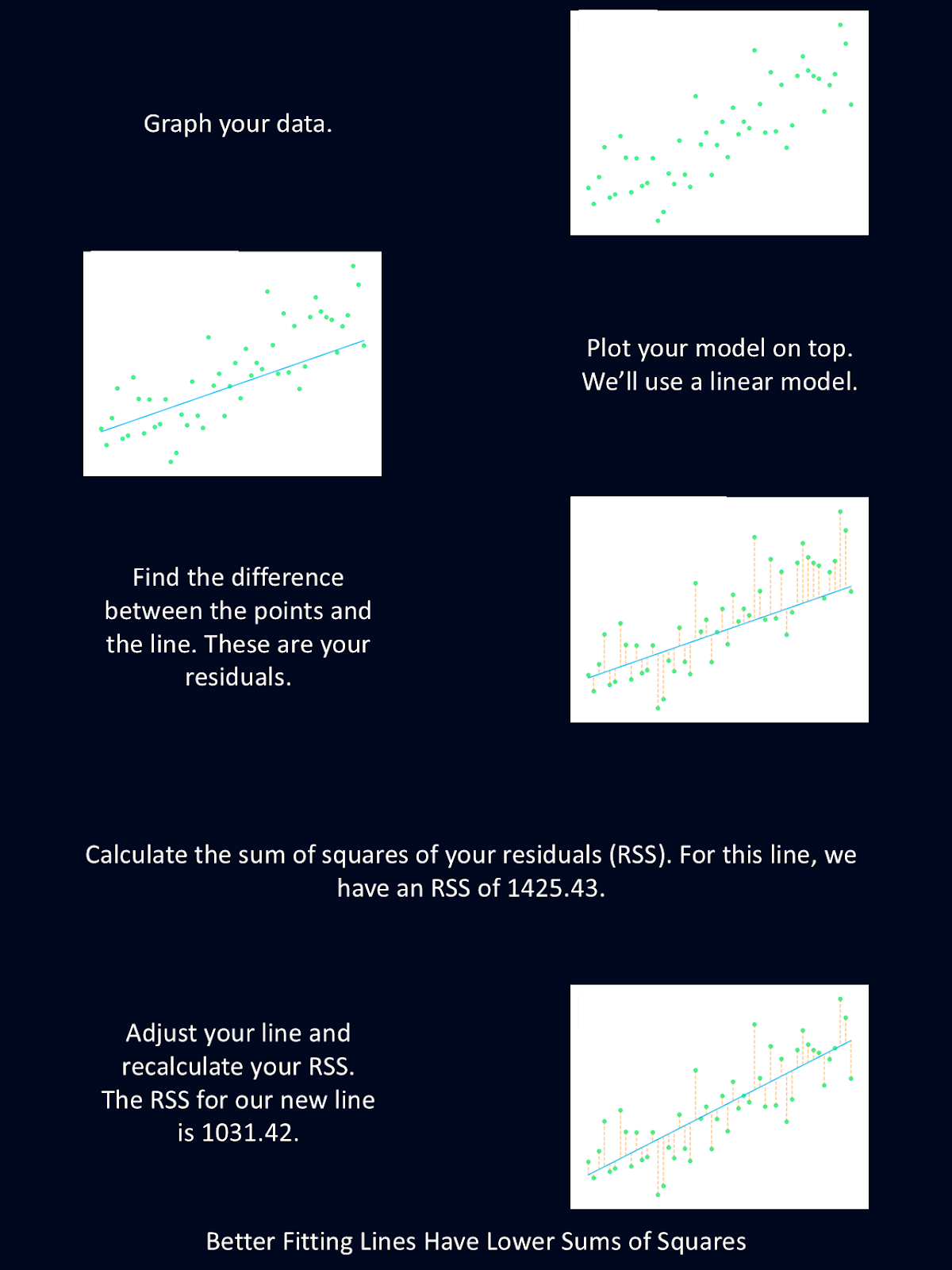
Le diagramme ci-dessus explique brièvement les étapes de la méthode des moindres carrés.

Cette méthode a été élaborée par Carl Friedrich Gauss, âgé de 18 ans, en 1895 (son nom est peut-être associé à la distribution gaussienne). Adrien-Marie Legendre a formalisé la technique en 1805 et a été le premier à écrire un article utilisant la méthode des moindres carrés pour reconstruire l'orbite d'un astéroïde. 

Comment fonctionne la méthode des moindres carrés

La méthode des moindres carrés permet de trouver la ligne qui s'ajuste le mieux à un ensemble de points en minimisant la somme des carrés des différences entre les valeurs observées et les valeurs prédites. Cette méthode est utilisée pour trouver les paramètres du modèle qui correspondent le mieux possible à la réalité.

Essayons ceci avec un ensemble de données extrêmement réduit : seulement 10 points. Tout d'abord, nous devons choisir un modèle adapté à nos données. Pour cet exemple simple, nous choisirons une régression linéaire simple, ce qui signifie que nous effectuons une régression pour laquelle nous n'avons qu'une seule variable indépendante et une seule variable dépendante.

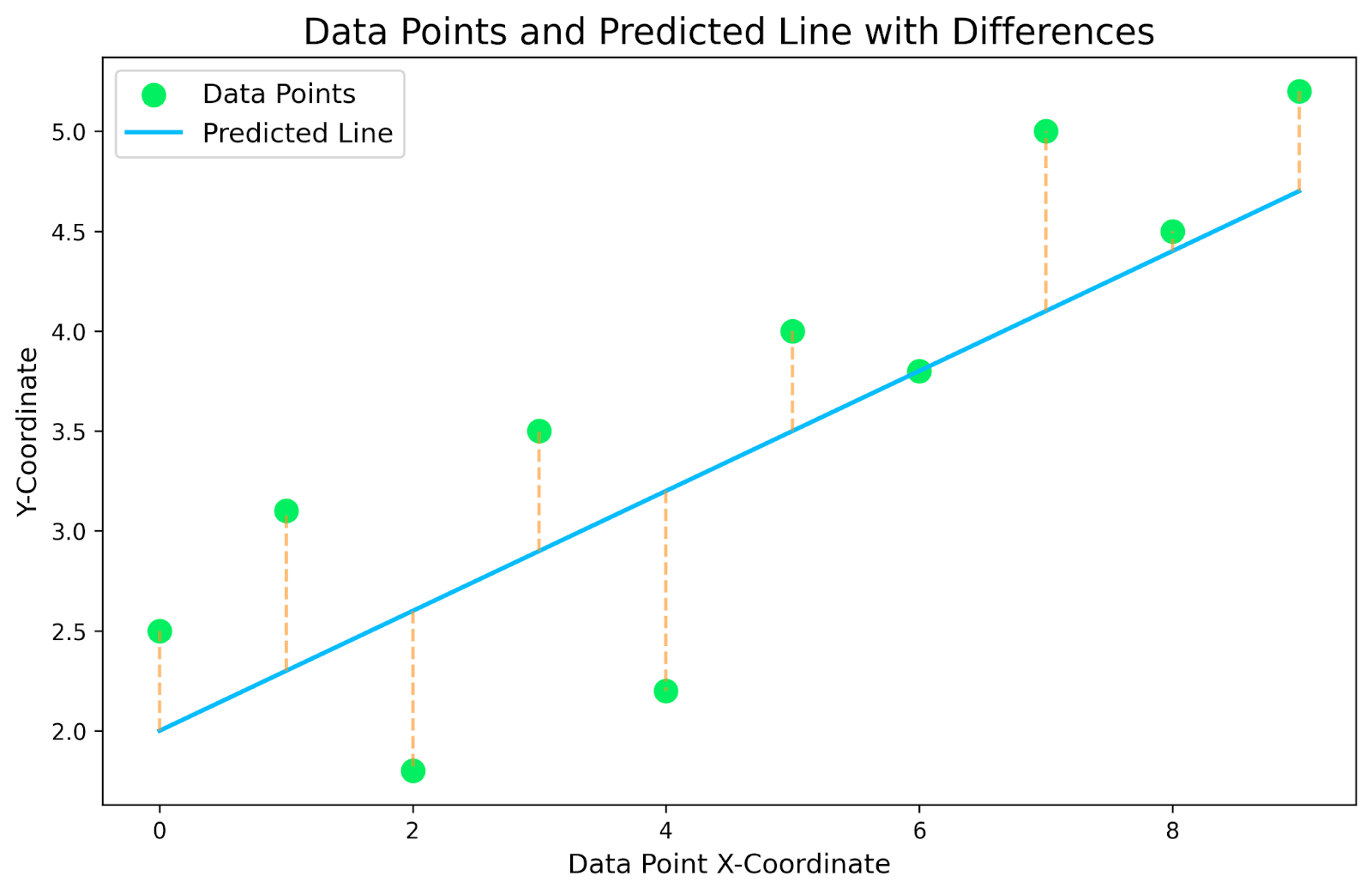
Le graphique ci-dessus est une représentation graphique de notre petit ensemble de données, sur laquelle figure une régression linéaire. Les lignes jaunes en pointillés reliant les points de données à la ligne prédite sont les résidus. L'objectif est de trouver le modèle de régression linéaire qui minimise ces lignes résiduelles en pointillés jaunes.

Pour chaque point de données de notre ensemble de données, nous devons trouver la différence de coordonnées y entre le point de données et la ligne. Il s'agit de nos résidus. Nous élevons ensuite chaque résidu au carré afin d'éliminer les nombres négatifs ( ) et nous obtenons la somme totale. Cela nous donnera une idée de l'adéquation de notre ligne avec nos données. Vous trouverez dans le tableau ci-dessous la répartition pour notre graphique spécifique.

Maintenant que nous avons une idée de la façon dont cette droite s'ajuste à nos données, nous pouvons modifieres paramètres de la droite, que ce soit sa pente ou son ordonnée à l'origine, et recommencer nos calculs. La ligne qui présente la plus faible somme des résidus quadratiques est celle qui correspond le mieux à nos données. C'est donc cette ligne qui nous donnera les meilleures prédictions.

Utilisation de la méthode des moindres carrés pour trouver la meilleure ligne

Dans l'exemple ci-dessus, nous n'avons pas trouvé la ligne la mieux adaptée. Au lieu de cela, nous avons simplement calculé dans quelle mesure cette ligne correspondait aux données. Nous pourrions maintenant passer en revue un certain nombre de lignes potentielles et effectuer le même calcul pour trouver celles qui conviennent le mieux. Nous pouvons également utiliser un peu d'algèbre pour trouver la meilleure ligne plus rapidement. Essayons cela.

Nous commencerons par l'équation de la régression linéaire : y=mx+b, où b est l'ordonnée à l'origine et m la pente. Maintenant, inventons quelques données.

Tout d'abord, nous devons calculer la moyenne des valeurs X et Y. Ces valeurs serviront de valeurs prédites :

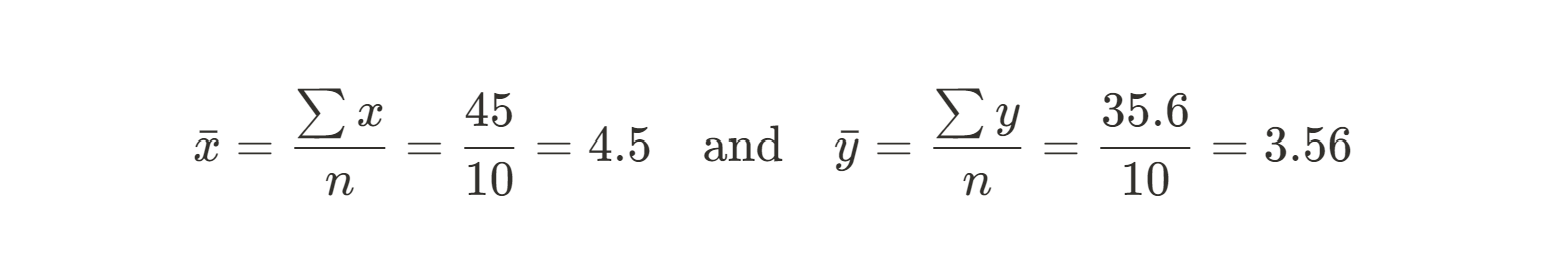
Ensuite, nous pouvons utiliser la somme des carrés de nos résidus entre chaque point de données et notre valeur prédite (la moyenne) pour trouver la pente. Voici l'équation que nous allons utiliser :

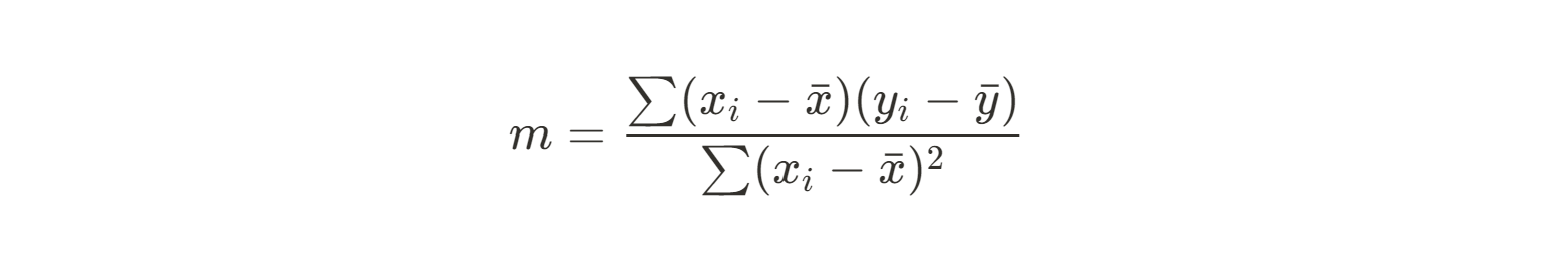
Comme il s'agit d'une équation assez difficile à réaliser à la main, nous allons calculer le numérateuret le dénominateur séparément. Commençons par le numérateur :

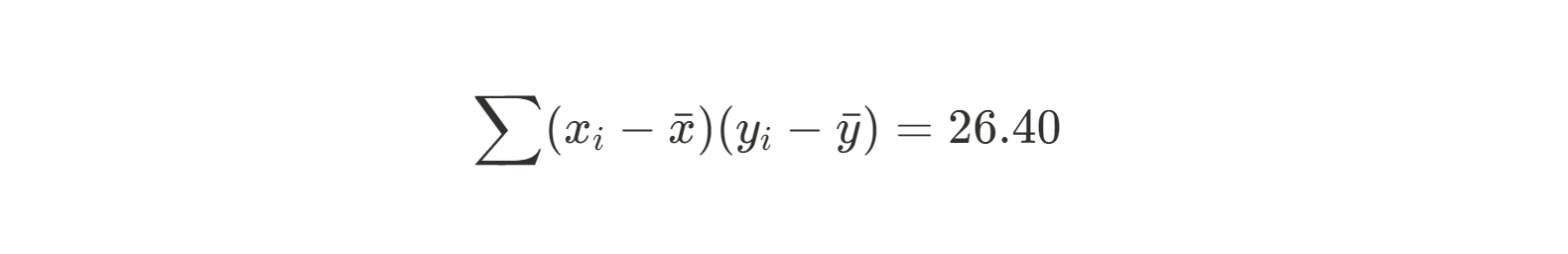
Faisons de même pour le dénominateur :

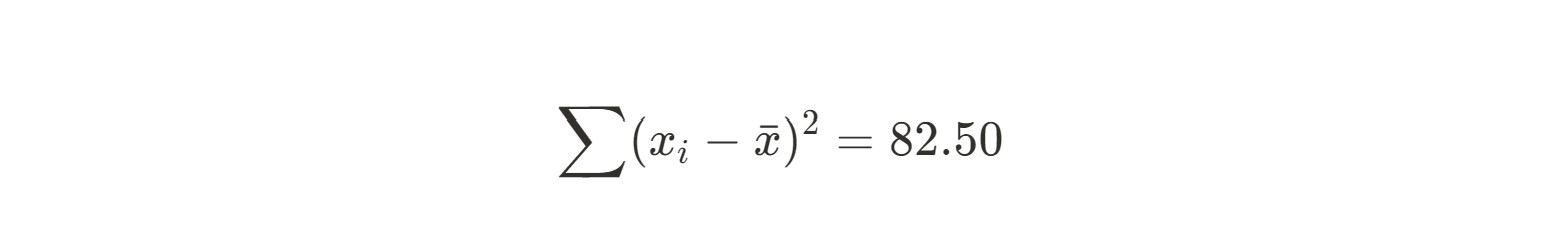
Nous pouvons maintenant calculer la pente de notre ligne de meilleur ajustement.

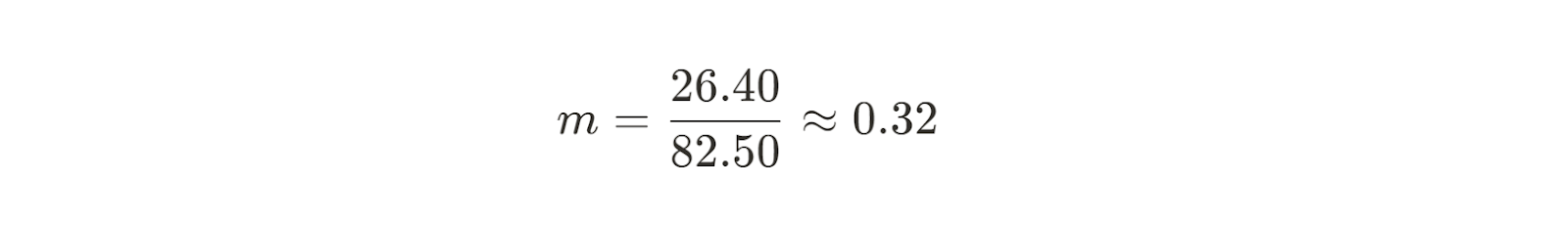
Nous connaissons maintenant la pente de la droite qui s'adapte le mieux à nos données. Ensuite, nous devons trouver l'ordonnée à l'origine. La formule pour l'ordonnée à l'origine b est facile à trouver en utilisant un peu de réarrangement algébrique :

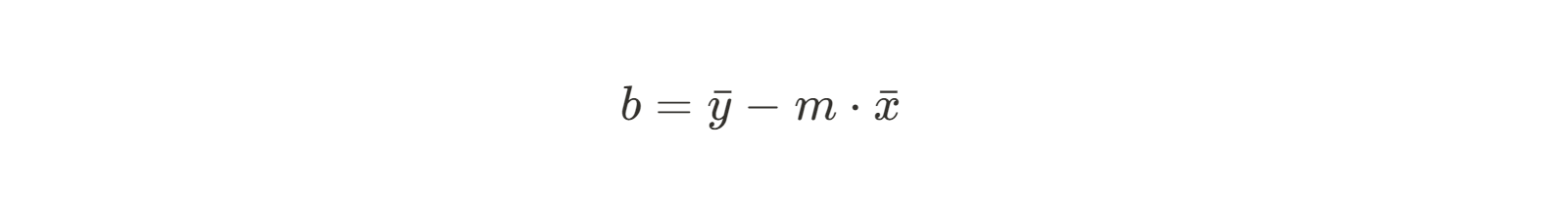
Puisque nous connaissons déjà la pente, nous pouvons simplement insérer nos moyennes x et y et résoudre pour b.

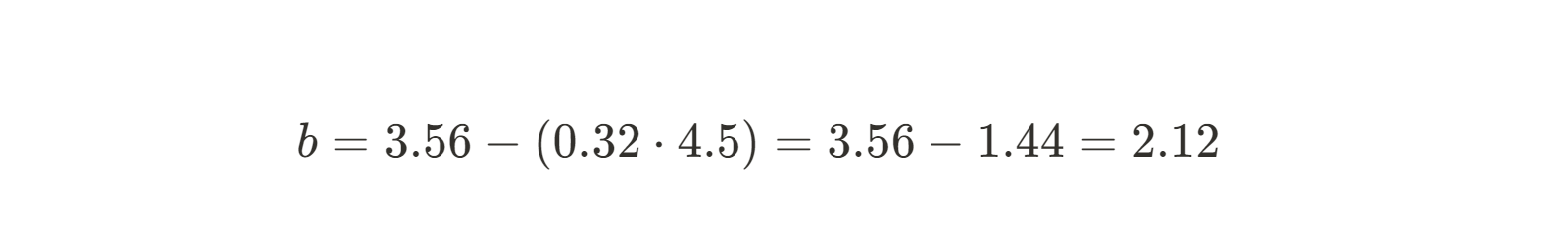
Maintenant que nous connaissons m et b, nous pouvons écrire l'équation de la droite la mieux ajustée :

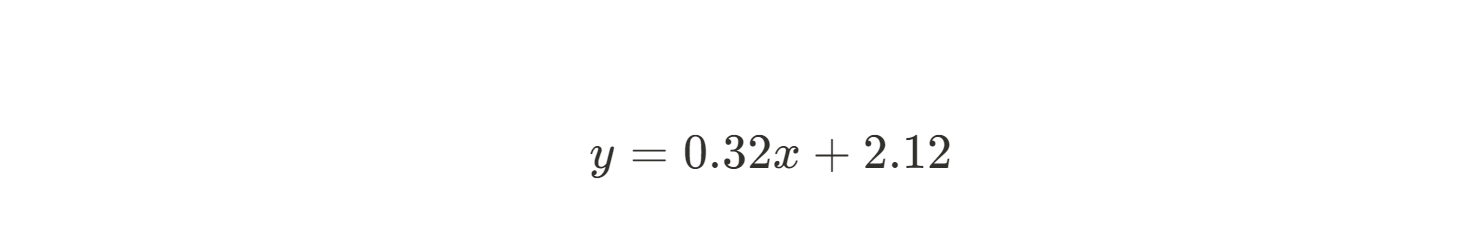
La méthode des moindres carrés nous a permis de dériver rapidement et facilement la meilleure droite de régression linéaire, même à la main ! Évidemment, plus vous avez de données, plus il sera difficile de le faire à la main. Heureusement, puisque les mathématiques sont assez simples, il est très facile de mettre en œuvre cette méthode en Python ou en R. Pour des explications détaillées sur la façon de procéder, consultez Essentials of Linear Regression in Python et How to Do Linear Regression in R.

Fondements mathématiques de la méthode des moindres carrés

Ci-dessus, nous avons utilisé un exemple de régression linéaire simple et trouvé la pente et l'ordonnée à l'origine à l'aide de belles équations fermées, et nous avons modélisé la variable dépendante comme une fonction de la variable indépendante : y=mx+b.

Cependant, les équations que j'ai montrées ci-dessus ne fonctionnent que lorsque vous avez une seule variable indépendante. Une autre façon de trouver les coefficients d'une régression est d'utiliser ce que l'on appelle l'équation normale, qui fournit une solution matricielle au problème des moindres carrés. L'équation normale est l'équation matricielle qui résulte de la minimisation de la somme des carrés des résidus à l'aide de la méthode des moindres carrés. Géométriquement, et en utilisant le langage de l'algèbre linéaire, la solution des moindres carrés peut être visualisée comme la projection orthogonale du vecteur des données observées sur l'espace des colonnes de la matrice du modèle. En termes simples, cela signifie que les erreurs sont minimisées de manière à ce que les valeurs prédites soient aussi proches que possible des données observées, compte tenu des contraintes du modèle.

Dans les cas où la matrice n'est pas inversible (ce qui signifie que le système d'équations n'a pas de solution unique), la pseudo-inverse de Moore-Penrose permet de calculer une solution par les moindres carrés. Cela nous donne la flexibilité nécessaire pour gérer les situations où le système est sous-déterminé (ce qui signifie qu'il y a plus d'inconnues que d'équations) ou surdéterminé (ce qui signifie qu'il y a plus d'équations que d'inconnues).

Si vous avez besoin d'une remise à niveau sur l'algèbre matricielle, je vous recommande le cours Linear Algebra for Data Science in R.

Types de méthodes des moindres carrés

Jusqu'à présent, nous n'avons parlé que de l'utilisation de la méthode des moindres carrés avec un estimateur des moindres carrés ordinaires. Cependant, il s'agit d'un outil polyvalent qui peut être adapté à de nombreux scénarios en fonction de la nature du problème que vous abordez. Examinons quelques types de méthodes des moindres carrés, ce qui les rend uniques et leurs utilisations pratiques.

Moindres carrés linéaires

À ce stade, vous devriez être assez familier avec les moindres carrés linéaires (également appelés moindres carrés ordinaires). Il est utilisé avec les modèles qui ont des coefficients linéaires, comme dans larégression linéaire simple ou multiple . L'objectif est de trouver la ligne (ou l'hyperplan, dans le cas de régressions linéaires multiples) qui minimise la somme des carrés des résidus.

Ce type de moindres carrés suppose que les résidus ont une variance constante et qu'il n'y a pas de valeurs aberrantes significatives dans les données. Elle peut s'appliquer à la plupart des choses qui ont une relation linéaire. Par exemple, vous pourriez l'utiliser pour les relations entre la durée de la gestation et le poids à la naissance ou entre les dépenses publicitaires et le chiffre d'affaires. C'est le type de moindres carrés que j'utilise le plus souvent et dont j'entends le plus souvent parler.

Moindres carrés pondérés

La méthode des moindres carrés pondérés est une extension de cette méthode qui fonctionne lorsque la variance des résidus n'est pas constante. En attribuant des poids à chaque point de données, les moindres carrés pondérés donnent plus d'importance aux observations dont la variance est plus faible. L'équation est similaire à la somme des carrés précédente, mais avec une pondération (w_i) appliqué à chaque résidu :

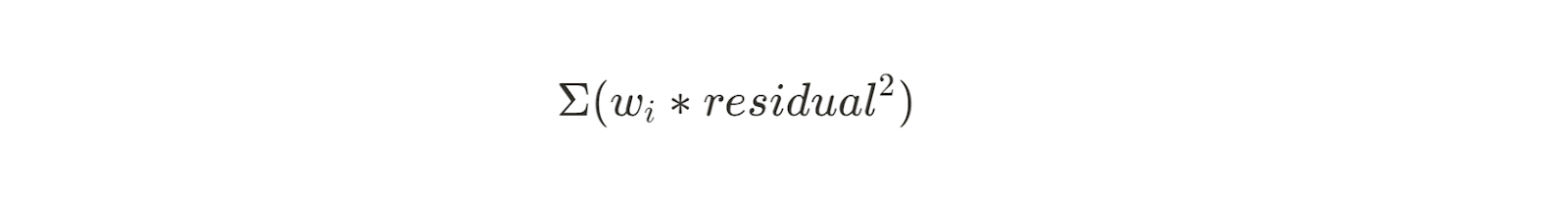
Cette méthode est utile pour les ensembles de données où l'erreur de mesure varie d'une observation à l'autre, par exemple lors de l'étalonnage de capteurs. Les poids sont généralement l'inverse de la variance de chaque observation.

Moindres carrés robustes

Les moindres carrés robustes sont conçus pour traiter les ensembles de données comportant des valeurs aberrantes qui peuvent influencer de manière disproportionnée les résultats des moindres carrés ordinaires. Il utilise des techniques de repondération itératives pour réduire l'impact des valeurs aberrantes.

Dans les moindres carrés robustes, vous pouvez utiliser des méthodes telles que les moindres résidus absolus (LAR) ou les poids bisquare pour ajuster itérativement les poids et minimiser l'influence des valeurs aberrantes.

Un exemple d'utilisation est la modélisation financière, où l'on veut tenir compte des krachs boursiers extrêmes. Si vous disposez d'un ensemble de données pour lequel vous ne souhaitez pas supprimer les valeurs aberrantes, mais que vous voulez tout de même en tenir compte, la méthode des moindres carrés robustes peut être la voie à suivre.

Moindres carrés non linéaires

La méthode des moindres carrés ne s'applique pas uniquement aux régressions linéaires. Les moindres carrés non linéaires sont utilisés lorsque le modèle que vous appliquez n'est pas linéaire dans ses coefficients. Cette méthode est plus complexe que la méthode des moindres carrés linéaires et peut nécessiter des techniques d'optimisation itératives (comme Gauss-Newton ou Levenberg-Marquardt) pour trouver le meilleur ajustement.

Il est important d'être prudent avec les moindres carrés non linéaires. Le calcul peut être sensible aux estimations initiales des paramètres ainsi qu'aux problèmes de convergence. Vous pouvez par exemple modéliser la croissance exponentielle des virus dans un corps lors d'une infection ou modéliser les taux de réaction chimique en laboratoire.

Moindres carrés totaux

Jusqu'à présent, nous avons surtout parlé de cas où seule la variable dépendante présentait des erreurs. Et nous avons minimisé les distances verticales entre notre modèle et nos données. Mais que se passe-t-il si vos mesures indépendantes sont également entachées d'erreurs ?

La méthode des moindres carrés totaux est utile lorsque les variables indépendantes et dépendantes présentent des erreurs de mesure. Cette méthode tient compte des erreurs dans toutes les variables. Cela peut être particulièrement utile dans des domaines tels que l'astronomie et la géodésie (le domaine qui mesure la forme de la Terre et le champ de gravité), où les erreurs de mesure sont présentes dans toutes les dimensions en raison du haut niveau de précision nécessaire. La méthode des moindres carrés totaux est souvent utilisée conjointement avec la décomposition en valeurs singulières.

Moindres carrés généralisés

La méthode des moindres carrés généralisés est une extension de la méthode des moindres carrés qui permet de résoudre les problèmes posés par les résidus corrélés. Avec les moindres carrés généralisés, nous transformons les données dans une forme où les moindres carrés ordinaires peuvent être appliqués. Cette transformation consiste à utiliser la matrice de covariance des résidus pour tenir compte de leur structure de corrélation, ce qui permet d'obtenir des estimations de paramètres plus précises.

Cela peut être particulièrement utile dans des situations telles que les analyses de séries temporelles, où les résidus peuvent présenter une autocorrélation. 

Applications de la méthode des moindres carrés

La méthode des moindres carrés est une technique statistique largement utilisée dans de nombreux domaines.

En statistique et en science des données, les moindres carrés sont utilisés pour construire des modèles de régression linéaires et non linéaires afin de faire des prédictions basées sur des données connues. Elle est également utile pour analyser les tendances, en particulier dans les séries chronologiques.

En finance, les moindres carrés sont utilisés dans l'analyse de la performance des actions, aidant à déterminer la relation entre la performance d'une action et les indices du marché. Par exemple, il peut être utilisé pour calculer la sensibilité d'un titre aux mouvements du marché. Il contribue également à la modélisation du risque en adaptant les modèles aux données financières historiques afin d'estimer le risque et le rendement.

Les ingénieurs utilisent la méthode des moindres carrés pour l'étalonnage des capteurs afin d'adapter les modèles aux données observées et de minimiser les erreurs de mesure. Elle est également utilisée dans le traitement des signaux pour le filtrage et la réduction du bruit, ce qui permet une interprétation plus claire des données.

Bien entendu, la méthode des moindres carrés a vu le jour en astronomie ; elle a été utilisée pour la première fois par Carl Friedrich Gauss pour prédire l'orbite de l'astéroïde Cérès. Elle est également utilisée en géodésie pour modéliser la forme de la Terre à partir de données d'observation, ce qui est essentiel pour obtenir des mesures géographiques précises.

Si vous avez un peu tâté de l'apprentissage automatique, vous reconnaîtrez la méthode des moindres carrés comme une méthode permettant de minimiser la fonction de perte lors de l'apprentissage de modèles de régression linéaire. Vous l'avez peut-être également utilisé lors de la sélection des caractéristiques pour identifier les variables les plus importantes contribuant au modèle.

Elle joue également un rôle dans de nombreuses autres sciences exactes, telles que la physique et la chimie. Il peut être utilisé pour ajuster des courbes à des données expérimentales, telles que des taux de réaction ou des mesures physiques, et aider à minimiser les erreurs dans les montages expérimentaux.

La méthode des moindres carrés est un outil statistique polyvalent. Personnellement, j'ai utilisé cette méthode pour calibrer des capteurs de pression, faire des prédictions sur la base de mes données expérimentales et lors de l'entraînement à l'apprentissage automatique. La capacité à modéliser de manière fiable les relations et à minimiser les erreurs est une caractéristique qui offre de la valeur à de nombreuses disciplines différentes.

Hypothèses et diagnostics

La méthode des moindres carrés repose sur quelques hypothèses clés concernant vos données et le modèle utilisé. Il est important de comprendre ces hypothèses, car leur violation peut entraîner des résultats biaisés ou peu fiables. Discutons donc de ces hypothèses, ainsi que de la manière de diagnostiquer et de traiter les problèmes potentiels.

L'une des hypothèses est l'indépendance des erreurs, ce qui signifie que les résidus ne doivent pas être corrélés. Si les erreurs sont corrélées entre elles, en particulier dans les données séquentielles ou spatiales, les estimations peuvent être faussées. Le test de Durbin-Watson permet de détecter l'autocorrélation dans les résidus, en particulier pour les ensembles de données dépendant du temps. Si vous trouvez une corrélation, vous pouvez utiliser les moindres carrés généralisés pour en tenir compte.

Une autre hypothèse est que la variance des résidus reste constante pour tous les niveaux de la variable indépendante. Si les résidus présentent une dispersion en forme d'entonnoir lorsqu'ils sont représentés par rapport aux valeurs ajustées, il est probable que cette hypothèse ne soit pas respectée. Pour résoudre ce problème, vous pouvez utiliser la méthode des moindres carrés pondérés pour attribuer des poids appropriés à vos observations. Vous pouvez également utiliser des transformations telles que des ajustements logarithmiques ou de racine carrée pour stabiliser la variance inégale et résoudre les problèmes d'hétéroscédasticité.

Comme pour toute modélisation, il est important que la structure reflète la relation sous-jacente entre les variables. Si ce n'est pas le cas, peu importe que votre ajustement soit optimisé, les résultats seront toujours trompeurs. Les graphiques des résidus et les mesures d'adéquation telles que le ^R² peuvent vous aider à déterminer si le modèle que vous avez choisi capture les schémas des données. 

La méthode standard des moindres carrés suppose que les variables indépendantes sont mesurées sans erreur. Il est donc important de connaître la précision de votre mesure indépendante. Vous devriez avoir une idée de la précision de cette mesure en examinant les méthodes de collecte. S'il existe des erreurs de mesure dans votre prédicteur, veillez à utiliser la méthode des moindres carrés totaux pour atténuer les inexactitudes de votre modélisation.

Enfin, la distribution des erreurs résiduelles joue un rôle important, en particulier dans les tests d'hypothèse et l'estimation des intervalles de confiance. La méthode des moindres carrés suppose que les erreurs suivent une distribution normale (gaussienne), et les écarts par rapport à la normalité peuvent affecter l'inférence. Les histogrammes et les graphiques Q-Q permettent d'évaluer si les résidus correspondent aux distributions attendues. En cas d'écarts importants par rapport à la normalité, des techniques de régression robustes ou des méthodes de bootstrapping peuvent fournir des estimations plus fiables et moins sensibles aux valeurs aberrantes.

Avantages et inconvénients de la méthode des moindres carrés

La méthode des moindres carrés est un outil largement utilisé dans l'analyse des données. Mais cela ne signifie pas qu'il faille l'utiliser pour tous les ensembles de données.

La méthode des moindres carrés présente plusieurs avantages. Il est assez facile à calculer, en particulier pour les modèles linéaires. Il est facilement interprétable par un public technique et non technique. De plus, il existe différents styles, tels que la régression pondérée, la régression robuste et la régression non linéaire, ce qui le rend très polyvalent. Et surtout, elle repose sur un fondement théorique solide, le théorème de Gauss-Markov. Tout cela fait que les moindres carrés sont largement applicables et utilisés dans des domaines allant de l'économie à l'ingénierie.

Toutefois, la méthode est sensible aux valeurs aberrantes, qui peuvent affecter de manière disproportionnée les résultats du modèle. Elle suppose également qu'il n'y a pas d'erreurs dans les prédicteurs, ce qui peut ne pas être le cas dans les données réelles. En outre, les moindres carrés peuvent être limités par la multicolinéarité. Cela signifie que des prédicteurs fortement corrélés peuvent conduire à des coefficients instables et donc à des estimations peu fiables. Elle requiert également une variance constante des résidus, une condition qui n'est pas toujours remplie.

Il est important d'examiner attentivement votre ensemble de données et votre objectif avant de décider que la méthode des moindres carrés est le meilleur outil pour votre situation.

Conclusion

La méthode des moindres carrés est un outil fondamental pour tout analyste de données. En trouvant la meilleure adéquation à nos données, nous pouvons faire des prédictions plus précises et dégager des tendances plus perspicaces.

Pour en savoir plus sur la mesure des lignes droites dans l'espace euclidien, je vous recommande notre site Comprendre la distance euclidienne : De la théorie à la pratique tutorial. N'oubliez pas non plus de vous inscrire à nos cours de régression pour devenir un véritable expert. 

• Introduction à la régression avec statsmodels en Python
• Introduction à la régression en R