Softplus : La fonction d'activation en douceur qu'il est important de connaître

La fonction ReLU est la fonction d'activation par défaut dans le domaine de l'apprentissage profond depuis plusieurs années. Il y a une bonne raison à cela : c'est simple et cela fonctionne bien dans la plupart des cas. Cependant, lorsque les neurones commencent à produire des résultats nuls pendant l'entraînement, ils cessent d'apprendre, leurs gradients deviennent nuls et la rétropropagation ne peut plus mettre à jour leurs poids. Dans les réseaux plus profonds, ce problème peut affecter plusieurs neurones et réduire la capacité de votre modèle à capturer les modèles dans vos données.

En termes simples : votre réseau cesse d'apprendre.

Softplus propose une alternative fluide et différenciable qui résout ce problème, tout en conservant la plupart des avantages de ReLU. Elle se rapproche du comportement de ReLU pour les entrées positives, mais fournit des gradients non nuls pour les valeurs négatives. Cela permet de maintenir les neurones actifs tout au long de l'entraînement.

Dans cet article, vous découvrirez ce qu'est Softplus, comment il se compare mathématiquement à ReLU et dans quels cas il est préférable de le choisir plutôt que d'autres fonctions d'activation.

Si vous êtes totalement novice en matière d'apprentissage profond, veuillez consulter notre guide détaillé sur les fonctions d'activation dans les réseaux neuronaux.

Quelle est la fonction Softplus ?

Softplus est une fonction d'activation lisse qui agit comme une approximation différentiable de ReLU.

La fonction prend n'importe quel nombre réel en entrée et renvoie une valeur positive. Softplus ne présente pas d'angle aigu à zéro comme ReLU. Elle s'incurve en douceur à travers ce point de transition.

Voici la définition mathématique :

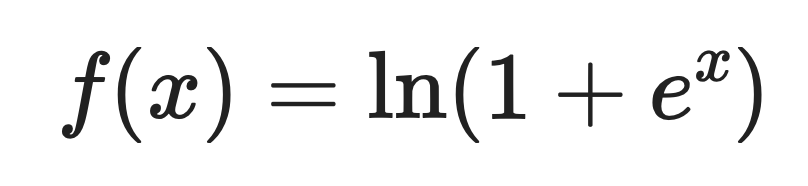
Où :

• x est la valeur d'entrée
• e est le nombre d'Euler (environ 2,718)
• ln est le logarithme naturel.

Pour les entrées positives importantes, Softplus renvoie des valeurs proches de l'entrée elle-même. Pour les entrées négatives, il renvoie de petites valeurs positives au lieu de zéro.

Dérivé de Softplus

La dérivée de Softplus est la fonction logistique sigmoïde. sigmoïde logistique.

Cela signifie :

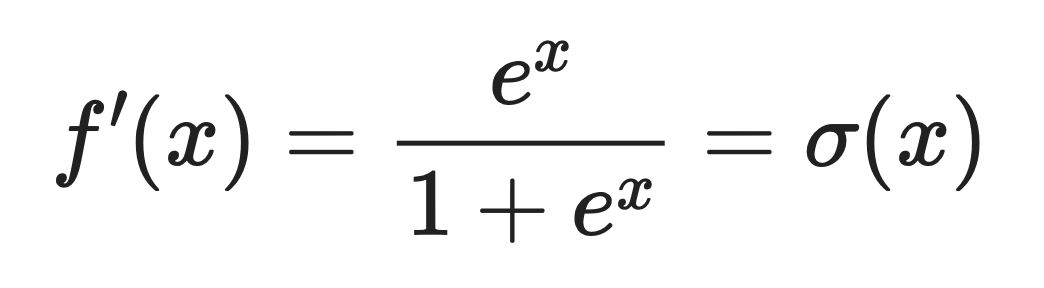
Où σ(x) est la fonction sigmoïde que vous avez probablement déjà rencontrée.

Cette propriété dérivée rend Softplus utile lorsque vous avez besoin d'un flux de gradient régulier pendant la rétropropagation. Les gradients ne descendent jamais à zéro. Cela signifie que les neurones peuvent constamment actualiser leurs poids et poursuivre leur apprentissage.

Comportement dans des situations extrêmes

Softplus se comporte différemment selon que l'entrée est grande et positive ou grande et négative.

Pour les grandes valeurs positives :

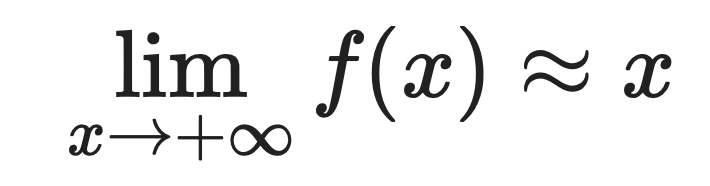
Pour les valeurs négatives importantes :

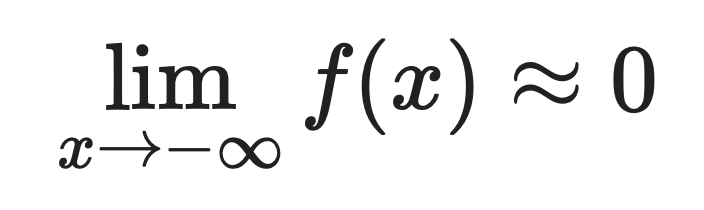
C'est pourquoi Softplus se rapproche si bien de ReLU. Lorsque x est positif et grand, les deux fonctions renvoient approximativement la même valeur.

La différence est visible sur les entrées négatives. ReLU produit exactement zéro pour les entrées négatives, tandis que Softplus produit de petites valeurs positives.

Cette légère différence permet d'éviter le problème de la mort des neurones. Les neurones utilisant Softplus peuvent se remettre d'activations négatives, car leurs gradients ne disparaissent jamais complètement.

Propriétés mathématiques et informatiques

Softplus possède des propriétés mathématiques qu'il est important de connaître. Ils en font bien plus qu'une simple version améliorée de ReLU.

Lissage et différentiabilité

Softplus est infiniment dérivable en tout point.

Cela signifie que vous pouvez dériver autant de fois que vous le souhaitez, et la fonction restera régulière. En termes mathématiques, il s'agit d'une fonction analytique.

ReLU, en revanche, présente un coude à zéro, c'est-à-dire un angle aigu où la dérivée n'existe pas. Ce point non différentiable peut poser des problèmes dans les algorithmes d'optimisation qui supposent des gradients réguliers.

Dans le domaine de l'apprentissage profond, l'optimisation lisse fonctionne mieux lorsque la surface de perte est lisse. Si vous utilisez des méthodes d'optimisation de second ordre ou tout algorithme reposant sur des transitions de gradient fluides, Softplus vous offre cette fluidité.

Stabilité numérique

Le calcul des exponentielles peut entraîner des problèmes de dépassement de capacité lorsque les entrées sont importantes.

Les frameworks d'apprentissage profond gèrent cela à l'aide d'un paramètre appelé « threshold ». Lorsque l'entrée dépasse ce seuil, la fonction passe du calcul du logarithme au renvoi d'une sortie linéaire.

Voici comment cela fonctionne :

• Pour les petites entrées : calculer directement Softplus
• Pour les entrées importantes dépassant le seuil : renvoyer directement les entrées.

Cela permet d'éviter les dépassements de capacité numérique tout en conservant le comportement souhaité. Pour les entrées positives importantes, Softplus se rapproche de toute façon d'une fonction linéaire, de sorte que le commutateur n'a pas d'incidence significative sur la sortie.

Relation avec d'autres fonctions

Softplus est relié à plusieurs autres fonctions d'activation et de probabilité. Voici comment procéder :

• sigmoïde: Comme vous l'avez observé précédemment, la dérivée de Softplus est la fonction sigmoïde. Cela signifie que Softplus est l'intégrale de la sigmoïde, ce qui est logique lorsque l'on considère leurs formes.

• LogSumExp: Softplus est en réalité un cas particulier de la fonction LogSumExp. Pour deux entrées, veuillez consulter le site LogSumExp(0, x) = ln(1 + e^x) = Softplus(x). Ceci relie Softplus aux techniques de stabilité numérique utilisées dans l'apprentissage automatique.

• Softmax: LogSumExp constitue la base de Softmax, donc Softplus partage cette lignée. Les deux fonctions utilisent l'astuce log-exp pour assurer la stabilité numérique.

• s de la fonction logit: La fonction logit est l'inverse de la fonction sigmoïde. Étant donné que la fonction sigmoïde est la dérivée de la fonction Softplus, ces trois fonctions forment une famille cohérente en théorie des probabilités.

• s de la fonction convexe conjuguée: En analyse convexe, le conjugué convexe de Softplus est l'entropie binaire négative. Cela relie Softplus aux principes de maximisation de l'entropie utilisés en théorie de l'information et en modélisation probabiliste.

Si vous travaillez avec des modèles probabilistes ou des cadres bayésiens, ce lien avec l'entropie fait de Softplus un choix naturel pour garantir que vos activations respectent les principes d'entropie maximale.

Avantages de l'utilisation de Softplus

Softplus résout des problèmes spécifiques que ReLU ne peut pas traiter efficacement. Voici quatre d'entre eux.

Lisse et différentiable

Softplus est régulier en tout point de la courbe.

Cela signifie que les gradients s'écoulent de manière continue pendant la rétropropagation, sans sauts ni ruptures soudains. Lorsque vous entraînez un réseau, un flux de gradient régulier conduit à des mises à jour de poids plus stables et à un meilleur comportement de convergence.

Le coin aigu de ReLU à zéro peut entraîner des discontinuités de gradient. Softplus ne rencontre pas ce problème.

Empêche la mort des neurones

Softplus ne produit jamais exactement zéro, même pour des entrées négatives importantes.

Cela signifie que chaque neurone peut continuer à apprendre l', car les gradients ne disparaissent jamais complètement. Avec ReLU, un neurone qui commence à produire une sortie nulle peut rester bloqué à ce niveau indéfiniment : son gradient est nul, donc les mises à jour des poids ne le modifient pas.

Softplus vous offre une sécurité. Les neurones peuvent se remettre d'activations négatives et recommencer à contribuer au réseau.

Le résultat est toujours positif.

Softplus garantit des résultats non négatifs pour toute entrée.

Ceci est important lorsque vous créez des modèles qui nécessitent des prédictions positives. La régression de Poisson modèles de régression de Poisson comptent les données (clients, événements, clics) pour lesquelles les valeurs négatives n'ont pas de sens. Les modèles génératifs ont souvent besoin de résultats positifs pour représenter des probabilités ou des intensités.

Plus adapté à certaines tâches

Certaines tâches bénéficient d'un comportement d'activation fluide et continu.

Les tâches de régression avec des fonctions cibles lisses fonctionnent mieux avec des activations lisses. Si vous prédisez des valeurs continues telles que la température, le prix ou la distance, Softplus s'aligne mieux avec la régularité sous-jacente de vos données.

Les modèles bayésiens et les cadres probabilistes privilégient également les fonctions lisses. Lorsque vous modélisez l'incertitude ou travaillez avec des distributions de probabilité, les dérivées continues de Softplus rendent les opérations mathématiques plus claires et plus stables.

Si vous travaillez dans ces domaines, Softplus vous offre de meilleures garanties théoriques et des résultats pratiques supérieurs à ceux obtenus avec les transitions abruptes de ReLU.

Limites et compromis

Il existe certaines limites que vous devez connaître concernant Softplus avant d'abandonner définitivement ReLU. Voici trois d'entre eux.

Coût de calcul plus élevé

ReLU utilise une opération max simple : max(0, x).

Softplus effectue des calculs exponentiels et logarithmiques : ln(1 + e^x). Ces opérations sont plus lentes, en particulier lorsque vous les exécutez des millions de fois sur de grands réseaux comportant des milliers de neurones.

La différence s'accumule. Cette charge de calcul peut augmenter la durée de la formation.

Convergence plus lente

Softplus présente des dégradés plus fluides, ce qui semble avantageux sur le papier.

Cependant, la fluidité n'est pas toujours synonyme de rapidité. Les transitions abruptes de ReLU génèrent des activations clairsemées : de nombreux neurones produisent exactement zéro sortie. Cette rareté permet aux gradients de se propager plus rapidement à travers le réseau pendant la rétropropagation.

Softplus ne présente pas cette rareté. Chaque neurone produit une valeur différente de zéro, ce qui implique davantage de calculs et une convergence potentiellement plus lente dans les architectures profondes.

Moins courant dans la pratique

ReLU domine le domaine de l'apprentissage profond depuis plusieurs années.

Cela signifie qu'il existe davantage de documentation, de problèmes/solutions et de ressources générales à ce sujet. Softplus ne bénéficie pas du même traitement. Moins de personnes l'utilisent, ce qui se traduit par une communauté moins informée, moins de réponses sur Stack Overflow et moins de modèles pré-entraînés qui l'utilisent.

En choisissant Softplus, vous optez pour une solution qui offre moins d'assistance et qui peut nécessiter davantage de débogage de votre part.

Softplus in PyTorch

PyTorch facilite l'utilisation de Softplus grâce à une prise en charge intégrée et deux paramètres qui contrôlent son comportement.

À titre de référence, voici la version de PyTorch que j'utilise :

import torch
import torch.nn as nn

print(torch.__version__)

Voici la mise en œuvre de base :

# Create a Softplus activation function
softplus = nn.Softplus(beta=1, threshold=20)

# Apply it to some input
x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
output = softplus(x)

print(output)

C'est assez simple. Cependant, ces deux paramètres - beta et threshold - modifient le comportement de la fonction. Examinons-les plus en détail.

Le paramètre bêta

Le paramètre « beta » (lissage de la courbe) contrôle le lissage de la courbe Softplus.

Lorsque vous augmentez beta, la fonction devient plus raide et se rapproche de ReLU. Lorsque vous la diminuez, la fonction devient plus fluide et plus progressive. Voici comment cela fonctionne dans le code :

x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])

# Steeper activation (closer to ReLU)
softplus_steep = nn.Softplus(beta=2, threshold=20)
output_steep = softplus_steep(x)

# Smoother activation
softplus_smooth = nn.Softplus(beta=0.5, threshold=20)
output_smooth = softplus_smooth(x)

print("Softplus - Steeper activation")
print(output_steep)

print()

print("Softplus - Smoother activation")
print(output_smooth)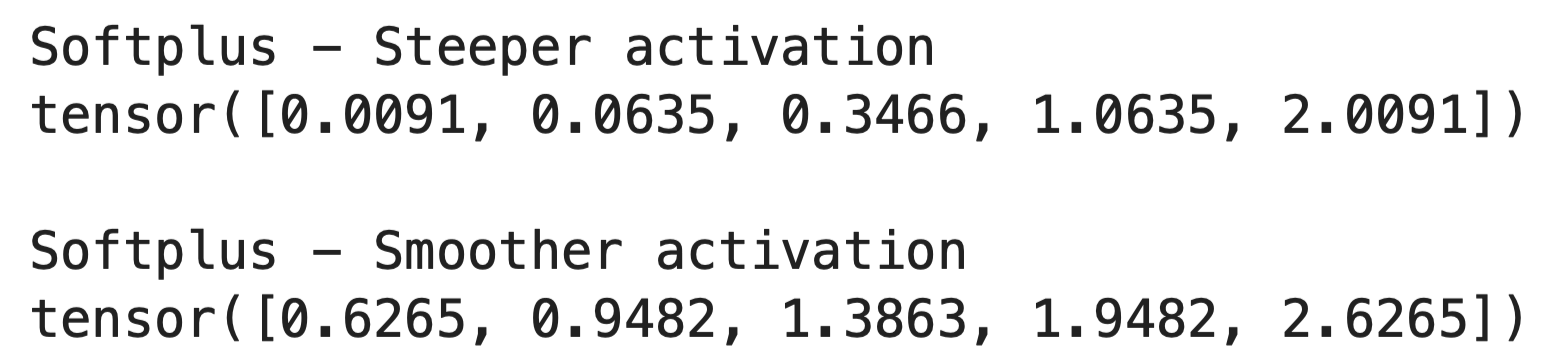

L'beta=1 e par défaut fonctionne bien dans la plupart des cas. Vous ne devriez modifier ce paramètre que si vous avez besoin d'ajuster la sensibilité de l'activation pour des tâches spécifiques.

Le paramètre seuil

Le paramètre threshold empêche le dépassement de capacité numérique pour les entrées volumineuses.

Veuillez noter que l'e^x e de calcul peut augmenter considérablement pour des valeurs x élevées. Lorsque l'entrée dépasse le seuil, PyTorch passe du calcul de la formule Softplus complète au simple renvoi direct de l'entrée :

softplus = nn.Softplus(beta=1, threshold=20)

# Large input bypasses the exponential
large_input = torch.tensor([25.0])
print(softplus(large_input))

L'threshold=20 e par défaut convient à la plupart des scénarios. À ce stade, Softplus se rapproche déjà d'une fonction linéaire, donc le changement n'affecte pas les résultats.

Quand utiliser Softplus

Veuillez sélectionner Softplus lorsque vous avez besoin d'une optimisation dela fluidité des dégradés. Si vous utilisez des méthodes d'optimisation du second ordre ou des algorithmes qui supposent des surfaces de perte lisses, Softplus vous fournit les dérivées continues sur lesquelles reposent ces méthodes.

Veuillez l'utiliser lorsque votre modèle nécessite des sorties non négatives.. Les données de comptage, les valeurs d'intensité et les paramètres de probabilité doivent tous rester positifs. Softplus gère cela de manière naturelle, sans contraintes supplémentaires.

Les réseaux peu profonds bénéficient davantage de Softplus que les réseaux profonds. Lorsque vous ne disposez que de quelques couches, la perte d'un seul neurone due au problème de ReLU affecte les performances. Softplus stimule l'activité et l'apprentissage de tous les neurones.

Vous pouvez également choisir Softplus pour les modèles probabilistes et les cadres bayésiens. Les gradients lisses et les connexions entropiques rendent les opérations mathématiques plus claires. Les modèles basés sur l'énergie bénéficient également de la nature continue de Softplus.

Les modèles dans lesquels il est nécessaire d'interpréter des gradients continus fonctionnent mieux avec Softplus. Si vous analysez la manière dont votre réseau réagit aux changements d'entrée ou étudiez le flux de gradient, les dérivées lisses vous fournissent des informations plus claires que les transitions abruptes de ReLU.

Quand ReLU est toujours plus performant

Il est déconseillé de passer à Softplus simplement parce que cela semble plus avantageux sur le papier ou parce que c'est une nouveauté.

• Les réseaux vastes et profonds s'entraînent plus rapidement avec ReLU. La charge de calcul de Softplus s'accumule à travers des centaines de couches et des millions de paramètres. La rareté de ReLU contribue également à améliorer la mémoire et la vitesse.
• Les systèmes de production privilégient souvent ReLU, car les optimisations matérielles le ciblent spécifiquement. Votre formation pourrait être 10 à 20 % plus lente avec Softplus sur le même matériel.
• Les tâches standard de vision par ordinateur et de traitement du langage naturel ( ) ne bénéficient généralement pas de Softplus. La communauté a consacré des années à optimiser les architectures autour de ReLU, et changer de fonction d'activation implique de reconstruire ces connaissances.

Pour la plupart des projets, il est recommandé de commencer par ReLU. Veuillez passer à Softplus uniquement lorsque vous rencontrez des problèmes spécifiques que ses propriétés permettent de résoudre.

Conclusion

En résumé, Softplus vous offre une alternative fluide à ReLU lorsque cela est nécessaire.

Elle ne remplacera pas ReLU en tant que fonction d'activation par défaut, et cela n'est pas nécessaire. Softplus résout des problèmes spécifiques : les neurones défaillants dans les réseaux peu profonds, les modèles qui nécessitent des sorties non négatives et les tâches où un flux de gradient régulier est important pour l'optimisation.

Vous obtenez de meilleures propriétés mathématiques au détriment de la vitesse de calcul. Pour la plupart des projets d'apprentissage profond, la simplicité et la rapidité de ReLU sont des atouts majeurs. Cependant, lorsque vous travaillez avec des modèles probabilistes, des cadres bayésiens ou des tâches de régression avec des fonctions cibles lisses, Softplus s'impose comme le choix le plus approprié.

Veuillez tester les deux. Veuillez mener des expériences. Veuillez laisser votre problème spécifique guider votre décision.

Souhaitez-vous en savoir davantage ? Veuillez consulter nos excellentes ressources :

• Apprentissage profond en Python
• Traitement du langage naturel en Python
• Principes d'ingénierie logicielle en Python