Curso
Definitivamente, vale a pena aprender a regressão OLS (mínimos quadrados ordinários), pois ela é uma grande parte da estatística e do aprendizado de máquina. Ele é usado para prever resultados ou analisar relações entre variáveis, e as aplicações desses dois usos incluem tudo, desde testes de hipóteses até previsões.
Neste artigo, ajudarei você a entender os fundamentos da regressão OLS, suas aplicações, pressupostos e como ela pode ser implementada no Excel, R e Python. Há muito o que aprender, portanto, quando você terminar, faça nossos cursos de regressão designados, como Introdução à Regressão em Python e Introdução à Regressão em R, e leia nossos tutoriais, como Regressão Linear no Excel.
O que é regressão OLS?
A regressão OLS estima a relação entre uma ou mais variáveis independentes (preditores) e uma variável dependente (resposta). Isso é feito por meio do ajuste de uma equação linear aos dados observados. Aqui está a aparência dessa equação:
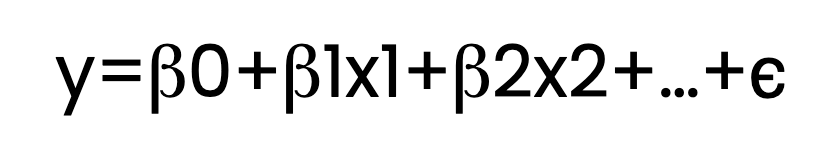
Aqui:
- y é a variável dependente.
- x1, x2,..., são variáveis independentes.
- β0 é a interceptação.
- β1, β2, …, são os coeficientes.
- ϵ representa o termo de erro.
Na equação acima, mostro vários termos β , como β1 e β2. Mas, para que fique claro, a equação de regressão poderia conter apenas um termo β além de β0, caso em que a chamaríamos de regressão linear simples. Com dois ou mais preditores, como β1 e β2 , chamaríamos isso de regressão linear múltipla. Ambos se qualificariam como regressão OLS se um estimador de mínimos quadrados ordinários fosse usado.
O que é o problema de minimização OLS?
No centro da regressão OLS está um desafio de otimização: encontrar a linha (ou hiperplano em dimensões mais altas) que melhor se ajusta aos dados. Mas o que significa "melhor ajuste"? "Melhor ajuste" aqui significa minimizar a soma dos resíduos ao quadrado.
Vou tentar explicar o problema de minimização e, ao mesmo tempo, explicar a ideia de resíduos.
- Explicação dos resíduos: Os resíduos são as diferenças entre os valores reais observados e os valores previstos pelo modelo de regressão. Para cada ponto de dados, o resíduo nos informa o quanto nossa previsão estava errada.
- Por que elevar os resíduos ao quadrado? Ao elevar cada resíduo ao quadrado, garantimos que as diferenças positivas e negativas não se anulem. A quadratura também dá mais peso a erros maiores, o que significa que o modelo prioriza a redução de erros maiores.
Ao minimizar a soma dos resíduos ao quadrado, a linha de regressão se torna uma representação precisa da relação entre as variáveis independentes e dependentes. De fato, ao minimizar a soma dos resíduos ao quadrado, nosso modelo apresenta o menor erro geral possível em suas previsões. Para saber mais sobre resíduos e decomposição de regressão, leia nosso tutorial, Understanding Sum of Squares: Um guia para SST, SSR e SSE.
O que é o estimador de mínimos quadrados ordinários?
No contexto da regressão, os estimadores são usados para calcular os coeficientes que descrevem a relação entre as variáveis independentes e a variável dependente. O estimador de mínimos quadrados ordinários (OLS) é um desses métodos. Ele encontra os valores de coeficiente que minimizam a soma das diferenças quadráticas entre os valores observados e os previstos pelo modelo.
Estou mencionando isso para manter os termos claros. A regressão pode ser feita com outros estimadores, cada um oferecendo vantagens diferentes, dependendo dos dados e dos objetivos da análise. Por exemplo, alguns estimadores são mais robustos em relação a outliers, enquanto outros ajudam a evitar o ajuste excessivo, regularizando os parâmetros do modelo.
Como os parâmetros de regressão OLS são estimados?
Para determinar os coeficientes que melhor se ajustam ao modelo de regressão, o estimador OLS emprega técnicas matemáticas para minimizar a soma dos resíduos ao quadrado. Um método possível é a equação normal, que fornece uma solução direta ao configurar um sistema de equações com base nos dados e resolver os coeficientes que atingem a menor soma possível de diferenças quadráticas entre os valores observados e previstos.
No entanto, a solução da equação normal pode exigir muito da computação, especialmente com grandes conjuntos de dados. Para resolver isso, outra técnica chamada decomposição QR é usada com frequência. A decomposição QR divide a matriz de variáveis independentes em duas matrizes mais simples: uma matriz ortogonal (Q) e uma matriz triangular superior (R). Essa simplificação torna os cálculos mais eficientes e também melhora a estabilidade numérica.
Quando usar a regressão OLS
Como decidimos usar a regressão OLS? Ao tomar essa decisão, precisamos avaliar as características do nosso conjunto de dados e também definir o problema específico que estamos tentando resolver.
Pressupostos da regressão OLS
Antes de aplicar a regressão OLS, devemos nos certificar de que nossos dados atendam às seguintes premissas para que tenhamos resultados confiáveis:
- Linearidade: A relação entre as variáveis independentes e dependentes deve ser linear.
- Independência de erros: Os resíduos não devem estar correlacionados entre si.
- Homocedasticidade: Os resíduos devem ter uma variação constante em todos os níveis das variáveis independentes.
- Normalidade dos erros: Os resíduos devem ser distribuídos normalmente.
Violações graves dessas premissas podem levar a estimativas distorcidas ou previsões não confiáveis. Portanto, temos que avaliar e resolver todos os possíveis problemas antes de prosseguir.
Aplicações da regressão OLS
Quando as premissas são satisfeitas, a regressão OLS pode ser usada para diferentes fins:
- Modelagem preditiva: Previsão de resultados, como vendas, receita ou tendências.
- Análise de relacionamento: Compreender a influência de variáveis independentes em uma variável dependente.
- Teste de hipóteses: Avaliar se preditores específicos afetam significativamente a variável de resultado.
Regressão OLS em R, Python e Excel
Vamos agora dar uma olhada em como realizar a regressão OLS no R, Python e Excel.
Regressão OLS no R
O R fornece a função lm() para regressão OLS. Aqui está um exemplo:
# Let's create sample data
predictor_variable <- c(1, 2, 3, 4, 5)
response_variable <- c(2, 4, 5, 4, 5)
# We now fit the OLS regression model using the lm() function from base R
ols_regression_model <- lm(response_variable ~ predictor_variable)
# OLS regression model summary
summary(ols_regression_model)Observe como não precisamos importar nenhum pacote adicional para realizar a regressão OLS no R.
Regressão OLS em Python
O Python oferece bibliotecas como statsmodels e scikit-learn para regressão OLS. Vamos tentar um exemplo usando statsmodels:
import statsmodels.api as sm
# We can create some sample data
ols_regression_predictor = [1, 2, 3, 4, 5]
ols_regression_response = [2, 4, 5, 4, 5]
# Adding a constant for the intercept
ols_regression_predictor = sm.add_constant(ols_regression_predictor)
# We now fit our OLS regression model
ols_regression_model = sm.OLS(ols_regression_response, ols_regression_predictor).fit()
# Summary of our OLS regression
print(ols_regression_model.summary())Regressão OLS no Excel
O Excel também oferece uma maneira de fazer a regressão OLS por meio de suas ferramentas internas. Basta você seguir estas etapas:
Prepare seus dados
Organize seus dados em duas colunas: uma para a(s) variável(is) independente(s) e outra para a variável dependente. Certifique-se de que não haja células em branco em seu conjunto de dados.
Ativar o Data Analysis ToolPak
Acesse File > Options > Add-Ins. Na caixa Gerenciar, selecione Excel Suplementose, em seguida, clique em Ir para. Marque a caixa para Análise ToolPak e clique em OK.
Execute a análise de regressão
Navegue até Data > Data Analysis e selecione Regressão na lista de opções. Clique em OK.
Na caixa de diálogo Regressão:
- Defina o Intervalo Y de entrada para a coluna de sua variável dependente.
- Defina o Intervalo X de entrada para sua(s) variável(eis) independente(s).
- Verificação Rótulos se o intervalo de entrada incluir cabeçalhos de coluna.
- Selecione um intervalo de saída ou uma nova planilha para os resultados.
Como avaliar modelos de regressão OLS
Agora criamos um modelo de regressão OLS. A próxima etapa é verificar se ele é eficaz, examinando os diagnósticos e as estatísticas do modelo.
Gráficos de diagnóstico
Podemos avaliar um modelo de regressão OLS usando ferramentas visuais para avaliar as suposições do modelo e a qualidade do ajuste. Algumas opções incluem umgráfico de residuais vs. valores ajustados, que verifica os padrões que podem indicar não linearidade ou heterocedasticidade, ou ográfico gráfico Q-Qque examina se os resíduos seguem uma distribuição como a normal.
Estatísticas do modelo
Também podemos avaliar nosso modelo com métricas estatísticas que fornecem insights sobre o desempenho do modelo e a significância do preditor. As estatísticas comuns do modelo incluem R -squared e R-quadrado ajustadoajustado, quemedem a proporção da variação explicada pelo modelo. Também podemos examinar as estatísticas F e os valores p, que testam a importância geral do modelo e dos preditores individuais .
Fluxo de trabalho de treinamento/teste
Por fim, devemos dizer que os analistas de dados também gostam de seguir um processo estruturado para validar os recursos preditivos de um modelo. Isso inclui um processo de divisão de dados, em que os dados são divididos em subconjuntos de treinamento e teste, um processo de treinamento para ajustar o modelo e, em seguida, um processo de teste para avaliar o desempenho do modelo em dados de teste não vistos. Esse processo também pode incluir etapas de validação cruzada, como a validação cruzada k-fold.
Insights mais profundos sobre a regressão OLS
Agora que exploramos os conceitos básicos da regressão OLS, vamos explorar alguns conceitos mais avançados.
Regressão OLS e estimativa de máxima verossimilhança
A estimativa de máxima verossimilhança (MLE) é outro conceito mencionado juntamente com a regressão OLS, e por um bom motivo. Até agora, falamos sobre como o OLS minimiza a soma dos resíduos ao quadrado para estimar os coeficientes. Agora vamos dar um passo atrás para falar sobre o MLE.
O MLE maximiza a probabilidade de observar os dados fornecidos de acordo com nosso modelo. Ele funciona assumindo uma distribuição de probabilidade específica para o termo de erro. Essa distribuição de probabilidade geralmente é uma distribuição normal ou gaussiana. Usando nossa distribuição de probabilidade, encontramos valores de parâmetros que tornam os dados observados mais prováveis.
O motivo pelo qual estou mencionando a estimativa de máxima verossimilhança neste momento é porque, no contexto da regressão OLS, a abordagem MLE leva às mesmas estimativas de coeficiente que obtemos ao minimizar a soma dos erros de quadrados, desde que os erros sejam normalmente distribuídos.
Interpretando a regressão OLS como uma média ponderada
Outra perspectiva fascinante sobre a regressão OLS é sua interpretação como uma média ponderada. Andrew Gelman discute a ideia de que os coeficientes em uma regressão OLS podem ser considerados como uma média ponderada dos pontos de dados observados, em que os pesos são determinados pela variação dos preditores e pela estrutura do modelo.
Essa visão fornece alguns insights sobre como o processo de regressão funciona e por que ele se comporta dessa maneira, porque a regressão OLS está realmente dando mais peso às observações que têm menos variação ou que estão mais próximas das previsões do modelo. Você também podeunir-se ao nosso episódio do podcast DataFramed, Election Forecasting and Polling, para ouvir o que o professor Gelman diz sobre o uso da regressão em pesquisas eleitorais.
Regressão OLS vs. Métodos de regressão semelhantes
Vários outros métodos de regressão têm nomes que podem soar semelhantes, mas servem a propósitos diferentes ou operam sob premissas diferentes. Vamos dar uma olhada em alguns que parecem semelhantes:
OLS vs. mínimos quadrados ponderados (WLS)
O WLS é uma extensão do OLS que atribui pesos diferentes a cada ponto de dados com base na variação de suas observações. O WLS é particularmente útil quando a suposição de variância constante dos resíduos é violada. Ao ponderar as observações inversamente à sua variação, o WLS fornece estimativas mais confiáveis ao lidar com dados heterocedásticos.
Regressão OLS vs.regressão por mínimos quadrados parciais(PLS)
O PLS combina recursos da análise de componentes principais e da regressão múltipla, extraindo variáveis latentes que capturam a covariância máxima entre os preditores e a variável de resposta. O PLS é vantajoso em situações com multicolinearidade ou quando o número de preditores excede o número de observações. Ele reduz a dimensionalidade e, ao mesmo tempo, maximiza o poder preditivo, o que o OLS não aborda de forma inerente.
OLS vs. gmínimos quadrados generalizados (GLS)
Semelhante ao WLS, o GLS generaliza o OLS ao permitir a variância correlacionada e/ou não constante dos resíduos. O GLS ajusta o processo de estimativa para levar em conta as violações das suposições do OLS em relação aos resíduos, fornecendo estimativas mais eficientes e imparciais em tais cenários.
OLS vs. mínimos quadrados totais (TLS)
Também conhecido como regressão ortogonal, o TLS minimiza as distâncias perpendiculares dos pontos de dados à linha de regressão, em vez das distâncias verticais minimizadas pelo OLS. O TLS é útil quando há erro nas variáveis independentes e dependentes, enquanto o OLS pressupõe que somente a variável dependente tem erro de medição.
Alternativas à regressão OLS
Quando a relação entre as variáveis é complexa ou não linear, os métodos de regressão não paramétricos oferecem alternativas flexíveis ao OLS, permitindo que os dados determinem a forma da função de regressão. Todos os exemplos anteriores (os que soam "semelhantes") pertencem à categoria de modelos paramétricos. Mas os modelos não paramétricos também podem ser usados quando você quiser modelar padrões sem as restrições das suposições paramétricas.
| Método | Descrição | Vantagens | Casos de uso comuns |
|---|---|---|---|
| Regressão de Kernel | Usa médias ponderadas com um kernel para suavizar os dados. | Captura relações não lineares Suavização flexível |
Análise exploratória Relações entre variáveis desconhecidas |
| Regressão local | Ajusta polinômios locais a subconjuntos de dados para uma curva suave. | Lida com padrões complexos Suavidade adaptável |
Visualização de tendências Suavização de gráficos de dispersão |
| Árvores de regressão | Divide os dados em ramos para ajustar modelos simples em cada segmento. | Fácil de interpretar Lida com interações |
Segmentação de dados Identificação de regimes de dados distintos |
| Regressão Spline | Usa polinômios por partes com continuidade nos nós para modelar dados. | Modelos de tendências não lineares suaves Ajuste flexível |
Séries temporais Curvas de crescimento |
Considerações finais
A regressão OLS é uma ferramenta fundamental para entender as relações entre os dados e fazer previsões. Ao dominar o OLS, você criará uma base sólida para explorar modelos e técnicas avançadas. Explore os cursos do DataCamp sobre regressão em R e Python para expandir seu conjunto de habilidades: Introdução à regressão com modelos estatísticos em Python e Introdução à regressão em R). Além disso, considere nossa popular carreira de Cientista de Aprendizado de Máquina em Python.
Torne-se um cientista de ML


