Course
What is Fuzzy String Matching?
A human may be able to distinguish the intention of a misspelled word with a quick glance. For a computer, the distinction is not as clear-cut.
Fuzzy string matching is the colloquial name used for approximate string matching – we will stick with the term fuzzy string matching for this tutorial. It’s a technique used to identify two elements of text strings that match partially but not exactly.
We typically see this phenomenon used in search engines. For example, if a user were to type “Londin” instead of “London” into Google, fuzzy string matching would identify that “London” was the intended word, and Google would return search results for that.
In this article, you will learn:
- How the fuzzy string matching algorithm determines the closeness of two strings using the Levenshtein edit distance.
- How to perform simple fuzzy string matching in Python using TheFuzz library.
- Some advanced fuzzy string matching techniques using TheFuzz advanced matches.
- How to integrate the TheFuzz library with Pandas.
Learn more Python techniques by starting our Cleaning Data in Python course today.
Check out the DataLab workbook to follow along with the code used in this article.
Learn Python From Scratch
Edits and edit distance
The fuzzy string matching algorithm seeks to determine the degree of closeness between two different strings. This is discovered using a distance metric known as the “edit distance.” The edit distance determines how close two strings are by finding the minimum number of “edits” required to transform one string to another.
If the edit distance counts the number of edit operations to tell us how many operations away one string is from another, an edit is an operation performed on a string to transform it into another string.
There are four main types of edits:
| Edit Operation | Description | Example |
|---|---|---|
| Insert | Add a letter | "Londn" -> "London" |
| Delete | Remove a letter | "Londoon" -> "London" |
| Switch | Swap two adjacent letters | "Lnodon" -> "London" |
| Replace | Change one letter to another | "Londin" -> "London" |
These four edit operations make it possible to modify any string.
Combining the edit operations together enables you to discover the list of possible strings that are N edits away, where N is the number of edit operations. For example, the edit distance between “London” and “Londin” is one since replacing the “i” with an “o” leads to an exact match.
But how specifically is the edit distance calculated, you ask?
There are different variations of how to calculate edit distance. For instance, there is the Levenshtein distance, Hamming distance, Jaro distance, and more.
The Levenshtein Distance
In this tutorial, we are only concerned with the Levenshtein distance.
It’s a metric named after Vladimir Levenshtein, who originally considered it in 1965 to measure the difference between two sequences of words. We can use it to discover the minimum number of edits that you need to do to change a one-word sequence into the other.
Here’s the formal calculation:
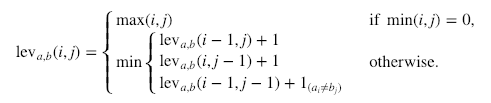
Where 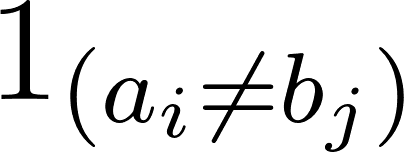 denotes 0 when a=b and 1 otherwise.
denotes 0 when a=b and 1 otherwise.
It is important to note that the rows on the minimum above correspond to a deletion, an insertion, and a substitution in that order.
It is also possible to calculate the Levenshtein similarity ratio based on the Levenshtein distance. This can be done using the following formula:
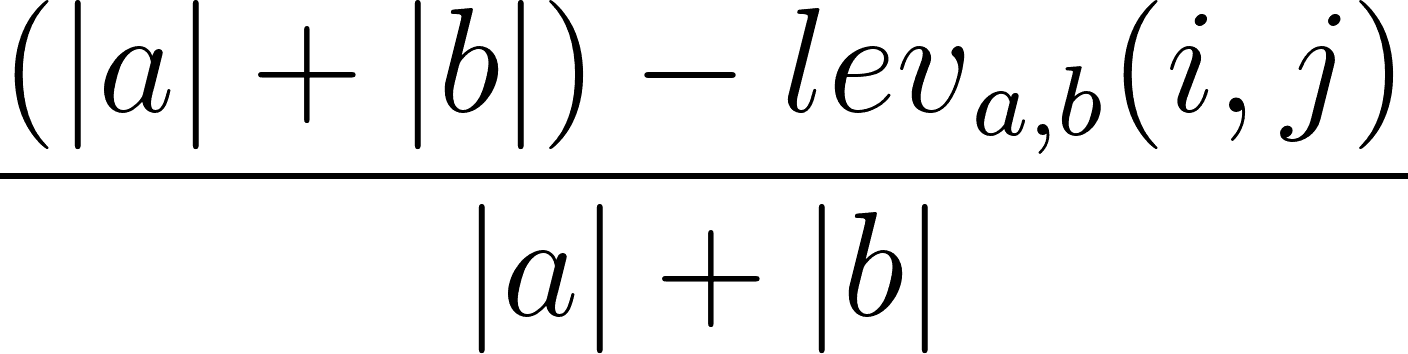
where |a| and |b| are the lengths of a sequence and b sequence, respectively.
Simple Fuzzy String Matching
One of the most popular packages for fuzzy string matching in Python was FuzzyWuzzy. However, FuzzyWuzzy was updated and renamed in 2021. It now goes by the name TheFuzz.
TheFuzz still holds as one of the most advanced open-source libraries for fuzzy string matching in Python. It was first developed by SeatGeek for the purpose of distinguishing whether two ticket listings with similar names were for the same event.
In accordance with FuzzyWuzzy, TheFuzz uses the Levenshtein edit distance to calculate the degree of closeness between two strings. It also provides features for determining string similarity in various situations, as you will see in this tutorial.
First, we must install thefuzz package. You can do this with pip using the following command:
!pip install thefuzzNote: This library comes pre-installed in the DataLab workbook.
Now, let’s take a look at some of the things we can do with thefuzz.
Follow along with the code in this DataLab workbook.
Simple ratio
We can determine the simple ratio between two strings using the ratio() method on the fuzz object. This simply calculates the edit distance based on the ordering of both input strings difflib.ratio() – see the difflib documentation to learn more.
# Check the similarity score
name = "Kurtis Pykes"
full_name = "Kurtis K D Pykes"
print(f"Similarity score: {fuzz.ratio(name, full_name)}")
"""
Similarity Score: 86
"""In the code, we used two variations of my name to compare the similarity score, which was given as 86.
Let’s check this against the partial ratio.
Partial ratio
To check the partial ratio, all we must do to the code above is call partial_ratio() on our fuzz object instead of ratio().
# Check the similarity score
name = "Kurtis Pykes"
full_name = "Kurtis K D Pykes"
print(f"Similarity score: {fuzz.partial_ratio(name, full_name)}")
"""
Similarity Score: 67
"""We see a decrease. What is going on?
Well, the partial_ratio() seeks to find how partially similar two strings are. Two strings are partially similar if they have some of the words in a common order.
The partial_ratio() calculates the similarity by taking the shortest string, which in this scenario is stored in the variable name, then compares it against the sub-strings of the same length in the longer string, which is stored in full_name.
Since order matters in partial ratio, our score dropped in this instance. Therefore, to get a 100% similarity match, you would have to move the "K D" part (signifying my middle name) to the end of the string. For example:
# Order matters with partial ratio
# Check the similarity score
name = "Kurtis Pykes"
full_name = "Kurtis Pykes K D"
print(f"Partial ratio similarity score: {fuzz.partial_ratio(name, full_name)}")
# But order will not effect simple ratio if strings do not match
print(f"Simple ratio similarity score: {fuzz.ratio(name, full_name)}")
"""
Partial ratio similarity score: 100
Simple ratio similarity score: 86
"""So what if we want our fuzzy string matcher to ignore order?
Then you may want to use the “token sort ratio.”
Token sort ratio
Okay, so we want to ignore the ordering of the words in the strings but still determine how similar they are – token sort helps you do exactly that. Token sort doesn’t care about what order words occur in. It accounts for similar strings that aren’t in order as expressed above.
Thus, we should get a 100% score using token sort ratio with the most recent example:
# Check the similarity score
full_name = "Kurtis K D Pykes"
full_name_reordered = "Kurtis Pykes K D"
# Order does not matter for token sort ratio
print(f"Token sort ratio similarity score: {fuzz.token_sort_ratio(full_name_reordered, full_name)}")
# Order matters for partial ratio
print(f"Partial ratio similarity score: {fuzz.partial_ratio(full_name, full_name_reordered)}")
# Order will not effect simple ratio if strings do not match
print(f"Simple ratio similarity score: {fuzz.ratio(name, full_name)}")
"""
Token sort ratio similarity score: 100
Partial ratio similarity score: 75
Simple ratio similarity score: 86
"""… and as expected, we did.
Let’s go back to the original name and full_name variables. What do you think will happen if we use token sort now?
# Check the similarity score
name = "Kurtis Pykes"
full_name = "Kurtis K D Pykes"
print(f"Token sort ratio similarity score: {fuzz.token_sort_ratio(name, full_name)}")
"""
Token sort ratio similarity score: 86
"""The score drops.
This is because token sort only disregards order. If there are words that are dissimilar words in the strings, it will negatively impact the similarity ratio, as we’ve seen above.
But there is a workaround.
Token set ratio
The token_set_ratio() method is pretty similar to the token_sort_ratio(), except it takes out common tokens before calculating how similar the strings are: this is extremely helpful when the strings are significantly different in length.
Since the name and full_name variables both have “Kurtis Pykes” in them, we can expect the token set ratio similarity to be 100%.
# Check the similarity score
name = "Kurtis Pykes"
full_name = "Kurtis K D Pykes"
print(f"Token sort ratio similarity score: {fuzz.token_set_ratio(name, full_name)}")
"""
Token sort ratio similarity score: 100
"""Process
The process module enables users to extract text from a collection using fuzzy string matching. Calling the extract() method on the process module returns the strings with a similarity score in a vector. For example:
from thefuzz import process
collection = ["AFC Barcelona", "Barcelona AFC", "barcelona fc", "afc barcalona"]
print(process.extract("barcelona", collection, scorer=fuzz.ratio))
"""
[('barcelona fc', 86), ('AFC Barcelona', 82), ('Barcelona AFC', 82), ('afc barcalona', 73)]
"""We can control the length of the vector returned by the extract() method by setting the limit parameter to the desired length.
print(process.extract("barcelona", collection, scorer=fuzz.ratio))
"""
[('barcelona fc', 86), ('AFC Barcelona', 82), ('Barcelona AFC', 82)]
"""In this instance, the extract() returns the three closest matching strings based on the scorer we defined.
Fuzzy string matching techniques with TheFuzz compapred
In the table below, you can see a quick comparison of the different types of techniques available in TheFuzz:
| Technique | Description | Code Example |
|---|---|---|
| Simple Ratio | Calculates similarity considering the order of input strings. | fuzz.ratio(name, full_name) |
| Partial Ratio | Finds partial similarity by comparing the shortest string with sub-strings. | fuzz.partial_ratio(name, full_name) |
| Token Sort Ratio | Ignores order of words in strings. | fuzz.token_sort_ratio(full_name_reordered, full_name) |
| Token Set Ratio | Removes common tokens before calculating similarity. | fuzz.token_set_ratio(name, full_name) |
Fuzzy String Matching with pandas
In this section, we will see how to do fuzzy string matching on a pandas dataframe.
Let’s say you have some data you have exported into a pandas dataframe, and you would like to join it to the existing data you have.
import pandas as pd
# Creating a dataframe
dict_one = {
"country": ["England", "Scotland", "Wales", "United Kingdom", "Northern Ireland"],
"population_in_millions": [55.98, 5.45, 3.14, 67.33, 1.89]
}
dict_two = {
"country": ["Northern Iland", "Wles", "Scotlnd", "Englnd", "United K."],
"GDP_per_capita": [24900, 23882, 37460, 45101, 46510.28]
}
existing_data = pd.DataFrame(dict_one)
exported_data = pd.DataFrame(dict_two)
print(existing_data, exported_data, sep="\n\n")
"""
country population_in_millions
0 England 55.98
1 Scotland 5.45
2 Wales 3.14
3 United Kingdom 67.33
4 Northern Ireland 1.89
country GDP_per_capita
0 Northern Iland 24900.00
1 Wles 23882.00
2 Scotlnd 37460.00
3 Englnd 45101.00
4 United K. 46510.28
"""There’s a major problem.
The existing data has the correct spellings for the countries, but the exported data does not. If we attempt to join the two dataframes on the country column, pandas would not recognize the misspelled words as being equal to the correctly spelled words. Thus, the result returned from the merge function will not be as expected.
Here is what would happen if we tried:
# Attempt to join the two dataframe
data = pd.merge(existing_data, exported_data, on="country", how="left")
print(data.head())
"""
country population_in_millions GDP_per_capita
0 England 55.98 NaN
1 Scotland 5.45 NaN
2 Wales 3.14 NaN
3 United Kingdom 67.33 NaN
4 Northern Ireland 1.89 NaN
"""This defeats the whole purpose of attempting to merge these dataframes together.
However, we can get around this problem with fuzzy string matching.
Let’s see how it looks in code:
# Rename the misspelled columns
exported_data["country"] = exported_data["country"].apply(
lambda x: process.extractOne(x, existing_data["country"], scorer=fuzz.partial_ratio)[0]
)
# Attempt to join the two dataframe
data = pd.merge(existing_data, exported_data, on="country", how="left")
print(data.head())
"""
country population_in_millions GDP_per_capita
0 England 55.98 45101.00
1 Scotland 5.45 37460.00
2 Wales 3.14 23882.00
3 United Kingdom 67.33 46510.28
4 Northern Ireland 1.89 24900.00
"""In this code, we have renamed the misspelled values in country column of the exported data using a neat lambda function in association with the process.extractOne() method. Note, we used an index of 0 on the result of the extractOne() to return online the similar string instead of a list containing the string and similarity value.
Next, we merged the dataframes on the country column using a left join. The result is a single dataframe containing the correctly spelled countries (including the political union of the United Kingdom).
Fuzzy string matching with pandas DataFrames
If you need a quick recap of the techniques mentioned above, you can find them in the table below:
| Step | Description | Code Snippet |
|---|---|---|
| Create DataFrames | Define data with possible misspellings. | existing_data = pd.DataFrame(dict_one), exported_data = pd.DataFrame(dict_two) |
| Attempt Merge with Errors | Initial merge fails due to mismatched strings. | data = pd.merge(existing_data, exported_data, on="country", how="left") |
| Correct Misspellings | Use fuzzy matching to correct misspelled country names. | exported_data["country"] = exported_data["country"].apply(lambda x: process.extractOne(x, existing_data["country"], scorer=fuzz.partial_ratio)[0]) |
| Successful Merge | Merge dataframes after correcting misspellings using fuzzy string matching. | data = pd.merge(existing_data, exported_data, on="country", how="left") |
Final thoughts
In this tutorial, you have learned:
- Edits and edit distance
- The Levenshtein edit distance and how it works
- How to do fuzzy string matching in Python with thefuzz library
- How to do fuzzy string matching with Pandas dataframes.
The examples presented here may be simple, but they are enough to illustrate how to handle various cases of what a computer thinks are mismatching strings. There are several applications of fuzzy matching in areas such as spell-checking and bioinformatics, where fuzzy logic is used to match DNA sequences.
Additional Resources
Fuzzy String Matching in Python FAQs
How does fuzzy string matching handle case sensitivity?
Fuzzy string matching is generally case-sensitive unless explicitly specified otherwise. You can convert strings to lowercase before matching to achieve case-insensitivity.
Can I use TheFuzz library with other data structures besides strings?
TheFuzz is primarily designed for string comparison. However, you can convert other data types to strings before applying fuzzy matching techniques.
How do I handle fuzzy matching with large datasets for performance optimization?
For large datasets, consider using indexing techniques or filtering to reduce the number of comparisons. Libraries like RapidFuzz, which is optimized for speed, can also be used.
What are some common applications of fuzzy string matching beyond search engines?
Fuzzy string matching is used in spell-checkers, data cleaning, bioinformatics for DNA sequence alignment, and record linkage in databases.
How does the Levenshtein distance differ from other edit distance algorithms?
Levenshtein distance considers insertions, deletions, and substitutions. Other algorithms like Hamming distance only consider substitutions and require strings of equal length.