Kurs
Explorative Datenanalyse in R
4 Std.
115.1K
Bei der Interpretation von Daten kann die Wahl des richtigen Maßes für die zentrale Tendenz über den Erfolg oder Misserfolg deiner Analyse entscheiden. Zu den gängigsten Kennzahlen gehören derMittelwert und der Median , zwei scheinbar einfache Konzepte, die bei der Dateninterpretation tiefgreifende Auswirkungen haben. Während der Mittelwert uns den arithmetischen Durchschnitt gibt, ist der Median der Mittelpunkt in einer sortierten Reihe von Werten, sodass die Hälfte der Beobachtungen auf jeder Seite liegt. Aber welches ist zuverlässiger? Die Antwort hängt oft davon ab, wie deine Daten verteilt sind, ob es Ausreißer gibt und was du damit sagen willst.
In diesem Artikel werde ich die Unterschiede zwischen Mittelwert und Median, ihre Vor- und Nachteile sowie die richtige Wahl für verschiedene Szenarien erläutern. Ich werde auch schauen, wie schiefe Verteilungen und Ausreißer diese Kennzahlen beeinflussen, und praktische Beispiele und Grafiken zeigen, damit du diese grundlegenden Konzepte besser verstehst. Wir werden auch ein bisschen in fortgeschrittenere Ideen reinschnuppern.
Definitionen von Mittelwert und Median
Um die Unterschiede zwischen dem Mittelwert und dem Median richtig zu verstehen, schauen wir uns diese beiden Maße genauer an und zeigen ihre wichtigsten Eigenschaften auf.
Was meinst du damit?
Der Mittelwert kann als „Gleichgewichtspunkt“ (oder Schwerpunkt) der Daten angesehen werden. Es berücksichtigt alle Datenpunkte in einem Datensatz und gibt einen einzigen Wert aus, der den Durchschnitt darstellt. Genauer gesagt wird der t-, den er meint, berechnet, indem man alle Werte in einem Datensatz zusammenzählt und dann durch die Anzahl der Werte teilt.
Was ist der Median?
Der Median ist der Mittelwert, wenn die Daten sortiert sind. Im Gegensatz zum Mittelwert ist er robuster gegenüber Ausreißern und liefert so ein besseres Maß für die zentrale Tendenz bei schiefverteilten Daten.
Was ist der Modus?
Der Modus ist ein anderes Maß für die zentrale Tendenz und zeigt den Wert an, der in einem Datensatz am häufigsten vorkommt. Schauen wir uns mal ein Beispiel an:
3, 3, 6, 8, 9Hier ist der Modus 3 , weil er zweimal vorkommt, während alle anderen Werte nur einmal auftauchen.
Wie man den Mittelwert und den Median berechnet
Eine Definition zu lesen ist eine Sache, aber zu rechnen ist was anderes. In diesem Abschnitt werde ich die Schritte zur Berechnung der einzelnen Kennzahlen aufschlüsseln und ihre rechnerischen Unterschiede hervorheben.
Wie man den Mittelwert findet
Der Mittelwert ist der arithmetische Durchschnitt eines Datensatzes und wird so berechnet:
- Summiere die Werte: Zähl einfach alle Zahlen in deinem Datensatz zusammen.
- Durch die Gesamtzahl der Werte teilen: Nimm die Gesamtsumme und teil sie durch die Anzahl der Werte.
Hier ist der Prozess als allgemeine Gleichung dargestellt:
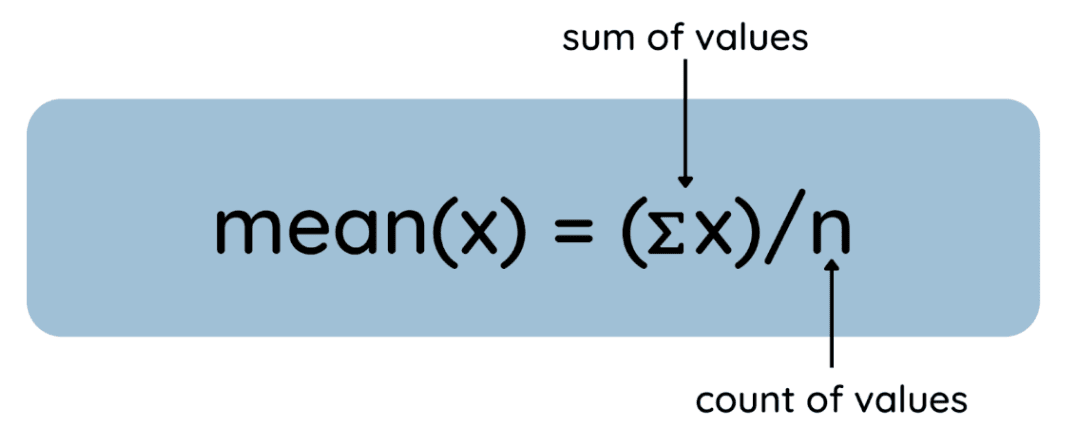
Wie man den Mittelwert findet. Bild vom Autor
Nimm zum Beispiel einen Datensatz mit Prüfungsergebnissen:
78, 85, 92, 88, 70- Schritt 1 (Summe): 78 + 85 + 92 + 88 + 70 = 413
- Schritt 2 (Teilen): 413 ÷ 5 = 82.6
Der Durchschnittswert ist 82,6.
Wie man den Median findet
Der Median ist der Mittelwert einer Reihe von Werten, wenn man sie in aufsteigender Reihenfolge sortiert. So findest du es:
- Sortiere die Daten: Ordne die Werte vom kleinsten zum größten Wert.
- Finde den mittleren Wert: Wenn der Datensatz eine ungerade Anzahl von Werten hat, ist der Median der Wert in der Mitte; wenn der Datensatz eine gerade Anzahl von Werten hat, ist der Median der Durchschnitt der beiden mittleren Werte.
Und hier sind diese Schritte als Gleichungen dargestellt:
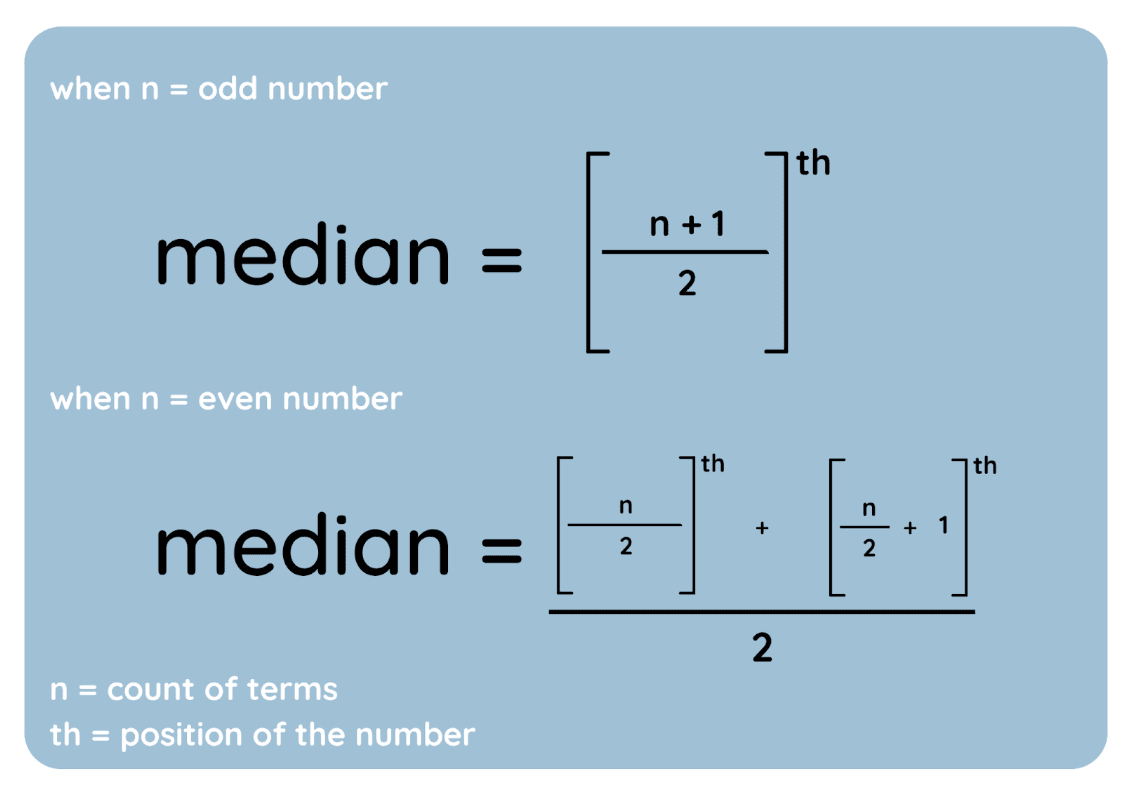
Medianformel. Bild vom Autor
Ich hab auch eine Grafik gemacht, um den Prozess zu zeigen.
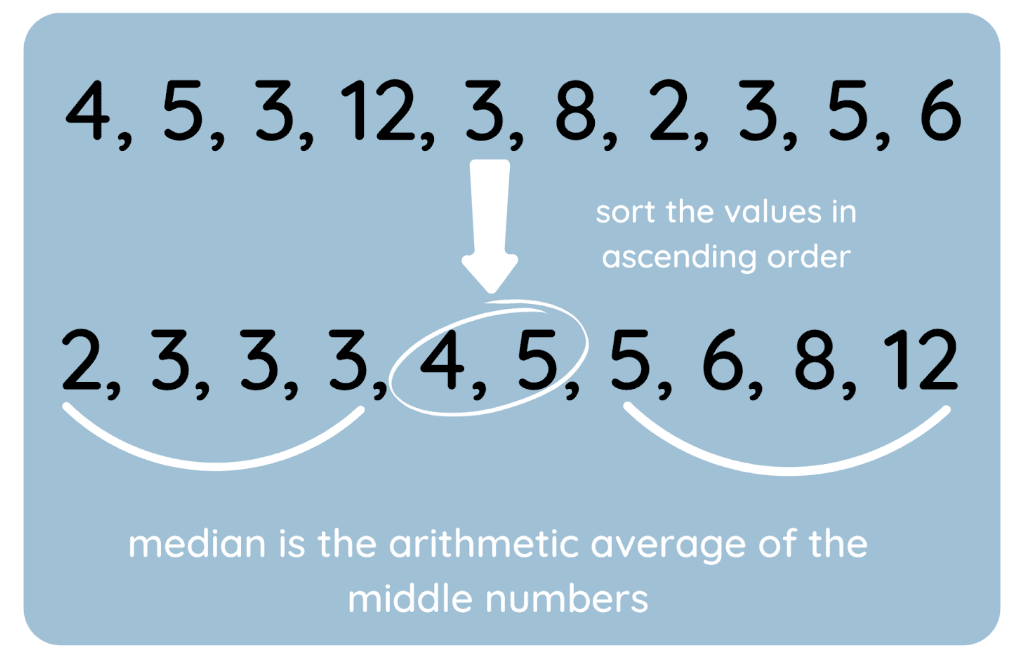
Wie man den Median findet. Bild vom Autor
Hier ist ein Beispiel für einen Datensatz mit einer ungeraden Anzahl von Werten:
70, 78, 85, 88, 92- Schritt 1 (Sortieren): Schon erledigt.
- Schritt 2 (mittlerer Wert): Der dritte Wert ist 85.
Der Median ist 85.
Hier ist noch ein Beispiel, aber mit einer geraden Anzahl von Werten:
70, 78, 85, 88- Schritt 1 (Sortieren): Schon erledigt.
- Schritt 2 (Durchschnitt der Mittelwerte): (78 + 85) ÷ 2 = 81,5
Der Median ist 81,5.
Warum der Unterschied wichtig ist: Ausreißer und Schiefe
Sowohl der Mittelwert als auch der Median zeigen, wo die Mitte eines Datensatzes liegt, aber sie verhalten sich ganz anders, wenn es Ausreißer und schiefe Verteilungen gibt. Es ist echt wichtig, diesen Unterschied zu verstehen, um Daten richtig zu interpretieren und falsche Schlussfolgerungen zu vermeiden.
Auswirkungen von Ausreißern
Ausreißer sind Werte, die deutlich höher oder niedriger sind als der Rest der Daten. Sie können den Mittelwert stark beeinflussen, haben aber kaum oder gar keinen Einfluss auf den Median.
Schauen wir uns mal einen Datensatz mit monatlichen Einkommen (in Tausend) an:
3, 3.5, 4, 4.5, 5, 6, 50Das durchschnittliche Einkommen hier ist 10,85k, was stark durch den Extremwert von 50.000.
Andererseits ist der Medianwert 4,5k, was meiner Meinung nach ein viel typischeres Bild vom Einkommen dieser Gruppe gibt.
Schiefe Verteilungen
Der Mittelwert und der Median unterscheiden sich auch in der Darstellung von Daten in schiefen Verteilungen (Datensätze, die nicht symmetrisch sind).
Zum BeispielBei rechtsschiefe Verteilungen (wie Einkommen oder Immobilienpreise) sind die meisten Werte am unteren Ende, und ein paar extreme Werte ziehen den Schwanz nach rechts.
- Durchschnitt: Verschiebungen zum Ende hin, was zu einem Wert führt, der über dem Median liegt.
- Median: Bleibt näher an den typischen Werten und spiegelt so besser den „typischen“ Fall wider.
Schau dir mal die Einkommen an:
30k, 35k, 40k, 45k, 50k, 100k, 200k- Durchschnitt: 71,4k (nach oben korrigiert um 100k und 200k).
- Median: 45.000 (näher an den meisten Einkommen).
Warum das wichtig ist
- Bei verzerrten Daten: Der Median ist oft repräsentativer für einen „typischen“ Datenpunkt, weil er nicht durch Extremwerte verzerrt wird.
- Bei symmetrischen Daten: Der Mittelwert und der Median sind fast gleich, also kann man beide als Maß für die zentrale Tendenz nehmen.
Was du daraus lernen solltest, ist, dass es wichtig ist, immer die Verteilung deiner Daten zu checken, bevor du dich entscheidest, ob du den Mittelwert oder den Median nimmst. Tools wie Histogramme und Boxplots können dabei helfen, Schiefe zu visualisieren und Ausreißer zu erkennen. Wir werden später darauf eingehen. Außerdem möchte ich sagen, dass die Untersuchung des Unterschieds zwischen Mittelwert und Median eine Möglichkeit ist, die Schiefe zu beurteilen.
Wann man den Mittelwert und wann den Median benutzt
Bei der Analyse von Daten hängt die Entscheidung, ob du den Mittelwert oder den Median verwenden solltest, von den Eigenschaften deines Datensatzes und den Erkenntnissen ab, die du gewinnen möchtest. Hier ist 'ne kurze Tabelle, die dir bei der Entscheidung hilft:
| Benutze den Mittelwert, wenn | Benutze den Median, wenn |
|---|---|
| Die Datenverteilung ist ungefähr normal (symmetrisch). | Die Daten sind ziemlich verzerrt (z. B. Einkommen, Immobilienwerte). |
| Ausreißer sind minimal oder für die Analyse nicht wichtig. | Es gibt Ausreißer, die die Ergebnisse verzerren könnten, wenn sie mit rein genommen werden. |
| Du brauchst eine Methode, die auf jeden einzelnen Datenpunkt eingeht, wie zum Beispiel bei der Vorhersagemodellierung oder beim Berechnen von Summen. | Du willst eher den „typischen“ Wert als den „mathematischen Mittelpunkt“ des Datensatzes zeigen. |
Hier ist ein praktischer Tipp, der dir echt helfen wird: Fang immer mit einer visuellen Analyse deiner Daten an (z. B. einem Histogramm oder Boxplot), um Symmetrie, Schiefe und das Vorhandensein von Ausreißern zu checken. Das hilft dir bei der Entscheidung, ob der Mittelwert oder der Median besser zu deinem Szenario passt.
Visualisierung von Mittelwert vs. Median
Visualisierungen sind echt nützliche Tools, um das Verhalten von Mittelwert und Median in verschiedenen Datensätzen zu verstehen. Sie können echt gut zeigen, wie diese Maßnahmen auf Ausreißer und schiefe Verteilungen reagieren, und helfen so, bessere datengestützte Entscheidungen zu treffen.
Beispiel für ein Balkendiagramm
Stell dir mal einen kleinen Datensatz mit Einkommen in Tausend vor:
30, 35, 40, 45, 50, 55, 1000Das folgende Balkendiagramm zeigt, wie ein einzelner Extremwert den Mittelwert stark beeinflussen kann, während der Median ziemlich stabil bleibt. In diesem Fall liegen die meisten Datenpunkte zwischen 30 und 55, aber der Ausreißer (1000) zieht den Mittelwert nach oben.
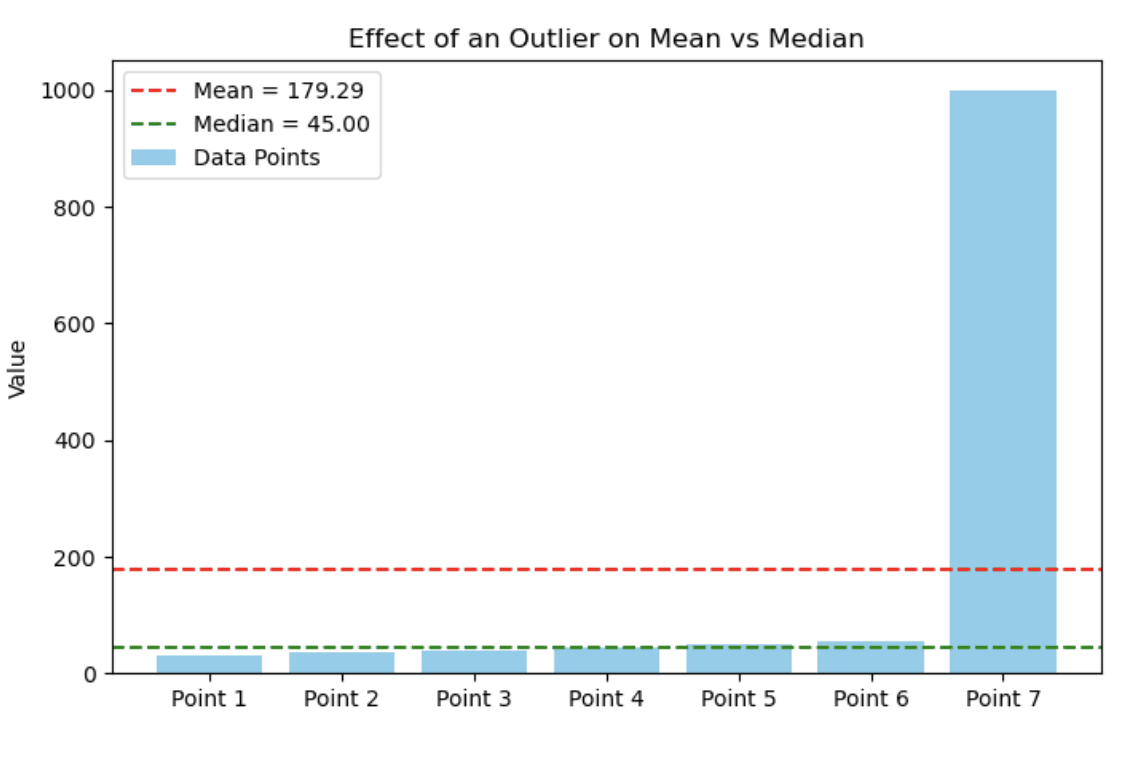
Balkendiagramm, das zeigt, wie ein Ausreißer den Mittelwert im Vergleich zum Median beeinflusst. Bild vom Autor
Histogramm-Beispiel
Bei einer rechtsverschobenen Verteilung (wie bei Einkommen oder Immobilienpreisen) wird der Mittelwert oft in Richtung der langen Reihe hoher Werte gezogen, während der Median näher am „typischen” Datenpunkt bleibt. Deshalb ist der Median in solchen Fällen ein besserer Maßstab für die zentrale Tendenz.
Das Histogramm unten zeigt eine simulierte Einkommensverteilung, bei der der Mittelwert (rote gestrichelte Linie) wegen der Schiefe deutlich größer ist als der Median (grüne gestrichelte Linie).
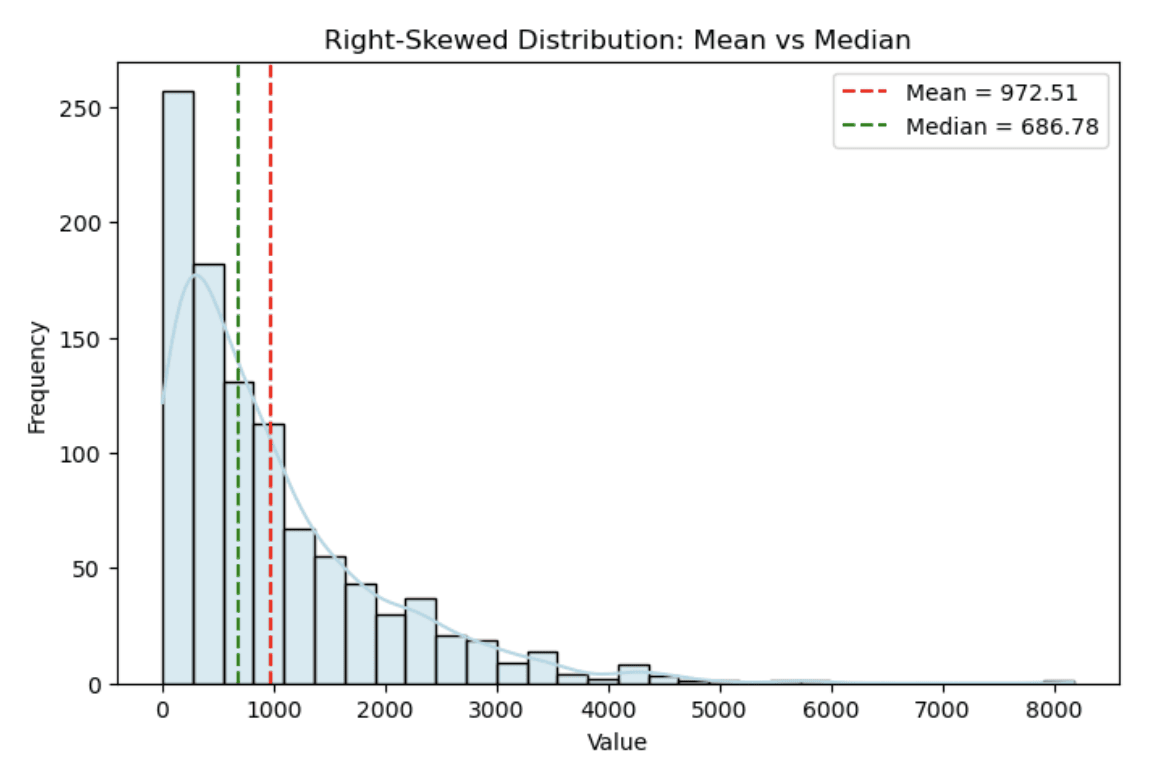
Histogramm, das eine rechtsschiefe Verteilung zeigt. Bild vom Autor
Du kannst sehen, wie die Rechtsverzerrung den Schwanz verlängert und so einen deutlichen Unterschied zwischen dem Mittelwert und dem Median macht.
Beispiel für ein Boxplot-Diagramm
Ein Boxplot ist super, um zu zeigen, wie Ausreißer den Median beeinflussen. Unten vergleichen wir zwei Gruppen: eine mit Ausreißern und eine ohne. Der Median (die vertikale Linie im Kasten) bleibt auch mit den Extremwerten stabil, aber der gesamte Bereich der Daten wird stark von den Ausreißern beeinflusst.
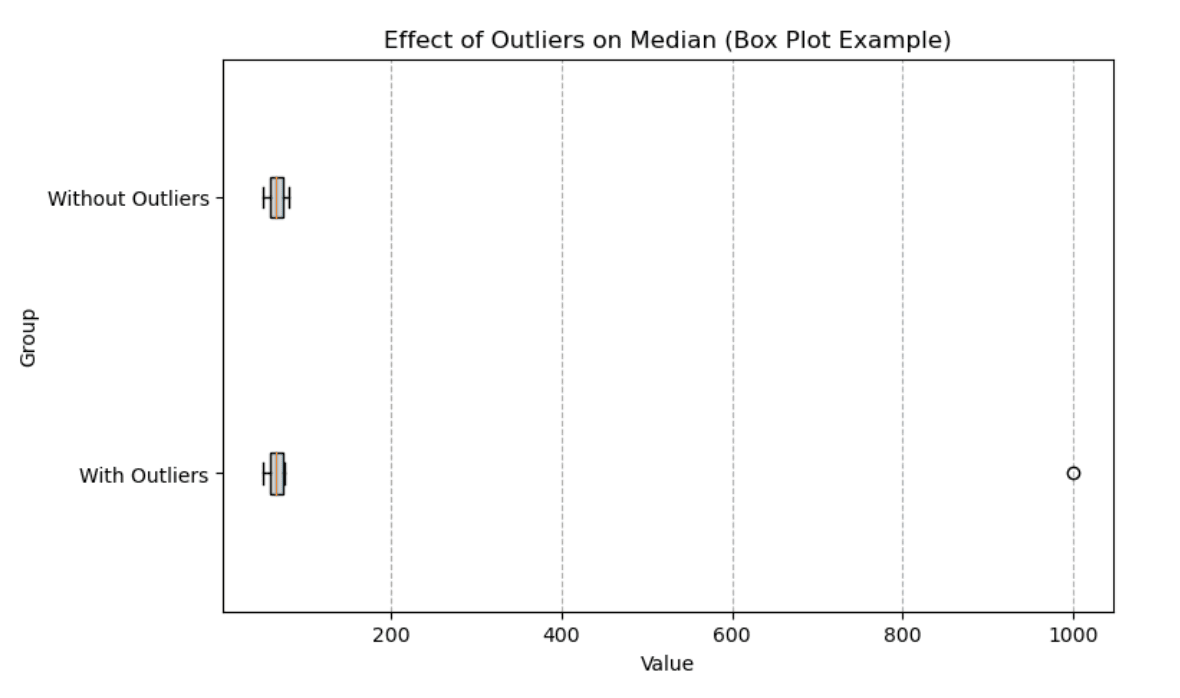
Boxplot, der zeigt, wie Ausreißer den Median beeinflussen. Bild vom Autor
Diese Visualisierungen zeigen, wie der Mittelwert und der Median auf verschiedene Datenmerkmale reagieren, und machen klar, wann man welche Messgröße verwenden sollte. Egal, ob du schiefe Daten oder Datensätze mit vielen Ausreißern analysierst oder Gruppen vergleichst – mit solchen visuellen Hilfsmitteln kannst du komplexe Zusammenhänge viel besser verstehen.
Fortgeschrittene Themen und moderne Best Practices
Schauen wir uns jetzt ein paar fortgeschrittenere Ideen an, falls du neugierig bist, mehr zu erfahren.
Mittelwert- und Medianimputation
Also, wenn du ein Datenwissenschaftler bist und Lücken in deinen Daten füllen musst, musst du vielleicht eine Imputationsmethode auswählen. Du fragst dich jetzt vielleicht, was der praktische Unterschied zwischen der Imputation des Mittelwerts und der Imputation des Medians ist?
Wie du dir vielleicht denken kannst, ersetzt die Mittelwertimputation fehlende Werte durch den Durchschnitt der verfügbaren Daten, der, wie wir schon gesagt haben, durch Extremwerte verzerrt sein kann. Bei der Medianimputation werden fehlende Werte durch den Mittelwert des Datensatzes ersetzt.
Eine gute Faustregel ist, dir die Verteilung deiner Daten anzuschauen. Wenn deine Datenverteilung durch viele fehlende Werte verzerrt war und du die Mittelwertimputation verwendet hast, dann hast du möglicherweise die Verteilung deiner Daten verändert!
BAber denk auch daran, dass die Imputation einzelner Werte (Mittelwert oder Median) die Varianz verringern und die Beziehungen zwischen Variablen abschwächen kann. Wenn es viele fehlende Werte gibt, solltest du eine multiple Imputation oder eine modellbasierte Imputation in Betracht ziehen, um Unsicherheit und Struktur besser zu bewahren.
Parametrische und rangbasierte Methoden
Bei vielen parametrischen Methoden sind der Mittelwert (und die Varianz) die wichtigsten Parameter. Ein einfaches lineares Regressionsmodell geht zum Beispiel davon aus, dass Fehler normalerweise um einen Mittelwert verteilt sind. Wenn deine Daten die Normalitätsannahme erfüllen, ist der Stichprobenmittelwert ein natürlicher Schätzer und passt gut in parametrische Rahmenbedingungen.
Heutzutage wird der Median oft in robusten und nichtparametrischen Umgebungen benutzt und ist eine gängige Wahl, wenn Daten schief verteilt sind oder Ausreißer enthalten. Viele Tests, wie der Mann-Whitney-Test, basieren auf Rangfolgen und vergleichen eher Verteilungen (oft als Lageverschiebung unter Annahmen interpretiert) als Mittelwerte, und sie testen nicht immer den Unterschied zwischen Medianwerten.
Das heißt, den Unterschied zwischen Mittelwert und Median zu verstehen, ist nicht nur wichtig, um Daten richtig zu beschreiben, sondern auch für die Hypothesenprüfung.
Bootstrap-Stabilität für Mittelwert und Median
Bei der Entscheidung, ob man den Mittelwert oder den Median nimmt, ist es wichtig zu wissen, wie stabil die Statistiken für einen bestimmten Datensatz sind. Bootstrapping ist eine Möglichkeit, mit der wir die Stichprobenverteilung sowohl des Mittelwerts als auch des Medians empirisch schätzen können, indem wir wiederholt (mit Zurücklegen) aus den Originaldaten neu stichproben.
Du könntest die Unterschiede in der mittleren und medianen Stabilität einfach mal empirisch zeigen. Du könntest ein paar Ausreißer in einen Datensatz einfügen und dann das Bootstrap-Verfahren nochmal laufen lassen. So kannst du zeigen, wie sich die Verteilung des Mittelwerts viel stärker verändert als die des Medians. Außerdem kann Bootstrapping das Ganze konkretisieren, indem es zeigt, wie groß oder klein deine Konfidenzintervalle in realistischen Szenarien sein könnten. Lies unser Tutorial über die Anwendung von Bootstrap-Methoden, um mehr zu erfahren.
Quadratischer Verlust und absoluter Verlust
Lass mich jetzt eine andere, aber genauso zutreffende Definition geben: Der Mittelwert ist der Wert, der die Summe der quadrierten Abweichungen von den Daten am kleinsten macht, während der Median der Wert ist, der die Summe der absoluten Abweichungen am kleinsten macht.
Schau dir mal diese Gleichung an:
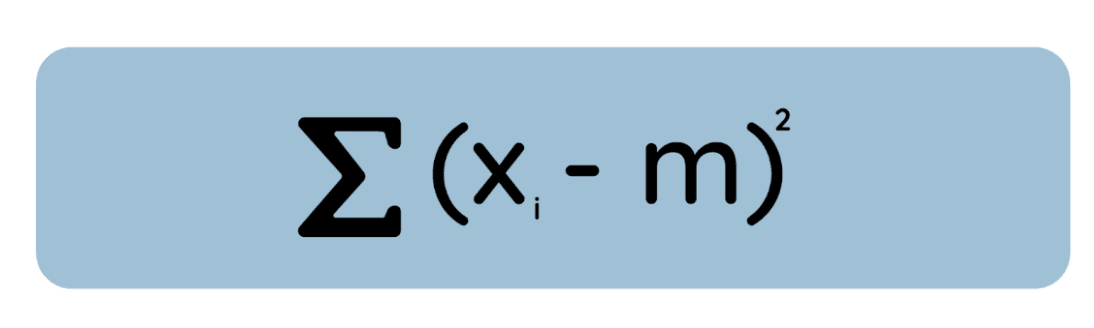
Wenn du die Ableitung dieser Gleichung nach , sie auf Null setzt und auflöst, wirst du feststellen, dass der Minimalwert einfach dem arithmetischen Mittel entspricht. Das ist wichtig, weil wir bei vielen statistischen Methoden, wie der OLS-Regression, die quadratischen Fehler aus mathematischen Gründen minimieren und um den Annahmen normalverteilter Fehler zu entsprechen.
Jetzt mal eine andere Idee: Anstatt jede Abweichung zu quadrieren, messen wir denabsoluten Fehler„ “ zwischen m und jedem Datenpunkt:
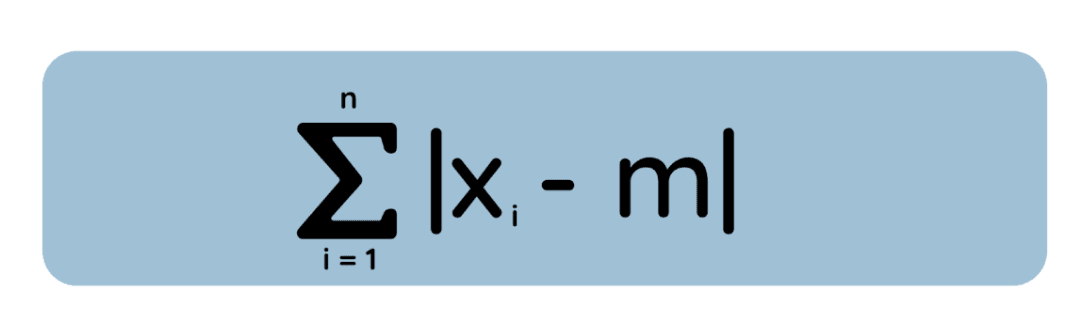
Hier wollen wir m finden, das diese gesamte absolute Abweichung minimiert. Es stellt sich heraus (durch Analyse der Ableitung des absoluten Verlusts oder durch ein geometrisches Argument), dass die Lösung derMedianwert des Datensatzes ist. (Und wenn du eine gerade Anzahl von Beobachtungen hast, minimiert jeder Wert zwischen den beiden Mittelpunkten die gesamte absolute Abweichung – der Minimierer ist also möglicherweise nicht eindeutig.)
Einfach gesagt, wenn links vom Median liegt, gibt es mehr Datenpunkte rechts davon, die ihn nach rechts ziehen. Nur in der Mitte gleicht sich der Sog von links und rechts aus, wodurch die absolute Gesamtentfernung minimiert wird.
Mittelwert und Median bei Maßstab
Zum Schluss möchte ich noch sagen, dass der Mittelwert in großem Maßstab rechnerisch einfacher ist. Das heißt, du kannst es nach und nach berechnen, während die Daten reinkommen, ohne sie sortieren zu müssen.
Der Median wird in der Praxis oft durch Sortieren berechnet, was bei großen Datenmengen ziemlich teuer sein kann. Aber der Median braucht nicht unbedingt eine komplette Sortierung (es gibt Auswahlalgorithmen), und bei sehr großen oder Streaming-Datensätzen werden oft Algorithmen für ungefähre Quantilsskizzen benutzt, um den Median effizient zu schätzen. Unser Kurs „Konzepte der Informatik“ ist super, um mehr über diese Sachen zu erfahren.
Nächste Schritte
Wie du gesehen hast, ist der Mittelwert der arithmetische Durchschnitt eines Datensatzes, was ihn empfindlich gegenüber Extremwerten macht, während der Median den Mittelwert in einem geordneten Datensatz darstellt. Die richtige Wahl kann echt einen Unterschied machen, aber in echten Analysen ist es oft am besten, sowohl den Mittelwert als auch den Median zusammen mit anderen Statistiken wie Modus, Standardabweichung und Perzentilen anzugeben. Das ist die beste Methode, weil sie ein umfassendes Bild liefert.
Wenn du dich mehr mit statistischen Konzepten beschäftigen willst, gibt es ein paar Bereiche, die du dir genauer anschauen solltest. Fang damit an, dich über fortgeschrittenere Varianten des Mittelwerts zu informieren, wie den getrimmten Mittelwert, den geometrischen Mittelwert und den gewichteten Mittelwert, die alle ihren eigenen Zweck haben. Ich würde auch unseren technologieunabhängigen Kurs „Einführung in die Statistik “ machen.
Um dann wirklich ein Experte zu werden, solltest du dir ein Tool aussuchen und es richtig gut beherrschen. Unser Kurs „Einführung in die Statistik mit R“ und der Lernpfad „Statistiker mit R“ sind super informative Einstiegspunkte, wenn du R nutzen willst, eine beliebte Sprache für Datenwissenschaft und Statistik. Wenn du lieber mit Tabellenkalkulationen und einer Programmiersprache wie Python arbeitest, bieten dir unsere Kurse „Einführung in die Statistik in Google Sheets“ und „Einführung in die Statistik in Python “ einen praxisorientierten Ansatz für die statistische Analyse mithilfe von Formeln und leistungsstarken Bibliotheken.
