Kurs
Supervised Learning in R: Regression
4 Std.
43.8K
Stell dir vor, du versuchst, die Wohnungspreise anhand der Quadratmeterzahl vorherzusagen. Du hast Datenpunkte aus den letzten Verkäufen, aber sie bilden kein perfektes Muster. Manche Häuser verkaufen sich teurer als erwartet, andere wiederum billiger. Wie findest du die beste Trendlinie, die die allgemeine Beziehung zwischen Größe und Preis widerspiegelt, ohne dass einzelne Häuser deine Vorhersage verfälschen?
Die Methode der kleinsten Quadrate könnte genau die Lösung sein, die du brauchst. In diesem Artikel werden wir die Kernkonzepte der Methode der kleinsten Quadrate, ihre Varianten und Anwendungen untersuchen. Am Ende wirst du ein solides Verständnis davon haben, wie man diese Methode anwendet und sie auf reale Probleme anwendet.
Was ist die Methode der kleinsten Quadrate?
Die Methode der kleinsten Quadrate ist ein statistisches Verfahren, das verwendet wird, um die am besten passende Linie oder Kurve für eine Reihe von Datenpunkten zu bestimmen. Es funktioniert, indem es die quadratischen Unterschiede zwischen den beobachteten und den vorhergesagten Werten in einem Datensatz minimiert. Die Differenz zwischen den tatsächlichen Datenpunkten und den vom Modell vorhergesagten Werten wird als Residuen bezeichnet. Das Ziel ist es, ein Modell zu finden, das die Summe dieser quadrierten Residuen minimiert und so zu möglichst genauen Vorhersagen führt.
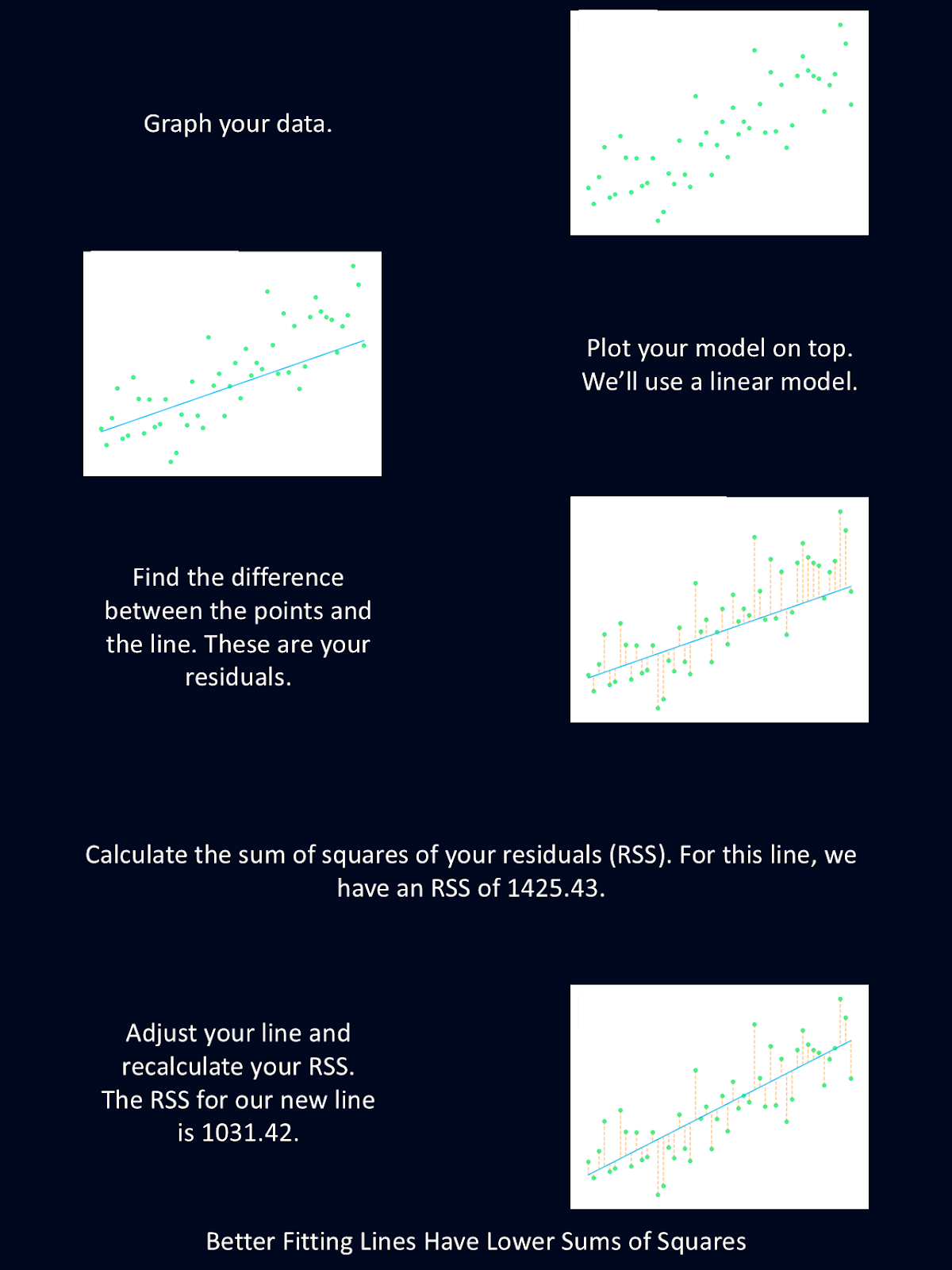
Das Diagramm oben erklärt kurz die Schritte der Methode der kleinsten Quadrate.
Diese Methode wurde 1895 von dem 18-jährigen Carl Friedrich Gauß entwickelt (du kennst seinen Namen vielleicht von der Gaußschen Verteilung). Adrien-Marie Legendre formalisierte die Technik später im Jahr 1805 und war der erste, der die Methode der kleinsten Quadrate zur Rekonstruktion der Bahn eines Asteroiden einsetzte.
So funktioniert die Methode der kleinsten Quadrate
Die Methode der kleinsten Quadrate findet die Linie, die am besten zu einer Reihe von Punkten passt, indem sie die Summe der quadratischen Differenzen zwischen den beobachteten Werten und den vorhergesagten Werten minimiert. Dies wird verwendet, um die Modellparameter mit der bestmöglichen Anpassung zu finden.
Versuchen wir das mal mit einem extrem kleinen Datensatz: nur 10 Punkte. Zuerst müssen wir ein Modell auswählen, das zu unseren Daten passt. Für dieses einfache Beispiel wählen wir eine einfache lineare Regression, d.h. wir führen eine Regression durch, bei der wir nur genau eine unabhängige und eine abhängige Variable haben.
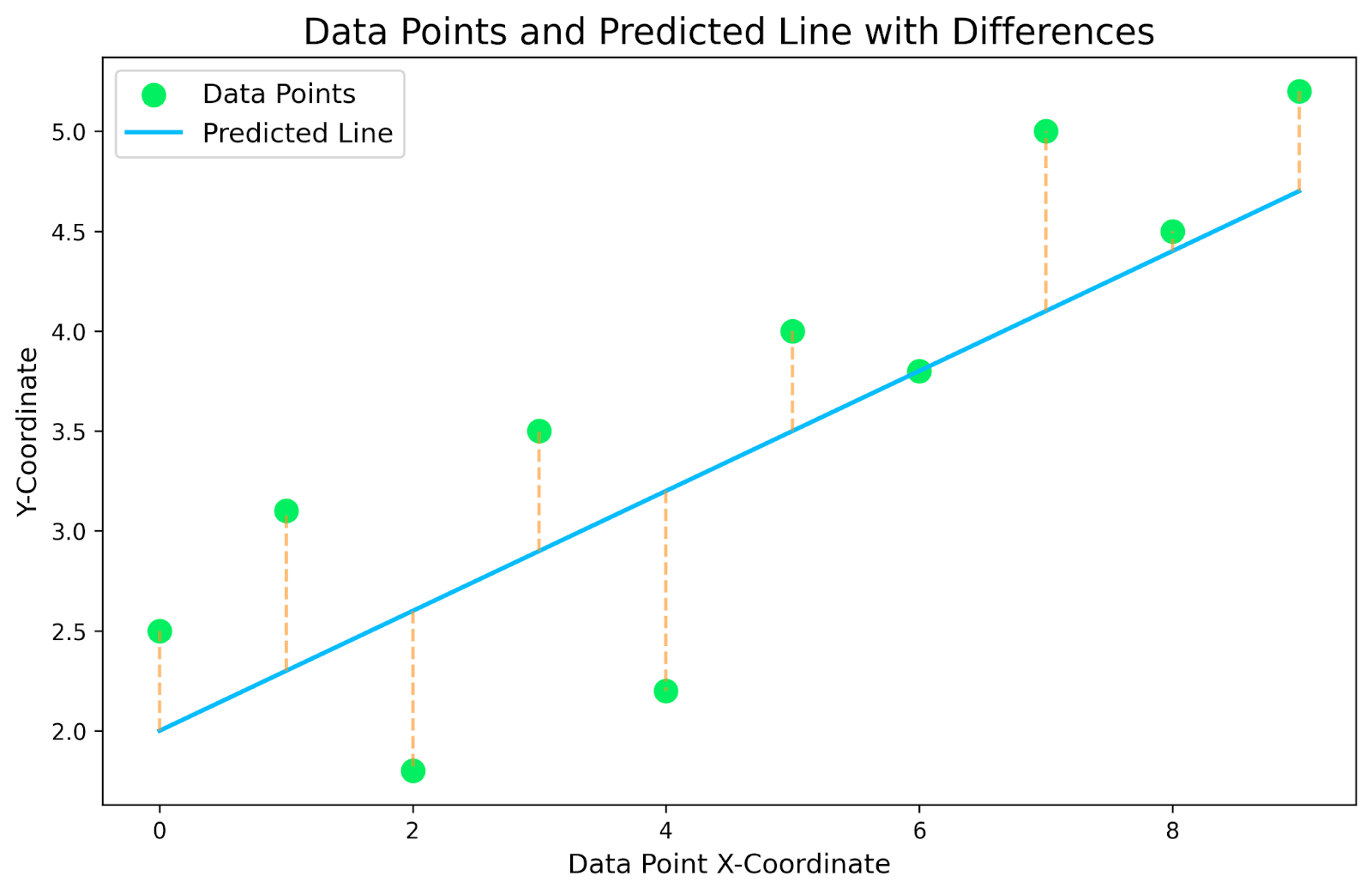
Die obige Grafik ist eine Darstellung unseres kleinen Datensatzes mit einer linearen Regression darüber. Die gelb gepunkteten Linien, die die Datenpunkte mit der vorhergesagten Linie verbinden, sind die Residuen. Das Ziel ist es, das lineare Regressionsmodell zu finden, das diese gelb gestrichelten Restlinien minimiert.
Für jeden Datenpunkt in unserem Datensatz müssen wir die Differenz der y-Koordinaten zwischen dem Datenpunkt und der Linie finden. Das werden unsere Residuen sein. Dann quadrieren wir jeden Rest, um alle negativen Zahlen von zu entfernen, und bilden die Gesamtsumme. So bekommen wir ein Gefühl dafür, wie gut unsere Linie zu unseren Daten passt. In der folgenden Tabelle findest du die Aufschlüsselung für unsere spezielle Grafik.
|
X-Koordinate |
Beobachtete Y-Koordinate (Datenpunkt) |
Vorausgesagte Y-Koordinate (Linie) |
Residuen (Beobachtet - Vorausgesagt) |
Quadratische Residuen |
|
0 |
2.5 |
2.0 |
0.5 |
0.25 |
|
1 |
3.1 |
2.3 |
0.8 |
0.64 |
|
2 |
1.8 |
2.6 |
-0.8 |
0.64 |
|
3 |
3.5 |
2.9 |
0.6 |
0.36 |
|
4 |
2.2 |
3.2 |
-1.0 |
1.0 |
|
5 |
4.0 |
3.5 |
0.5 |
0.25 |
|
6 |
3.8 |
3.8 |
0.0 |
0.0 |
|
7 |
5.0 |
4.1 |
0.9 |
0.81 |
|
8 |
4.5 |
4.4 |
0.1 |
0.01 |
|
9 |
5.2 |
4.7 |
0.5 |
0.25 |
|
Summe der quadrierten Residuen |
4.21 |
Jetzt, wo wir wissen, wie gut die Linie zu unseren Daten passt, können wir die Parameter der Linie, entweder die Steigung oder den Achsenabschnitt, ändern und unsere Berechnungen wiederholen. Die Linie mit der niedrigsten Summe der quadrierten Residuen ist die Linie, die am besten zu unseren Daten passt. Daher wird uns diese Linie die besten Vorhersagen liefern.
Die Methode der kleinsten Quadrate verwenden, um die beste Linie zu finden
Im obigen Beispiel haben wir nicht die am besten passende Linie gefunden. Stattdessen haben wir nur berechnet, wie gut diese Linie zu den Daten passt. Jetzt könnten wir eine Reihe von möglichen Linien durchgehen und dieselbe Berechnung durchführen, um die zu finden, die am besten passt. Oder wir könnten ein bisschen Algebra benutzen, um die beste Linie schneller zu finden. Lass uns das mal versuchen.
Wir beginnen mit der Gleichung für die lineare Regression: y=mx+b, wobei b der y-Achsenabschnitt und m die Steigung ist. Jetzt lass uns ein paar Daten zusammenstellen.
|
X-Koordinate |
Y-Koordinate |
|
0 |
2.5 |
|
1 |
3.1 |
|
2 |
1.8 |
|
3 |
3.5 |
|
4 |
2.2 |
|
5 |
4.0 |
|
6 |
3.8 |
|
7 |
5.0 |
|
8 |
4.5 |
|
9 |
5.2 |
Zuerst müssen wir den Mittelwert der X- und Y-Werte berechnen. Diese dienen als unsere voraussichtlichen Werte:
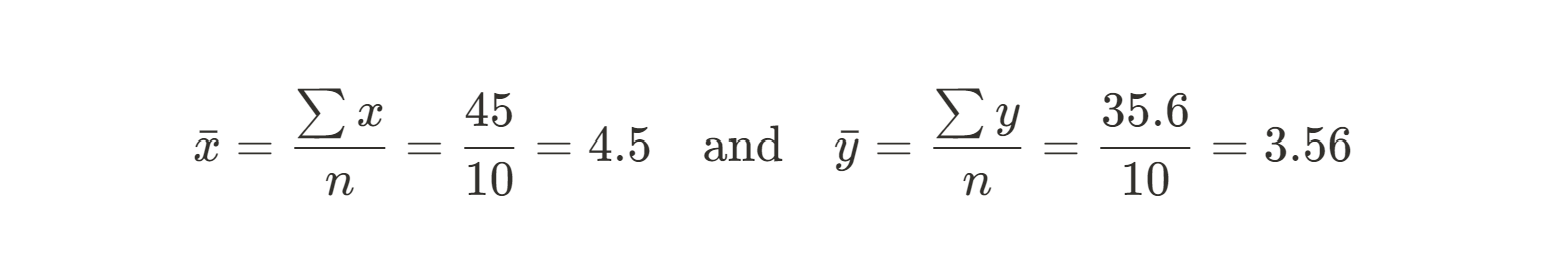
Als Nächstes können wir die Summe der Quadrate unserer Residuen zwischen jedem Datenpunkt und unserem vorhergesagten Wert (dem Mittelwert) verwenden, um die Steigung zu ermitteln. Hier ist die Gleichung, die wir verwenden werden:
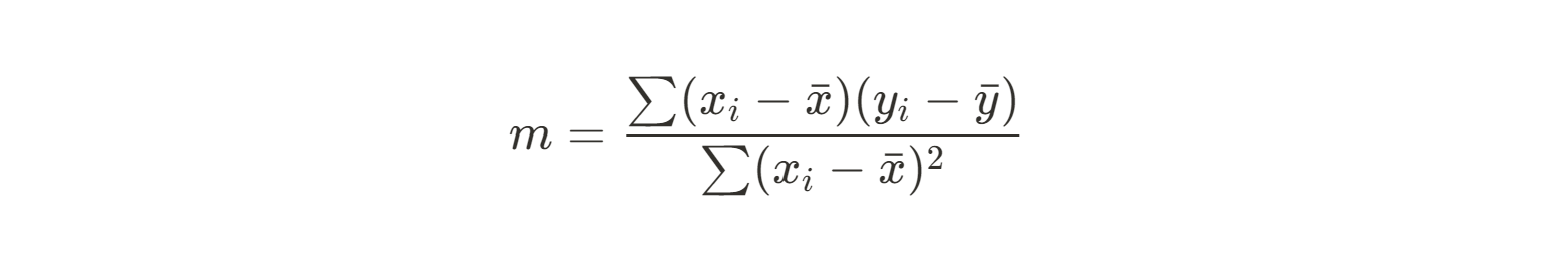
Da diese Gleichung ziemlich umständlich ist, berechnen wir Zählerund Nenner getrennt. Beginnen wir mit dem Zähler:
|
xi |
yi |
xi - xMittelwert |
yi - yMittelwert |
(xi - xMittel)(yi -yMittel) |
|
0 |
2.5 |
-4.5 |
-1.06 |
4.77 |
|
1 |
3.1 |
-3.5 |
-0.46 |
1.61 |
|
2 |
1.8 |
-2.5 |
-1.76 |
4.40 |
|
3 |
3.5 |
-1.5 |
-0.06 |
0.09 |
|
4 |
2.2 |
-0.5 |
-1.36 |
0.68 |
|
5 |
4.0 |
0.5 |
0.44 |
0.22 |
|
6 |
3.8 |
1.5 |
0.24 |
0.36 |
|
7 |
5.0 |
2.5 |
1.44 |
3.60 |
|
8 |
4.5 |
3.5 |
0.94 |
3.29 |
|
9 |
5.2 |
4.5 |
1.64 |
7.38 |
|
Summe von (xi - xMittelwert)(yi - yMittelwert) |
26.4 |
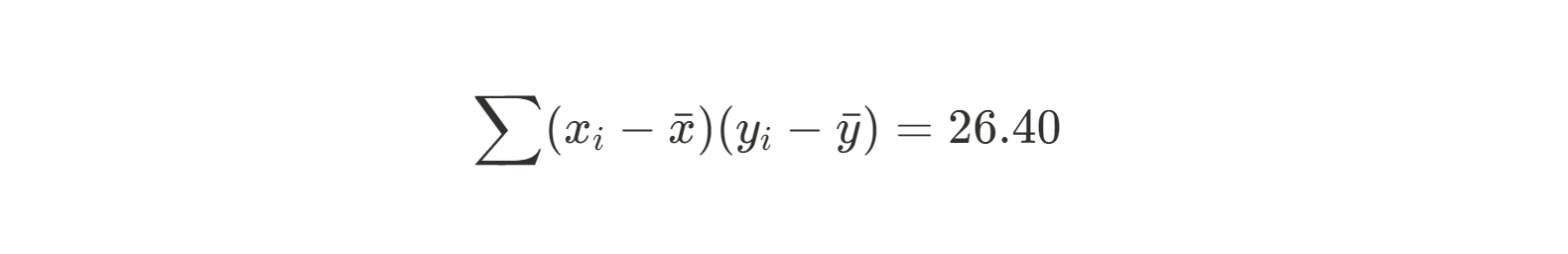
Jetzt machen wir das Gleiche für den Nenner:
|
xi |
xi - xMittelwert |
(xi - xMittel)2 |
|
0 |
-4.5 |
20.25 |
|
1 |
-3.5 |
12.25 |
|
2 |
-2.5 |
6.25 |
|
3 |
-1.5 |
2.25 |
|
4 |
-0.5 |
0.25 |
|
5 |
0.5 |
0.25 |
|
6 |
1.5 |
2.25 |
|
7 |
2.5 |
6.25 |
|
8 |
3.5 |
12.25 |
|
9 |
4.5 |
20.25 |
|
Summe aus (xi - xMittel)2 |
82.50 |
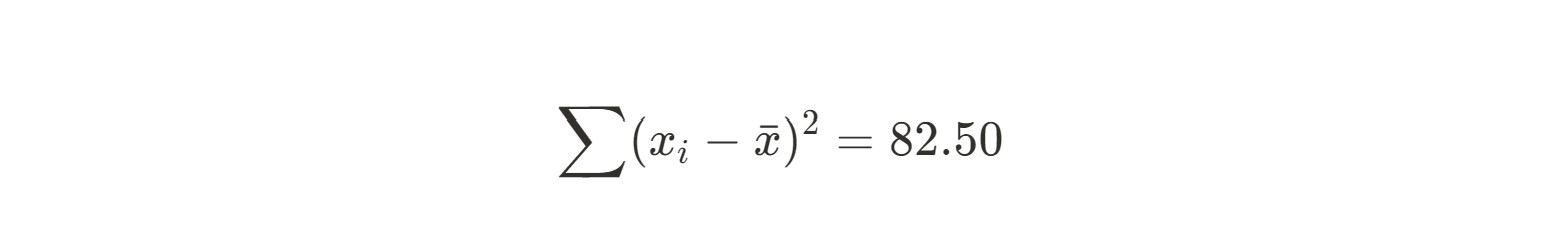
Jetzt können wir die Steigung für unsere beste Anpassungslinie berechnen.
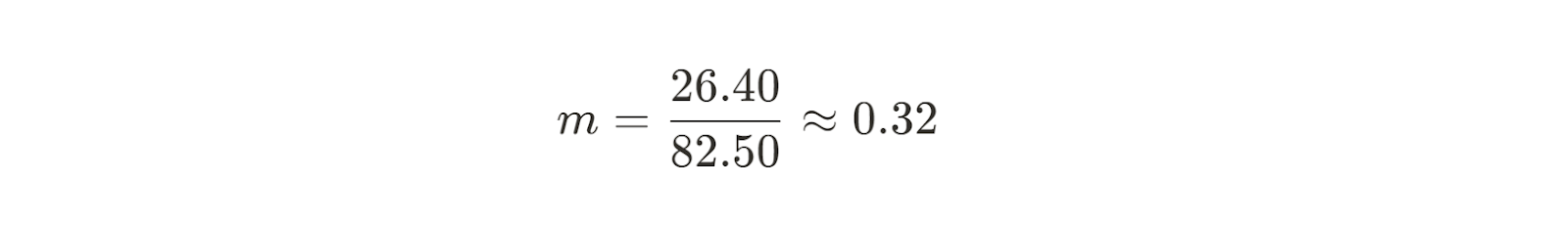
Jetzt kennen wir also die Steigung der Linie, die am besten zu unseren Daten passt. Als Nächstes müssen wir den y-Achsenabschnitt finden. Die Formel für den Achsenabschnitt b ist mit ein wenig algebraischer Umrechnung leicht zu finden:
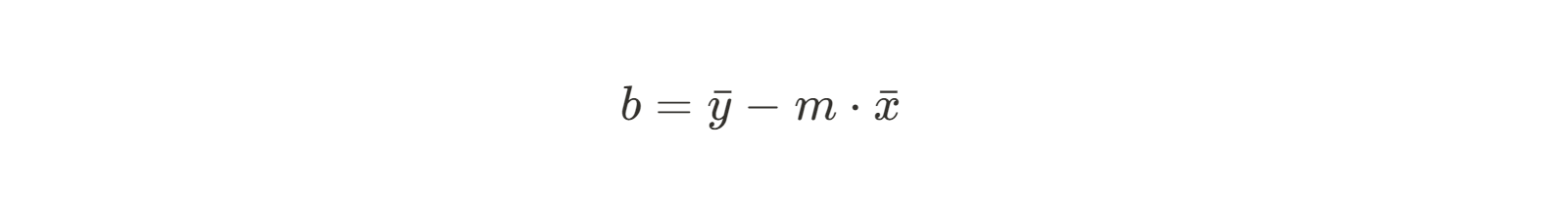
Da wir die Steigung bereits kennen, können wir einfach unsere Mittelwerte x und y einsetzen und b lösen.
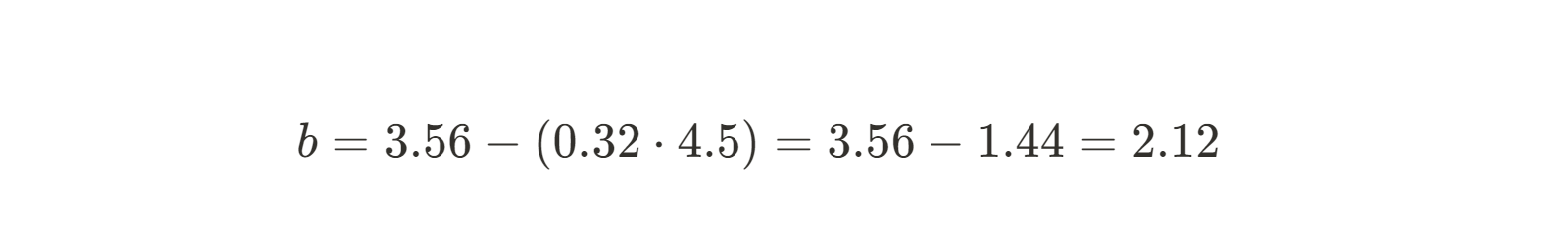
Da wir nun sowohl m als auch b kennen, können wir die Gleichung der besten Anpassungslinie aufstellen:
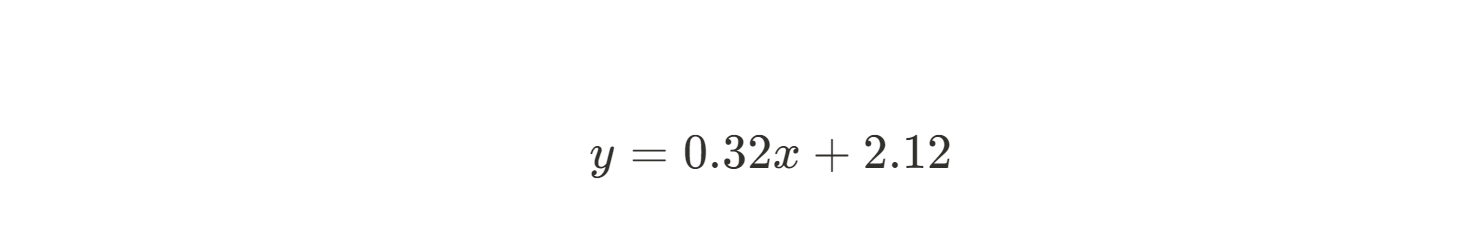
Mit der Methode der kleinsten Quadrate konnten wir schnell und einfach die beste lineare Regressionslinie ableiten, sogar per Hand! Je mehr Daten du hast, desto schwieriger wird es natürlich, dies von Hand zu tun. Glücklicherweise ist diese Methode sehr einfach in Python oder R zu implementieren, denn die Mathematik ist ziemlich unkompliziert. Ausführliche Erklärungen dazu findest du in Essentials of Linear Regression in Python und How to Do Linear Regression in R.
Mathematische Grundlagen der Methode der kleinsten Quadrate
Oben haben wir ein Beispiel mit einer einfachen linearen Regression verwendet und die Steigung und den Achsenabschnitt mit Hilfe schöner Gleichungen in geschlossener Form ermittelt und die abhängige Variable als Funktion der unabhängigen Variable modelliert : y=mx+b.
Die Gleichungen, die ich oben gezeigt habe, funktionieren jedoch nur, wenn du eine unabhängige Variable hast. Eine andere Möglichkeit, die Koeffizienten für eine Regression zu finden, ist die so genannte Normalgleichung, die eine matrixbasierte Lösung für das Problem der kleinsten Quadrate bietet. Die Normalgleichung bezieht sich auf die Matrixgleichung, die sich aus der Minimierung der Summe der quadrierten Residuen nach der Methode der kleinsten Quadrate ergibt. Geometrisch und in der Sprache der linearen Algebra kann die Lösung der kleinsten Quadrate als orthogonale Projektion des Vektors der beobachteten Daten auf den Spaltenraum der Modellmatrix dargestellt werden. Vereinfacht ausgedrückt bedeutet das, dass die Fehler so minimiert werden, dass die vorhergesagten Werte so nah wie möglich an den beobachteten Daten liegen, wenn man die Beschränkungen des Modells berücksichtigt.
In Fällen, in denen die Matrix nicht invertierbar ist (was bedeutet, dass das Gleichungssystem keine eindeutige Lösung hat), bietet die Moore-Penrose-Pseudoinverse eine Möglichkeit, eine Lösung der kleinsten Quadrate zu berechnen. Das gibt uns die Flexibilität, mit Situationen umzugehen, in denen das System unterbestimmt (das heißt, es gibt mehr Unbekannte als Gleichungen) oder überbestimmt (das heißt, es gibt mehr Gleichungen als Unbekannte) ist.
Wenn du eine Auffrischung der Matrixalgebra brauchst, empfehle ich dir den Kurs Lineare Algebra für Data Science in R.
Arten von Methoden der kleinsten Quadrate
Bisher haben wir nur über die Anwendung der Methode der kleinsten Quadrate mit einem gewöhnlichen Kleinstquadratschätzer gesprochen. Es ist jedoch ein vielseitiges Werkzeug, das an viele Szenarien angepasst werden kann, je nach der Art des Problems, das du angehen willst. Im Folgenden werden einige Arten von Methoden der kleinsten Quadrate vorgestellt, was sie einzigartig macht und wie sie in der Praxis eingesetzt werden.
Lineare kleinste Quadrate
Bis zu diesem Punkt solltest du mit der linearen kleinsten Quadrate (auch gewöhnliche kleinste Quadrategenannt) ziemlich vertraut sein. Sie wird bei Modellen mit linearen Koeffizienten verwendet, wie zum Beispiel bei der einfachen oder multiplen linearen Regression. Das Ziel ist es, die Linie (oder Hyperebene, im Fall von multiplen linearen Regressionen) zu finden, die die Summe der quadrierten Residuen minimiert.
Bei dieser Art der kleinsten Quadrate wird davon ausgegangen, dass die Residuen eine konstante Varianz haben und es keine signifikanten Ausreißer in den Daten gibt. Sie kann auf die meisten Dinge angewendet werden, die eine lineare Beziehung haben. Du könntest dies zum Beispiel für Beziehungen zwischen Trächtigkeitsdauer und Geburtsgewicht oder zwischen Werbeausgaben und Umsatz nutzen. Das ist die Art der kleinsten Quadrate, die ich am häufigsten verwende und über die ich andere am häufigsten sprechen höre.
Gewichtete kleinste Quadrate
Die gewichtete kleinste Quadratzahl ist eine Erweiterung dieser Methode, die funktioniert, wenn die Varianz der Residuen nicht konstant ist. Durch die Zuweisung von Gewichten für jeden Datenpunkt verleiht die gewichtete kleinste Quadratzahl den Beobachtungen mit geringerer Varianz mehr Bedeutung. Die Gleichung dafür ist ähnlich wie die vorherige Summe der Quadrate, aber mit einem Gewicht (wi) auf jedes Residuum angewandt:
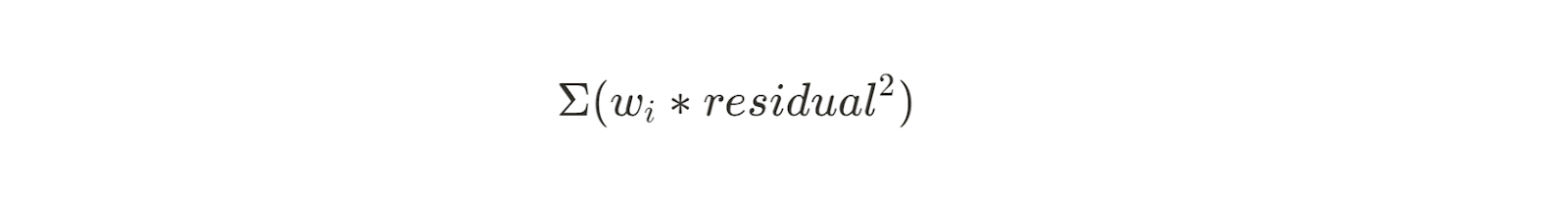
Diese Methode ist nützlich für Datensätze, bei denen der Messfehler zwischen den Beobachtungen variiert, zum Beispiel bei der Kalibrierung von Sensoren. Die Gewichte sind in der Regel der Kehrwert der Varianz für jede Beobachtung.
Robuste kleinste Quadrate
Die robuste kleinste Quadratzahl wurde entwickelt, um Datensätze mit Ausreißern zu behandeln, die die Ergebnisse der gewöhnlichen kleinsten Quadratzahl unverhältnismäßig stark beeinflussen können. Es verwendet iterative Neugewichtungstechniken, um die Auswirkungen von Ausreißern zu reduzieren.
Bei der robusten kleinsten Quadratzahl kannst du Methoden wie die kleinsten absoluten Residuen (LAR) oder bisquare Gewichte verwenden, um die Gewichte iterativ anzupassen und den Einfluss von Ausreißern zu verringern.
Ein Beispiel dafür ist die Finanzmodellierung, bei der du extreme Marktzusammenbrüche berücksichtigen willst. Wenn du einen Datensatz hast, bei dem du die Ausreißer nicht entfernen, aber dennoch berücksichtigen willst, ist die robuste kleinste Quadratzahl vielleicht der richtige Weg für dich.
Nichtlineare kleinste Quadrate
Die Methode der kleinsten Quadrate ist nicht nur für lineare Regressionen geeignet. Eine nichtlineare kleinste Quadrate wird verwendet, wenn das Modell, das du anwendest, in seinen Koeffizienten nichtlinear ist. Dies ist komplizierter als die lineare Kleinstquadrate und kann iterative Optimierungsverfahren (wie Gauss-Newton oder Levenberg-Marquardt) erfordern, um die beste Anpassung zu finden.
Bei nichtlinearen kleinsten Quadraten muss man vorsichtig sein. Die Berechnung kann empfindlich auf anfängliche Parameterschätzungen sowie auf Konvergenzprobleme reagieren. Du könntest zum Beispiel das exponentielle Wachstum von Viren in einem Körper während einer Infektion modellieren oder chemische Reaktionsraten im Labor modellieren.
Kleinste Quadrate insgesamt
Bis jetzt haben wir hauptsächlich über Fälle gesprochen, in denen nur die abhängige Variable Fehler aufweist. Und wir haben die vertikalen Abstände zwischen unserem Modell und unseren Daten minimiert. Aber was ist, wenn du auch bei deinen unabhängigen Messungen Fehler hast?
Die kleinste Quadratzahl ist nützlich, wenn sowohl die unabhängigen als auch die abhängigen Variablen Messfehler aufweisen. Bei dieser Methode werden Fehler in allen Variablen berücksichtigt. Dies kann besonders in Bereichen wie der Astronomie und der Geodäsie (dem Bereich, der die Form und das Schwerefeld der Erde misst) nützlich sein, wo Messfehler in allen Dimensionen auftreten, weil ein hohes Maß an Präzision erforderlich ist. Die Methode der kleinsten Quadrate wird oft in Verbindung mit der Singulärwertzerlegung verwendet.
Verallgemeinerte kleinste Quadrate
Die verallgemeinerte kleinste Quadrate ist eine Erweiterung der Methode der kleinsten Quadrate, die sich mit den Herausforderungen von korrelierten Residuen befasst. Bei der verallgemeinerten kleinsten Quadrate wandeln wir die Daten in eine Form um, in der gewöhnliche kleinste Quadrate angewendet werden können. Bei dieser Umwandlung wird die Kovarianzmatrix der Residuen verwendet, um ihre Korrelationsstruktur zu berücksichtigen, was eine genauere Parameterschätzung ermöglicht.
Dies kann besonders bei Zeitreihenanalysen nützlich sein, bei denen die Residuen eine Autokorrelation aufweisen können.
Anwendungen der Methode der kleinsten Quadrate
Die Methode der kleinsten Quadrate ist ein weit verbreitetes statistisches Verfahren, das in zahlreichen Bereichen Anwendung findet.
In der Statistik und den Datenwissenschaften wird die Methode der kleinsten Quadrate verwendet, um lineare und nichtlineare Regressionsmodelle zu erstellen, die Vorhersagen auf der Grundlage bekannter Eingaben machen. Sie ist auch nützlich bei der Analyse von Trends, insbesondere bei Zeitreihendaten.
In der Finanzwelt wird die Methode der kleinsten Quadrate bei der Analyse der Wertentwicklung von Aktien eingesetzt, um die Beziehung zwischen der Wertentwicklung einer Aktie und den Marktindizes zu bestimmen. Damit lässt sich zum Beispiel die Empfindlichkeit einer Aktie gegenüber Marktbewegungen berechnen. Sie hilft auch bei der Risikomodellierung, indem sie Modelle an historische Finanzdaten anpasst, um Risiko und Rendite abzuschätzen.
Bei der Sensorkalibrierung verwenden Ingenieure die Methode der kleinsten Quadrate, um Modelle an beobachtete Daten anzupassen und Messfehler zu minimieren. Sie wird auch in der Signalverarbeitung zur Filterung und Rauschunterdrückung eingesetzt und ermöglicht eine klarere Interpretation der Daten.
Die Methode der kleinsten Quadrate wurde erstmals von Carl Friedrich Gauß in der Astronomie eingesetzt, um die Umlaufbahn des Asteroiden Ceres vorherzusagen. Sie wird auch in der Geodäsie verwendet, um die Form der Erde anhand von Beobachtungsdaten zu modellieren, was für genaue geografische Messungen unerlässlich ist.
Wenn du dich mit maschinellem Lernen befasst hast, kennst du die Methode der kleinsten Quadrate als eine Methode zur Minimierung der Verlustfunktion beim Training von linearen Regressionsmodellen. Vielleicht hast du sie auch schon bei der Merkmalsauswahl verwendet, um die wichtigsten Variablen zu identifizieren, die zum Modell beitragen.
Sie spielt auch in vielen anderen Naturwissenschaften eine Rolle, zum Beispiel in der Physik und der Chemie. Sie kann verwendet werden, um Kurven an experimentelle Daten wie Reaktionsgeschwindigkeiten oder physikalische Messungen anzupassen, und hilft, Fehler in Versuchsaufbauten zu minimieren.
Die Methode der kleinsten Quadrate ist ein vielseitiges statistisches Werkzeug. Ich persönlich habe diese Methode verwendet, um Drucksensoren zu kalibrieren, Vorhersagen auf der Grundlage meiner experimentellen Daten zu treffen und beim Training von maschinellem Lernen. Die Fähigkeit, Beziehungen zuverlässig zu modellieren und Fehler zu minimieren, ist eine Eigenschaft, die für viele verschiedene Disziplinen von Nutzen ist.
Annahmen und Diagnosen
Die Methode der kleinsten Quadrate macht einige wichtige Annahmen über deine Daten und das verwendete Modell. Es ist wichtig, diese Annahmen zu verstehen, denn ein Verstoß gegen sie kann zu verzerrten oder unzuverlässigen Ergebnissen führen. Lass uns also über diese Annahmen sprechen und darüber, wie du mögliche Probleme diagnostizieren und lösen kannst.
Eine Annahme ist die Unabhängigkeit der Fehler, was bedeutet, dass die Residuen nicht korreliert sein sollten. Wenn Fehler miteinander korreliert sind, insbesondere bei sequentiellen oder räumlichen Daten, können die Schätzungen verzerrt werden. Der Durbin-Watson-Test kann Autokorrelation in den Residuen aufdecken, insbesondere bei zeitabhängigen Datensätzen. Wenn du eine Korrelation findest, kannst du die verallgemeinerte kleinste Quadrate verwenden, um sie zu berücksichtigen.
Eine weitere Annahme ist, dass die Varianz der Residuen über alle Stufen der unabhängigen Variable hinweg konstant bleibt. Wenn die Residuen eine trichterförmige Streuung aufweisen, wenn sie gegen die angepassten Werte aufgetragen werden, ist diese Annahme wahrscheinlich verletzt worden. Um dieses Problem zu lösen, kannst du die gewichtete kleinste Quadrate verwenden, um deine Beobachtungen entsprechend zu gewichten. Alternativ kannst du auch Transformationen wie Logarithmus- oder Quadratwurzelanpassungen verwenden, um ungleiche Varianz zu stabilisieren und Probleme mit Heteroskedastizität zu beheben.
Wie bei jeder Modellierung ist es wichtig, dass die Struktur die zugrunde liegende Beziehung zwischen den Variablen widerspiegelt. Wenn das nicht der Fall ist, spielt es keine Rolle, wie gut deine Passform optimiert ist; die Ergebnisse werden trotzdem irreführend sein. Residualdiagramme und Anpassungskennzahlen wie R² können dir dabei helfen festzustellen, ob dein gewähltes Modell die Muster in den Daten erfasst.
Die Standardmethode der kleinsten Quadrate geht davon aus, dass die unabhängigen Variablen ohne Fehler gemessen werden. Es ist also wichtig, die Genauigkeit deiner unabhängigen Messung zu kennen. Du solltest eine Vorstellung von der Genauigkeit dieser Messung haben, wenn du dir die Erhebungsmethoden ansiehst. Wenn dein Prädiktor mit Messfehlern behaftet ist, solltest du die Methode der kleinsten Quadrate anwenden, um Ungenauigkeiten in deiner Modellierung zu verringern.
Schließlich spielt auch die Verteilung der Restfehler eine wichtige Rolle, insbesondere bei Hypothesentests und Konfidenzintervallschätzungen. Bei der kleinsten Quadratzahl wird davon ausgegangen, dass die Fehler einer normalen (Gaußschen) Verteilung folgen, und Abweichungen von der Normalität können die Schlussfolgerungen beeinträchtigen. Histogramme und Q-Q-Diagramme helfen zu beurteilen, ob die Residuen mit den erwarteten Verteilungen übereinstimmen. Bei erheblichen Abweichungen von der Normalität können robuste Regressionsverfahren oder Bootstrapping-Methoden zuverlässigere Schätzungen liefern, die weniger empfindlich auf Ausreißer reagieren.
Vorteile und Nachteile von Least Squares
Die Methode der kleinsten Quadrate ist ein weit verbreitetes Instrument der Datenanalyse. Das heißt aber nicht, dass sie für jeden Datensatz verwendet werden sollte.
Die Methode der kleinsten Quadrate bietet mehrere Vorteile. Sie ist ziemlich einfach zu berechnen, vor allem für lineare Modelle. Sie ist sowohl für ein technisches als auch für ein nichttechnisches Publikum leicht zu interpretieren. Außerdem gibt es verschiedene Stile wie die gewichtete, die robuste und die nichtlineare Regression, was sie sehr vielseitig macht. Und was noch wichtiger ist: Das Gauß-Markov-Theorem bietet eine solide theoretische Grundlage. Dadurch sind die kleinsten Quadrate breit anwendbar und werden in vielen Bereichen eingesetzt, von der Wirtschaft bis zum Ingenieurwesen.
Die Methode ist jedoch anfällig für Ausreißer, die die Ergebnisse des Modells unverhältnismäßig stark beeinflussen können. Außerdem wird davon ausgegangen, dass die Prädiktoren keine Fehler enthalten, was in der Realität möglicherweise nicht der Fall ist. Außerdem kann die kleinste Quadratzahl durch Multikollinearität eingeschränkt werden. Das bedeutet, dass stark korrelierte Prädiktoren zu instabilen Koeffizienten und damit zu unzuverlässigen Schätzungen führen können. Sie erfordert außerdem eine konstante Varianz der Residuen, eine Bedingung, die nicht immer erfüllt werden kann.
Es ist wichtig, dass du deinen Datensatz und dein Ziel genau unter die Lupe nimmst, bevor du entscheidest, dass die Methode der kleinsten Quadrate das beste Werkzeug für deine Situation ist.
|
Vorteile |
Benachteiligungen |
|
Leichtigkeit der Berechnung |
Empfindlichkeit gegenüber Ausreißern |
|
Interpretierbarkeit |
Geht davon aus, dass die Prädiktoren keine Fehler aufweisen |
|
Breite Anwendbarkeit |
Begrenzt durch Multikollinearität |
|
Starkes theoretisches Fundament |
Annahme einer konstanten Varianz |
Fazit
Die Methode der kleinsten Quadrate ist ein grundlegendes Werkzeug für jeden Datenanalysten. Indem wir die beste Anpassung für unsere Daten finden, können wir genauere Vorhersagen treffen und aufschlussreichere Trends finden.
Wenn du mehr über das Messen von Geraden im euklidischen Raum erfahren möchtest, empfehle ich dir unsere Seite Euklidische Distanz verstehen: Von der Theorie zur Praxis tutorial. Außerdem solltest du dich für unsere Regressionskurse anmelden, um wirklich ein Experte zu werden.
