Softplus: The Smooth Activation Function Worth Knowing

ReLU has been the default activation function in deep learning for years. And there's a good reason for it - it's simple and works well in most cases. But when neurons start outputting zero during training, they stop learning, their gradients become zero, and backpropagation can't update their weights. In deeper networks, this problem can affect multiple neurons and reduce your model's ability to capture patterns in your data.

In plain English: your network stops learning.

Softplus offers a smooth, differentiable alternative that addresses this issue, all while maintaining most of ReLU's benefits. It approximates ReLU's behavior for positive inputs but provides non-zero gradients for negative values. This keeps neurons active throughout training.

In this article, you'll learn what Softplus is, how it compares to ReLU mathematically, and when you should choose it over other activation functions.

If you're completely new to deep learning, check out our in-depth guide to activation functions in neural networks.

What Is the Softplus Function?

Softplus is a smooth activation function that acts as a differentiable approximation of ReLU.

The function takes any real number as input and outputs a positive value. Softplus doesn't have a sharp corner at zero like ReLU. It curves smoothly through that transition point.

Here's the mathematical definition:

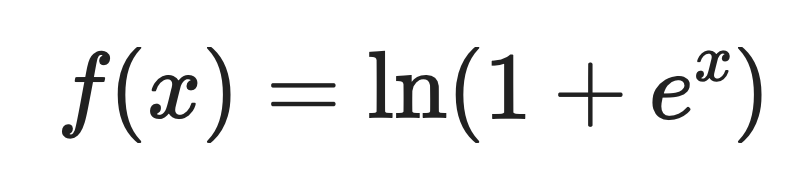
Where:

• x is the input value
• e is Euler's number (approximately 2.718)
• ln is the natural logarithm

For large positive inputs, Softplus returns values close to the input itself. For negative inputs, it returns small positive values instead of zero.

Derivative of Softplus

The derivative of Softplus is the logistic sigmoid function.

This means:

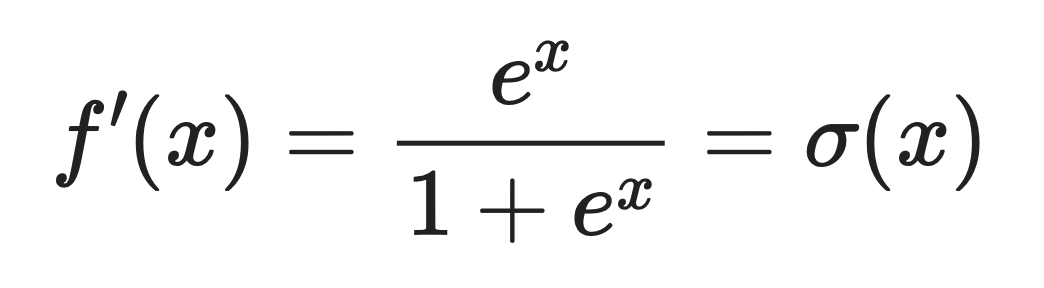
Where σ(x) is the sigmoid function you've probably seen before. 

This derivative property makes Softplus useful when you need smooth gradient flow during backpropagation. The gradients never drop to zero. This means neurons can always update their weights and continue learning.

Behavior at extremes

Softplus behaves differently depending on whether the input is large and positive or large and negative.

For large positive values:

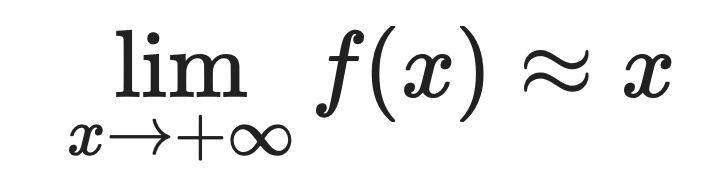
For large negative values:

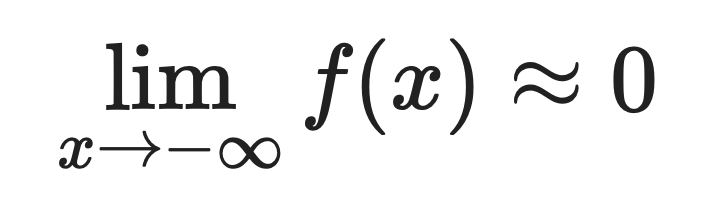
This is why Softplus approximates ReLU so well. When x is positive and large, both functions return approximately the same value.

The difference is visible on negative inputs. ReLU outputs exactly zero for negative inputs, and Softplus outputs small positive values.

That small difference prevents the dying neuron problem. Neurons using Softplus can recover from negative activations because their gradients never completely vanish.

Mathematical and Computational Properties

Softplus has mathematical properties you need to know. They make it more than just a smooth version of ReLU.

Smoothness and differentiability

Softplus is infinitely differentiable at every point.

This means you can take the derivative as many times as you want, and the function remains smooth. In mathematical terms, it's an analytic function.

ReLU, on the other hand, has a kink at zero - a sharp corner where the derivative doesn't exist. This non-differentiable point can cause issues in optimization algorithms that assume smooth gradients.

In deep learning, smooth optimization works better when the loss surface is smooth. If you're using second-order optimization methods or any algorithm that relies on smooth gradient transitions, Softplus gives you that smoothness.

Numerical stability

Computing exponentials can cause overflow problems when inputs get large.

Deep learning frameworks handle this with a threshold parameter. When the input exceeds this threshold, the function switches from computing the logarithm to returning a linear output.

Here's how it works:

• For small inputs: compute Softplus directly
• For large inputs beyond the threshold: return inputs directly

This prevents numerical overflow while maintaining the behavior you need. For large positive inputs, Softplus approximates a linear function anyway, so the switch doesn't affect the output meaningfully.

Relation to other functions

Softplus connects to a couple of other activation and probability functions. Here's how:

• Sigmoid: As you saw earlier, the derivative of Softplus is the sigmoid function. This means Softplus is the integral of the sigmoid, which makes sense when you think about their shapes.

• LogSumExp: Softplus is actually a special case of the LogSumExp function. For two inputs, LogSumExp(0, x) = ln(1 + e^x) = Softplus(x). This connects Softplus to numerical stability techniques used in machine learning.

• Softmax: LogSumExp is the foundation of Softmax, so Softplus shares that lineage. Both functions use the log-exp trick for numerical stability.

• Logit function: The logit is the inverse of sigmoid. Since sigmoid is the derivative of Softplus, these three functions form a connected family in probability theory.

• Convex conjugate: In convex analysis, the convex conjugate of Softplus is negative binary entropy. This connects Softplus to entropy maximization principles used in information theory and probabilistic modeling.

If you're working with probabilistic models or Bayesian frameworks, this entropy connection makes Softplus a natural choice for ensuring your activations align with maximum entropy principles.

Advantages of Using Softplus

Softplus solves specific problems that ReLU can't handle well. Here are four of them.

Smooth and differentiable

Softplus is smooth at every point on the curve.

This means gradients flow continuously during backpropagation without sudden jumps or breaks. When you're training a network, smooth gradient flow leads to more stable weight updates and better convergence behavior.

ReLU's sharp corner at zero can cause gradient discontinuities. Softplus doesn't have this problem.

Prevents dying neurons

Softplus never outputs exactly zero, even for large negative inputs.

This means every neuron can continue learning because gradients never completely vanish. With ReLU, a neuron that starts outputting zero can stay stuck there forever - its gradient is zero, so weight updates don't move it.

Softplus gives you a safety net. Neurons can recover from negative activations and start contributing to the network again.

Output is always positive

Softplus guarantees non-negative outputs for any input.

This matters when you're building models that need positive predictions. Poisson regression models count data (customers, events, clicks) where negative values don't make sense. Generative models often need positive outputs to represent probabilities or intensities.

Better suited for certain tasks

Some tasks benefit from smooth, continuous activation behavior.

Regression tasks with smooth target functions work better with smooth activations. If you're predicting continuous values like temperature, price, or distance, Softplus aligns better with the underlying smoothness of your data.

Bayesian models and probabilistic frameworks also prefer smooth functions. When you're modeling uncertainty or working with probability distributions, the continuous derivatives of Softplus make mathematical operations cleaner and more stable.

If you're working in these domains, Softplus gives you better theoretical guarantees and practical results than ReLU's sharp transitions.

Limitations and Trade-Offs

There are some limitations you need to know about Softplus before you ditch ReLU for good. Here are three of them.

Higher computational cost

ReLU uses a simple max operation: max(0, x).

Softplus computes exponentials and logarithms: ln(1 + e^x). These operations are slower, especially when you're running them millions of times across large networks with thousands of neurons.

The difference adds up. This computational overhead can increase training time.

Slower convergence

Softplus has smoother gradients, which sounds good on paper.

But smooth doesn't always mean fast. ReLU's sharp transitions create sparse activations - many neurons output exactly zero. This sparsity helps gradients propagate faster through the network during backpropagation.

Softplus doesn't have this sparsity. Every neuron outputs some non-zero value, which means more computation and potentially slower convergence in deep architectures.

Less common in practice

ReLU has dominated in deep learning for years.

This means there's more documentation, problems/solutions, and general resources around it. Softplus doesn't get the same treatment. Fewer people use it, so there's less community knowledge, fewer Stack Overflow answers, and fewer pre-trained models using it.

When you pick Softplus, you're choosing a path with less support and potentially more debugging on your own.

Softplus in PyTorch

PyTorch makes Softplus easy to use with built-in support and two parameters that control its behavior.

For reference, this is the version of PyTorch I'm using:

import torch
import torch.nn as nn

print(torch.__version__)

Here's the basic implementation:

# Create a Softplus activation function
softplus = nn.Softplus(beta=1, threshold=20)

# Apply it to some input
x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
output = softplus(x)

print(output)

Simple enough. But those two parameters - beta and threshold - change how the function behaves. Let's explore them in more depth.

The beta parameter

The beta parameter controls the smoothness of the Softplus curve.

When you increase beta, the function becomes steeper and closer to ReLU. When you decrease it, the function becomes smoother and more gradual. Here's how it works in code:

x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])

# Steeper activation (closer to ReLU)
softplus_steep = nn.Softplus(beta=2, threshold=20)
output_steep = softplus_steep(x)

# Smoother activation
softplus_smooth = nn.Softplus(beta=0.5, threshold=20)
output_smooth = softplus_smooth(x)

print("Softplus - Steeper activation")
print(output_steep)

print()

print("Softplus - Smoother activation")
print(output_smooth)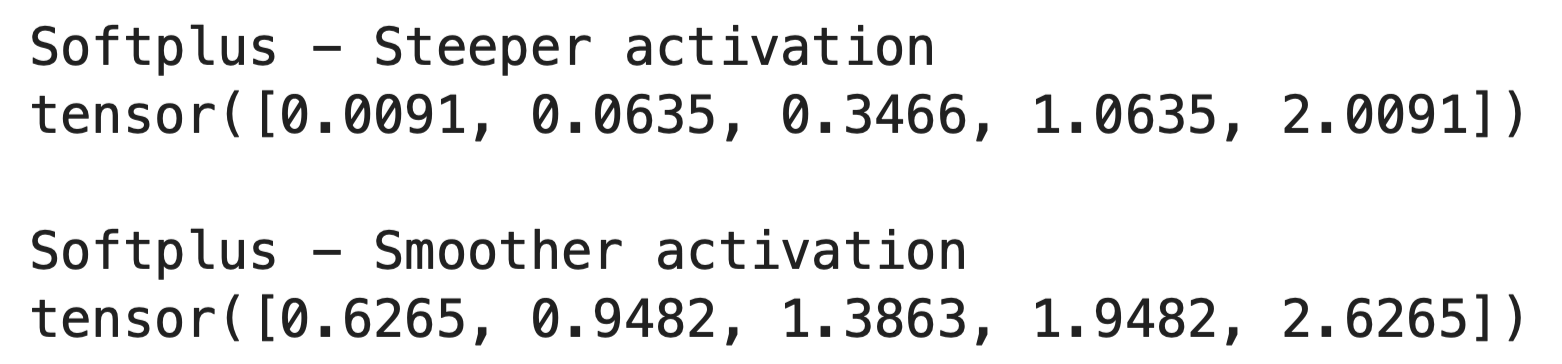

The default beta=1 works well for most cases. You'd only change this if you need to tune the activation's sharpness for specific tasks.

The threshold parameter

The threshold parameter prevents numerical overflow for large inputs.

Remember how computing e^x can explode for large x values? When the input exceeds the threshold, PyTorch switches from computing the full Softplus formula to just returning the input directly:

softplus = nn.Softplus(beta=1, threshold=20)

# Large input bypasses the exponential
large_input = torch.tensor([25.0])
print(softplus(large_input))

The default threshold=20 works for most scenarios. At this point, Softplus already approximates a linear function anyway, so the switch doesn't affect results.

When to Use Softplus

Choose Softplus when you need gradient smoothness for optimization. If you're using second-order optimization methods or algorithms that assume smooth loss surfaces, Softplus gives you the continuous derivatives those methods rely on.

Use it when your model requires non-negative outputs. Count data, intensity values, and probability parameters all need to stay positive. Softplus handles this naturally without extra constraints.

Shallow networks benefit from Softplus more than deep ones. When you only have a few layers, losing even one neuron to the dying ReLU problem hurts performance. Softplus keeps all neurons active and learning.

You can also pick Softplus for probabilistic models and Bayesian frameworks. The smooth gradients and entropy connections make mathematical operations cleaner. Energy-based models also benefit from Softplus's continuous nature.

Models where you need to interpret continuous gradients work better with Softplus. If you're analyzing how your network responds to input changes or studying gradient flow, the smooth derivatives give you clearer insights than ReLU's sharp transitions.

When ReLU is still better

Don't switch to Softplus just because it sounds better on paper or because it's a shiny new thing.

• Large, deep networks train faster with ReLU. The computational overhead of Softplus adds up across hundreds of layers and millions of parameters. ReLU's sparsity also helps with memory and speed.
• Production systems often favor ReLU because hardware optimizations target it specifically. Your training might be 10-20% slower with Softplus on the same hardware.
• Standard computer vision and NLP tasks don't usually benefit from Softplus. The community has spent years optimizing architectures around ReLU, and switching activation functions means rebuilding that knowledge.

Start with ReLU for most projects. Switch to Softplus only when you hit specific problems that its properties solve.

Conclusion

In short, Softplus gives you a smooth alternative to ReLU when you need it.

It won't replace ReLU as the default activation function - and it doesn't need to. Softplus solves specific problems: dying neurons in shallow networks, models that need non-negative outputs, and tasks where smooth gradient flow matters for optimization.

You get better mathematical properties at the cost of computational speed. For most deep learning projects, ReLU's simplicity and speed win. But when you're working with probabilistic models, Bayesian frameworks, or regression tasks with smooth target functions, Softplus becomes the better choice.

Test both. Run experiments. Let your specific problem guide the decision.

Want to learn more? Check out our great resources:

• Deep Learning in Python
• Natural Language Processing in Python
• Software Engineering Principles in Python