Softplus: La función de activación suave que vale la pena conocer

ReLU ha sido la función de activación predeterminada en el aprendizaje profundo durante años. Y hay una buena razón para ello: es sencillo y funciona bien en la mayoría de los casos. Pero cuando las neuronas comienzan a generar un resultado cero durante el entrenamiento, dejan de aprender, sus gradientes se vuelven nulos y la retropropagación no puede actualizar sus pesos. En redes más profundas, este problema puede afectar a múltiples neuronas y reducir la capacidad de tu modelo para capturar patrones en tus datos.

En lenguaje sencillo: tu red deja de aprender.

Softplus ofrece una alternativa fluida y diferenciable que aborda este problema, al tiempo que mantiene la mayoría de las ventajas de ReLU. Se aproxima al comportamiento de ReLU para entradas positivas, pero proporciona gradientes distintos de cero para valores negativos. Esto mantiene las neuronas activas durante todo el entrenamiento.

En este artículo, aprenderás qué es Softplus, cómo se compara matemáticamente con ReLU y cuándo debes elegirlo frente a otras funciones de activación.

Si eres completamente nuevo en el aprendizaje profundo, consulta nuestra guía detallada sobre funciones de activación en redes neuronales.

¿Qué es la función Softplus?

Softplus es una función de activación suave que actúa como una aproximación diferenciable de ReLU.

La función toma cualquier número real como entrada y devuelve un valor positivo. Softplus no tiene una esquina afilada en cero como ReLU. Se curva suavemente a través de ese punto de transición.

Aquí está la definición matemática:

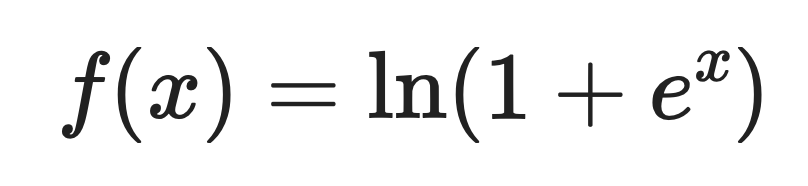
Dónde:

• x es el valor de entrada
• e es el número de Euler (aproximadamente 2,718).
• ln es el logaritmo natural.

Para entradas positivas grandes, Softplus devuelve valores cercanos a la propia entrada. Para entradas negativas, devuelve pequeños valores positivos en lugar de cero.

Derivada de Softplus

La derivada de Softplus es la función logística sigmoide logística.

Esto significa:

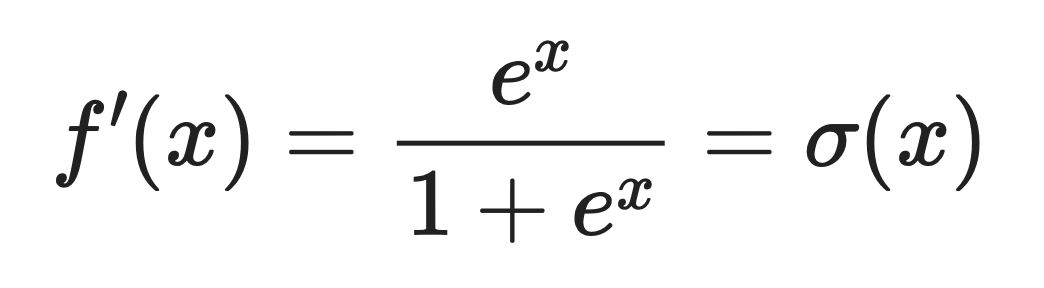
Donde σ(x) es la función sigmoide que probablemente ya hayas visto antes.

Esta propiedad derivada hace que Softplus sea útil cuando necesitas un flujo de gradiente suave durante la retropropagación. Los gradientes nunca bajan a cero. Esto significa que las neuronas pueden actualizar constantemente sus pesos y seguir aprendiendo.

Comportamiento en situaciones extremas

Softplus se comporta de manera diferente dependiendo de si la entrada es grande y positiva o grande y negativa.

Para valores positivos grandes:

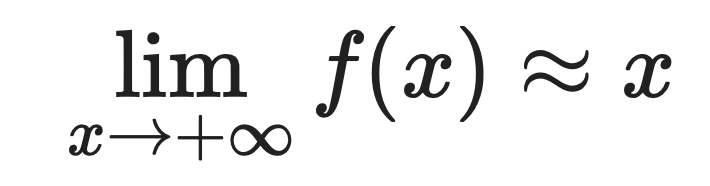
Para valores negativos grandes:

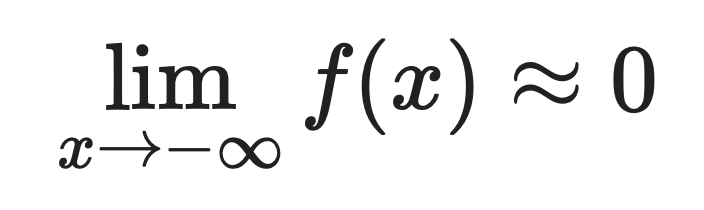
Por eso Softplus se aproxima tan bien a ReLU. Cuando x es positivo y grande, ambas funciones devuelven aproximadamente el mismo valor.

La diferencia es visible en las entradas negativas. ReLU genera exactamente cero para entradas negativas, y Softplus genera pequeños valores positivos.

Esa pequeña diferencia evita el problema de la muerte neuronal. Las neuronas que utilizan Softplus pueden recuperarse de activaciones negativas porque sus gradientes nunca desaparecen por completo.

Propiedades matemáticas y computacionales

Softplus tiene propiedades matemáticas que debes conocer. Lo hacen más que una simple versión suavizada de ReLU.

Suavidad y diferenciabilidad

Softplus es infinitamente diferenciable en cada punto.

Esto significa que puedes derivar tantas veces como quieras y la función seguirá siendo continua. En términos matemáticos, es una función analítica.

Por otro lado, ReLU tiene un punto de inflexión en cero, una esquina pronunciada donde la derivada no existe. Este punto no diferenciable puede causar problemas en los algoritmos de optimización que asumen gradientes suaves.

En el aprendizaje profundo, la optimización suave funciona mejor cuando la superficie de pérdida es suave. Si utilizas métodos de optimización de segundo orden o cualquier algoritmo que se base en transiciones de gradiente suaves, Softplus te ofrece esa suavidad.

Estabilidad numérica

El cálculo de exponenciales puede causar problemas de desbordamiento cuando las entradas son grandes.

Los marcos de aprendizaje profundo gestionan esto con un parámetro « threshold ». Cuando la entrada supera este umbral, la función pasa de calcular el logaritmo a devolver una salida lineal.

Así es como funciona:

• Para entradas pequeñas: calcula Softplus directamente.
• Para entradas grandes que superen el umbral: devuelve las entradas directamente.

Esto evita el desbordamiento numérico y mantiene el comportamiento que necesitas. Para entradas positivas grandes, Softplus se aproxima a una función lineal de todos modos, por lo que el cambio no afecta significativamente a la salida.

Relación con otras funciones

Softplus se conecta a otras funciones de activación y probabilidad. Así es como se hace:

• e sigmoide: Como viste anteriormente, la derivada de Softplus es la función sigmoide. Esto significa que Softplus es la integral de la sigmoide, lo cual tiene sentido si pensamos en sus formas.

• LogSumExp: Softplus es en realidad un caso especial de la función LogSumExp. Para dos entradas, LogSumExp(0, x) = ln(1 + e^x) = Softplus(x). Esto conecta Softplus con las técnicas de estabilidad numérica utilizadas en machine learning.

• : LogSumExp es la base de Softmax, por lo que Softplus comparte ese linaje. Ambas funciones utilizan el truco log-exp para garantizar la estabilidad numérica.

• Función logit: El logit es la inversa de la sigmoide. Dado que la sigmoide es la derivada de Softplus, estas tres funciones forman una familia conectada en la teoría de la probabilidad.

• Conjugado convexo: En el análisis convexo, el conjugado convexo de Softplus es la entropía binaria negativa. Esto conecta Softplus con los principios de maximización de la entropía utilizados en la teoría de la información y el modelado probabilístico.

Si trabajas con modelos probabilísticos o marcos bayesianos, esta conexión con la entropía hace que Softplus sea la elección natural para garantizar que tus activaciones se ajusten a los principios de máxima entropía.

Ventajas de utilizar Softplus

Softplus resuelve problemas específicos que ReLU no puede manejar bien. Aquí hay cuatro de ellos.

Suave y diferenciable

Softplus es suave en todos los puntos de la curva.

Esto significa que los gradientes fluyen continuamente durante la retropropagación sin saltos ni interrupciones repentinas. Cuando estás entrenando una red, un flujo de gradiente suave conduce a actualizaciones de peso más estables y a un mejor comportamiento de convergencia.

La esquina afilada de ReLU en cero puede causar discontinuidades en el gradiente. Softplus no tiene este problema.

Evita la muerte de las neuronas.

Softplus nunca da como resultado exactamente cero, incluso con entradas negativas grandes.

Esto significa que cada neurona puede seguir aprendiendo e, ya que los gradientes nunca desaparecen por completo. Con ReLU, una neurona que comienza a generar un resultado cero puede quedarse estancada ahí para siempre: su gradiente es cero, por lo que las actualizaciones de peso no la mueven.

Softplus te ofrece una red de seguridad. Las neuronas pueden recuperarse de activaciones negativas y volver a contribuir a la red.

El resultado siempre es positivo.

Softplus garantiza resultados no negativos para cualquier entrada.

Esto es importante cuando se crean modelos que necesitan predicciones positivas. La regresión de Poisson Los modelos cuentan datos (clientes, eventos, clics) en los que los valores negativos no tienen sentido. Los modelos generativos suelen necesitar resultados positivos para representar probabilidades o intensidades.

Más adecuado para determinadas tareas

Algunas tareas se benefician de un comportamiento de activación fluido y continuo.

Las tareas de regresión con funciones objetivo suaves funcionan mejor con activaciones suaves. Si estás prediciendo valores continuos como la temperatura, el precio o la distancia, Softplus se ajusta mejor a la suavidad subyacente de tus datos.

Los modelos bayesianos y los marcos probabilísticos también prefieren funciones suaves. Cuando modelas la incertidumbre o trabajas con distribuciones de probabilidad, las derivadas continuas de Softplus hacen que las operaciones matemáticas sean más claras y estables.

Si trabajas en estos ámbitos, Softplus te ofrece mejores garantías teóricas y resultados prácticos que las transiciones bruscas de ReLU.

Limitaciones y compensaciones

Hay algunas limitaciones que debes conocer sobre Softplus antes de abandonar ReLU definitivamente. Aquí hay tres de ellos.

Mayor coste computacional

ReLU utiliza una operación máxima simple: max(0, x).

Softplus calcula exponenciales y logaritmos: ln(1 + e^x). Estas operaciones son más lentas, especialmente cuando se ejecutan millones de veces en grandes redes con miles de neuronas.

La diferencia se acumula. Esta sobrecarga computacional puede aumentar el tiempo de entrenamiento.

Convergencia más lenta

Softplus tiene gradientes más suaves, lo que suena bien sobre el papel.

Pero suave no siempre significa rápido. Las transiciones bruscas de ReLU crean activaciones dispersas: muchas neuronas producen exactamente cero. Esta escasez ayuda a que los gradientes se propaguen más rápidamente a través de la red durante la retropropagación.

Softplus no tiene esta escasez. Cada neurona genera un valor distinto de cero, lo que implica un mayor esfuerzo computacional y una convergencia potencialmente más lenta en las arquitecturas profundas.

Menos común en la práctica

ReLU ha dominado el aprendizaje profundo durante años.

Esto significa que hay más documentación, problemas/soluciones y recursos generales al respecto. Softplus no recibe el mismo trato. Hay menos gente que lo utiliza, por lo que hay menos conocimientos comunitarios, menos respuestas en Stack Overflow y menos modelos preentrenados que lo utilizan.

Cuando eliges Softplus, estás optando por un camino con menos asistencia y, potencialmente, más depuración por tu cuenta.

Softplus en PyTorch

PyTorch facilita el uso de Softplus con soporte integrado y dos parámetros que controlan su comportamiento.

A modo de referencia, esta es la versión de PyTorch que estoy utilizando:

import torch
import torch.nn as nn

print(torch.__version__)

Aquí está la implementación básica:

# Create a Softplus activation function
softplus = nn.Softplus(beta=1, threshold=20)

# Apply it to some input
x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
output = softplus(x)

print(output)

Es bastante sencillo. Pero esos dos parámetros — beta y threshold — cambian el comportamiento de la función. Explorémoslos más a fondo.

El parámetro beta

El parámetro « beta » controla la suavidad de la curva Softplus.

Cuando aumentas beta, la función se vuelve más pronunciada y se acerca más a ReLU. Cuando lo reduces, la función se vuelve más suave y gradual. Así es como funciona en el código:

x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])

# Steeper activation (closer to ReLU)
softplus_steep = nn.Softplus(beta=2, threshold=20)
output_steep = softplus_steep(x)

# Smoother activation
softplus_smooth = nn.Softplus(beta=0.5, threshold=20)
output_smooth = softplus_smooth(x)

print("Softplus - Steeper activation")
print(output_steep)

print()

print("Softplus - Smoother activation")
print(output_smooth)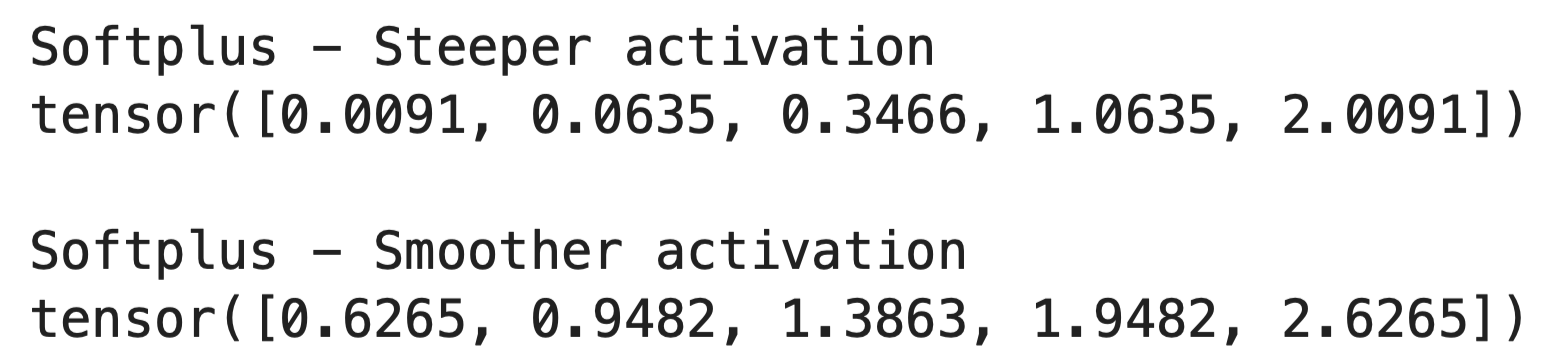

El valor predeterminado beta=1 funciona bien en la mayoría de los casos. Solo cambiarías esto si necesitas ajustar la precisión de la activación para tareas específicas.

El parámetro umbral

El parámetro threshold evita el desbordamiento numérico para entradas grandes.

¿Recuerdas cómo el cálculo de e^x puede explotar para valores grandes de x? Cuando la entrada supera el umbral, PyTorch pasa de calcular la fórmula Softplus completa a simplemente devolver la entrada directamente:

softplus = nn.Softplus(beta=1, threshold=20)

# Large input bypasses the exponential
large_input = torch.tensor([25.0])
print(softplus(large_input))

El valor predeterminado threshold=20 funciona en la mayoría de los casos. En este punto, Softplus ya se aproxima a una función lineal, por lo que el cambio no afecta a los resultados.

Cuándo utilizar Softplus

Elige Softplus cuando necesites suavidad de degradado para la optimización. Si utilizas métodos de optimización de segundo orden o algoritmos que asumen superficies de pérdida suaves, Softplus te proporciona las derivadas continuas en las que se basan esos métodos.

Úsalo cuando tu modelo requiera salidas no negativas. Los datos de recuento, los valores de intensidad y los parámetros de probabilidad deben mantenerse positivos. Softplus gestiona esto de forma natural sin restricciones adicionales.

Las redes poco profundas se benefician más de Softplus que las profundas. Cuando solo tienes unas pocas capas, perder incluso una neurona por el problema de ReLU moribundo perjudica el rendimiento. Softplus mantiene todas las neuronas activas y aprendiendo.

También puedes elegir Softplus para modelos probabilísticos y marcos bayesianos. Los gradientes suaves y las conexiones de entropía hacen que las operaciones matemáticas sean más limpias. Los modelos basados en la energía también se benefician de la naturaleza continua de Softplus.

Los modelos en los que es necesario interpretar gradientes continuos funcionan mejor con Softplus. Si estás analizando cómo responde tu red a los cambios de entrada o estudiando el flujo gradiente, las derivadas suaves te proporcionan una visión más clara que las transiciones bruscas de ReLU.

Cuando ReLU sigue siendo mejor

No cambies a Softplus solo porque suena mejor sobre el papel o porque es algo nuevo y brillante.

• Las redes grandes y profundas se entrenan más rápido con ReLU. La sobrecarga computacional de Softplus se acumula a lo largo de cientos de capas y millones de parámetros. La escasez de ReLU también ayuda con la memoria y la velocidad.
• Los sistemas de producción suelen favorecer a ReLU porque las optimizaciones de hardware se centran específicamente en él. Tu entrenamiento podría ser entre un 10 y un 20 % más lento con Softplus en el mismo hardware.
• Las tareas estándar de visión artificial y procesamiento del lenguaje natural (NLP) no suelen beneficiarse de Softplus. La comunidad ha dedicado años a optimizar las arquitecturas en torno a ReLU, y cambiar las funciones de activación significa reconstruir ese conocimiento.

Empieza con ReLU para la mayoría de los proyectos. Cambia a Softplus solo cuando te encuentres con problemas específicos que sus propiedades puedan resolver.

Conclusión

En resumen, Softplus te ofrece una alternativa fluida a ReLU cuando la necesitas.

No sustituirá a ReLU como función de activación predeterminada, ni es necesario que lo haga. Softplus resuelve problemas específicos: neuronas moribundas en redes poco profundas, modelos que necesitan resultados no negativos y tareas en las que el flujo de gradiente suave es importante para la optimización.

Se obtienen mejores propiedades matemáticas a costa de la velocidad de cálculo. Para la mayoría de los proyectos de aprendizaje profundo, la simplicidad y velocidad de ReLU resultan ganadoras. Pero cuando trabajas con modelos probabilísticos, marcos bayesianos o tareas de regresión con funciones objetivo suaves, Softplus se convierte en la mejor opción.

Prueba ambos. Realiza experimentos. Deja que tu problema específico guíe la decisión.

¿Quieres saber más? Echa un vistazo a nuestros fantásticos recursos:

• Aprendizaje profundo en Python
• Procesamiento del lenguaje natural en Python
• Principios de ingeniería de software en Python