Cauchy-Verteilung: Heavy-Tailed-Daten verstehen

Die Cauchy-Verteilung stellt ein faszinierendes statistisches Rätsel dar. Obwohl sie die bekannte glockenförmige Form mit vielen anderen kontinuierlichen Wahrscheinlichkeitsverteilungen teilt, entzieht sie sich der konventionellen Analyse, da sie weder einen definierten Mittelwert noch eine Varianz hat. Diese nach dem Mathematiker Augustin-Louis Cauchy benannte Verteilung kommt in vielen Bereichen zum Einsatz, von der Finanzmodellierung bis zur Bayes'schen Statistik.

Als Lehrmittel veranschaulicht die Cauchy-Verteilung grundlegende statistische Konzepte mit bemerkenswerter Klarheit. Sie demonstriert die Nicht-Konvergenz der Stichprobenmittelwerte, unterstreicht die Bedeutung von Verteilungsannahmen und zeigt, wie die Schätzer unter verschiedenen Bedingungen abschneiden.

Willst du diese statistischen Konzepte und ihre Anwendungen in der Datenwissenschaft beherrschen? In unserem Lernpfad "Machine Learning Scientist in R" lernst du, wie du diese Ideen mit Hilfe der R-Programmierung umsetzen kannst.

Was ist die Cauchy-Verteilung?

Die Cauchy-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die für ihre einzigartigen Eigenschaften und ihre starken Schwänze bekannt ist. Sie ist durch zwei wichtige Parameter gekennzeichnet:

1. Standortparameter (θ): Dieser Parameter bestimmt, wo die Spitze (oder das Zentrum) der Verteilung auf der x-Achse liegt. Stell dir vor, dass du die gesamte Verteilung nach links oder rechts verschiebst, ohne ihre Form zu verändern.
2. Skalenparameter (σ): Dieser Parameter bestimmt, wie breit die Verteilung ist. Größere Werte von σ erzeugen breitere, flachere Verteilungen mit stärkeren Schwänzen. Du kannst dir das so vorstellen, dass die Verteilung horizontal gestreckt oder gequetscht wird.

Die Verteilung wird mathematisch durch ihre Wahrscheinlichkeitsdichtefunktion (PDF) definiert:

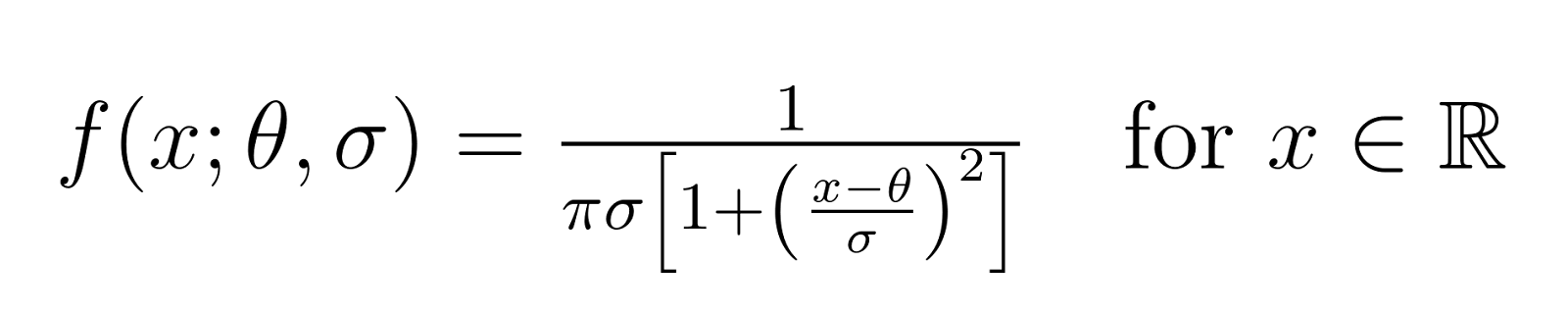
Wenn wir θ = 0 und σ = 1 setzen, erhalten wir die so genannte Cauchy-Standardverteilung. Dies ist die einfachste Form der Verteilung und dient als Bezugspunkt für das Verständnis komplexerer Fälle.

Die wichtigsten Merkmale der Cauchy-Verteilung

Die definierenden Eigenschaften von Cauchy-Verteilungen

Schwänze

Stell dir die Cauchy-Verteilung als Verteilung der "Extremereignisse" vor. Während eine Normalverteilung darauf hindeutet, dass Werte, die weit von der Mitte entfernt sind, sehr selten sind (wie z. B. eine Person zu finden, die zwei Meter groß ist), sagt uns die Cauchy-Verteilung, dass Extremwerte häufiger vorkommen, als du vielleicht erwartest. 

Bei den Aktienmarktrenditen zum Beispiel treten massive eintägige Kursänderungen (wie bei Marktcrashs oder -rallys) häufiger auf, als eine Normalverteilung vorhersagen würde. Die schweren Schwänze der Cauchy-Verteilung können diese "schwarzen Schwäne" besser erfassen.

Unbestimmter Mittelwert und Varianz

Dies ist vielleicht die faszinierendste Eigenschaft der Cauchy-Verteilung. Anders als die meisten Verteilungen, die du kennst, hat die Cauchy-Verteilung keinen aussagekräftigen Durchschnitt (Mittelwert) oder Streuung (Varianz). 

Um zu verstehen, warum das wichtig ist: Wenn du wiederholte Stichproben aus einer Cauchy-Verteilung nimmst und versuchst, ihren Durchschnitt zu berechnen, wirst du nicht zu einem bestimmten Wert konvergieren, selbst bei Millionen von Stichproben. Dies hat Auswirkungen auf die statistische Analyse, da herkömmliche statistische Methoden, die auf Mittelwerten und Varianzen basieren (wie t-Tests oder ANOVA), mit Cauchy-verteilten Daten nicht funktionieren.

Symmetrie

Die Cauchy-Verteilung ist um ihren Lageparameter (θ) perfekt ausgeglichen, wie ein Spiegelbild auf beiden Seiten. Diese Symmetrie bedeutet jedoch nicht, dass sie sich wie die bekannte Normalverteilung verhält. Während beide Verteilungen symmetrisch sind, streut die Cauchy-Verteilung ihre Wahrscheinlichkeit viel breiter. Das bedeutet, dass es zwar einen klaren Mittelpunkt gibt, die Werte aber mit großer Wahrscheinlichkeit sehr weit von diesem Mittelpunkt abweichen können.

Stabilität

Die Cauchy-Verteilung hat eine bemerkenswerte Eigenschaft: Wenn du zwei unabhängige Variablen mit Cauchy-Verteilung zusammenzählst, erhältst du eine weitere Cauchy-Verteilung! Diese Eigenschaft, die als Stabilität bekannt ist, wird nur von wenigen anderen Verteilungen (wie der Normalverteilung) geteilt. Sie ist besonders nützlich in der Physik und der Finanzmodellierung, wo wir oft verstehen müssen, wie sich kombinierte Zufallsprozesse im Laufe der Zeit verhalten.

Was du bei der Verwendung der Cauchy-Verteilung beachten solltest

Umgang mit Ausreißern

Die Cauchy-Verteilung eignet sich besonders gut für die Behandlung von Ausreißern, weil sie deren Auftreten erwartet. Das macht sie besonders nützlich in Szenarien, in denen Extremwerte natürliche Bestandteile der Daten sind und keine Fehler, die entfernt werden müssen. In diesen Fällen können herkömmliche Methoden zur Erkennung von Ausreißern zu aggressiv sein und unberechtigterweise legitime Datenpunkte zum Entfernen markieren. Die Cauchy-Verteilung bietet einen Rahmen für den Aufbau robuster Modelle, die von extremen Beobachtungen nicht übermäßig beeinflusst werden. Das macht sie zu einem wertvollen Werkzeug bei der Arbeit mit Datensätzen, bei denen Ausreißer eher ein inhärentes Merkmal als eine zu eliminierende Anomalie sind.

Modellauswahl

Die Entscheidung, ob du eine Cauchy-Verteilung verwendest, hängt von deinen Daten und Zielen ab. Die Cauchy-Verteilung ist besonders wertvoll, wenn deine Daten häufig Extremwerte aufweisen, wenn du mit Verhältnissen normalverteilter Variablen arbeitest oder wenn du ein robustes Modell brauchst, das mit Daten mit hohem Schwanzanteil umgehen kann. In bestimmten Situationen solltest du jedoch vorsichtig mit der Cauchy-Verteilung sein: wenn du dich auf Mittelwerte und Varianzen verlassen musst, wenn deine Daten tatsächlich einer Verteilung mit leichterem Schwanz folgen oder wenn die Effizienz deiner Berechnungen ein Hauptanliegen ist. Wenn du diese Kompromisse verstehst, kannst du besser entscheiden, ob die Cauchy-Verteilung für deine spezifischen Analyseanforderungen geeignet ist.

Berechnungseffizienz

Während die mathematische Formel der Cauchy-Verteilung einfach ist, kann die Arbeit mit ihr rechnerisch eine Herausforderung sein. Die Schätzung von Parametern erfordert oft spezielle Techniken wie Markov Chain Monte Carlo (MCMC), und die Standard-Maximum-Likelihood-Methoden haben mit den starken Schwänzen zu kämpfen. Glücklicherweise enthalten moderne Statistiksoftwarepakete oft spezielle Werkzeuge für den Umgang mit Cauchy-Verteilungen, so dass die Arbeit mit dieser Verteilung in der Praxis trotz ihrer rechnerischen Komplexität leichter möglich ist.

Mathematische Eigenschaften der Cauchy-Verteilung

Die Cauchy-Verteilung besitzt mehrere wichtige mathematische Eigenschaften, die sie einzigartig und nützlich machen:

• Eine stabile Verteilung mit einem interessanten Verhalten: Wenn du zwei Variablen mit Cauchy-Verteilung addierst, erhältst du eine weitere Cauchy-Verteilung mit skalierten Parametern. Das macht sie nützlich für die Untersuchung kumulativer Effekte in der Physik und im Finanzwesen.
• Unbestimmte Momente, einschließlich Mittelwert und Varianz, was sie zu einem faszinierenden Gegenbeispiel in der Wahrscheinlichkeitstheorie macht. Diese Eigenschaft hilft den Schülern zu verstehen, warum der zentrale Grenzwertsatz eine endliche Varianz erfordert.
• Eine elegante, einfache mathematische Form, mit einem einfachen PDF und einer charakteristischen Funktion. Trotz seines komplexen Verhaltens ist seine grundlegende mathematische Beschreibung erstaunlich gut nachvollziehbar.
• Die Verhältnis-Eigenschaft: Wenn du eine normale Zufallsvariable durch eine andere unabhängige normale Zufallsvariable teilst, erhältst du eine Cauchy-Verteilung. Dadurch eignet sie sich hervorragend zum Modellieren von Verhältnissen und Proportionen.
• Starke Bayes'sche Anwendungen, insbesondere als Prioritätsverteilung in hierarchischen Modellen. Mit seinen schweren Schwänzen ist er eine ausgezeichnete Wahl für Skalenparameter, bei denen Robustheit wichtig ist.

Visualisierung der Cauchy-Verteilung in R und Python

Das Verhalten der Cauchy-Verteilung lässt sich am besten durch eine Visualisierung verstehen. Verwenden wir R, um Diagramme verschiedener Cauchy-Verteilungen zu erstellen, die zeigen, wie die Parameter Ort (θ) und Skala (σ) die Form und Position der Verteilung beeinflussen.

Cauchy-Verteilung in R

R bietet mit dem Paket stats Funktionen für die Arbeit mit Cauchy-Verteilungen. Außerdem werden wir ggplot2 nutzen, um klare, publikationsreife Grafiken zu erstellen:

# Load required libraries
library(ggplot2)  # for plotting
# Note: dcauchy is from the stats package which is loaded by default in R

# Create a sequence of x values
x <- seq(-10, 10, length.out = 1000)

# Generate different Cauchy distributions using stats::dcauchy
# Standard Cauchy (θ = 0, σ = 1)
standard_cauchy <- dcauchy(x, location = 0, scale = 1)

# Location and Scale Adjusted (θ = 2, σ = 3)
adjusted_cauchy <- dcauchy(x, location = 2, scale = 3)

# Highly Scaled (θ = -1, σ = 5)
scaled_cauchy <- dcauchy(x, location = -1, scale = 5)

# Create a data frame for plotting
plot_data <- data.frame(
  x = rep(x, 3),
  density = c(standard_cauchy, adjusted_cauchy, scaled_cauchy),
  distribution = rep(c("Standard (θ=0, σ=1)", 
                      "Adjusted (θ=2, σ=3)", 
                      "Scaled (θ=-1, σ=5)"), 
                    each = length(x))
)

# Create the plot
ggplot(plot_data, aes(x = x, y = density, color = distribution)) +
  geom_line(size = 1) +
  theme_minimal() +
  labs(title = "Comparison of Cauchy Distributions",
       x = "x",
       y = "Density",
       color = "Parameters") +
  theme(legend.position = "bottom",
        plot.title = element_text(hjust = 0.5)) +
  scale_color_brewer(palette = "Set1")

Dieser Code erzeugt einen Vergleichsplot von drei verschiedenen Cauchy-Verteilungen:

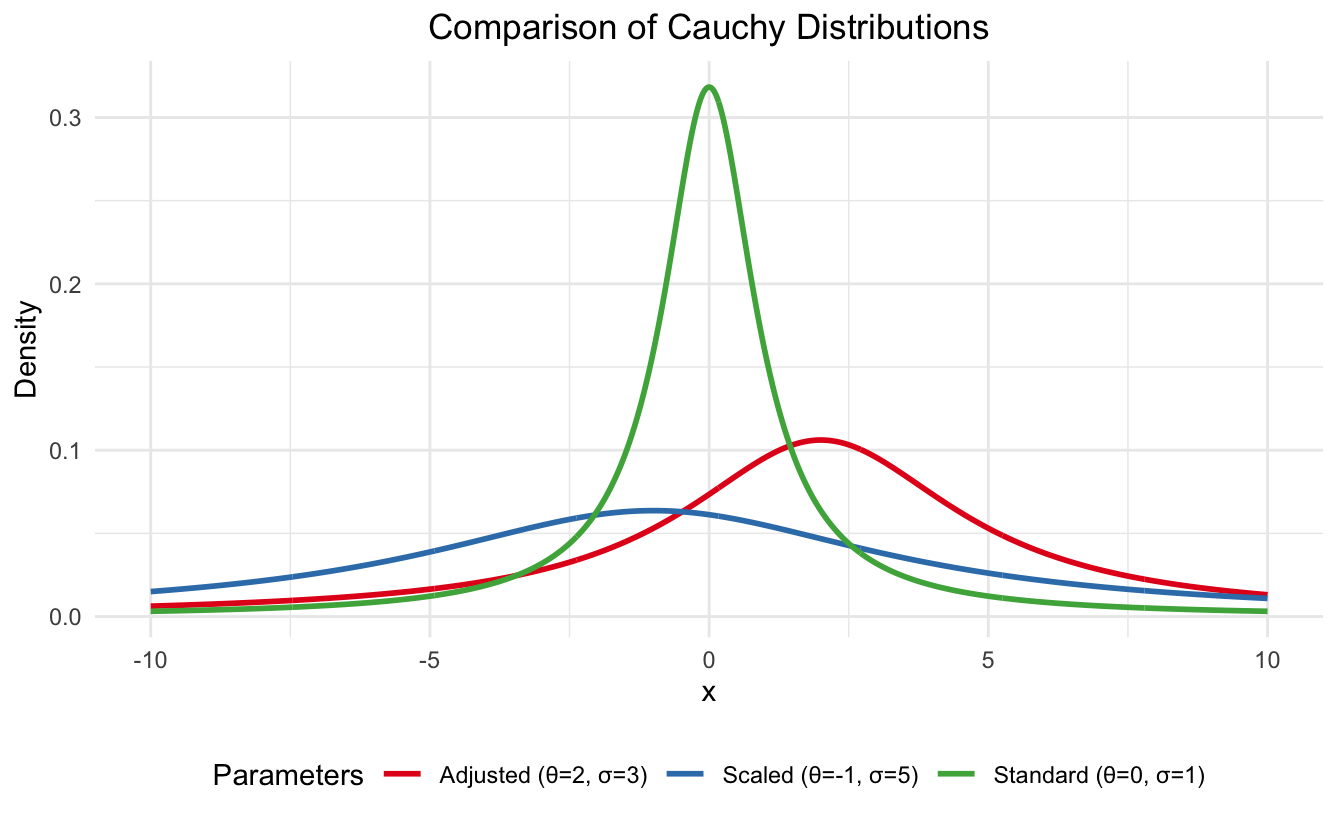
Cauchy-Verteilung in R. Bild vom Autor

1. Standard Cauchy (grüne Linie): Mit θ = 0 und σ = 1 ist dies der Basisfall. Beachte die scharfe Spitze bei x = 0 und die symmetrischen schweren Schwänze.
2. Standortangepasster Cauchy (rote Linie): Wenn du θ = 2 einstellst, verschiebt sich die Spitze nach rechts, während die Form erhalten bleibt. Dies zeigt, wie der Standortparameter das Zentrum der Verteilung beeinflusst, ohne die Streuung zu verändern.
3. Hoch skalierter Cauchy (blaue Linie): Mit θ = -1 und σ = 5 zeigt dies eine verschobene und viel flachere Verteilung. Der größere Skalenparameter führt zu breiteren, schwereren Ausläufern und verringert die Spitzenhöhe, was zeigt, wie σ die Streuung kontrolliert.

Die Visualisierung zeigt deutlich, wie eine Erhöhung des Skalenparameters (σ) zu einer flacheren, breiteren Verteilung führt, während der Ortsparameter (θ) einfach die gesamte Verteilung nach links oder rechts verschiebt.

Cauchy-Verteilung in Python

Nachdem wir die Parameter der Cauchy-Verteilung in R untersucht haben, wollen wir die Cauchy-Verteilung mit ihrem bekannteren Cousin, der Normalverteilung, in Python vergleichen. Der Scientific Computing Stack von Python, insbesondere scipy.stats, bietet hervorragende Werkzeuge für die Arbeit mit Wahrscheinlichkeitsverteilungen.

Während wir mit dem stats-Paket von R direkten Zugriff auf die Funktionen der Cauchy-Verteilung haben, bietet das scipy.stats-Modul von Python eine ähnliche Funktionalität mit einer etwas anderen Schnittstelle. Wir verwenden matplotlib, die wichtigste Plot-Bibliothek von Python, um eine übersichtliche Visualisierung zu erstellen:

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Set style parameters for better visualization
plt.style.use('seaborn')
plt.rcParams.update({
    'font.size': 16,
    'axes.labelsize': 18,
    'axes.titlesize': 24,
    'xtick.labelsize': 16,
    'ytick.labelsize': 16,
    'legend.fontsize': 16,
})

# Create data
x = np.linspace(-10, 10, 1000)
cauchy = stats.cauchy.pdf(x, loc=0, scale=1)
normal = stats.norm.pdf(x, loc=0, scale=1)

# Create the plot
plt.figure(figsize=(12, 8))

# Plot distributions
plt.plot(x, cauchy, 'b-', linewidth=2.5, label='Cauchy(0,1)')
plt.plot(x, normal, 'r--', linewidth=2.5, label='Normal(0,1)')

# Customize the plot
plt.title('Cauchy vs Normal Distribution', pad=20)
plt.xlabel('x', labelpad=10)
plt.ylabel('Density', labelpad=10)

# Customize legend
plt.legend(fontsize=16, bbox_to_anchor=(0.99, 0.99), 
          loc='upper right', borderaxespad=0.)

# Add grid and adjust layout
plt.grid(True, alpha=0.3)
plt.tight_layout()

plt.show()

Der obige Code erstellt einen Vergleich zwischen der Standard-Cauchy-Verteilung (blaue durchgezogene Linie) und der Standard-Normalverteilung (rote gestrichelte Linie), beide zentriert bei 0 mit einem Skalenparameter von 1.

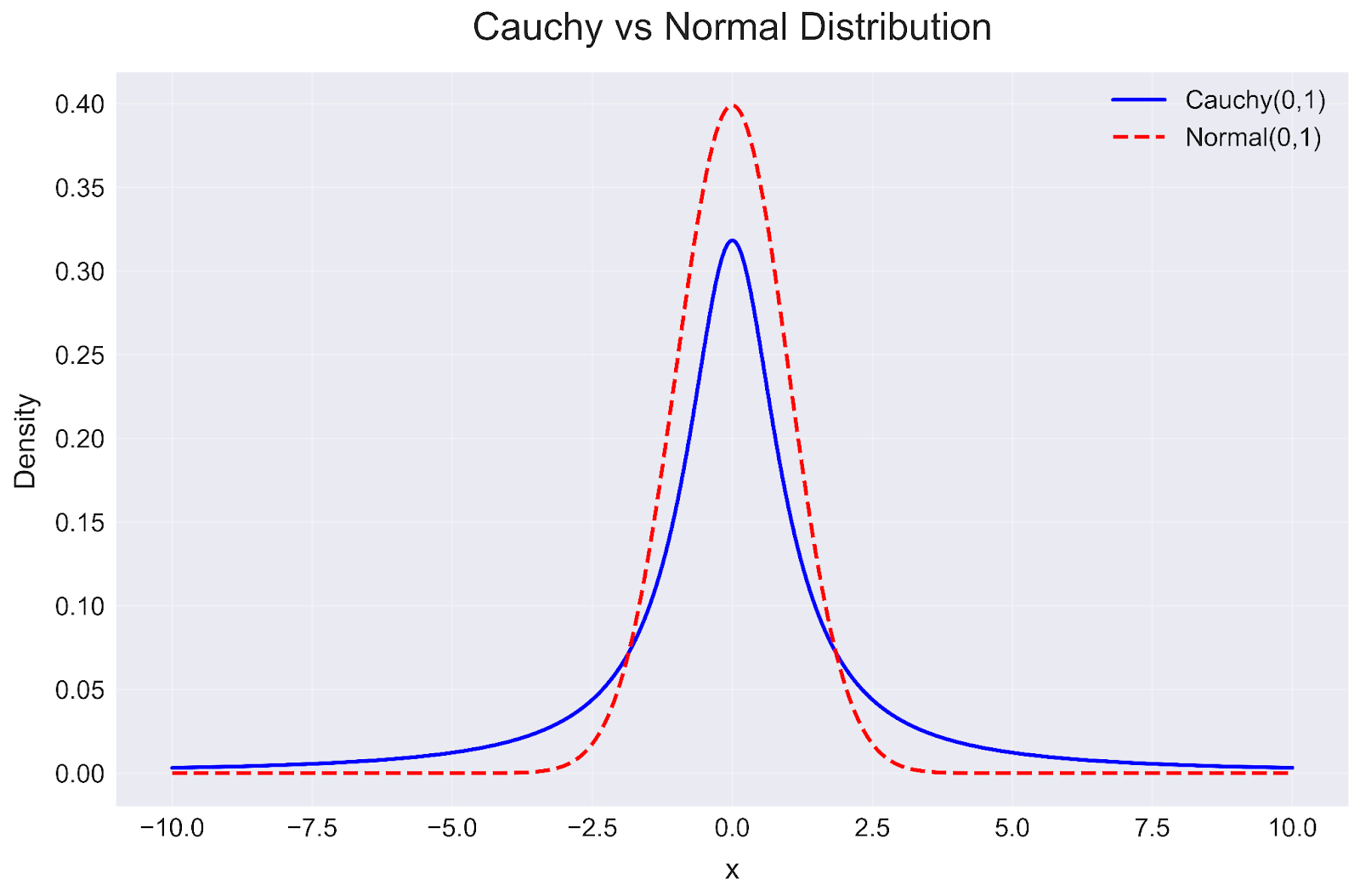
Cauchy-Verteilung in Python. Bild vom Autor

Diese Visualisierung zeigt mehrere wichtige Erkenntnisse:

1. Scheitelhöhe: Die Normalverteilung erreicht eine höhere Spitzendichte (ca. 0,4) als die Cauchy-Verteilung (ca. 0,32), was darauf hindeutet, dass die Werte bei der Normalverteilung stärker um den Mittelpunkt konzentriert sind.
2. Heavy Tails: Beachte, dass die blaue Linie der Cauchy-Verteilung höher bleibt als die rot gestrichelte Linie der Normalverteilung, je weiter wir uns vom Zentrum entfernen. Diese "schweren Schwänze" bedeuten, dass Extremwerte bei einer Cauchy-Verteilung viel wahrscheinlicher sind als bei einer Normalverteilung.
3. Praktische Implikationen: Da die Schwänze der Cauchy-Verteilung schwerer sind, eignet sie sich besser für die Modellierung von Phänomenen, bei denen Extremereignisse häufiger auftreten, als sie von einer Normalverteilung vorhergesagt würden, z. B. bei Finanzmarktrenditen oder bestimmten physikalischen Phänomenen.

Dieser Vergleich hilft zu erklären, warum die Cauchy-Verteilung oft in Szenarien verwendet wird, in denen die Normalverteilung die Wahrscheinlichkeit von Extremereignissen unterschätzt. Während beide Verteilungen um ihren Mittelpunkt symmetrisch sind, eignet sich die Cauchy-Verteilung aufgrund ihrer starken Schwänze besser für die Modellierung von Systemen, in denen Ausreißer keine seltenen Ausnahmen sind, sondern häufig auftreten.

Wann die Cauchy-Verteilung nützlich ist

Die Cauchy-Verteilung dient bestimmten Zwecken bei der Datenanalyse und Modellierung. Sehen wir uns an, wie sie in verschiedenen Bereichen effektiv eingesetzt wird.

Finanzen: Marktunsicherheit bewältigen

Renditen modellieren

Die Finanzmärkte sind für ihre Unberechenbarkeit bekannt und erleben oft dramatische Kursschwankungen, die unter der Annahme einer Normalverteilung als "unmöglich" gelten würden. Die Cauchy-Verteilung glänzt hier, denn:

• Sie fängt natürlich "schwarze Schwäne" wie Marktcrashs oder plötzliche Erholungen ein.
• Sie spiegelt die Realität besser wider, dass extreme Marktbewegungen häufiger vorkommen, als traditionelle Modelle vorhersagen.
• Er unterschätzt das Risiko großer Preisbewegungen nicht.

Während der Finanzkrise 2008 sind zum Beispiel viele traditionelle Modelle gescheitert, weil sie von einer Normalverteilung ausgingen. Ein auf Cauchy basierendes Modell hätte die Möglichkeit solch extremer Marktbewegungen besser vorhersehen können.

Risikobewertung

Bei der Bewertung von Investitionsrisiken bietet die Cauchy-Verteilung eine konservativere und realistischere Sichtweise. Es hilft Risikomanagern, angemessenere Kapitalreserven festzulegen, indem es Extremszenarien berücksichtigt, die Wahrscheinlichkeit signifikanter Verluste oder Gewinne besser einschätzt und ein realistischeres Modell für Stresstests von Portfolios bietet. Dieser Ansatz zur Risikobewertung hilft Finanzinstituten, sich auf unwahrscheinliche, aber folgenreiche Marktereignisse vorzubereiten.

Bayessche Statistik: Robuste statistische Inferenz

Frühere Ausschüttungen

Bei der Bayes'schen Analyse ist die Wahl der richtigen Prioritätsverteilung entscheidend. Die Cauchy-Verteilung ist hier besonders wertvoll, denn:

• Durch die starken Schwänze ist es weniger wahrscheinlich, dass wichtige Parameterwerte versehentlich ausgeschlossen werden.
• Es ist besonders nützlich für Skalenparameter (wie Standardabweichungen) in hierarchischen Modellen
• Es hilft zu verhindern, dass das Modell zu viel Vertrauen in seine Schätzungen hat

Wenn wir zum Beispiel die Wirksamkeit einer neuen medizinischen Behandlung analysieren, können wir mit einem Cauchy-Prior für die Effektgröße sicherstellen, dass wir die Möglichkeit großer Behandlungseffekte nicht unterschätzen.

Robuste Regression

Die traditionelle Regression kann durch Ausreißer stark beeinflusst werden. Die Verwendung von Cauchy-verteilten Fehlertermen hilft dabei, robustere Modelle zu erstellen, indem sie das Modell weniger empfindlich gegenüber extremen Beobachtungen macht. Die Ergebnisse bleiben auch dann zuverlässig, wenn die Daten Ausreißer enthalten, und die Vorhersagen sind stabiler, wenn ungewöhnliche Datenpunkte vorhanden sind. Diese Robustheit macht Cauchy-verteilte Fehlerterme besonders wertvoll bei der Arbeit mit realen Datensätzen, die oft unerwartete oder extreme Werte enthalten.

Maschinelles Lernen und Datenwissenschaft: Resiliente Modelle bauen

Robuste Algorithmen

Modernes maschinelles Lernen arbeitet oft mit verrauschten Daten aus der realen Welt. Die Cauchy-Verteilung hilft dabei, belastbarere Algorithmen zu entwickeln:

• Ein besseres Modell für Rauschen in Sensordaten erstellen
• Hilfe beim Umgang mit Ausreißern in Trainingsdaten, ohne sie zu entfernen
• Lernalgorithmen robuster gegenüber beschädigten Datenpunkten machen

In der Computer Vision zum Beispiel kann die Verwendung von Cauchy-verteilten Rauschmodellen den Algorithmen helfen, besser mit Bildartefakten oder Sensorfehlern umzugehen.

Generative Modelle

In fortgeschrittenen Anwendungen des maschinellen Lernens hilft die Cauchy-Verteilung, flexiblere Modelle zu erstellen. Sie ist nützlich für Variations-Autoencoder, wenn die Daten stark schwanzlastig sind, hilft bei der Erzeugung realistischerer synthetischer Daten, die gelegentlich Extremwerte enthalten, und ist wertvoll für die Modellierung latenter Räume, in denen Normalverteilungen zu restriktiv sind. Diese Flexibilität macht die Cauchy-Verteilung besonders nützlich für generative Modellierungsaufgaben, bei denen es darauf ankommt, die gesamte Bandbreite der möglichen Datenvariationen zu erfassen.

Verwechslung der Cauchy-Verteilung mit anderen Verteilungen

Es ist üblich, die Cauchy-Verteilung mit anderen ähnlichen Verteilungen zu verwechseln. Wir wollen uns die wichtigsten Unterschiede ansehen, damit du die richtige Wahl für deine Analyse treffen kannst.

Cauchy-Verteilung vs. Normalverteilung

Die Normalverteilung ist oft die Standardwahl für viele Analysen, aber es gibt wichtige Unterschiede zwischen ihr und der Cauchy-Verteilung:

Schwanzverhalten 

Obwohl beide Verteilungen symmetrisch sind, erzählen ihre Schwänze sehr unterschiedliche Geschichten: Die Normalverteilung legt nahe, dass Werte über drei Standardabweichungen extrem selten sind. Die Cauchy-Verteilung sagt uns, dass Extremwerte viel häufiger vorkommen, als du vielleicht erwartest.

Statistische Eigenschaften 

Diese Verteilungen unterscheiden sich grundlegend darin, wie wir sie analysieren können: Die Normalverteilung hat wohldefinierte Momente (Mittelwert = μ, Varianz = σ²). Die Cauchy-Verteilung hat keinen definierten Mittelwert und keine Varianz, was traditionelle statistische Methoden unbrauchbar macht.

Praktische Implikationen 

Dieser Unterschied ist in realen Anwendungen wichtig: Verwende die Normalverteilung, wenn sich deine Daten um einen zentralen Wert mit vorhersehbarer Streuung gruppieren. Verwende die Cauchy-Verteilung, wenn deine Daten häufig Extremwerte aufweisen, die unter normalen Annahmen "unmöglich" wären.

Cauchy vs. Laplace-Verteilung

Die Laplace-Verteilung mag auf den ersten Blick der Cauchy-Verteilung ähneln, aber es gibt wichtige Unterschiede, die sie voneinander unterscheiden:

Schwanzverhalten 

Beide Verteilungen haben schwerere Schwänze als die Normalverteilung, aber sie unterscheiden sich darin, wie schwer sie sind: Die Schwänze der Laplace-Verteilung nehmen exponentiell ab. Die Schwänze der Cauchy-Verteilung zerfallen langsamer (polynomial), wodurch Extremwerte noch wahrscheinlicher werden.

Symmetrie 

Beide Verteilungen sind symmetrisch um ihren Mittelpunkt, aber sie unterscheiden sich darin, wie sich ihre Schwänze verhalten: Die Laplace-Verteilung zeigt einen exponentiellen Zerfall in den Schwänzen. Die Cauchy-Verteilung zeigt einen polynomialen Zerfall, wodurch ihre Schwänze schwerer sind als die Laplace-Verteilung.

Praktische Anwendungsfälle 

Wenn du diese Unterschiede kennst, kannst du das richtige Werkzeug auswählen: Verwende die Laplace-Verteilung, wenn du gelegentliche Ausreißer erwartest, aber trotzdem definierte Momente brauchst. Verwende die Cauchy-Verteilung, wenn du häufige Extremwerte erwartest und keine Mittelwerte berechnen musst.

Fazit

Die Cauchy-Verteilung wird zwar nicht so häufig verwendet wie die Normalverteilung, ist aber in Bereichen, in denen Daten ein starkes Schwanzverhalten aufweisen, Robustheit gegenüber Ausreißern erforderlich ist oder theoretische Eigenschaften stabiler Verteilungen von Interesse sind, von großer Bedeutung. Ob in der Physik, im Finanzwesen oder in der Bayes'schen Statistik - das Verständnis der Cauchy-Verteilung verbessert die Fähigkeit, Daten zu modellieren und zu interpretieren, die erhebliche Schwankungen und Ausreißer aufweisen.

Für ein tieferes Verständnis verwandter Wahrscheinlichkeitsverteilungen könnte dir die folgende Serie nützlich sein: In unserem Leitfaden zur Gauß-Verteilung geht es um die am weitesten verbreitete Wahrscheinlichkeitsverteilung, die einen ausgezeichneten Kontrast zur Cauchy-Verteilung mit ihren starken Schwänzen darstellt. Unser Leitfaden zur Poisson-Verteilung befasst sich mit der Modellierung von diskreten Ereignissen über Zeit und Raum, während unser Leitfaden zur Binomialverteilung die Mathematik hinter der Abfolge von unabhängigen Versuchen erklärt. Für diejenigen, die sich für die Grundlagen der Wahrscheinlichkeitstheorie interessieren, bietet unser Leitfaden zur Bernoulli-Verteilung Einblicke in die Bausteine komplexerer Verteilungen.