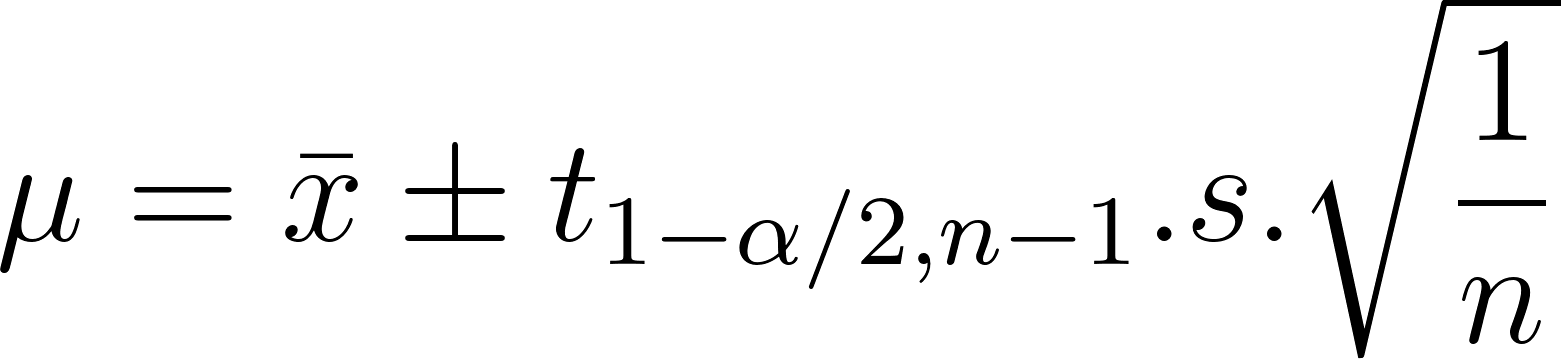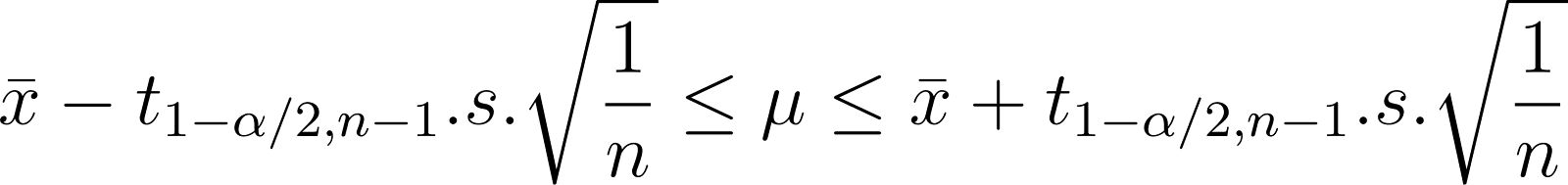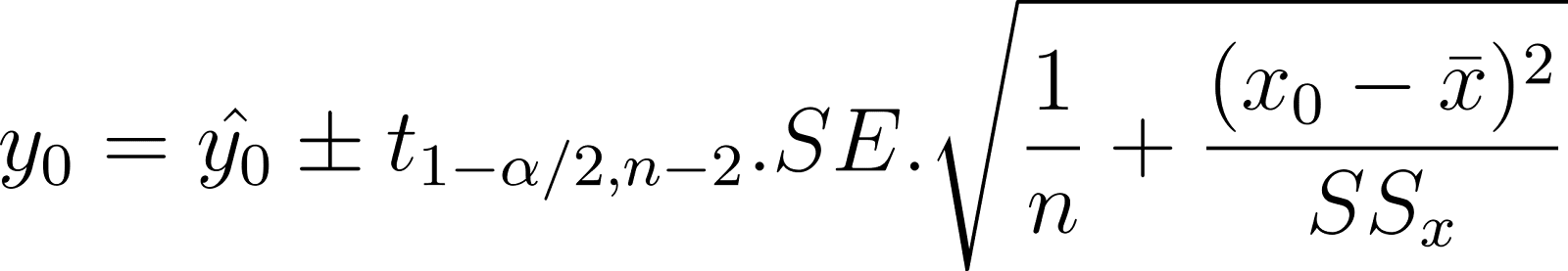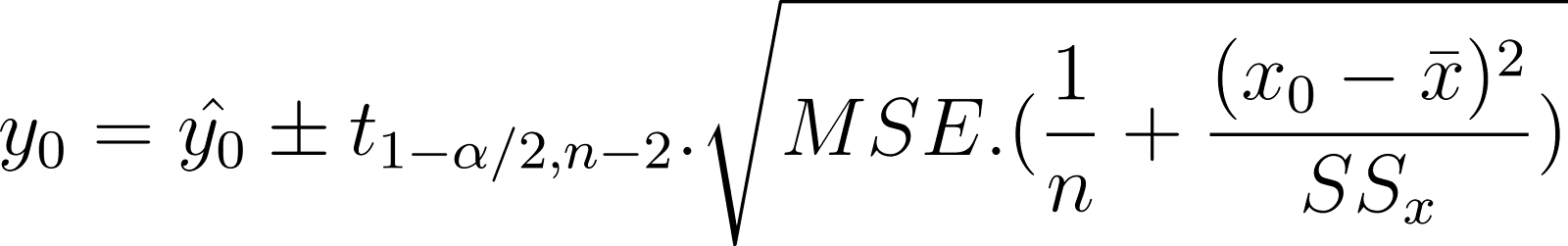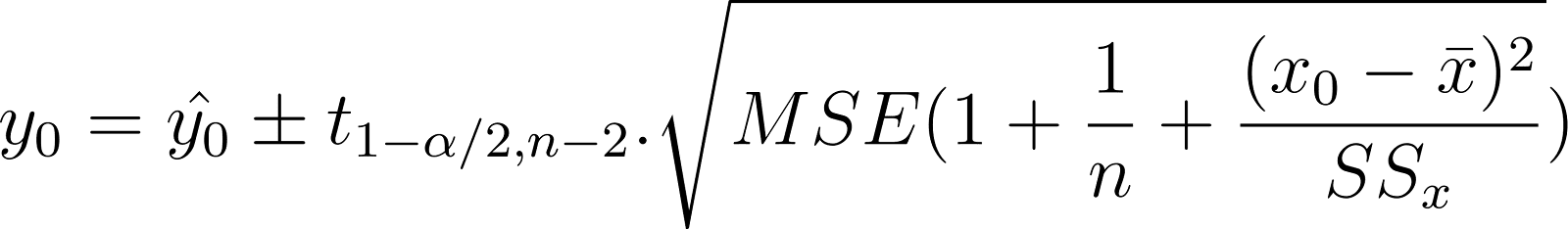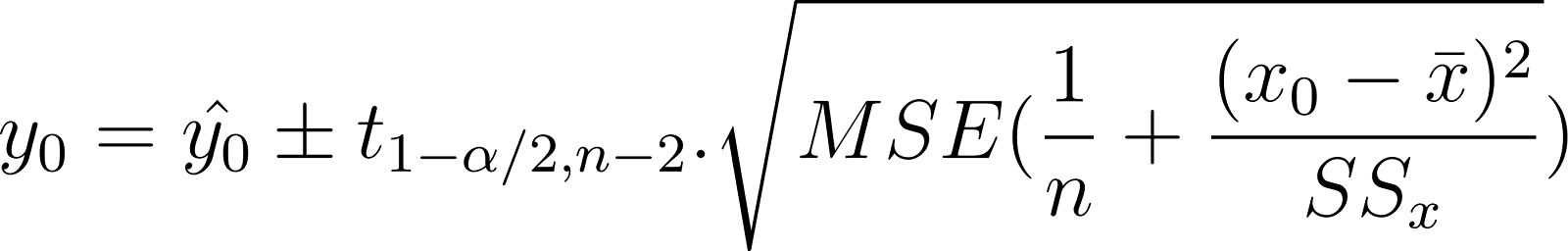Confidence vs Prediction Intervals: Understanding the Difference

Differences Between Prediction Intervals and Confidence Intervals

The two concepts - prediction intervals and confidence intervals are closely related. The same analysis can often involve the use of both kinds of intervals. So, it is helpful to compare them head to head. 

Purpose and interpretation

When you need to know a population parameter, such as a mean, you use a sample to estimate this parameter. Since the sample size is typically much smaller than the population, the sample’s parameter estimate is imperfect. The confidence interval is the range (of the sample estimate) expected to contain the population parameter. 

Regression coefficients are also considered population parameters. Because they are estimated based on a sample (and not the whole population), some error is baked into these parameters. Thus, regression coefficients can also be expressed with a confidence interval. 

Furthermore, you can use regression to predict either:

• The average value of a dependent variable (like the average weight of 2-year-old dogs) or
• The value of an individual data point (like an individual 2-year-old dog). 

The former uses a confidence interval, and the latter uses a prediction interval. The following section explains this difference in greater detail.

Calculation and width of the interval

Calculating the confidence interval for statistical inference 

As explained previously, the confidence interval is proportional to the standard deviation and inversely proportional to the sample size. The confidence interval of the population mean, 𝛍, is expressed as:

In the above expression:

• x is the sample mean, the estimate, which you can measure
• 𝛍 is the population mean, the population parameter you want to estimate. 
• n is the sample size
• s is the sample standard deviation
• t is the critical value of the Student’s T-distribution at
• Significance level of 1 - α
• n-1  degrees of freedom
• You can find the T values from standardized tables - just Google for “Student’s T table.” 

Thus, the range of 𝛍 is:

Understanding confidence levels and significance levels 

Notice also that the size of the interval is proportional to the t-value. If you want an extremely high degree of confidence (certainty) that the actual value lies within the given range, that range has to be very large. The lower the degree of confidence, the narrower the interval. But, a very low degree of confidence is not very useful. So, in practice, it is common to choose confidence levels of 90%, 95%, 99%, etc. 

If you have a confidence level of 95%, it leads to a significance level of 5%. Assuming a two-sided interval, you need to find the t-critical value at 2.5% (0.025). 

Conceptually, all intervals are expressed as follows:

Observe that in all cases, the larger the error, the wider the interval. This error is calculated differently depending on the use case. For inference, the error is the standard deviation. For regression, the error is shown in the next sections. 

Calculating the confidence interval for regression 

When you predict the average value of the dependent variable, you estimate its range using the confidence interval. For example, you want to predict a range for the average weight of 2-year-old dogs based on their age. This is called the confidence interval of the mean response. It is also considered a population parameter because it is a property of the entire population. The interval is expressed as:

In the above expression:

• y0 is the true value of the predicted parameter. 
• y0  is the value predicted using the regression relationship. 
• The critical t-value is explained in the previous section
• n is the sample size
• (x0  - x) is the difference between the mean value of x and x0, for which you are trying to predict y0. Notice that the larger this difference, the larger the interval. Thus, you get narrow intervals (and more accurate predictions) for values of x close to the sample average. 
• SSx is the squared deviation of the sample of x values. It is expressed as:

• SE is the standard error of the estimate. It is the square root of the mean square error (MSE). The MSE is the variance of the error. So, the SE is analogous to the standard deviation of the error. The MSE is based on the residual error. It is expressed as: 

In the above expression, the summation term is also called the sum of squares of the residuals. The residual is the difference between the true value of y and the predicted value of y. 

Using the MSE instead of the SE, the confidence interval of the mean response can also be written as:

Compare the above expression to the conceptual relation shown earlier. 

Observe that the error takes into account:

• The difference between the actual and predicted values of y. 
• The difference between the average value of x and the value of xo, for which you want to generate the prediction
• The overall dispersion of x values (relative to their mean) 

Calculating the prediction interval for regression 

To predict the exact value of an individual data point (not the average), you estimate its range using the prediction interval. For example, you want to predict the range for one specific 2-year-old dog's actual weight based on age. This is called the prediction interval, and it is expressed as:

Compare this to the confidence interval shown earlier:

Notice that both expressions are pretty similar. The only difference is the additional error term in the prediction interval. The prediction interval has an additional MSE term inside the square root than the confidence interval. This is to take into account the variability in y values, which you want to predict. This makes the prediction interval wider than the confidence interval. 

The sketch below shows the confidence and prediction intervals in relation to the point estimate (predicted value).

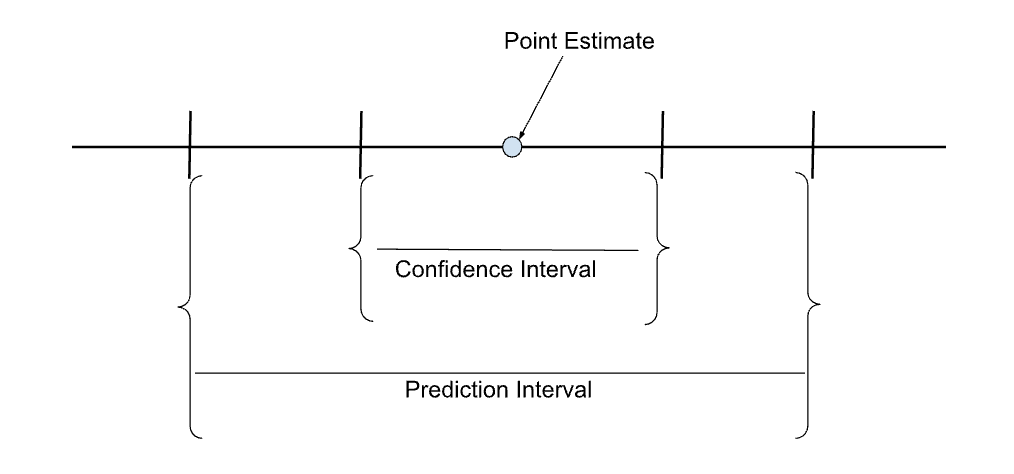
Comparing confidence and prediction intervals of a point estimate. Image by author.

The schematic sketch below shows the confidence and prediction intervals in relation to the regression—notice also that the intervals are the narrowest in the region of the mean. 

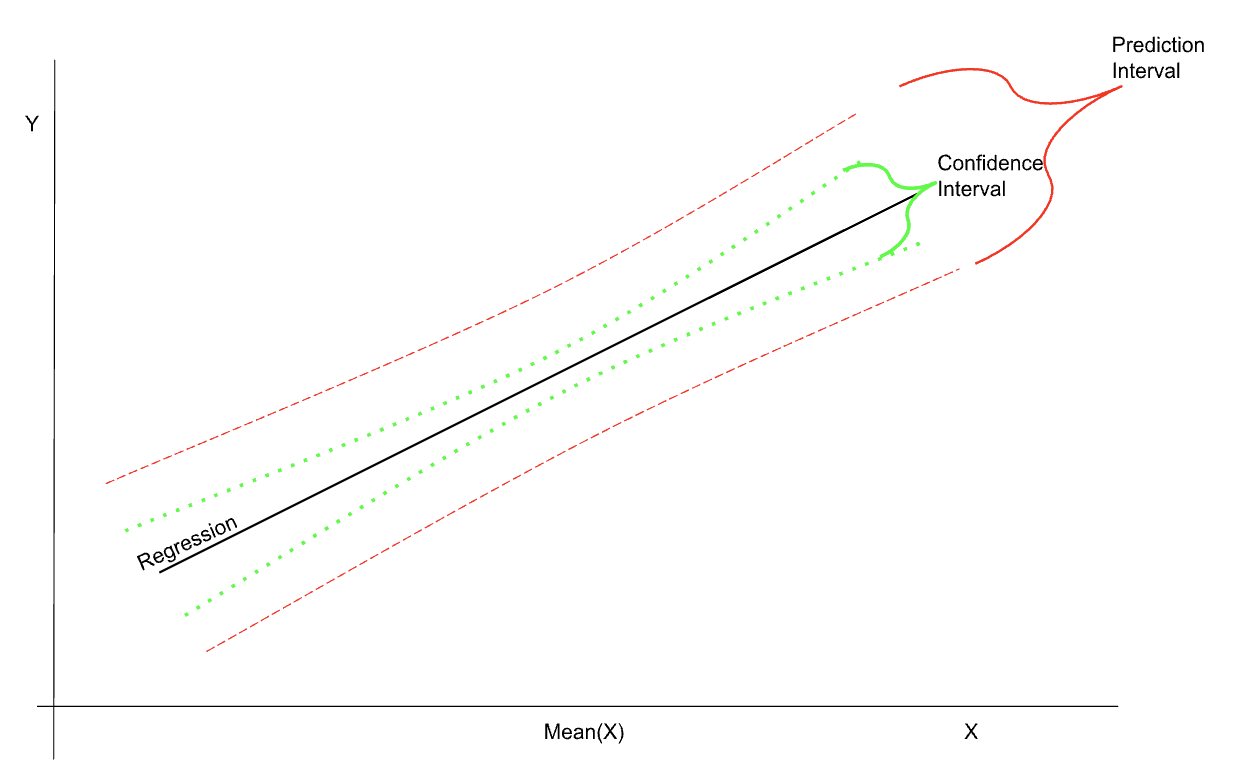
Illustration of confidence and prediction intervals in regression. Image by author.

When to Use a Confidence Interval

The previous sections discussed the basics of confidence and prediction intervals, their uses, and the formulae used to calculate them. This section gives practical examples of when to use confidence and prediction intervals. 

A confidence interval is used when estimating a population parameter. To estimate the population parameter, you can either:

1. Use direct measurements based on a random sample
2. Use a regression model based on a random sample

Some example use cases of the confidence interval are:

• Estimating a population parameter based on measuring a random sample. For example, to estimate the average height and weight of newborn infants, you take the measurements of a random sample of newborns. 
• Estimating a population’s behavior by studying a random sample. This use case is common clinical trials, where you try to estimate the effects of a drug on the population by studying its effects on a random sample. 
• Predicting the mean response of a dependent variable based on a regression analysis done on a random sample. For instance, you want to predict the average weight of 55-day-old puppies based on a sample of puppy weights measured every 15 days. 
• Setting tolerance limits in manufacturing processes. For example, if a machine produces parts of a specified weight, not every part has precisely the same weight as the specification. The weight of each part lies within a confidence interval of the specified weight. This interval is the tolerance limit. Any parts with weights beyond the tolerance limits are rejected. The machine is expected to produce parts that are mostly within the tolerance limit. 
• Quality control. Suppose you want to establish whether the parts produced by a machine are within the tolerance limit. It is not possible to measure every single part. You have to rely on taking random samples, measuring them, and then using the sample estimates to gauge the population parameters. 
• Testing hypotheses. Confidence levels and significance levels are two sides of the same coin. Significance level = 1 - Confidence level.  A confidence interval, with a specified confidence level, includes those data points for which the null hypothesis is true at a significance level of (1 - the specified confidence level). 

When to Use a Prediction Interval

Prediction intervals are used whenever you predict the expected value of an individual data point based on observations of (and regression analysis on) a random sample. 

Some practical examples include: 

• Predicting the range of an individual data point based on a regression analysis. Because individual data points can have higher variability (than the sample mean), you need a wider range of the prediction interval. For instance, you want to predict the weight of an individual 55-day-old puppy based on a random sample of puppy weights measured every 15 days. 
• You can use Monte Carlo simulations to predict the value of an unknown variable. Because Monte Carlo methods are probabilistic, you get a slightly different output each time you run the model. These differences between different outputs are encoded in the Monte Carlo Uncertainty Interval, which is conceptually similar to a prediction interval. 
• In standard regression, you build a relationship to predict the mean value of a parameter. In quantile regression, you build different models to predict each quantile of the target parameter. This also allows you to construct more granular prediction intervals. 
• Machine learning models are concerned with predicting the value of an unknown parameter. These models are typically based on statistical methods and, hence, predict the average value of the unknown quantity. Thus, the model’s output includes both the expected (average) value and the prediction interval. 
• Deep learning models use a series of neural networks to make predictions. To assess the uncertainty in the output, it is common to randomly drop different neurons to study the variability in the output. The variance in these predictions is used to construct the prediction interval. 
• In time series forecasting, the goal is to predict the value of an observable in a future time step. Predictions are based on statistical models like ARIMA, which performs auto-regression on a moving average. Thus, it predicts the expected value. The actual observed values are contained within a prediction interval of the expected value. This prediction interval is calculated as a function of the standard deviation. For example, for a 95% confidence level, the prediction interval is within 1.96 standard deviations of the expected value. Furthermore, multi-step predictions, which involve a longer forecast horizon, also involve a larger prediction interval. To learn more about time series, refer to the DataCamp course on time series analysis. 

Confidence Interval vs Prediction Interval: A Summary

Confidence intervals and prediction intervals are often used in the same context, making it important to understand how they differ. 

This table summarizes the differences based on the discussion in the previous sections:

Implementing Confidence Intervals and Prediction Intervals in R

This section shows hands-on examples of using the R programming language to estimate confidence and prediction intervals. R is a language designed for statistical applications, and it comes with inbuilt datasets and statistical functions. 

To learn more about regressions using R, follow the DataCamp tutorial on linear regressions in R.

The examples below use the inbuilt Orange dataset. This dataset tracks the circumference (in millimeters) and age (in days) of orange trees. Naturally, one would expect that the older the tree, the larger its circumference. 

Implementing confidence intervals in R

The examples below show how to estimate confidence intervals for summary statistics and regression analyses. 

Confidence interval in summary statistics

To get the confidence interval for the mean, run the standard T-test using the t.test() function on the dataset:

t.test(Orange$circumference)

The output looks like the example below:

t = 11.923, df = 34, p-value = 1.076e-13 
alternative hypothesis: true mean is not equal to 0 
95 percent confidence interval:
   96.10926 135.60502 
sample estimates: 
mean of x
   115.8571 

It gives you the mean estimate and the 95% confidence interval. By default, the T-Test function uses a confidence level of 95%. Use the conf.level parameter to specify a different confidence interval, such as 99%. 

> t.test(Orange$circumference, conf.level = 0.99)

This command yields the following output:

t = 11.923, df = 34, p-value = 1.076e-13 
alternative hypothesis: true mean is not equal to 0
99 percent confidence interval:
   89.34458 142.36970 
sample estimates: 
mean of x
   115.8571 

Notice that the estimated mean is the same in either case. However, the interval needs to be wider to have a higher confidence level. Based on the data, I am 99% confident that the mean lies between 89.3 and 142.4, but only 95% confident that it lies between 96.1 and 135.6. For a parameter estimated from a given sample, the narrower the confidence interval, the lower the confidence level. 

Confidence interval in regression 

In regression analyses, you need the confidence intervals for the regression coefficients and predicted values. 

For an in-depth understanding of how to do R regressions, follow the DataCamp course on Inference for Linear Regression in R.

Confidence interval of regression coefficients 

Regression coefficients are estimated by analyzing a random sample. Thus, they are not the true coefficients for the entire population. The estimates of the regression parameters have some errors associated with them. In addition to their estimated values, it is helpful to give a confidence interval for the parameters. 

Use the lm() function to build a linear model based on the Orange dataset to predict the circumference (in mm) of orange trees given their age (in days):

model_orange <- lm(circumference ~ age, data = Orange)

Check the coefficients of this linear model:

model_orange

This command shows the model’s parameters (intercept and slope) as below:

Coefficients: (Intercept)          age
                              17.3997       0.1068  

Use the confint() function to calculate the 95% confidence intervals:

confint(model_orange, level = 0.95)

You can now see the 95% confidence intervals of the slope and intercept estimated by the model:

                          2.5 %                   97.5 %
(Intercept)     -0.14328303       34.9425835 
age                  0.08993141          0.1236092

Confidence interval of a mean response prediction 

Use the regression model created above to predict the expected average circumference of 900-day-old trees. Use the interval parameter to specify a confidence interval. 

predict(model_orange, data.frame(age = 900), interval = "confidence", level = 0.95)  

The output includes the prediction (fit) and the confidence interval (lwr and upr for lower and upper limits), as shown below:

       fit                    lwr              upr
 1     113.4929        105.3211       121.6647

Implementing prediction intervals in R

Use the same model as above to predict the specific circumference of an individual orange tree that is 900 days old. Use the interval parameter to specify that you want the prediction interval. 

> predict(model, data.frame(age = 900), interval = "prediction", level = 0.95)  

The output resembles the example below:

       fit                    lwr              upr
1      113.4929        64.5118        162.4741

Notice that in both cases, the predicted value of the circumference is the same - 113.49. However, the prediction interval is much wider than the confidence interval. The confidence interval of the prediction is the range that is expected to contain the average circumference of 900-day-old trees. The prediction interval is the expected range of the circumference of an individual 900-day-old tree. This is because there can be considerably more variation in individual trees which is smoothened out when considering the average value. 

Common Misconceptions and Pitfalls

Statistical intervals are commonly used in applied statistical fields like data analysis, pharmaceuticals, econometrics, etc. For those without an academic background in statistics, it is easy to confuse confidence intervals and prediction intervals. 

Some common misconceptions are discussed below: 

• Making a prediction without considering the prediction interval. 
• When you use a regression model to predict the value of the dependent variable for a given value of the independent variable, the regression equation gives you the expected value of the dependent variable. The actual value rarely matches the expected value but lies within a certain range of the expected value, as specified by the prediction interval. 
• Assuming that a regression analysis involves only prediction intervals.
• You make two types of predictions using regression models - 1) predicting a future value and 2) predicting the mean response. In the orange tree example, you can try to predict 1) the circumference of a specific orange tree that is 900 days old or 2) the average circumference of all trees that are 900 days old. In both cases, the expected value is the same. However, the former involves the prediction interval, and the latter involves the confidence interval. 
• Believing that the narrower interval is the better one.
• You might sometimes be tempted to just use the narrower interval while using the result of a regression study. The confidence interval is not somehow “better” because it is narrower. It is narrower because it gives the range for something different than the prediction interval does. Consider whether you are trying to predict the average value of the dependent variable or whether you want to predict an individual data point.
• Mistaking a confidence interval for a prediction interval. 
• If your prediction involves determining the value of a population parameter from a sample or predicting the mean response (average value) from a regression, you use the confidence interval. If you try to predict some property of an individual data point based on a regression, use the prediction interval. 

Conclusion

This article provided an overview of confidence intervals and prediction intervals. It also explains the difference between these similar-sounding concepts and offers practical examples of when to use each type of interval. The article also showed how to calculate prediction and confidence intervals using the R programming language. 

To learn how to apply statistical formulas using Python, refer to the DataCamp course on statistics in Python. Lastly, if you are preparing for job interviews involving statistics, check out the DataCamp course on statistics interview questions in Python.