Distribuição de Cauchy: Entendendo os dados de cauda pesada

A distribuição de Cauchy apresenta um intrigante quebra-cabeça estatístico. Embora compartilhe a conhecida forma de sino com muitas outras distribuições de probabilidade contínua, ela desafia a análise convencional por não ter uma média e uma variância definidas. Com o nome do matemático Augustin-Louis Cauchy, essa distribuição surge naturalmente em campos que vão desde a modelagem financeira até a estatística bayesiana.

Como ferramenta de ensino, a distribuição de Cauchy ilustra conceitos estatísticos fundamentais com notável clareza. Ele demonstra a não convergência das médias das amostras, destaca a importância das suposições de distribuição e mostra o desempenho dos estimadores em condições variadas.

Você quer dominar esses conceitos estatísticos e suas aplicações na ciência de dados? Explore nossa carreira de Cientista de Machine Learning em R, onde você aprenderá a implementar essas ideias usando a programação em R.

O que é a distribuição de Cauchy?

A distribuição de Cauchy é uma distribuição de probabilidade contínua famosa por suas propriedades exclusivas e caudas pesadas. Ele é caracterizado por dois parâmetros principais:

1. Parâmetro de localização (θ): Esse parâmetro determina onde o pico (ou centro) da distribuição se encontra no eixo x. Pense nisso como se você estivesse deslocando toda a distribuição para a esquerda ou para a direita sem alterar sua forma.
2. Parâmetro de escala (σ): Esse parâmetro controla o grau de dispersão da distribuição. Valores maiores de σ criam distribuições mais amplas e planas com caudas mais pesadas. Você pode pensar nisso como se estivesse esticando ou apertando a distribuição horizontalmente.

A distribuição é definida matematicamente por sua função de densidade de probabilidade (PDF):

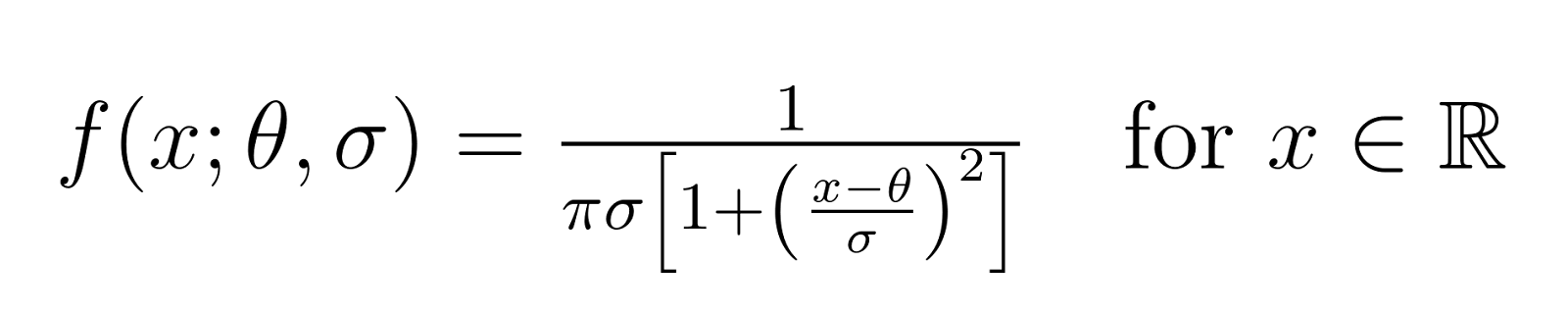
Quando definimos θ = 0 e σ = 1, obtemos o que chamamos de distribuição padrão de Cauchy. Essa é a forma mais simples de distribuição e serve como ponto de referência para você entender casos mais complexos.

As principais características da distribuição de Cauchy

As propriedades definidoras das distribuições de Cauchy

Caudas pesadas

Pense na distribuição de Cauchy como a distribuição de "eventos extremos". Enquanto uma distribuição normal sugere que os valores distantes do centro são muito raros (como encontrar uma pessoa com 2,5 metros de altura), a distribuição de Cauchy nos diz que os valores extremos ocorrem com mais frequência do que você poderia esperar. 

Por exemplo, nos retornos do mercado de ações, grandes mudanças de preço em um único dia (como durante quedas ou altas do mercado) ocorrem com mais frequência do que uma distribuição normal poderia prever. As caudas pesadas da distribuição de Cauchy podem capturar melhor esses eventos de "cisne negro".

Média e variância indefinidas

Essa talvez seja a propriedade mais fascinante da distribuição de Cauchy. Diferentemente da maioria das distribuições que você já encontrou, a distribuição de Cauchy não tem uma média significativa (mean) ou dispersão (variance). 

Para entender por que isso é importante: se você pegar amostras repetidas de uma distribuição de Cauchy e tentar calcular a média delas, não convergirá para nenhum valor específico, mesmo com milhões de amostras. Isso tem implicações para a análise estatística, pois os métodos estatísticos tradicionais que dependem de médias e variâncias (como testes t ou ANOVA) não funcionam com dados com distribuição de Cauchy.

Simetria

A distribuição de Cauchy é perfeitamente equilibrada em torno de seu parâmetro de localização (θ), como uma imagem espelhada em ambos os lados. Entretanto, essa simetria não significa que ela se comporte como a distribuição normal conhecida. Embora ambas as distribuições sejam simétricas, a distribuição de Cauchy espalha sua probabilidade de forma muito mais ampla. Isso significa que, embora tenha um centro claro, os valores podem se afastar muito desse centro com probabilidade significativa.

Estabilidade

A distribuição de Cauchy tem uma propriedade notável: quando você soma duas variáveis independentes com distribuição de Cauchy, obtém outra distribuição de Cauchy! Essa propriedade, conhecida como estabilidade, é compartilhada apenas com algumas outras distribuições (como a distribuição normal). É particularmente útil em física e modelagem financeira, onde frequentemente precisamos entender como os processos aleatórios combinados se comportam ao longo do tempo.

O que você deve observar ao usar a distribuição de Cauchy

Manuseio de valores discrepantes

A distribuição de Cauchy é excelente para lidar com valores discrepantes porque espera que eles ocorram. Isso o torna particularmente útil em cenários em que os valores extremos são partes naturais dos dados, e não erros a serem removidos. Nesses casos, os métodos tradicionais de detecção de outliers podem ser muito agressivos, sinalizando de forma inadequada pontos de dados legítimos para remoção. A distribuição de Cauchy fornece uma estrutura para a criação de modelos robustos que não serão indevidamente influenciados por observações extremas, o que a torna uma ferramenta valiosa ao trabalhar com conjuntos de dados em que os valores discrepantes são um recurso inerente e não uma anomalia a ser eliminada.

Seleção de modelos

A escolha do uso de uma distribuição de Cauchy depende de seus dados e objetivos. A distribuição de Cauchy é particularmente valiosa quando seus dados frequentemente apresentam valores extremos, quando você está trabalhando com proporções de variáveis normalmente distribuídas ou quando precisa de um modelo robusto que possa lidar com dados de cauda pesada. No entanto, você deve ser cauteloso ao usar a distribuição de Cauchy em determinadas situações: quando precisar confiar em médias e variâncias, quando os dados realmente seguirem uma distribuição de cauda mais leve ou quando a eficiência computacional for a principal preocupação. Compreender essas compensações é útil para que você possa tomar decisões informadas sobre se a distribuição de Cauchy é apropriada para suas necessidades específicas de análise.

Eficiência computacional

Embora a fórmula matemática da distribuição de Cauchy seja simples, trabalhar com ela em termos computacionais pode ser um desafio. A estimativa de parâmetros geralmente requer técnicas especializadas, como Markov Chain Monte Carlo (MCMC), e os métodos padrão de máxima verossimilhança podem ter dificuldades com as caudas pesadas. Felizmente, os pacotes modernos de software estatístico geralmente incluem ferramentas específicas para lidar com as distribuições de Cauchy, tornando mais viável trabalhar com essa distribuição na prática, apesar de suas complexidades computacionais.

Propriedades matemáticas da distribuição de Cauchy

A distribuição de Cauchy possui várias propriedades matemáticas importantes que a tornam única e útil:

• Uma distribuição estável com um comportamento interessante: quando você adiciona duas variáveis com distribuição de Cauchy, obtém outra distribuição de Cauchy com parâmetros em escala. Isso o torna útil no estudo de efeitos cumulativos em física e finanças.
• Momentos indefinidos, incluindo a média e a variância, o que o torna um contraexemplo fascinante na teoria da probabilidade. Essa propriedade ajuda os alunos a entender por que o Teorema do Limite Central exige uma variação finita.
• Uma forma matemáticaelegantemente simples, com um PDF direto e uma função característica. Apesar de seu comportamento complexo, sua descrição matemática básica é surpreendentemente fácil.
• A propriedade de proporção: se você dividir uma variável aleatória normal por outra variável aleatória normal independente, obterá uma distribuição de Cauchy. Isso o torna naturalmente adequado para modelar razões e proporções.
• Fortes aplicações bayesianas, particularmente como uma distribuição prévia em modelos hierárquicos. Suas caudas pesadas o tornam uma excelente opção para parâmetros de escala em que a robustez é importante.

Visualizando a distribuição de Cauchy em R e Python

O comportamento da distribuição de Cauchy é melhor compreendido por meio da visualização. Vamos usar o R para criar gráficos de diferentes distribuições de Cauchy, demonstrando como os parâmetros de localização (θ) e escala (σ) afetam a forma e a posição da distribuição.

Distribuição de Cauchy em R

O R fornece funções para você trabalhar com distribuições de Cauchy por meio do pacote stats. Também usaremos o site ggplot2 para criar visuais claros e com qualidade de publicação:

# Load required libraries
library(ggplot2)  # for plotting
# Note: dcauchy is from the stats package which is loaded by default in R

# Create a sequence of x values
x <- seq(-10, 10, length.out = 1000)

# Generate different Cauchy distributions using stats::dcauchy
# Standard Cauchy (θ = 0, σ = 1)
standard_cauchy <- dcauchy(x, location = 0, scale = 1)

# Location and Scale Adjusted (θ = 2, σ = 3)
adjusted_cauchy <- dcauchy(x, location = 2, scale = 3)

# Highly Scaled (θ = -1, σ = 5)
scaled_cauchy <- dcauchy(x, location = -1, scale = 5)

# Create a data frame for plotting
plot_data <- data.frame(
  x = rep(x, 3),
  density = c(standard_cauchy, adjusted_cauchy, scaled_cauchy),
  distribution = rep(c("Standard (θ=0, σ=1)", 
                      "Adjusted (θ=2, σ=3)", 
                      "Scaled (θ=-1, σ=5)"), 
                    each = length(x))
)

# Create the plot
ggplot(plot_data, aes(x = x, y = density, color = distribution)) +
  geom_line(size = 1) +
  theme_minimal() +
  labs(title = "Comparison of Cauchy Distributions",
       x = "x",
       y = "Density",
       color = "Parameters") +
  theme(legend.position = "bottom",
        plot.title = element_text(hjust = 0.5)) +
  scale_color_brewer(palette = "Set1")

Esse código gera um gráfico de comparação de três distribuições de Cauchy diferentes:

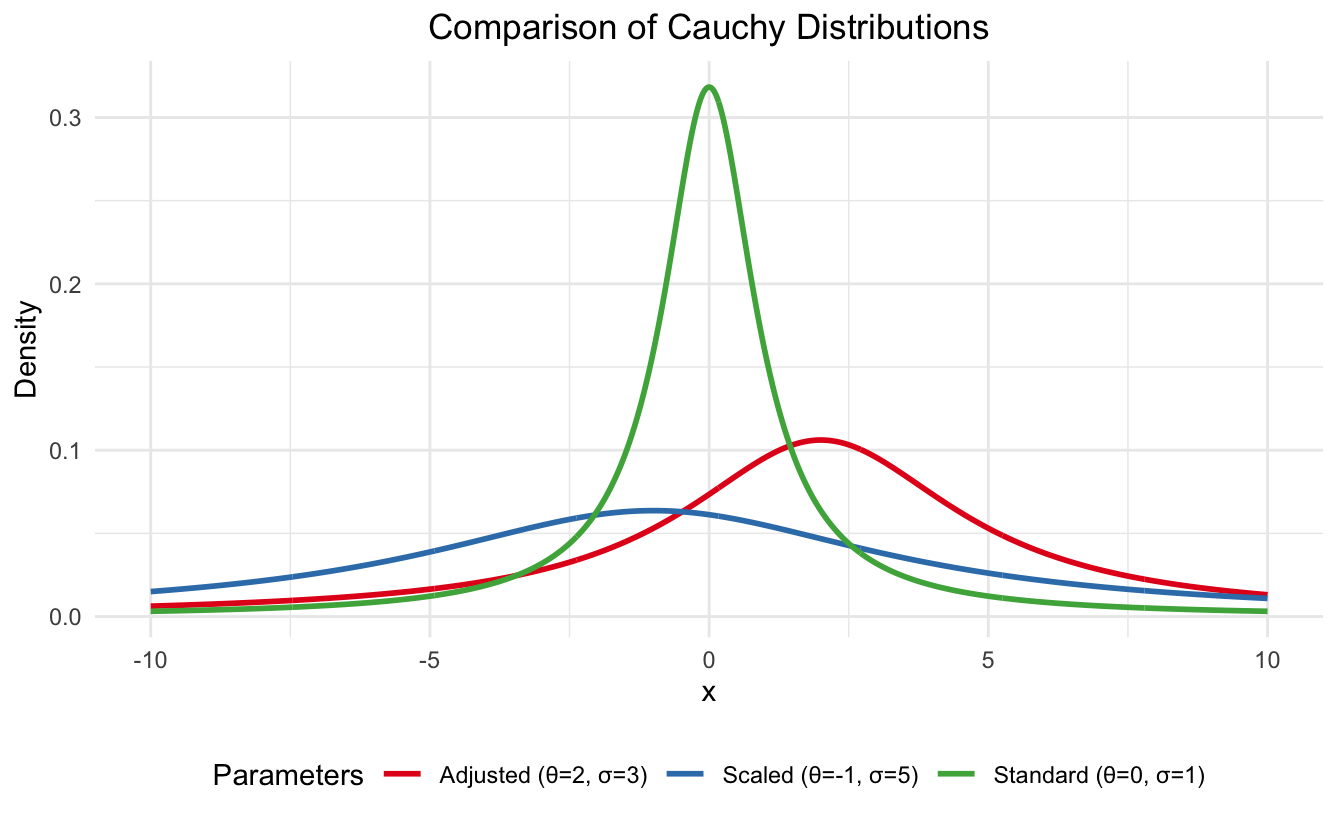
Distribuição de Cauchy no R. Imagem do autor

1. Cauchy padrão (linha verde): Com θ = 0 e σ = 1, isso representa o caso de linha de base. Observe seu pico acentuado em x = 0 e as caudas pesadas simétricas.
2. Cauchy ajustado ao local (linha vermelha): Ao definir θ = 2, você desloca o pico para a direita e mantém a forma. Isso demonstra como o parâmetro de localização afeta o centro da distribuição sem alterar sua dispersão.
3. Cauchy em alta escala (linha azul): Com θ = -1 e σ = 5, isso mostra uma distribuição deslocada e muito mais plana. O parâmetro de escala maior cria caudas mais largas e pesadas e reduz a altura do pico, ilustrando como σ controla a propagação.

A visualização mostra claramente como o aumento do parâmetro de escala (σ) leva a uma distribuição mais plana e espalhada, enquanto o parâmetro de localização (θ) simplesmente desloca toda a distribuição para a esquerda ou para a direita.

Distribuição de Cauchy em Python

Depois de explorar os parâmetros da distribuição de Cauchy no R, vamos usar o Python para comparar a distribuição de Cauchy com sua prima mais conhecida, a distribuição Normal. A pilha de computação científica do Python, particularmente scipy.stats, fornece excelentes ferramentas para que você trabalhe com distribuições de probabilidade.

Embora o pacote stats do R tenha nos dado acesso direto às funções de distribuição de Cauchy, o módulo scipy.stats do Python oferece funcionalidade semelhante com uma interface ligeiramente diferente. Usaremos a matplotlib, a principal biblioteca de plotagem do Python, para criar uma visualização clara:

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# Set style parameters for better visualization
plt.style.use('seaborn')
plt.rcParams.update({
    'font.size': 16,
    'axes.labelsize': 18,
    'axes.titlesize': 24,
    'xtick.labelsize': 16,
    'ytick.labelsize': 16,
    'legend.fontsize': 16,
})

# Create data
x = np.linspace(-10, 10, 1000)
cauchy = stats.cauchy.pdf(x, loc=0, scale=1)
normal = stats.norm.pdf(x, loc=0, scale=1)

# Create the plot
plt.figure(figsize=(12, 8))

# Plot distributions
plt.plot(x, cauchy, 'b-', linewidth=2.5, label='Cauchy(0,1)')
plt.plot(x, normal, 'r--', linewidth=2.5, label='Normal(0,1)')

# Customize the plot
plt.title('Cauchy vs Normal Distribution', pad=20)
plt.xlabel('x', labelpad=10)
plt.ylabel('Density', labelpad=10)

# Customize legend
plt.legend(fontsize=16, bbox_to_anchor=(0.99, 0.99), 
          loc='upper right', borderaxespad=0.)

# Add grid and adjust layout
plt.grid(True, alpha=0.3)
plt.tight_layout()

plt.show()

O código acima cria uma comparação entre a distribuição Cauchy padrão (linha sólida azul) e a distribuição Normal padrão (linha tracejada vermelha), ambas centradas em 0 com um parâmetro de escala de 1.

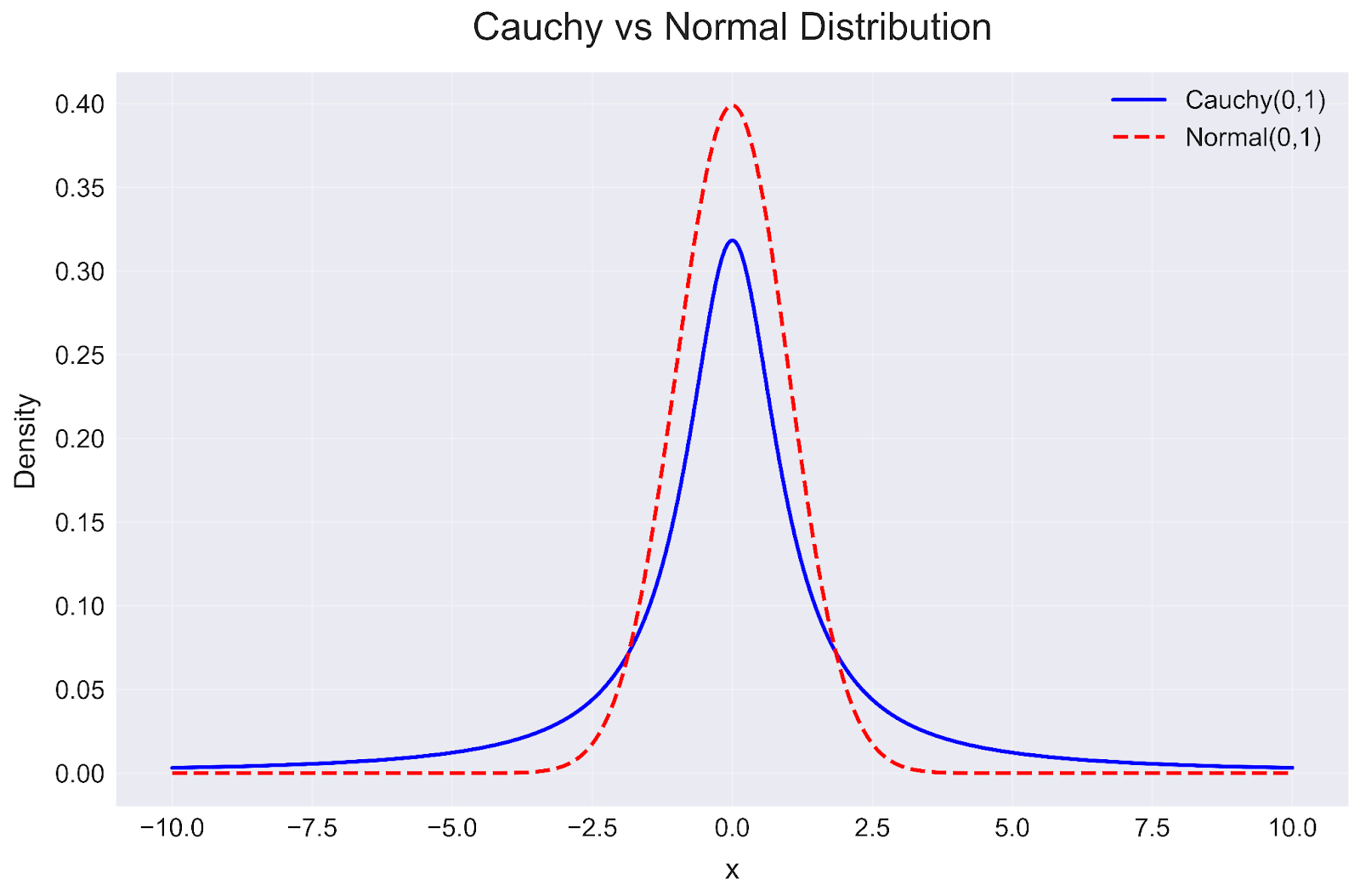
Distribuição de Cauchy em Python. Imagem do autor

Essa visualização revela várias percepções importantes:

1. Altura do pico: A distribuição Normal atinge uma densidade de pico mais alta (aproximadamente 0,4) em comparação com a distribuição Cauchy (aproximadamente 0,32), indicando que os valores estão mais concentrados em torno do centro na distribuição Normal.
2. Caudas pesadas: Observe como a linha azul da distribuição de Cauchy permanece mais alta do que a linha vermelha tracejada da distribuição Normal à medida que nos afastamos do centro. Essas "caudas pesadas" significam que os valores extremos são muito mais prováveis em uma distribuição Cauchy do que em uma distribuição Normal.
3. Implicações práticas: As caudas mais pesadas da distribuição de Cauchy a tornam mais adequada para modelar fenômenos em que eventos extremos ocorrem com mais frequência do que seria previsto por uma distribuição Normal, como retornos do mercado financeiro ou determinados fenômenos físicos.

Essa comparação ajuda a explicar por que a distribuição de Cauchy é frequentemente usada em cenários em que a distribuição Normal subestima a probabilidade de eventos extremos. Embora ambas as distribuições sejam simétricas em torno de seu centro, as caudas pesadas da distribuição de Cauchy a tornam mais apropriada para modelar sistemas em que os valores discrepantes são comuns em vez de raras exceções.

Quando a distribuição de Cauchy é útil

A distribuição de Cauchy tem finalidades específicas na análise e modelagem de dados. Vamos examinar como ele é usado de forma eficaz em diferentes domínios.

Finanças: Gerenciando a incerteza do mercado

Modelagem de retornos

Os mercados financeiros são conhecidos por sua natureza imprevisível, muitas vezes apresentando oscilações drásticas de preços que seriam consideradas "impossíveis" sob as premissas de distribuição normal. A distribuição de Cauchy se destaca aqui porque:

• Ele captura naturalmente eventos do tipo "cisne negro", como quedas de mercado ou altas repentinas.
• Ele reflete melhor a realidade de que os movimentos extremos do mercado ocorrem com mais frequência do que os modelos tradicionais preveem.
• Ele não subestima o risco de grandes movimentos de preços.

Por exemplo, durante a crise financeira de 2008, muitos modelos tradicionais falharam porque assumiram distribuições normais. Um modelo baseado em Cauchy teria previsto melhor a possibilidade de tais movimentos extremos do mercado.

Avaliação de riscos

Ao avaliar os riscos de investimento, a distribuição de Cauchy oferece uma visão mais conservadora e realista. Ele ajuda os gerentes de risco a definir reservas de capital mais adequadas, levando em conta cenários extremos, estimando melhor a probabilidade de perdas ou ganhos significativos e fornecendo um modelo mais realista para portfólios de teste de estresse. Essa abordagem de avaliação de risco ajuda as instituições financeiras a se prepararem para eventos de mercado improváveis, mas impactantes.

Estatística bayesiana: Inferência estatística robusta

Distribuições anteriores

Na análise bayesiana, é fundamental escolher a distribuição prévia correta. A distribuição de Cauchy é particularmente valiosa aqui porque:

• Suas caudas pesadas tornam menos provável que você exclua acidentalmente valores de parâmetros importantes
• É especialmente útil para parâmetros de escala (como desvios padrão) em modelos hierárquicos
• Isso ajuda a evitar que o modelo seja excessivamente confiante em suas estimativas

Por exemplo, ao analisar a eficácia de um novo tratamento médico, o uso de uma prévia de Cauchy para o tamanho do efeito ajuda a garantir que não subestimemos a possibilidade de grandes efeitos do tratamento.

Regressão robusta

A regressão tradicional pode ser muito influenciada por outliers. O uso de termos de erro com distribuição de Cauchy ajuda a criar modelos mais robustos, tornando o modelo menos sensível a observações extremas. Os resultados permanecem confiáveis mesmo quando os dados contêm valores discrepantes, e as previsões são mais estáveis na presença de pontos de dados incomuns. Essa robustez torna os termos de erro distribuídos de Cauchy particularmente valiosos quando se trabalha com conjuntos de dados reais que frequentemente contêm valores inesperados ou extremos.

Machine learning e ciência de dados: Criação de modelos resilientes

Algoritmos robustos

O machine learning moderno geralmente lida com dados ruidosos do mundo real. A distribuição de Cauchy ajuda a criar algoritmos mais resistentes:

• Fornecimento de um modelo melhor para o ruído nos dados do sensor
• Ajudar a lidar com exceções nos dados de treinamento sem removê-las
• Tornar os algoritmos de aprendizado mais robustos em relação a pontos de dados corrompidos

Por exemplo, na visão computacional, o uso de modelos de ruído distribuído de Cauchy pode ajudar os algoritmos a lidar melhor com artefatos de imagem ou falhas no sensor.

Modelos generativos

Em aplicativos avançados de machine learning, a distribuição de Cauchy ajuda a criar modelos mais flexíveis. É útil em autoencodificadores variacionais em que os dados podem ter características de cauda pesada, ajuda a gerar dados sintéticos mais realistas que incluem valores extremos ocasionais e é útil na modelagem de espaços latentes em que as distribuições normais podem ser muito restritivas. Essa flexibilidade torna a distribuição de Cauchy particularmente útil em tarefas de modelagem generativa em que é importante capturar toda a gama de possíveis variações de dados.

Confundindo a distribuição de Cauchy com outras distribuições

É comum você confundir a distribuição de Cauchy com outras distribuições semelhantes. Vamos explorar as principais diferenças para ajudar você a fazer a escolha certa para a sua análise.

Distribuição de Cauchy vs. distribuição normal

A distribuição normal costuma ser a opção padrão para muitas análises, mas há diferenças importantes entre ela e a distribuição de Cauchy:

Comportamento da cauda 

Embora ambas as distribuições sejam simétricas, suas caudas contam histórias muito diferentes: A distribuição normal sugere que valores acima de três desvios padrão são extremamente raros. A distribuição de Cauchy nos diz que os valores extremos são muito mais comuns do que você poderia esperar.

Propriedades estatísticas 

Essas distribuições diferem fundamentalmente na forma como podemos analisá-las: A distribuição normal tem momentos bem definidos (média = μ, variância = σ²). A distribuição de Cauchy não tem média ou variância definidas, o que torna os métodos estatísticos tradicionais inutilizáveis.

Implicações práticas 

Essa diferença é importante em aplicativos reais: Use a distribuição normal quando seus dados se agruparem em torno de um valor central com dispersão previsível. Use a distribuição de Cauchy quando seus dados frequentemente apresentarem valores extremos que seriam "impossíveis" sob suposições normais.

Cauchy vs. Distribuição de Laplace

À primeira vista, a distribuição de Laplace pode parecer semelhante à de Cauchy, mas há diferenças importantes que as diferenciam:

Comportamento da cauda 

Ambas as distribuições têm caudas mais pesadas do que a distribuição normal, mas diferem quanto ao peso: As caudas da distribuição de Laplace decaem exponencialmente. As caudas da distribuição de Cauchy decaem mais lentamente (polinomialmente), tornando os valores extremos ainda mais prováveis.

Simetria 

Ambas as distribuições são simétricas em torno de seu centro, mas diferem na forma como suas caudas se comportam: A distribuição de Laplace mostra um decaimento exponencial em suas caudas. A distribuição de Cauchy apresenta decaimento polinomial, tornando suas caudas mais pesadas do que a de Laplace.

Casos práticos de uso 

Entender essas diferenças ajuda você a escolher a ferramenta certa: Use a distribuição de Laplace quando você espera outliers ocasionais, mas ainda precisa de momentos definidos. Use a distribuição de Cauchy quando você espera valores extremos frequentes e não precisa calcular as médias.

Conclusão

A distribuição de Cauchy, embora não seja tão aplicada como a distribuição normal, tem uma importância significativa em áreas em que os dados apresentam um comportamento de cauda pesada, em que é necessária a robustez em relação a valores discrepantes ou em que as propriedades teóricas de distribuições estáveis são de interesse. Seja na física, nas finanças ou na estatística bayesiana, a compreensão da distribuição de Cauchy aumenta a capacidade de modelar e interpretar dados que apresentam variabilidade significativa e valores discrepantes.

Para uma compreensão mais profunda das distribuições de probabilidade relacionadas, você pode achar valiosa a série a seguir: Nosso guia de distribuição gaussiana explora a distribuição de probabilidade mais amplamente usada, que serve como um excelente contraste com o comportamento de cauda pesada da distribuição de Cauchy. Nosso guia de Distribuição de Poisson se aprofunda na modelagem de eventos discretos no tempo ou no espaço, enquanto nosso guia de Distribuição Binomial explica a matemática por trás das sequências de tentativas independentes. Para os interessados nos fundamentos da teoria da probabilidade, nosso guia de Distribuição de Bernoulli fornece insights sobre os blocos de construção de distribuições mais complexas.