Explicación del RMSE: Guía para la precisión de la predicción de regresión

El RMSE (error cuadrático medio) es una métrica de evaluación de la precisión muy utilizada en el análisis de regresión que mide la magnitud media de los errores de un modelo de regresión.

A diferencia de la R-cuadrado, que cuantifica la varianza explicada, el RMSE proporciona una medida directa del error de predicción en las mismas unidades que la variable de respuesta. Esto lo hace especialmente útil cuando el objetivo es minimizar las magnitudes de error e interpretar el rendimiento del modelo en términos del mundo real.

En este artículo, exploraremos el significado, el cálculo, la interpretación y los errores más comunes en torno al RMSE. También recorreremos ejemplos en Python y R para ver cómo se comporta el RMSE en diferentes condiciones de modelado.

¿Qué es el RMSE?

El RMSE es la raíz cuadrada de la media de las diferencias al cuadrado entre los valores observados y los predichos. Es una métrica de regresión muy utilizada que nos indica cuánto error debemos esperar de nuestras predicciones, por término medio. 

La fórmula matemática para calcular el RMSE es:

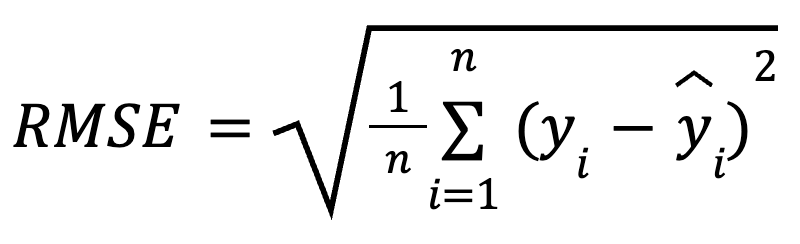
aquí:

• y_i es el valor real de la observación i,
• _ŷ, es el valor previsto para la observación i,
• n es el número total de observaciones.

Al elevar al cuadrado los residuos antes de promediarlos, el RMSE penaliza más los errores grandes que los pequeños. Esta sensibilidad hace que sea una buena elección cuando no se desean grandes errores de predicción. El RMSE siempre es no negativo, y los valores más bajos indican un modelo mejor ajustado.

Tres formas iguales de calcular el RMSE

El RMSE es fácil de calcular. Se trata simplemente de calcular los residuos, elevarlos al cuadrado, hallar la media y sacar la raíz cuadrada.

Consideremos algunas formas diferentes de calcularlo.

Utilizar los residuos

En este método, empezamos restando las predicciones de los valores reales para obtener los residuos. A continuación, elevamos al cuadrado cada residuo, hacemos la media de todos ellos y, por último, sacamos la raíz cuadrada.

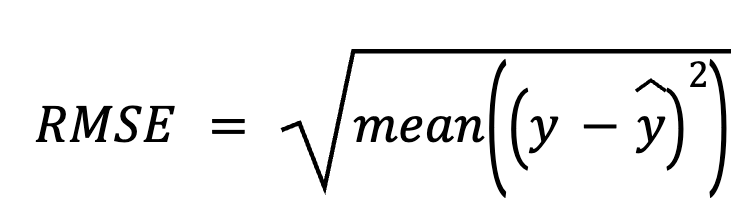
aquí:

• y es el vector de valores reales,
• ŷes el vector de valores previstos.

Este enfoque directo hace hincapié en los propios errores de predicción.

Utilizando el error cuadrático medio (ECM)

Esto parece una reafirmación, pero en realidad hay algo más: El RMSE es simplemente la raíz cuadrada del MSE. 

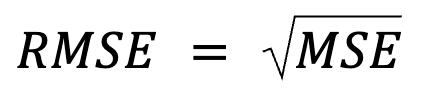
donde:

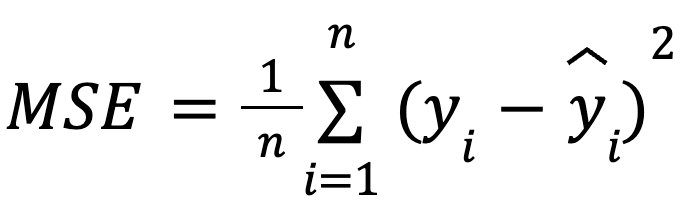
con:

• y_i como el valor real de la observación i,
• ŷ, como valor previsto para la observación i,
• n como el número total de observaciones.

Esta formulación es útil porque el MSE es una función de pérdida habitual en la optimización de modelos. Esta equivalencia es especialmente importante en el machine learning, donde el MSE suele ser la función de pérdida minimizada durante el entrenamiento mediante el descenso de gradiente. 

Más información: Precisamente porque el RMSE introduce una raíz cuadrada, muchos algoritmos de machine learning optan por no hacer RMSE durante el entrenamiento del modelo. Se prefiere el MSE para estas optimizaciones porque tiene derivadas más sencillas (de nuevo, porque la raíz cuadrada introduce no linealidad). A continuación, el RMSE se suele utilizar post hoc para informar del rendimiento en unidades interpretables.

En forma de matriz

En la regresión múltiple, el RMSE también puede derivarse del vector residual utilizando el álgebra matricial:

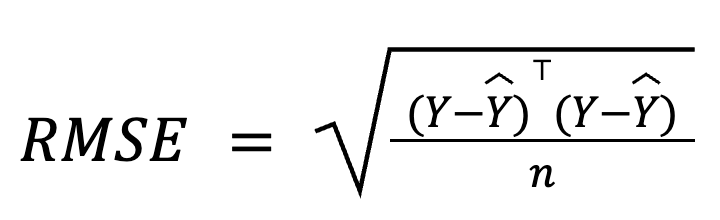
donde:

• Y es el vector columna de los valores reales,
• ŷ es el vector columna de los valores predichos,
• n es el número de observaciones.

Esta formulación basada en matrices es especialmente compacta y eficiente desde el punto de vista informático, sobre todo para grandes conjuntos de datos o cadenas de modelos. Tenemos un curso dedicado al álgebra lineal si quieres estudiar las matemáticas.

Interpretar el RMSE

El RMSE se interpreta como el error medio de predicción, que determina la precisión de predicción del modelo. En pocas palabras, muestra, por término medio, lo lejos que están las predicciones de los valores reales, en la misma escala que la variable de resultado.

Un RMSE menor sugiere menores errores medios de predicción y, por tanto, predicciones más precisas, pero el RMSE "aceptable" depende totalmente del contexto. Por ejemplo, un RMSE de 2 puede ser bueno para predecir el tamaño de las almendras en milímetros, pero no tan convincente para predecir el rendimiento anual de la cosecha de almendras en toneladas.

Para que sea significativo, el RMSE debe compararse entre modelos entrenados con los mismos datos o mediante la evaluación comparativa del rendimiento histórico.

Cuándo utilizar el RMSE

El RMSE es especialmente útil en estos casos:

• Cuando la precisión absoluta de la predicción es clave
• Al comparar modelos en el mismo conjunto de datos
• Cuando los errores del modelo se distribuyen normalmente
• Cuando nuestro objetivo es minimizar los grandes errores
• Cuando es importante interpretar los errores en unidades naturales

Sin embargo, el RMSE tiene sus inconvenientes:

• Es sensible a los valores atípicos. Unos pocos residuos grandes pueden afectar desproporcionadamente al RMSE y hacerlo engañoso.
• No está normalizado. Esto significa que no puede comparar entre diferentes conjuntos de datos y escalas objetivo, a menos que la variable objetivo esté escalada.

Ejemplos de RMSE en Python y R

Ilustremos ahora cómo calcular el RMSE tanto en Python como en R utilizando el conjunto de datos Kaggle de Clasificación de Tipos de Almendra. Aunque el conjunto de datos está pensado originalmente para la clasificación, aquí lo reutilizaremos para la regresión, prediciendo el grosor del núcleo como una variable continua basada en otros atributos físicos.

Construiremos dos modelos en cada lenguaje de programación y luego calcularemos el RMSE de cada modelo:

• Modelo 1: Utiliza predictores relevantes (longitud y anchura).
• Modelo 2: Añade un predictor aleatorio e irrelevante.

Ejemplo en Python

Empecemos con Python.

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from math import sqrt

# Load data
data = pd.read_csv("almond_dataset.csv")

# Model 1
X1 = data[['Length', 'Width']]
y = data['Thickness']
model1 = LinearRegression().fit(X1, y)
preds1 = model1.predict(X1)
rmse1 = sqrt(mean_squared_error(y, preds1))
print("Model 1 RMSE:", round(rmse1, 3))

# Model 2 with an irrelevant predictor
np.random.seed(42)
data['random_noise'] = np.random.randn(len(data))
X2 = data[['Length', 'Width', 'random_noise']]
model2 = LinearRegression().fit(X2, y)
preds2 = model2.predict(X2)
rmse2 = sqrt(mean_squared_error(y, preds2))
print("Model 2 RMSE:", round(rmse2, 3))

Model 1 RMSE: 0.251
Model 2 RMSE: 0.253

Podemos ver que el RMSE aumentó tras añadir un predictor irrelevante en el Modelo 2. Aunque el Modelo 2 pueda parecer más complejo, su precisión de predicción real puede empeorar (¡y mucho!), ya que acabamos de añadir ruido aleatorio.

Para mejorar tus habilidades de regresión en Python, inscríbete en estos cursos:

• Introducción a la regresión con modelos estadísticos en Python
• Regresión intermedia con modelos estadísticos en Python

R ejemplo

Ahora, probemos en R.

# Load data
almonds <- read.csv("almond_dataset.csv")

# Model 1
model1 <- lm(Thickness ~ Length + Width, data = almonds)
preds1 <- predict(model1)
rmse1 <- sqrt(mean((almonds$Thickness - preds1)^2))
print(paste("Model 1 RMSE:", round(rmse1, 3)))

# Model 2 with an irrelevant predictor
set.seed(42)
almonds$random_noise <- rnorm(nrow(almonds))
model2 <- lm(Thickness ~ Length + Width + random_noise, data = almonds)
preds2 <- predict(model2)
rmse2 <- sqrt(mean((almonds$Thickness - preds2)^2))
print(paste("Model 2 RMSE:", round(rmse2, 3)))

[1] "Model 1 RMSE: 0.251"
[1] "Model 2 RMSE: 0.253"

Aquí he reformulado el mismo ejemplo en R. El RMSE aumenta cuando incluimos un predictor irrelevante en R. Esto confirma que el RMSE puede crecer cuando un modelo se vuelve innecesariamente complejo, reduciendo la capacidad de generalización del modelo.

Si has tenido problemas para conseguir que tu código R compile, o si has tenido problemas para interpretar el resultado, prueba nuestros cursos:

• Introducción a la regresión en R
• Regresión intermedia en R

RMSE vs. Métricas relacionadas

El RMSE forma parte de una familia más amplia de métricas de error de regresión. Comparémoslo brevemente con otros, aclaremos las diferencias entre ellos y destaquemos cuándo es más útil cada uno.

RMSE vs. MAE

El RMSE penaliza más los errores grandes porque eleva los residuos al cuadrado, lo que lo hace más sensible a los valores atípicos. En cambio, el error medio absoluto (MAE) es más robusto frente a los valores atípicos, trata todos los errores por igual y funciona mejor para medir el tamaño típico del error cuando los valores atípicos no son un problema. Mientras que el RMSE minimizala pérdida al cuadrado , el MAE minimiza la pérdida absoluta.

En general, deberíamos utilizar el RMSE cuando los errores grandes pueden ser especialmente costosos, y el MAE cuando queremos una visión del error similar a la mediana, menos sensible a los valores atípicos.

RMSE vs. R-cuadrado

El RMSE proporciona el error medio en unidades originales, lo que lo hace más intuitivopara la interpretación práctica. En cambio, R-cuadrado describe cuánta varianza explica el modelo, pero no indica el tamaño del error de predicción.

A menudo se utilizan juntos: R-cuadrado para el ajuste relativo, y RMSE para el rendimiento absoluto.

RMSE vs. MSE

El RMSE no es más que la raíz cuadrada del MSE, lo que facilita su interpretación porque está en las mismas unidades que la variable de resultado. 

Sin embargo, aparte de la mera interpretación, el MSE es especialmente útil para la optimización durante el entrenamiento para el machine learning. Recuerda que si optimizas en RMSE, la función raíz cuadrada significa que el modelo pondrá más énfasis en los errores más grandes. Además, el MSE tiene una derivada suave, por lo que funciona bien con algoritmos basados en gradientes, como el descenso de gradiente estocástico, lo que permite una convergencia eficaz durante el entrenamiento del modelo. En resumen, el RMSE es más fácil de interpretar porque estamos viendo los resultados a escala de los datos, pero debemos saber que el aprendizaje profundo a menudo optimiza el MSE, no el RMSE.

RMSE vs. MAPE

El MAPE (error porcentual medio absoluto) devuelve los errores como porcentajes, lo que resulta útil para comparar conjuntos de datos. Sin embargo, se rompe cuando los valores reales se acercan a cero, lo que la hace inestable. El RMSE evita este problema y es más fiable cuando los valores objetivo son pequeños.

RMSE vs. log-verosimilitud

He aquí otra relación interesante: El RMSE es formalmente equivalente a la log-verosimilitud negativa bajo errores gaussianos. Más bien, quizá deberíamos decir que minimizar el RMSE equivale a maximizar la log-verosimilitud (de un modelo de regresión) bajo el supuesto de errores distribuidos normalmente (con varianza constante). No digo que el RMSE estime por sí mismo la log-verosimilitud completa, pero sí que la minimización delRMSE maximiza implícitamente la log-verosimilitud bajo un supuesto de error normal.

Sin embargo, cuando los errores son asimétricos o tienen valores atípicos, alternativas como la pérdida de Huber o de cuantiles pueden funcionar mejor. En cualquier caso, debemos tratar nuestra elección métrica como una decisión de diseño del modelo, no como una ocurrencia tardía.

Errores comunes sobre el RMSE

Aclaremos algunos mitos muy extendidos sobre el RMSE:

• "Un RMSE bajo garantiza una buena generalización del modelo". Esto no es necesariamente cierto. Un modelo puede tener un valor bajo de RMSE en los datos de entrenamiento, pero aún así tener un rendimiento deficiente en los datos nuevos, no vistos, debido al sobreajuste. Para evaluar eficazmente la generalización, necesitamos realizar una validación cruzada o utilizar un conjunto de pruebas independiente.
• "El RMSE puede determinar si un modelo está sobreajustado". El RMSE por sí solo no puede hacerlo. Debe compararse entre los conjuntos de datos de entrenamiento y validación: si el RMSE de entrenamiento es bajo pero el de validación es mucho mayor, eso me significa sobreajuste.
• "Hay un umbral universal fijo para un buen RMSE". No, no lo hay. Que el valor del RMSE sea "bueno" depende totalmente del contexto, el dominio y las unidades de la variable de resultado. En otras palabras, los valores de RMSE no tienen sentido sin contexto.

Conclusión

En resumen, el RMSE es una medida práctica, interpretable e intuitiva de la precisión de la predicción que comunica el error medio de predicción en las unidades de la variable objetivo. Es una métrica a la que acudir para evaluar el rendimiento de la regresión, especialmente cuando las magnitudes de error son importantes.

Sin embargo, el RMSE debe utilizarse junto con otras métricas, como R-cuadrado, MAE y puntuaciones de validación cruzada, para obtener una imagen más completa de la calidad del modelo. No debemos confiar ciegamente en esta medida, sino tener siempre en cuenta la escala, el contexto y la complejidad del modelo. Además, emparejar el RMSE con diagnósticos visuales puede ayudar a detectar sesgos. 

En resumen, el RMSE nos dice lo erróneo que es nuestro modelo, por término medio, en términos reales, lo cual es una perspectiva poderosa a tener en cuenta a la hora de construir sistemas predictivos.

Si algo de este artículo te ha resultado confuso, no te preocupes: Tenemos muchos recursos estupendos para ayudarte: 

• Regresión lineal simple: Todo lo que necesitas saber tutorial
• Comprender la suma de cuadrados: Guía de TSM, TSS y TSE tutorial
• Curso de Introducción a la Regresión con modelos estadísticos en Python
• Curso de Introducción a la Regresión en R