Comment normaliser les données : Un guide complet avec des exemples

Un réseau neuronal qui ne parvient pas à converger, avec une perte qui stagne et des gradients qui disparaissent ou explosent, s'avère souvent ne présenter aucun problème au niveau de son architecture. Le problème est souvent beaucoup plus simple : les caractéristiques d'entrée se situent à des échelles très différentes, où une colonne va de 0 à 1 tandis qu'une autre atteint des dizaines de milliers. 

D'après mon expérience, ce schéma se présente fréquemment dans la pratique. Cinq minutes de prétraitement peuvent résoudre ce que plusieurs jours de réglage des hyperparamètres n'ont pas réussi à accomplir.

Dans ce tutoriel, je vais vous expliquer comment normaliser des données. Je vais vous présenter différentes techniques de normalisation, ainsi que leurs cas d'application respectifs, avec des implémentations Python incluses. De plus, vous découvrirez les erreurs courantes et les idées reçues, ainsi que les moyens de les éviter.

Si vous souhaitez en savoir plus sur la préparation des données pour les algorithmes d'apprentissage automatique, je vous recommande de suivre notre cours « Prétraitement pour l'apprentissage automatique en Python ». .

Qu'est-ce que la normalisation des données ?

La normalisation des données désigne le processus de transformation des caractéristiques numériques afin qu'elles occupent des plages comparables ou suivent une échelle cohérente. 

Ce terme revêt différentes significations selon le contexte : en apprentissage automatique, il désigne généralement le recalibrage des valeurs des caractéristiques afin d'éviter que leur ampleur ne détermine leur importance, tandis qu'en conception de bases de données, il fait référence à l'organisation des tables afin d'éliminer les redondances.

Je me concentrerai principalement sur la signification du machine learning, bien que nous aborderons brièvement la normalisation des bases de données plus tard afin de clarifier le chevauchement des termes.

Pourquoi la normalisation des données est-elle importante ?

Lorsque les caractéristiques existent à différentes échelles, certains algorithmes accordent une importance disproportionnée aux valeurs qui se trouvent être numériquement plus élevées. 

Une variable mesurant le revenu en milliers prévaudra sur une variable mesurant l'âge en décennies, non pas parce que le revenu est plus important pour la prédiction, mais simplement parce que les chiffres sont plus élevés. La normalisation place les caractéristiques sur un pied d'égalité afin que le modèle puisse déterminer celles qui sont réellement pertinentes.

Au-delà de la formation des modèles, la normalisation contribue également à :

• Combiner des mesures utilisant différentes unités
• Intégration de données provenant de sources multiples avec des conventions incohérentes
• Concevoir des schémas de bases de données qui doivent conserver leur cohérence au fil du temps.

Normalisation des données, mise à l'échelle et standardisation

Quelle est donc la différence entre la normalisation, la mise à l'échelle et la standardisation ? Ces trois termes apparaissent fréquemment dans la documentation et sont souvent utilisés de manière interchangeable, bien qu'ils aient des significations distinctes.

La distinction pratique réside dans le fait que votre modèle nécessite ou non des valeurs comprises dans des limites spécifiques. La normalisation min-max garantit des limites, contrairement à la standardisation. Le tableau suivant résume les différences :

Pour une comparaison plus approfondie des cas où chaque approche peut avoir des effets négatifs, veuillez consulter notre blog sur Normalization vs. La normalisation expliquée couvre bien les cas limites.

Cas d'utilisation de la normalisation des données

Maintenant que nous avons défini les termes, examinons quelques cas d'utilisation classiques. La normalisation peut servir à différentes fins selon votre cas d'utilisation, depuis l'amélioration de la dynamique d'entraînement des modèles jusqu'à la possibilité d'effectuer des comparaisons significatives entre des sources de données hétérogènes.

Améliorer les performances des modèles d'apprentissage automatique

Réseaux neuronaux et régression logistique mettent à jour les poids par la descente de gradient, où la contribution de chaque caractéristique à l'erreur de prédiction détermine l'ampleur de l'ajustement du poids correspondant. 

Lorsque les magnitudes des caractéristiques diffèrent considérablement, les gradients qui en résultent diffèrent également : les grandes caractéristiques produisent de grands gradients, tandis que les petites caractéristiques produisent de petits gradients. Ce déséquilibre conduit l'optimiseur à prendre des mesures importantes dans certaines directions tout en restant pratiquement inactif dans d'autres, ce qui entraîne un apprentissage instable ou une absence totale de convergence.

Les algorithmes basés sur la distance, tels que kNN et K-means rencontrent un problème similaire. Ils calculent la similarité à l'aide de mesures de distance, généralement la distance euclidienne, où les valeurs numériques plus élevées contribuent davantage au calcul simplement parce qu'elles sont plus grandes. Une caractéristique comprise entre 0 et 10 000 prévaudra sur une caractéristique comprise entre 0 et 1, quelle que soit la caractéristique réellement pertinente pour la tâche de prédiction. 

La mise à l'échelle garantit que toutes les caractéristiques contribuent proportionnellement à leur valeur prédictive réelle plutôt qu'à leur plage numérique arbitraire.

Permettre une comparaison équitable entre les différentes fonctionnalités

Lors de la création de scores composites ou de la combinaison de mesures avec différentes unités, les valeurs brutes peuvent conduire à des comparaisons trompeuses. 

Un indicateur de santé client qui combine les dépenses mensuelles en dollars, la fréquence de connexion en nombre et l'ancienneté du compte en jours accordera davantage d'importance aux montants en dollars, simplement parce que ces chiffres sont plus élevés. 

La normalisation vous permet de combiner ces mesures d'une manière qui reflète leur importance réelle plutôt que leur ampleur accidentelle.

Cela s'applique également à l'analyse exploratoire et à la visualisation. La création de graphiques à différentes échelles rend plus difficile la détection de tendances ou la comparaison de distributions. Les données normalisées offrent une image plus claire des relations entre les caractéristiques.

Améliorer la qualité et l'intégrité des données

Les pipelines de production puisent souvent dans plusieurs sources de données dont les conventions ne sont pas cohérentes. Les revenus peuvent être déclarés en dollars dans un système et en milliers dans un autre. Les dates apparaissent sous forme d'horodatages Unix dans une API et sous forme de chaînes formatées dans une autre. 

Définir une échelle et un format cohérents avant le traitement en aval permet d'éviter des erreurs subtiles difficiles à diagnostiquer par la suite.

Dans le contexte des bases de données, la normalisation revêt une signification différente mais connexe : organiser les tables de manière à ce que chaque information se trouve à un seul endroit. 

Cela permet d'éviter les anomalies de mise à jour qui surviennent lorsqu'une modification apportée à une valeur à un endroit entraîne des valeurs contradictoires ailleurs. Bien que les techniques diffèrent du redimensionnement des caractéristiques, la motivation sous-jacente est similaire : maintenir la cohérence et la prévisibilité des données.

Techniques courantes de normalisation des données

Chaque approche de normalisation repose sur des hypothèses différentes concernant vos données et produit des caractéristiques de sortie différentes. Le choix approprié dépend de la distribution de vos données, de la présence de valeurs aberrantes et des attentes de votre modèle en aval.

Normalisation min-max

La normalisation min-max compresse les valeurs dans une plage fixe, généralement comprise entre 0 et 1, en soustrayant le minimum et en divisant par la plage. Cette approche préserve la forme de distribution d'origine tout en garantissant que toutes les valeurs se situent dans des limites connues.

Fonctionnement : Soustrayez la valeur minimale, divisez par l'intervalle. C'est tout.

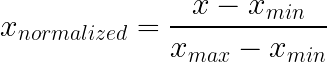
Fonctionnalités :

• Garantit que la production reste dans les limites définies.
• Conserve la forme de distribution d'origine, simplement redimensionnée.
• Zéro devient votre plancher, un devient votre plafond

Idéal pour :

• Intensités des pixels (toujours comprises entre 0 et 255 par définition)
• Probabilités et pourcentages
• Notes d'examen, évaluations, tout ce qui comporte un seuil minimal et maximal naturel
• Réseaux neuronaux qui attendent des entrées limitées, comme les classificateurs d'images

À surveiller :

Les valeurs aberrantes peuvent compromettre la normalisation min-max. Imaginez des données dont la plupart se situent entre 10 et 100, mais dont une seule vaut 99 999. Ce point unique élargit tellement votre champ d'action que tout ce qui est normal se comprime en une minuscule fraction proche de zéro. Une seule observation négative, et l'ensemble du reportage est compromis.

Veuillez également considérer ce qui se produit lorsque de nouvelles données se situent en dehors de la plage d'entraînement. Les valeurs de test supérieures au maximum d'entraînement produisent un résultat supérieur à 1. La question de savoir si cela entraîne des problèmes dépend de votre modèle.

Normalisation du score Z

La normalisation par score Z transforme les données de manière à ce que la moyenne soit égale à zéro et l'écart type égal à un, sans imposer de limites fixes aux résultats. Cette approche est efficace pour les données sans limites naturelles évidentes et est largement adoptée ou recommandée par de nombreuses implémentations d'algorithmes.

Fonctionnement : Soustrayez la moyenne, divisez par l'écart type.

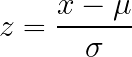
Fonctionnalités :

• Recentre tous les éléments de manière à ce que la moyenne soit égale à zéro.
• Échelle où un écart type équivaut à une unité
• La sortie peut devenir négative et dépasser toute limite spécifique.

Idéal pour :

• Données sans limites naturelles apparentes
• Distributions approximativement en forme de cloche
• Algorithmes qui supposent ou recommandent la normalisation (la plupart des tutoriels sur les réseaux neuronaux, implémentations de régression logistique)
• Lorsque vous n'êtes pas certain de ce qu'il convient d'utiliser (une valeur par défaut raisonnable)

Compromis :

L'interprétabilité est affectée. « Cette observation se situe à 1,7 écart-type au-dessus de la moyenne » nécessite un effort intellectuel plus important que « cela correspond à 80 % de la fourchette ». Si les parties prenantes ont besoin de comprendre directement les valeurs échelonnées, l'intervalle min-max pourrait être plus efficace.

Les valeurs aberrantes continuent de gonfler la moyenne et l'écart type, faussant ainsi la mise à l'échelle des données en vrac, mais elles posent moins de problèmes que dans la normalisation min-max.

Mise à l'échelle robuste

La mise à l'échelle robuste traite la sensibilité aux valeurs aberrantes des approches min-max et z-score en utilisant médiane et l'écart interquartile (IQR) à la place de la moyenne et de l'écart type. Ces statistiques restent stables, quelles que soient les valeurs extrêmes aux extrémités de votre distribution.

Fonctionnement : Soustrayez la médiane, divisez par l'écart interquartile (différence entre les 25e et 75e centiles).

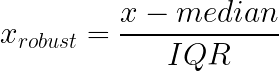
Fonctionnalités :

• Échelles basées sur la partie centrale de vos données, en ignorant les valeurs extrêmes
• Les queues peuvent agir à leur guise sans altérer la transformation pour les valeurs typiques.
• Plus stable lorsque vos données contiennent des valeurs aberrantes légitimes que vous ne pouvez pas supprimer

Idéal pour :

• Transactions financières, où la plupart des achats sont de faible valeur, mais où des transactions occasionnelles de grande valeur peuvent se produire.
• Les données relatives aux revenus, qui présentent généralement une longue queue à droite
• Lectures des capteurs où les pics représentent des événements réels
• Toute distribution très asymétrique et toute situation où les approches basées sur la moyenne sont influencées par des valeurs extrêmes.

Pourquoi cela est utile en cas de données asymétriques :

La répartition des revenus en est un bon exemple. La plupart des individus gagnent des montants modérés, tandis que certains gagnent des montants considérables : il s'agit d'une distribution classique asymétrique à droite. L'écart type est amplifié par les revenus élevés, ce qui rend la standardisation moins utile pour la majorité des observations. La médiane et l'IQR restent néanmoins ancrés au milieu de la distribution.

Normalisation des vecteurs unitaires

La normalisation par norme unitaire (L1/L2) fonctionne différemment des techniques ci-dessus : au lieu de mettre à l'échelle les caractéristiques (colonnes), elle met généralement à l'échelle les échantillons individuels (lignes). Chaque vecteur d'échantillon est redimensionné de manière à ce que sa longueur soit égale à 1 selon une norme choisie (souvent L2), ce qui élimine l'amplitude globale et ne conserve que la direction/les proportions.

Veuillez ne pas confondre cela avec la régularisation L1/L2. régularisation (Lasso/Ridge) : la régularisation modifie l'objectif d'apprentissage en ajoutant une pénalité sur les poids du modèle afin de réduire le surajustement, et non en redimensionnant les vecteurs d'entrée.

Fonctionnement : Dans la normalisation L2, chaque ligne est divisée par sa norme euclidienne, de sorte que la somme des valeurs au carré soit égale à un. L1 utilise plutôt la somme des valeurs absolues.

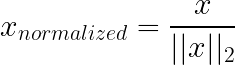
Fonctionnalités :

• Supprime la magnitude de l'équation
• Rend les lignes comparables en fonction de leur proportion plutôt que de leur taille brute.
• L'angle entre les vecteurs devient le signal ; la longueur du vecteur n'a plus d'importance.

Idéal pour :

• Données textuelles représentées sous forme de vecteurs de nombre de mots : un rapport de 50 000 mots comporte naturellement un nombre de mots plus élevé qu'un e-mail de 500 mots, mais L2 vous permet de comparer les proportions de contenu.
• Tout ce qui concerne la similarité cosinus
• Classification de documents, recherche d'informations et systèmes de recommandation basés sur le contenu

Non utile pour :

Situations où l'importance est réellement significative. Si le nombre total de mots est pertinent pour votre tâche, le normaliser entraînerait une perte d'informations.

Normalisation de base de données

La normalisation d'une base de données consiste à restructurer les tables relationnelles afin d'éliminer les redondances et d'améliorer l'intégrité des données. Par exemple, cela permet de garantir que l'adresse e-mail d'un client est stockée à un seul endroit plutôt que d'être répétée dans chaque enregistrement de commande.

Cela n'a aucun rapport avec la mise à l'échelle des fonctionnalités.

Le terme se recoupe simplement. Dans le domaine de l'apprentissage automatique, la « normalisation » fait presque toujours référence à la mise à l'échelle des valeurs numériques. En ingénierie des données ou en SQL, cela fait référence à l'organisation des structures de tables (souvent désignées par les termes 1NF, 2NF ou 3NF).

Distinction essentielle :

• Normalisation des caractéristiques (ML) : Transformation des nombres (par exemple, mise à l'échelle 0-1) pour faciliter l'apprentissage des modèles.
• Normalisation de base de données (SQL) : Organiser le schéma afin d'éviter la duplication des données.

Si un ingénieur de données vous demande de « normaliser la base de données », il souhaite que vous modifiiez la structure de la table, et non que vous exécutiez la commande ` MinMaxScaler`.

Pour approfondir le sujet, veuillez consulter ce guide sur la normalisation des bases de données en SQL.

Comment normaliser les données dans la pratique

Pour mettre en œuvre correctement la normalisation, il est nécessaire de prêter attention à l'ordre des opérations, en particulier en ce qui concerne la répartition entre entraînement et test. Le code en lui-même est simple, mais de petites erreurs dans l'ordre des opérations peuvent invalider l'ensemble de votre évaluation.

Normalisation des données en Python

Scikit-learn vous fournit les scalers, mais la règle principale est procédurale, et non mathématique : divisez d'abord, ajustez uniquement sur l'entraînement, puis réutilisez ce transformateur ajusté partout ailleurs.

Pourquoi tant d'agitation ? Étant donné que la mise à l'échelle apprend les chiffres à partir des données : min/max, moyenne/écart type, médiane/intervalle interquartile. Si ces chiffres sont calculés à l'aide de l'ensemble de test, vous avez discrètement laissé des informations futures s'infiltrer dans l'entraînement. Rien ne plante, mais vos indicateurs cessent simplement d'avoir le sens que vous leur attribuez.

Un exemple minimal :

import pandas as pd
from sklearn.preprocessing import MinMaxScaler, StandardScaler, RobustScaler
from sklearn.model_selection import train_test_split

# Example data
data = pd.DataFrame({
    'age': [25, 32, 47, 51, 62, 28, 35, 44],
    'income': [30000, 45000, 72000, 85000, 120000, 38000, 55000, 67000],
    'score': [0.2, 0.5, 0.7, 0.4, 0.9, 0.3, 0.6, 0.8]
})

# Split happens before any scaling
train_data, test_data = train_test_split(data, test_size=0.25, random_state=42)

À ce stade, vous considérez la répartition de l'entraînement comme « ce à quoi ressemblait le monde lorsque j'ai construit le modèle ». Le test est divisé en « données nouvelles, non vues ». Votre scaler doit apprendre le monde à partir du premier uniquement.

MinMaxScaler

La normalisation min-max est simple : elle enregistre les valeurs minimales et maximales d'apprentissage pour chaque colonne, puis applique le même mappage ultérieurement.

scaler = MinMaxScaler()
scaler.fit(train_data)  # training only

train_scaled = scaler.transform(train_data)
test_scaled = scaler.transform(test_data)

Si vous vous surprenez à appeler « fit() » sur le test set, veuillez vous arrêter. Cela va à l'encontre de l'objectif initial de la mise en place d'un ensemble de tests.

StandardScaler

StandardScaler stocke la moyenne et l'écart type à partir de la division d'entraînement, puis utilise ces mêmes valeurs pour transformer à la fois l'entraînement et le test.

scaler = StandardScaler()
scaler.fit(train_data)

train_standardized = scaler.transform(train_data)
test_standardized = scaler.transform(test_data)

C'est celui qui se brise discrètement en cas de fuite, car la moyenne et l'écart-type sont faciles à « stabiliser » en utilisant accidentellement plus de données que nécessaire.

RobustScaler

RobustScaler utilise la même méthode « ajuster une fois, réutiliser indéfiniment », mais utilise la médiane et l'IQR, de sorte que quelques points extrêmes ne dictent pas l'échelle.

scaler = RobustScaler()
scaler.fit(train_data)

train_robust = scaler.transform(train_data)
test_robust = scaler.transform(test_data)

Un indicateur pratique qui montre que la mise à l'échelle robuste en vaut la peine : vous avez une longue traîne que vous souhaitez réellement conserver (paiements, réclamations, pics de capteurs) et vous ne souhaitez pas qu'une journée inhabituelle réduise le reste de la fonctionnalité à presque zéro.

Calculs rapides avec Pandas

Pour un travail exploratoire rapide, il est tout à fait acceptable d'effectuer les calculs directement dans pandas, à condition d'être transparent sur votre démarche : il s'agit d'examiner les distributions, et non d'évaluer des modèles.

# Min-max
df_minmax = (data - data.min()) / (data.max() - data.min())

# Z-score
df_zscore = (data - data.mean()) / data.std()

Prévention des fuites de données

Attention : les statistiques sont basées sur l'ensemble des données. Veuillez effectuer cette opération avant la division, et les valeurs de test influencent la transformation. Votre évaluation perd de sa pertinence car le prétraitement a déjà examiné des réponses qu'il n'aurait pas dû consulter.

Le schéma de fuite se présente généralement comme suit :

Une approche inadéquate :

scaler = MinMaxScaler()
scaled_all = scaler.fit_transform(full_data)  # problem
train, test = split(scaled_all)

Cette approche normalise les données avant leur fractionnement, de sorte que les données de test ont déjà influencé la transformation.

Procéder de manière appropriée :

En divisant d'abord les données, nous nous assurons que le scaler apprend les statistiques uniquement à partir de l'ensemble d'apprentissage, en gardant les données de test véritablement invisibles.

scaler = MinMaxScaler()
scaler.fit(train_data)
train_scaled = scaler.transform(train_data)
test_scaled = scaler.transform(test_data)

Les mêmes opérations, mais dans un ordre différent. Et l'ordre est essentiel.

Si vous préférez vous exercer au prétraitement de bout en bout (y compris la normalisation correcte et la prévention des fuites), ce cours est conçu pour cela : Pré-traitement pour l'apprentissage automatique en Python.

Normalisation en SQL

Comme nous l'avons mentionné précédemment, un même mot peut avoir différentes significations. Ici, la « normalisation » n'est pas une transformation numérique. Il s'agit d'une décision structurelle visant à éviter la duplication des faits.

customer_email Si votre table de commandes stocke des informations sur chaque ligne, la base de données vous permettra de le faire. La base de données acceptera également volontiers les contradictions ultérieures : un e-mail dans une ligne, un autre e-mail dans une autre ligne, sans moyen évident de déterminer lequel est « authentique ».

Avant la normalisation :

CREATE TABLE orders_denormalized (
    order_id INT,
    customer_name VARCHAR(100),
    customer_email VARCHAR(100),
    product_name VARCHAR(100),
    product_price DECIMAL(10,2),
    quantity INT
);

Les informations relatives aux clients sont répétées dans chaque ligne. Mettre à jour les adresses e-mail implique de localiser et de modifier toutes leurs commandes.

Après normalisation :

CREATE TABLE customers (
    customer_id INT PRIMARY KEY,
    name VARCHAR(100),
    email VARCHAR(100)
);

CREATE TABLE products (
    product_id INT PRIMARY KEY,
    name VARCHAR(100),
    price DECIMAL(10,2)
);

CREATE TABLE orders (
    order_id INT PRIMARY KEY,
    customer_id INT REFERENCES customers(customer_id),
    product_id INT REFERENCES products(product_id),
    quantity INT
);

Les informations client sont enregistrées une seule fois. Les requêtes nécessitent des jointures, mais les mises à jour s'effectuent à un seul endroit.

Comment sélectionner la technique de normalisation appropriée

Enfin, je souhaite vous fournir un cadre décisionnel pour la prochaine fois que vous vous demanderez quelle technique de normalisation utiliser.

Min-max lorsque des limites existent

Le redimensionnement min-max est particulièrement efficace lorsque vos données ont des limites connues et stables qui ne changeront pas entre l'entraînement et le déploiement. Les valeurs de pixels sont toujours comprises entre 0 et 255. Les scores de probabilité ne peuvent pas dépasser 1. Les notes d'examen ont des minima et des maxima définis.

Cette approche convient également lorsque votre modèle attend spécifiquement des entrées limitées, comme c'est le cas pour certaines architectures de réseaux neuronaux. Cependant, il est recommandé d'éviter le redimensionnement min-max en présence de valeurs aberrantes, car une seule valeur extrême peut comprimer toutes les observations normales dans une plage étroite proche de zéro.

La normalisation en tant que solution de repli

La normalisation constitue une valeur par défaut raisonnable lorsque vous ne disposez pas d'hypothèses solides concernant les limites ou la distribution de vos données. Il est particulièrement adapté aux caractéristiques présentant des plages variables, des limites inconnues ou des distributions approximativement en forme de cloche.

De nombreuses implémentations d'algorithmes supposent ou recommandent des entrées standardisées, notamment la plupart des frameworks de réseaux neuronaux et des bibliothèques de régression logistique. Si vous n'êtes pas certain de l'approche à adopter et que vos données ne présentent pas de limites naturelles évidentes, la normalisation constitue généralement un choix prudent.

Robuste pour faire face aux aléas du monde réel

Une mise à l'échelle robuste s'avère être le choix approprié lorsque vos données contiennent des valeurs aberrantes significatives qui représentent des valeurs légitimes plutôt que des erreurs. Les données relatives aux transactions financières présentent généralement la caractéristique suivante : la plupart des achats sont modestes, mais il arrive que des montants importants soient facturés, et ceux-ci doivent être conservés dans l'ensemble de données.

Les distributions de revenus, les relevés de capteurs présentant des pics occasionnels et toutes les données présentant un fort biais ou de longues queues bénéficient d'une mise à l'échelle robuste. La médiane et l'écart interquartile restent ancrés à la majeure partie de votre distribution, indépendamment de ce qui se produit aux extrêmes.

Quand ne pas normaliser

Les modèles basés sur les arbres, tels que les forêts aléatoires, XGBoost et les arbres boostés par gradient, se divisent en fonction de valeurs seuils et ne calculent jamais les distances ou les gradients entre les caractéristiques. L'échelle leur est invisible, donc la normalisation ajoute de la complexité sans apporter d'avantage.

Les caractéristiques codées en one-hot sont déjà binaires (0 et 1), donc les mettre à l'échelle n'apporte aucune valeur ajoutée. Les ensembles de données uniquement catégoriels relèvent de la même catégorie.

Parfois, les transformations spécifiques à un domaine sont plus efficaces que la normalisation générique :

• La mise à l'échelle logarithmique compresse les longues queues droites tout en répartissant les valeurs inférieures regroupées, ce qui fonctionne souvent mieux pour les données relatives aux revenus ou aux prix que les approches standard. 
• Le regroupement est pertinent lorsque l'appartenance à une catégorie est plus importante que les valeurs numériques précises. 
• Les transformateurs de puissance contribuent à stabiliser les variations dans des situations spécifiques.

Tableau récapitulatif comparatif

Voici un aperçu des techniques et de leurs cas d'utilisation :

Conclusion

Les différences d'échelle posent de réels problèmes aux modèles qui en tiennent compte. Les mesures de distance privilégient les caractéristiques de grande ampleur. La descente de gradient rencontre des difficultés lorsque les gradients couvrent plusieurs ordres de grandeur. La formation se bloque ou plante pour des raisons qui ne sont pas évidentes à première vue en examinant le code ou l'architecture.

La normalisation répond à ce problème. Veuillez utiliser la normalisation min-max pour les données bornées, la mise à l'échelle robuste lorsque les valeurs aberrantes sont réelles et ne peuvent être supprimées, et la normalisation comme valeur par défaut raisonnable. La mécanique est simple : intégrez l'entraînement, appliquez-le partout de manière cohérente. 

D'après mon expérience, ce qui prend du temps, c'est de ne pas reconnaître quand la mise à l'échelle est importante, puis de passer des jours à déboguer le comportement du modèle alors que la solution résidait dans le prétraitement. Ou l'erreur inverse, comme appliquer systématiquement la mise à l'échelle à des modèles qui n'en ont pas besoin, ce qui ajoute de la complexité sans apporter d'avantage.

Êtes-vous prêt à passer au niveau supérieur ? Notre programme complet ingénieur en apprentissage automatique le cursus vous enseigne tout ce que vous devez savoir sur le processus d'apprentissage automatique.