Cómo normalizar datos: Una guía completa con ejemplos

Una red neuronal que se niega a converger, con pérdidas estancadas y gradientes que desaparecen o explotan, a menudo resulta no tener ningún problema en su arquitectura. El problema suele ser mucho más sencillo: características de entrada que se encuentran en escalas muy diferentes, donde una columna va de 0 a 1, mientras que otra alcanza decenas de miles. 

Según mi experiencia, este patrón se repite constantemente en la práctica. Cinco minutos de preprocesamiento pueden resolver lo que días de ajuste de hiperparámetros no han podido resolver.

En este tutorial, te mostraré cómo normalizar datos. Te explicaré diferentes técnicas de normalización y cuándo se aplica cada una, incluyendo implementaciones en Python. Además, aprenderás cuáles son los errores y conceptos erróneos más comunes y cómo evitarlos.

Si deseas obtener más información sobre cómo preparar datos para algoritmos de machine learning, te recomiendo que realices nuestro curso Preprocesamiento para el machine learning en Python .

¿Qué es la normalización de datos?

La normalización de datos se refiere al proceso de transformar características numéricas para que ocupen rangos comparables o sigan una escala coherente. 

El término tiene diferentes significados según el contexto: en el machine learning, normalmente significa reescalar los valores de las características para evitar que la magnitud dicte la importancia, mientras que en el diseño de bases de datos, se refiere a organizar tablas para eliminar la redundancia.

Me centraré principalmente en el significado del machine learning, aunque más adelante abordaremos brevemente la normalización de bases de datos para aclarar la superposición de vocabulario.

Por qué es importante la normalización de datos

Cuando las características existen en diferentes escalas, ciertos algoritmos otorgan una importancia desproporcionada a los valores que resultan ser numéricamente mayores. 

Una variable que mide los ingresos en miles predominará sobre otra que mide la edad en décadas, no porque los ingresos sean más importantes para la tarea de predicción, sino simplemente porque las cifras son mayores. La normalización pone las características en pie de igualdad para que el modelo pueda aprender cuáles son realmente importantes.

Más allá del entrenamiento de modelos, la normalización también ayuda a:

• Combinar mediciones que utilizan diferentes unidades.
• integrar datos de múltiples fuentes con convenciones inconsistentes
• Diseñar esquemas de bases de datos que deban mantener la coherencia a lo largo del tiempo.

Normalización de datos frente a escalado frente a estandarización

Entonces, ¿cuál es la diferencia entre normalización, escalado y estandarización? Estos tres términos aparecen con frecuencia en la documentación y, a menudo, se utilizan indistintamente a pesar de tener significados distintos.

La distinción práctica se reduce a si tu modelo necesita valores dentro de límites específicos. La normalización mín-máx garantiza los límites, mientras que la estandarización no. La siguiente tabla resume las diferencias:

Para una comparación más detallada de cuándo cada enfoque resulta contraproducente, consulta nuestro blog sobre « Normalization vs. Explicación de la estandarización cubre bien los casos extremos.

Casos de uso de la normalización de datos

Ahora que ya hemos establecido los términos, veamos algunos casos de uso clásicos. La normalización tiene diferentes propósitos según el caso de uso, desde mejorar la dinámica del entrenamiento de modelos hasta permitir comparaciones significativas entre fuentes de datos heterogéneas.

Mejorar el rendimiento del modelo de machine learning

Redes neuronales y regresión logística actualizan los pesos mediante descenso de gradiente, donde la contribución de cada característica al error de predicción determina cuánto se ajusta el peso correspondiente. 

Cuando las magnitudes de las características difieren drásticamente, los gradientes resultantes también lo hacen: las características grandes producen gradientes grandes, las características pequeñas producen gradientes pequeños. Este desequilibrio hace que el optimizador dé pasos enormes en algunas direcciones, mientras que apenas se mueve en otras, lo que conduce a un entrenamiento inestable o a la imposibilidad de converger.

Los algoritmos basados en la distancia, como kNN y K-means se enfrentan a un problema relacionado. Calculan la similitud utilizando métricas de distancia, normalmente la distancia euclídea, en la que los valores numéricos más grandes contribuyen más al cálculo simplemente por ser más grandes. Una característica que abarca de 0 a 10 000 dominará una que abarca de 0 a 1, independientemente de cuál sea realmente importante para la tarea de predicción. 

El escalado garantiza que todas las características contribuyan proporcionalmente a su valor predictivo real, en lugar de a su rango numérico arbitrario.

Permite una comparación justa entre las distintas funciones.

Al crear puntuaciones compuestas o combinar mediciones con diferentes unidades, los valores brutos pueden dar lugar a comparaciones engañosas. 

Una métrica de salud del cliente que combina el gasto mensual en dólares, la frecuencia de inicio de sesión como recuento y la antigüedad de la cuenta en días dará mayor peso a las cantidades en dólares, simplemente porque esas cifras son más elevadas. 

La normalización permite combinar estas mediciones de manera que reflejen su importancia real, en lugar de su magnitud accidental.

Esto también se aplica al análisis exploratorio y la visualización. Gráficar características en diferentes escalas dificulta la detección de patrones o la comparación de distribuciones. Los datos normalizados ofrecen una imagen más clara de cómo se relacionan entre sí las características.

Mejorar la calidad y la integridad de los datos.

Los procesos de producción suelen extraer información de múltiples fuentes de datos con convenciones inconsistentes. Los ingresos pueden aparecer en dólares en un sistema y en miles en otro. Las fechas aparecen como marcas de tiempo Unix en una API y como cadenas formateadas en otra. 

Establecer una escala y un formato coherentes antes del procesamiento posterior evita errores sutiles que son difíciles de diagnosticar más adelante.

En el contexto de las bases de datos, la normalización adquiere un significado diferente, pero relacionado: organizar las tablas de manera que cada dato se encuentre en un único lugar. 

Esto evita anomalías en las actualizaciones, en las que al cambiar un valor en un lugar se generan valores contradictorios en otros. Aunque las técnicas difieren del escalado de características, la motivación subyacente es similar: mantener los datos coherentes y predecibles.

Técnicas comunes de normalización de datos

Cada enfoque de normalización parte de supuestos diferentes sobre tus datos y produce características de salida diferentes. La elección correcta depende de la distribución de tus datos, la presencia de valores atípicos y lo que espera tu modelo descendente.

Normalización mín-máx.

La normalización mín-máx comprime los valores en un rango fijo, normalmente de 0 a 1, restando el mínimo y dividiendo por el rango. Este enfoque conserva la forma de distribución original y garantiza que todos los valores se encuentren dentro de los límites conocidos.

Cómo funciona: Resta el mínimo y divide por el rango. Eso es todo.

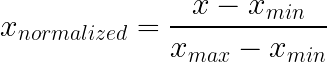
Qué hace:

• Garantiza que la producción se mantenga dentro de los límites definidos.
• Conserva la forma de distribución original, solo que a otra escala.
• El cero se convierte en tu piso, el uno se convierte en tu techo.

Ideal para:

• Intensidades de píxeles (siempre de 0 a 255 por definición)
• Probabilidades y porcentajes
• Calificaciones de exámenes, valoraciones, cualquier cosa con un mínimo y un máximo naturales.
• Redes neuronales que esperan entradas limitadas, como los clasificadores de imágenes.

Qué hay que tener en cuenta:

Los valores atípicos pueden arruinar por completo la normalización min-max. Imagina unos datos que en su mayoría se sitúan entre 10 y 100, pero con un valor de 99 999. Ese único punto amplía tu rango hasta tal punto que todo lo normal se comprime en una pequeña franja cercana a cero. Una mala observación, toda la función arruinada.

Ten en cuenta también lo que ocurre cuando los nuevos datos quedan fuera del rango de entrenamiento. Los valores de prueba que superan el máximo de entrenamiento producen un resultado superior a 1. Que eso rompa algo depende de tu modelo.

Estandarización de la puntuación Z

La estandarización de la puntuación Z transforma los datos de modo que la media sea cero y la desviación estándar sea uno, sin imponer límites fijos a los resultados. Este enfoque funciona bien con datos que no tienen límites naturales evidentes y es ampliamente aceptado o recomendado por muchas implementaciones de algoritmos.

Cómo funciona: Resta la media y divide por la desviación estándar.

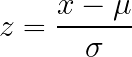
Qué hace:

• Reencuentra todo para que la media sea cero.
• Escalas en las que una desviación estándar equivale a una unidad.
• La salida puede ser negativa, puede exceder cualquier límite concreto.

Ideal para:

• Datos sin límites naturales evidentes
• Distribuciones con forma aproximada de campana
• Algoritmos que asumen o recomiendan la estandarización (la mayoría de los tutoriales sobre redes neuronales, implementaciones de regresión logística).
• Cuando no estás seguro de qué más utilizar (una opción predeterminada razonable)

Compensación:

La interpretabilidad se ve afectada. «Esta observación está 1,7 desviaciones estándar por encima de la media» requiere más esfuerzo mental que «esto está en el 80 % del rango». Si las partes interesadas necesitan comprender directamente los valores escalados, el rango mínimo-máximo podría ser más claro.

Los valores atípicos siguen inflando la media y la desviación estándar, distorsionando la escala de los datos masivos, pero suponen un problema menor que en la normalización mín-máx.

Escalabilidad robusta

El escalado robusto aborda la sensibilidad a los valores atípicos de los enfoques min-max y z-score mediante el uso de mediana y el rango intercuartílico (IQR) en lugar de la media y la desviación estándar. Estas estadísticas se mantienen estables independientemente de los valores extremos en los extremos de tu distribución.

Cómo funciona: Resta la mediana y divide por el IQR (diferencia entre los percentiles 25 y 75).

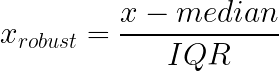
Qué hace:

• Escalas basadas en la parte media de tus datos, ignorando los extremos.
• Las colas pueden hacer lo que quieran sin alterar la transformación para los valores típicos.
• Más estable cuando tus datos contienen valores atípicos legítimos que no puedes eliminar.

Ideal para:

• Transacciones financieras, en las que la mayoría de las compras son pequeñas, pero ocasionalmente se producen transacciones legítimas de alto valor.
• Los datos sobre ingresos, que tienden a tener colas largas a la derecha.
• Lecturas del sensor en las que los picos representan eventos reales.
• Cualquier distribución muy sesgada y situación en la que los enfoques basados en la media se vean arrastrados por valores extremos.

Por qué ayuda con los datos sesgados:

La distribución de los ingresos es un buen ejemplo. La mayoría de la gente gana cantidades moderadas, y algunos ganan cantidades enormes: una distribución clásica sesgada hacia la derecha. La desviación estándar se ve inflada por los ingresos elevados, lo que hace que la estandarización sea menos útil para la mayoría de las observaciones. La mediana y el IQR permanecen anclados en el centro de la distribución independientemente.

Normalización de vectores con norma unitaria

La normalización de norma unitaria (L1/L2) funciona de manera diferente a las técnicas anteriores: en lugar de escalar características (columnas), normalmente escala muestras individuales (filas). Cada vector de muestra se reescala, de modo que su longitud es 1 según una norma elegida (a menudo L2), lo que elimina la magnitud global y solo conserva la dirección/proporciones.

No confundas esto con la regularización L1/L2 regularización (Lasso/Ridge): la regularización modifica el objetivo de entrenamiento añadiendo una penalización a los pesos del modelo para reducir el sobreajuste, no reescalando los vectores de entrada.

Cómo funciona: En la normalización L2, cada fila se divide por su norma euclídea, de modo que los valores al cuadrado suman uno. L1 utiliza en su lugar la suma de los valores absolutos.

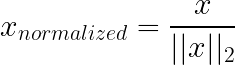
Qué hace:

• Elimina la magnitud de la ecuación.
• Hace que las filas sean comparables por proporción en lugar de por tamaño bruto.
• El ángulo entre los vectores se convierte en la señal; la longitud del vector deja de ser relevante.

Ideal para:

• Datos de texto representados como vectores de recuento de palabras: un informe de 50 000 palabras tiene, naturalmente, un recuento mayor que un correo electrónico de 500 palabras, pero L2 te permite comparar las proporciones del contenido.
• Cualquier cosa relacionada con la similitud coseno.
• Clasificación de documentos, recuperación de información y sistemas de recomendación basados en el contenido.

No es útil para:

Situaciones en las que la magnitud realmente importa. Si el recuento total de palabras es significativo para tu tarea, normalizarlo supone perder información.

Normalización de bases de datos

La normalización de bases de datos se refiere a la reestructuración de tablas relacionales para eliminar la redundancia y mejorar la integridad de los datos; por ejemplo, asegurarse de que el correo electrónico de un cliente se almacene en un solo lugar en lugar de repetirse en cada registro de pedido.

No tiene ninguna relación con el escalado de funciones.

El término simplemente se superpone. En machine learning, la «normalización» casi siempre se refiere al escalado de valores numéricos. En ingeniería de datos o SQL, se refiere a la organización de estructuras de tablas (a menudo denominadas 1NF, 2NF o 3NF).

Diferencia clave:

• Normalización de características (ML): Transformación de números (por ejemplo, escala de 0 a 1) para ayudar a los modelos a aprender.
• Normalización de bases de datos (SQL): Organizar el esquema para evitar la duplicación de datos.

Si un ingeniero de datos te pide que «normalices la base de datos», lo que quiere es que corrijas la estructura de las tablas, no que ejecutes MinMaxScaler.

Para obtener más información, consulta esta guía sobre normalización de bases de datos en SQL.

Cómo normalizar datos en la práctica

Para implementar correctamente la normalización, es necesario prestar atención al orden de las operaciones, especialmente en lo que respecta a las divisiones entre entrenamiento y prueba. El código en sí es sencillo, pero pequeños errores en la secuenciación pueden invalidar toda la evaluación.

Normalización de datos en Python

Scikit-learn te proporciona los escaladores, pero la regla principal es procedimental, no matemática: primero dividir, ajustar solo en el entrenamiento y luego reutilizar ese transformador ajustado en todas partes.

¿Por qué tanto alboroto? Porque el escalado aprende números a partir de datos: mínimo/máximo, media/desviación estándar, mediana/IQR. Si esos números se calculan utilizando el conjunto de pruebas, habrás dejado que la información futura se filtre silenciosamente en el entrenamiento. Nada se bloquea, pero tus métricas dejan de significar lo que crees que significan.

Un ejemplo mínimo:

import pandas as pd
from sklearn.preprocessing import MinMaxScaler, StandardScaler, RobustScaler
from sklearn.model_selection import train_test_split

# Example data
data = pd.DataFrame({
    'age': [25, 32, 47, 51, 62, 28, 35, 44],
    'income': [30000, 45000, 72000, 85000, 120000, 38000, 55000, 67000],
    'score': [0.2, 0.5, 0.7, 0.4, 0.9, 0.3, 0.6, 0.8]
})

# Split happens before any scaling
train_data, test_data = train_test_split(data, test_size=0.25, random_state=42)

En este punto, consideras la división del entrenamiento como «cómo era el mundo cuando creaste el modelo». La división de la prueba es «datos nuevos, no vistos». Tu escalador solo necesita aprender del mundo a partir del primero.

MinMaxScaler

La estandarización mín-máx es sencilla: almacena el mínimo y el máximo de entrenamiento para cada columna y, posteriormente, aplica la misma asignación.

scaler = MinMaxScaler()
scaler.fit(train_data)  # training only

train_scaled = scaler.transform(train_data)
test_scaled = scaler.transform(test_data)

Si alguna vez te ves llamando a fit() en el conjunto de pruebas, haz una pausa. Eso contradice el objetivo de realizar una prueba en primer lugar.

StandardScaler

StandardScaler almacena la media y la desviación estándar de la división de entrenamiento, y luego utiliza esos mismos valores para transformar tanto el entrenamiento como la prueba.

scaler = StandardScaler()
scaler.fit(train_data)

train_standardized = scaler.transform(train_data)
test_standardized = scaler.transform(test_data)

Este es el que se rompe silenciosamente cuando se produce una fuga, porque la media y la desviación estándar son fáciles de «estabilizar» utilizando accidentalmente más datos de los que deberías.

RobustScaler

RobustScaler Hace lo mismo que «ajustar una vez, reutilizar siempre», pero utiliza la mediana y el IQR, por lo que unos pocos puntos extremos no dictan la escala.

scaler = RobustScaler()
scaler.fit(train_data)

train_robust = scaler.transform(train_data)
test_robust = scaler.transform(test_data)

Una señal práctica de que vale la pena realizar un escalado robusto: tienes una cola larga que realmente deseas conservar (pagos, reclamaciones, picos de sensores) y no quieres que un día extraño reduzca el resto de la función a casi cero.

Cálculos rápidos con pandas

Para un trabajo exploratorio rápido, realizar los cálculos directamente en pandas está bien, siempre y cuando seas sincero sobre lo que estás haciendo: esto es para observar distribuciones, no para evaluar modelos.

# Min-max
df_minmax = (data - data.min()) / (data.max() - data.min())

# Z-score
df_zscore = (data - data.mean()) / data.std()

Prevención de la fuga de datos

Peligro aquí: las estadísticas se basan en el conjunto de datos completo. Hazlo antes de dividir, y los valores de prueba influirán en la transformación. Tu evaluación pierde sentido porque el preprocesamiento ya ha visto respuestas que no debería haber visto.

El patrón de fuga suele ser el siguiente:

Haciéndolo mal:

scaler = MinMaxScaler()
scaled_all = scaler.fit_transform(full_data)  # problem
train, test = split(scaled_all)

Este enfoque normaliza los datos antes de dividirlos, por lo que los datos de prueba ya han influido en la transformación.

Hacerlo de la manera correcta:

Al dividir primero los datos, nos aseguramos de que el escalador aprenda las estadísticas únicamente a partir del conjunto de entrenamiento, manteniendo los datos de prueba realmente ocultos.

scaler = MinMaxScaler()
scaler.fit(train_data)
train_scaled = scaler.transform(train_data)
test_scaled = scaler.transform(test_data)

Las mismas operaciones, en diferente orden. Y el orden es lo más importante.

Si prefieres practicar el preprocesamiento de principio a fin (incluyendo la estandarización correcta y cómo evitar fugas), este curso está diseñado para eso: Preprocesamiento para el machine learning en Python.

Normalización en SQL

Como mencionamos anteriormente, tenemos diferentes significados para la misma palabra. Aquí, la «normalización» no es una transformación numérica. Es una decisión estructural dejar de duplicar datos.

Si tu tabla de pedidos almacena customer_email en cada fila, la base de datos te permitirá hacerlo. La base de datos también aceptará sin problemas contradicciones posteriores: un correo electrónico en una fila, otro correo electrónico diferente en otra, y sin una forma clara de saber cuál es «real».

Antes de la normalización:

CREATE TABLE orders_denormalized (
    order_id INT,
    customer_name VARCHAR(100),
    customer_email VARCHAR(100),
    product_name VARCHAR(100),
    product_price DECIMAL(10,2),
    quantity INT
);

Los datos de los clientes se repiten en cada fila. Actualizar el correo electrónico significa buscar y modificar todos tus pedidos.

Después de la normalización:

CREATE TABLE customers (
    customer_id INT PRIMARY KEY,
    name VARCHAR(100),
    email VARCHAR(100)
);

CREATE TABLE products (
    product_id INT PRIMARY KEY,
    name VARCHAR(100),
    price DECIMAL(10,2)
);

CREATE TABLE orders (
    order_id INT PRIMARY KEY,
    customer_id INT REFERENCES customers(customer_id),
    product_id INT REFERENCES products(product_id),
    quantity INT
);

La información del cliente existe una sola vez. Las consultas requieren uniones, pero las actualizaciones se realizan en un solo lugar.

Cómo elegir la técnica de normalización adecuada

Por último, quiero ofrecerte un marco de decisión para la próxima vez que te preguntes qué técnica de normalización utilizar.

Mínimo-máximo cuando existen límites

El escalado mínimo-máximo funciona mejor cuando tus datos tienen límites conocidos y estables que no cambiarán entre el entrenamiento y la implementación. Los valores de píxeles siempre están comprendidos entre 0 y 255. Las puntuaciones de probabilidad no pueden superar 1. Las calificaciones de los exámenes tienen mínimos y máximos definidos.

Este enfoque también es adecuado cuando tu modelo espera específicamente entradas limitadas, como ocurre con algunas arquitecturas de redes neuronales. Sin embargo, evita el escalado mínimo-máximo cuando haya valores atípicos, ya que un solo valor extremo puede comprimir todas las observaciones normales en un rango estrecho cercano a cero.

La estandarización como alternativa

La estandarización sirve como un valor predeterminado razonable cuando no se tienen hipótesis sólidas sobre los límites o la distribución de los datos. Funciona bien para características con rangos variables, límites desconocidos o distribuciones aproximadamente en forma de campana.

Muchas implementaciones de algoritmos asumen o recomiendan entradas estandarizadas, incluyendo la mayoría de los marcos de redes neuronales y bibliotecas de regresión logística. Si no estás seguro de qué enfoque utilizar y tus datos no tienen límites naturales evidentes, la estandarización suele ser una opción segura.

Robusto para el desorden del mundo real

El escalado robusto se convierte en la opción adecuada cuando tus datos contienen valores atípicos significativos que representan valores legítimos en lugar de errores. Los datos de transacciones financieras suelen tener esta característica: la mayoría de las compras son pequeñas, pero ocasionalmente se producen cargos elevados que son reales y deben permanecer en el conjunto de datos.

Las distribuciones de ingresos, las lecturas de sensores con picos ocasionales y cualquier dato con gran sesgo o colas largas se benefician de un escalado robusto. La mediana y el rango intercuartílico permanecen anclados a la mayor parte de tu distribución, independientemente de lo que ocurra en los extremos.

Cuándo no normalizar

Los modelos basados en árboles, como los bosques aleatorios, XGBoost y los árboles impulsados por gradientes, se dividen en valores umbral y nunca calculan distancias o gradientes entre características. La escala es invisible para ustedes, por lo que la normalización añade complejidad sin aportar ningún beneficio.

Las características codificadas con un solo valor ya son binarias (0 y 1), por lo que escalarlas no aporta nada útil. Los conjuntos de datos solo categóricos entran en la misma categoría.

A veces, las transformaciones específicas del dominio funcionan mejor que la normalización genérica:

• La escala logarítmica comprime las colas largas a la derecha y dispersa los valores más bajos agrupados, lo que a menudo funciona mejor para los datos de ingresos o precios que los enfoques estándar. 
• La agrupación tiene sentido cuando la pertenencia a una categoría es más importante que los valores numéricos precisos. 
• Los transformadores de potencia ayudan a estabilizar la varianza en situaciones específicas.

Tabla comparativa resumida

A continuación, se ofrece una descripción general de las técnicas y sus casos de uso:

Conclusión

Las diferencias de escala causan verdaderos problemas a los modelos que se preocupan por ellas. Las métricas de distancia favorecen las características de gran magnitud. El descenso por gradiente tiene dificultades cuando los gradientes abarcan órdenes de magnitud. El entrenamiento se detiene o explota por razones que no son evidentes al observar el código o la arquitectura.

La normalización aborda este problema. Utiliza la normalización mín-máx para datos acotados, el escalado robusto cuando los valores atípicos son reales y no se pueden eliminar, y la estandarización como valor predeterminado razonable. La mecánica es sencilla: encaja en el entrenamiento, aplícalo en todas partes de forma coherente. 

Según mi experiencia, lo que lleva tiempo es no reconocer cuándo es importante el escalado y luego pasar días depurando el comportamiento del modelo cuando la solución era el preprocesamiento. O el error contrario, como aplicar el escalado de forma refleja a modelos que no lo necesitan, añadiendo complejidad sin aportar ningún beneficio.

¿Listo para subir de nivel? Nuestro completo ingeniero de machine learning el programa te enseña todo lo que necesitas saber sobre el flujo de trabajo del machine learning.