R-Squared expliqué : Quel est le degré d'adéquation de votre modèle de régression ?

Au fond, le R au carré explique la proportion de la variance de la variable dépendante qui peut être attribuée à la (ou aux) variable(s) indépendante(s). Nous pouvons considérer qu'il s'agit d'une mesure de la capacité de notre modèle à capturer l'histoire des données, et de la part de bruit inexpliquée. Sa simplicité et son interprétation directe en font un outil très répandu dans les diagnostics de régression linéaire, en particulier dans les régressions linéaires simples et multiples.

Dans cet article, nous examinerons la signification, le calcul, l'interprétation et les pièges courants du R au carré, afin de pouvoir l'utiliser avec confiance et prudence. En outre, nous examinerons quelques exemples d'extraits de code pour le calcul du R-carré dans R et Python.

Qu'est-ce que le R au carré ?

Le R au carré, noté ^R², est une mesure statistique de la qualité de l'ajustement des modèles de régression. Il nous indique dans quelle mesure la variation de la variable dépendante peut être expliquée par le modèle.

La valeur de R-carré est comprise entre 0 et 1 :

• ^R² = 0 signifie que le modèle n'explique aucune partie de la variabilité ;
• ^R² = 1 signifie que le modèle explique tout.

Si le concept est simple, son interprétation nécessite une approche nuancée, en particulier lorsqu'il s'agit de passer de la théorie à la pratique.

Comment calculer le R au carré

Il existe plusieurs méthodes équivalentes sur le plan mathématique pour calculer le R au carré, chacune offrant un aperçu différent de ce que signifie réellement l'"adéquation", en fonction du contexte : régression simple, régression multiple, algèbre matricielle ou modélisation bayésienne. Examinons les approches les plus fréquemment utilisées.

1. Utilisation de la somme des carrés résiduels et de la somme totale des carrés

Il s'agit de la formule la plus standard et la plus largement utilisée :

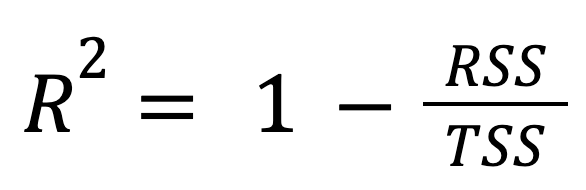
où :

• RSS est la somme des carrés résiduels, qui mesure la variation inexpliquée par le modèle,
• SCT est la somme totale des carrés, qui mesure la variation totale des données.

En d'autres termes, le R au carré représente la fraction de la variation totale que le modèle prend en compte. 

Cette approche met en évidence l'amélioration des performances du modèle de régression par rapport à la simple prédiction de la moyenne de la réponse.

2. Utilisation de la somme des carrés expliquée et de la somme totale des carrés

Le R au carré peut également être exprimé directement en termes de variance expliquée :

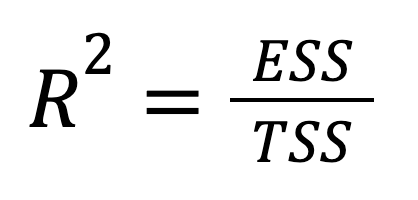
où :

• ESS est la somme des carrés expliqués, qui mesure l'ampleur de la variance capturée par le modèle,
• SCT est la somme totale des carrés, qui mesure la variation totale des données.

Nous pouvons constater que cette version met l'accent sur la part de la variation totale du résultat qui est prise en compte par les prédictions du modèle. En d'autres termes, l'accent n'est plus mis sur ce que nous n'avons pas réussi à expliquer (RSS), mais sur ce que nous avons fait (ESS), ce qui donne un cadre plus optimiste.

Pour une analyse approfondie des trois composantes de la somme des carrés, consultez Comprendre la somme des carrés : Un guide pour les SST, SSR et SSE.

3. Utilisation de la somme des carrés expliqués et de la somme des carrés résiduels

Dans le contexte d'un tableau d'ANOVA, le R au carré émerge naturellement de la décomposition de la variabilité totale : 

où :

• ESS est la somme des carrés expliqués, qui mesure l'ampleur de la variance capturée par le modèle,
• RSS est la somme des carrés résiduels, qui mesure la variation inexpliquée par le modèle.

Cette formulation montre quelle part de la variance totale est prise en compte par le modèle et quelle part reste inexpliquée.

Cette perspective est un peu unique parce qu'elle lie le R-carré aux tests d'hypothèse. En effet, le rapport entre ESS et RSS est utilisé pour calculer la statistique F ( ), ce qui fait du R-carré un élément important des tests de signification dans les rapports de type ANOVA.

4. Utilisation du coefficient de corrélation dans une régression linéaire simple

Les trois dernières méthodes sont toutes des formules algébriques équivalentes dérivées de la décomposition de la régression. Voici une nouvelle perspective :

Dans le cas d'une régression linéaire simple avec un seul prédicteur, le R-carré a un raccourci :

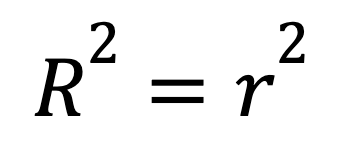
où

• r est le coefficient de corrélation de Pearson entre x et y.

Cette formule montre comment une forte relation linéaire entre deux variables se traduit directement par un R-carré élevé. 

Pour comprendre la théorie sous-jacente à la régression linéaire simple, consultez le site Régression linéaire simple : Tout ce que vous devez savoir.

5. Utilisation de l'erreur quadratique moyenne et de la variance du résultat

Le R au carré peut être calculé comme une mesure normalisée de l'erreur du modèle : 

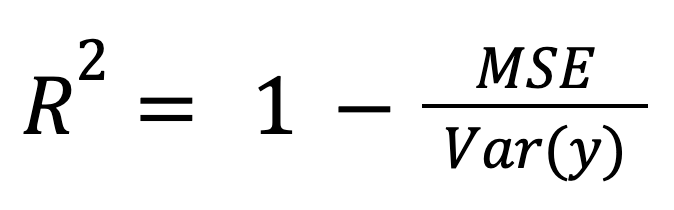
où :

• MSE est l'erreur quadratique moyenne du modèle,
• Var(y) est la variance du résultat réel.

Ce cadrage est particulièrement pertinent lorsque l'on compare des modèles à différentes échelles ou unités, car il normalise l'erreur du modèle en fonction de la dispersion globale des données.

6. Utilisation de la variance des valeurs prédites

En supposant que les résidus ne sont pas corrélés avec les prédictions, le R au carré peut également être interprété comme la fraction de variance capturée par le modèle :

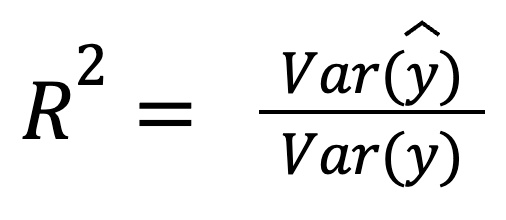
où :

• Var(ŷ) est la variance des prédictions du modèle,
• Var(y) est la variance du résultat réel.

Cette version met en évidence la manière dont les prédictions elles-mêmes reflètent la dispersion des données réelles.

Interprétation du R au carré

Comme nous l'avons déjà mentionné, le R au carré est facile à calculer, mais son interprétation est un peu plus délicate.

• Un R-carré élevé signifie que le modèle explique une grande partie de la variance. Toutefois, cela ne signifie pas que notre modèle est nécessairement correct ou utile.
• Un faible R-carré signifie que le modèle explique peu de variance. Ce n'est pas toujours une mauvaise chose, en particulier dans le domaine des sciences sociales ou des données bruitées, où l'on s'attend souvent à un faible R-carré.

Il est important de se rappeler que le R au carré mesure la corrélation, mais pas la causalité. Ce n'est pas parce que nos prédicteurs expliquent le résultat qu'ils sont la cause de celui-ci, car corrélation ne signifie toujours pas causalité. En outre, le R au carré n'indique pas si les prédictions sont exactes.

Voici deux ressources utiles sur des sujets plus avancés liés à la régression linéaire : 

• Facteur d'inflation de la variance (VIF) : Traitement de la multicolinéarité dans l'analyse de régression
• Décomposition QR dans l'apprentissage automatique : Un guide détaillé

Quand utiliser le R au carré

Le R-carré peut être très utile s'il est utilisé dans les bonnes situations. Il est approprié pour :

• Comparaison de modèles avec le même nombre de prédicteurs.
• Explication de la variance d'un ensemble de données prise en compte par le modèle.

D'autre part, le R au carré peut être trompeur dans les cas suivants :

• Ajout de prédicteurs non pertinents, ce qui entraîne un surajustement. Dans ce cas, le R au carré augmente toujours, même si la performance prédictive du modèle ne s'améliore pas.
• Comparer des modèles avec différents nombres de prédicteurs, c'est-à-dire avec différentes complexités. Dans ce cas, le R au carré ajusté est un meilleur choix. Je reviendrai plus tard sur le R au carré ajusté.

Exemples de R-carré dans R et Python

Illustrons maintenant le concept de R-carré dans R et Python en utilisant le jeu de données Kaggle Fish Market. Dans les deux langages de programmation, nous construirons deux modèles :

• Modèle 1 : Prédire le poids des poissons à l'aide de quatre prédicteurs.
• Modèle 2 : Ajoutez un prédicteur aléatoire et non pertinent.

Exemple R

Commençons par R.

Modèle 1

# Load data
fish <- read.csv("Fish.csv")

# Model 1
model1 <- lm(Weight ~ Length1 + Length2 + Height + Width, data=fish)
summary(model1)$r.squared

Sortie :

[1] 0.8673

Modèle 2

# Model 2 with an irrelevant predictor
fish$random_noise <- rnorm(nrow(fish))
model2 <- lm(Weight ~ Length1 + Length2 + Height + Width + random_noise, data=fish)
summary(model2)$r.squared

Sortie :

[1] 0.8679

Comme nous pouvons le voir, le R au carré augmente légèrement après l'ajout d'un prédicteur non pertinent (modèle 2). Cela ne signifie pas pour autant que le modèle s'est amélioré. Après tout, nous n'avons fait qu'ajouter un bruit aléatoire.

Pour en savoir plus sur le sujet, consultez les tutoriels suivants :

• Comment effectuer une régression linéaire dans R
• Régression linéaire multiple dans R : Tutoriel avec exemples

Et n'oubliez pas de vous inscrire à notre cours désigné :

• Introduction à la régression en R

Exemple en Python

Essayons maintenant en Python.

Modèle 1

import pandas as pd
import statsmodels.api as sm
import numpy as np

# Load data
fish = pd.read_csv('Fish.csv')
X1 = fish[['Length1', 'Length2', 'Height', 'Width']]
y = fish['Weight']

# Model 1
X1 = sm.add_constant(X1)
model1 = sm.OLS(y, X1).fit()
print(model1.rsquared)

Sortie :

0.8673

Modèle 2

# Model 2 with an irrelevant predictor
fish['random_noise'] = np.random.randn(len(fish))
X2 = fish[['Length1', 'Length2', 'Height', 'Width', 'random_noise']]
X2 = sm.add_constant(X2)
model2 = sm.OLS(y, X2).fit()
print(model2.rsquared)

Sortie :

0.8679

Une fois de plus, nous observons une légère augmentation de la valeur du R au carré, mais il s'agit simplement d'un bruit aléatoire.

Pour continuer à apprendre, inscrivez-vous à nos cours :

• Introduction à la régression avec statsmodels en Python et
• Régression intermédiaire avec statsmodels en Python

R au carré vs. Mesures connexes

Nous allons maintenant comparer brièvement le R-carré à deux mesures apparentées : le R-carré ajusté et le R-carré prédit.

R-carré vs. R-carré ajusté

Contrairement au R au carré, le R au carré ajusté tient compte du nombre de prédicteurs. En particulier, il pénalise le modèle pour l'inclusion de prédicteurs inutiles :

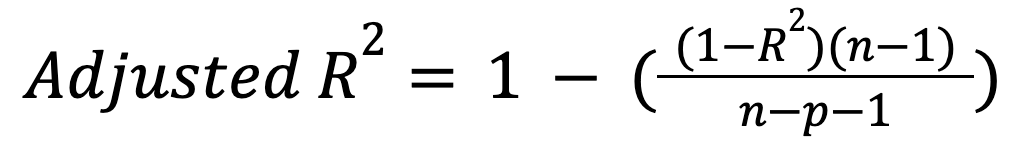
où :

• n est le nombre d'observations,
• p est le nombre de prédicteurs.

Cette mesure n'augmente que si un nouveau prédicteur améliore effectivement le modèle de manière significative, et peut diminuer dans le cas contraire. Lisez notre tutoriel pour en savoir plus sur cette extension importante : R-carré ajusté : Une explication claire avec des exemples.

R-carré vs. R-carré prédit

Alors que le R-carré normal indique les performances du modèle sur les données d'apprentissage, le R-carré prédit nous indique les performances du modèle sur de nouvelles données inédites. Cette mesure évalue donc la capacité de généralisation du modèle.

Le R au carré prédit est calculé à l'aide de la validation croisée ou en conservant une partie des données d'apprentissage pour des tests supplémentaires. Il peut être nettement inférieur au R au carré normal si le modèle est surajusté. Par conséquent, un scénario dans lequel nous obtenons une valeur élevée de R-carré régulier mais une valeur faible de R-carré prédit peut très probablement indiquer un surajustement du modèle.

Idées reçues sur le R au carré

Examinons quelques mythes populaires sur le R-carré, ainsi que la réalité des choses : 

• "Un R au carré élevé est toujours synonyme d'un bon modèle. Ce n'est pas nécessairement vrai. Le R au carré peut être élevé pour un modèle surajusté ou construit sur des corrélations fallacieuses. Naturellement, dans les deux cas, le modèle ne peut être qualifié de bon.
• "Le R au carré mesure le pouvoir de prédiction. En réalité, il ne mesure que l'adéquation du modèle aux données d'apprentissage et ne dit rien sur les données inédites. Pour évaluer les performances futures du modèle, nous avons besoin d'autres mesures telles que le R-carré prédit évoqué ci-dessus.
• "Nous devrions toujours viser un R au carré élevé". Enfin, pas toujours. Cela dépend du domaine, ainsi que de la qualité des données elles-mêmes. Comme nous l'avons mentionné plus haut dans cet article, pour les sciences sociales telles que la psychologie ou l'histoire, la valeur du R au carré peut être très faible (0,1 ou même moins) et rester significative. Il en va de même pour les données bruitées, pour lesquelles une faible valeur de R-carré est fortement attendue.

Conclusion

Pour résumer, nous avons appris ce qu'est le R au carré, comment calculer cette métrique (à la fois mathématiquement et dans R et Python), quand l'utiliser et quand l'éviter, et comment interpréter les résultats. En outre, nous avons abordé deux mesures connexes et quelques idées fausses très répandues sur le R-carré. 

En bref, le R au carré est une mesure utile, intuitive et directe de l'adéquation d'un modèle de régression. Il s'agit d'un excellent point de départ pour l'évaluation d'un modèle, mais il doit être utilisé à bon escient, interprété en parallèle avec d'autres mesures et ne pas être confondu avec l'ensemble du tableau. C'est particulièrement vrai dans les contextes de régression multiple et de sélection de modèles.