R-Quadrat Erklärt: Wie gut passt dein Regressionsmodell?

Im Kern erklärt R-Quadrat den Anteil der Varianz in der abhängigen Variable, der auf die unabhängige(n) Variable(n) zurückgeführt werden kann. Wir können sie als Maß dafür betrachten, wie gut unser Modell die Geschichte in den Daten erfasst und wie viel als unerklärtes Rauschen übrig bleibt. Aufgrund ihrer Einfachheit und direkten Interpretation ist sie in der linearen Regressionsdiagnostik weit verbreitet, insbesondere bei der einfachen und multiplen linearen Regression.

In diesem Artikel werden wir die Bedeutung, die Berechnung, die Interpretation und die häufigsten Fallstricke von R-Quadrat besprechen, damit wir es mit Zuversicht und Sorgfalt verwenden können. Außerdem sehen wir uns einige Beispiele für Codeschnipsel zur Berechnung von R-Quadrat in R und Python an.

Was ist R-Quadrat?

Das R-Quadrat (^R²) ist ein statistisches Maß für die Anpassungsgüte von Regressionsmodellen. Sie sagt uns, wie viel der Variation in der abhängigen Variable durch das Modell erklärt werden kann.

Der Wert von R-Quadrat liegt zwischen 0 und 1:

• ^R² = 0 bedeutet, dass das Modell keinen Teil der Variabilität erklärt;
• ^R² = 1 bedeutet, dass das Modell alles erklärt.

Das Konzept ist zwar einfach, aber seine Auslegung erfordert einen differenzierten Ansatz, vor allem, wenn man von der Theorie zur Praxis übergeht.

Wie man das R-Quadrat berechnet

Es gibt mehrere mathematisch äquivalente Methoden zur Berechnung des R-Quadrats, die je nach Kontext einen anderen Einblick in die Bedeutung von "Passung" bieten: einfache Regression, multiple Regression, Matrixalgebra oder Bayes'sche Modellierung. Schauen wir uns die am häufigsten verwendeten Ansätze an.

1. Verwendung der Residualsumme der Quadrate und der Gesamtsumme der Quadrate

Dies ist die gängigste und am häufigsten verwendete Formel:

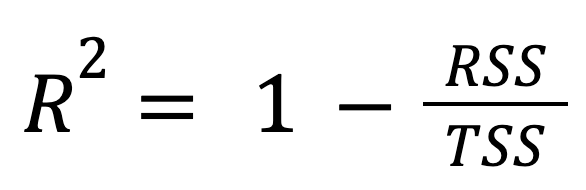
wo:

• RSS ist die Residualsumme der Quadrate, die die unerklärte Variation durch das Modell misst,
• TSS ist die Gesamtsumme der Quadrate, die die gesamte Variation in den Daten misst.

Mit anderen Worten: Das R-Quadrat gibt den Anteil der Gesamtvariation an, den das Modell abdeckt. 

Dieser Ansatz verdeutlicht, wie viel besser das Regressionsmodell im Vergleich zur einfachen Vorhersage des Mittelwerts der Antwort abschneidet.

2. Verwendung der erklärten Summe der Quadrate und der gesamten Summe der Quadrate

Das R-Quadrat kann auch direkt in Form der erklärten Varianz ausgedrückt werden:

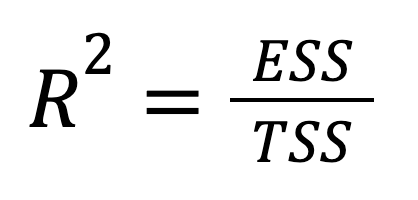
wo:

• ESS ist die erklärte Summe der Quadrate, die angibt, wie viel der Varianz durch das Modell erfasst wird,
• TSS ist die Gesamtsumme der Quadrate, die die gesamte Variation in den Daten misst.

Wir sehen, dass diese Version hervorhebt, wie viel von der Gesamtvariation des Ergebnisses von den Vorhersagen des Modells erfasst wird. Mit anderen Worten: Der Schwerpunkt wird von dem, was wir nicht erklären konnten (RSS), auf das verlagert, was wir erklärt haben (ESS), was eine optimistischere Sichtweise ermöglicht.

Einen tieferen Einblick in die drei Komponenten der Quadratsumme erhältst du unter Summen der Quadrate verstehen: Ein Leitfaden für SST, SSR und SSE.

3. Verwendung der erklärten Summe der Quadrate und der Residualsumme der Quadrate

Im Zusammenhang mit einer ANOVA-Tabelle ergibt sich das R-Quadrat natürlich aus der Zerlegung der Gesamtvariabilität: 

wo:

• ESS ist die erklärte Summe der Quadrate, die angibt, wie viel der Varianz durch das Modell erfasst wird,
• RSS ist die Residualsumme der Quadrate, die die unerklärte Variation durch das Modell misst.

Diese Formulierung zeigt, wie viel von der Gesamtvarianz durch das Modell erfasst wird und wie viel unerklärt bleibt.

Diese Perspektive ist ein wenig einzigartig, weil sie das R-Quadrat mit dem Hypothesentest verbindet. Das liegt daran, dass das Verhältnis von ESS zu RSS zur Berechnung der F-Statistik verwendet wird, wodurch das R-Quadrat ein wichtiger Bestandteil der Signifikanztests in der ANOVA-Berichterstattung ist.

4. Verwendung des Korrelationskoeffizienten in der einfachen linearen Regression

Die letzten drei Methoden waren alle algebraisch gleichwertige Formeln, die aus der Regressionszerlegung abgeleitet wurden. Jetzt gibt es eine neue Perspektive:

Bei einer einfachen linearen Regression mit nur einem Prädiktor hat das R-Quadrat eine Abkürzung:

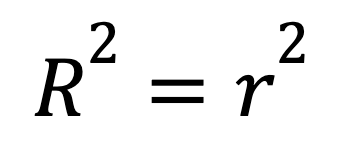
wo

• r ist der Pearson-Korrelationskoeffizient zwischen x und y.

Diese Formel zeigt, wie sich eine starke lineare Beziehung zwischen zwei Variablen direkt in einem hohen R-Quadrat niederschlägt. 

Um die zugrundeliegende Theorie hinter der einfachen linearen Regression zu verstehen, besuche Einfache lineare Regression: Alles, was du wissen musst.

5. Verwendung des mittleren quadratischen Fehlers und der Varianz des Ergebnisses

Das R-Quadrat kann als normalisiertes Maß für den Modellfehler berechnet werden: 

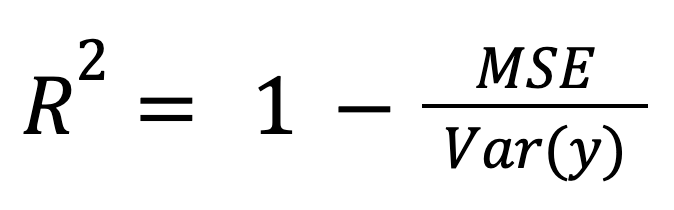
wo:

• MSE ist der mittlere quadratische Fehler des Modells,
• Var(y) ist die Varianz des wahren Ergebnisses.

Dieser Rahmen ist besonders wichtig, wenn du Modelle in verschiedenen Maßstäben oder Einheiten vergleichst, da er den Modellfehler durch die Gesamtdatenstreuung normalisiert.

6. Verwendung der Varianz der vorhergesagten Werte

Unter der Annahme, dass die Residuen nicht mit den Vorhersagen korreliert sind, kann R-Quadrat auch als der Anteil der Varianz interpretiert werden, den das Modell erfasst:

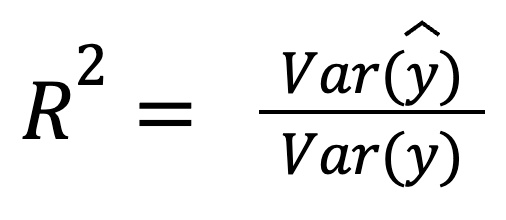
wo:

• Var(ŷ) ist die Varianz der Vorhersagen des Modells,
• Var(y) ist die Varianz des wahren Ergebnisses.

Diese Version zeigt, wie gut die Vorhersagen selbst die Streuung der tatsächlichen Daten widerspiegeln.

R-Quadrat interpretieren

Wie wir bereits erwähnt haben, ist das R-Quadrat leicht zu berechnen, aber etwas schwieriger zu interpretieren.

• Ein hohes R-Quadrat bedeutet, dass das Modell einen großen Teil der Varianz erklärt. Das heißt aber nicht, dass unser Modell unbedingt richtig oder nützlich ist.
• Ein niedriges R-Quadrat bedeutet, dass nur wenig Varianz durch das Modell erklärt wird. Das ist nicht immer schlecht, vor allem in den Sozialwissenschaften oder bei verrauschten Daten, wo oft ein niedriges R-Quadrat erwartet wird.

Es ist wichtig, daran zu denken, dass das R-Quadrat die Korrelationmisst , aber nicht die Kausalität. Nur weil unsere Prädiktoren das Ergebnis erklären, bedeutet das nicht, dass sie Ursache essind, denn Korrelation bedeutet noch lange nicht Kausalität. Außerdem sagt das R-Quadrat nichts darüber aus, ob die Vorhersagen richtig sind.

Hier sind zwei nützliche Ressourcen zu fortgeschrittenen Themen im Zusammenhang mit der linearen Regression: 

• Varianz-Inflations-Faktor (VIF): Umgang mit Multikollinearität in der Regressionsanalyse
• QR-Zerlegung beim maschinellen Lernen: Ein detaillierter Leitfaden

Wann man R-Quadrat verwendet

R-Quadrat kann sehr hilfreich sein, wenn es in den richtigen Situationen eingesetzt wird. Es ist geeignet für:

• Vergleich von Modellen mit der gleichen Anzahl von Prädiktoren.
• Erklären, wie viel Varianz in einem Datensatz durch das Modell erklärt wird.

Andererseits kann das R-Quadrat in den folgenden Szenarien irreführend sein:

• Hinzufügen irrelevanter Prädiktoren, was zu einer Überanpassung führt. In diesem Fall steigt das R-Quadrat immer, auch wenn sich die Vorhersageleistung des Modells nicht verbessert.
• Vergleich von Modellen mit einer unterschiedlichen Anzahl von Prädiktoren, d. h. mit unterschiedlicher Komplexität. Hier ist das bereinigte R-Quadrat die bessere Wahl. Ich werde später mehr über das bereinigte R-Quadrat sprechen.

R-Quadrat Beispiele in R und Python

Veranschaulichen wir uns nun das Konzept von R-Quadrat in R und Python anhand des Fish Market Kaggle-Datensatzes. In beiden Programmiersprachen werden wir zwei Modelle erstellen:

• Modell 1: Sage das Fischgewicht mithilfe von vier Prädiktoren voraus.
• Modell 2: Füge einen zufälligen, irrelevanten Prädiktor hinzu.

R Beispiel

Fangen wir mit R an.

Modell 1

# Load data
fish <- read.csv("Fish.csv")

# Model 1
model1 <- lm(Weight ~ Length1 + Length2 + Height + Width, data=fish)
summary(model1)$r.squared

Ausgabe:

[1] 0.8673

Modell 2

# Model 2 with an irrelevant predictor
fish$random_noise <- rnorm(nrow(fish))
model2 <- lm(Weight ~ Length1 + Length2 + Height + Width + random_noise, data=fish)
summary(model2)$r.squared

Ausgabe:

[1] 0.8679

Wie wir sehen können, steigt das R-Quadrat leicht an, wenn wir einen irrelevanten Prädiktor hinzufügen (Modell 2). Das heißt aber nicht, dass das Modell besser geworden ist. Schließlich haben wir nur zufälliges Rauschen hinzugefügt.

Weitere Informationen zu diesem Thema findest du in den folgenden Tutorials:

• Wie man eine lineare Regression in R durchführt
• Multiple lineare Regression in R: Tutorial mit Beispielen

Und vergiss nicht, dich für den vorgesehenen Kurs anzumelden:

• Kurs Einführung in die Regression in R

Python Beispiel

Versuchen wir es jetzt in Python.

Modell 1

import pandas as pd
import statsmodels.api as sm
import numpy as np

# Load data
fish = pd.read_csv('Fish.csv')
X1 = fish[['Length1', 'Length2', 'Height', 'Width']]
y = fish['Weight']

# Model 1
X1 = sm.add_constant(X1)
model1 = sm.OLS(y, X1).fit()
print(model1.rsquared)

Ausgabe:

0.8673

Modell 2

# Model 2 with an irrelevant predictor
fish['random_noise'] = np.random.randn(len(fish))
X2 = fish[['Length1', 'Length2', 'Height', 'Width', 'random_noise']]
X2 = sm.add_constant(X2)
model2 = sm.OLS(y, X2).fit()
print(model2.rsquared)

Ausgabe:

0.8679

Auch hier beobachten wir einen leichten Anstieg des R-Quadratwerts, aber das ist nur ein zufälliges Rauschen.

Um weiter zu lernen, melde dich für unsere Kurse an:

• Einführung in die Regression mit Statsmodels in Python und
• Mittlere Regression mit statsmodels in Python

R-Quadrat vs. Verwandte Metriken

Wir werden nun kurz das R-Quadrat mit zwei verwandten Kennzahlen vergleichen: dem bereinigten R-Quadrat und dem vorhergesagten R-Quadrat.

R-Quadrat vs. bereinigtes R-Quadrat

Im Gegensatz zum R-Quadrat berücksichtigt das bereinigte R-Quadrat die Anzahl der Prädiktoren. Insbesondere wird das Modell für die Einbeziehung unnötiger Prädiktoren bestraft:

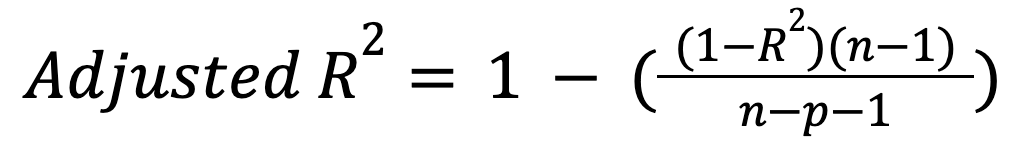
wo:

• n ist die Anzahl der Beobachtungen,
• p ist die Anzahl der Prädiktoren.

Diese Kennzahl steigt nur, wenn ein neuer Prädiktor das Modell tatsächlich sinnvoll verbessert, und kann im umgekehrten Fall sinken. Lies unseren Leitfaden, um mehr über diese wichtige Erweiterung zu erfahren: Bereinigtes R-Quadrat: Eine klare Erläuterung mit Beispielen.

R-Quadrat vs. vorhergesagtes R-Quadrat

Während das reguläre R-Quadrat zeigt, wie gut das Modell in den Trainingsdaten abschneidet, sagt das vorhergesagte R-Quadrat aus, wie gut es in neuen, ungesehenen Daten abschneidet. Mit dieser Kennzahl wird also die Generalisierungsfähigkeit des Modells bewertet.

Das vorhergesagte R-Quadrat wird mithilfe einer Kreuzvalidierung oder durch das Zurückhalten eines Teils der Trainingsdaten für weitere Tests berechnet. Er kann deutlich niedriger sein als das reguläre R-Quadrat, wenn das Modell überangepasst ist. Ein Szenario, in dem wir einen hohen Wert für das reguläre R-Quadrat, aber einen niedrigen Wert für das vorhergesagte R-Quadrat erhalten, kann daher höchstwahrscheinlich auf eine Überanpassung des Modells hinweisen.

Häufige Missverständnisse über R-Quadrat

Werfen wir einen Blick auf einige populäre Mythen über das R-Quadrat und den wahren Stand der Dinge: 

• "Ein hohes R-Quadrat bedeutet immer ein gutes Modell." Das ist nicht unbedingt richtig. Das R-Quadrat kann bei einem überangepassten Modell oder einem Modell, das auf falschen Korrelationen beruht, hoch sein. Natürlich kann man das Modell in beiden Fällen nicht als gut bezeichnen.
• "R-Quadrat misst die Vorhersagekraft." In Wirklichkeit misst sie nur die Anpassung des Modells an die Trainingsdaten und sagt nichts über ungesehene Daten aus. Um die künftige Leistung des Modells zu bewerten, brauchen wir andere Messgrößen wie das oben beschriebene R-Quadrat.
• "Wir sollten immer ein hohes R-Quadrat anstreben." Nun, nicht immer. Das hängt sowohl von der Domäne als auch von der Datenqualität selbst ab. Wie wir bereits in diesem Artikel erwähnt haben, kann der Wert des R-Quadrats in den Sozialwissenschaften wie Psychologie oder Geschichte sehr niedrig sein (0,1 oder sogar weniger) und trotzdem aussagekräftig sein. Das Gleiche gilt für verrauschte Daten, bei denen ein niedriger Wert von R-Quadrat sehr zu erwarten ist.

Fazit

Zusammenfassend haben wir gelernt, was R-Quadrat ist, wie man diese Kennzahl berechnet (sowohl mathematisch als auch in R und Python), wann man sie verwenden und wann man sie vermeiden sollte und wie man die Ergebnisse interpretiert. Außerdem haben wir zwei verwandte Metriken und einige weit verbreitete Missverständnisse über das R-Quadrat angesprochen. 

Kurz gesagt ist das R-Quadrat ein nützliches, intuitives und einfaches Maß für die Anpassung eines Regressionsmodells. Sie ist ein guter Ausgangspunkt für die Bewertung von Modellen, sollte aber mit Bedacht eingesetzt und zusammen mit anderen Kennzahlen interpretiert werden und nicht mit dem Gesamtbild verwechselt werden. Das gilt vor allem für die multiple Regression und die Modellauswahl.