R-Squared explicado: Qual é o nível de ajuste do seu modelo de regressão?

Em sua essência, o R-quadrado explica a proporção da variação na variável dependente que pode ser atribuída à variável (ou variáveis) independente(s). Podemos pensar nisso como uma medida de quão bem nosso modelo captura a história nos dados e quanto é deixado como ruído inexplicável. Sua simplicidade e interpretação direta fazem com que seja amplamente utilizado em diagnósticos de regressão linear, especialmente em regressão linear simples e múltipla.

Neste artigo, discutiremos o significado, o cálculo, a interpretação e as armadilhas comuns relacionadas ao R-quadrado, para que você possa usá-lo com confiança e cuidado. Além disso, daremos uma olhada em alguns exemplos de trechos de código para calcular o R-quadrado no R e no Python.

O que é R-Squared?

O R-quadrado, denotado como ^R², é uma medida estatística da qualidade do ajuste em modelos de regressão. Ele nos informa quanto da variação na variável dependente pode ser explicada pelo modelo.

O valor do R-quadrado está entre 0 e 1:

• ^R² = 0 significa que o modelo não explica nenhuma das variações;
• ^R² = 1 significa que o modelo explica tudo.

Embora o conceito seja simples, sua interpretação exige uma abordagem diferenciada, especialmente quando se passa da teoria para a prática.

Como calcular o R-Squared

Há várias maneiras matematicamente equivalentes de calcular o R-quadrado, cada uma oferecendo uma visão diferente do que realmente significa "ajuste", dependendo do contexto - regressão simples, regressão múltipla, álgebra matricial ou modelagem bayesiana. Vamos explorar as abordagens usadas com mais frequência.

1. Usando a soma residual de quadrados e a soma total de quadrados

Essa é a fórmula mais padrão e amplamente utilizada:

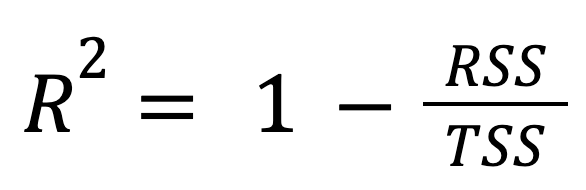
where:

• RSS é a soma residual de quadrados, que mede a variação não explicada pelo modelo,
• TSS é a soma total de quadrados, que mede a variação total dos dados.

Em outras palavras, o R-quadrado representa a fração da variação total que o modelo considera. 

Essa abordagem destaca o desempenho muito melhor do modelo de regressão em comparação com a simples previsão da média da resposta.

2. Usando a soma de quadrados explicada e a soma total de quadrados

O R-quadrado também pode ser expresso diretamente em termos de variação explicada:

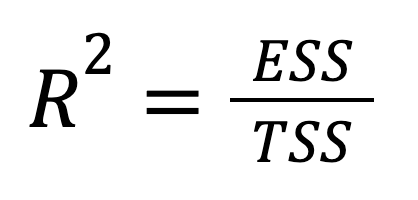
where:

• ESS é a soma de quadrados explicada, que mede o quanto da variação é capturada pelo modelo,
• TSS é a soma total de quadrados, que mede a variação total dos dados.

Podemos ver que essa versão enfatiza o quanto da variação total do resultado é capturada pelas previsões do modelo. Em outras palavras, o foco aqui é deslocado do que não conseguimos explicar (RSS) para o que conseguimos (ESS), proporcionando um enquadramento mais otimista.

Para se aprofundar nos três componentes da soma de quadrados, leia Understanding Sum of Squares: Um guia para SST, SSR e SSE.

3. Usando a soma de quadrados explicada e a soma de quadrados residual

No contexto de uma tabela ANOVA, o R-quadrado surge naturalmente da decomposição da variabilidade total: 

where:

• ESS é a soma de quadrados explicada, que mede o quanto da variação é capturada pelo modelo,
• RSS é a soma residual de quadrados, que mede a variação não explicada pelo modelo.

Essa formulação mostra quanto da variação total é captada pelo modelo e quanto é deixado sem explicação.

Essa perspectiva é um pouco diferente porque vincula o R-quadrado ao teste de hipóteses. Isso ocorre porque a proporção de ESS para RSS é usada para calcular a estatística F , tornando o R-quadrado uma parte importante do teste de significância em relatórios no estilo ANOVA.

4. Uso do coeficiente de correlação na regressão linear simples

Os três últimos métodos eram todos fórmulas algebricamente equivalentes derivadas da decomposição da regressão. Agora, aqui está uma nova perspectiva:

Na regressão linear simples com apenas um preditor, o R-quadrado tem um atalho:

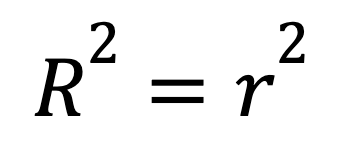
onde

• r é o coeficiente de correlação de Pearson entre x e y.

Essa fórmula mostra como uma forte relação linear entre duas variáveis se traduz diretamente em um R-quadrado alto. 

Para entender a teoria subjacente à regressão linear simples, acesse Simple Linear Regression: Tudo o que você precisa saber.

5. Usando o erro quadrático médio e a variância do resultado

O R-quadrado pode ser calculado como uma medida normalizada do erro do modelo: 

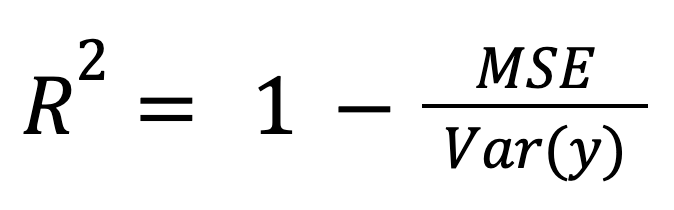
where:

• MSE é o erro quadrático médio do modelo,
• Var(y) é a variação do resultado real.

Esse enquadramento é especialmente relevante na comparação de modelos em diferentes escalas ou unidades, pois normaliza o erro do modelo pela dispersão geral dos dados.

6. Usando a variância dos valores previstos

Supondo que os resíduos não estejam correlacionados com as previsões, o R-quadrado também pode ser interpretado como a fração da variação capturada pelo modelo:

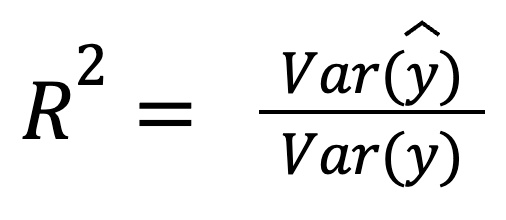
where:

• Var(ŷ) é a variação das previsões do modelo,
• Var(y) é a variação do resultado real.

Essa versão destaca o quanto as próprias previsões refletem a dispersão dos dados reais.

Interpretação do R-Squared

Como mencionamos anteriormente, o R-quadrado é fácil de calcular, mas um pouco mais complicado de interpretar de forma significativa.

• Um R-quadrado alto significa que o modelo explica uma grande parte da variação. No entanto, isso não significa que nosso modelo seja necessariamente correto ou útil.
• Um R-quadrado baixo significa que pouca variação é explicada pelo modelo. Isso nem sempre é ruim, especialmente em ciências sociais ou dados ruidosos, em que se espera um R-quadrado baixo.

É importante lembrar que o R-quadrado mede a correlação, mas não mede a causalidade. O fato de nossos preditores explicarem o resultado não significa que eles causam isso, pois a correlação ainda não significa causalidade. Além disso, o R-quadrado não indica se as previsões são precisas.

Aqui estão dois recursos úteis sobre tópicos mais avançados relacionados à regressão linear: 

• Fator de inflação de variância (VIF): Como lidar com a multicolinearidade na análise de regressão
• Decomposição de QR no machine learning: Um guia detalhado

Quando usar o R-Squared

O R-quadrado pode ser muito útil se usado nas situações certas. É apropriado para você:

• Comparação de modelos com o mesmo número de preditores.
• Explicação de quanta variação em um conjunto de dados é considerada pelo modelo.

Por outro lado, o R-quadrado pode ser enganoso nos seguintes cenários:

• Adição de preditores irrelevantes, o que resulta em sobreajuste. Nesse caso, o R-quadrado sempre aumenta, mesmo que o desempenho preditivo do modelo não melhore.
• Comparação de modelos com diferentes números de preditores, ou seja, com diferentes complexidades. Nesse caso, o R-quadrado ajustado é uma opção melhor. Falarei mais sobre o R-quadrado ajustado mais adiante.

Exemplos de R-Squared em R e Python

Vamos agora ilustrar o conceito de R-quadrado em R e Python usando o conjunto de dados do Fish Market do Kaggle. Em ambas as linguagens de programação, criaremos dois modelos:

• Modelo 1: Prever o peso do peixe usando quatro preditores.
• Modelo 2: Adicione um preditor aleatório e irrelevante.

Exemplo de R

Vamos começar com o R.

Modelo 1

# Load data
fish <- read.csv("Fish.csv")

# Model 1
model1 <- lm(Weight ~ Length1 + Length2 + Height + Width, data=fish)
summary(model1)$r.squared

Saída:

[1] 0.8673

Modelo 2

# Model 2 with an irrelevant predictor
fish$random_noise <- rnorm(nrow(fish))
model2 <- lm(Weight ~ Length1 + Length2 + Height + Width + random_noise, data=fish)
summary(model2)$r.squared

Saída:

[1] 0.8679

Como podemos ver, o R-quadrado aumenta ligeiramente após a adição de um preditor irrelevante (Modelo 2). No entanto, isso não significa que o modelo ficou melhor. Afinal, apenas adicionamos ruído aleatório.

Para ler mais sobre o assunto, consulte os tutoriais a seguir:

• Como fazer regressão linear no R
• Regressão linear múltipla no R: Tutorial com exemplos

E lembre-se de se inscrever em nosso curso designado:

• Curso de Introdução à Regressão em R

Exemplo em Python

Agora, vamos tentar em Python.

Modelo 1

import pandas as pd
import statsmodels.api as sm
import numpy as np

# Load data
fish = pd.read_csv('Fish.csv')
X1 = fish[['Length1', 'Length2', 'Height', 'Width']]
y = fish['Weight']

# Model 1
X1 = sm.add_constant(X1)
model1 = sm.OLS(y, X1).fit()
print(model1.rsquared)

Saída:

0.8673

Modelo 2

# Model 2 with an irrelevant predictor
fish['random_noise'] = np.random.randn(len(fish))
X2 = fish[['Length1', 'Length2', 'Height', 'Width', 'random_noise']]
X2 = sm.add_constant(X2)
model2 = sm.OLS(y, X2).fit()
print(model2.rsquared)

Saída:

0.8679

Novamente, observamos um ligeiro aumento no valor R-quadrado, mas isso é apenas a captura de ruído aleatório.

Para continuar aprendendo, inscreva-se em nossos cursos:

• Introdução à regressão com statsmodels em Python e
• Regressão intermediária com statsmodels em Python

R-Squared vs. Métricas relacionadas

Agora, faremos uma breve comparação do R-quadrado com duas métricas relacionadas: R-quadrado ajustado e R-quadrado previsto.

R-quadrado vs. R-quadrado ajustado

Ao contrário do R-quadrado, o R-quadrado ajustado leva em conta o número de preditores. Em particular, ele penaliza o modelo por incluir preditores desnecessários:

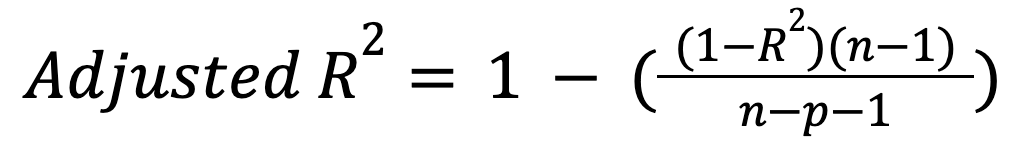
where:

• n é o número de observações,
• p é o número de preditores.

Essa métrica só aumenta se um novo preditor realmente melhorar o modelo de forma significativa, e pode diminuir no caso oposto. Leia nosso tutorial para saber mais sobre essa importante extensão: R-quadrado ajustado: Uma explicação clara com exemplos.

R-quadrado vs. R-quadrado previsto

Enquanto o R-quadrado normal mostra o desempenho do modelo nos dados de treinamento, o R-quadrado previsto nos informa o desempenho do modelo em dados novos e não vistos. Portanto, essa métrica avalia a capacidade de generalização do modelo.

O R-quadrado previsto é calculado usando validação cruzada ou retendo parte dos dados de treinamento para testes adicionais. Ele pode ser significativamente menor do que o R-quadrado regular se o modelo for ajustado em excesso. Portanto, um cenário em que obtemos um valor alto de R-quadrado regular, mas um valor baixo de R-quadrado previsto, provavelmente indica um ajuste excessivo do modelo.

Equívocos comuns sobre o R-Squared

Vamos dar uma olhada em alguns mitos populares sobre o R-quadrado, juntamente com a situação real: 

• "Um R-quadrado alto sempre significa um bom modelo." Isso não é necessariamente verdade. O R-quadrado pode ser alto para um modelo excessivamente ajustado ou construído com base em correlações espúrias. Naturalmente, em ambos os casos, o modelo não pode ser considerado bom.
• "O R-quadrado mede o poder de previsão." Na realidade, ele mede apenas o ajuste do modelo nos dados de treinamento e não diz nada sobre os dados não vistos. Para avaliar o desempenho futuro do modelo, precisamos de outras métricas, como o R-quadrado previsto discutido acima.
• "Devemos sempre buscar um R-quadrado alto." Bem, nem sempre. Depende do domínio, bem como da própria qualidade dos dados. Como mencionamos anteriormente neste artigo, para ciências sociais como psicologia ou história, o valor de R-quadrado pode ser muito baixo (0,1 ou até menos) e ainda assim significativo. O mesmo se aplica a dados ruidosos, em que um valor baixo de R-quadrado é altamente esperado.

Conclusão

Em resumo, aprendemos o que é o R-quadrado, como calcular essa métrica (matematicamente e em R e Python), quando usá-la e quando evitá-la e como interpretar os resultados. Além disso, abordamos duas métricas relacionadas e alguns equívocos generalizados sobre o R-quadrado. 

Em resumo, o R-quadrado é uma medida útil, intuitiva e direta do ajuste de um modelo de regressão. É um ótimo ponto de partida para a avaliação do modelo, mas deve ser usado com sabedoria, interpretado juntamente com outras métricas e não deve ser confundido com o panorama geral. Isso é especialmente verdadeiro para contextos de regressão múltipla e seleção de modelos.