RMSE explicado: Um guia para a precisão da previsão de regressão

O RMSE (root mean squared error, erro quadrático médio) é uma métrica de avaliação de precisão comumente usada na análise de regressão que mede a magnitude média dos erros em um modelo de regressão.

Ao contrário do R-quadrado, que quantifica a variação explicada, o RMSE fornece uma medida direta do erro de previsão nas mesmas unidades que a variável de resposta. Isso o torna especialmente útil quando o objetivo é minimizar as magnitudes de erro e interpretar o desempenho do modelo em termos do mundo real.

Neste artigo, exploraremos o significado, o cálculo, a interpretação e as concepções errôneas comuns sobre o RMSE. Você também verá exemplos em Python e R para saber como o RMSE se comporta em diferentes condições de modelagem.

O que é RMSE?

RMSE é a raiz quadrada da média das diferenças quadráticas entre os valores observados e previstos. É uma métrica de regressão amplamente usada que nos informa quanto erro você deve esperar de nossas previsões, em média. 

A fórmula matemática para calcular o RMSE é:

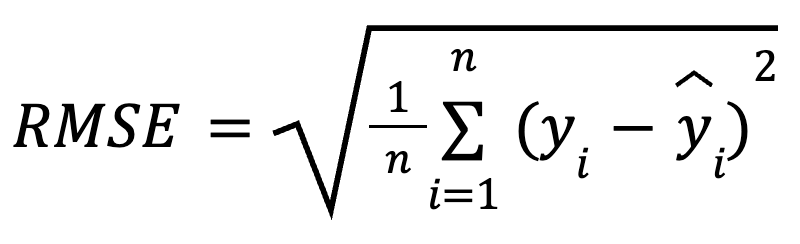
aqui:

• y_i é o valor real da observação i,
• _ŷ, é o valor previsto para a observação i,
• n é o número total de observações.

Ao elevar os resíduos ao quadrado antes de calcular a média, o RMSE penaliza mais os erros maiores do que os menores. Essa sensibilidade faz com que ele seja uma boa opção quando grandes erros de previsão são especialmente indesejáveis. O RMSE é sempre não negativo, e valores mais baixos indicam um modelo mais bem ajustado.

Três maneiras iguais de calcular o RMSE

O RMSE é fácil de calcular. É simplesmente uma questão de calcular os resíduos, elevá-los ao quadrado, encontrar a média e tirar a raiz quadrada.

Vamos considerar algumas maneiras diferentes de calculá-la.

Usando resíduos

Nesse método, começamos subtraindo as previsões dos valores reais para obter os resíduos. Em seguida, elevamos cada resíduo ao quadrado, calculamos a média de todos eles e, por fim, tiramos a raiz quadrada.

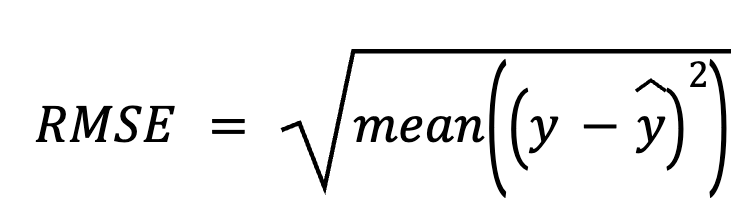
aqui:

• y é o vetor de valores reais,
• ŷé o vetor de valores previstos.

Essa abordagem direta enfatiza os próprios erros de previsão.

Usando o erro quadrático médio (MSE)

Esta parece ser apenas uma reafirmação, mas na verdade há mais do que isso: O RMSE é simplesmente a raiz quadrada do MSE. 

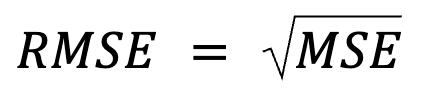
where:

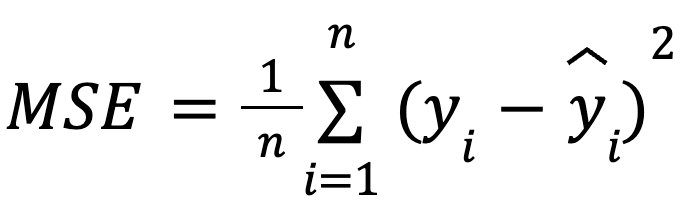
com:

• y_i como o valor real da observação i,
• ŷ, como o valor previsto para a observação i,
• n como o número total de observações.

Essa formulação é útil porque o MSE é uma função de perda comum na otimização de modelos. Essa equivalência é especialmente importante no machine learning, em que o MSE costuma ser a função de perda minimizada durante o treinamento por meio da descida do gradiente. 

Mais sobre isso: É justamente porque o RMSE introduz uma raiz quadrada que muitos algoritmos de machine learning optam por não usar o RMSE durante o treinamento do modelo. O MSE é preferível para essas otimizações porque tem derivados mais simples (novamente, porque a raiz quadrada introduz a não linearidade). O RMSE é frequentemente usado post hoc para relatar o desempenho em unidades interpretáveis.

Em forma de matriz

Na regressão múltipla, o RMSE também pode ser derivado do vetor residual usando álgebra matricial:

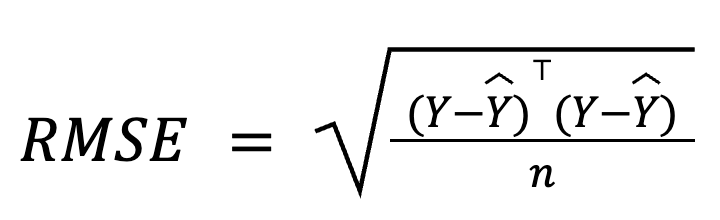
where:

• Y é o vetor de coluna dos valores reais,
• ŷ é o vetor de coluna dos valores previstos,
• n é o número de observações.

Essa formulação baseada em matriz é particularmente compacta e eficiente do ponto de vista computacional, especialmente para grandes conjuntos de dados ou pipelines de modelos. Temos um curso dedicado de álgebra linear se você quiser estudar matemática.

Interpretação do RMSE

O RMSE é interpretado como o erro médio de previsão, que determina a precisão da previsão do modelo. Simplificando, ele mostra, em média, a distância entre as previsões e os valores reais, na mesma escala da variável de resultado.

Um RMSE menor sugere erros de previsão médios menores e, portanto, previsões mais precisas, mas o RMSE "aceitável" depende inteiramente do contexto. Por exemplo, um RMSE de 2 pode ser bom para prever o tamanho da amêndoa em milímetros, mas não é tão convincente para prever a produção anual de amêndoas em toneladas.

Para ser significativo, o RMSE deve ser comparado entre modelos treinados com os mesmos dados ou por meio de benchmarking do desempenho histórico.

Quando usar o RMSE

O RMSE é particularmente útil nesses cenários:

• Quando a precisão absoluta da previsão é fundamental
• Ao comparar modelos no mesmo conjunto de dados
• Quando os erros do modelosão normalmente distribuídos
• Quando nosso objetivo é minimizar grandes erros
• Quando interpretar erros em unidades naturais é importante

No entanto, o RMSE tem suas desvantagens:

• É sensível a valores discrepantes. Alguns resíduos grandes podem afetar desproporcionalmente o RMSE e torná-lo enganoso.
• Isso não é normalizado. Isso significa que não é possível comparar conjuntos de dados e escalas de destino diferentes, a menos que a variável de destino seja dimensionada.

Exemplos de RMSE em Python e R

Vamos agora ilustrar como você pode calcular o RMSE no Python e no R usando o conjunto de dados do Kaggle Almond Types Classification. Embora o conjunto de dados seja originalmente destinado à classificação, nós o reutilizaremos aqui para regressão, prevendo a espessura do kernel como uma variável contínua com base em outros atributos físicos.

Criaremos dois modelos em cada linguagem de programação e, em seguida, calcularemos o RMSE para cada modelo:

• Modelo 1: Usa preditores relevantes (comprimento e largura).
• Modelo 2: Adiciona um preditor aleatório e irrelevante.

Exemplo em Python

Vamos começar com o Python.

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from math import sqrt

# Load data
data = pd.read_csv("almond_dataset.csv")

# Model 1
X1 = data[['Length', 'Width']]
y = data['Thickness']
model1 = LinearRegression().fit(X1, y)
preds1 = model1.predict(X1)
rmse1 = sqrt(mean_squared_error(y, preds1))
print("Model 1 RMSE:", round(rmse1, 3))

# Model 2 with an irrelevant predictor
np.random.seed(42)
data['random_noise'] = np.random.randn(len(data))
X2 = data[['Length', 'Width', 'random_noise']]
model2 = LinearRegression().fit(X2, y)
preds2 = model2.predict(X2)
rmse2 = sqrt(mean_squared_error(y, preds2))
print("Model 2 RMSE:", round(rmse2, 3))

Model 1 RMSE: 0.251
Model 2 RMSE: 0.253

Podemos ver que o RMSE aumentou depois de adicionar um preditor irrelevante no Modelo 2. Embora o Modelo 2 possa parecer mais complexo, sua precisão de previsão real pode piorar (e significativamente!), pois acabamos de adicionar ruído aleatório.

Para elevar o nível de suas habilidades de regressão em Python, inscreva-se nestes cursos:

• Introdução à regressão com statsmodels em Python
• Regressão intermediária com statsmodels em Python

Exemplo de R

Agora, vamos tentar no R.

# Load data
almonds <- read.csv("almond_dataset.csv")

# Model 1
model1 <- lm(Thickness ~ Length + Width, data = almonds)
preds1 <- predict(model1)
rmse1 <- sqrt(mean((almonds$Thickness - preds1)^2))
print(paste("Model 1 RMSE:", round(rmse1, 3)))

# Model 2 with an irrelevant predictor
set.seed(42)
almonds$random_noise <- rnorm(nrow(almonds))
model2 <- lm(Thickness ~ Length + Width + random_noise, data = almonds)
preds2 <- predict(model2)
rmse2 <- sqrt(mean((almonds$Thickness - preds2)^2))
print(paste("Model 2 RMSE:", round(rmse2, 3)))

[1] "Model 1 RMSE: 0.251"
[1] "Model 2 RMSE: 0.253"

Aqui, reformulei o mesmo exemplo no R. O RMSE aumenta quando incluímos um preditor irrelevante no R. Isso confirma que o RMSE pode aumentar quando um modelo se torna desnecessariamente complexo, reduzindo a capacidade de generalização do modelo.

Se você teve problemas para compilar seu código R ou para interpretar o resultado, experimente nossos cursos:

• Introdução à regressão em R
• Regressão intermediária no R

RMSE vs. Métricas relacionadas

O RMSE faz parte de uma família mais ampla de métricas de erro de regressão. Vamos compará-lo brevemente com outros, esclarecer as diferenças entre eles e destacar quando cada um é mais útil.

RMSE vs. MAE

O RMSE penaliza mais os erros grandes porque ele eleva os resíduos ao quadrado, o que o torna mais sensível a valores discrepantes. O MAE (erro absoluto médio), por outro lado, é mais robusto em relação aos outliers, trata todos os erros igualmente e funciona melhor para medir o tamanho típico do erro quando os outliers não são uma preocupação. Enquanto o RMSE minimizaa perda quadrada, o MAE minimiza a perda absoluta.

Em geral, devemos usar o RMSE quando erros grandes podem ser especialmente onerosos, e o MAE quando quisermos uma visão de erro semelhante à mediana, menos sensível a outliers.

RMSE vs. R-quadrado

O RMSE fornece o erro médio em unidades originais, o que o torna mais intuitivopara a interpretação prática. Em vez disso, o R-quadrado descreve a quantidade de variação explicada pelo modelo, mas não indica o tamanho do erro de previsão.

Eles costumam ser usados juntos: R-quadrado para ajuste relativo e RMSE para desempenho absoluto.

RMSE vs. MSE

O RMSE é apenas a raiz quadrada do MSE, o que facilita a interpretação, pois está nas mesmas unidades que a variável de resultado. 

Além da simples interpretação, no entanto, o MSE é especialmente útil para a otimização durante o treinamento para machine learning. Lembre-se de que, se você otimizar com base no RMSE, a função de raiz quadrada significa que o modelo dará mais ênfase a erros maiores. Além disso, o MSE tem uma derivada suave, portanto, funciona bem com algoritmos baseados em gradiente, como a descida de gradiente estocástica, permitindo uma convergência eficiente durante o treinamento do modelo. Em resumo, o RMSE é mais fácil de interpretar porque estamos analisando os resultados na escala dos dados, mas devemos saber que a aprendizagem profunda geralmente otimiza o MSE, não o RMSE.

RMSE vs. MAPE

O MAPE (erro percentual absoluto médio) retorna erros como porcentagens, o que é útil para comparar conjuntos de dados. No entanto, ele é interrompido quando os valores reais estão próximos de zero, o que o torna instável. O RMSE evita esse problema e é mais confiável quando há valores-alvo pequenos.

RMSE vs. log-likelihood

Aqui está outra relação interessante: O RMSE é formalmente equivalente à probabilidade de logaritmo negativo sob erros gaussianos. Em vez disso, talvez devêssemos dizer que minimizar o RMSE é equivalente a maximizar a probabilidade logarítmica (de um modelo de regressão) sob a suposição de erros normalmente distribuídos (com variância constante). Não estou dizendo que o RMSE, por si só, estima a verossimilhança total, mas estou dizendo que a minimização doRMSE maximiza implicitamente a verossimilhança sob uma suposição de erro normal.

No entanto, quando os erros são distorcidos ou têm valores discrepantes, alternativas como Huber ou perda de quantis podem ter um desempenho melhor. De qualquer forma, devemos tratar nossa escolha de métrica como uma decisão de projeto de modelo, não como uma reflexão tardia.

Equívocos comuns sobre o RMSE

Vamos esclarecer alguns mitos muito difundidos sobre o RMSE:

• "Um RMSE baixo garante uma boa generalização do modelo." Isso não é necessariamente verdade. Um modelo pode ter um valor baixo de RMSE nos dados de treinamento, mas ainda assim ter um desempenho ruim em dados novos e não vistos devido ao excesso de ajuste. Para avaliar a generalização de forma eficiente, precisamos realizar a validação cruzada ou usar um conjunto de testes separado.
• "O RMSE pode determinar se um modelo está se ajustando demais." O RMSE sozinho não é suficiente. Ele deve ser comparado entre os conjuntos de dados de treinamento e validação: se o RMSE de treinamento for baixo, mas o RMSE de validação for muito mais alto, isso significa que você está se adaptando demais.
• "Há um limite universal fixo para um bom RMSE." Não, não há. O fato de o valor de RMSE ser "bom" depende inteiramente do contexto, do domínio e das unidades da variável de resultado. Em outras palavras, os valores de RMSE não fazem sentido sem contexto.

Conclusão

Em resumo, o RMSE é uma medida prática, interpretável e intuitiva da precisão da previsão que comunica o erro médio da previsão nas unidades da variável-alvo. É uma métrica essencial para a avaliação do desempenho da regressão, especialmente quando as magnitudes de erro são importantes.

No entanto, o RMSE deve ser usado juntamente com outras métricas, como R-quadrado, MAE e pontuações de validação cruzada, para que você tenha uma visão mais completa da qualidade do modelo. Não devemos confiar cegamente nessa medida, mas sempre considerar a escala, o contexto e a complexidade do modelo. Além disso, a combinação do RMSE com diagnósticos visuais pode ajudar a detectar distorções. 

Em suma, o RMSE nos informa o quanto nosso modelo está errado, em média, em termos reais, o que é uma perspectiva poderosa a ser mantida ao criar sistemas preditivos.

Se algo neste artigo foi confuso, não se preocupe: Temos muitos recursos excelentes para ajudar você: 

• Regressão linear simples: Tudo o que você precisa saber tutorial
• Compreensão da soma de quadrados: Um guia para SST, SSR e SSE tutorial
• Introdução à regressão com modelos estatísticos no curso Python
• Curso de Introdução à Regressão em R