Compreensão da soma de quadrados: Um guia para SST, SSR e SSE

A soma dos quadrados é uma medida estatística complexa que desempenha uma função essencial na análise de regressão. Ele descreve a variabilidade da variável dependente e pode ser decomposto em três componentes - a soma dos quadrados total (SST), a soma dos quadrados da regressão (SSR) e a soma dos quadrados do erro (SSE) - que, juntos, ajudam a avaliar o desempenho de um modelo de regressão.

Neste artigo, discutiremos os três componentes da soma de quadrados, bem como o R-quadrado. Primeiro, daremos uma visão geral de cada soma de quadrados separadamente. Em seguida, consideraremos a relação matemática entre eles. Por fim, exploraremos a conexão do SST, SSR e SSE com o R-quadrado, uma métrica importante de avaliação de modelos.

O que são SST, SSR e SSE?

Vamos começar definindo o que são SST, SSR e SSE, como cada medida reflete a variabilidade total e como cada uma delas ajuda a avaliar a qualidade do ajuste de um modelo de regressão. Além disso, veremos como é cada soma de quadrados em uma regressão linear simples com uma variável dependente e uma independente.

Se, ao analisarmos as definições, você quiser revisar as estatísticas sem codificação, confira nosso curso Introduction to Statistics. Para cursos introdutórios de estatística ancorados em uma tecnologia específica, temos opções, incluindo Introdução à estatística no Planilhas Google, Introdução à estatística em Python e Introdução à estatística em R.

Soma total de quadrados (SST)

A soma dos quadrados totais (SST) é a soma das diferenças quadráticas entre cada valor da variável dependente observada e a média dessa variável. Também é conhecido como a soma total de quadrados (TSS). 

A soma total dos quadrados representa a variabilidade total da variável dependente, incluindo as partes da variabilidade explicadas e não explicadas pelo modelo de regressão. Por sua natureza, a SST reflete a dispersão geral dos valores individuais da variável dependente observada em relação ao seu valor médio.

Abaixo você encontra a fórmula matemática para calcular o SST:

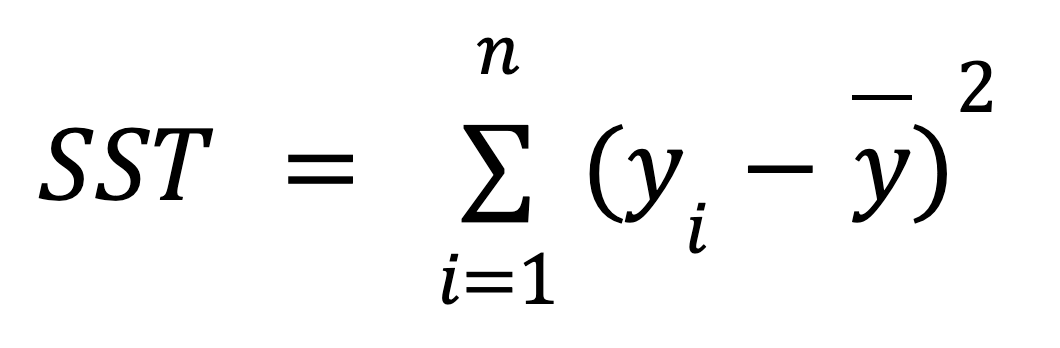
onde:

• y_i é o valor da variável dependente observada para cada um dos n pontos de dados.
• ȳ é o valor médio da variável dependente observada.

O gráfico a seguir para uma regressão linear simples demonstra graficamente o significado da fórmula acima:

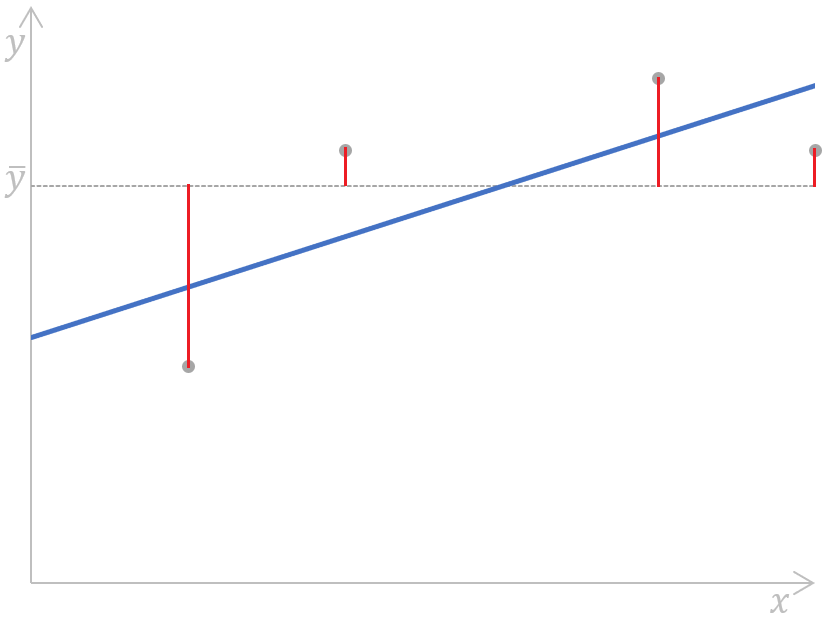
Cálculo da soma dos quadrados totais para uma regressão linear simples. Imagem do autor

Como podemos ver, as distâncias (os segmentos vermelhos no gráfico) entre o valor médio (a linha tracejada cinza) da variável dependente observada e cada valor (os pontos cinza) dessa variável são medidos, elevados ao quadrado e somados. Além disso, esse gráfico mostra claramente que a SST não depende do modelo de regressão; ela depende apenas dos valores y observados e da média da variável dependente observada.

Soma de quadrados de regressão (SSR)

A soma dos quadrados da regressão (SSR) é a soma das diferenças quadráticas entre cada valor da variável dependente prevista por um modelo de regressão para cada ponto de dados da variável independente e a média da variável dependente observada. Outros termos para essa métrica incluem: soma de quadrados de regressão, soma de quadrados devido à regressão e soma de quadrados explicada. Há até mesmo outra abreviação para isso: ESS. 

A regressão da soma de quadrados capta a parte da variabilidade total da variável dependente explicada pelo modelo de regressão (daí um de seus termos alternativos -somaexplicadade quadrados). Você também pode pensar nisso como o erro reduzido devido ao modelo de regressão.

Para calcular o SSR, usamos a seguinte fórmula:

onde:

• y_i é o valor da variável dependente previsto por um modelo de regressão para cada um dos n pontos de dados da variável independente,
• ȳ é o valor médio da variável dependente observada.

Podemos ilustrar essa fórmula no seguinte gráfico de regressão linear simples:

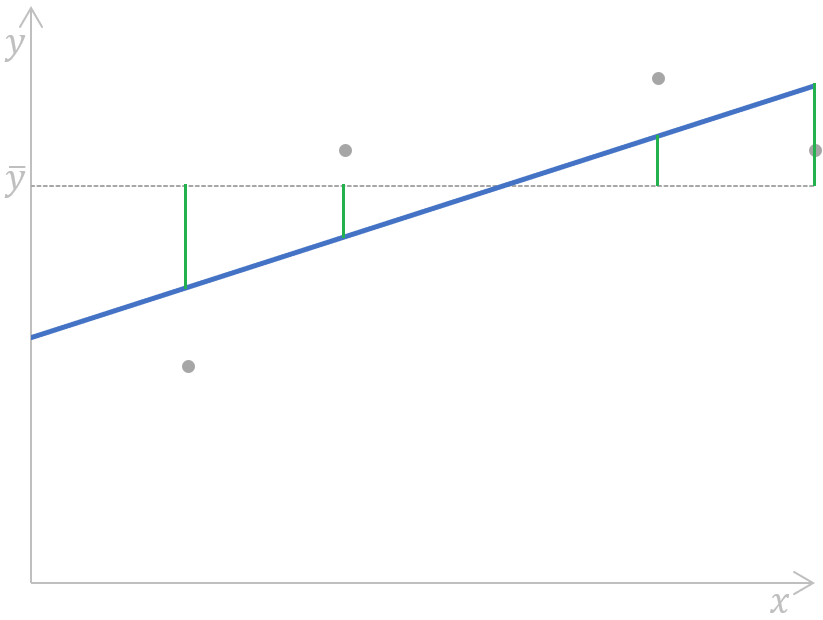a Calculando a regressão da soma dos quadrados para uma regressão linear simples. Imagem do autor

Simplificando, as distâncias (os segmentos verdes no gráfico) entre o valor médio (a linha tracejada cinza) da variável dependente observada e cada valor da variável dependente previsto por um modelo de regressão (a linha azul) para cada ponto de dados da variável independente são medidas, elevadas ao quadrado e somadas.

Na análise de regressão, o SSR contribui para medir o ajuste de um modelo de regressão, ajudando a determinar o grau de acerto do modelo na previsão dos pontos de dados. Teremos uma visão mais clara de como isso acontece mais adiante neste tutorial, quando discutirmos a relação entre as três métricas da soma de quadrados.

Soma de quadrados de erro (SSE)

A soma do erro de quadrados (SSE) é a soma das diferenças quadráticas entre cada valor da variável dependente observada e o valor da variável dependente previsto por um modelo de regressão para o mesmo ponto de dados da variável independente. Em outras palavras, essa métrica mede a diferença entre os valores reais e previstos da variável dependente. 

O erro da soma de quadrados também é chamado de soma de quadrados de erro, soma de quadrados residual, soma de quadrados residual ou soma de quadrados não explicada. Além de SSE, ele também pode ser abreviado como RSS, ESS ou até SSR - no último caso, ele pode ser facilmente confundido com o SSR discutido anteriormente, que significa a regressão da soma dos quadrados.

O erro da soma de quadrados reflete o erro restante, ou variabilidade não explicada, que é a parte da variabilidade total na variável dependente que não pode ser explicada pelo modelo de regressão (por isso também é chamada de soma de quadrados não explicada).

Você pode usar a seguinte fórmula para calcular o SSE:

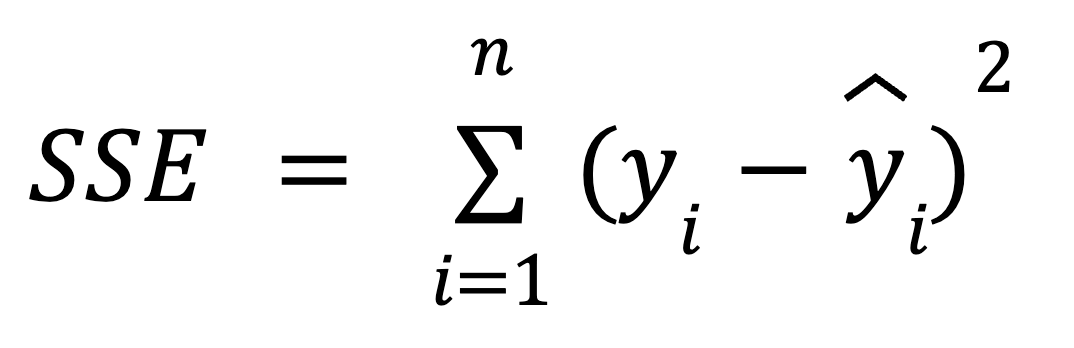
onde:

• y_i é o valor real da variável dependente para cada um dos n pontos de dados da variável independente.
• ŷ é o valor previsto da variável dependente para cada um dos n pontos de dados da variável independente.

Graficamente, essa fórmula pode ser exibida como:

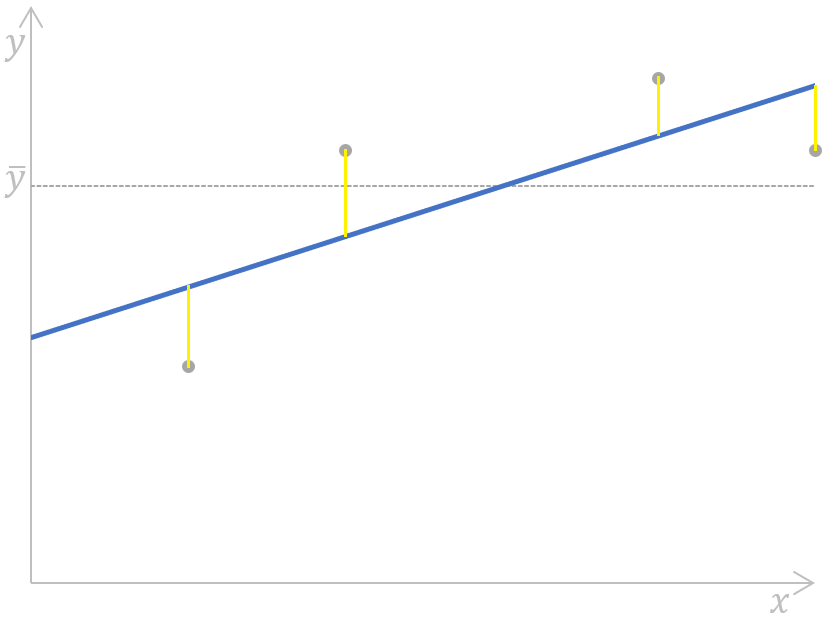Calculando a soma do erro de quadrados para uma regressão linear simples. Imagem do autor

Aqui, as distâncias (os segmentos amarelos no gráfico) para cada par de valores reais e previstos da variável dependente são medidas, elevadas ao quadrado e somadas.

Na análise de regressão, a minimização do SSE é fundamental para melhorar a precisão do modelo de regressão, e vamos desenvolver a intuição em torno disso no próximo capítulo.

Também temos uma coleção de tutoriais específicos de tecnologia para ajudar você a adquirir as habilidades necessárias para criar modelos simples de regressão linear e logística, incluindo Essentials of Linear Regression in Python, How to Do Linear Regression in R e Linear Regression in Excel: Um guia abrangente para iniciantes.

Relação matemática entre SST, SSR e SSE

A relação matemática entre o SST, o SSR e o SSE é expressa pela seguinte fórmula:

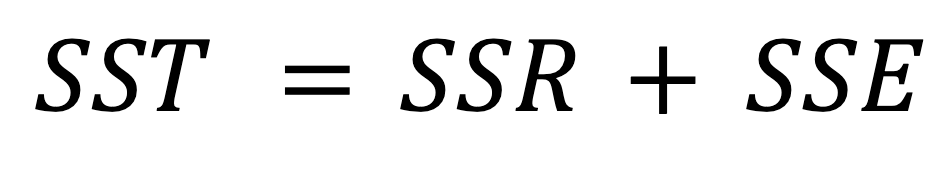
Anteriormente, mencionamos que a variabilidade total (SST) é composta tanto pela variabilidade explicada (SSR) quanto pela variabilidade não explicada (SSE), o que se reflete na fórmula acima.

Como vimos anteriormente, o SST não depende do modelo de regressão, enquanto as outras duas métricas dependem. Isso significa que o aprimoramento da precisão do modelo está relacionado a alterações na SSR ou na SSE, em particular, minimizando a SSE e, portanto, maximizando a SSR. Com base na fórmula acima, podemos dizer que quanto menor o SSE, mais próximo o SSR está do SST; portanto, melhor nosso modelo de regressão se ajusta aos valores observados da variável dependente. 

Se o SSE fosse igual a 0, a SSR coincidiria com a SST, o que significaria que todos os valores observados da variável dependente seriam perfeitamente explicados pelo modelo de regressão, ou seja, todos eles estariam localizados exatamente na linha de regressão. Em cenários do mundo real, isso não ocorrerá, mas devemos procurar minimizar o SSE para obter um modelo de regressão mais confiável.

Interpretação geométrica

Como a SST representa a variabilidade total nos dados, quando ajustamos um modelo de regressão, decompomos essa variabilidade total em duas partes: SSR e SSE. Essa decomposição é geometricamente interessante porque reflete o teorema de Pitágoras em um espaço de alta dimensão. Isso ocorre porque a variabilidade total é dividida em dois componentes ortogonais: a variabilidade explicada pelo modelo e o erro não explicado. Essa interpretação faz sentido porque a regressão trata essencialmente da projeção de dados em um espaço de dimensão inferior, que é o espaço abrangido por nossos preditores. Faça nosso curso Álgebra linear para ciência de dados em R para saber mais sobre conceitos como subespaços.

Quando SST não for igual a SSR + SSE

Na regressão ridge e lasso, a decomposição de SST em SSR e SSE não segue a mesma relação. Isso ocorre porque tanto o ridge quanto o lasso adicionam termos de regularização, ou penalidades, às suas respectivas funções de custo, o que altera a relação. No caso das versões regularizadas da regressão, a SST ainda é bem definida, mas a variabilidade explicada e a variabilidade residual não somam mais a SST devido ao termo de regularização. Leia nosso tutorial Regularization in R Tutorial: Ridge, Lasso e Elastic Net para saber mais.

Soma de quadrados e R-quadrado

O R-quadrado, também conhecido como coeficiente de determinação, é uma medida estatística importante para avaliar a qualidade do ajuste de um modelo de regressão e, portanto, seu poder preditivo. Representa a proporção da variabilidade na variável dependente que pode ser explicada pela variável independente. O R-quadrado pode ser calculado elevando-se o coeficiente de correlação r ao quadrado, e também pode ser calculado de acordo com esta fórmula:

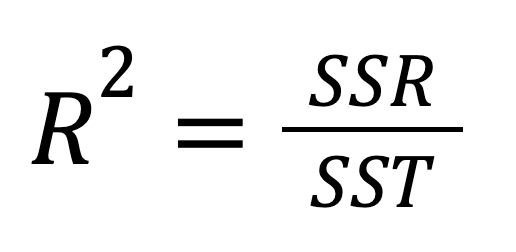
Ou, alternativamente:

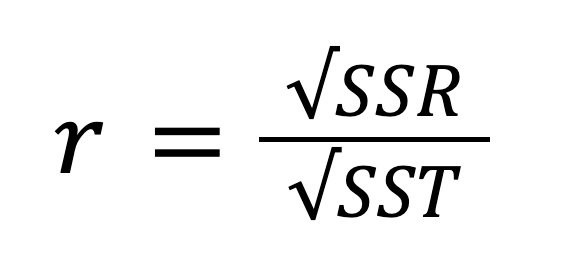
Considerando a relação entre SST, SSR e SSE, a fórmula acima pode ser reescrita como:

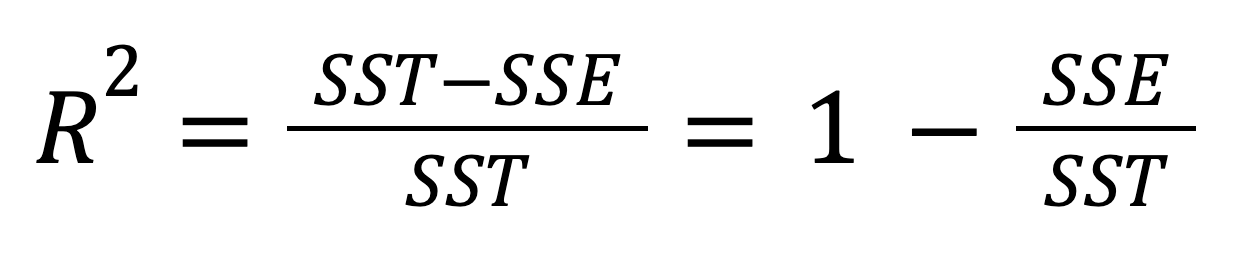
O valor do R-quadrado pode ser de 0 a 1, inclusive. Se R² = 0, isso significa que nosso modelo de regressão não explica nenhuma parte da variabilidade da variável dependente. Em vez disso, se R² = 1, isso significa que nosso modelo de regressão explica perfeitamente toda a variabilidade da variável dependente. Na prática, é quase impossível encontrar esses valores extremos - muito provavelmente, em casos reais, veremos algo intermediário.

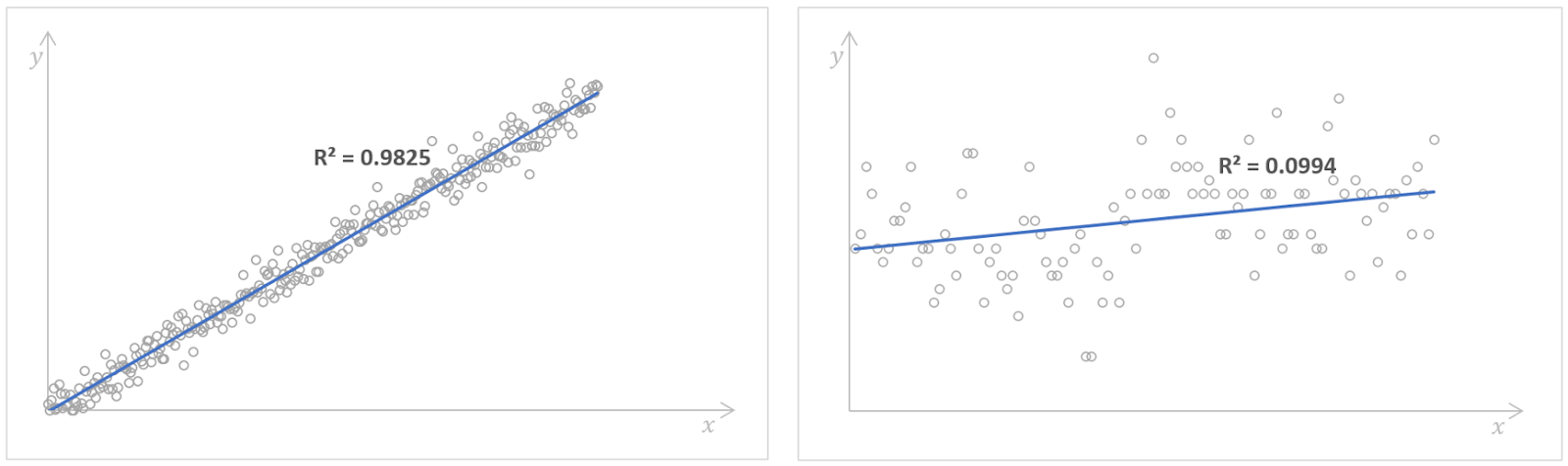
Modelos de regressão com valores altos (esquerda) e baixos (direita) do R-quadrado. Fonte: Número de livros lidos no Kaggle e Regressão de gambás no Kaggle. Imagem do autor.

Um valor alto do R-quadrado indica um bom desempenho do modelo, o que significa que a variável dependente pode ser prevista pela variável independente com alta precisão. No entanto, não existe uma regra geral sobre qual valor do R-quadrado deve ser considerado suficientemente bom. Depende de cada caso específico, dos requisitos de precisão de um modelo de regressão e da variabilidade que esperamos ver nos dados. Muitas vezes, isso também depende do domínio ao qual nossa análise de regressão está relacionada. Por exemplo, nos campos científicos, buscaríamos um valor de R-quadrado superior a 0,8, enquanto nas ciências sociais, o valor de 0,3 já seria suficiente. 

Como observação final, devemos dizer que, na regressão linear múltipla, ou seja, na regressão com mais de uma variável independente, geralmente consideramos o R-quadrado ajustado, que é uma extensão do R-quadrado que leva em conta o número de preditores e o tamanho da amostra.

Conclusão

Embora hoje em dia possamos calcular de forma fácil e rápida o SST, o SSR e o SSE na maioria dos softwares estatísticos e linguagens de programação, ainda vale a pena entender realmente o que eles significam, sua interconexão e, em particular, sua importância na análise de regressão. A compreensão da relação entre os três componentes da variabilidade e o R-quadrado ajuda os analistas e cientistas de dados a melhorar o desempenho do modelo, minimizando o SSE e maximizando o SSR, para que possam tomar decisões informadas sobre seus modelos de regressão.

Para criar uma base sólida em estatística e aprender técnicas estatísticas avançadas trabalhando com dados do mundo real, considere as seguintes trilhas de habilidades exaustivas e fáceis de usar para iniciantes: Fundamentos de Estatística em Python e Fundamentos de Estatística em R. Por fim, se você estiver interessado em saber como os coeficientes de regressão são calculados, confira nosso tutorial Equação normal para regressão linear e QR Decomposition in Machine Learning: Um guia detalhado.