Track
Root-mean squared propagation (RMSprop) is a powerful optimization algorithm used in machine learning to find the model parameters that correspond to the best fit between actual values and model predictions. The algorithm is widely used in deep learning in combination with backpropagation during neural network training.
In this tutorial, you will learn:
- The intuition behind RMSprop optimizer
- How to use RMSprop in PyTorch
- How to implement it in pure NumPy for a deeper understanding
- Its differences from other optimization algorithms such as SGD and Adam
What is RMSprop? The Short Answer
RMSprop is an adaptive learning rate optimization algorithm designed to accelerate the convergence of gradient descent. Key features of RMSprop include:
- Adaptive learning rates: It adjusts the learning rate for each parameter based on the historical gradient information.
- Moving average of squared gradients: RMSprop maintains a moving average of squared gradients for each parameter, which helps to normalize the gradient updates.
- Momentum-like behavior: By using the moving average, RMSprop achieves a momentum-like effect without explicitly incorporating momentum terms.
- Improved performance on non-stationary problems: RMSprop is particularly effective for optimizing non-convex loss functions and handling non-stationary objectives.
- Hyperparameter sensitivity reduction: Compared to standard SGD, RMSprop reduces the need for manual tuning of the learning rate hyperparameter.
In essence, RMSprop addresses the diminishing learning rates problem of AdaGrad while providing adaptive per-parameter learning rates, making it a popular choice for training deep neural networks.
Before you continue, please read our separate tutorial on Stochastic Gradient Descent that covers the fundamentals of gradient descent crucial for understanding RMSprop.
The Intuition Behind RMSprop Optimizer
It helps to think of optimization as finding the lowest point in a hilly terrain while being blindfolded. Since you are limited to your touch, you can find which way is down by only feeling the ground immediately around you.
This analogy represents finding the best model parameters for the best fit between model predictions and actual values by optimizing a loss function. You can think of the surface of the loss function plotted on Cartesian coordinates as our hilly terrain.
Different optimization functions, like RMSprop, provide different strategies for navigating this terrain. A key aspect of RMSprop’s strategy is adaptive movement based on the recent history of the terrain.
Specifically, it allows you to adjust your step size (stride length) for each direction you can move. In flat directions, you can take larger steps for acceleration, while in steep areas, take careful small steps to prevent overshooting over sharp declines. Also, in rapidly changing terrain like rocky surfaces, it balances out your path, preventing erratic movements.
Due to its characteristics, RMSprop’s strategy is particularly effective for optimizing non-convex functions. In other words, RMSprop is specifically designed for optimization problems where the graph of the function can have multiple local minima, maxima, or saddle points. Visually, a non-convex function would have multiple valleys, hills, small dips, and rocky surfaces rather than a single, smooth bowl-shape (which would be convex).
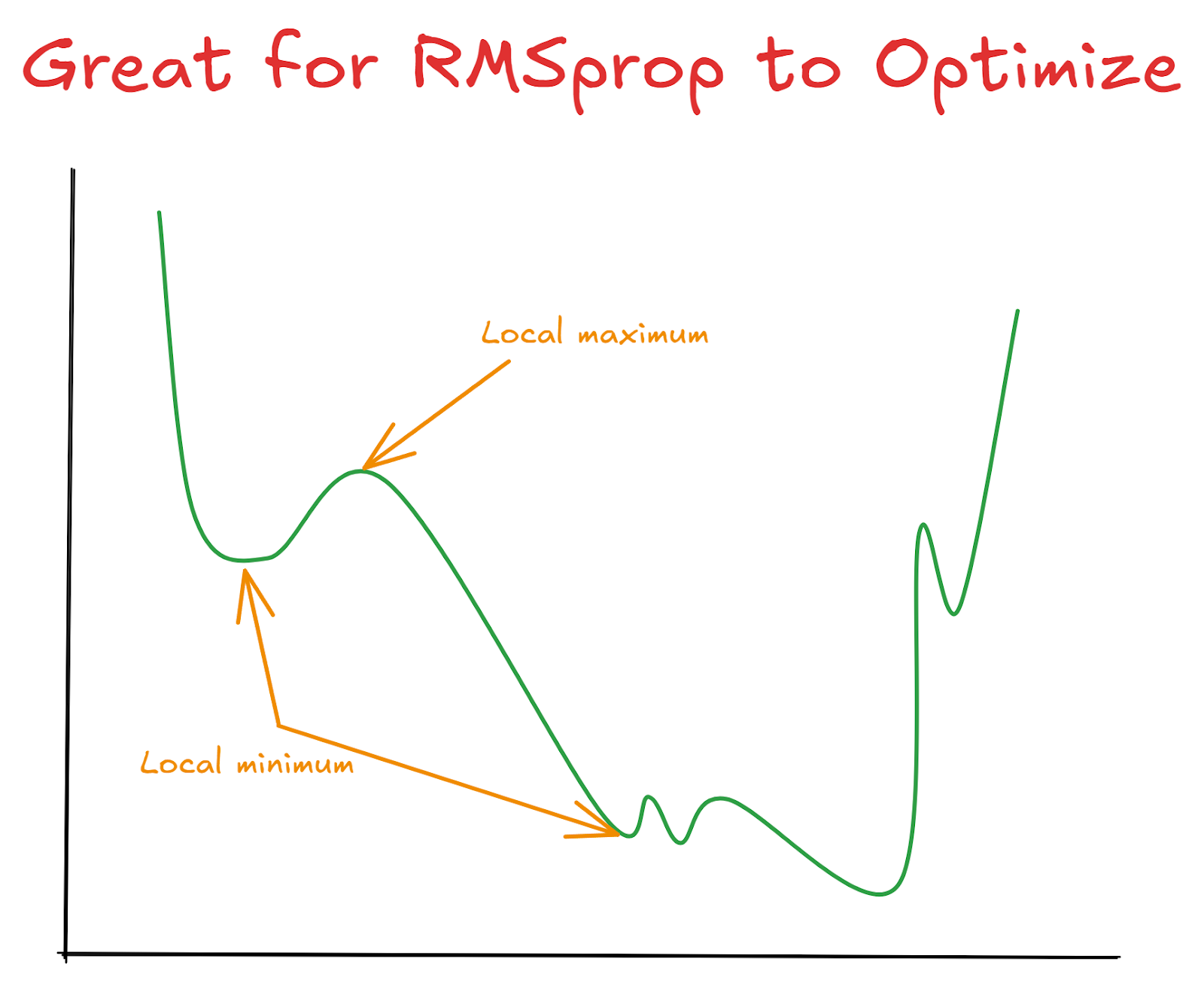
Using RMSprop in PyTorch and TensorFlow
In practice, you rarely have to implement RMSprop manually. Since it is a widely used algorithm, it is available in popular frameworks such as PyTorch and TensorFlow.
RMSprop in PyTorch
In PyTorch, the algorithm is implemented under the optim module:
import torch
torch.optim.RMSprop
torch.optim.rmsprop.RMSpropHere is how you can use it to optimize (find the minimum) of any function f(x):
import torch.optim as optim
# Define the loss function: f(x) = x / log(x)
def f(x):
return x / torch.log(x)
# Create a tensor with requires_grad=True
x = torch.tensor([364.0], requires_grad=True)
# Create an RMSprop optimizer
optimizer = optim.RMSprop([x], lr=0.3)
# Optimization loop
for i in range(1500):
# Forward pass: compute the loss
loss = f(x)
# Backward pass: compute the gradients
loss.backward()
# Update the parameter
optimizer.step()
# Zero the gradients
optimizer.zero_grad()
if i % 100 == 0:
print(f'Iteration {i}: x = {x.item():.4f}')
print(f'Final result: x = {x.item():.4f}')Output:
Iteration 0: x = 361.0000
Iteration 100: x = 302.5840
Iteration 200: x = 268.0156
Iteration 300: x = 236.2579
Iteration 400: x = 205.2928
Iteration 500: x = 174.5349
Iteration 600: x = 143.7643
Iteration 700: x = 112.8619
Iteration 800: x = 81.7036
Iteration 900: x = 50.0471
Iteration 1000: x = 17.0591
Iteration 1100: x = 2.7183
Iteration 1200: x = 2.7183
Iteration 1300: x = 2.7183
Iteration 1400: x = 2.7183
Final result: x = 2.7183In this case, we are optimizing x / log(x) function, which has a minimum at e. When we are initializing the RMSprop class, we are giving it an arbitrary start value, 364. After about 1100 iterations, the minimum is correctly found.
Here is the explanation of the code:
1. Function definition:
def f(x):
return x / torch.log(x)2. Initialization:
x = torch.tensor([364.0], requires_grad=True)Creates a PyTorch tensor with an initial value of 364.0. requires_grad=True allows PyTorch to compute gradients for this tensor.
3. Optimizer setup:
optimizer = optim.RMSprop([x], lr=0.3)4. Optimization loop:
for i in range(1500):Runs the optimization process for 1500 iterations.
- Inside the loop:
loss = f(x): Computes the current value of the function.loss.backward(): Computes the gradient of the loss with respect to x.optimizer.step(): Updates x using the RMSprop algorithm.optimizer.zero_grad(): Resets the gradients to zero for the next iteration.
- Progress tracking:
if i % 100 == 0:
print(f'Iteration {i}: x = {x.item():.4f}')- Final result:
print(f'Final result: x = {x.item():.4f}')To use RMSprop in supervised learning problems, you can refer to our Introduction to PyTorch course.
RMSprop in Tensorflow and Keras
Let’s see how to optimize the same function with RMSprop in Tensorflow and Keras:
import tensorflow as tf
# Define the loss function: f(x) = x / log(x)
def f(x):
return x / tf.math.log(x)
# Create a variable
x = tf.Variable([364.0])
# Create an RMSprop optimizer
optimizer = tf.keras.optimizers.RMSprop(learning_rate=0.3)
# Optimization loop
for i in range(1500):
with tf.GradientTape() as tape:
loss = f(x)
# Compute gradients
gradients = tape.gradient(loss, [x])
# Apply gradients
optimizer.apply_gradients(zip(gradients, [x]))
if i % 100 == 0:
print(f'Iteration {i}: x = {x.numpy()[0]:.4f}')
print(f'Final result: x = {x.numpy()[0]:.4f}')Output:
Iteration 0: x = 363.0513
Iteration 100: x = 330.9281
Iteration 200: x = 300.8935
Iteration 300: x = 270.8544
Iteration 400: x = 240.8105
Iteration 500: x = 210.7600
Iteration 600: x = 180.7007
Iteration 700: x = 150.6295
Iteration 800: x = 120.5406
Iteration 900: x = 90.4234
Iteration 1000: x = 60.2539
Iteration 1100: x = 29.9579
Iteration 1200: x = 2.7183
Iteration 1300: x = 2.7183
Iteration 1400: x = 2.7183
Final result: x = 2.7183This time, the optimizer class is located at tf.keras.optimizers module. As you can see, the algorithm correctly converged at e, just like PyTorch, but it took slightly more iterations.
Here is an explanation of the code:
1. Variable initialization:
x = tf.Variable([364.0])2. Optimizer setup:
optimizer = tf.keras.optimizers.RMSprop(learning_rate=0.3)3. Optimization loop:
for i in range(1500):4. Inside the loop:
with tf.GradientTape() as tape:
loss = f(x)Uses TensorFlow’s GradientTape to record operations for automatic differentiation.
5. Gradient computation:
gradients = tape.gradient(loss, [x])6. Gradient application:
optimizer.apply_gradients(zip(gradients, [x]))Updates x using the computed gradients and the RMSprop algorithm.
Implementing RMSprop in Python Step-by-Step
Your interactions with RMSprop will be mostly limited to those classes in either TensorFlow or PyTorch in practice. However, a deep understanding of their implementation and hyperparameters will go a long way in solidifying your ability to fine-tune them for various problems. Therefore, in this section, we will create a function, rmsprop, step-by-step that will output the best model parameters given x and y arrays.
1. Defining the model and loss function
Our implementation of RMSprop will be designed to find the best parameters for a Simple Linear Regression model—f(x) = mx + b. Here:
mis the slopebis the interceptxis the inputf(x)is the model prediction given the input and parameters.
Let’s define the model as a function:
import numpy as np
def model(m, x, b):
"""Simple linear regression model with slope m and intercept b"""
return m * x + bFor regression problems, Mean Squared Error is commonly used as a loss function:
def mean_squared_error(y_true, y_pred):
"""Mean squared error loss function"""
return np.mean((y_true - y_pred) ** 2)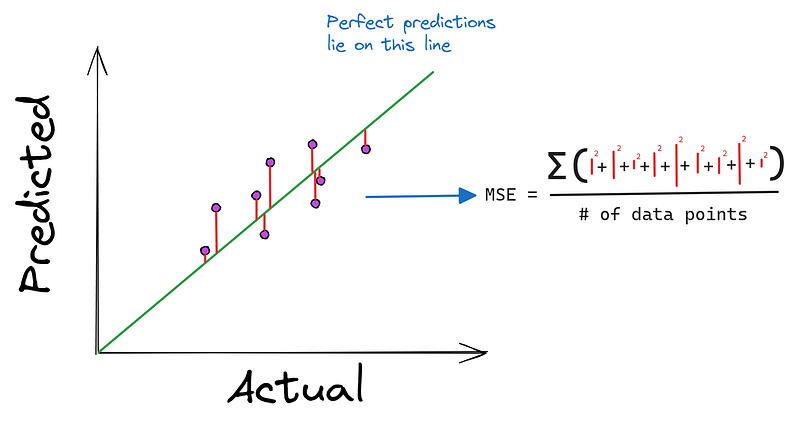
2. Defining the optimization algorithm function
Now, we define a function named rmsprop that accepts seven parameters:
def rmsprop(
x,
y,
initial_params,
learning_rate=0.001,
decay_rate=0.9,
epsilon=1e-8,
n_iter=1000,
):
passHere are the explanations of the parameters:
x: Input featuresy: Target valuesinitial_params: Starting values for the model parameters (slope and intercept)learn_rate: Step size for parameter updates (default: 0.001)decay_rate: Decay factor for moving average of squared gradients (default: 0.9)epsilon: Small value to prevent division by zero (default: 1e-8)n_iter: Number of iterations for optimization (default: 1000)
Don’t worry too much about the hyperparameters. We will explain them in detail later on.
3. Initialize an empty array for squared gradients
Inside the function body, we will create an empty array to store the squared gradients:
def rmsprop(...):
params = np.array(initial_params, dtype=float) # Use float
squared_grad = np.zeros_like(params)params will be an array containing random start values like [0, 1]. squared_grad will look the same:
params = np.array([0, 1])
squared_grad = np.zeros_like(params)
print(squared_grad)Output:
[0 0]4. Writing the optimization loop
In the next step, we start an optimization loop. A single iteration of the loop represents a single pass through the entire dataset, x. The number of iterations depends on the given initial parameters and the complexity of the problem we are solving. In the TensorFlow and PyTorch sections, we have seen that we needed at least 1100 iterations for the algorithm to converge. The same logic applies here:
def rmsprop(...):
params = ...
squared_grad = ...
for _ in range(n_iter):
# Forward pass
y_pred = model(params[0], x, params[1])
# Compute error
error = y_pred - yThe first step in the loop is performing a forward pass, or in other words, computing predictions with the current set of parameters and then, the error. You might be wondering why we are using y_pred - y as error instead of using the mean_squared_error function we defined above. You will find the explanation of this step in a later section.
5. Computing the gradients
Once we have the error, we can compute the gradients for both parameters:
def rmsprop(...):
params = ...
squared_grad = ...
for _ in range(n_iter):
# Forward pass
y_pred = model(params[0], x, params[1])
# Compute error
error = y_pred - y
# Compute gradients
grad_m = np.mean(error * x)
grad_b = np.mean(error)
grad = np.array([grad_m, grad_b])The formula for computing grad_m and grad_b comes from the partial derivatives of Mean Squared Error. Again, we will see the explanation of the formula in a later section. For now, think of each gradient as how much MSE changes when we slightly adjust m and b.
6. Writing RMSprop’s update rule
We now have the gradients that show us in which direction we should adjust the parameters. This is where we use all of learning_rate, decay_rate, and epsilon parameters in a single operation known as RMSprop's update rule.
This is where the algorithm is distinguished from other optimization processes. This is where RMSprop adjusts learning rates for each of our parameters m and b based on the history of the terrain stored in squared_grad array:
def rmsprop(...):
params = ...
squared_grad = ...
for _ in range(n_iter):
# Forward pass
...
# Compute error
...
# Compute gradients
...
# RMSprop update rule
squared_grad = decay_rate * squared_grad + (1 - decay_rate) * grad ** 2
params -= learn_rate * grad / (np.sqrt(squared_grad) + epsilon)The update is carried out in two steps:
- Updating the history of squared gradients using
decay_rateand the gradients - Updating the parameters based on the updated squared gradients
Both steps require some math we need to go over, but again, we will keep that to a later section so that we don’t get distracted. For now, all you need to know is that each RMSprop update changes the parameters in a way that conforms to the overall optimization strategy we discussed earlier.
Once the optimization loop ends, we return the tuned parameters:
def rmsprop(...):
params = ...
squared_grad = ...
for _ in range(n_iter):
# Forward pass
...
# Compute error
...
# Compute gradients
...
# RMSprop update rule
...
return paramsHere is the full function so far:
def rmsprop(
x, y, initial_params, learn_rate=0.001, decay_rate=0.9, epsilon=1e-8, n_iter=10000
):
params = np.array(initial_params, dtype=float)
squared_grad = np.zeros_like(params)
for _ in range(n_iter):
# Forward pass
y_pred = model(params[0], x, params[1])
# Compute error
error = y_pred - y
# Compute gradients
grad_m = np.mean(error * x)
grad_b = np.mean(error)
grad = np.array([grad_m, grad_b])
# RMSprop update
squared_grad = decay_rate * squared_grad + (1 - decay_rate) * grad**2
params -= learn_rate * grad / (np.sqrt(squared_grad) + epsilon)
return paramsLet’s use it on a small sample dataset with just six values:
# Example usage
x = np.array([5, 15, 25, 35, 45, 55])
y = np.array([5, 20, 14, 32, 22, 38])
initial_params = np.array([3.0, 5.0]) # Change: Use float values
result = rmsprop(x, y, initial_params, n_iter=5000)
print("Optimized parameters (m, b):", result)
# Make predictions
y_pred = model(result[0], x, result[1])
print("Predictions:", y_pred)
print("Actual values:", y)
print("Root Mean Squared Error", mean_squared_error(y, y_pred) ** 0.5)Output:
Optimized parameters (m, b): [0.54935276 5.24240429]
Predictions: [ 7.98916807 13.48269564 18.97622321 24.46975078 29.96327835 35.45680592]
Actual values: [ 5 20 14 32 22 38]
Root Mean Squared Error 5.813195776655382The predictions using the found parameters are reasonably close to actual values. We can confirm this by plotting the regression line:
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.scatter(x, y, alpha=0.5, label="Actual")
plt.plot(x, y_pred, alpha=0.5, label="Predicted", color="red")
plt.xlabel("X")
plt.ylabel("Y")
plt.title("Simple Linear Regression")
plt.legend()
plt.show()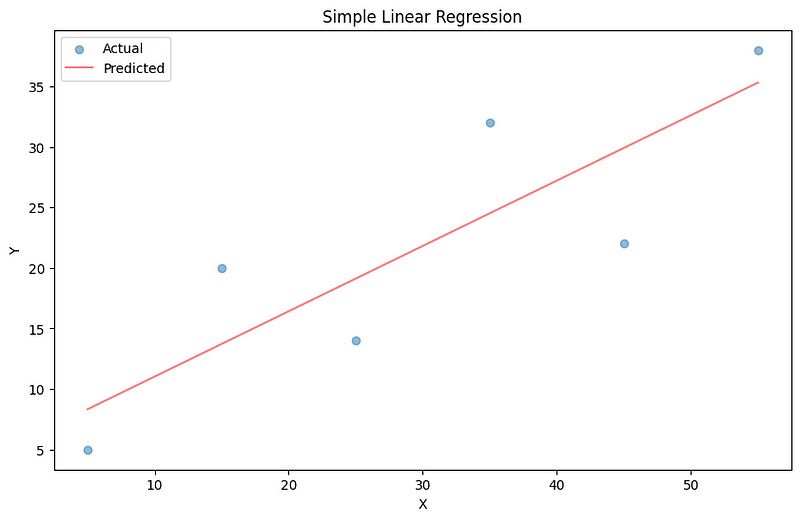
It is the line of best fit.
Adding mini-batches to RMSprop
The rmsprop function is a bare-bones implementation of our algorithm. In a practical version, RMSprop would have a few differences.
The most important one is mini-batches. In our version, each parameter update uses the entire dataset, regardless of whether it has 10 data points or 10 million:
...
for _ in range(n_iter):
# Forward pass
y_pred = model(params[0], x, params[1]) # <-- This is using the entire dataset
# Compute error
error = y_pred - y
# Compute gradients
grad_m = np.mean(error * x)
grad_b = np.mean(error)
grad = np.array([grad_m, grad_b])
...In practice, this can become a huge bottleneck for large datasets. For this reason, we introduce mini-batches to the algorithm using the batch_size hyperparameter. Here is how it affects the process:
- The optimization loop starts.
- In each iteration, the dataset is shuffled to prevent learning order-dependent patterns.
- The dataset is divided into groups of data points whose lengths are equal to batch_size. For example, if the dataset size is 640 and batch size is 32, 20 batches will be created in total.
- Error, gradient computation and parameter updates will be performed for each batch.
Let’s see what this version looks like in code:
def rmsprop(
x,
y,
initial_params,
learning_rate=0.01,
decay_rate=0.9,
epsilon=1e-8,
n_iter=1000,
batch_size=32,
):
params = np.array(initial_params, dtype=float)
squared_grad = np.zeros_like(params)
n_samples = len(x)What’s new in this snippet:
- We introduce the new
batch_sizeparameter - We store the dataset length in
n_samples
Then, we start the optimization loop:
def rmsprop(...):
...
for _ in range(n_iter):
indices = np.random.permutation(n_samples)
x_shuffled = x[indices]
y_shuffled = y[indices]What’s new in this snippet:
- We shuffle the data using
np.random.permutation
Next, we start another loop:
def rmsprop(...):
...
for _ in range(n_iter):
...
for i in range(0, n_samples, batch_size):
x_batch = x_shuffled[i : i + batch_size]
y_batch = y_shuffled[i : i + batch_size]What’s new in this snippet:
- We start a loop that divides the dataset into multiple groups of
batch_sizesamples. - In each iteration, we extract the current X and Y arrays from the current batch.
The rest will be familiar:
def rmsprop(...):
...
for _ in range(n_iter):
...
for i in range(0, n_samples, batch_size):
x_batch = ...
y_batch = ...
y_pred = params[0] * x_batch + params[1]
error = y_pred - y_batch
grad_m = np.mean(error * x_batch)
grad_b = np.mean(error)
grad = np.array([grad_m, grad_b])
squared_grad = decay_rate * squared_grad + (1 - decay_rate) * grad**2
params -= learning_rate * grad / (np.sqrt(squared_grad) + epsilon)
return paramsWhat’s new in this snippet:
- The error is calculated for the current batch
- The gradients are also calculated for the current batch using
x_batch
Here is the full function so far:
def rmsprop(
x,
y,
initial_params,
learning_rate=0.01,
decay_rate=0.9,
epsilon=1e-8,
n_iter=1000,
batch_size=32,
):
params = np.array(initial_params, dtype=float)
squared_grad = np.zeros_like(params)
n_samples = len(x)
for _ in range(n_iter):
indices = np.random.permutation(n_samples)
x_shuffled = x[indices]
y_shuffled = y[indices]
for i in range(0, n_samples, batch_size):
x_batch = x_shuffled[i : i + batch_size]
y_batch = y_shuffled[i : i + batch_size]
y_pred = params[0] * x_batch + params[1]
error = y_pred - y_batch
grad_m = np.mean(error * x_batch)
grad_b = np.mean(error)
grad = np.array([grad_m, grad_b])
squared_grad = decay_rate * squared_grad + (1 - decay_rate) * grad**2
params -= learning_rate * grad / (np.sqrt(squared_grad) + epsilon)
return paramsLet’s test it on an actual dataset:
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# Load the diamonds dataset
diamonds = sns.load_dataset("diamonds")
# Extract carat and price
X = diamonds["carat"].values.reshape(-1, 1)
y = diamonds["price"].values
# Normalize the data
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X_normalized = scaler_X.fit_transform(X)
y_normalized = scaler_y.fit_transform(y.reshape(-1, 1)).flatten()
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(
X_normalized, y_normalized, test_size=0.2, random_state=42
)Here is what we are doing in the above snippet:
- Loading the Diamonds dataset from Seaborn
- Choosing its
caratfeature to predict diamondpricesand storing the arrays asXandy - Normalizing the arrays since Linear Regression requires features in similar scales
- Splitting the data into training and test sets
Now, let’s use our rmsprop function on the dataset:
# Train the model using RMSprop
initial_params = np.array([1.0, 0.0])
optimized_params = rmsprop(
X_train.flatten(),
y_train,
initial_params,
learning_rate=0.01,
n_iter=5000,
batch_size=512,
)Diamonds dataset has over 50k samples, so we are choosing a batch size of 512. Let’s make predictions with the tuned parameters and calculate the loss on the test set:
# Make predictions on the test set
y_pred_normalized = model(optimized_params[0], X_test.flatten(), optimized_params[1])
# Denormalize the predictions
y_pred = scaler_y.inverse_transform(y_pred_normalized.reshape(-1, 1)).flatten()
y_test_denormalized = scaler_y.inverse_transform(y_test.reshape(-1, 1)).flatten()
# Calculate Mean Squared Error
mse = mean_squared_error(y_test_denormalized, y_pred)
print(f"Root Mean Squared Error: {mse ** 0.5:.2f}")
# Print optimized parameters
print(f"Optimized slope (m): {optimized_params[0]:.4f}")
print(f"Optimized intercept (b): {optimized_params[1]:.4f}")Output:
Root Mean Squared Error: 1550.76
Optimized slope (m): 0.9269
Optimized intercept (b): 0.0089The RMSE score is $1550. Let’s plot the regression line:
# Plot the results
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.scatter(X_test, y_test_denormalized, alpha=0.5, label="Actual")
plt.scatter(X_test, y_pred, alpha=0.5, label="Predicted")
plt.xlabel("Carat")
plt.ylabel("Price")
plt.title("Diamond Price Prediction")
plt.legend()
plt.show()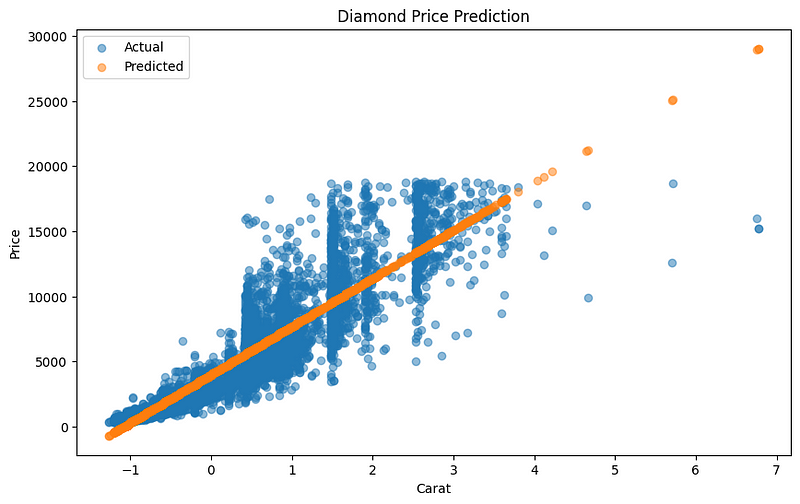
Again, we see that the line fits the data well.
In summary, using mini-batches in RMSprop offers several interconnected benefits. By processing smaller batches, it improves computational efficiency, requiring less memory and potentially speeding up calculations.
This approach introduces beneficial noise that aids in generalization and helps prevent overfitting. The more frequent parameter updates enabled by mini-batches can lead to faster convergence while also allowing for training on large datasets that might not fit entirely in memory.
Additionally, the stochastic nature of mini-batch selection enhances the algorithm’s ability to escape local minima, increasing the likelihood of finding better global solutions.
The Gradient of Mean Squared Error
To understand how RMSprop updates the model parameters, we need to first understand the gradient of the mean squared error (MSE) loss function. The gradient tells us how to adjust our parameters to minimize the error.
For our simple linear regression model f(x) = mx + b, the mean squared error is:
MSE = (1/n) * Σ(y_i - (m * x_i + b))^2Where:
nis the number of samplesy_iis the actual valuem * x_i + bis the predicted value
To find the gradients, we need to calculate the partial derivatives of MSE with respect to m and b:
1. Gradient with respect to m (∂MSE/∂m):
∂MSE/∂m = (-2/n) * Σ(y_i - (m * x_i + b)) * x_i
2. Gradient with respect to b (∂MSE/∂b):
∂MSE/∂b = (-2/n) * Σ(y_i - (m * x_i + b))
Let’s break down these formulas:
1. For the slope m:
- We sum the product of the error
(y_i - (mx_i + b))and the input x_ifor each sample. - This is multiplied by
-2/nto get the average gradient.
2. For the intercept b:
- We sum the error
(y_i - (mx_i + b))for each sample. - This is also multiplied by
-2/nto get the average gradient.
In our implementation, we simplified these formulas slightly:
error = y_pred - y
grad_m = np.mean(error x)
grad_b = np.mean(error)Here’s how this simplification works:
- We calculate the error as
(y_pred - y)instead of(y - y_pred). This flips the sign, eliminating the need for the negative sign in our gradient formulas. - We use
np.mean()instead of summing and dividing byn, which gives us the average directly. - For
grad_m, we multiply the error byxbefore taking the mean, which is equivalent to the formula above. - For
grad_b, we just take the mean of the error, which is equivalent to the formula above (sincex_i ^ 0 = 1for alli).
These gradients tell us how to adjust m and b to reduce the error. A positive gradient means we should decrease the parameter, while a negative gradient means we should increase it. The magnitude of the gradient indicates how large this adjustment should be.
RMSprop uses these gradients in its update rule, but it doesn’t apply them directly. Instead, it uses them to compute adaptive learning rates for each parameter, which we’ll explore in the next section.
Intuition Behind RMSprop’s Update Rule
RMSprop’s update rule is designed to address some of the limitations of basic gradient descent methods. Let’s break down the update rule and understand its components:
squared_grad = decay_rate * squared_grad + (1 - decay_rate) * grad ** 2
params -= learning_rate * grad / (np.sqrt(squared_grad) + epsilon)1. Adaptive learning rates
The key idea behind RMSprop is to use adaptive learning rates for each parameter. Instead of using a fixed learning rate for all parameters, RMSprop adjusts the learning rate based on the historical gradient information.
2. Moving average of squared gradients
squared_grad = decay_rate * squared_grad + (1 - decay_rate) * grad ** 2This line computes a moving average of squared gradients. Here’s why this is important:
- Squaring the gradients eliminates negative values, focusing on the magnitude of the gradient.
- The moving average provides a smoothed history of gradient magnitudes.
- The
decay_rate(typically 0.9) determines how much weight is given to recent vs. older gradients.
Values close to 1 give more weight to older gradients (the left side of the plus sign), while values close to 0 make the latest gradients more important (the right side of the plus sign).
3. Normalizing the update
params -= learning_rate * grad / (np.sqrt(squared_grad) + epsilon)This line performs the actual parameter update. The key insight is dividing the gradient by the square root of the moving average of squared gradients:
- If a parameter has consistently large gradients,
sqrt(squared_grad)will be large, reducing the effective learning rate for that parameter. - If a parameter has small or infrequent gradients,
sqrt(squared_grad)will be small, increasing the effective learning rate.
4. Balancing the learning
This adaptive approach helps balance the learning process:
- It prevents the learning rate from becoming too small for parameters with small gradients.
- It slows down learning for parameters with large gradients, preventing overshooting.
5. Handling different scales
RMSprop is particularly effective when dealing with features of different scales or when the optimal scale of parameters is unknown:
- Parameters that need larger updates will naturally receive them.
- Parameters that need finer adjustments will get smaller updates.
6. Momentum-like behavior
While RMSprop doesn’t explicitly use momentum, the moving average of squared gradients provides a form of momentum:
- It helps smooth out oscillations in the gradient.
- It allows the algorithm to build up “speed” in directions with consistent gradients.
7. Epsilon for numerical stability
The small epsilon value (typically 1e-8) is added to prevent division by zero and to provide a minimum scale of update.
In essence, RMSprop’s update rule adapts the learning process to the characteristics of each parameter, allowing for more efficient and stable optimization. This makes it particularly well-suited for non-convex optimization problems, such as those encountered in deep learning.
RMSprop vs Other Optimizers
Below, you can find a comparison table that highlights the differences between RMSprop and other optimizers:
|
Feature/Optimizer |
SGD |
AdaGrad |
RMSprop |
Adam |
|
Learning Rate |
Fixed learning rate |
Adaptive, but decreases over time |
Adaptive, based on recent gradient magnitudes |
Adaptive, combines momentum and RMSprop-style learning rates |
|
Momentum |
Optional (Momentum term can be added) |
No |
No (momentum-like behavior via moving average of gradients) |
Yes, built-in momentum via moving averages of gradients |
|
Gradient Scaling |
Uniform across all parameters |
Per-parameter scaling (based on historical gradients) |
Per-parameter scaling (moving average of squared gradients) |
Per-parameter scaling (moving averages of first and second moments) |
|
Performance on Non-Convex Functions |
Struggles with non-convex functions, can get stuck in local minima |
Struggles due to diminishing learning rates over time |
Effective, especially on non-stationary and non-convex problems |
Very effective due to adaptive learning rates and momentum |
|
Convergence Speed |
Slow without momentum |
Slows down over time due to shrinking learning rate |
Faster convergence compared to AdaGrad and SGD |
Fast convergence, especially on large and complex datasets |
|
Hyperparameters |
Learning rate (and momentum if used) |
Learning rate |
Learning rate, decay rate, epsilon |
Learning rate, beta1, beta2, epsilon |
|
Memory Usage |
Low |
High (accumulates squared gradients) |
Moderate (stores moving average of squared gradients) |
Higher (stores moving averages of gradients and squared gradients) |
|
Use Cases |
Simple tasks, convex functions |
Sparse data, convex problems |
RNNs, non-convex optimization problems, non-stationary objectives |
Deep learning, large datasets, complex models (CNNs, RNNs) |
Key Insights:
- SGD is often used for simple problems or when memory and computational resources are limited. It may require momentum to improve convergence.
- AdaGrad excels in sparse data situations but tends to slow down over time due to its learning rate decay.
- RMSprop is great for non-convex optimization problems, balancing learning rates across parameters and stabilizing learning with adaptive rates.
- Adam combines the best of both worlds: adaptive learning rates and momentum, making it highly effective for large, complex models, especially in deep learning tasks.
Conclusion
In this article, we have learned about the RMSprop optimization algorithm. Its optimization strategy is valuable for many deep learning applications, especially in complex optimization landscapes involving non-convex functions.
It differs from other optimization algorithms in that its adaptive learning rates per parameter are calculated using the moving average of squared gradients. This adaptability balances learning across parameters while also providing momentum-like behavior.
To learn more about how RMSprop compares to other optimization algorithms, you can refer to our separate article on Adam optimizer.
If you want to master more topics related to deep learning, you can check out our Deep Learning in Python skill track.
RMSprop FAQs
What is RMSprop and why is it important?
RMSprop is an optimization algorithm used in machine learning. It's important because it adapts learning rates for each parameter, making it effective for training deep neural networks and solving non-convex optimization problems.
How does RMSprop differ from standard gradient descent?
Unlike standard gradient descent, RMSprop uses adaptive learning rates for each parameter based on the history of gradients. This allows it to handle different scales of parameters more effectively and potentially converge faster.
Can I implement RMSprop from scratch in Python?
Yes, the article provides a step-by-step guide to implementing RMSprop in Python using NumPy. It also shows how to add mini-batch functionality to the implementation.
What are the key hyperparameters in RMSprop?
The key hyperparameters in RMSprop are the learning rate, decay rate, epsilon (for numerical stability), number of iterations, and batch size (if using mini-batches).
Is RMSprop better than other optimization algorithms like Adam?
RMSprop performs well in many scenarios, especially for non-convex optimization. However, its performance relative to other algorithms like Adam can depend on the specific problem. The article mentions a separate tutorial on Adam for comparison.

I am a data science content creator with over 2 years of experience and one of the largest followings on Medium. I like to write detailed articles on AI and ML with a bit of a sarcastıc style because you've got to do something to make them a bit less dull. I have produced over 130 articles and a DataCamp course to boot, with another one in the makıng. My content has been seen by over 5 million pairs of eyes, 20k of whom became followers on both Medium and LinkedIn.
