Adagrad Optimizer Explained: How It Works, Implementation, & Comparisons

Imagine you're walking down a hill, but the ground changes as you go—some parts are steep, and others are flat. If you take the same-sized step every time, you might struggle or take too long to reach the bottom. In machine learning, a similar challenge happens with gradient descent, where using the same learning rate for all parameters can slow down learning.

This is where Adagrad comes in. It adjusts the step size for each parameter based on how much it's changed during training, helping the model learn faster and more effectively, especially when different features have different scales. In this article, we'll explore how Adagrad works and break down the math behind it. Also, we’ll show you how to implement it using PyTorch and compare it with other optimizers so you can choose the best for your projects.

What is Adagrad?

Adagrad (Adaptive Gradient) is an optimization algorithm used in machine learning, specifically for training deep neural networks. It is designed to adapt the learning rate for each parameter based on its historical gradients. This approach allows Adagrad to improve the efficiency of machine learning models, especially in scenarios where sparse data is involved or when different parameters have varying rates of convergence.

Adagrad provides higher learning rates for less frequent features and lower rates for more frequent ones, which makes it well-suited for working with sparse data. Additionally, it reduces the need to manually adjust the learning rate!

The Adagrad Algorithm Explained

Let’s break down the Adagrad algorithm:

Step 1: Initialize Parameters

First, start with:

• The initial values of the parameters,0, which you want to optimize.
• A small constant ϵ to prevent division by zero (this is usually a very small number, like 10^-8.
• The initial learning rate η, which determines how large the parameter updates should be at the beginning.

Step 2: Compute the Gradient

For each parameter 0_t​ at the time step _t, you compute the gradient of the loss function with respect to that parameter. This gradient tells us how much and in what direction we should update the parameter to reduce the loss. Let’s call this gradient g_t, where _t is the current time step.

Step 3: Accumulate the Squared Gradients

Instead of updating the parameters directly, Adagrad keeps track of the squared sum of gradients for each parameter. For each parameter i, you compute and accumulate the squared gradient at every time step. This accumulated gradient is denoted as G_t.

G_t =G_t-1 + g_t²

Here:

• G_t-1 is the sum of squared gradients up to the previous time step.
• g_t² is the square of the current gradient for the parameter.

This accumulated gradient helps Adagrad adjust the learning rate differently for each parameter based on how much it has been updated.

Step 4: Update the Parameters

Now that you have the accumulated squared gradient G_t​, we can update each parameter 0_t​. The update rule for Adagrad is as follows:

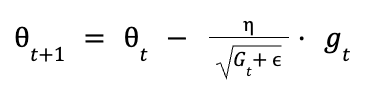
Here’s what’s happening:

• η is the initial learning rate
• G_t is the accumulated squared gradients up to the time step t.
• ϵ is a small value to avoid division by zero.
• g_t​ is the gradient at the current time step.

The term:

​

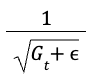
effectively reduces the learning rate for parameters that have a large accumulated gradient. In contrast, parameters with smaller accumulated gradients will have a larger learning rate.

Adagrad’s formula automatically adapts the learning rate, here’s how:

• Frequent updates (large accumulated gradient): For parameters that are updated often, G_t become large, making the learning rate smaller. This prevents the parameter from changing too drastically and stabilizes learning.
• Infrequent updates (small accumulated gradient): For parameters that are updated less frequently, G_t stay small, keeping the learning rate larger. This allows for more significant updates when necessary.

Implementing Adagrad in PyTorch

PyTorch provides a built-in implementation of Adagrad, which can be accessed through the torch.optim module. First, install PyTorch using pip:

pip install torch torchvision

Learn how to build your first neural network with our free course, Introduction to Deep Learning with PyTorch.

Here’s a step-by-step guide to implementing the Adagrad optimizer in PyTorch:

Step 1: Import Necessary Libraries

import torch
import torch.nn as nn
import torch.optim as optim

Step 2: Define a Simple Neural Network

class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(10, 5)
        self.fc2 = nn.Linear(5, 2)
    
    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.fc2(x)
        return x

Step 3: Initialize the Model and Optimizer

model = SimpleNN()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adagrad(model.parameters(), lr=0.01)

Step 4: Training Loop

for epoch in range(10):  # loop over the dataset multiple times
    inputs = torch.randn(1, 10)  # random input tensor
    labels = torch.tensor([1])   # target labels

    # Zero the parameter gradients
    optimizer.zero_grad()

    # Forward pass
    outputs = model(inputs)
    loss = criterion(outputs, labels)

    # Backward pass and optimize
    loss.backward()
    optimizer.step()

    print(f'Epoch {epoch+1}, Loss: {loss.item()}')

In this code, a simple linear model is trained using the AdaGrad optimizer. The learning rate is set to 0.01, but AdaGrad will adjust it for each parameter based on the accumulated squared gradients.

Run the code and you’ll see output similar to this:

The output shows the loss after each epoch, which indicates how well the model is learning. Initially, the loss is higher, but as the training progresses, the loss generally decreases, meaning the model is improving. Some fluctuations are normal, especially with random inputs, but overall, the model is gradually learning to make better predictions.

If you want to discover deep learning and explore how this branch of machine learning is changing the world. Check out our course on Deep Learning in Python.

Adagrad vs. Other Optimizers

Let’s compare the Adagrad with other optimizers such as Adam, SGD, and RMSProp.

Adagard vs. Adam

Learning Rate Adaptation

Both Adagrad and Adam adapt the learning rate for each parameter, but they do so in different ways. Adagrad scales the learning rate based on the sum of squared gradients, which can lead to diminishing learning rates over time. On the other hand, Adam uses both the first and second moments of the gradients, allowing it to maintain a more stable learning rate throughout training.

Handling Sparse Data: 

Adagrad is particularly well-suited for handling sparse data due to its ability to assign larger learning rates to infrequent features. This makes it a good choice for applications like natural language processing, where sparse gradients are common. Adam, while also capable of handling sparse data, is generally preferred for its overall robustness and efficiency across a wider range of applications.

Convergence and Performance

Adam is often favored for its faster convergence and superior performance in practice, especially in deep learning models with large datasets. Its use of momentum and bias correction helps it avoid getting stuck in local minima and saddle points, which can be a limitation for Adagrad.

Learn about fundamental deep learning architectures such as CNNs, RNNs, LSTMs, and GRUs for modeling image and sequential data. Check out our course Intermediate Deep Learning with PyTorch.

Adagrad vs. other gradient descent algorithms

Let’s compare the Adagrad with SGD and RMSProp

AdaGrad vs. Stochastic Gradient Descent (SGD)

Stochastic Gradient Descent is a basic optimization algorithm that updates the model parameters using the gradient of the loss function with respect to the parameters. It is known for its simplicity and ease of implementation. However, SGD has a constant learning rate, which can be a limitation when dealing with sparse data or varying feature scales.

AdaGrad vs. RMSProp

RMSProp is an extension of AdaGrad that addresses its diminishing learning rate issue by introducing a decay factor. This decay factor allows RMSProp to maintain a more stable learning rate throughout the training process.

Let’s summarise the pros and cons of Adagrad, SGD, and RMSProp:

Common Use Cases and Limitations

Let’s explore the use cases and limitations of AdaGrad in various contexts.

Use cases of Adagrad

Adagrad's unique ability to adapt learning rates for each parameter makes it ideal for several scenarios:

1. Natural Language Processing (NLP): One of the most significant applications of Adagrad is in natural language processing (NLP). In NLP, word embeddings are crucial components, and Adagrad is used to optimize these embeddings by adapting the learning rates of each parameter.
2. Recommender systems: In recommender systems, Adagrad is used to optimize the weights of the recommendation model. This is important for predicting the likelihood of a user liking a particular product.
3. Image recognition: In image recognition, Adagrad is used to optimize the weights of deep neural networks. By adapting the learning rates of each parameter, Adagrad ensures that the weights are updated appropriately for the task at hand, improving the accuracy of the image recognition model

Limitations of Adagrad

While Adagrad is powerful in certain situations, it does come with some set of limitations:

1. Diminishing learning rate: One of the primary limitations of Adagrad is its tendency to reduce the learning rate too aggressively over time. As the algorithm accumulates the squared gradients from the beginning of training, the effective learning rate can become very small, leading to slow convergence or even causing the model to stop learning altogether.
2. Memory requirements: Adagrad requires more memory to store the historical gradients for each parameter, making it less efficient for larger datasets. This can be a significant drawback when working with large-scale machine learning models, where memory efficiency is crucial.

Strategies to mitigate limitations

There are several strategies you can use to address Adagrad’s limitations:

1. Use of AdaDelta and RMSProp: To address the issue of diminishing learning rates, extensions of AdaGrad such as AdaDelta and RMSProp have been developed.
2. Combining with momentum: Another strategy to mitigate the limitations of AdaGrad is to combine it with momentum-based methods. The Adam optimizer, for example, combines the adaptive learning rate of AdaGrad with the concept of momentum, which helps accelerate convergence and improve performance in practice.
3. Hyperparameter tuning: Careful tuning of hyperparameters, such as the initial learning rate and the epsilon value used to prevent division by zero, can also help mitigate some of the limitations of AdaGrad.

Hands-On Exercise: Optimizing a Model with Adagrad

Let’s build a simple neural network, train it using the Adagrad optimizer, and compare its performance with other popular optimizers.

If you want to learn more about PyTorch, then check out our guide on PyTorch Tutorial: Building a Simple Neural Network From Scratch.

Let's start by creating a basic neural network model in PyTorch. We'll design a network suitable for binary classification on sparse data where Adagrad shines well.

import torch
import torch.nn as nn

class SparseNN(nn.Module):
    def __init__(self, input_size):
        super(SparseNN, self).__init__()
        self.fc1 = nn.Linear(input_size, 50)
        self.fc2 = nn.Linear(50, 1)
        self.activation = nn.ReLU()
        self.output_activation = nn.Sigmoid()

    def forward(self, x):
        x = self.activation(self.fc1(x))
        x = self.output_activation(self.fc2(x))
        return x

This neural network has an input layer, one hidden layer with 50 neurons, and an output layer with a single neuron. We use ReLU activation for the hidden layer and Sigmoid activation for the output layer, making it suitable for binary classification.

Now, let's set up our training process using the Adagrad optimizer. We'll create a function to handle the training:

import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset

# Function to train the model
def train_model(model, optimizer, criterion, train_loader, num_epochs=100):
    losses = []
    for epoch in range(num_epochs):  # loop for each training epoch
        for inputs, targets in train_loader:
            # Clear gradients before each batch to avoid accumulation
            optimizer.zero_grad() # Reset gradients to zero

            # Forward pass - get model predictions
            outputs = model(inputs)

            # Calculate loss based on predictions and targets
            loss = criterion(outputs, targets)

            # Backward pass - calculate gradients for parameter updates based on the loss
            loss.backward()

            # Update model parameters based on calculated gradients
            optimizer.step()

        # Track loss for monitoring training progress
        losses.append(loss.item())
    return losses

# Setup for training
X, y = generate_sparse_data()  # This function generates our sparse dataset
input_size = X.shape[1]
train_size = int(0.8 * len(X))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]

train_dataset = TensorDataset(X_train, y_train)
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)

model = SparseNN(input_size)
criterion = nn.BCELoss()  # Assuming binary classification with BCE loss
optimizer = optim.Adagrad(model.parameters(), lr=0.01)

# Train the model
losses = train_model(model, optimizer, criterion, train_loader)

In this setup, we:

1. Create our SparseNN model.
2. Define the loss function (Binary Cross Entropy).
3. Initialize the Adagrad optimizer with a learning rate of 0.01.
4. Train the model for 100 epochs, recording the loss at each epoch.

Now, to assess our model's performance, we'll create an evaluation function:

def evaluate_model(model, test_loader):
    model.eval()
    correct = 0
    total = 0
    with torch.no_grad():
        for inputs, targets in test_loader:
            outputs = model(inputs)
            predicted = (outputs > 0.5).float()
            total += targets.size(0)
            correct += (predicted == targets).sum().item()
    accuracy = correct / total
    return accuracy

# Evaluate the model
test_dataset = TensorDataset(X_test, y_test)
test_loader = DataLoader(test_dataset, batch_size=32)
accuracy = evaluate_model(model, test_loader)
print(f"Adagrad Accuracy: {accuracy:.4f}")

This function calculates the accuracy of our model on the test set.

Next, let's compare it with other popular optimizers: SGD, Adam, and RMSprop. We'll create a function to run the experiment for each optimizer:

def run_experiment(optimizer_class, lr=0.01):
    model = SparseNN(input_size)
    criterion = nn.BCELoss()
    
    if optimizer_class == optim.SGD:
        optimizer = optimizer_class(model.parameters(), lr=lr, momentum=0.9)
    elif optimizer_class == optim.RMSprop:
        optimizer = optimizer_class(model.parameters(), lr=lr, alpha=0.99)
    else:
        optimizer = optimizer_class(model.parameters(), lr=lr)

    losses = train_model(model, optimizer, criterion, train_loader)
    accuracy = evaluate_model(model, test_loader)
    return losses, accuracy

# Compare optimizers
optimizers = {
    'Adagrad': optim.Adagrad,
    'SGD': optim.SGD,
    'Adam': optim.Adam,
    'RMSprop': optim.RMSprop
}

results = {}
for name, opt_class in optimizers.items():
    losses, accuracy = run_experiment(opt_class)
    results[name] = {'losses': losses, 'accuracy': accuracy}

print("Final accuracies:")
for name, data in results.items():
    print(f"{name}: {data['accuracy']:.4f}")

After running this code, we get the following results:

Final accuracies:
Adagrad: 0.9350
SGD: 0.8950
Adam: 0.9300
RMSprop: 0.8600

These results show that Adagrad performed the best on our sparse data problem, achieving the highest accuracy of 95.00%. This shows that Adagrad is well-suited for sparse data scenarios. Adam came in a close second, while SGD and RMSprop performed less well in this particular case.

To visualize the training process, we can plot the loss curves:

import matplotlib.pyplot as plt

plt.figure(figsize=(12, 6))
for name, data in results.items():
    plt.plot(data['losses'], label=f"{name} (Accuracy: {data['accuracy']:.4f})")
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Training Loss Comparison (Sparse Data)')
plt.legend()
plt.show()

Let’s combine all the code snippets and here is the complete code.

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
import matplotlib.pyplot as plt

# Step 1: Generate sparse synthetic data
def generate_sparse_data(n_samples=1000, n_features=100, sparsity=0.95):
    X = torch.randn(n_samples, n_features)
    mask = torch.rand(n_samples, n_features) < sparsity
    X[mask] = 0
    weights = torch.randn(n_features)
    y = (torch.matmul(X, weights) > 0).float().view(-1, 1)
    return X, y

# Step 2: Define the neural network
class SparseNN(nn.Module):
    def __init__(self, input_size):
        super(SparseNN, self).__init__()
        self.fc1 = nn.Linear(input_size, 50)
        self.fc2 = nn.Linear(50, 1)
        self.activation = nn.ReLU()
        self.output_activation = nn.Sigmoid()

    def forward(self, x):
        x = self.activation(self.fc1(x))
        x = self.output_activation(self.fc2(x))
        return x

# Step 3: Train the model
def train_model(model, optimizer, criterion, train_loader, num_epochs=100):
    losses = []
    for epoch in range(num_epochs):
        for inputs, targets in train_loader:
            optimizer.zero_grad()
            outputs = model(inputs)
            loss = criterion(outputs, targets)
            loss.backward()
            optimizer.step()
        losses.append(loss.item())
    return losses

# Step 4: Evaluate the model
def evaluate_model(model, test_loader):
    model.eval()
    correct = 0
    total = 0
    with torch.no_grad():
        for inputs, targets in test_loader:
            outputs = model(inputs)
            predicted = (outputs > 0.5).float()
            total += targets.size(0)
            correct += (predicted == targets).sum().item()
    accuracy = correct / total
    return accuracy

# Step 5: Main function to run the experiment
def run_experiment(optimizer_class, lr=0.01):
    # Generate sparse data
    X, y = generate_sparse_data()
    input_size = X.shape[1]
    train_size = int(0.8 * len(X))
    X_train, X_test = X[:train_size], X[train_size:]
    y_train, y_test = y[:train_size], y[train_size:]

    # Create data loaders
    train_dataset = TensorDataset(X_train, y_train)
    test_dataset = TensorDataset(X_test, y_test)
    train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
    test_loader = DataLoader(test_dataset, batch_size=32)

    # Initialize model and training components
    model = SparseNN(input_size)
    criterion = nn.BCELoss()
    
    # Use default hyperparameters for each optimizer
    if optimizer_class == optim.SGD:
        optimizer = optimizer_class(model.parameters(), lr=lr, momentum=0.9)
    elif optimizer_class == optim.RMSprop:
        optimizer = optimizer_class(model.parameters(), lr=lr, alpha=0.99)
    else:
        optimizer = optimizer_class(model.parameters(), lr=lr)

    # Train the model
    losses = train_model(model, optimizer, criterion, train_loader)

    # Evaluate the model
    accuracy = evaluate_model(model, test_loader)

    return losses, accuracy

# Step 6: Compare Adagrad with other optimizers
optimizers = {
    'Adagrad': optim.Adagrad,
    'SGD': optim.SGD,
    'Adam': optim.Adam,
    'RMSprop': optim.RMSprop
}

results = {}

for name, opt_class in optimizers.items():
    losses, accuracy = run_experiment(opt_class)
    results[name] = {'losses': losses, 'accuracy': accuracy}

# Step 7: Plot results
plt.figure(figsize=(12, 6))
for name, data in results.items():
    plt.plot(data['losses'], label=f"{name} (Accuracy: {data['accuracy']:.4f})")
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Training Loss Comparison (Sparse Data)')
plt.legend()
plt.show()

print("Final accuracies:")
for name, data in results.items():
    print(f"{name}: {data['accuracy']:.4f}")

Here’s the result:

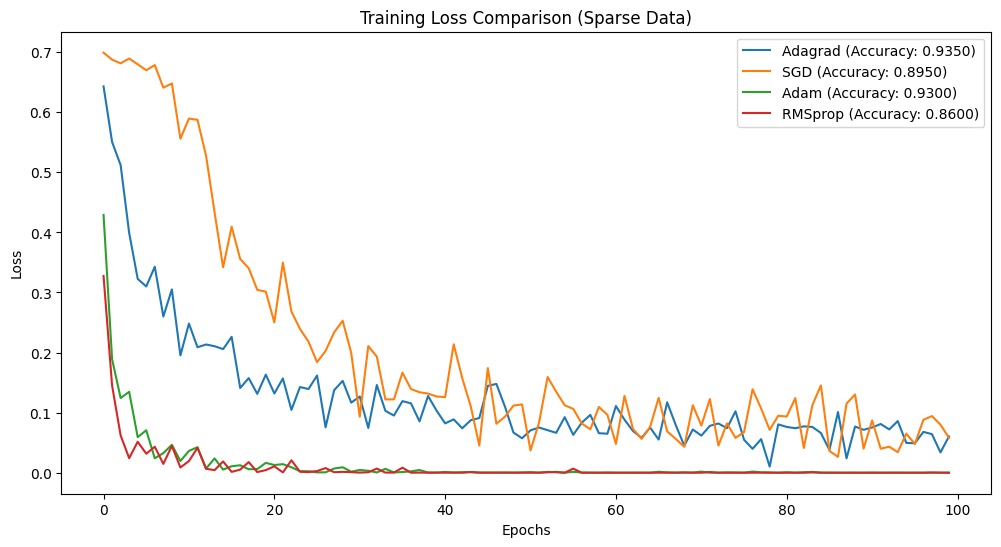
Conclusion

Adagrad is useful when working with sparse data due to its adaptive learning rate. We built a basic neural network and trained it using Adagrad, and then compared its performance to other well-known optimization algorithms. The results strongly favoured Adagrad showing that it handles sparse data better.

I've also handpicked some of the best resources on PyTorch, deep learning, and other optimization algorithms. Make sure to check them out to learn more in-depth:

• PyTorch Tutorial: Building a Simple Neural Network From Scratch
• Adam Optimizer Tutorial: Intuition and Implementation in Python
• Stochastic Gradient Descent in Python: A Complete Guide for ML Optimization
• Introduction to Deep Learning with PyTorch
• Intermediate Deep Learning with PyTorch
• Deep Learning for Images with PyTorch