Scikit-Learn Tutorial: Baseball Analytics Pt 2

A Scikit-Learn tutorial to using logistic regression and random forest models to predict which baseball players will be voted into the Hall of Fame

Jun 20, 2017 · 32 min read

Importing Data
Data Cleaning and Preprocessing
Feature Engineering: Creating New Features
Selecting Error Metric and Model
Your Future Sports Analytics Projects

In Part I of this tutorial the focus was determining the number of games that a Major-League Baseball (MLB) team won that season, based on the team’s statistics and other variables from that season.

In the second part of this project, you’ll test out a logistic regression model and a random forest model from Scikit-Learn (sklearn) to predict which players will be voted into the Hall of Fame, based on the player’s career statistics and awards. Each row will consist of a single player and data related to their career. There are four main position subgroups in baseball: Infielders, Outfielders, Pitchers, and Catchers. The focus of this project will be on Infielders and Outfielders.

The National Baseball Hall of Fame and Museum is located in Cooperstown, New York and was dedicated in 1939. A baseball player can be elected to the Hall of Fame if they meet the following criteria:

The player must have competed in at least ten seasons;
The player has been retired for at least five seasons;
A screening committee must approve the player’s worthiness to be included on the ballot and most players who played regularly for ten or more years are deemed worthy;
The player must not be on the ineligible list (that means that the player should not be banned from baseball);
A player is considered elected if he receives at least 75% of the vote in the election; and
A player stays on the ballot the following year if they receive at least 5% of the vote and can appear on ballots for a maximum of 10 years.

A player who does not get elected to the Hall of Fame can be added by the Veterans Committee or a Special Committee appointed by the Commissioner of Major League Baseball, but this project will focus only on players who were voted into the Hall of Fame. Fundamentally, what you want to know is:

“Can you build a machine learning model that can accurately predict if an MLB baseball player will be voted into the Hall of Fame?”.

In the first part of this project, you loaded the data from an SQLite database. This time, you’ll load the data from CSV files. Sean Lahman compiled this data on his website.

Importing Data

You will need to read in the data from the following CSV files into pandas DataFrames:

The Master.csv will tell you more about the player names, Date Of Birth (DOB), and biographical info;
The Fielding.csv contains the fielding statistics, while
the Batting.csv contains the Batting statistics;
You’ll also read in the AwardsPlayers.csv, in which you’ll find data on the awards won by baseball players;
The AllstarFull.csv file wil give you all the All-Star appearances;
You’ll also need the Hall of Fame voting data, which you can find in HallOfFame.csv; and
Appearances.csv, which contains details on the positions at which a player appeared.

Don’t worry if some concepts aren’t clear yet, you’ll get more information as you go through the tutorial!

First, download the CSV files by clicking here. Ideally, put all of the data into one specific folder which will contain all the files for this project. Next, open up your terminal or start the Jupyter Notebook Application and you can start working!

Load pandas and rename to pd, then read in each of the CSV files. You’ll only include certain columns, and you can review the available columns here.

# Import data to DataFramesimport pandas as pd# Read in the CSV filesmaster_df = pd.read_csv('Master.csv',usecols=['playerID','nameFirst','nameLast','bats','throws','debut','finalGame'])fielding_df = pd.read_csv('Fielding.csv',usecols=['playerID','yearID','stint','teamID','lgID','POS','G','GS','InnOuts','PO','A','E','DP'])batting_df = pd.read_csv('Batting.csv')awards_df = pd.read_csv('AwardsPlayers.csv', usecols=['playerID','awardID','yearID'])allstar_df = pd.read_csv('AllstarFull.csv', usecols=['playerID','yearID'])hof_df = pd.read_csv('HallOfFame.csv',usecols=['playerID','yearid','votedBy','needed_note','inducted','category'])appearances_df = pd.read_csv('Appearances.csv')

Note that for this tutorial, the data will be loaded in for you!

Data Cleaning and Preprocessing

Now that you have imported the data, you can start cleaning and preprocessing it. Because you’re working with 7 CSV files, it’s best to start by looking at them one by one: in the following sections, you’ll go over the separate DataFrames and this in the following order: batting_df, fielding_df, awards_df, allstar_df, hof_df, appearances_df, and master_df.

`batting_df`

First, you’ll be working on the batting_df DataFrame. Print out the first few rows with the help of the head() function:

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxuYmF0dGluZ19kZiA9IHBkLnJlYWRfY3N2KCdodHRwczovL3MzLmFtYXpvbmF3cy5jb20vYXNzZXRzLmRhdGFjYW1wLmNvbS9ibG9nX2Fzc2V0cy9NTEIrRGF0YS9CYXR0aW5nLmNzdicpIiwic2FtcGxlIjoiIyBQcmludCBmaXJzdCBmZXcgcm93cyBvZiBgYmF0dGluZ19kZmBcbmJhdHRpbmdfZGYuX19fX19fIiwic29sdXRpb24iOiIjIFByaW50IGZpcnN0IGZldyByb3dzIG9mIGBiYXR0aW5nX2RmYFxuYmF0dGluZ19kZi5oZWFkKCkiLCJzY3QiOiJFeCgpLnRlc3RfZnVuY3Rpb24oXCJiYXR0aW5nX2RmLmhlYWRcIilcbnN1Y2Nlc3NfbXNnKFwiV2VsbCBkb25lISBZb3UncmUgb2ZmIHRvIGEgZ29vZCBzdGFydCFcIikifQ==

Tip because you pulled in all columns from this data table, it’s wise to use the columns attribute to also pull up the columns of the batting_df DataFrame to see what you’re dealing with. Also, feel free to use any other Pandas functions to inspect your data thoroughly!

When you inspect the results, you’ll notice three things about the batting_df and its columns:

There are a lot of IDs. Remember that this is nothing abnormal: because the data originally comes from a database, all your tables will be linked to each other, as is normal (and required) for relational databases.

playerID, for the Player ID code.
yearID, which lists the year;
teamID identifies the team for which a player plays;
lgID identifies the league;

As you’d expect from the batting_df, there are a lot of statistics on the players; Here are some examples:

G for the number of games,
ABfor the number at bats;
R to indicate the number of runs;
H for the number of hits;
HR for the number of Homeruns;
RBI for the Runs Batted In;
SO or Strikeouts.

At this moment, your data is not tidy. If you don’t know what is meant with the concept of “tidy data”, read a detailed explanation of tidy data here. Making sure that it is tidy is very important; In short, this means that you need to get to a point where each row is an observation, in this case a player’s career, and each column is a variable. Most of the rows in the current DataFrames are from individual seasons. Each of these seasons need to be compiled into one row for the player’s career.

To do this, you’ll be creating dictionaries for each player within a dictionary. Each player’s stats will be aggregated to their dictionary, and then the main dictionary can be converted to a DataFrame.

To start, create a dictionary for player’s stats and one for years played. Aggregate each player’s statistics from batting_df into player_stats and data on which years they played into years_played:

# Initialize dictionaries for player stats and years playedplayer_stats = {}years_played = {}# Create dictionaries for player stats and years played from `batting_df`for i, row in batting_df.iterrows():    playerID = row['playerID']    if playerID in player_stats:        player_stats[playerID]['G'] = player_stats[playerID]['G'] + row['G']        player_stats[playerID]['AB'] = player_stats[playerID]['AB'] + row['AB']        player_stats[playerID]['R'] = player_stats[playerID]['R'] + row['R']        player_stats[playerID]['H'] = player_stats[playerID]['H'] + row['H']        player_stats[playerID]['2B'] = player_stats[playerID]['2B'] + row['2B']        player_stats[playerID]['3B'] = player_stats[playerID]['3B'] + row['3B']        player_stats[playerID]['HR'] = player_stats[playerID]['HR'] + row['HR']        player_stats[playerID]['RBI'] = player_stats[playerID]['RBI'] + row['RBI']        player_stats[playerID]['SB'] = player_stats[playerID]['SB'] + row['SB']        player_stats[playerID]['BB'] = player_stats[playerID]['BB'] + row['BB']        player_stats[playerID]['SO'] = player_stats[playerID]['SO'] + row['SO']        player_stats[playerID]['IBB'] = player_stats[playerID]['IBB'] + row['IBB']        player_stats[playerID]['HBP'] = player_stats[playerID]['HBP'] + row['HBP']        player_stats[playerID]['SH'] = player_stats[playerID]['SH'] + row['SH']        player_stats[playerID]['SF'] = player_stats[playerID]['SF'] + row['SF']        years_played[playerID].append(row['yearID'])    else:        player_stats[playerID] = {}        player_stats[playerID]['G'] = row['G']        player_stats[playerID]['AB'] = row['AB']        player_stats[playerID]['R'] = row['R']        player_stats[playerID]['H'] = row['H']        player_stats[playerID]['2B'] = row['2B']        player_stats[playerID]['3B'] = row['3B']        player_stats[playerID]['HR'] = row['HR']        player_stats[playerID]['RBI'] = row['RBI']        player_stats[playerID]['SB'] = row['SB']        player_stats[playerID]['BB'] = row['BB']        player_stats[playerID]['SO'] = row['SO']        player_stats[playerID]['IBB'] = row['IBB']        player_stats[playerID]['HBP'] = row['HBP']        player_stats[playerID]['SH'] = row['SH']        player_stats[playerID]['SF'] = row['SF']        years_played[playerID] = []        years_played[playerID].append(row['yearID'])

Now, iterate through the years_played dictionary and add the number of years played by each player into the player_stats dictionary:

# Iterate through `years_played` and add the number of years played to `player_stats`for k, v in years_played.items():    player_stats[k]['Years_Played'] = len(list(set(v)))

`fielding_df`

Next up is the fielding_df. The data from this table contains more player statistics and is therefore very similar to the batting_df. As you aggregated each player’s statistics in the player_stats dictionary above, it’s a good idea to also aggregate the statistics from fielding_df into the player_stats dictionary.

More specifically, you’ll need to add new keys to each player’s dictionary within the player_stats dictionary as you iterate through fielding_df. First, make sure to create a fielder_list to identify which players have had their fielding keys entered so the stats can be added properly:

# Initialize `fielder_list`fielder_list = []# Add fielding stats to `player_stats` from `fielding_df`for i, row in fielding_df.iterrows():    playerID = row['playerID']    Gf = row['G']    GSf = row['GS']    POf = row['PO']    Af = row['A']    Ef = row['E']    DPf = row['DP']    if playerID in player_stats and playerID in fielder_list:        player_stats[playerID]['Gf'] = player_stats[playerID]['Gf'] + Gf        player_stats[playerID]['GSf'] = player_stats[playerID]['GSf'] + GSf        player_stats[playerID]['POf'] = player_stats[playerID]['POf'] + POf        player_stats[playerID]['Af'] = player_stats[playerID]['Af'] + Af        player_stats[playerID]['Ef'] = player_stats[playerID]['Ef'] + Ef        player_stats[playerID]['DPf'] = player_stats[playerID]['DPf'] + DPf    else:        fielder_list.append(playerID)        player_stats[playerID]['Gf'] = Gf        player_stats[playerID]['GSf'] = GSf        player_stats[playerID]['POf'] = POf        player_stats[playerID]['Af'] = Af        player_stats[playerID]['Ef'] = Ef        player_stats[playerID]['DPf'] = DPf

`awards_df`

Next up is the awards_df DataFrame: throughout a player’s career, there are many different awards they may receive for excellent achievement. The awards_df contains all the data on the awards won by players.

A good way to inspect your data here is to print out the unique awards within awards_df using the unique() method. Alternatively, you can also experiment with the head(), tail(), info(), … functions to get to know the data in this DataFrame better.

Tip: from the first code chunk, you know that you only read in three columns from the original data table: playerID, awardID, and yearID.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxuYXdhcmRzX2RmID0gcGQucmVhZF9jc3YoJ2h0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL0F3YXJkc1BsYXllcnMuY3N2JywgdXNlY29scz1bJ3BsYXllcklEJywnYXdhcmRJRCcsJ3llYXJJRCddKSIsInNhbXBsZSI6IiMgUHJpbnQgb3V0IHVuaXF1ZSBhd2FyZHMgZnJvbSBgYXdhcmRzX2RmYFxucHJpbnQoYXdhcmRzX2RmWydhd2FyZElEJ10uX19fX19fX18pIiwic29sdXRpb24iOiIjIFByaW50IG91dCB1bmlxdWUgYXdhcmRzIGZyb20gYGF3YXJkc19kZmBcbnByaW50KGF3YXJkc19kZlsnYXdhcmRJRCddLnVuaXF1ZSgpKSIsInNjdCI6IkV4KCkudGVzdF9mdW5jdGlvbihcInByaW50XCIpXG5zdWNjZXNzX21zZyhcIkdvb2Qgam9iISBOb3cgdGFrZSB0aGUgb3Bwb3J0dW5pdHkgdG8gYWxzbyB1c2Ugb3RoZXIgZnVuY3Rpb25zIHN1Y2ggYXMgYGhlYWQoKWAsIGB0YWlsKClgIG9yIGBpbmZvKClgIHRvIGluc3BlY3QgeW91ciBkYXRhIVwiKSJ9

As you can see, there are quite a few options in awards_df… Do you know all these awards?

As mentioned in Part I of this tutorial, knowledge of the data you’re working with is very important. For example, the best awards to include are the Most Valuable Player, Rookie of the Year, Gold Glove, Silver Slugger, and World Series MVP awards and I determined that entirely based on my experience following MLB Baseball.

It obviously could be determined which of these awards is most correlated with being voted into the Hall of Fame, but that would require much more coding.

Now you need to add a count for each award into each player’s dictionary within the player_stats dictionary: first, filter the awards_df for each of the awards listed above, creating five new series. Then create a list called awards_list and include each of the five series in the list. As you did above with fielding_df, create a list to identify which keys have been added to the dictionaries within player_stats for each of the five awards series. Now create a list called lists and include each of the five lists. You’re now ready to loop through awards_list, and iterate through each of the awards series counting how many of each award each player has:

# Create DataFrames for each awardmvp = awards_df[awards_df['awardID'] == 'Most Valuable Player']roy = awards_df[awards_df['awardID'] == 'Rookie of the Year']gg = awards_df[awards_df['awardID'] == 'Gold Glove']ss = awards_df[awards_df['awardID'] == 'Silver Slugger']ws_mvp = awards_df[awards_df['awardID'] == 'World Series MVP']# Include each DataFrame in `awards_list`awards_list = [mvp,roy,gg,ss,ws_mvp]# Initialize lists for each of the above DataFramesmvp_list = []roy_list = []gg_list = []ss_list = []ws_mvp_list = []# Include each of the above lists in `lists`lists = [mvp_list,roy_list,gg_list,ss_list,ws_mvp_list]# Add a count for each award for each player in `player_stats`for index, v in enumerate(awards_list):    for i, row in v.iterrows():        playerID = row['playerID']        award = row['awardID']        if playerID in player_stats and playerID in lists[index]:            player_stats[playerID][award] += 1        else:            lists[index].append(playerID)            player_stats[playerID][award] = 1

`allstar_df`

The allstar_df DataFrame contains information on which players made appearances in Allstar games. The Allstar game is an exhibition game played each year at mid-season. Major League Baseball consists of two leagues: the American league and the National league. The top 25 players from each league are selected to represent their league in the Allstar game.

As you did previously, iterate through allstar_df and add a count of Allstar game appearances to each dictionary within player_stats.

# Initialize `allstar_list`allstar_list = []# Add a count for each Allstar game appearance for each player in `player_stats`for i, row in allstar_df.iterrows():    playerID = row['playerID']    if playerID in player_stats and playerID in allstar_list:        player_stats[playerID]['AS_games'] += 1    else:        allstar_list.append(playerID)        player_stats[playerID]['AS_games'] = 1

`hof_df`

Next up is the hof_df DataFrame, which contains information on which players, managers, and executives have been nominated or inducted into the Hall of Fame, and by what method.

Adding this type of information to your player_stats might be valuable! To do this, filter hof_df first to include only players who were inducted into the Hall of Fame. Then iterate through hof_df indicating which players in player_stats have been inducted into the Hall of Fame as well as how they were inducted:

# filter `hof_df` to include only instances where a player was inducted into the Hall of Famehof_df = hof_df[(hof_df['inducted'] == 'Y') & (hof_df['category'] == 'Player')]# Indicate which players in `player_stats` were inducted into the Hall of Famefor i, row in hof_df.iterrows():    playerID = row['playerID']    if playerID in player_stats:        player_stats[playerID]['HoF'] = 1        player_stats[playerID]['votedBy'] = row['votedBy']

`player_stats`

You’ve now compiled data from batting_df, fielding_df, awards_df, allstar_df, and hof_df into the player_stats dictionary. You have a bit more work to do with the appearances_df DataFrame, but now is a good time to convert the player_stats dictionary into a DataFrame.

Use the pandas from_dict() method to convert the dictionary to a DataFrame called stats_df:

# Convert `player_stats` into a DataFramestats_df = pd.DataFrame.from_dict(player_stats, orient='index')

The stats_df DataFrame is using each player’s unique player ID as the index. Add a column to stats_df called playerID derived from the index. Then join stats_df with master_df using an inner join.

Remember that an inner join selects all rows from both tables as long as there is a match between the columns. In this case, you use an inner join because you want to match the information of stats_df with the master_df data: you want to keep on working with the rows that are common to both DataFrames.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxuaG9mX2RmID0gcGQucmVhZF9jc3YoJ2h0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL0hhbGxPZkZhbWUuY3N2JywgdXNlY29scz1bJ3BsYXllcklEJywneWVhcmlkJywndm90ZWRCeScsJ25lZWRlZF9ub3RlJywnaW5kdWN0ZWQnLCdjYXRlZ29yeSddKVxubWFzdGVyX2RmID0gcGQucmVhZF9jc3YoJ2h0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL01hc3Rlci5jc3YnLCB1c2Vjb2xzPVsncGxheWVySUQnLCduYW1lRmlyc3QnLCduYW1lTGFzdCcsJ2JhdHMnLCd0aHJvd3MnLCdkZWJ1dCcsJ2ZpbmFsR2FtZSddKVxuc3RhdHNfZGYgPSBwZC5yZWFkX2NzdihcImh0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL3BsYXllclN0YXRzLmNzdlwiLCBuYW1lcyA9WycnLCAnRycsICdBQicsICdSJywgJ0gnLCAnMkInLCAnM0InLCAnSFInLCAnUkJJJywgJ1NCJywgJ0JCJywgJ1NPJywgJ0lCQicsICdIQlAnLCAnU0gnLCAnU0YnLCAnWWVhcnNfUGxheWVkJywgJ0dmJywgJ0dTZicsICdQT2YnLCAnQWYnLCAnRWYnLCAnRFBmJywgJ0hvRicsICd2b3RlZEJ5JywgJ01vc3QgVmFsdWFibGUgUGxheWVyJywgJ0FTX2dhbWVzJywgJ0dvbGQgR2xvdmUnLCAnUm9va2llIG9mIHRoZSBZZWFyJywgJ1dvcmxkIFNlcmllcyBNVlAnLCAnU2lsdmVyIFNsdWdnZXInLCAncGxheWVySUQnXSwgc2tpcHJvd3M9MSwgaW5kZXhfY29sPTApIiwic2FtcGxlIjoiIyBBZGQgYSBjb2x1bW4gZm9yIHBsYXllcklEIGZyb20gdGhlIGBzdGF0c19kZmAgaW5kZXhcbnN0YXRzX2RmWydwbGF5ZXJJRCddID0gc3RhdHNfZGYuX19fX19cblxuIyBKb2luIGBzdGF0c19kZmAgYW5kIGBtYXN0ZXJfZGZgXG5tYXN0ZXJfZGYgPSBtYXN0ZXJfZGYuam9pbihfX19fX19fXyxvbj0ncGxheWVySUQnLGhvdz0naW5uZXInLCByc3VmZml4PSdtc3RyJylcblxuIyBJbnNwZWN0IGZpcnN0IHJvd3Mgb2YgYG1hc3Rlcl9kZmBcbm1hc3Rlcl9kZi5fX19fX18iLCJzb2x1dGlvbiI6IiMgQWRkIGEgY29sdW1uIGZvciBwbGF5ZXJJRCBmcm9tIHRoZSBgc3RhdHNfZGZgIGluZGV4XG5zdGF0c19kZlsncGxheWVySUQnXSA9IHN0YXRzX2RmLmluZGV4XG5cbiMgSm9pbiBgc3RhdHNfZGZgIGFuZCBgbWFzdGVyX2RmYFxubWFzdGVyX2RmID0gbWFzdGVyX2RmLmpvaW4oc3RhdHNfZGYsb249J3BsYXllcklEJyxob3c9J2lubmVyJywgcnN1ZmZpeD0nbXN0cicpXG5cbiMgSW5zcGVjdCBmaXJzdCByb3dzIG9mIGBtYXN0ZXJfZGZgXG5tYXN0ZXJfZGYuaGVhZCgpIiwic2N0IjoiRXgoKS50ZXN0X29iamVjdChcInN0YXRzX2RmXCIpXG5FeCgpLnRlc3Rfb2JqZWN0KFwibWFzdGVyX2RmXCIpXG5FeCgpLnRlc3RfZnVuY3Rpb24oXCJtYXN0ZXJfZGYuaGVhZFwiKVxuc3VjY2Vzc19tc2coXCJBd2Vzb21lIVwiKSJ9

`appearances_df`

The last DataFrame that you loaded in and need to look at before you can start creating new features for your data is appearances_df. This DataFrame contains information on how many appearances each player had at each position for each year.

Print out the first few rows using the head() method:

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxuYXBwZWFyYW5jZXNfZGYgPSBwZC5yZWFkX2NzdignaHR0cHM6Ly9zMy5hbWF6b25hd3MuY29tL2Fzc2V0cy5kYXRhY2FtcC5jb20vYmxvZ19hc3NldHMvTUxCK0RhdGEvQXBwZWFyYW5jZXMuY3N2JykiLCJzYW1wbGUiOiJwcmludChhcHBlYXJhbmNlc19kZi5fX19fX18pIiwic29sdXRpb24iOiJwcmludChhcHBlYXJhbmNlc19kZi5oZWFkKCkpIiwic2N0IjoiRXgoKS50ZXN0X2Z1bmN0aW9uKFwicHJpbnRcIilcbnN1Y2Nlc3NfbXNnKFwiR29vZCBqb2IhXCIpIn0=

Tip: use the IPython Console to inspect your data with other functions such as info(), tail(), the attributes columns and index, … You’ll see that the appearances_df has 21 columns, which in some cases are pretty straightforward (think of the ID columns that you already saw in other DataFrames), but in other cases, you see that they have somewhat cryptic names, such as G_3b, G_dh, and so on.

Now is a good time to take a look at the information that the the README page gives you:

G_all Total games played
GS Games started
G_batting Games in which player batted
G_defense Games in which player appeared on defense
G_p Games as pitcher
G_c Games as catcher
G_1b Games as firstbaseman
G_2b Games as secondbaseman
G_3b Games as thirdbaseman
G_ss Games as shortstop
G_lf Games as leftfielder
G_cf Games as centerfielder
G_rf Games as right fielder
G_of Games as outfielder
G_dh Games as designated hitter
G_ph Games as pinch hitter
G_pr Games as pinch runner

In an instant, you see that there is a lot of information in appearances_df that needs to be extracted. You also see that you need to aggregate each players number of appearances to find the total number of career appearances at each position.

As you may recall from the first part of this tutorial, as MLB progressed, different eras emerged where the amount of runs per game increased or decreased significantly. This means that when a player played has a large influence on that player’s career statistics. The Hall of Fame (HoF) voters take this into account when voting players in, so your model needs that information too.

To gather this information, create a dictionary called pos_dict. Loop through appearances_df and add a dictionary for each player as you did above with the player_stats dictionary. Aggregate each player’s appearances at each position for each season they played using the position as a key and the appearances count as the value. You’ll also need to aggregate the number of games each player played in each era using the era as a key and the games played count as the value.

# Initialize a dictionarypos_dict = {}# Iterate through `appearances_df`# Add a count for the number of appearances for each player at each position# Also add a count for the number of games played for each player in each era.for i, row in appearances_df.iterrows():    ID = row['playerID']    year = row['yearID']    if ID in pos_dict:        pos_dict[ID]['G_all'] = pos_dict[ID]['G_all'] + row['G_all']        pos_dict[ID]['G_p'] = pos_dict[ID]['G_p'] + row['G_p']        pos_dict[ID]['G_c'] = pos_dict[ID]['G_c'] + row['G_c']        pos_dict[ID]['G_1b'] = pos_dict[ID]['G_1b'] + row['G_1b']        pos_dict[ID]['G_2b'] = pos_dict[ID]['G_2b'] + row['G_2b']        pos_dict[ID]['G_3b'] = pos_dict[ID]['G_3b'] + row['G_3b']        pos_dict[ID]['G_ss'] = pos_dict[ID]['G_ss'] + row['G_ss']        pos_dict[ID]['G_lf'] = pos_dict[ID]['G_lf'] + row['G_lf']        pos_dict[ID]['G_cf'] = pos_dict[ID]['G_cf'] + row['G_cf']        pos_dict[ID]['G_rf'] = pos_dict[ID]['G_rf'] + row['G_rf']        pos_dict[ID]['G_of'] = pos_dict[ID]['G_of'] + row['G_of']        pos_dict[ID]['G_dh'] = pos_dict[ID]['G_dh'] + row['G_dh']        if year < 1920:            pos_dict[ID]['pre1920'] = pos_dict[ID]['pre1920'] + row['G_all']        elif year >= 1920 and year <= 1941:            pos_dict[ID]['1920-41'] = pos_dict[ID]['1920-41'] + row['G_all']        elif year >= 1942 and year <= 1945:            pos_dict[ID]['1942-45'] = pos_dict[ID]['1942-45'] + row['G_all']        elif year >= 1946 and year <= 1962:            pos_dict[ID]['1946-62'] = pos_dict[ID]['1946-62'] + row['G_all']        elif year >= 1963 and year <= 1976:            pos_dict[ID]['1963-76'] = pos_dict[ID]['1963-76'] + row['G_all']        elif year >= 1977 and year <= 1992:            pos_dict[ID]['1977-92'] = pos_dict[ID]['1977-92'] + row['G_all']        elif year >= 1993 and year <= 2009:            pos_dict[ID]['1993-2009'] = pos_dict[ID]['1993-2009'] + row['G_all']        elif year > 2009:            pos_dict[ID]['post2009'] = pos_dict[ID]['post2009'] + row['G_all']    else:        pos_dict[ID] = {}        pos_dict[ID]['G_all'] = row['G_all']        pos_dict[ID]['G_p'] = row['G_p']        pos_dict[ID]['G_c'] = row['G_c']        pos_dict[ID]['G_1b'] = row['G_1b']        pos_dict[ID]['G_2b'] = row['G_2b']        pos_dict[ID]['G_3b'] = row['G_3b']        pos_dict[ID]['G_ss'] = row['G_ss']        pos_dict[ID]['G_lf'] = row['G_lf']        pos_dict[ID]['G_cf'] = row['G_cf']        pos_dict[ID]['G_rf'] = row['G_rf']        pos_dict[ID]['G_of'] = row['G_of']        pos_dict[ID]['G_dh'] = row['G_dh']        pos_dict[ID]['pre1920'] = 0        pos_dict[ID]['1920-41'] = 0        pos_dict[ID]['1942-45'] = 0        pos_dict[ID]['1946-62'] = 0        pos_dict[ID]['1963-76'] = 0        pos_dict[ID]['1977-92'] = 0        pos_dict[ID]['1993-2009'] = 0        pos_dict[ID]['post2009'] = 0        if year < 1920:            pos_dict[ID]['pre1920'] = row['G_all']        elif year >= 1920 and year <= 1941:            pos_dict[ID]['1920-41'] = row['G_all']        elif year >= 1942 and year <= 1945:            pos_dict[ID]['1942-45'] = row['G_all']        elif year >= 1946 and year <= 1962:            pos_dict[ID]['1946-62'] = row['G_all']        elif year >= 1963 and year <= 1976:            pos_dict[ID]['1963-76'] = row['G_all']        elif year >= 1977 and year <= 1992:            pos_dict[ID]['1977-92'] = row['G_all']        elif year >= 1993 and year <= 2009:            pos_dict[ID]['1993-2009'] = row['G_all']        elif year > 2009:            pos_dict[ID]['post2009'] = row['G_all']

Now that you’re dictionary is complete, you can convert pos_dict into a DataFrame with the help of the from_dict() function:

# Convert the `pos_dict` to a DataFramepos_df = pd.DataFrame.from_dict(pos_dict, orient='index')

Also, print the columns and inspect the data some further:

Next you want to determine the percentage of times each player played at each position and within each era.

First, create a list called pos_col_list from the columns of pos_df and remove the string ‘G_all’. Then create new columns in pos_df for the percentage each player played at each position and within each era by looping through pos_col_list and dividing the games played at each position or era by the total games played by that player. Finally, print out the first few rows of pos_df:

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxucG9zX2RmID0gcGQucmVhZF9jc3YoXCJodHRwczovL3MzLmFtYXpvbmF3cy5jb20vYXNzZXRzLmRhdGFjYW1wLmNvbS9ibG9nX2Fzc2V0cy9NTEIrRGF0YS9Qb3NpdGlvbkRmLmNzdlwiLG5hbWVzPVsnJywgJ0dfYWxsJywgJ0dfcCcsICdHX2MnLCAnR18xYicsICdHXzJiJywgJ0dfM2InLCAnR19zcycsICdHX2xmJywgJ0dfY2YnLCAnR19yZicsICdHX29mJywgJ0dfZGgnLCAncHJlMTkyMCcsICcxOTIwLTQxJywgJzE5NDItNDUnLCcxOTQ2LTYyJywgJzE5NjMtNzYnLCAnMTk3Ny05MicsICcxOTkzLTIwMDknLCAncG9zdDIwMDknXSxza2lwcm93cz0xLCBpbmRleF9jb2w9MCkiLCJzYW1wbGUiOiIjIENyZWF0ZSBhIGxpc3QgZnJvbSB0aGUgY29sdW1ucyBvZiBgcG9zX2RmYFxucG9zX2NvbF9saXN0ID0gcG9zX2RmLmNvbHVtbnMuX19fX19fX19cblxuIyBSZW1vdmUgdGhlIHN0cmluZyAnR19hbGwnXG5wb3NfY29sX2xpc3QucmVtb3ZlKCdHX2FsbCcpXG5cbiMgTG9vcCB0aHJvdWdoIHRoZSBsaXN0IGFuZCBkaXZpZGUgZWFjaCBjb2x1bW4gYnkgdGhlIHBsYXllcnMgdG90YWwgZ2FtZXMgcGxheWVkXG5mb3IgY29sIGluIHBvc19jb2xfbGlzdDpcbiAgICBjb2x1bW4gPSBjb2wgKyAnX3BlcmNlbnQnXG4gICAgcG9zX2RmW2NvbHVtbl0gPSBwb3NfZGZbY29sXSAvIHBvc19kZlsnR19hbGwnXVxuXG4jIFByaW50IG91dCB0aGUgZmlyc3Qgcm93cyBvZiBgcG9zX2RmYCAgICBcbnByaW50KHBvc19kZi5fX19fX19fKSIsInNvbHV0aW9uIjoiIyBDcmVhdGUgYSBsaXN0IGZyb20gdGhlIGNvbHVtbnMgb2YgYHBvc19kZmBcbnBvc19jb2xfbGlzdCA9IHBvc19kZi5jb2x1bW5zLnRvbGlzdCgpXG5cbiMgUmVtb3ZlIHRoZSBzdHJpbmcgJ0dfYWxsJ1xucG9zX2NvbF9saXN0LnJlbW92ZSgnR19hbGwnKVxuXG4jIExvb3AgdGhyb3VnaCB0aGUgbGlzdCBhbmQgZGl2aWRlIGVhY2ggY29sdW1uIGJ5IHRoZSBwbGF5ZXJzIHRvdGFsIGdhbWVzIHBsYXllZFxuZm9yIGNvbCBpbiBwb3NfY29sX2xpc3Q6XG4gICAgY29sdW1uID0gY29sICsgJ19wZXJjZW50J1xuICAgIHBvc19kZltjb2x1bW5dID0gcG9zX2RmW2NvbF0gLyBwb3NfZGZbJ0dfYWxsJ11cblxuIyBQcmludCBvdXQgdGhlIGZpcnN0IHJvd3Mgb2YgYHBvc19kZmAgICAgXG5wcmludChwb3NfZGYuaGVhZCgpKSIsInNjdCI6IkV4KCkudGVzdF9vYmplY3QoXCJwb3NfY29sX2xpc3RcIilcbkV4KCkudGVzdF9mdW5jdGlvbihcInByaW50XCIpXG5zdWNjZXNzX21zZyhcIk5vdyB5b3UgY2FuIHRha2UgYSBsb29rIGF0IHRoZSBwZXJjZW50YWdlIG9mIHRpbWVzIGVhY2ggcGxheWVyIHBsYXllZCBhdCBlYWNoIHBvc2l0aW9uIGFuZCB3aXRoaW4gZWFjaCBlcmEhXCIpIn0=

As mentioned earlier, this project is focused on infielders and outfielders since each position is judged differently when determining HoF worthiness. Infielders and outfielders are judged similarly, while pitchers and catchers are judged based on much different playing statistics predominately based on defense. This is beyond the scope of this project as it would require much more data cleaning and feature engineering.

Since many players played at multiple different positions in the earlier years of MLB, eliminate the pitchers and catchers by filtering out players who played more than 10% of their games at either of those positions.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxucG9zX2RmID0gcGQucmVhZF9jc3YoXCJodHRwczovL3MzLmFtYXpvbmF3cy5jb20vYXNzZXRzLmRhdGFjYW1wLmNvbS9ibG9nX2Fzc2V0cy9NTEIrRGF0YS9Qb3NpdGlvbkRmLmNzdlwiLG5hbWVzPVsnJywgJ0dfYWxsJywgJ0dfcCcsICdHX2MnLCAnR18xYicsICdHXzJiJywgJ0dfM2InLCAnR19zcycsICdHX2xmJywgJ0dfY2YnLCAnR19yZicsICdHX29mJywgJ0dfZGgnLCAncHJlMTkyMCcsICcxOTIwLTQxJywgJzE5NDItNDUnLCcxOTQ2LTYyJywgJzE5NjMtNzYnLCAnMTk3Ny05MicsICcxOTkzLTIwMDknLCAncG9zdDIwMDknXSxza2lwcm93cz0xLCBpbmRleF9jb2w9MClcbnBvc19jb2xfbGlzdCA9IHBvc19kZi5jb2x1bW5zLnRvbGlzdCgpXG5wb3NfY29sX2xpc3QucmVtb3ZlKCdHX2FsbCcpXG5mb3IgY29sIGluIHBvc19jb2xfbGlzdDpcbiAgICBjb2x1bW4gPSBjb2wgKyAnX3BlcmNlbnQnXG4gICAgcG9zX2RmW2NvbHVtbl0gPSBwb3NfZGZbY29sXSAvIHBvc19kZlsnR19hbGwnXSIsInNhbXBsZSI6IiMgRmlsdGVyIGBwb3NfZGZgIHRvIGVsaW1pbmF0ZSBwbGF5ZXJzIHdobyBwbGF5ZWQgMTAlIG9yIG1vcmUgb2YgdGhlaXIgZ2FtZXMgYXMgUGl0Y2hlcnMgb3IgQ2F0Y2hlcnNcbnBvc19kZiA9IHBvc19kZlsoX19fX19fWydHX3BfcGVyY2VudCddIDwgMC4xKSAmIChwb3NfZGZbJ0dfY19wZXJjZW50J10gPCAwLjEpXVxuXG4jIEdldCBpbmZvIG9uIGBwb3NfZGZgXG5wb3NfZGYuX19fX19fIiwic29sdXRpb24iOiIjIEZpbHRlciBgcG9zX2RmYCB0byBlbGltaW5hdGUgcGxheWVycyB3aG8gcGxheWVkIDEwJSBvciBtb3JlIG9mIHRoZWlyIGdhbWVzIGFzIFBpdGNoZXJzIG9yIENhdGNoZXJzXG5wb3NfZGYgPSBwb3NfZGZbKHBvc19kZlsnR19wX3BlcmNlbnQnXSA8IDAuMSkgJiAocG9zX2RmWydHX2NfcGVyY2VudCddIDwgMC4xKV1cblxuIyBHZXQgaW5mbyBvbiBgcG9zX2RmYFxucG9zX2RmLmluZm8oKSIsInNjdCI6IkV4KCkudGVzdF9vYmplY3QoXCJwb3NfZGZcIilcbkV4KCkudGVzdF9mdW5jdGlvbihcInBvc19kZi5pbmZvXCIpXG5zdWNjZXNzX21zZyhcIkdyZWF0IGpvYiEgWW91IGhhdmUgc3VjY2Vzc2Z1bGx5IGZpbHRlcmVkIG91dCB0aGUgIHBsYXllcnMgd2hvIHBsYXllZCBsZXNzIHRoYW4gMTAlIG9mIHRoZWlyIGdhbWVzIGF0IHRoZSBjYXRjaGVycyBvciBwaXRjaGVycyBwb3NpdGlvbnMuIEhvd2V2ZXIsIHlvdXIgd29yayBkb2Vzbid0IHN0b3AgdGhlcmUuIFlvdSBuZWVkIHRvIGluY2x1ZGUgdGhpcyBpbmZvcm1hdGlvbiBhbHNvIGluIHRoZSBgbWFzdGVyX2RmYC4uLlwiKSJ9

`master_df`

Remember that you performed an inner join on the master_df and the stats_df, composed of information gathered from batting_df, fielding_df, awards_df, allstar_df and hof_df, to get a more uniform data set of your players’ statistics and the player master data, which was composed of player names, date of birth and biographical information.

Now, you want to join the uniform master_df with pos_df; Be careful! You need to use a right join here because you only want to keep players who are in pos_df:

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxubWFzdGVyX2RmID0gcGQucmVhZF9jc3YoJ2h0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL01hc3Rlci5jc3YnLCB1c2Vjb2xzPVsncGxheWVySUQnLCduYW1lRmlyc3QnLCduYW1lTGFzdCcsJ2JhdHMnLCd0aHJvd3MnLCdkZWJ1dCcsJ2ZpbmFsR2FtZSddKVxuc3RhdHNfZGYgPSBwZC5yZWFkX2NzdihcImh0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL3BsYXllclN0YXRzLmNzdlwiLCBuYW1lcyA9WycnLCAnRycsICdBQicsICdSJywgJ0gnLCAnMkInLCAnM0InLCAnSFInLCAnUkJJJywgJ1NCJywgJ0JCJywgJ1NPJywgJ0lCQicsICdIQlAnLCAnU0gnLCAnU0YnLCAnWWVhcnNfUGxheWVkJywgJ0dmJywgJ0dTZicsICdQT2YnLCAnQWYnLCAnRWYnLCAnRFBmJywgJ0hvRicsICd2b3RlZEJ5JywgJ01vc3QgVmFsdWFibGUgUGxheWVyJywgJ0FTX2dhbWVzJywgJ0dvbGQgR2xvdmUnLCAnUm9va2llIG9mIHRoZSBZZWFyJywgJ1dvcmxkIFNlcmllcyBNVlAnLCAnU2lsdmVyIFNsdWdnZXInLCAncGxheWVySUQnXSwgc2tpcHJvd3M9MSwgaW5kZXhfY29sPTApXG5zdGF0c19kZlsncGxheWVySUQnXSA9IHN0YXRzX2RmLmluZGV4XG5tYXN0ZXJfZGYgPSBtYXN0ZXJfZGYuam9pbihzdGF0c19kZixvbj0ncGxheWVySUQnLGhvdz0naW5uZXInLCByc3VmZml4PSdtc3RyJylcbnBvc19kZiA9IHBkLnJlYWRfY3N2KFwiaHR0cHM6Ly9zMy5hbWF6b25hd3MuY29tL2Fzc2V0cy5kYXRhY2FtcC5jb20vYmxvZ19hc3NldHMvTUxCK0RhdGEvUG9zaXRpb25EZi5jc3ZcIixuYW1lcz1bJycsICdHX2FsbCcsICdHX3AnLCAnR19jJywgJ0dfMWInLCAnR18yYicsICdHXzNiJywgJ0dfc3MnLCAnR19sZicsICdHX2NmJywgJ0dfcmYnLCAnR19vZicsICdHX2RoJywgJ3ByZTE5MjAnLCAnMTkyMC00MScsICcxOTQyLTQ1JywnMTk0Ni02MicsICcxOTYzLTc2JywgJzE5NzctOTInLCAnMTk5My0yMDA5JywgJ3Bvc3QyMDA5J10sc2tpcHJvd3M9MSwgaW5kZXhfY29sPTApXG5wb3NfY29sX2xpc3QgPSBwb3NfZGYuY29sdW1ucy50b2xpc3QoKVxucG9zX2NvbF9saXN0LnJlbW92ZSgnR19hbGwnKVxuZm9yIGNvbCBpbiBwb3NfY29sX2xpc3Q6XG4gICAgY29sdW1uID0gY29sICsgJ19wZXJjZW50J1xuICAgIHBvc19kZltjb2x1bW5dID0gcG9zX2RmW2NvbF0gLyBwb3NfZGZbJ0dfYWxsJ11cbnBvc19kZiA9IHBvc19kZlsocG9zX2RmWydHX3BfcGVyY2VudCddIDwgMC4xKSAmIChwb3NfZGZbJ0dfY19wZXJjZW50J10gPCAwLjEpXSIsInNhbXBsZSI6IiMgSm9pbiBgcG9zX2RmYCBhbmQgYG1hc3Rlcl9kZmBcbm1hc3Rlcl9kZiA9IG1hc3Rlcl9kZi5qb2luKF9fX19fXyxvbj0ncGxheWVySUQnLGhvdz0ncmlnaHQnKVxuXG4jIFByaW50IG91dCB0aGUgZmlyc3Qgcm93cyBvZiBgbWFzdGVyX2RmYFxucHJpbnQobWFzdGVyX2RmLl9fX19fXykiLCJzb2x1dGlvbiI6IiMgSm9pbiBgcG9zX2RmYCBhbmQgYG1hc3Rlcl9kZmBcbm1hc3Rlcl9kZiA9IG1hc3Rlcl9kZi5qb2luKHBvc19kZixvbj0ncGxheWVySUQnLGhvdz0ncmlnaHQnKVxuXG4jIFByaW50IG91dCB0aGUgZmlyc3Qgcm93cyBvZiBgbWFzdGVyX2RmYFxucHJpbnQobWFzdGVyX2RmLmhlYWQoKSkiLCJzY3QiOiJFeCgpLnRlc3Rfb2JqZWN0KFwibWFzdGVyX2RmXCIpXG5FeCgpLnRlc3RfZnVuY3Rpb24oXCJwcmludFwiKVxuc3VjY2Vzc19tc2coXCJOb3cgeW91IGNhbiBiZSBzdXJlIHRoYXQgYG1hc3Rlcl9kZmAgb25seSBpbmNsdWRlcyBwbGF5ZXJzIHdobyBwbGF5ZWQgbW9yZSB0aGFuIDEwJSBvZiB0aGVpciBnYW1lcyBhdCBlaXRoZXIgdGhlIHBpdGNoZXIgb3IgY2F0Y2hlciBwb3NpdGlvbnMhXCIpIn0=

Now filter master_df to only include players who were voted into the Hall of Fame or didn’t make it at all.

Some players make it into the Hall by selection from the Veterans Committee, or by a specially appointed committee. These players are typically selected for reasons other than purely their statistics which your model may find difficult to quantify, so it’s best to leave them out of the data set.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxubWFzdGVyX2RmPXBkLnJlYWRfY3N2KFwiaHR0cHM6Ly9zMy5hbWF6b25hd3MuY29tL2Fzc2V0cy5kYXRhY2FtcC5jb20vYmxvZ19hc3NldHMvTUxCK0RhdGEvbWFzdGVycG9zLmNzdlwiLCBcbiAgICAgICAgICAgICAgICAgICAgICBuYW1lcz1bJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdiYXRzJywgJ3Rocm93cycsXG4gICAgICAgJ2RlYnV0JywgJ2ZpbmFsR2FtZScsICdHJywgJ0FCJywgJ1InLCAnSCcsICcyQicsICczQicsICdIUicsICdSQkknLFxuICAgICAgICdTQicsICdCQicsICdTTycsICdJQkInLCAnSEJQJywgJ1NIJywgJ1NGJywgJ1llYXJzX1BsYXllZCcsICdHZicsICdHU2YnLFxuICAgICAgICdQT2YnLCAnQWYnLCAnRWYnLCAnRFBmJywgJ0hvRicsICd2b3RlZEJ5JywgJ01vc3QgVmFsdWFibGUgUGxheWVyJyxcbiAgICAgICAnQVNfZ2FtZXMnLCAnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnV29ybGQgU2VyaWVzIE1WUCcsXG4gICAgICAgJ1NpbHZlciBTbHVnZ2VyJywgJ3BsYXllcklEbXN0cicsICdHX2FsbCcsICdHX3AnLCAnR19jJywgJ0dfMWInLCAnR18yYicsXG4gICAgICAgJ0dfM2InLCAnR19zcycsICdHX2xmJywgJ0dfY2YnLCAnR19yZicsICdHX29mJywgJ0dfZGgnLCAncHJlMTkyMCcsXG4gICAgICAgJzE5MjAtNDEnLCAnMTk0Mi00NScsICcxOTQ2LTYyJywgJzE5NjMtNzYnLCAnMTk3Ny05MicsICcxOTkzLTIwMDknLFxuICAgICAgICdwb3N0MjAwOScsICdHX3BfcGVyY2VudCcsICdHX2NfcGVyY2VudCcsICdHXzFiX3BlcmNlbnQnLFxuICAgICAgICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywgJ0dfc3NfcGVyY2VudCcsICdHX2xmX3BlcmNlbnQnLFxuICAgICAgICdHX2NmX3BlcmNlbnQnLCAnR19yZl9wZXJjZW50JywgJ0dfb2ZfcGVyY2VudCcsICdHX2RoX3BlcmNlbnQnLFxuICAgICAgICdwcmUxOTIwX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsXG4gICAgICAgJzE5NDYtNjJfcGVyY2VudCcsICcxOTYzLTc2X3BlcmNlbnQnLCAnMTk3Ny05Ml9wZXJjZW50JyxcbiAgICAgICAnMTk5My0yMDA5X3BlcmNlbnQnLCAncG9zdDIwMDlfcGVyY2VudCddLCBza2lwcm93cz0xLCBpbmRleF9jb2w9MCkiLCJzYW1wbGUiOiIjIFJlcGxhY2UgTkEgdmFsdWVzIHdpdGggYE5vbmVgXG5tYXN0ZXJfZGZbJ3ZvdGVkQnknXSA9IG1hc3Rlcl9kZlsndm90ZWRCeSddLmZpbGxuYSgnTm9OZScpXG5cbiMgRmlsdGVyIGBtYXN0ZXJfZGZgIHRvIGluY2x1ZGUgb25seSBwbGF5ZXJzIHdobyB3ZXJlIHZvdGVkIGludG8gdGhlIEhhbGwgb2YgRmFtZSBvciBQbGF5ZXJzIHdobyBkaWQgbm90IG1ha2UgaXQgYXQgYWxsXG5tYXN0ZXJfZGYgPSBtYXN0ZXJfZGZbKG1hc3Rlcl9kZlsnX19fX19fXyddID09ICdOb25lJykgfCAobWFzdGVyX2RmWyd2b3RlZEJ5J10gPT0gJ0JCV0FBJykgfCAobWFzdGVyX2RmWyd2b3RlZEJ5J10gPT0gJ1J1biBPZmYnKV1cblxuIyBJbnNwZWN0IGBtYXN0ZXJfZGZgXG5tYXN0ZXJfZGYuaW5mbygpIiwic29sdXRpb24iOiIjIFJlcGxhY2UgTkEgdmFsdWVzIHdpdGggYE5vbmVgXG5tYXN0ZXJfZGZbJ3ZvdGVkQnknXSA9IG1hc3Rlcl9kZlsndm90ZWRCeSddLmZpbGxuYSgnTm9uZScpXG5cbiMgRmlsdGVyIGBtYXN0ZXJfZGZgIHRvIGluY2x1ZGUgb25seSBwbGF5ZXJzIHdobyB3ZXJlIHZvdGVkIGludG8gdGhlIEhhbGwgb2YgRmFtZSBvciBQbGF5ZXJzIHdobyBkaWQgbm90IG1ha2UgaXQgYXQgYWxsXG5tYXN0ZXJfZGYgPSBtYXN0ZXJfZGZbKG1hc3Rlcl9kZlsndm90ZWRCeSddID09ICdOb25lJykgfCAobWFzdGVyX2RmWyd2b3RlZEJ5J10gPT0gJ0JCV0FBJykgfCAobWFzdGVyX2RmWyd2b3RlZEJ5J10gPT0gJ1J1biBPZmYnKV1cblxuIyBJbnNwZWN0IGBtYXN0ZXJfZGZgXG5tYXN0ZXJfZGYuaW5mbygpIiwic2N0IjoiRXgoKS50ZXN0X29iamVjdChcIm1hc3Rlcl9kZlwiKVxuRXgoKS50ZXN0X2Z1bmN0aW9uKFwibWFzdGVyX2RmLmluZm9cIilcbnN1Y2Nlc3NfbXNnKFwiWW91IGhhdmUgbm93IHN1Y2Nlc3NmdWxseSBleGNsdWRlZCBwbGF5ZXJzIHdobyB3ZXJlIHNlbGVjdGVkIGJ5IHRoZSBWZXRlcmFucyBDb21taXR0ZWUgb3IgYnkgYSBzcGVjaWFsbHkgYXBwb2ludGVkIGNvbW1pdHRlZSFcIikifQ==

The bats and throws columns need to be converted to numeric: you can easily do this by creating a function to convert each R to a 1 and each L to a 0. Use the apply() method to create numeric columns called bats_R and throws_R:

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxubWFzdGVyX2RmPXBkLnJlYWRfY3N2KFwiaHR0cHM6Ly9zMy5hbWF6b25hd3MuY29tL2Fzc2V0cy5kYXRhY2FtcC5jb20vYmxvZ19hc3NldHMvTUxCK0RhdGEvbWFzdGVycG9zLmNzdlwiLCBcbiAgICAgICAgICAgICAgICAgICAgICBuYW1lcz1bJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdiYXRzJywgJ3Rocm93cycsXG4gICAgICAgJ2RlYnV0JywgJ2ZpbmFsR2FtZScsICdHJywgJ0FCJywgJ1InLCAnSCcsICcyQicsICczQicsICdIUicsICdSQkknLFxuICAgICAgICdTQicsICdCQicsICdTTycsICdJQkInLCAnSEJQJywgJ1NIJywgJ1NGJywgJ1llYXJzX1BsYXllZCcsICdHZicsICdHU2YnLFxuICAgICAgICdQT2YnLCAnQWYnLCAnRWYnLCAnRFBmJywgJ0hvRicsICd2b3RlZEJ5JywgJ01vc3QgVmFsdWFibGUgUGxheWVyJyxcbiAgICAgICAnQVNfZ2FtZXMnLCAnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnV29ybGQgU2VyaWVzIE1WUCcsXG4gICAgICAgJ1NpbHZlciBTbHVnZ2VyJywgJ3BsYXllcklEbXN0cicsICdHX2FsbCcsICdHX3AnLCAnR19jJywgJ0dfMWInLCAnR18yYicsXG4gICAgICAgJ0dfM2InLCAnR19zcycsICdHX2xmJywgJ0dfY2YnLCAnR19yZicsICdHX29mJywgJ0dfZGgnLCAncHJlMTkyMCcsXG4gICAgICAgJzE5MjAtNDEnLCAnMTk0Mi00NScsICcxOTQ2LTYyJywgJzE5NjMtNzYnLCAnMTk3Ny05MicsICcxOTkzLTIwMDknLFxuICAgICAgICdwb3N0MjAwOScsICdHX3BfcGVyY2VudCcsICdHX2NfcGVyY2VudCcsICdHXzFiX3BlcmNlbnQnLFxuICAgICAgICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywgJ0dfc3NfcGVyY2VudCcsICdHX2xmX3BlcmNlbnQnLFxuICAgICAgICdHX2NmX3BlcmNlbnQnLCAnR19yZl9wZXJjZW50JywgJ0dfb2ZfcGVyY2VudCcsICdHX2RoX3BlcmNlbnQnLFxuICAgICAgICdwcmUxOTIwX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsXG4gICAgICAgJzE5NDYtNjJfcGVyY2VudCcsICcxOTYzLTc2X3BlcmNlbnQnLCAnMTk3Ny05Ml9wZXJjZW50JyxcbiAgICAgICAnMTk5My0yMDA5X3BlcmNlbnQnLCAncG9zdDIwMDlfcGVyY2VudCddLCBza2lwcm93cz0xLCBpbmRleF9jb2w9MClcbm1hc3Rlcl9kZlsndm90ZWRCeSddID0gbWFzdGVyX2RmWyd2b3RlZEJ5J10uZmlsbG5hKCdOb25lJylcbm1hc3Rlcl9kZiA9IG1hc3Rlcl9kZlsobWFzdGVyX2RmWyd2b3RlZEJ5J10gPT0gJ05vbmUnKSB8IChtYXN0ZXJfZGZbJ3ZvdGVkQnknXSA9PSAnQkJXQUEnKSB8IChtYXN0ZXJfZGZbJ3ZvdGVkQnknXSA9PSAnUnVuIE9mZicpXSIsInNhbXBsZSI6IiMgQ3JlYXRlIGEgZnVuY3Rpb24gdG8gY29udmVydCB0aGUgYmF0cyBhbmQgdGhyb3dzIGNvbHVtcyB0byBudW1lcmljXG5kZWYgYmF0c190aHJvd3MoY29sKTpcbiAgICBpZiBjb2wgPT0gXCJSXCI6XG4gICAgICAgIHJldHVybiAxXG4gICAgZWxzZTpcbiAgICAgICAgcmV0dXJuIDBcblxuIyBVc2UgdGhlIGBhcHBseSgpYCBtZXRob2QgdG8gY3JlYXRlIG51bWVyaWMgY29sdW1ucyBmcm9tIHRoZSBiYXRzIGFuZCB0aHJvd3MgY29sdW1uc1xubWFzdGVyX2RmWydiYXRzX1InXSA9IG1hc3Rlcl9kZlsnYmF0cyddLmFwcGx5KF9fX19fX19fX19fKVxubWFzdGVyX2RmWyd0aHJvd3NfUiddID0gbWFzdGVyX2RmWyd0aHJvd3MnXS5hcHBseShiYXRzX3Rocm93cylcblxuIyBQcmludCBvdXQgdGhlIGZpcnN0IHJvd3Mgb2YgYG1hc3Rlcl9kZmBcbnByaW50KG1hc3Rlcl9kZi5oZWFkKCkpIiwic29sdXRpb24iOiIjIENyZWF0ZSBhIGZ1bmN0aW9uIHRvIGNvbnZlcnQgdGhlIGJhdHMgYW5kIHRocm93cyBjb2x1bXMgdG8gbnVtZXJpY1xuZGVmIGJhdHNfdGhyb3dzKGNvbCk6XG4gICAgaWYgY29sID09IFwiUlwiOlxuICAgICAgICByZXR1cm4gMVxuICAgIGVsc2U6XG4gICAgICAgIHJldHVybiAwXG5cbiMgVXNlIHRoZSBgYXBwbHkoKWAgbWV0aG9kIHRvIGNyZWF0ZSBudW1lcmljIGNvbHVtbnMgZnJvbSB0aGUgYmF0cyBhbmQgdGhyb3dzIGNvbHVtbnNcbm1hc3Rlcl9kZlsnYmF0c19SJ10gPSBtYXN0ZXJfZGZbJ2JhdHMnXS5hcHBseShiYXRzX3Rocm93cylcbm1hc3Rlcl9kZlsndGhyb3dzX1InXSA9IG1hc3Rlcl9kZlsndGhyb3dzJ10uYXBwbHkoYmF0c190aHJvd3MpXG5cbiMgUHJpbnQgb3V0IHRoZSBmaXJzdCByb3dzIG9mIGBtYXN0ZXJfZGZgXG5wcmludChtYXN0ZXJfZGYuaGVhZCgpKSIsInNjdCI6IkV4KCkuY2hlY2tfZnVuY3Rpb25fZGVmKFwiYmF0c190aHJvd3NcIilcbkV4KCkudGVzdF9vYmplY3QoXCJtYXN0ZXJfZGZcIilcbkV4KCkudGVzdF9mdW5jdGlvbihcInByaW50XCIpXG5zdWNjZXNzX21zZyhcIlRoZSBgYmF0c19SYCBhbmQgYHRocm93c19SYCBjb2x1bW5zIGhhdmUgc3VjY2Vzc2Z1bGx5IGJlZW4gY29udmVydGVkIHRvIG51bWVyaWMgY29sdW1ucyFcIikifQ==

The debut and finalGame columns are currently strings. You’ll need to parse out the years from these columns. First, import datetime. Next, convert the debut and finalGame columns to a datetime object using pd.to_datetime(). Then parse out the year using dt.strftime(‘%Y’) and convert to numeric with pd.to_numeric().

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxubWFzdGVyX2RmPXBkLnJlYWRfY3N2KFwiaHR0cHM6Ly9zMy5hbWF6b25hd3MuY29tL2Fzc2V0cy5kYXRhY2FtcC5jb20vYmxvZ19hc3NldHMvTUxCK0RhdGEvbWFzdGVycG9zLmNzdlwiLCBcbiAgICAgICAgICAgICAgICAgICAgICBuYW1lcz1bJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdiYXRzJywgJ3Rocm93cycsXG4gICAgICAgJ2RlYnV0JywgJ2ZpbmFsR2FtZScsICdHJywgJ0FCJywgJ1InLCAnSCcsICcyQicsICczQicsICdIUicsICdSQkknLFxuICAgICAgICdTQicsICdCQicsICdTTycsICdJQkInLCAnSEJQJywgJ1NIJywgJ1NGJywgJ1llYXJzX1BsYXllZCcsICdHZicsICdHU2YnLFxuICAgICAgICdQT2YnLCAnQWYnLCAnRWYnLCAnRFBmJywgJ0hvRicsICd2b3RlZEJ5JywgJ01vc3QgVmFsdWFibGUgUGxheWVyJyxcbiAgICAgICAnQVNfZ2FtZXMnLCAnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnV29ybGQgU2VyaWVzIE1WUCcsXG4gICAgICAgJ1NpbHZlciBTbHVnZ2VyJywgJ3BsYXllcklEbXN0cicsICdHX2FsbCcsICdHX3AnLCAnR19jJywgJ0dfMWInLCAnR18yYicsXG4gICAgICAgJ0dfM2InLCAnR19zcycsICdHX2xmJywgJ0dfY2YnLCAnR19yZicsICdHX29mJywgJ0dfZGgnLCAncHJlMTkyMCcsXG4gICAgICAgJzE5MjAtNDEnLCAnMTk0Mi00NScsICcxOTQ2LTYyJywgJzE5NjMtNzYnLCAnMTk3Ny05MicsICcxOTkzLTIwMDknLFxuICAgICAgICdwb3N0MjAwOScsICdHX3BfcGVyY2VudCcsICdHX2NfcGVyY2VudCcsICdHXzFiX3BlcmNlbnQnLFxuICAgICAgICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywgJ0dfc3NfcGVyY2VudCcsICdHX2xmX3BlcmNlbnQnLFxuICAgICAgICdHX2NmX3BlcmNlbnQnLCAnR19yZl9wZXJjZW50JywgJ0dfb2ZfcGVyY2VudCcsICdHX2RoX3BlcmNlbnQnLFxuICAgICAgICdwcmUxOTIwX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsXG4gICAgICAgJzE5NDYtNjJfcGVyY2VudCcsICcxOTYzLTc2X3BlcmNlbnQnLCAnMTk3Ny05Ml9wZXJjZW50JyxcbiAgICAgICAnMTk5My0yMDA5X3BlcmNlbnQnLCAncG9zdDIwMDlfcGVyY2VudCddLCBza2lwcm93cz0xLCBpbmRleF9jb2w9MClcbm1hc3Rlcl9kZlsndm90ZWRCeSddID0gbWFzdGVyX2RmWyd2b3RlZEJ5J10uZmlsbG5hKCdOb25lJylcbm1hc3Rlcl9kZiA9IG1hc3Rlcl9kZlsobWFzdGVyX2RmWyd2b3RlZEJ5J10gPT0gJ05vbmUnKSB8IChtYXN0ZXJfZGZbJ3ZvdGVkQnknXSA9PSAnQkJXQUEnKSB8IChtYXN0ZXJfZGZbJ3ZvdGVkQnknXSA9PSAnUnVuIE9mZicpXVxuZGVmIGJhdHNfdGhyb3dzKGNvbCk6XG4gICAgaWYgY29sID09IFwiUlwiOlxuICAgICAgICByZXR1cm4gMVxuICAgIGVsc2U6XG4gICAgICAgIHJldHVybiAwXG5cbm1hc3Rlcl9kZlsnYmF0c19SJ10gPSBtYXN0ZXJfZGZbJ2JhdHMnXS5hcHBseShiYXRzX3Rocm93cylcbm1hc3Rlcl9kZlsndGhyb3dzX1InXSA9IG1hc3Rlcl9kZlsndGhyb3dzJ10uYXBwbHkoYmF0c190aHJvd3MpIiwic2FtcGxlIjoiIyBJbXBvcnQgZGF0ZXRpbWUgXG5mcm9tIGRhdGV0aW1lIGltcG9ydCBkYXRldGltZVxuXG4jIENvbnZlcnQgdGhlIGBkZWJ1dGAgY29sdW1uIHRvIGRhdGV0aW1lXG5tYXN0ZXJfZGZbJ2RlYnV0J10gPSAgcGQuX19fX19fX19fX18obWFzdGVyX2RmWydkZWJ1dCddKVxuIyBDb252ZXJ0IHRoZSBgZmluYWxHYW1lYCBjb2x1bW4gdG8gZGF0ZXRpbWVcbm1hc3Rlcl9kZlsnZmluYWxHYW1lJ10gPSBwZC50b19kYXRldGltZShtYXN0ZXJfZGZbJ2ZpbmFsR2FtZSddKVxuXG4jIENyZWF0ZSBuZXcgY29sdW1ucyBmb3IgZGVidXRZZWFyIGFuZCBmaW5hbFllYXJcbm1hc3Rlcl9kZlsnZGVidXRZZWFyJ10gPSBwZC50b19udW1lcmljKG1hc3Rlcl9kZlsnZGVidXQnXS5kdC5zdHJmdGltZSgnJVknKSwgZXJyb3JzPSdjb2VyY2UnKVxubWFzdGVyX2RmWydmaW5hbFllYXInXSA9IF9fX19fX19fX19fX18obWFzdGVyX2RmWydmaW5hbEdhbWUnXS5kdC5zdHJmdGltZSgnJVknKSwgZXJyb3JzPSdjb2VyY2UnKVxuXG4jIFJldHVybiB0aGUgZmlyc3Qgcm93cyBvZiBgbWFzdGVyX2RmYFxucHJpbnQobWFzdGVyX2RmLmhlYWQoKSkiLCJzb2x1dGlvbiI6IiMgSW1wb3J0IGRhdGV0aW1lIFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcblxuIyBDb252ZXJ0IHRoZSBgZGVidXRgIGNvbHVtbiB0byBkYXRldGltZVxubWFzdGVyX2RmWydkZWJ1dCddID0gIHBkLnRvX2RhdGV0aW1lKG1hc3Rlcl9kZlsnZGVidXQnXSlcbiMgQ29udmVydCB0aGUgYGZpbmFsR2FtZWAgY29sdW1uIHRvIGRhdGV0aW1lXG5tYXN0ZXJfZGZbJ2ZpbmFsR2FtZSddID0gcGQudG9fZGF0ZXRpbWUobWFzdGVyX2RmWydmaW5hbEdhbWUnXSlcblxuIyBDcmVhdGUgbmV3IGNvbHVtbnMgZm9yIGRlYnV0WWVhciBhbmQgZmluYWxZZWFyXG5tYXN0ZXJfZGZbJ2RlYnV0WWVhciddID0gcGQudG9fbnVtZXJpYyhtYXN0ZXJfZGZbJ2RlYnV0J10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbm1hc3Rlcl9kZlsnZmluYWxZZWFyJ10gPSBwZC50b19udW1lcmljKG1hc3Rlcl9kZlsnZmluYWxHYW1lJ10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcblxuIyBSZXR1cm4gdGhlIGZpcnN0IHJvd3Mgb2YgYG1hc3Rlcl9kZmBcbnByaW50KG1hc3Rlcl9kZi5oZWFkKCkpIiwic2N0IjoiRXgoKS50ZXN0X2ltcG9ydChcImRhdGV0aW1lLmRhdGV0aW1lXCIpXG5FeCgpLnRlc3Rfb2JqZWN0KFwibWFzdGVyX2RmXCIpXG5FeCgpLnRlc3RfZnVuY3Rpb24oXCJwcmludFwiKVxuc3VjY2Vzc19tc2coXCJDb25ncmF0cywgeW91IGhhdmUgc3VjY2Vzc2Z1bGx5IHBhcnNlZCBvdXQgdGhlIHllYXJzIVwiKSJ9

There are currently some unnecessary columns in master_df. Use the drop() method on master_df and create a new DataFrame called df. Now is a good time to print the columns in df and display the count of null values for each column.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcbm1hc3Rlcl9kZj1wZC5yZWFkX2NzdihcImh0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL21hc3RlcnBvcy5jc3ZcIiwgXG4gICAgICAgICAgICAgICAgICAgICAgbmFtZXM9WydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnYmF0cycsICd0aHJvd3MnLFxuICAgICAgICdkZWJ1dCcsICdmaW5hbEdhbWUnLCAnRycsICdBQicsICdSJywgJ0gnLCAnMkInLCAnM0InLCAnSFInLCAnUkJJJyxcbiAgICAgICAnU0InLCAnQkInLCAnU08nLCAnSUJCJywgJ0hCUCcsICdTSCcsICdTRicsICdZZWFyc19QbGF5ZWQnLCAnR2YnLCAnR1NmJyxcbiAgICAgICAnUE9mJywgJ0FmJywgJ0VmJywgJ0RQZicsICdIb0YnLCAndm90ZWRCeScsICdNb3N0IFZhbHVhYmxlIFBsYXllcicsXG4gICAgICAgJ0FTX2dhbWVzJywgJ0dvbGQgR2xvdmUnLCAnUm9va2llIG9mIHRoZSBZZWFyJywgJ1dvcmxkIFNlcmllcyBNVlAnLFxuICAgICAgICdTaWx2ZXIgU2x1Z2dlcicsICdwbGF5ZXJJRG1zdHInLCAnR19hbGwnLCAnR19wJywgJ0dfYycsICdHXzFiJywgJ0dfMmInLFxuICAgICAgICdHXzNiJywgJ0dfc3MnLCAnR19sZicsICdHX2NmJywgJ0dfcmYnLCAnR19vZicsICdHX2RoJywgJ3ByZTE5MjAnLFxuICAgICAgICcxOTIwLTQxJywgJzE5NDItNDUnLCAnMTk0Ni02MicsICcxOTYzLTc2JywgJzE5NzctOTInLCAnMTk5My0yMDA5JyxcbiAgICAgICAncG9zdDIwMDknLCAnR19wX3BlcmNlbnQnLCAnR19jX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JyxcbiAgICAgICAnR18yYl9wZXJjZW50JywgJ0dfM2JfcGVyY2VudCcsICdHX3NzX3BlcmNlbnQnLCAnR19sZl9wZXJjZW50JyxcbiAgICAgICAnR19jZl9wZXJjZW50JywgJ0dfcmZfcGVyY2VudCcsICdHX29mX3BlcmNlbnQnLCAnR19kaF9wZXJjZW50JyxcbiAgICAgICAncHJlMTkyMF9wZXJjZW50JywgJzE5MjAtNDFfcGVyY2VudCcsICcxOTQyLTQ1X3BlcmNlbnQnLFxuICAgICAgICcxOTQ2LTYyX3BlcmNlbnQnLCAnMTk2My03Nl9wZXJjZW50JywgJzE5NzctOTJfcGVyY2VudCcsXG4gICAgICAgJzE5OTMtMjAwOV9wZXJjZW50JywgJ3Bvc3QyMDA5X3BlcmNlbnQnXSwgc2tpcHJvd3M9MSwgaW5kZXhfY29sPTApXG5tYXN0ZXJfZGZbJ3ZvdGVkQnknXSA9IG1hc3Rlcl9kZlsndm90ZWRCeSddLmZpbGxuYSgnTm9uZScpXG5tYXN0ZXJfZGYgPSBtYXN0ZXJfZGZbKG1hc3Rlcl9kZlsndm90ZWRCeSddID09ICdOb25lJykgfCAobWFzdGVyX2RmWyd2b3RlZEJ5J10gPT0gJ0JCV0FBJykgfCAobWFzdGVyX2RmWyd2b3RlZEJ5J10gPT0gJ1J1biBPZmYnKV1cbmRlZiBiYXRzX3Rocm93cyhjb2wpOlxuICAgIGlmIGNvbCA9PSBcIlJcIjpcbiAgICAgICAgcmV0dXJuIDFcbiAgICBlbHNlOlxuICAgICAgICByZXR1cm4gMFxuXG5tYXN0ZXJfZGZbJ2JhdHNfUiddID0gbWFzdGVyX2RmWydiYXRzJ10uYXBwbHkoYmF0c190aHJvd3MpXG5tYXN0ZXJfZGZbJ3Rocm93c19SJ10gPSBtYXN0ZXJfZGZbJ3Rocm93cyddLmFwcGx5KGJhdHNfdGhyb3dzKVxubWFzdGVyX2RmWydkZWJ1dCddID0gIHBkLnRvX2RhdGV0aW1lKG1hc3Rlcl9kZlsnZGVidXQnXSlcbm1hc3Rlcl9kZlsnZmluYWxHYW1lJ10gPSBwZC50b19kYXRldGltZShtYXN0ZXJfZGZbJ2ZpbmFsR2FtZSddKVxubWFzdGVyX2RmWydkZWJ1dFllYXInXSA9IHBkLnRvX251bWVyaWMobWFzdGVyX2RmWydkZWJ1dCddLmR0LnN0cmZ0aW1lKCclWScpLCBlcnJvcnM9J2NvZXJjZScpXG5tYXN0ZXJfZGZbJ2ZpbmFsWWVhciddID0gcGQudG9fbnVtZXJpYyhtYXN0ZXJfZGZbJ2ZpbmFsR2FtZSddLmR0LnN0cmZ0aW1lKCclWScpLCBlcnJvcnM9J2NvZXJjZScpIiwic2FtcGxlIjoiIyBFbGltaW5hdGluZyB1bm5lY2Vzc2FyeSBjb2x1bW5zXG5kZiA9IG1hc3Rlcl9kZi5fX19fKFsndm90ZWRCeScsICdJQkInLCAnYmF0cycsICd0aHJvd3MnLCAnR1NmJywgJ1BPZicsJ0dmJywgJ3BsYXllcklEbXN0ciddLCBheGlzPTEpXG5cbiMgUHJpbnQgYGRmYCBjb2x1bW5zIFxucHJpbnQoZGYuX19fX19fXylcblxuIyBQcmludCBhIGxpc3Qgb2YgbnVsbCB2YWx1ZXNcbnByaW50KGRmLmlzbnVsbCgpLnN1bShheGlzPTApLl9fX19fXykiLCJzb2x1dGlvbiI6IiMgRWxpbWluYXRpbmcgdW5uZWNlc3NhcnkgY29sdW1uc1xuZGYgPSBtYXN0ZXJfZGYuZHJvcChbJ3ZvdGVkQnknLCAnSUJCJywgJ2JhdHMnLCAndGhyb3dzJywgJ0dTZicsICdQT2YnLCdHZicsICdwbGF5ZXJJRG1zdHInXSwgYXhpcz0xKVxuXG4jIFByaW50IGBkZmAgY29sdW1ucyBcbnByaW50KGRmLmNvbHVtbnMpXG5cbiMgUHJpbnQgYSBsaXN0IG9mIG51bGwgdmFsdWVzXG5wcmludChkZi5pc251bGwoKS5zdW0oYXhpcz0wKS50b2xpc3QoKSkiLCJzY3QiOiJFeCgpLnRlc3Rfb2JqZWN0KFwiZGZcIilcbkV4KCkudGVzdF9mdW5jdGlvbihcInByaW50XCIsIGluZGV4PTEpXG5FeCgpLnRlc3RfZnVuY3Rpb24oXCJwcmludFwiLCBpbmRleD0yKVxuc3VjY2Vzc19tc2coXCJBd2Vzb21lIGpvYiFcIikifQ==

In the first part of this tutorial, you were dealing with team statistics and the null values were likely due to missing data. A team is never going to make it through an entire season without a double play, for example.

With players, it is much more likely that null values are zeros.

That’s why you’re going to create a list of the numeric columns and loop through the list, filling the null values with zeros using the fillna() method. Then use the dropna() method to eliminate any remaining null values.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcbmRmID0gcGQucmVhZF9jc3YoXCJodHRwczovL3MzLmFtYXpvbmF3cy5jb20vYXNzZXRzLmRhdGFjYW1wLmNvbS9ibG9nX2Fzc2V0cy9NTEIrRGF0YS9kZi1kcm9wcGVkLmNzdlwiLCBuYW1lcz1bJycsICdwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnZGVidXQnLCAnZmluYWxHYW1lJywgJ0cnLCAnQUInLFxuICAgICAgICdSJywgJ0gnLCAnMkInLCAnM0InLCAnSFInLCAnUkJJJywgJ1NCJywgJ0JCJywgJ1NPJywgJ0hCUCcsICdTSCcsICdTRicsXG4gICAgICAgJ1llYXJzX1BsYXllZCcsICdBZicsICdFZicsICdEUGYnLCAnSG9GJywgJ01vc3QgVmFsdWFibGUgUGxheWVyJyxcbiAgICAgICAnQVNfZ2FtZXMnLCAnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnV29ybGQgU2VyaWVzIE1WUCcsXG4gICAgICAgJ1NpbHZlciBTbHVnZ2VyJywgJ0dfYWxsJywgJ0dfcCcsICdHX2MnLCAnR18xYicsICdHXzJiJywgJ0dfM2InLCAnR19zcycsXG4gICAgICAgJ0dfbGYnLCAnR19jZicsICdHX3JmJywgJ0dfb2YnLCAnR19kaCcsICdwcmUxOTIwJywgJzE5MjAtNDEnLCAnMTk0Mi00NScsXG4gICAgICAgJzE5NDYtNjInLCAnMTk2My03NicsICcxOTc3LTkyJywgJzE5OTMtMjAwOScsICdwb3N0MjAwOScsICdHX3BfcGVyY2VudCcsXG4gICAgICAgJ0dfY19wZXJjZW50JywgJ0dfMWJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JyxcbiAgICAgICAnR19zc19wZXJjZW50JywgJ0dfbGZfcGVyY2VudCcsICdHX2NmX3BlcmNlbnQnLCAnR19yZl9wZXJjZW50JyxcbiAgICAgICAnR19vZl9wZXJjZW50JywgJ0dfZGhfcGVyY2VudCcsICdwcmUxOTIwX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JyxcbiAgICAgICAnMTk0Mi00NV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsICcxOTYzLTc2X3BlcmNlbnQnLFxuICAgICAgICcxOTc3LTkyX3BlcmNlbnQnLCAnMTk5My0yMDA5X3BlcmNlbnQnLCAncG9zdDIwMDlfcGVyY2VudCcsICdiYXRzX1InLFxuICAgICAgICd0aHJvd3NfUicsICdkZWJ1dFllYXInLCAnZmluYWxZZWFyJ10sIGhlYWRlcj0wLCBpbmRleF9jb2w9MClcbmRmWydkZWJ1dCddID0gIHBkLnRvX2RhdGV0aW1lKGRmWydkZWJ1dCddKVxuZGZbJ2ZpbmFsR2FtZSddID0gcGQudG9fZGF0ZXRpbWUoZGZbJ2ZpbmFsR2FtZSddKVxuZGZbJ2RlYnV0WWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZGVidXQnXS5kdC5zdHJmdGltZSgnJVknKSwgZXJyb3JzPSdjb2VyY2UnKVxuZGZbJ2ZpbmFsWWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZmluYWxHYW1lJ10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJykiLCJzYW1wbGUiOiIjIEZpbGwgbnVsbCB2YWx1ZXMgaW4gbnVtZXJpYyBjb2x1bW5zIHdpdGggMFxuZmlsbF9jb2xzID0gWydBU19nYW1lcycsICdTaWx2ZXIgU2x1Z2dlcicsICdSb29raWUgb2YgdGhlIFllYXInLCAnR29sZCBHbG92ZScsICdNb3N0IFZhbHVhYmxlIFBsYXllcicsICdIb0YnLCAnMTk3Ny05MicsICdwcmUxOTIwJywgJzE5NDItNDUnLCAnMTk0Ni02MicsICcxOTYzLTc2JywgJzE5MjAtNDEnLCAnMTk5My0yMDA5JywgJ0hCUCcsICdTQicsICdTRicsICdTSCcsICdSQkknLCAnU08nLCAnV29ybGQgU2VyaWVzIE1WUCcsICdHX2RoX3BlcmNlbnQnLCAnR19kaCcsICdBZicsICdEUGYnLCAnRWYnXVxuXG5mb3IgY29sIGluIGZpbGxfY29sczpcbiAgICBkZltjb2xdID0gZGZbY29sXS5maWxsbmEoMClcblxuIyBEcm9wIGFueSBhZGRpdGlvbmFsIHJvd3Mgd2l0aCBudWxsIHZhbHVlc1xuZGYgPSBkZi5fX19fX19fX1xuXG4jIENoZWNrIHRvIG1ha2Ugc3VyZSBudWxsIHZhbHVlcyBoYXZlIGJlZW4gcmVtb3ZlZFxucHJpbnQoZGYuaXNudWxsKCkuc3VtKGF4aXM9MCkudG9saXN0KCkpIiwic29sdXRpb24iOiIjIEZpbGwgbnVsbCB2YWx1ZXMgaW4gbnVtZXJpYyBjb2x1bW5zIHdpdGggMFxuZmlsbF9jb2xzID0gWydBU19nYW1lcycsICdTaWx2ZXIgU2x1Z2dlcicsICdSb29raWUgb2YgdGhlIFllYXInLCAnR29sZCBHbG92ZScsICdNb3N0IFZhbHVhYmxlIFBsYXllcicsICdIb0YnLCAnMTk3Ny05MicsICdwcmUxOTIwJywgJzE5NDItNDUnLCAnMTk0Ni02MicsICcxOTYzLTc2JywgJzE5MjAtNDEnLCAnMTk5My0yMDA5JywgJ0hCUCcsICdTQicsICdTRicsICdTSCcsICdSQkknLCAnU08nLCAnV29ybGQgU2VyaWVzIE1WUCcsICdHX2RoX3BlcmNlbnQnLCAnR19kaCcsICdBZicsICdEUGYnLCAnRWYnXVxuXG5mb3IgY29sIGluIGZpbGxfY29sczpcbiAgICBkZltjb2xdID0gZGZbY29sXS5maWxsbmEoMClcblxuIyBEcm9wIGFueSBhZGRpdGlvbmFsIHJvd3Mgd2l0aCBudWxsIHZhbHVlc1xuZGYgPSBkZi5kcm9wbmEoKVxuXG4jIENoZWNrIHRvIG1ha2Ugc3VyZSBudWxsIHZhbHVlcyBoYXZlIGJlZW4gcmVtb3ZlZFxucHJpbnQoZGYuaXNudWxsKCkuc3VtKGF4aXM9MCkudG9saXN0KCkpIiwic2N0IjoiRXgoKS50ZXN0X29iamVjdChcImZpbGxfY29sc1wiKVxuRXgoKS50ZXN0X29iamVjdChcImRmXCIpXG5FeCgpLnRlc3RfZnVuY3Rpb24oXCJwcmludFwiKVxuc3VjY2Vzc19tc2coXCJQaGV3ISBZb3UgZmluYWxseSBzZWVtIHRvIGhhdmUgYSBmdWxsIHZpZXcgb24geW91ciBwbGF5ZXJzJyBkYXRhIVwiKSJ9

Congratulations! You have finally gathered a totally uniform view on your players: you have the player statistics and the master data in one place, the df DataFrame.

Feature Engineering: Creating New Features

Now that the data has been cleaned up, you can add new features. The important baseball statistics that are missing from our data are batting average, on-base percentage, slugging percentage, and on-base plus slugging percentage.

Add each of these statistics by using the following formulas:

Batting Ave. = At Bats / Hits
Plate Appearances = At Bats + Walks + Sacrifice Flys & Hits + Hit by Pitch
On-base % = (Hits + Walks + Hit by Pitch) / Plate Appearances
Slugging % = ((Home Runs x 4) + (Triples x 3) + (Doubles x 2) + Singles) / At Bats
On-Base plus Slugging % = On-base % + Slugging %

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcbmRmID0gcGQucmVhZF9jc3YoXCJodHRwczovL3MzLmFtYXpvbmF3cy5jb20vYXNzZXRzLmRhdGFjYW1wLmNvbS9ibG9nX2Fzc2V0cy9NTEIrRGF0YS9kZi1kcm9wcGVkLmNzdlwiLCBuYW1lcz1bJycsICdwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnZGVidXQnLCAnZmluYWxHYW1lJywgJ0cnLCAnQUInLFxuICAgICAgICdSJywgJ0gnLCAnMkInLCAnM0InLCAnSFInLCAnUkJJJywgJ1NCJywgJ0JCJywgJ1NPJywgJ0hCUCcsICdTSCcsICdTRicsXG4gICAgICAgJ1llYXJzX1BsYXllZCcsICdBZicsICdFZicsICdEUGYnLCAnSG9GJywgJ01vc3QgVmFsdWFibGUgUGxheWVyJyxcbiAgICAgICAnQVNfZ2FtZXMnLCAnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnV29ybGQgU2VyaWVzIE1WUCcsXG4gICAgICAgJ1NpbHZlciBTbHVnZ2VyJywgJ0dfYWxsJywgJ0dfcCcsICdHX2MnLCAnR18xYicsICdHXzJiJywgJ0dfM2InLCAnR19zcycsXG4gICAgICAgJ0dfbGYnLCAnR19jZicsICdHX3JmJywgJ0dfb2YnLCAnR19kaCcsICdwcmUxOTIwJywgJzE5MjAtNDEnLCAnMTk0Mi00NScsXG4gICAgICAgJzE5NDYtNjInLCAnMTk2My03NicsICcxOTc3LTkyJywgJzE5OTMtMjAwOScsICdwb3N0MjAwOScsICdHX3BfcGVyY2VudCcsXG4gICAgICAgJ0dfY19wZXJjZW50JywgJ0dfMWJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JyxcbiAgICAgICAnR19zc19wZXJjZW50JywgJ0dfbGZfcGVyY2VudCcsICdHX2NmX3BlcmNlbnQnLCAnR19yZl9wZXJjZW50JyxcbiAgICAgICAnR19vZl9wZXJjZW50JywgJ0dfZGhfcGVyY2VudCcsICdwcmUxOTIwX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JyxcbiAgICAgICAnMTk0Mi00NV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsICcxOTYzLTc2X3BlcmNlbnQnLFxuICAgICAgICcxOTc3LTkyX3BlcmNlbnQnLCAnMTk5My0yMDA5X3BlcmNlbnQnLCAncG9zdDIwMDlfcGVyY2VudCcsICdiYXRzX1InLFxuICAgICAgICd0aHJvd3NfUicsICdkZWJ1dFllYXInLCAnZmluYWxZZWFyJ10sIGhlYWRlcj0wLCBpbmRleF9jb2w9MClcbmRmWydkZWJ1dCddID0gIHBkLnRvX2RhdGV0aW1lKGRmWydkZWJ1dCddKVxuZGZbJ2ZpbmFsR2FtZSddID0gcGQudG9fZGF0ZXRpbWUoZGZbJ2ZpbmFsR2FtZSddKVxuZGZbJ2RlYnV0WWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZGVidXQnXS5kdC5zdHJmdGltZSgnJVknKSwgZXJyb3JzPSdjb2VyY2UnKVxuZGZbJ2ZpbmFsWWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZmluYWxHYW1lJ10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmZpbGxfY29scyA9IFsnQVNfZ2FtZXMnLCAnU2lsdmVyIFNsdWdnZXInLCAnUm9va2llIG9mIHRoZSBZZWFyJywgJ0dvbGQgR2xvdmUnLCAnTW9zdCBWYWx1YWJsZSBQbGF5ZXInLCAnSG9GJywgJzE5NzctOTInLCAncHJlMTkyMCcsICcxOTQyLTQ1JywgJzE5NDYtNjInLCAnMTk2My03NicsICcxOTIwLTQxJywgJzE5OTMtMjAwOScsICdIQlAnLCAnU0InLCAnU0YnLCAnU0gnLCAnUkJJJywgJ1NPJywgJ1dvcmxkIFNlcmllcyBNVlAnLCAnR19kaF9wZXJjZW50JywgJ0dfZGgnLCAnQWYnLCAnRFBmJywgJ0VmJ11cbmZvciBjb2wgaW4gZmlsbF9jb2xzOlxuICAgIGRmW2NvbF0gPSBkZltjb2xdLmZpbGxuYSgwKVxuZGYgPSBkZi5kcm9wbmEoKSIsInNhbXBsZSI6IiMgQ3JlYXRlIEJhdHRpbmcgQXZlcmFnZSAoYEFWRWApIGNvbHVtblxuZGZbJ0FWRSddID0gZGZbJ0gnXSAvIGRmWydBQiddXG5cbiMgQ3JlYXRlIE9uIEJhc2UgUGVyY2VudCAoYE9CUGApIGNvbHVtblxucGxhdGVfYXBwZWFyYW5jZXMgPSAoZGZbJ0FCJ10gKyBkZlsnQkInXSArIGRmWydTRiddICsgZGZbJ1NIJ10gKyBkZlsnSEJQJ10pXG5kZlsnT0JQJ10gPSAoZGZbJ0gnXSArIGRmWydCQiddICsgZGZbJ0hCUCddKSAvIHBsYXRlX2FwcGVhcmFuY2VzXG5cbiMgQ3JlYXRlIFNsdWdnaW5nIFBlcmNlbnQgKGBTbHVnX1BlcmNlbnRgKSBjb2x1bW5cbnNpbmdsZSA9ICgoZGZbJ0gnXSAtIGRmWycyQiddKSAtIGRmWyczQiddKSAtIGRmWydIUiddXG5kZlsnU2x1Z19QZXJjZW50J10gPSAoKGRmWydIUiddICogNCkgKyAoZGZbJzNCJ10gKiAzKSArIChkZlsnMkInXSAqIDIpICsgc2luZ2xlKSAvIGRmWydBQiddXG5cbiMgQ3JlYXRlIE9uIEJhc2UgcGx1cyBTbHVnZ2luZyBQZXJjZW50IChgT1BTYCkgY29sdW1uXG5ociA9IGRmWydIUiddICogNFxudHJpcGxlID0gZGZbJzNCJ10gKiAzXG5kb3VibGUgPSBkZlsnMkInXSAqIDJcbmRmWydPUFMnXSA9IGRmWydPQlAnXSArIGRmWydTbHVnX1BlcmNlbnQnXVxuXG4jIERvdWJsZSBjaGVjayB0aGUgYGRmYCBjb2x1bW5zIFxucHJpbnQoZGYuY29sdW1ucykifQ==

There are a few anomalies in your data that need to be resolved, which you might know if you have some knowledge on MLB history:

The first two involve players who had Hall of Fame worthy statistics, but were banned from baseball for life. For example, Shoeless Joe Jackson (playerID == jacksjo01) was an incredible player but got caught up in the 1919 Black Sox scandal when multiple players from the Chicago White Sox accepted money from Mobsters and intentionally lost. Even though he played extremely well in that series, he was banned for life.
In addition, you have Pete Rose (playerID == rosepe01), the all-time hits leader. Nicknamed Charlie Hussle, he was the everyman who had an incredible career playing for the Cincinnati Reds. Shortly after he retired as a player he became the Manager of the Reds and got caught betting on baseball games including betting on his own team to win. He was also banned for life. It’s best to remove these two players from the dataset.

The other anomaly that needs to be resolved is a much different situation than the two above. Jackie Robinson was an all-time great, and played for the Brooklyn Dodgers putting up incredible statistics during the years he played. He also broke the color barrier in Major League Baseball, becoming the first African American Major Leaguer. The problem is, his career started very late at the age of 26 which was completely outside of his control and limited his career statistics.

Out of respect for Jackie Robinson (playerID == robinja02) and the incredible impact he had on the game of baseball, instead of removing him, create a function to identify him as the first African American to play in the Major Leagues.

Now it’s time to visualize some of the data to gain a better understanding. Filter df to only include Hall of Fame players and print the length.

You have 70 Hall of Famers left in the data set. Plot out distributions for Hits, Home Runs, Years Played, and All-Star Game Appearances for these Hall of Famers.

# Import the `pyplot` module from `matplotlib`import matplotlib.pyplot as plt# Initialize the figure and add subplotsfig = plt.figure(figsize=(15, 12))ax1 = fig.add_subplot(2,2,1)ax2 = fig.add_subplot(2,2,2)ax3 = fig.add_subplot(2,2,3)ax4 = fig.add_subplot(2,2,4)# Create distribution plots for Hits, Home Runs, Years Played and All Star Gamesax1.hist(df_hof['H'])ax1.set_title('Distribution of Hits')ax1.set_ylabel('HoF Careers')ax2.hist(df_hof['HR'])ax2.set_title('Distribution of Home Runs')ax3.hist(df_hof['Years_Played'])ax3.set_title('Distribution of Years Played')ax3.set_ylabel('HoF Careers')ax4.hist(df_hof['AS_games'])ax4.set_title('Distribution of All Star Game Appearances')# Show the plotplt.show()

Note that if you’re working in a Jupyter notebook, you can easily make use of the %matplotlib inline magic to plot these distribution plots!

Next, create a scatter plot for Hits vs. Batting Average and one for Home Runs vs. Batting Average. First, filter df to only include players who played 10 or more seasons which is the minimum for Hall of Fame eligibility.

# Filter `df` for players with 10 or more years of experiencedf_10 = df[(df['Years_Played'] >= 10) & (df['HoF'] == 0)]# Initialize the figure and add subplotsfig = plt.figure(figsize=(14, 7))ax1 = fig.add_subplot(1,2,1)ax2 = fig.add_subplot(1,2,2)# Create Scatter plots for Hits vs. Average and Home Runs vs. Averageax1.scatter(df_hof['H'], df_hof['AVE'], c='r', label='HoF Player')ax1.scatter(df_10['H'], df_10['AVE'], c='b', label='Non HoF Player')ax1.set_title('Career Hits vs. Career Batting Average')ax1.set_xlabel('Career Hits')ax1.set_ylabel('Career Average')ax2.scatter(df_hof['HR'], df_hof['AVE'], c='r', label='HoF Player')ax2.scatter(df_10['HR'], df_10['AVE'], c='b', label='Non HoF Player')ax2.set_title('Career Home Runs vs. Career Batting Average')ax2.set_xlabel('Career Home Runs')ax2.legend(loc='lower right', scatterpoints=1)# Show the plotplt.show()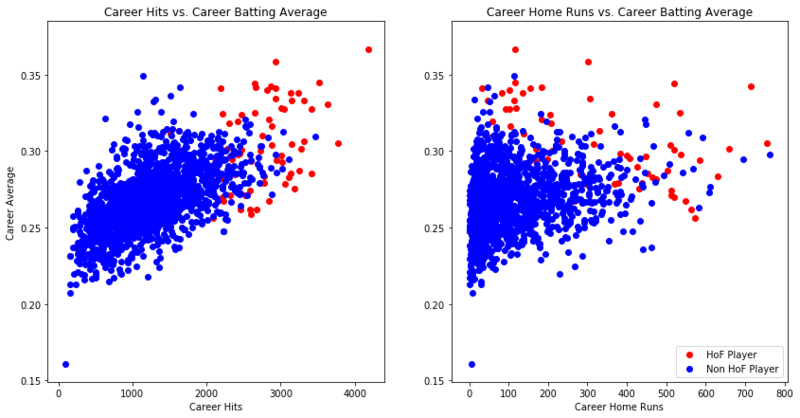

When you created new features, you may have also created new null values. Print out the count of null values for each column.

As you can see, there are not many null values, so you can easily drop the rows that have null values in them.

In the first part of this tutorial series, the data was split into testing and training sets by taking a random slice of the data for each. This time you’ll be using cross-validation to train and test the models. Since a player must wait 5 years to become eligible for the HoF ballot, and can remain on the ballot for as many as 10 years then there are still eligible players who played their final season in the last 15 years.

Make sure to separate out the players who played their most recent season in the last 15 years so you can use this as “new” data once you have a model that’s trained and tested.

Add a column to df for years since last season (YSLS) by subtracting the finalYear column from 2016. Next, create a new DataFrame called df_hitters by filtering df for players whose last season was more than 15 years ago and create one called df_eligible for players whose last season was 15 or less years ago.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcbmRmID1wZC5yZWFkX2NzdihcImh0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL2NhbGNkZi5jc3ZcIixcbiAgICAgICAgICAgICAgICBuYW1lcz1bJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdkZWJ1dCcsICdmaW5hbEdhbWUnLCAnRycsICdBQicsJ1InLCAnSCcsICcyQicsICczQicsICdIUicsICdSQkknLCAnU0InLCAnQkInLCAnU08nLCAnSEJQJywgJ1NIJywgJ1NGJywnWWVhcnNfUGxheWVkJywgJ0FmJywgJ0VmJywgJ0RQZicsICdIb0YnLCAnTW9zdCBWYWx1YWJsZSBQbGF5ZXInLCdBU19nYW1lcycsICdHb2xkIEdsb3ZlJywgJ1Jvb2tpZSBvZiB0aGUgWWVhcicsICdXb3JsZCBTZXJpZXMgTVZQJywnU2lsdmVyIFNsdWdnZXInLCAnR19hbGwnLCAnR19wJywgJ0dfYycsICdHXzFiJywgJ0dfMmInLCAnR18zYicsICdHX3NzJywnR19sZicsICdHX2NmJywgJ0dfcmYnLCAnR19vZicsICdHX2RoJywgJ3ByZTE5MjAnLCAnMTkyMC00MScsICcxOTQyLTQ1JywnMTk0Ni02MicsICcxOTYzLTc2JywgJzE5NzctOTInLCAnMTk5My0yMDA5JywgJ3Bvc3QyMDA5JywgJ0dfcF9wZXJjZW50JywnR19jX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJ0dfMmJfcGVyY2VudCcsICdHXzNiX3BlcmNlbnQnLCdHX3NzX3BlcmNlbnQnLCAnR19sZl9wZXJjZW50JywgJ0dfY2ZfcGVyY2VudCcsICdHX3JmX3BlcmNlbnQnLCdHX29mX3BlcmNlbnQnLCAnR19kaF9wZXJjZW50JywgJ3ByZTE5MjBfcGVyY2VudCcsICcxOTIwLTQxX3BlcmNlbnQnLCAnMTk0Mi00NV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsJzE5NjMtNzZfcGVyY2VudCcsJzE5NzctOTJfcGVyY2VudCcsJzE5OTMtMjAwOV9wZXJjZW50JywgJ3Bvc3QyMDA5X3BlcmNlbnQnLCAnYmF0c19SJywndGhyb3dzX1InLCAnZGVidXRZZWFyJywgJ2ZpbmFsWWVhcicsICdBVkUnLCAnT0JQJywnU2x1Z19QZXJjZW50JywgJ09QUyddLCBza2lwcm93cz0xLCBpbmRleF9jb2w9MClcbmRmWydkZWJ1dCddID0gIHBkLnRvX2RhdGV0aW1lKGRmWydkZWJ1dCddKVxuZGZbJ2ZpbmFsR2FtZSddID0gcGQudG9fZGF0ZXRpbWUoZGZbJ2ZpbmFsR2FtZSddKVxuZGZbJ2RlYnV0WWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZGVidXQnXS5kdC5zdHJmdGltZSgnJVknKSwgZXJyb3JzPSdjb2VyY2UnKVxuZGZbJ2ZpbmFsWWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZmluYWxHYW1lJ10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmRmID0gZGZbKGRmWydwbGF5ZXJJRCddICE9ICdyb3NlcGUwMScpICYgKGRmWydwbGF5ZXJJRCddICE9ICdqYWNrc2pvMDEnKV1cbmRlZiBmaXJzdF9hYXAoY29sKTpcbiAgICBpZiBjb2wgPT0gJ3JvYmluamEwMic6XG4gICAgICAgIHJldHVybiAxXG4gICAgZWxzZTpcbiAgICAgICAgcmV0dXJuIDBcbiAgICBcbmRmWydmaXJzdF9hYXAnXSA9IGRmWydwbGF5ZXJJRCddLmFwcGx5KGZpcnN0X2FhcClcbmRmX2hvZiA9IGRmW2RmWydIb0YnXSA9PSAxXVxuZGYgPSBkZi5kcm9wbmEoKSIsInNhbXBsZSI6IiMgQ3JlYXRlIGNvbHVtbiBmb3IgeWVhcnMgc2luY2UgcmV0aXJlbWVudFxuZGZbJ1lTTFMnXSA9IDIwMTYgLSBkZlsnZmluYWxZZWFyJ11cblxuIyBGaWx0ZXIgYGRmYCBmb3IgcGxheWVycyB3aG8gcmV0aXJlZCBtb3JlIHRoYW4gMTUgeWVhcnMgYWdvXG5kZl9oaXR0ZXJzID0gZGZbX19bJ1lTTFMnXSA+IDE1XVxuXG5wcmludChkZl9oaXR0ZXJzLmhlYWQoKSlcblxuIyBGaWx0ZXIgYGRmYCBmb3IgcGxheWVycyB3aG8gcmV0aXJlZCBsZXNzIHRoYW4gMTUgeWVhcnMgYWdvIGFuZCBmb3IgY3VycmVudGx5IGFjdGl2ZSBwbGF5ZXJzXG5kZl9lbGlnaWJsZSA9IGRmW2RmWydZU0xTJ108PSAxNV1cblxucHJpbnQoZGZfZWxpZ2libGUuX19fX19fKSIsInNvbHV0aW9uIjoiIyBDcmVhdGUgY29sdW1uIGZvciB5ZWFycyBzaW5jZSByZXRpcmVtZW50XG5kZlsnWVNMUyddID0gMjAxNiAtIGRmWydmaW5hbFllYXInXVxuXG4jIEZpbHRlciBgZGZgIGZvciBwbGF5ZXJzIHdobyByZXRpcmVkIG1vcmUgdGhhbiAxNSB5ZWFycyBhZ29cbmRmX2hpdHRlcnMgPSBkZltkZlsnWVNMUyddID4gMTVdXG5cbnByaW50KGRmX2hpdHRlcnMuaGVhZCgpKVxuXG4jIEZpbHRlciBgZGZgIGZvciBwbGF5ZXJzIHdobyByZXRpcmVkIGxlc3MgdGhhbiAxNSB5ZWFycyBhZ28gYW5kIGZvciBjdXJyZW50bHkgYWN0aXZlIHBsYXllcnNcbmRmX2VsaWdpYmxlID0gZGZbZGZbJ1lTTFMnXTw9IDE1XVxuXG5wcmludChkZl9lbGlnaWJsZS5oZWFkKCkpIiwic2N0IjoiRXgoKS50ZXN0X29iamVjdChcImRmXCIpXG5FeCgpLnRlc3Rfb2JqZWN0KFwiZGZfaGl0dGVyc1wiKVxuRXgoKS50ZXN0X2Z1bmN0aW9uKFwicHJpbnRcIiwgaW5kZXg9MSlcbkV4KCkudGVzdF9vYmplY3QoXCJkZl9lbGlnaWJsZVwiKVxuRXgoKS50ZXN0X2Z1bmN0aW9uKFwicHJpbnRcIiwgaW5kZXg9MilcbnN1Y2Nlc3NfbXNnKFwiV2VsbCBkb25lIVwiKSJ9

Now you need to select the columns to include in the model. First, print out the columns.

Make a list with the columns to include in the model and create a new DataFrame called data from df_hitters using the list of columns. Include playerID, nameFirst, and nameLast in the list, as you’ll want those columns when you display the results of your predictions with the new data.

You’ll need to drop those three columns for any data used in the model.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcbmRmID1wZC5yZWFkX2NzdihcImh0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL2NhbGNkZi5jc3ZcIixcbiAgICAgICAgICAgICAgICBuYW1lcz1bJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdkZWJ1dCcsICdmaW5hbEdhbWUnLCAnRycsICdBQicsJ1InLCAnSCcsICcyQicsICczQicsICdIUicsICdSQkknLCAnU0InLCAnQkInLCAnU08nLCAnSEJQJywgJ1NIJywgJ1NGJywnWWVhcnNfUGxheWVkJywgJ0FmJywgJ0VmJywgJ0RQZicsICdIb0YnLCAnTW9zdCBWYWx1YWJsZSBQbGF5ZXInLCdBU19nYW1lcycsICdHb2xkIEdsb3ZlJywgJ1Jvb2tpZSBvZiB0aGUgWWVhcicsICdXb3JsZCBTZXJpZXMgTVZQJywnU2lsdmVyIFNsdWdnZXInLCAnR19hbGwnLCAnR19wJywgJ0dfYycsICdHXzFiJywgJ0dfMmInLCAnR18zYicsICdHX3NzJywnR19sZicsICdHX2NmJywgJ0dfcmYnLCAnR19vZicsICdHX2RoJywgJ3ByZTE5MjAnLCAnMTkyMC00MScsICcxOTQyLTQ1JywnMTk0Ni02MicsICcxOTYzLTc2JywgJzE5NzctOTInLCAnMTk5My0yMDA5JywgJ3Bvc3QyMDA5JywgJ0dfcF9wZXJjZW50JywnR19jX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJ0dfMmJfcGVyY2VudCcsICdHXzNiX3BlcmNlbnQnLCdHX3NzX3BlcmNlbnQnLCAnR19sZl9wZXJjZW50JywgJ0dfY2ZfcGVyY2VudCcsICdHX3JmX3BlcmNlbnQnLCdHX29mX3BlcmNlbnQnLCAnR19kaF9wZXJjZW50JywgJ3ByZTE5MjBfcGVyY2VudCcsICcxOTIwLTQxX3BlcmNlbnQnLCAnMTk0Mi00NV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsJzE5NjMtNzZfcGVyY2VudCcsJzE5NzctOTJfcGVyY2VudCcsJzE5OTMtMjAwOV9wZXJjZW50JywgJ3Bvc3QyMDA5X3BlcmNlbnQnLCAnYmF0c19SJywndGhyb3dzX1InLCAnZGVidXRZZWFyJywgJ2ZpbmFsWWVhcicsICdBVkUnLCAnT0JQJywnU2x1Z19QZXJjZW50JywgJ09QUyddLCBza2lwcm93cz0xLCBpbmRleF9jb2w9MClcbmRmWydkZWJ1dCddID0gIHBkLnRvX2RhdGV0aW1lKGRmWydkZWJ1dCddKVxuZGZbJ2ZpbmFsR2FtZSddID0gcGQudG9fZGF0ZXRpbWUoZGZbJ2ZpbmFsR2FtZSddKVxuZGZbJ2RlYnV0WWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZGVidXQnXS5kdC5zdHJmdGltZSgnJVknKSwgZXJyb3JzPSdjb2VyY2UnKVxuZGZbJ2ZpbmFsWWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZmluYWxHYW1lJ10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmRmID0gZGZbKGRmWydwbGF5ZXJJRCddICE9ICdyb3NlcGUwMScpICYgKGRmWydwbGF5ZXJJRCddICE9ICdqYWNrc2pvMDEnKV1cbmRlZiBmaXJzdF9hYXAoY29sKTpcbiAgICBpZiBjb2wgPT0gJ3JvYmluamEwMic6XG4gICAgICAgIHJldHVybiAxXG4gICAgZWxzZTpcbiAgICAgICAgcmV0dXJuIDBcbiAgICBcbmRmWydmaXJzdF9hYXAnXSA9IGRmWydwbGF5ZXJJRCddLmFwcGx5KGZpcnN0X2FhcClcbmRmX2hvZiA9IGRmW2RmWydIb0YnXSA9PSAxXVxuZGYgPSBkZi5kcm9wbmEoKVxuZGZbJ1lTTFMnXSA9IDIwMTYgLSBkZlsnZmluYWxZZWFyJ11cbmRmX2hpdHRlcnMgPSBkZltkZlsnWVNMUyddID4gMTVdIiwic2FtcGxlIjoiIyBTZWxlY3QgY29sdW1ucyB0byB1c2UgZm9yIG1vZGVscywgYW5kIGlkZW50aWZpY2F0aW9uIGNvbHVtbnNcbm51bV9jb2xzX2hpdHRlcnMgPSBbJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdIb0YnLCAnWWVhcnNfUGxheWVkJywgJ0gnLCAnQkInLCAnSFInLCAnQVZFJywgJ09CUCcsICdTbHVnX1BlcmNlbnQnLCAnT1BTJywgICdSQkknLCdSJywgJ1NCJywgJzJCJywgJzNCJywgJ0FCJywgJ1NPJywgJ01vc3QgVmFsdWFibGUgUGxheWVyJywgJ1dvcmxkIFNlcmllcyBNVlAnLCAnQVNfZ2FtZXMnLCdHb2xkIEdsb3ZlJywgJ1Jvb2tpZSBvZiB0aGUgWWVhcicsICdTaWx2ZXIgU2x1Z2dlcicsICdiYXRzX1InLCAndGhyb3dzX1InLCAnRFBmJywgJ0FmJywgJ0VmJywgJ1lTTFMnLCAnR19hbGwnLCAnMTk2My03Nl9wZXJjZW50JywgJzE5OTMtMjAwOV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsICdHXzFiX3BlcmNlbnQnLCAnMTk0Mi00NV9wZXJjZW50JywnR19kaF9wZXJjZW50JywgJzE5MjAtNDFfcGVyY2VudCcsICdHX3NzX3BlcmNlbnQnLCdwb3N0MjAwOV9wZXJjZW50JywgJzE5NzctOTJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywnR19vZl9wZXJjZW50JywgJ3ByZTE5MjBfcGVyY2VudCcsICdmaXJzdF9hYXAnXVxuXG4jIENyZWF0ZSBhIG5ldyBEYXRhRnJhbWUgKGBkYXRhYCkgZnJvbSB0aGUgYGRmX2hpdHRlcnNgIHVzaW5nIHRoZSBjb2x1bW5zIGFib3ZlXG5kYXRhID0gZGZfaGl0dGVyc1tfX19fX19fX19fX19fX19fXVxuXG4jIFJldHVybiB0aGUgZmlyc3Qgcm93cyBvZiBgZGF0YWBcbnByaW50KGRhdGEuaGVhZCgpKSIsInNvbHV0aW9uIjoiIyBTZWxlY3QgY29sdW1ucyB0byB1c2UgZm9yIG1vZGVscywgYW5kIGlkZW50aWZpY2F0aW9uIGNvbHVtbnNcbm51bV9jb2xzX2hpdHRlcnMgPSBbJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdIb0YnLCAnWWVhcnNfUGxheWVkJywgJ0gnLCAnQkInLCAnSFInLCAnQVZFJywgJ09CUCcsICdTbHVnX1BlcmNlbnQnLCAnT1BTJywgICdSQkknLCdSJywgJ1NCJywgJzJCJywgJzNCJywgJ0FCJywgJ1NPJywgJ01vc3QgVmFsdWFibGUgUGxheWVyJywgJ1dvcmxkIFNlcmllcyBNVlAnLCAnQVNfZ2FtZXMnLCdHb2xkIEdsb3ZlJywgJ1Jvb2tpZSBvZiB0aGUgWWVhcicsICdTaWx2ZXIgU2x1Z2dlcicsICdiYXRzX1InLCAndGhyb3dzX1InLCAnRFBmJywgJ0FmJywgJ0VmJywgJ1lTTFMnLCAnR19hbGwnLCAnMTk2My03Nl9wZXJjZW50JywgJzE5OTMtMjAwOV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsICdHXzFiX3BlcmNlbnQnLCAnMTk0Mi00NV9wZXJjZW50JywnR19kaF9wZXJjZW50JywgJzE5MjAtNDFfcGVyY2VudCcsICdHX3NzX3BlcmNlbnQnLCdwb3N0MjAwOV9wZXJjZW50JywgJzE5NzctOTJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywnR19vZl9wZXJjZW50JywgJ3ByZTE5MjBfcGVyY2VudCcsICdmaXJzdF9hYXAnXVxuXG4jIENyZWF0ZSBhIG5ldyBEYXRhRnJhbWUgKGBkYXRhYCkgZnJvbSB0aGUgYGRmX2hpdHRlcnNgIHVzaW5nIHRoZSBjb2x1bW5zIGFib3ZlXG5kYXRhID0gZGZfaGl0dGVyc1tudW1fY29sc19oaXR0ZXJzXVxuXG4jIFJldHVybiB0aGUgZmlyc3Qgcm93cyBvZiBgZGF0YWBcbnByaW50KGRhdGEuaGVhZCgpKSIsInNjdCI6IkV4KCkudGVzdF9vYmplY3QoXCJudW1fY29sc19oaXR0ZXJzXCIpXG5FeCgpLnRlc3Rfb2JqZWN0KFwiZGF0YVwiKVxuRXgoKS50ZXN0X2Z1bmN0aW9uKFwiZGF0YS5oZWFkXCIpIn0=

Print out how many rows are in data and how many of those rows are Hall of Famers.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcbmRmID1wZC5yZWFkX2NzdihcImh0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL2NhbGNkZi5jc3ZcIixcbiAgICAgICAgICAgICAgICBuYW1lcz1bJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdkZWJ1dCcsICdmaW5hbEdhbWUnLCAnRycsICdBQicsJ1InLCAnSCcsICcyQicsICczQicsICdIUicsICdSQkknLCAnU0InLCAnQkInLCAnU08nLCAnSEJQJywgJ1NIJywgJ1NGJywnWWVhcnNfUGxheWVkJywgJ0FmJywgJ0VmJywgJ0RQZicsICdIb0YnLCAnTW9zdCBWYWx1YWJsZSBQbGF5ZXInLCdBU19nYW1lcycsICdHb2xkIEdsb3ZlJywgJ1Jvb2tpZSBvZiB0aGUgWWVhcicsICdXb3JsZCBTZXJpZXMgTVZQJywnU2lsdmVyIFNsdWdnZXInLCAnR19hbGwnLCAnR19wJywgJ0dfYycsICdHXzFiJywgJ0dfMmInLCAnR18zYicsICdHX3NzJywnR19sZicsICdHX2NmJywgJ0dfcmYnLCAnR19vZicsICdHX2RoJywgJ3ByZTE5MjAnLCAnMTkyMC00MScsICcxOTQyLTQ1JywnMTk0Ni02MicsICcxOTYzLTc2JywgJzE5NzctOTInLCAnMTk5My0yMDA5JywgJ3Bvc3QyMDA5JywgJ0dfcF9wZXJjZW50JywnR19jX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJ0dfMmJfcGVyY2VudCcsICdHXzNiX3BlcmNlbnQnLCdHX3NzX3BlcmNlbnQnLCAnR19sZl9wZXJjZW50JywgJ0dfY2ZfcGVyY2VudCcsICdHX3JmX3BlcmNlbnQnLCdHX29mX3BlcmNlbnQnLCAnR19kaF9wZXJjZW50JywgJ3ByZTE5MjBfcGVyY2VudCcsICcxOTIwLTQxX3BlcmNlbnQnLCAnMTk0Mi00NV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsJzE5NjMtNzZfcGVyY2VudCcsJzE5NzctOTJfcGVyY2VudCcsJzE5OTMtMjAwOV9wZXJjZW50JywgJ3Bvc3QyMDA5X3BlcmNlbnQnLCAnYmF0c19SJywndGhyb3dzX1InLCAnZGVidXRZZWFyJywgJ2ZpbmFsWWVhcicsICdBVkUnLCAnT0JQJywnU2x1Z19QZXJjZW50JywgJ09QUyddLCBza2lwcm93cz0xLCBpbmRleF9jb2w9MClcbmRmWydkZWJ1dCddID0gIHBkLnRvX2RhdGV0aW1lKGRmWydkZWJ1dCddKVxuZGZbJ2ZpbmFsR2FtZSddID0gcGQudG9fZGF0ZXRpbWUoZGZbJ2ZpbmFsR2FtZSddKVxuZGZbJ2RlYnV0WWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZGVidXQnXS5kdC5zdHJmdGltZSgnJVknKSwgZXJyb3JzPSdjb2VyY2UnKVxuZGZbJ2ZpbmFsWWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZmluYWxHYW1lJ10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmRmID0gZGZbKGRmWydwbGF5ZXJJRCddICE9ICdyb3NlcGUwMScpICYgKGRmWydwbGF5ZXJJRCddICE9ICdqYWNrc2pvMDEnKV1cbmRlZiBmaXJzdF9hYXAoY29sKTpcbiAgICBpZiBjb2wgPT0gJ3JvYmluamEwMic6XG4gICAgICAgIHJldHVybiAxXG4gICAgZWxzZTpcbiAgICAgICAgcmV0dXJuIDBcbiAgICBcbmRmWydmaXJzdF9hYXAnXSA9IGRmWydwbGF5ZXJJRCddLmFwcGx5KGZpcnN0X2FhcClcbmRmX2hvZiA9IGRmW2RmWydIb0YnXSA9PSAxXVxuZGYgPSBkZi5kcm9wbmEoKVxuZGZbJ1lTTFMnXSA9IDIwMTYgLSBkZlsnZmluYWxZZWFyJ11cbmRmX2hpdHRlcnMgPSBkZltkZlsnWVNMUyddID4gMTVdXG5udW1fY29sc19oaXR0ZXJzID0gWydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnSG9GJywgJ1llYXJzX1BsYXllZCcsICdIJywgJ0JCJywgJ0hSJywgJ0FWRScsICdPQlAnLCAnU2x1Z19QZXJjZW50JywgJ09QUycsICAnUkJJJywnUicsICdTQicsICcyQicsICczQicsICdBQicsICdTTycsICdNb3N0IFZhbHVhYmxlIFBsYXllcicsICdXb3JsZCBTZXJpZXMgTVZQJywgJ0FTX2dhbWVzJywnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnU2lsdmVyIFNsdWdnZXInLCAnYmF0c19SJywgJ3Rocm93c19SJywgJ0RQZicsICdBZicsICdFZicsICdZU0xTJywgJ0dfYWxsJywgJzE5NjMtNzZfcGVyY2VudCcsICcxOTkzLTIwMDlfcGVyY2VudCcsICcxOTQ2LTYyX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsJ0dfZGhfcGVyY2VudCcsICcxOTIwLTQxX3BlcmNlbnQnLCAnR19zc19wZXJjZW50JywgJ3Bvc3QyMDA5X3BlcmNlbnQnLCAnMTk3Ny05Ml9wZXJjZW50JywgJ0dfMmJfcGVyY2VudCcsICdHXzNiX3BlcmNlbnQnLCdHX29mX3BlcmNlbnQnLCAncHJlMTkyMF9wZXJjZW50JywgJ2ZpcnN0X2FhcCddXG5kYXRhID0gZGZfaGl0dGVyc1tudW1fY29sc19oaXR0ZXJzXSIsInNhbXBsZSI6IiMgUHJpbnQgbGVuZ3RoIG9mIGBkYXRhYFxucHJpbnQobGVuKF9fX18pKVxuXG4jIFByaW50IGhvdyBtYW55IEhhbGwgb2YgRmFtZSBtZW1iZXJzIGFyZSBpbiBkYXRhXG5wcmludChsZW4oZGF0YVtkYXRhWydfX18nXSA9PSAxXSkpIiwic29sdXRpb24iOiIjIFByaW50IGxlbmd0aCBvZiBgZGF0YWBcbnByaW50KGxlbihkYXRhKSlcblxuIyBQcmludCBob3cgbWFueSBIYWxsIG9mIEZhbWUgbWVtYmVycyBhcmUgaW4gZGF0YVxucHJpbnQobGVuKGRhdGFbZGF0YVsnSG9GJ10gPT0gMV0pKSIsInNjdCI6IkV4KCkudGVzdF9mdW5jdGlvbihcInByaW50XCIsIGluZGV4PTEpXG5FeCgpLnRlc3RfZnVuY3Rpb24oXCJwcmludFwiLCBpbmRleD0yKVxuc3VjY2Vzc19tc2coXCJIb3cgbWFueSByb3dzIGFyZSBIYWxsIG9mIEZhbWVycz9cIikifQ==

There are 6,239 rows and 61 of those are Hall of Famers for your model to identify. Create your target Series from the HoF column of data and your features DataFrame by dropping the identification columns and the target column with the help of drop().

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiaW1wb3J0IHBhbmRhcyBhcyBwZFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcbmRmID1wZC5yZWFkX2NzdihcImh0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL2NhbGNkZi5jc3ZcIixcbiAgICAgICAgICAgICAgICBuYW1lcz1bJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdkZWJ1dCcsICdmaW5hbEdhbWUnLCAnRycsICdBQicsJ1InLCAnSCcsICcyQicsICczQicsICdIUicsICdSQkknLCAnU0InLCAnQkInLCAnU08nLCAnSEJQJywgJ1NIJywgJ1NGJywnWWVhcnNfUGxheWVkJywgJ0FmJywgJ0VmJywgJ0RQZicsICdIb0YnLCAnTW9zdCBWYWx1YWJsZSBQbGF5ZXInLCdBU19nYW1lcycsICdHb2xkIEdsb3ZlJywgJ1Jvb2tpZSBvZiB0aGUgWWVhcicsICdXb3JsZCBTZXJpZXMgTVZQJywnU2lsdmVyIFNsdWdnZXInLCAnR19hbGwnLCAnR19wJywgJ0dfYycsICdHXzFiJywgJ0dfMmInLCAnR18zYicsICdHX3NzJywnR19sZicsICdHX2NmJywgJ0dfcmYnLCAnR19vZicsICdHX2RoJywgJ3ByZTE5MjAnLCAnMTkyMC00MScsICcxOTQyLTQ1JywnMTk0Ni02MicsICcxOTYzLTc2JywgJzE5NzctOTInLCAnMTk5My0yMDA5JywgJ3Bvc3QyMDA5JywgJ0dfcF9wZXJjZW50JywnR19jX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJ0dfMmJfcGVyY2VudCcsICdHXzNiX3BlcmNlbnQnLCdHX3NzX3BlcmNlbnQnLCAnR19sZl9wZXJjZW50JywgJ0dfY2ZfcGVyY2VudCcsICdHX3JmX3BlcmNlbnQnLCdHX29mX3BlcmNlbnQnLCAnR19kaF9wZXJjZW50JywgJ3ByZTE5MjBfcGVyY2VudCcsICcxOTIwLTQxX3BlcmNlbnQnLCAnMTk0Mi00NV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsJzE5NjMtNzZfcGVyY2VudCcsJzE5NzctOTJfcGVyY2VudCcsJzE5OTMtMjAwOV9wZXJjZW50JywgJ3Bvc3QyMDA5X3BlcmNlbnQnLCAnYmF0c19SJywndGhyb3dzX1InLCAnZGVidXRZZWFyJywgJ2ZpbmFsWWVhcicsICdBVkUnLCAnT0JQJywnU2x1Z19QZXJjZW50JywgJ09QUyddLCBza2lwcm93cz0xLCBpbmRleF9jb2w9MClcbmRmWydkZWJ1dCddID0gIHBkLnRvX2RhdGV0aW1lKGRmWydkZWJ1dCddKVxuZGZbJ2ZpbmFsR2FtZSddID0gcGQudG9fZGF0ZXRpbWUoZGZbJ2ZpbmFsR2FtZSddKVxuZGZbJ2RlYnV0WWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZGVidXQnXS5kdC5zdHJmdGltZSgnJVknKSwgZXJyb3JzPSdjb2VyY2UnKVxuZGZbJ2ZpbmFsWWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZmluYWxHYW1lJ10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmRmID0gZGZbKGRmWydwbGF5ZXJJRCddICE9ICdyb3NlcGUwMScpICYgKGRmWydwbGF5ZXJJRCddICE9ICdqYWNrc2pvMDEnKV1cbmRlZiBmaXJzdF9hYXAoY29sKTpcbiAgICBpZiBjb2wgPT0gJ3JvYmluamEwMic6XG4gICAgICAgIHJldHVybiAxXG4gICAgZWxzZTpcbiAgICAgICAgcmV0dXJuIDBcbiAgICBcbmRmWydmaXJzdF9hYXAnXSA9IGRmWydwbGF5ZXJJRCddLmFwcGx5KGZpcnN0X2FhcClcbmRmX2hvZiA9IGRmW2RmWydIb0YnXSA9PSAxXVxuZGYgPSBkZi5kcm9wbmEoKVxuZGZbJ1lTTFMnXSA9IDIwMTYgLSBkZlsnZmluYWxZZWFyJ11cbmRmX2hpdHRlcnMgPSBkZltkZlsnWVNMUyddID4gMTVdXG5udW1fY29sc19oaXR0ZXJzID0gWydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnSG9GJywgJ1llYXJzX1BsYXllZCcsICdIJywgJ0JCJywgJ0hSJywgJ0FWRScsICdPQlAnLCAnU2x1Z19QZXJjZW50JywgJ09QUycsICAnUkJJJywnUicsICdTQicsICcyQicsICczQicsICdBQicsICdTTycsICdNb3N0IFZhbHVhYmxlIFBsYXllcicsICdXb3JsZCBTZXJpZXMgTVZQJywgJ0FTX2dhbWVzJywnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnU2lsdmVyIFNsdWdnZXInLCAnYmF0c19SJywgJ3Rocm93c19SJywgJ0RQZicsICdBZicsICdFZicsICdZU0xTJywgJ0dfYWxsJywgJzE5NjMtNzZfcGVyY2VudCcsICcxOTkzLTIwMDlfcGVyY2VudCcsICcxOTQ2LTYyX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsJ0dfZGhfcGVyY2VudCcsICcxOTIwLTQxX3BlcmNlbnQnLCAnR19zc19wZXJjZW50JywncG9zdDIwMDlfcGVyY2VudCcsICcxOTc3LTkyX3BlcmNlbnQnLCAnR18yYl9wZXJjZW50JywgJ0dfM2JfcGVyY2VudCcsJ0dfb2ZfcGVyY2VudCcsICdwcmUxOTIwX3BlcmNlbnQnLCAnZmlyc3RfYWFwJ11cbmRhdGEgPSBkZl9oaXR0ZXJzW251bV9jb2xzX2hpdHRlcnNdIiwic2FtcGxlIjoiIyBDcmVhdGUgYHRhcmdldGAgU2VyaWVzXG50YXJnZXQgPSBkYXRhWydfX18nXVxuXG4jIENyZWF0ZSBgZmVhdHVyZXNgIERhdGFGcmFtZVxuZmVhdHVyZXMgPSBkYXRhLl9fX18oWydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnSG9GJ10sIGF4aXM9MSkiLCJzb2x1dGlvbiI6IiMgQ3JlYXRlIGB0YXJnZXRgIFNlcmllc1xudGFyZ2V0ID0gZGF0YVsnSG9GJ11cblxuIyBDcmVhdGUgYGZlYXR1cmVzYCBEYXRhRnJhbWVcbmZlYXR1cmVzID0gZGF0YS5kcm9wKFsncGxheWVySUQnLCAnbmFtZUZpcnN0JywgJ25hbWVMYXN0JywgJ0hvRiddLCBheGlzPTEpIiwic2N0IjoiRXgoKS50ZXN0X29iamVjdChcInRhcmdldFwiKVxuRXgoKS50ZXN0X29iamVjdChcImZlYXR1cmVzXCIpXG5zdWNjZXNzX21zZyhcIkdyZWF0ISBZb3UncmUgbm93IHJlYWR5IHRvIGJ1aWxkIHlvdXIgbW9kZWwhXCIpIn0=

Now that you have isolated your target and features, it’s time to build your model!

Selecting Error Metric and Model

As was indicated earlier, the question you’re trying to answer is:

“Can you build a machine learning model that can accurately predict if an MLB baseball player will be voted into the Hall of Fame?”

The error metric for Part II is simple. How accurate are your predictions?

How many “True Positives” have you predicted where the player was predicted to be in the HoF and they are a HoF member. How many “False Positives” have you predicted where the player was predicted to be in the HoF and they are not a HoF member. Lastly, How many “False Negatives” where the player was predicted to not be in the HoF when the player was actually a HoF member.

Logistic Regression

The first model you’ll try is a Logistic Regression model. You’ll be using the Kfold cross-validation technique and you can learn more here.

Import cross_val_predict, and KFold from sklearn.cross_validation and LogisticRegression from sklearn.linear_model. Create a logistic regression model lr and be sure to set the class_weight perameter to ‘balanced’ because there are significantly more non-HoF members in the data.

Create an instance of the KFold class (kf) and finally, make predictions (predictions_lr) with cross_val_predict() using your model lr, features, target, and setting the cv parameter to kf.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiZnJvbSBudW1weSBpbXBvcnQgcmFuZG9tXG5yYW5kb20uc2VlZCg0MilcbmltcG9ydCBwYW5kYXMgYXMgcGRcbmZyb20gZGF0ZXRpbWUgaW1wb3J0IGRhdGV0aW1lXG5kZiA9cGQucmVhZF9jc3YoXCJodHRwczovL3MzLmFtYXpvbmF3cy5jb20vYXNzZXRzLmRhdGFjYW1wLmNvbS9ibG9nX2Fzc2V0cy9NTEIrRGF0YS9jYWxjZGYuY3N2XCIsXG4gICAgICAgICAgICAgICAgbmFtZXM9WydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnZGVidXQnLCAnZmluYWxHYW1lJywgJ0cnLCAnQUInLCdSJywgJ0gnLCAnMkInLCAnM0InLCAnSFInLCAnUkJJJywgJ1NCJywgJ0JCJywgJ1NPJywgJ0hCUCcsICdTSCcsICdTRicsJ1llYXJzX1BsYXllZCcsICdBZicsICdFZicsICdEUGYnLCAnSG9GJywgJ01vc3QgVmFsdWFibGUgUGxheWVyJywnQVNfZ2FtZXMnLCAnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnV29ybGQgU2VyaWVzIE1WUCcsJ1NpbHZlciBTbHVnZ2VyJywgJ0dfYWxsJywgJ0dfcCcsICdHX2MnLCAnR18xYicsICdHXzJiJywgJ0dfM2InLCAnR19zcycsJ0dfbGYnLCAnR19jZicsICdHX3JmJywgJ0dfb2YnLCAnR19kaCcsICdwcmUxOTIwJywgJzE5MjAtNDEnLCAnMTk0Mi00NScsJzE5NDYtNjInLCAnMTk2My03NicsICcxOTc3LTkyJywgJzE5OTMtMjAwOScsICdwb3N0MjAwOScsICdHX3BfcGVyY2VudCcsJ0dfY19wZXJjZW50JywgJ0dfMWJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywnR19zc19wZXJjZW50JywgJ0dfbGZfcGVyY2VudCcsICdHX2NmX3BlcmNlbnQnLCAnR19yZl9wZXJjZW50JywnR19vZl9wZXJjZW50JywgJ0dfZGhfcGVyY2VudCcsICdwcmUxOTIwX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsICcxOTQ2LTYyX3BlcmNlbnQnLCcxOTYzLTc2X3BlcmNlbnQnLCcxOTc3LTkyX3BlcmNlbnQnLCcxOTkzLTIwMDlfcGVyY2VudCcsICdwb3N0MjAwOV9wZXJjZW50JywgJ2JhdHNfUicsJ3Rocm93c19SJywgJ2RlYnV0WWVhcicsICdmaW5hbFllYXInLCAnQVZFJywgJ09CUCcsJ1NsdWdfUGVyY2VudCcsICdPUFMnXSwgc2tpcHJvd3M9MSwgaW5kZXhfY29sPTApXG5kZlsnZGVidXQnXSA9ICBwZC50b19kYXRldGltZShkZlsnZGVidXQnXSlcbmRmWydmaW5hbEdhbWUnXSA9IHBkLnRvX2RhdGV0aW1lKGRmWydmaW5hbEdhbWUnXSlcbmRmWydkZWJ1dFllYXInXSA9IHBkLnRvX251bWVyaWMoZGZbJ2RlYnV0J10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmRmWydmaW5hbFllYXInXSA9IHBkLnRvX251bWVyaWMoZGZbJ2ZpbmFsR2FtZSddLmR0LnN0cmZ0aW1lKCclWScpLCBlcnJvcnM9J2NvZXJjZScpXG5kZiA9IGRmWyhkZlsncGxheWVySUQnXSAhPSAncm9zZXBlMDEnKSAmIChkZlsncGxheWVySUQnXSAhPSAnamFja3NqbzAxJyldXG5kZWYgZmlyc3RfYWFwKGNvbCk6XG4gICAgaWYgY29sID09ICdyb2JpbmphMDInOlxuICAgICAgICByZXR1cm4gMVxuICAgIGVsc2U6XG4gICAgICAgIHJldHVybiAwXG4gICAgXG5kZlsnZmlyc3RfYWFwJ10gPSBkZlsncGxheWVySUQnXS5hcHBseShmaXJzdF9hYXApXG5kZl9ob2YgPSBkZltkZlsnSG9GJ10gPT0gMV1cbmRmID0gZGYuZHJvcG5hKClcbmRmWydZU0xTJ10gPSAyMDE2IC0gZGZbJ2ZpbmFsWWVhciddXG5kZl9oaXR0ZXJzID0gZGZbZGZbJ1lTTFMnXSA+IDE1XVxubnVtX2NvbHNfaGl0dGVycyA9IFsncGxheWVySUQnLCAnbmFtZUZpcnN0JywgJ25hbWVMYXN0JywgJ0hvRicsICdZZWFyc19QbGF5ZWQnLCAnSCcsICdCQicsICdIUicsICdBVkUnLCAnT0JQJywgJ1NsdWdfUGVyY2VudCcsICdPUFMnLCAgJ1JCSScsXG4gICAgICAgJ1InLCAnU0InLCAnMkInLCAnM0InLCAnQUInLCAnU08nLCAnTW9zdCBWYWx1YWJsZSBQbGF5ZXInLCAnV29ybGQgU2VyaWVzIE1WUCcsICdBU19nYW1lcycsJ0dvbGQgR2xvdmUnLCAnUm9va2llIG9mIHRoZSBZZWFyJywgXG4gICAgICAgJ1NpbHZlciBTbHVnZ2VyJywgJ2JhdHNfUicsICd0aHJvd3NfUicsICdEUGYnLCAnQWYnLCAnRWYnLCAnWVNMUycsICdHX2FsbCcsIFxuICAgICAgICcxOTYzLTc2X3BlcmNlbnQnLCAnMTk5My0yMDA5X3BlcmNlbnQnLCAnMTk0Ni02Ml9wZXJjZW50JywgJ0dfMWJfcGVyY2VudCcsICcxOTQyLTQ1X3BlcmNlbnQnLFxuICAgICAgICdHX2RoX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JywgJ0dfc3NfcGVyY2VudCcsXG4gICAgICAgJ3Bvc3QyMDA5X3BlcmNlbnQnLCAnMTk3Ny05Ml9wZXJjZW50JywgJ0dfMmJfcGVyY2VudCcsICdHXzNiX3BlcmNlbnQnLFxuICAgICAgICdHX29mX3BlcmNlbnQnLCAncHJlMTkyMF9wZXJjZW50JywgJ2ZpcnN0X2FhcCddXG5kYXRhID0gZGZfaGl0dGVyc1tudW1fY29sc19oaXR0ZXJzXVxudGFyZ2V0ID0gZGF0YVsnSG9GJ11cbmZlYXR1cmVzID0gZGF0YS5kcm9wKFsncGxheWVySUQnLCAnbmFtZUZpcnN0JywgJ25hbWVMYXN0JywgJ0hvRiddLCBheGlzPTEpIiwic2FtcGxlIjoiIyBJbXBvcnQgY3Jvc3NfdmFsX3ByZWRpY3QsIEtGb2xkIGFuZCBMb2dpc3RpY1JlZ3Jlc3Npb24gZnJvbSAnc2tsZWFybidcbmZyb20gc2tsZWFybi5jcm9zc192YWxpZGF0aW9uIGltcG9ydCBjcm9zc192YWxfcHJlZGljdCwgS0ZvbGRcbmZyb20gc2tsZWFybi5saW5lYXJfbW9kZWwgaW1wb3J0IExvZ2lzdGljUmVncmVzc2lvblxuXG4jIENyZWF0ZSBMb2dpc3RpYyBSZWdyZXNzaW9uIG1vZGVsXG5sciA9IExvZ2lzdGljUmVncmVzc2lvbihjbGFzc193ZWlnaHQ9J2JhbGFuY2VkJylcblxuIyBDcmVhdGUgYW4gaW5zdGFuY2Ugb2YgdGhlIEtGb2xkIGNsYXNzXG5rZiA9IEtGb2xkKGZlYXR1cmVzLnNoYXBlWzBdLCByYW5kb21fc3RhdGU9MSlcblxuIyBDcmVhdGUgcHJlZGljdGlvbnMgdXNpbmcgY3Jvc3MgdmFsaWRhdGlvblxucHJlZGljdGlvbnNfbHIgPSBjcm9zc192YWxfcHJlZGljdChsciwgZmVhdHVyZXMsIHRhcmdldCwgY3Y9a2YpIn0=

To determine accuracy, you need to compare your predictions to the target. Import numpy as np and convert predictions_lr and target to NumPy arrays.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiZnJvbSBudW1weSBpbXBvcnQgcmFuZG9tXG5yYW5kb20uc2VlZCg0MilcbmltcG9ydCBwYW5kYXMgYXMgcGRcbmZyb20gZGF0ZXRpbWUgaW1wb3J0IGRhdGV0aW1lXG5kZiA9cGQucmVhZF9jc3YoXCJodHRwczovL3MzLmFtYXpvbmF3cy5jb20vYXNzZXRzLmRhdGFjYW1wLmNvbS9ibG9nX2Fzc2V0cy9NTEIrRGF0YS9jYWxjZGYuY3N2XCIsbmFtZXM9WydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnZGVidXQnLCAnZmluYWxHYW1lJywgJ0cnLCAnQUInLCdSJywgJ0gnLCAnMkInLCAnM0InLCAnSFInLCAnUkJJJywgJ1NCJywgJ0JCJywgJ1NPJywgJ0hCUCcsICdTSCcsICdTRicsJ1llYXJzX1BsYXllZCcsICdBZicsICdFZicsICdEUGYnLCAnSG9GJywgJ01vc3QgVmFsdWFibGUgUGxheWVyJywnQVNfZ2FtZXMnLCAnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnV29ybGQgU2VyaWVzIE1WUCcsJ1NpbHZlciBTbHVnZ2VyJywgJ0dfYWxsJywgJ0dfcCcsICdHX2MnLCAnR18xYicsICdHXzJiJywgJ0dfM2InLCAnR19zcycsJ0dfbGYnLCAnR19jZicsICdHX3JmJywgJ0dfb2YnLCAnR19kaCcsICdwcmUxOTIwJywgJzE5MjAtNDEnLCAnMTk0Mi00NScsJzE5NDYtNjInLCAnMTk2My03NicsICcxOTc3LTkyJywgJzE5OTMtMjAwOScsICdwb3N0MjAwOScsICdHX3BfcGVyY2VudCcsJ0dfY19wZXJjZW50JywgJ0dfMWJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywnR19zc19wZXJjZW50JywgJ0dfbGZfcGVyY2VudCcsICdHX2NmX3BlcmNlbnQnLCAnR19yZl9wZXJjZW50JywnR19vZl9wZXJjZW50JywgJ0dfZGhfcGVyY2VudCcsICdwcmUxOTIwX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsICcxOTQ2LTYyX3BlcmNlbnQnLCcxOTYzLTc2X3BlcmNlbnQnLCcxOTc3LTkyX3BlcmNlbnQnLCcxOTkzLTIwMDlfcGVyY2VudCcsICdwb3N0MjAwOV9wZXJjZW50JywgJ2JhdHNfUicsJ3Rocm93c19SJywgJ2RlYnV0WWVhcicsICdmaW5hbFllYXInLCAnQVZFJywgJ09CUCcsJ1NsdWdfUGVyY2VudCcsICdPUFMnXSwgc2tpcHJvd3M9MSwgaW5kZXhfY29sPTApXG5kZlsnZGVidXQnXSA9ICBwZC50b19kYXRldGltZShkZlsnZGVidXQnXSlcbmRmWydmaW5hbEdhbWUnXSA9IHBkLnRvX2RhdGV0aW1lKGRmWydmaW5hbEdhbWUnXSlcbmRmWydkZWJ1dFllYXInXSA9IHBkLnRvX251bWVyaWMoZGZbJ2RlYnV0J10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmRmWydmaW5hbFllYXInXSA9IHBkLnRvX251bWVyaWMoZGZbJ2ZpbmFsR2FtZSddLmR0LnN0cmZ0aW1lKCclWScpLCBlcnJvcnM9J2NvZXJjZScpXG5kZiA9IGRmWyhkZlsncGxheWVySUQnXSAhPSAncm9zZXBlMDEnKSAmIChkZlsncGxheWVySUQnXSAhPSAnamFja3NqbzAxJyldXG5kZWYgZmlyc3RfYWFwKGNvbCk6XG4gICAgaWYgY29sID09ICdyb2JpbmphMDInOlxuICAgICAgICByZXR1cm4gMVxuICAgIGVsc2U6XG4gICAgICAgIHJldHVybiAwXG4gICAgXG5kZlsnZmlyc3RfYWFwJ10gPSBkZlsncGxheWVySUQnXS5hcHBseShmaXJzdF9hYXApXG5kZl9ob2YgPSBkZltkZlsnSG9GJ10gPT0gMV1cbmRmID0gZGYuZHJvcG5hKClcbmRmWydZU0xTJ10gPSAyMDE2IC0gZGZbJ2ZpbmFsWWVhciddXG5kZl9oaXR0ZXJzID0gZGZbZGZbJ1lTTFMnXSA+IDE1XVxubnVtX2NvbHNfaGl0dGVycyA9IFsncGxheWVySUQnLCAnbmFtZUZpcnN0JywgJ25hbWVMYXN0JywgJ0hvRicsICdZZWFyc19QbGF5ZWQnLCAnSCcsICdCQicsICdIUicsICdBVkUnLCAnT0JQJywgJ1NsdWdfUGVyY2VudCcsICdPUFMnLCAgJ1JCSScsJ1InLCAnU0InLCAnMkInLCAnM0InLCAnQUInLCAnU08nLCAnTW9zdCBWYWx1YWJsZSBQbGF5ZXInLCAnV29ybGQgU2VyaWVzIE1WUCcsICdBU19nYW1lcycsJ0dvbGQgR2xvdmUnLCAnUm9va2llIG9mIHRoZSBZZWFyJywnU2lsdmVyIFNsdWdnZXInLCAnYmF0c19SJywgJ3Rocm93c19SJywgJ0RQZicsICdBZicsICdFZicsICdZU0xTJywgJ0dfYWxsJywgJzE5NjMtNzZfcGVyY2VudCcsICcxOTkzLTIwMDlfcGVyY2VudCcsICcxOTQ2LTYyX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsJ0dfZGhfcGVyY2VudCcsICcxOTIwLTQxX3BlcmNlbnQnLCAnR19zc19wZXJjZW50JywgJ3Bvc3QyMDA5X3BlcmNlbnQnLCAnMTk3Ny05Ml9wZXJjZW50JywgJ0dfMmJfcGVyY2VudCcsICdHXzNiX3BlcmNlbnQnLCdHX29mX3BlcmNlbnQnLCAncHJlMTkyMF9wZXJjZW50JywgJ2ZpcnN0X2FhcCddXG5kYXRhID0gZGZfaGl0dGVyc1tudW1fY29sc19oaXR0ZXJzXVxudGFyZ2V0ID0gZGF0YVsnSG9GJ11cbmZlYXR1cmVzID0gZGF0YS5kcm9wKFsncGxheWVySUQnLCAnbmFtZUZpcnN0JywgJ25hbWVMYXN0JywgJ0hvRiddLCBheGlzPTEpXG5mcm9tIHNrbGVhcm4uY3Jvc3NfdmFsaWRhdGlvbiBpbXBvcnQgY3Jvc3NfdmFsX3ByZWRpY3QsIEtGb2xkXG5mcm9tIHNrbGVhcm4ubGluZWFyX21vZGVsIGltcG9ydCBMb2dpc3RpY1JlZ3Jlc3Npb25cbmxyID0gTG9naXN0aWNSZWdyZXNzaW9uKGNsYXNzX3dlaWdodD0nYmFsYW5jZWQnKVxua2YgPSBLRm9sZChmZWF0dXJlcy5zaGFwZVswXSwgcmFuZG9tX3N0YXRlPTEpXG5wcmVkaWN0aW9uc19sciA9IGNyb3NzX3ZhbF9wcmVkaWN0KGxyLCBmZWF0dXJlcywgdGFyZ2V0LCBjdj1rZikiLCJzYW1wbGUiOiIjIEltcG9ydCBOdW1QeSBhcyBucFxuaW1wb3J0IG51bXB5IGFzIF9fXG5cbiMgQ29udmVydCBwcmVkaWN0aW9ucyBhbmQgdGFyZ2V0IHRvIE51bVB5IGFycmF5c1xubnBfcHJlZGljdGlvbnNfbHIgPSBucC5hc2FycmF5KHByZWRpY3Rpb25zX2xyKVxubnBfdGFyZ2V0ID0gdGFyZ2V0LmFzX21hdHJpeCgpIiwic29sdXRpb24iOiIjIEltcG9ydCBOdW1QeSBhcyBucFxuaW1wb3J0IG51bXB5IGFzIG5wXG5cbiMgQ29udmVydCBwcmVkaWN0aW9ucyBhbmQgdGFyZ2V0IHRvIE51bVB5IGFycmF5c1xubnBfcHJlZGljdGlvbnNfbHIgPSBucC5hc2FycmF5KHByZWRpY3Rpb25zX2xyKVxubnBfdGFyZ2V0ID0gdGFyZ2V0LmFzX21hdHJpeCgpIiwic2N0IjoiRXgoKS50ZXN0X2ltcG9ydChcIm51bXB5XCIpXG5FeCgpLnRlc3Rfb2JqZWN0KFwibnBfcHJlZGljdGlvbnNfbHJcIilcbkV4KCkudGVzdF9vYmplY3QoXCJucF90YXJnZXRcIilcbnN1Y2Nlc3NfbXNnKFwiQXdlc29tZSFcIikifQ==

Create a filter for each of the four possible prediction scenarios:

True Positive: Predictions = 1, Target = 1
Fales Negative: Predictions = 0, Target = 1
False Positive: Predictions = 1, Target = 0
True Negative: Predictions = 0, Target = 0

Then determine the count by applying the filter to your predictions. Now you can determine your accuracy rate using the following formulas:

True Positive rate: True Positives / (True Positives + False Negatives)
False Negative rate: False Negatives / (False Negatives + True Positives)
False Positive rate: False Positives / (False Positives + True Negatives)

Print out the count for each except True Negatives and each of your accuracy rates.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiZnJvbSBudW1weSBpbXBvcnQgcmFuZG9tXG5yYW5kb20uc2VlZCg0MilcbmltcG9ydCBwYW5kYXMgYXMgcGRcbmltcG9ydCBudW1weSBhcyBucFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcbmRmID1wZC5yZWFkX2NzdihcImh0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL2NhbGNkZi5jc3ZcIixuYW1lcz1bJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdkZWJ1dCcsICdmaW5hbEdhbWUnLCAnRycsICdBQicsJ1InLCAnSCcsICcyQicsICczQicsICdIUicsICdSQkknLCAnU0InLCAnQkInLCAnU08nLCAnSEJQJywgJ1NIJywgJ1NGJywnWWVhcnNfUGxheWVkJywgJ0FmJywgJ0VmJywgJ0RQZicsICdIb0YnLCAnTW9zdCBWYWx1YWJsZSBQbGF5ZXInLCdBU19nYW1lcycsICdHb2xkIEdsb3ZlJywgJ1Jvb2tpZSBvZiB0aGUgWWVhcicsICdXb3JsZCBTZXJpZXMgTVZQJywnU2lsdmVyIFNsdWdnZXInLCAnR19hbGwnLCAnR19wJywgJ0dfYycsICdHXzFiJywgJ0dfMmInLCAnR18zYicsICdHX3NzJywnR19sZicsICdHX2NmJywgJ0dfcmYnLCAnR19vZicsICdHX2RoJywgJ3ByZTE5MjAnLCAnMTkyMC00MScsICcxOTQyLTQ1JywnMTk0Ni02MicsICcxOTYzLTc2JywgJzE5NzctOTInLCAnMTk5My0yMDA5JywgJ3Bvc3QyMDA5JywgJ0dfcF9wZXJjZW50JywnR19jX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJ0dfMmJfcGVyY2VudCcsICdHXzNiX3BlcmNlbnQnLCdHX3NzX3BlcmNlbnQnLCAnR19sZl9wZXJjZW50JywgJ0dfY2ZfcGVyY2VudCcsICdHX3JmX3BlcmNlbnQnLCdHX29mX3BlcmNlbnQnLCAnR19kaF9wZXJjZW50JywgJ3ByZTE5MjBfcGVyY2VudCcsICcxOTIwLTQxX3BlcmNlbnQnLCAnMTk0Mi00NV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsJzE5NjMtNzZfcGVyY2VudCcsJzE5NzctOTJfcGVyY2VudCcsJzE5OTMtMjAwOV9wZXJjZW50JywgJ3Bvc3QyMDA5X3BlcmNlbnQnLCAnYmF0c19SJywndGhyb3dzX1InLCAnZGVidXRZZWFyJywgJ2ZpbmFsWWVhcicsICdBVkUnLCAnT0JQJywnU2x1Z19QZXJjZW50JywgJ09QUyddLCBza2lwcm93cz0xLCBpbmRleF9jb2w9MClcbmRmWydkZWJ1dCddID0gIHBkLnRvX2RhdGV0aW1lKGRmWydkZWJ1dCddKVxuZGZbJ2ZpbmFsR2FtZSddID0gcGQudG9fZGF0ZXRpbWUoZGZbJ2ZpbmFsR2FtZSddKVxuZGZbJ2RlYnV0WWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZGVidXQnXS5kdC5zdHJmdGltZSgnJVknKSwgZXJyb3JzPSdjb2VyY2UnKVxuZGZbJ2ZpbmFsWWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZmluYWxHYW1lJ10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmRmID0gZGZbKGRmWydwbGF5ZXJJRCddICE9ICdyb3NlcGUwMScpICYgKGRmWydwbGF5ZXJJRCddICE9ICdqYWNrc2pvMDEnKV1cbmRlZiBmaXJzdF9hYXAoY29sKTpcbiAgICBpZiBjb2wgPT0gJ3JvYmluamEwMic6XG4gICAgICAgIHJldHVybiAxXG4gICAgZWxzZTpcbiAgICAgICAgcmV0dXJuIDBcbiAgICBcbmRmWydmaXJzdF9hYXAnXSA9IGRmWydwbGF5ZXJJRCddLmFwcGx5KGZpcnN0X2FhcClcbmRmX2hvZiA9IGRmW2RmWydIb0YnXSA9PSAxXVxuZGYgPSBkZi5kcm9wbmEoKVxuZGZbJ1lTTFMnXSA9IDIwMTYgLSBkZlsnZmluYWxZZWFyJ11cbmRmX2hpdHRlcnMgPSBkZltkZlsnWVNMUyddID4gMTVdXG5udW1fY29sc19oaXR0ZXJzID0gWydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnSG9GJywgJ1llYXJzX1BsYXllZCcsICdIJywgJ0JCJywgJ0hSJywgJ0FWRScsICdPQlAnLCAnU2x1Z19QZXJjZW50JywgJ09QUycsICAnUkJJJywnUicsICdTQicsICcyQicsICczQicsICdBQicsICdTTycsICdNb3N0IFZhbHVhYmxlIFBsYXllcicsICdXb3JsZCBTZXJpZXMgTVZQJywgJ0FTX2dhbWVzJywnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnU2lsdmVyIFNsdWdnZXInLCAnYmF0c19SJywgJ3Rocm93c19SJywgJ0RQZicsICdBZicsICdFZicsICdZU0xTJywgJ0dfYWxsJywgJzE5NjMtNzZfcGVyY2VudCcsICcxOTkzLTIwMDlfcGVyY2VudCcsICcxOTQ2LTYyX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsJ0dfZGhfcGVyY2VudCcsICcxOTIwLTQxX3BlcmNlbnQnLCAnR19zc19wZXJjZW50JywgJ3Bvc3QyMDA5X3BlcmNlbnQnLCAnMTk3Ny05Ml9wZXJjZW50JywgJ0dfMmJfcGVyY2VudCcsICdHXzNiX3BlcmNlbnQnLCdHX29mX3BlcmNlbnQnLCAncHJlMTkyMF9wZXJjZW50JywgJ2ZpcnN0X2FhcCddXG5kYXRhID0gZGZfaGl0dGVyc1tudW1fY29sc19oaXR0ZXJzXVxudGFyZ2V0ID0gZGF0YVsnSG9GJ11cbmZlYXR1cmVzID0gZGF0YS5kcm9wKFsncGxheWVySUQnLCAnbmFtZUZpcnN0JywgJ25hbWVMYXN0JywgJ0hvRiddLCBheGlzPTEpXG5mcm9tIHNrbGVhcm4uY3Jvc3NfdmFsaWRhdGlvbiBpbXBvcnQgY3Jvc3NfdmFsX3ByZWRpY3QsIEtGb2xkXG5mcm9tIHNrbGVhcm4ubGluZWFyX21vZGVsIGltcG9ydCBMb2dpc3RpY1JlZ3Jlc3Npb25cbmxyID0gTG9naXN0aWNSZWdyZXNzaW9uKGNsYXNzX3dlaWdodD0nYmFsYW5jZWQnKVxua2YgPSBLRm9sZChmZWF0dXJlcy5zaGFwZVswXSwgcmFuZG9tX3N0YXRlPTEpXG5wcmVkaWN0aW9uc19sciA9IGNyb3NzX3ZhbF9wcmVkaWN0KGxyLCBmZWF0dXJlcywgdGFyZ2V0LCBjdj1rZilcbm5wX3ByZWRpY3Rpb25zX2xyID0gbnAuYXNhcnJheShwcmVkaWN0aW9uc19scilcbm5wX3RhcmdldCA9IHRhcmdldC5hc19tYXRyaXgoKSIsInNhbXBsZSI6IiMgRGV0ZXJtaW5lIFRydWUgUG9zaXRpdmUgY291bnRcbnRwX2ZpbHRlcl9sciA9IChucF9wcmVkaWN0aW9uc19sciA9PSAxKSAmIChucF90YXJnZXQgPT0gMSlcbnRwX2xyID0gbGVuKG5wX3ByZWRpY3Rpb25zX2xyW3RwX2ZpbHRlcl9scl0pXG5cbiMgRGV0ZXJtaW5lIEZhbHNlIE5lZ2F0aXZlIGNvdW50XG5mbl9maWx0ZXJfbHIgPSAobnBfcHJlZGljdGlvbnNfbHIgPT0gMCkgJiAobnBfdGFyZ2V0ID09IDEpXG5mbl9sciA9IGxlbihucF9wcmVkaWN0aW9uc19scltmbl9maWx0ZXJfbHJdKVxuXG4jIERldGVybWluZSBGYWxzZSBQb3NpdGl2ZSBjb3VudFxuZnBfZmlsdGVyX2xyID0gKG5wX3ByZWRpY3Rpb25zX2xyID09IDEpICYgKG5wX3RhcmdldCA9PSAwKVxuZnBfbHIgPSBsZW4obnBfcHJlZGljdGlvbnNfbHJbZnBfZmlsdGVyX2xyXSlcblxuIyBEZXRlcm1pbmUgVHJ1ZSBOZWdhdGl2ZSBjb3VudFxudG5fZmlsdGVyX2xyID0gKG5wX3ByZWRpY3Rpb25zX2xyID09IDApICYgKG5wX3RhcmdldCA9PSAwKVxudG5fbHIgPSBsZW4obnBfcHJlZGljdGlvbnNfbHJbdG5fZmlsdGVyX2xyXSlcblxuIyBEZXRlcm1pbmUgVHJ1ZSBQb3NpdGl2ZSByYXRlXG50cHJfbHIgPSB0cF9sciAvIChfX19fX19fX19fX19fKVxuXG4jIERldGVybWluZSBGYWxzZSBOZWdhdGl2ZSByYXRlXG5mbnJfbHIgPSBfX19fXyAvIChmbl9sciArIHRwX2xyKVxuXG4jIERldGVybWluZSBGYWxzZSBQb3NpdGl2ZSByYXRlXG5mcHJfbHIgPSBmcF9sciAvIChfX19fXyArIHRuX2xyKVxuXG4jIFByaW50IGVhY2ggY291bnRcbnByaW50KHRwX2xyKVxucHJpbnQoZm5fbHIpXG5wcmludChmcF9scilcblxuIyBQcmludCBlYWNoIHJhdGVcbnByaW50KHRwcl9scilcbnByaW50KGZucl9scilcbnByaW50KGZwcl9scikiLCJzb2x1dGlvbiI6IiMgRGV0ZXJtaW5lIFRydWUgUG9zaXRpdmUgY291bnRcbnRwX2ZpbHRlcl9sciA9IChucF9wcmVkaWN0aW9uc19sciA9PSAxKSAmIChucF90YXJnZXQgPT0gMSlcbnRwX2xyID0gbGVuKG5wX3ByZWRpY3Rpb25zX2xyW3RwX2ZpbHRlcl9scl0pXG5cbiMgRGV0ZXJtaW5lIEZhbHNlIE5lZ2F0aXZlIGNvdW50XG5mbl9maWx0ZXJfbHIgPSAobnBfcHJlZGljdGlvbnNfbHIgPT0gMCkgJiAobnBfdGFyZ2V0ID09IDEpXG5mbl9sciA9IGxlbihucF9wcmVkaWN0aW9uc19scltmbl9maWx0ZXJfbHJdKVxuXG4jIERldGVybWluZSBGYWxzZSBQb3NpdGl2ZSBjb3VudFxuZnBfZmlsdGVyX2xyID0gKG5wX3ByZWRpY3Rpb25zX2xyID09IDEpICYgKG5wX3RhcmdldCA9PSAwKVxuZnBfbHIgPSBsZW4obnBfcHJlZGljdGlvbnNfbHJbZnBfZmlsdGVyX2xyXSlcblxuIyBEZXRlcm1pbmUgVHJ1ZSBOZWdhdGl2ZSBjb3VudFxudG5fZmlsdGVyX2xyID0gKG5wX3ByZWRpY3Rpb25zX2xyID09IDApICYgKG5wX3RhcmdldCA9PSAwKVxudG5fbHIgPSBsZW4obnBfcHJlZGljdGlvbnNfbHJbdG5fZmlsdGVyX2xyXSlcblxuIyBEZXRlcm1pbmUgVHJ1ZSBQb3NpdGl2ZSByYXRlXG50cHJfbHIgPSB0cF9sciAvICh0cF9sciArIGZuX2xyKVxuXG4jIERldGVybWluZSBGYWxzZSBOZWdhdGl2ZSByYXRlXG5mbnJfbHIgPSBmbl9sciAvIChmbl9sciArIHRwX2xyKVxuXG4jIERldGVybWluZSBGYWxzZSBQb3NpdGl2ZSByYXRlXG5mcHJfbHIgPSBmcF9sciAvIChmcF9sciArIHRuX2xyKVxuXG4jIFByaW50IGVhY2ggY291bnRcbnByaW50KHRwX2xyKVxucHJpbnQoZm5fbHIpXG5wcmludChmcF9scilcblxuIyBQcmludCBlYWNoIHJhdGVcbnByaW50KHRwcl9scilcbnByaW50KGZucl9scilcbnByaW50KGZwcl9scikiLCJzY3QiOiJFeCgpLnRlc3Rfb2JqZWN0KFwidHBfZmlsdGVyX2xyXCIpXG5FeCgpLnRlc3Rfb2JqZWN0KFwidHBfbHJcIilcbkV4KCkudGVzdF9vYmplY3QoXCJmbl9maWx0ZXJfbHJcIilcbkV4KCkudGVzdF9vYmplY3QoXCJmbl9sclwiKVxuRXgoKS50ZXN0X29iamVjdChcImZwX2ZpbHRlcl9sclwiKVxuRXgoKS50ZXN0X29iamVjdChcImZwX2xyXCIpXG5FeCgpLnRlc3Rfb2JqZWN0KFwidG5fZmlsdGVyX2xyXCIpXG5FeCgpLnRlc3Rfb2JqZWN0KFwidG5fbHJcIilcbkV4KCkudGVzdF9vYmplY3QoXCJ0cHJfbHJcIilcbkV4KCkudGVzdF9vYmplY3QoXCJmbnJfbHJcIilcbkV4KCkudGVzdF9vYmplY3QoXCJmcHJfbHJcIilcbkV4KCkudGVzdF9mdW5jdGlvbihcInByaW50XCIsIGluZGV4PTEpXG5FeCgpLnRlc3RfZnVuY3Rpb24oXCJwcmludFwiLCBpbmRleD0yKVxuRXgoKS50ZXN0X2Z1bmN0aW9uKFwicHJpbnRcIiwgaW5kZXg9MylcbkV4KCkudGVzdF9mdW5jdGlvbihcInByaW50XCIsIGluZGV4PTQpXG5FeCgpLnRlc3RfZnVuY3Rpb24oXCJwcmludFwiLCBpbmRleD01KVxuRXgoKS50ZXN0X2Z1bmN0aW9uKFwicHJpbnRcIiwgaW5kZXg9NilcbnN1Y2Nlc3NfbXNnKFwiTm93IHdoYXQgZG8gdGhlc2UgcmVzdWx0cyBvZiB0aGUgZXZhbHVhdGlvbiB0ZWxsIHlvdT9cIikifQ==

That first model was fairly accurate, selecting 54 of 61 Hall of Famers, but it had a relatively high false negative count at 36.

Random Forest

Next up is a Random Forest model. Import RandomForestClassifier from sklearn.ensemble. For this model, instead of setting class_weight to balanced, you’ll set it to penalty which is a dictionary you need to create with key 0 set to 100 and key 1 set to 1.

Create your model rf and set the parameters as follows: random_state= 1, n_estimators= 12, max_depth= 11, min_samples_leaf= 1, and class_weight= penalty.

Finally, make your predictions (predictions_rf) using cross_val_predict() the same as the previous model and again, convert your predictions to a NumPy array.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiZnJvbSBudW1weSBpbXBvcnQgcmFuZG9tXG5yYW5kb20uc2VlZCg0MilcbmltcG9ydCBwYW5kYXMgYXMgcGRcbmltcG9ydCBudW1weSBhcyBucFxuZnJvbSBza2xlYXJuLmNyb3NzX3ZhbGlkYXRpb24gaW1wb3J0IGNyb3NzX3ZhbF9wcmVkaWN0LCBLRm9sZFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcbmRmID1wZC5yZWFkX2NzdihcImh0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL2NhbGNkZi5jc3ZcIiwgbmFtZXM9WydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnZGVidXQnLCAnZmluYWxHYW1lJywgJ0cnLCAnQUInLCdSJywgJ0gnLCAnMkInLCAnM0InLCAnSFInLCAnUkJJJywgJ1NCJywgJ0JCJywgJ1NPJywgJ0hCUCcsICdTSCcsICdTRicsJ1llYXJzX1BsYXllZCcsICdBZicsICdFZicsICdEUGYnLCAnSG9GJywgJ01vc3QgVmFsdWFibGUgUGxheWVyJywnQVNfZ2FtZXMnLCAnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnV29ybGQgU2VyaWVzIE1WUCcsJ1NpbHZlciBTbHVnZ2VyJywgJ0dfYWxsJywgJ0dfcCcsICdHX2MnLCAnR18xYicsICdHXzJiJywgJ0dfM2InLCAnR19zcycsJ0dfbGYnLCAnR19jZicsICdHX3JmJywgJ0dfb2YnLCAnR19kaCcsICdwcmUxOTIwJywgJzE5MjAtNDEnLCAnMTk0Mi00NScsJzE5NDYtNjInLCAnMTk2My03NicsICcxOTc3LTkyJywgJzE5OTMtMjAwOScsICdwb3N0MjAwOScsICdHX3BfcGVyY2VudCcsJ0dfY19wZXJjZW50JywgJ0dfMWJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywnR19zc19wZXJjZW50JywgJ0dfbGZfcGVyY2VudCcsICdHX2NmX3BlcmNlbnQnLCAnR19yZl9wZXJjZW50JywnR19vZl9wZXJjZW50JywgJ0dfZGhfcGVyY2VudCcsICdwcmUxOTIwX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsICcxOTQ2LTYyX3BlcmNlbnQnLCcxOTYzLTc2X3BlcmNlbnQnLCcxOTc3LTkyX3BlcmNlbnQnLCcxOTkzLTIwMDlfcGVyY2VudCcsICdwb3N0MjAwOV9wZXJjZW50JywgJ2JhdHNfUicsJ3Rocm93c19SJywgJ2RlYnV0WWVhcicsICdmaW5hbFllYXInLCAnQVZFJywgJ09CUCcsJ1NsdWdfUGVyY2VudCcsICdPUFMnXSwgc2tpcHJvd3M9MSwgaW5kZXhfY29sPTApXG5kZlsnZGVidXQnXSA9ICBwZC50b19kYXRldGltZShkZlsnZGVidXQnXSlcbmRmWydmaW5hbEdhbWUnXSA9IHBkLnRvX2RhdGV0aW1lKGRmWydmaW5hbEdhbWUnXSlcbmRmWydkZWJ1dFllYXInXSA9IHBkLnRvX251bWVyaWMoZGZbJ2RlYnV0J10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmRmWydmaW5hbFllYXInXSA9IHBkLnRvX251bWVyaWMoZGZbJ2ZpbmFsR2FtZSddLmR0LnN0cmZ0aW1lKCclWScpLCBlcnJvcnM9J2NvZXJjZScpXG5kZiA9IGRmWyhkZlsncGxheWVySUQnXSAhPSAncm9zZXBlMDEnKSAmIChkZlsncGxheWVySUQnXSAhPSAnamFja3NqbzAxJyldXG5kZWYgZmlyc3RfYWFwKGNvbCk6XG4gICAgaWYgY29sID09ICdyb2JpbmphMDInOlxuICAgICAgICByZXR1cm4gMVxuICAgIGVsc2U6XG4gICAgICAgIHJldHVybiAwXG4gICAgXG5kZlsnZmlyc3RfYWFwJ10gPSBkZlsncGxheWVySUQnXS5hcHBseShmaXJzdF9hYXApXG5kZl9ob2YgPSBkZltkZlsnSG9GJ10gPT0gMV1cbmRmID0gZGYuZHJvcG5hKClcbmRmWydZU0xTJ10gPSAyMDE2IC0gZGZbJ2ZpbmFsWWVhciddXG5kZl9oaXR0ZXJzID0gZGZbZGZbJ1lTTFMnXSA+IDE1XVxubnVtX2NvbHNfaGl0dGVycyA9IFsncGxheWVySUQnLCAnbmFtZUZpcnN0JywgJ25hbWVMYXN0JywgJ0hvRicsICdZZWFyc19QbGF5ZWQnLCAnSCcsICdCQicsICdIUicsICdBVkUnLCAnT0JQJywgJ1NsdWdfUGVyY2VudCcsICdPUFMnLCAgJ1JCSScsJ1InLCAnU0InLCAnMkInLCAnM0InLCAnQUInLCAnU08nLCAnTW9zdCBWYWx1YWJsZSBQbGF5ZXInLCAnV29ybGQgU2VyaWVzIE1WUCcsICdBU19nYW1lcycsJ0dvbGQgR2xvdmUnLCAnUm9va2llIG9mIHRoZSBZZWFyJywgJ1NpbHZlciBTbHVnZ2VyJywgJ2JhdHNfUicsICd0aHJvd3NfUicsICdEUGYnLCAnQWYnLCAnRWYnLCAnWVNMUycsICdHX2FsbCcsICcxOTYzLTc2X3BlcmNlbnQnLCAnMTk5My0yMDA5X3BlcmNlbnQnLCAnMTk0Ni02Ml9wZXJjZW50JywgJ0dfMWJfcGVyY2VudCcsICcxOTQyLTQ1X3BlcmNlbnQnLCAnR19kaF9wZXJjZW50JywgJzE5MjAtNDFfcGVyY2VudCcsICdHX3NzX3BlcmNlbnQnLCdwb3N0MjAwOV9wZXJjZW50JywgJzE5NzctOTJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywnR19vZl9wZXJjZW50JywgJ3ByZTE5MjBfcGVyY2VudCcsICdmaXJzdF9hYXAnXVxuZGF0YSA9IGRmX2hpdHRlcnNbbnVtX2NvbHNfaGl0dGVyc11cbnRhcmdldCA9IGRhdGFbJ0hvRiddXG5ucF90YXJnZXQgPSB0YXJnZXQuYXNfbWF0cml4KClcbmZlYXR1cmVzID0gZGF0YS5kcm9wKFsncGxheWVySUQnLCAnbmFtZUZpcnN0JywgJ25hbWVMYXN0JywgJ0hvRiddLCBheGlzPTEpXG5rZiA9IEtGb2xkKGZlYXR1cmVzLnNoYXBlWzBdLCByYW5kb21fc3RhdGU9MSkiLCJzYW1wbGUiOiIjIEltcG9ydCBSYW5kb21Gb3Jlc3RDbGFzc2lmaWVyIGZyb20gc2tsZWFyblxuZnJvbSBza2xlYXJuLmVuc2VtYmxlIGltcG9ydCBSYW5kb21Gb3Jlc3RDbGFzc2lmaWVyXG5cbiMgQ3JlYXRlIHBlbmFsdHkgZGljdGlvbmFyeVxucGVuYWx0eSA9IHtcbiAgICAwOiAxMDAsXG4gICAgMTogMVxufVxuXG4jIENyZWF0ZSBSYW5kb20gRm9yZXN0IG1vZGVsXG5yZiA9IFJhbmRvbUZvcmVzdENsYXNzaWZpZXIocmFuZG9tX3N0YXRlPTEsbl9lc3RpbWF0b3JzPTEyLCBtYXhfZGVwdGg9MTEsIG1pbl9zYW1wbGVzX2xlYWY9MSwgY2xhc3Nfd2VpZ2h0PXBlbmFsdHkpXG5cbiMgQ3JlYXRlIHByZWRpY3Rpb25zIHVzaW5nIGNyb3NzIHZhbGlkYXRpb25cbnByZWRpY3Rpb25zX3JmID0gY3Jvc3NfdmFsX3ByZWRpY3QocmYsIGZlYXR1cmVzLCB0YXJnZXQsIGN2PWtmKVxuXG4jIENvbnZlcnQgcHJlZGljdGlvbnMgdG8gTnVtUHkgYXJyYXlcbm5wX3ByZWRpY3Rpb25zX3JmID0gbnAuYXNhcnJheShwcmVkaWN0aW9uc19yZikifQ==

As you did with the previous model, determine your True Positive, False Negative, and False Positive counts and rates.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiZnJvbSBudW1weSBpbXBvcnQgcmFuZG9tXG5yYW5kb20uc2VlZCg0MilcbmZyb20gc2tsZWFybi5lbnNlbWJsZSBpbXBvcnQgUmFuZG9tRm9yZXN0Q2xhc3NpZmllclxuaW1wb3J0IHBhbmRhcyBhcyBwZFxuaW1wb3J0IG51bXB5IGFzIG5wXG5mcm9tIHNrbGVhcm4uY3Jvc3NfdmFsaWRhdGlvbiBpbXBvcnQgY3Jvc3NfdmFsX3ByZWRpY3QsIEtGb2xkXG5mcm9tIGRhdGV0aW1lIGltcG9ydCBkYXRldGltZVxuZGYgPSBwZC5yZWFkX2NzdihcImh0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL2NhbGNkZi5jc3ZcIixuYW1lcz1bJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdkZWJ1dCcsICdmaW5hbEdhbWUnLCAnRycsICdBQicsJ1InLCAnSCcsICcyQicsICczQicsICdIUicsICdSQkknLCAnU0InLCAnQkInLCAnU08nLCAnSEJQJywgJ1NIJywgJ1NGJywnWWVhcnNfUGxheWVkJywgJ0FmJywgJ0VmJywgJ0RQZicsICdIb0YnLCAnTW9zdCBWYWx1YWJsZSBQbGF5ZXInLCdBU19nYW1lcycsICdHb2xkIEdsb3ZlJywgJ1Jvb2tpZSBvZiB0aGUgWWVhcicsICdXb3JsZCBTZXJpZXMgTVZQJywnU2lsdmVyIFNsdWdnZXInLCAnR19hbGwnLCAnR19wJywgJ0dfYycsICdHXzFiJywgJ0dfMmInLCAnR18zYicsICdHX3NzJywnR19sZicsICdHX2NmJywgJ0dfcmYnLCAnR19vZicsICdHX2RoJywgJ3ByZTE5MjAnLCAnMTkyMC00MScsICcxOTQyLTQ1JywnMTk0Ni02MicsICcxOTYzLTc2JywgJzE5NzctOTInLCAnMTk5My0yMDA5JywgJ3Bvc3QyMDA5JywgJ0dfcF9wZXJjZW50JywnR19jX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJ0dfMmJfcGVyY2VudCcsICdHXzNiX3BlcmNlbnQnLCdHX3NzX3BlcmNlbnQnLCAnR19sZl9wZXJjZW50JywgJ0dfY2ZfcGVyY2VudCcsICdHX3JmX3BlcmNlbnQnLCdHX29mX3BlcmNlbnQnLCAnR19kaF9wZXJjZW50JywgJ3ByZTE5MjBfcGVyY2VudCcsICcxOTIwLTQxX3BlcmNlbnQnLCAnMTk0Mi00NV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsJzE5NjMtNzZfcGVyY2VudCcsJzE5NzctOTJfcGVyY2VudCcsJzE5OTMtMjAwOV9wZXJjZW50JywgJ3Bvc3QyMDA5X3BlcmNlbnQnLCAnYmF0c19SJywndGhyb3dzX1InLCAnZGVidXRZZWFyJywgJ2ZpbmFsWWVhcicsICdBVkUnLCAnT0JQJywnU2x1Z19QZXJjZW50JywgJ09QUyddLCBza2lwcm93cz0xLCBpbmRleF9jb2w9MClcbmRmWydkZWJ1dCddID0gIHBkLnRvX2RhdGV0aW1lKGRmWydkZWJ1dCddKVxuZGZbJ2ZpbmFsR2FtZSddID0gcGQudG9fZGF0ZXRpbWUoZGZbJ2ZpbmFsR2FtZSddKVxuZGZbJ2RlYnV0WWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZGVidXQnXS5kdC5zdHJmdGltZSgnJVknKSwgZXJyb3JzPSdjb2VyY2UnKVxuZGZbJ2ZpbmFsWWVhciddID0gcGQudG9fbnVtZXJpYyhkZlsnZmluYWxHYW1lJ10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmRmID0gZGZbKGRmWydwbGF5ZXJJRCddICE9ICdyb3NlcGUwMScpICYgKGRmWydwbGF5ZXJJRCddICE9ICdqYWNrc2pvMDEnKV1cbmRlZiBmaXJzdF9hYXAoY29sKTpcbiAgICBpZiBjb2wgPT0gJ3JvYmluamEwMic6XG4gICAgICAgIHJldHVybiAxXG4gICAgZWxzZTpcbiAgICAgICAgcmV0dXJuIDBcbiAgICBcbmRmWydmaXJzdF9hYXAnXSA9IGRmWydwbGF5ZXJJRCddLmFwcGx5KGZpcnN0X2FhcClcbmRmX2hvZiA9IGRmW2RmWydIb0YnXSA9PSAxXVxuZGYgPSBkZi5kcm9wbmEoKVxuZGZbJ1lTTFMnXSA9IDIwMTYgLSBkZlsnZmluYWxZZWFyJ11cbmRmX2hpdHRlcnMgPSBkZltkZlsnWVNMUyddID4gMTVdXG5udW1fY29sc19oaXR0ZXJzID0gWydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnSG9GJywgJ1llYXJzX1BsYXllZCcsICdIJywgJ0JCJywgJ0hSJywgJ0FWRScsICdPQlAnLCAnU2x1Z19QZXJjZW50JywgJ09QUycsICAnUkJJJywnUicsICdTQicsICcyQicsICczQicsICdBQicsICdTTycsICdNb3N0IFZhbHVhYmxlIFBsYXllcicsICdXb3JsZCBTZXJpZXMgTVZQJywgJ0FTX2dhbWVzJywnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnU2lsdmVyIFNsdWdnZXInLCAnYmF0c19SJywgJ3Rocm93c19SJywgJ0RQZicsICdBZicsICdFZicsICdZU0xTJywgJ0dfYWxsJywgJzE5NjMtNzZfcGVyY2VudCcsICcxOTkzLTIwMDlfcGVyY2VudCcsICcxOTQ2LTYyX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsICdHX2RoX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JywgJ0dfc3NfcGVyY2VudCcsJ3Bvc3QyMDA5X3BlcmNlbnQnLCAnMTk3Ny05Ml9wZXJjZW50JywgJ0dfMmJfcGVyY2VudCcsICdHXzNiX3BlcmNlbnQnLCdHX29mX3BlcmNlbnQnLCAncHJlMTkyMF9wZXJjZW50JywgJ2ZpcnN0X2FhcCddXG5kYXRhID0gZGZfaGl0dGVyc1tudW1fY29sc19oaXR0ZXJzXVxudGFyZ2V0ID0gZGF0YVsnSG9GJ11cbm5wX3RhcmdldCA9IHRhcmdldC5hc19tYXRyaXgoKVxuZmVhdHVyZXMgPSBkYXRhLmRyb3AoWydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnSG9GJ10sIGF4aXM9MSlcbmtmID0gS0ZvbGQoZmVhdHVyZXMuc2hhcGVbMF0sIHJhbmRvbV9zdGF0ZT0xKVxucGVuYWx0eSA9IHtcbiAgICAwOiAxMDAsXG4gICAgMTogMVxufVxucmYgPSBSYW5kb21Gb3Jlc3RDbGFzc2lmaWVyKHJhbmRvbV9zdGF0ZT0xLG5fZXN0aW1hdG9ycz0xMiwgbWF4X2RlcHRoPTExLCBtaW5fc2FtcGxlc19sZWFmPTEsIGNsYXNzX3dlaWdodD1wZW5hbHR5KVxucHJlZGljdGlvbnNfcmYgPSBjcm9zc192YWxfcHJlZGljdChyZiwgZmVhdHVyZXMsIHRhcmdldCwgY3Y9a2YpXG5ucF9wcmVkaWN0aW9uc19yZiA9IG5wLmFzYXJyYXkocHJlZGljdGlvbnNfcmYpIiwic2FtcGxlIjoiIyBEZXRlcm1pbmUgVHJ1ZSBQb3NpdGl2ZSBjb3VudFxudHBfZmlsdGVyX3JmID0gKG5wX3ByZWRpY3Rpb25zX3JmID09IDEpICYgKG5wX3RhcmdldCA9PSAxKVxudHBfcmYgPSBsZW4obnBfcHJlZGljdGlvbnNfcmZbdHBfZmlsdGVyX3JmXSlcblxuIyBEZXRlcm1pbmUgRmFsc2UgTmVnYXRpdmUgY291bnRcbmZuX2ZpbHRlcl9yZiA9IChucF9wcmVkaWN0aW9uc19yZiA9PSAwKSAmIChucF90YXJnZXQgPT0gMSlcbmZuX3JmID0gbGVuKG5wX3ByZWRpY3Rpb25zX3JmW2ZuX2ZpbHRlcl9yZl0pXG5cbiMgRGV0ZXJtaW5lIEZhbHNlIFBvc2l0aXZlIGNvdW50XG5mcF9maWx0ZXJfcmYgPSAobnBfcHJlZGljdGlvbnNfcmYgPT0gMSkgJiAobnBfdGFyZ2V0ID09IDApXG5mcF9yZiA9IGxlbihucF9wcmVkaWN0aW9uc19yZltmcF9maWx0ZXJfcmZdKVxuXG4jIERldGVybWluZSBUcnVlIE5lZ2F0aXZlIGNvdW50XG50bl9maWx0ZXJfcmYgPSAobnBfcHJlZGljdGlvbnNfcmYgPT0gMCkgJiAobnBfdGFyZ2V0ID09IDApXG50bl9yZiA9IGxlbihucF9wcmVkaWN0aW9uc19yZlt0bl9maWx0ZXJfcmZdKVxuXG4jIERldGVybWluZSBUcnVlIFBvc2l0aXZlIHJhdGVcbnRwcl9yZiA9IHRwX3JmIC8gKHRwX3JmICsgZm5fcmYpXG5cbiMgRGV0ZXJtaW5lIEZhbHNlIE5lZ2F0aXZlIHJhdGVcbmZucl9yZiA9IGZuX3JmIC8gKGZuX3JmICsgdHBfcmYpXG5cbiMgRGV0ZXJtaW5lIEZhbHNlIFBvc2l0aXZlIHJhdGVcbmZwcl9yZiA9IGZwX3JmIC8gKGZwX3JmICsgdG5fcmYpXG5cbiMgUHJpbnQgZWFjaCBjb3VudFxucHJpbnQodHBfcmYpXG5wcmludChmbl9yZilcbnByaW50KGZwX3JmKVxuXG4jIFByaW50IGVhY2ggcmF0ZVxucHJpbnQodHByX3JmKVxucHJpbnQoZm5yX3JmKVxucHJpbnQoZnByX3JmKSJ9

The Random Forest model was slightly less accurate predicting 50 of 61 Hall of Famers, but with a very low false negative count of only 2.

The Random Forest model seems to perform better overall, so that’s the one you’ll use to make predictions with the “new” data you set aside.

Create a new DataFrame (new_data) from df_eligible using the num_cols_hitters list. Now create another DataFrame (new_features) by dropping the identification columns and the target column with drop().

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiZnJvbSBudW1weSBpbXBvcnQgcmFuZG9tXG5yYW5kb20uc2VlZCg0MilcbmltcG9ydCBwYW5kYXMgYXMgcGRcbmZyb20gZGF0ZXRpbWUgaW1wb3J0IGRhdGV0aW1lXG5kZiA9cGQucmVhZF9jc3YoXCJodHRwczovL3MzLmFtYXpvbmF3cy5jb20vYXNzZXRzLmRhdGFjYW1wLmNvbS9ibG9nX2Fzc2V0cy9NTEIrRGF0YS9jYWxjZGYuY3N2XCIsbmFtZXM9WydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnZGVidXQnLCAnZmluYWxHYW1lJywgJ0cnLCAnQUInLCdSJywgJ0gnLCAnMkInLCAnM0InLCAnSFInLCAnUkJJJywgJ1NCJywgJ0JCJywgJ1NPJywgJ0hCUCcsICdTSCcsICdTRicsJ1llYXJzX1BsYXllZCcsICdBZicsICdFZicsICdEUGYnLCAnSG9GJywgJ01vc3QgVmFsdWFibGUgUGxheWVyJywnQVNfZ2FtZXMnLCAnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnV29ybGQgU2VyaWVzIE1WUCcsJ1NpbHZlciBTbHVnZ2VyJywgJ0dfYWxsJywgJ0dfcCcsICdHX2MnLCAnR18xYicsICdHXzJiJywgJ0dfM2InLCAnR19zcycsJ0dfbGYnLCAnR19jZicsICdHX3JmJywgJ0dfb2YnLCAnR19kaCcsICdwcmUxOTIwJywgJzE5MjAtNDEnLCAnMTk0Mi00NScsJzE5NDYtNjInLCAnMTk2My03NicsICcxOTc3LTkyJywgJzE5OTMtMjAwOScsICdwb3N0MjAwOScsICdHX3BfcGVyY2VudCcsJ0dfY19wZXJjZW50JywgJ0dfMWJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywnR19zc19wZXJjZW50JywgJ0dfbGZfcGVyY2VudCcsICdHX2NmX3BlcmNlbnQnLCAnR19yZl9wZXJjZW50JywnR19vZl9wZXJjZW50JywgJ0dfZGhfcGVyY2VudCcsICdwcmUxOTIwX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsICcxOTQ2LTYyX3BlcmNlbnQnLCcxOTYzLTc2X3BlcmNlbnQnLCcxOTc3LTkyX3BlcmNlbnQnLCcxOTkzLTIwMDlfcGVyY2VudCcsICdwb3N0MjAwOV9wZXJjZW50JywgJ2JhdHNfUicsJ3Rocm93c19SJywgJ2RlYnV0WWVhcicsICdmaW5hbFllYXInLCAnQVZFJywgJ09CUCcsJ1NsdWdfUGVyY2VudCcsICdPUFMnXSwgc2tpcHJvd3M9MSwgaW5kZXhfY29sPTApXG5kZlsnZGVidXQnXSA9ICBwZC50b19kYXRldGltZShkZlsnZGVidXQnXSlcbmRmWydmaW5hbEdhbWUnXSA9IHBkLnRvX2RhdGV0aW1lKGRmWydmaW5hbEdhbWUnXSlcbmRmWydkZWJ1dFllYXInXSA9IHBkLnRvX251bWVyaWMoZGZbJ2RlYnV0J10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmRmWydmaW5hbFllYXInXSA9IHBkLnRvX251bWVyaWMoZGZbJ2ZpbmFsR2FtZSddLmR0LnN0cmZ0aW1lKCclWScpLCBlcnJvcnM9J2NvZXJjZScpXG5kZiA9IGRmWyhkZlsncGxheWVySUQnXSAhPSAncm9zZXBlMDEnKSAmIChkZlsncGxheWVySUQnXSAhPSAnamFja3NqbzAxJyldXG5kZWYgZmlyc3RfYWFwKGNvbCk6XG4gICAgaWYgY29sID09ICdyb2JpbmphMDInOlxuICAgICAgICByZXR1cm4gMVxuICAgIGVsc2U6XG4gICAgICAgIHJldHVybiAwXG4gICAgXG5kZlsnZmlyc3RfYWFwJ10gPSBkZlsncGxheWVySUQnXS5hcHBseShmaXJzdF9hYXApXG5kZl9ob2YgPSBkZltkZlsnSG9GJ10gPT0gMV1cbmRmID0gZGYuZHJvcG5hKClcbmRmWydZU0xTJ10gPSAyMDE2IC0gZGZbJ2ZpbmFsWWVhciddXG5kZl9lbGlnaWJsZSA9IGRmW2RmWydZU0xTJ108PSAxNV1cbm51bV9jb2xzX2hpdHRlcnMgPSBbJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdIb0YnLCAnWWVhcnNfUGxheWVkJywgJ0gnLCAnQkInLCAnSFInLCAnQVZFJywgJ09CUCcsICdTbHVnX1BlcmNlbnQnLCAnT1BTJywgICdSQkknLCdSJywgJ1NCJywgJzJCJywgJzNCJywgJ0FCJywgJ1NPJywgJ01vc3QgVmFsdWFibGUgUGxheWVyJywgJ1dvcmxkIFNlcmllcyBNVlAnLCAnQVNfZ2FtZXMnLCdHb2xkIEdsb3ZlJywgJ1Jvb2tpZSBvZiB0aGUgWWVhcicsICdTaWx2ZXIgU2x1Z2dlcicsICdiYXRzX1InLCAndGhyb3dzX1InLCAnRFBmJywgJ0FmJywgJ0VmJywgJ1lTTFMnLCAnR19hbGwnLCAnMTk2My03Nl9wZXJjZW50JywgJzE5OTMtMjAwOV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsICdHXzFiX3BlcmNlbnQnLCAnMTk0Mi00NV9wZXJjZW50JywnR19kaF9wZXJjZW50JywgJzE5MjAtNDFfcGVyY2VudCcsICdHX3NzX3BlcmNlbnQnLCdwb3N0MjAwOV9wZXJjZW50JywgJzE5NzctOTJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywnR19vZl9wZXJjZW50JywgJ3ByZTE5MjBfcGVyY2VudCcsICdmaXJzdF9hYXAnXSIsInNhbXBsZSI6IiMgQ3JlYXRlIGEgbmV3IERhdGFGcmFtZSBmcm9tIGBkZl9lbGlnaWJsZWAgdXNpbmcgYG51bV9jb2xfaGl0dGVyc2Bcbm5ld19kYXRhID0gZGZfZWxpZ2libGVbbnVtX2NvbHNfaGl0dGVyc11cblxuIyBDcmVhdGUgYSBuZXcgZmVhdHVyZXMgRGF0YUZyYW1lXG5uZXdfZmVhdHVyZXMgPSBuZXdfZGF0YS5fX19fKFsncGxheWVySUQnLCAnbmFtZUZpcnN0JywgJ25hbWVMYXN0JywgJ0hvRiddLCBheGlzPTEpIiwic29sdXRpb24iOiIjIENyZWF0ZSBhIG5ldyBEYXRhRnJhbWUgZnJvbSBgZGZfZWxpZ2libGVgIHVzaW5nIGBudW1fY29sX2hpdHRlcnNgXG5uZXdfZGF0YSA9IGRmX2VsaWdpYmxlW251bV9jb2xzX2hpdHRlcnNdXG5cbiMgQ3JlYXRlIGEgbmV3IGZlYXR1cmVzIERhdGFGcmFtZVxubmV3X2ZlYXR1cmVzID0gbmV3X2RhdGEuZHJvcChbJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdIb0YnXSwgYXhpcz0xKSIsInNjdCI6IkV4KCkudGVzdF9vYmplY3QoXCJuZXdfZGF0YVwiKVxuRXgoKS50ZXN0X29iamVjdChcIm5ld19mZWF0dXJlc1wiKVxuc3VjY2Vzc19tc2coXCJHcmVhdCEgTm93IHlvdSdyZSByZWFkeSB0byBnZXQgc3RhcnRlZCB3aXRoIHRoZSBSYW5kb20gRm9yZXN0IE1vZGVsIVwiKSJ9

Now you can use the fit() method to fit the rf model using the features and target you used earlier. Next, you can predict the probability that a player in the “new” data will be voted into the Hall of Fame. Use the predict_proba() method on the rf model using new_features.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiZnJvbSBudW1weSBpbXBvcnQgcmFuZG9tXG5yYW5kb20uc2VlZCg0MilcbmZyb20gc2tsZWFybi5lbnNlbWJsZSBpbXBvcnQgUmFuZG9tRm9yZXN0Q2xhc3NpZmllclxuaW1wb3J0IHBhbmRhcyBhcyBwZFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcbmRmID0gcGQucmVhZF9jc3YoXCJodHRwczovL3MzLmFtYXpvbmF3cy5jb20vYXNzZXRzLmRhdGFjYW1wLmNvbS9ibG9nX2Fzc2V0cy9NTEIrRGF0YS9jYWxjZGYuY3N2XCIsIG5hbWVzPVsncGxheWVySUQnLCAnbmFtZUZpcnN0JywgJ25hbWVMYXN0JywgJ2RlYnV0JywgJ2ZpbmFsR2FtZScsICdHJywgJ0FCJywnUicsICdIJywgJzJCJywgJzNCJywgJ0hSJywgJ1JCSScsICdTQicsICdCQicsICdTTycsICdIQlAnLCAnU0gnLCAnU0YnLCdZZWFyc19QbGF5ZWQnLCAnQWYnLCAnRWYnLCAnRFBmJywgJ0hvRicsICdNb3N0IFZhbHVhYmxlIFBsYXllcicsJ0FTX2dhbWVzJywgJ0dvbGQgR2xvdmUnLCAnUm9va2llIG9mIHRoZSBZZWFyJywgJ1dvcmxkIFNlcmllcyBNVlAnLCdTaWx2ZXIgU2x1Z2dlcicsICdHX2FsbCcsICdHX3AnLCAnR19jJywgJ0dfMWInLCAnR18yYicsICdHXzNiJywgJ0dfc3MnLCdHX2xmJywgJ0dfY2YnLCAnR19yZicsICdHX29mJywgJ0dfZGgnLCAncHJlMTkyMCcsICcxOTIwLTQxJywgJzE5NDItNDUnLCcxOTQ2LTYyJywgJzE5NjMtNzYnLCAnMTk3Ny05MicsICcxOTkzLTIwMDknLCAncG9zdDIwMDknLCAnR19wX3BlcmNlbnQnLCdHX2NfcGVyY2VudCcsICdHXzFiX3BlcmNlbnQnLCAnR18yYl9wZXJjZW50JywgJ0dfM2JfcGVyY2VudCcsJ0dfc3NfcGVyY2VudCcsICdHX2xmX3BlcmNlbnQnLCAnR19jZl9wZXJjZW50JywgJ0dfcmZfcGVyY2VudCcsJ0dfb2ZfcGVyY2VudCcsICdHX2RoX3BlcmNlbnQnLCAncHJlMTkyMF9wZXJjZW50JywgJzE5MjAtNDFfcGVyY2VudCcsICcxOTQyLTQ1X3BlcmNlbnQnLCAnMTk0Ni02Ml9wZXJjZW50JywnMTk2My03Nl9wZXJjZW50JywnMTk3Ny05Ml9wZXJjZW50JywnMTk5My0yMDA5X3BlcmNlbnQnLCAncG9zdDIwMDlfcGVyY2VudCcsICdiYXRzX1InLCd0aHJvd3NfUicsICdkZWJ1dFllYXInLCAnZmluYWxZZWFyJywgJ0FWRScsICdPQlAnLCdTbHVnX1BlcmNlbnQnLCAnT1BTJ10sIHNraXByb3dzPTEsIGluZGV4X2NvbD0wKVxuZGZbJ2RlYnV0J10gPSAgcGQudG9fZGF0ZXRpbWUoZGZbJ2RlYnV0J10pXG5kZlsnZmluYWxHYW1lJ10gPSBwZC50b19kYXRldGltZShkZlsnZmluYWxHYW1lJ10pXG5kZlsnZGVidXRZZWFyJ10gPSBwZC50b19udW1lcmljKGRmWydkZWJ1dCddLmR0LnN0cmZ0aW1lKCclWScpLCBlcnJvcnM9J2NvZXJjZScpXG5kZlsnZmluYWxZZWFyJ10gPSBwZC50b19udW1lcmljKGRmWydmaW5hbEdhbWUnXS5kdC5zdHJmdGltZSgnJVknKSwgZXJyb3JzPSdjb2VyY2UnKVxuZGYgPSBkZlsoZGZbJ3BsYXllcklEJ10gIT0gJ3Jvc2VwZTAxJykgJiAoZGZbJ3BsYXllcklEJ10gIT0gJ2phY2tzam8wMScpXVxuZGVmIGZpcnN0X2FhcChjb2wpOlxuICAgIGlmIGNvbCA9PSAncm9iaW5qYTAyJzpcbiAgICAgICAgcmV0dXJuIDFcbiAgICBlbHNlOlxuICAgICAgICByZXR1cm4gMFxuICAgIFxuZGZbJ2ZpcnN0X2FhcCddID0gZGZbJ3BsYXllcklEJ10uYXBwbHkoZmlyc3RfYWFwKVxuZGZfaG9mID0gZGZbZGZbJ0hvRiddID09IDFdXG5kZiA9IGRmLmRyb3BuYSgpXG5kZlsnWVNMUyddID0gMjAxNiAtIGRmWydmaW5hbFllYXInXVxuZGZfZWxpZ2libGUgPSBkZltkZlsnWVNMUyddPD0gMTVdXG5kZl9oaXR0ZXJzID0gZGZbZGZbJ1lTTFMnXSA+IDE1XVxubnVtX2NvbHNfaGl0dGVycyA9IFsncGxheWVySUQnLCAnbmFtZUZpcnN0JywgJ25hbWVMYXN0JywgJ0hvRicsICdZZWFyc19QbGF5ZWQnLCAnSCcsICdCQicsICdIUicsICdBVkUnLCAnT0JQJywgJ1NsdWdfUGVyY2VudCcsICdPUFMnLCAgJ1JCSScsICdSJywgJ1NCJywgJzJCJywgJzNCJywgJ0FCJywgJ1NPJywgJ01vc3QgVmFsdWFibGUgUGxheWVyJywgJ1dvcmxkIFNlcmllcyBNVlAnLCAnQVNfZ2FtZXMnLCdHb2xkIEdsb3ZlJywgJ1Jvb2tpZSBvZiB0aGUgWWVhcicsICdTaWx2ZXIgU2x1Z2dlcicsICdiYXRzX1InLCAndGhyb3dzX1InLCAnRFBmJywgJ0FmJywgJ0VmJywgJ1lTTFMnLCAnR19hbGwnLCAnMTk2My03Nl9wZXJjZW50JywgJzE5OTMtMjAwOV9wZXJjZW50JywgJzE5NDYtNjJfcGVyY2VudCcsICdHXzFiX3BlcmNlbnQnLCAnMTk0Mi00NV9wZXJjZW50JywnR19kaF9wZXJjZW50JywgJzE5MjAtNDFfcGVyY2VudCcsICdHX3NzX3BlcmNlbnQnLCdwb3N0MjAwOV9wZXJjZW50JywgJzE5NzctOTJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywnR19vZl9wZXJjZW50JywgJ3ByZTE5MjBfcGVyY2VudCcsICdmaXJzdF9hYXAnXVxuZGF0YSA9IGRmX2hpdHRlcnNbbnVtX2NvbHNfaGl0dGVyc11cbnRhcmdldCA9IGRhdGFbJ0hvRiddXG5mZWF0dXJlcyA9IGRhdGEuZHJvcChbJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdIb0YnXSwgYXhpcz0xKVxucGVuYWx0eSA9IHtcbiAgICAwOiAxMDAsXG4gICAgMTogMVxufVxucmYgPSBSYW5kb21Gb3Jlc3RDbGFzc2lmaWVyKHJhbmRvbV9zdGF0ZT0xLG5fZXN0aW1hdG9ycz0xMiwgbWF4X2RlcHRoPTExLCBtaW5fc2FtcGxlc19sZWFmPTEsIGNsYXNzX3dlaWdodD1wZW5hbHR5KVxubmV3X2RhdGEgPSBkZl9lbGlnaWJsZVtudW1fY29sc19oaXR0ZXJzXVxubmV3X2ZlYXR1cmVzID0gbmV3X2RhdGEuZHJvcChbJ3BsYXllcklEJywgJ25hbWVGaXJzdCcsICduYW1lTGFzdCcsICdIb0YnXSwgYXhpcz0xKSIsInNhbXBsZSI6IiMgRml0IHRoZSBSYW5kb20gRm9yZXN0IG1vZGVsXG5yZi5maXQoZmVhdHVyZXMsIF9fX19fXylcblxuIyBFc3RpbWF0ZSBwcm9iYWJpbGl0aWVzIG9mIEhhbGwgb2YgRmFtZSBpbmR1Y3Rpb25cbnByb2JhYmlsaXRpZXMgPSByZi5wcmVkaWN0X3Byb2JhKF9fX19fX19fX19fXykiLCJzb2x1dGlvbiI6IiMgRml0IHRoZSBSYW5kb20gRm9yZXN0IG1vZGVsXG5yZi5maXQoZmVhdHVyZXMsIHRhcmdldClcblxuIyBFc3RpbWF0ZSBwcm9iYWJpbGl0aWVzIG9mIEhhbGwgb2YgRmFtZSBpbmR1Y3Rpb25cbnByb2JhYmlsaXRpZXMgPSByZi5wcmVkaWN0X3Byb2JhKG5ld19mZWF0dXJlcykiLCJzY3QiOiJFeCgpLnRlc3RfZnVuY3Rpb24oXCJyZi5maXRcIilcbkV4KCkudGVzdF9vYmplY3QoXCJwcm9iYWJpbGl0aWVzXCIpXG5zdWNjZXNzX21zZyhcIlByaW50IG91dCB0aGUgcHJvYmFiaWxpdGllcy4gV2hhdCBkbyB5b3Ugbm90aWNlP1wiKSJ9

Finally, convert probabilities to a pandas DataFrame called hof_predictions. Sort hof_predictions in descending order.

Now, print out each of the first 50 rows from hof_predictions along with the names and important statistics found in new_data. These are the 50 players your model has predicted to be the most likely to be voted into the Hall of Fame, along with the estimated probability and the players career statistics.

eyJsYW5ndWFnZSI6InB5dGhvbiIsInByZV9leGVyY2lzZV9jb2RlIjoiZnJvbSBudW1weSBpbXBvcnQgcmFuZG9tXG5yYW5kb20uc2VlZCg0MilcbmZyb20gc2tsZWFybi5lbnNlbWJsZSBpbXBvcnQgUmFuZG9tRm9yZXN0Q2xhc3NpZmllclxuaW1wb3J0IHBhbmRhcyBhcyBwZFxuZnJvbSBkYXRldGltZSBpbXBvcnQgZGF0ZXRpbWVcblxuZGYgPSBwZC5yZWFkX2NzdihcImh0dHBzOi8vczMuYW1hem9uYXdzLmNvbS9hc3NldHMuZGF0YWNhbXAuY29tL2Jsb2dfYXNzZXRzL01MQitEYXRhL2NhbGNkZi5jc3ZcIiwgbmFtZXM9WydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnZGVidXQnLCAnZmluYWxHYW1lJywgJ0cnLCAnQUInLCdSJywgJ0gnLCAnMkInLCAnM0InLCAnSFInLCAnUkJJJywgJ1NCJywgJ0JCJywgJ1NPJywgJ0hCUCcsICdTSCcsICdTRicsJ1llYXJzX1BsYXllZCcsICdBZicsICdFZicsICdEUGYnLCAnSG9GJywgJ01vc3QgVmFsdWFibGUgUGxheWVyJywnQVNfZ2FtZXMnLCAnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnV29ybGQgU2VyaWVzIE1WUCcsJ1NpbHZlciBTbHVnZ2VyJywgJ0dfYWxsJywgJ0dfcCcsICdHX2MnLCAnR18xYicsICdHXzJiJywgJ0dfM2InLCAnR19zcycsJ0dfbGYnLCAnR19jZicsICdHX3JmJywgJ0dfb2YnLCAnR19kaCcsICdwcmUxOTIwJywgJzE5MjAtNDEnLCAnMTk0Mi00NScsJzE5NDYtNjInLCAnMTk2My03NicsICcxOTc3LTkyJywgJzE5OTMtMjAwOScsICdwb3N0MjAwOScsICdHX3BfcGVyY2VudCcsJ0dfY19wZXJjZW50JywgJ0dfMWJfcGVyY2VudCcsICdHXzJiX3BlcmNlbnQnLCAnR18zYl9wZXJjZW50JywnR19zc19wZXJjZW50JywgJ0dfbGZfcGVyY2VudCcsICdHX2NmX3BlcmNlbnQnLCAnR19yZl9wZXJjZW50JywnR19vZl9wZXJjZW50JywgJ0dfZGhfcGVyY2VudCcsICdwcmUxOTIwX3BlcmNlbnQnLCAnMTkyMC00MV9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsICcxOTQ2LTYyX3BlcmNlbnQnLCcxOTYzLTc2X3BlcmNlbnQnLCcxOTc3LTkyX3BlcmNlbnQnLCcxOTkzLTIwMDlfcGVyY2VudCcsICdwb3N0MjAwOV9wZXJjZW50JywgJ2JhdHNfUicsJ3Rocm93c19SJywgJ2RlYnV0WWVhcicsICdmaW5hbFllYXInLCAnQVZFJywgJ09CUCcsJ1NsdWdfUGVyY2VudCcsICdPUFMnXSwgc2tpcHJvd3M9MSwgaW5kZXhfY29sPTApXG5kZlsnZGVidXQnXSA9ICBwZC50b19kYXRldGltZShkZlsnZGVidXQnXSlcbmRmWydmaW5hbEdhbWUnXSA9IHBkLnRvX2RhdGV0aW1lKGRmWydmaW5hbEdhbWUnXSlcbmRmWydkZWJ1dFllYXInXSA9IHBkLnRvX251bWVyaWMoZGZbJ2RlYnV0J10uZHQuc3RyZnRpbWUoJyVZJyksIGVycm9ycz0nY29lcmNlJylcbmRmWydmaW5hbFllYXInXSA9IHBkLnRvX251bWVyaWMoZGZbJ2ZpbmFsR2FtZSddLmR0LnN0cmZ0aW1lKCclWScpLCBlcnJvcnM9J2NvZXJjZScpXG5kZiA9IGRmWyhkZlsncGxheWVySUQnXSAhPSAncm9zZXBlMDEnKSAmIChkZlsncGxheWVySUQnXSAhPSAnamFja3NqbzAxJyldXG5kZWYgZmlyc3RfYWFwKGNvbCk6XG4gICAgaWYgY29sID09ICdyb2JpbmphMDInOlxuICAgICAgICByZXR1cm4gMVxuICAgIGVsc2U6XG4gICAgICAgIHJldHVybiAwXG4gICAgXG5kZlsnZmlyc3RfYWFwJ10gPSBkZlsncGxheWVySUQnXS5hcHBseShmaXJzdF9hYXApXG5kZl9ob2YgPSBkZltkZlsnSG9GJ10gPT0gMV1cbmRmID0gZGYuZHJvcG5hKClcbmRmWydZU0xTJ10gPSAyMDE2IC0gZGZbJ2ZpbmFsWWVhciddXG5kZl9lbGlnaWJsZSA9IGRmW2RmWydZU0xTJ108PSAxNV1cbmRmX2hpdHRlcnMgPSBkZltkZlsnWVNMUyddID4gMTVdXG5udW1fY29sc19oaXR0ZXJzID0gWydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnSG9GJywgJ1llYXJzX1BsYXllZCcsICdIJywgJ0JCJywgJ0hSJywgJ0FWRScsICdPQlAnLCAnU2x1Z19QZXJjZW50JywgJ09QUycsICAnUkJJJywnUicsICdTQicsICcyQicsICczQicsICdBQicsICdTTycsICdNb3N0IFZhbHVhYmxlIFBsYXllcicsICdXb3JsZCBTZXJpZXMgTVZQJywgJ0FTX2dhbWVzJywnR29sZCBHbG92ZScsICdSb29raWUgb2YgdGhlIFllYXInLCAnU2lsdmVyIFNsdWdnZXInLCAnYmF0c19SJywgJ3Rocm93c19SJywgJ0RQZicsICdBZicsICdFZicsICdZU0xTJywgJ0dfYWxsJywgJzE5NjMtNzZfcGVyY2VudCcsICcxOTkzLTIwMDlfcGVyY2VudCcsICcxOTQ2LTYyX3BlcmNlbnQnLCAnR18xYl9wZXJjZW50JywgJzE5NDItNDVfcGVyY2VudCcsJ0dfZGhfcGVyY2VudCcsICcxOTIwLTQxX3BlcmNlbnQnLCAnR19zc19wZXJjZW50JywncG9zdDIwMDlfcGVyY2VudCcsICcxOTc3LTkyX3BlcmNlbnQnLCAnR18yYl9wZXJjZW50JywgJ0dfM2JfcGVyY2VudCcsJ0dfb2ZfcGVyY2VudCcsICdwcmUxOTIwX3BlcmNlbnQnLCAnZmlyc3RfYWFwJ11cbmRhdGEgPSBkZl9oaXR0ZXJzW251bV9jb2xzX2hpdHRlcnNdXG50YXJnZXQgPSBkYXRhWydIb0YnXVxuZmVhdHVyZXMgPSBkYXRhLmRyb3AoWydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnSG9GJ10sIGF4aXM9MSlcbnBlbmFsdHkgPSB7XG4gICAgMDogMTAwLFxuICAgIDE6IDFcbn1cbnJmID0gUmFuZG9tRm9yZXN0Q2xhc3NpZmllcihyYW5kb21fc3RhdGU9MSxuX2VzdGltYXRvcnM9MTIsIG1heF9kZXB0aD0xMSwgbWluX3NhbXBsZXNfbGVhZj0xLCBjbGFzc193ZWlnaHQ9cGVuYWx0eSlcbm5ld19kYXRhID0gZGZfZWxpZ2libGVbbnVtX2NvbHNfaGl0dGVyc11cbm5ld19mZWF0dXJlcyA9IG5ld19kYXRhLmRyb3AoWydwbGF5ZXJJRCcsICduYW1lRmlyc3QnLCAnbmFtZUxhc3QnLCAnSG9GJ10sIGF4aXM9MSlcbnJmLmZpdChmZWF0dXJlcywgdGFyZ2V0KVxucHJvYmFiaWxpdGllcyA9IHJmLnByZWRpY3RfcHJvYmEobmV3X2ZlYXR1cmVzKSIsInNhbXBsZSI6IiMgQ29udmVydCBwcmVkaWN0aW9ucyB0byBhIERhdGFGcmFtZVxuaG9mX3ByZWRpY3Rpb25zID0gcGQuRGF0YUZyYW1lKHByb2JhYmlsaXRpZXNbOiwxXSlcblxuIyBTb3J0IHRoZSBEYXRhRnJhbWUgKGRlc2NlbmRpbmcpXG5ob2ZfcHJlZGljdGlvbnMgPSBob2ZfcHJlZGljdGlvbnMuc29ydF92YWx1ZXMoMCwgYXNjZW5kaW5nPUZhbHNlKVxuXG5ob2ZfcHJlZGljdGlvbnNbJ1Byb2JhYmlsaXR5J10gPSBob2ZfcHJlZGljdGlvbnNbMF1cblxuIyBQcmludCA1MCBoaWdoZXN0IHByb2JhYmlsaXR5IEhvRiBpbmR1Y3RlZXMgZnJvbSBzdGlsbCBlbGlnaWJsZSBwbGF5ZXJzXG5mb3IgaSwgcm93IGluIGhvZl9wcmVkaWN0aW9ucy5oZWFkKDUwKS5pdGVycm93cygpOlxuICAgIHByb2IgPSAnICcuam9pbigoJ0hvRiBQcm9iYWJpbGl0eSA9Jywgc3RyKHJvd1snUHJvYmFiaWxpdHknXSkpKVxuICAgIHByaW50KCcnKVxuICAgIHByaW50KHByb2IpXG4gICAgcHJpbnQobmV3X2RhdGEuaWxvY1tpLDE6MjddKSJ9

As it stands, the model appears to do a really good job of making predictions, with a few exceptions:

Harold Baines, for example, was a solid player and has a legitimate argument for making the HoF, but the model predicts he has a 100% chance of making it and that is not accurate.
Additionally, the model is not accounting for players who were caught or accused of steroid use, which may prevent them from being elected to the HoF.

Your Future Sports Analytics Projects

This concludes the second part of our tutorial series on Scikit-Learn and sports analytics. You imported the data from CSV files, cleaned and aggregated it. You generated new features in the data and got a better understanding by visualizing it. You learned how to create a Logistic Regression model and a Random Forest model. You also learned how to use K-Fold Cross Validation to train and test your model, how to check the accuracy of your classification models, and you made predictions using new data.

If you enjoyed this project, try to build your own model for predicting which Pitchers will be voted into the Hall of Fame.

Good Luck!

Topics

Python

Data Science

Machine Learning

Learn more about Python

course

Supervised Learning with scikit-learn

4 hr

115.6K

Grow your machine learning skills with scikit-learn in Python. Use real-world datasets in this interactive course and learn how to make powerful predictions!

See Details

Start Course

course

Unsupervised Learning in Python

4 hr

137.1K

Learn how to cluster, transform, visualize, and extract insights from unlabeled datasets using scikit-learn and scipy.

See Details

Start Course

course

Introduction to Importing Data in Python

3 hr

284.2K

Learn to import data into Python from various sources, such as Excel, SQL, SAS and right from the web.

See Details

Start Course

tutorial

Scikit-Learn Tutorial: Baseball Analytics Pt 1

A scikit-learn tutorial to predicting MLB wins per season by modeling data to KMeans clustering model and linear regression models.

Daniel Poston

17 min

tutorial

Random Forest Classification with Scikit-Learn

This article covers how and when to use random forest classification with scikit-learn, focusing on concepts, workflow, and examples. We also cover how to use the confusion matrix and feature importances.

Adam Shafi

14 min

tutorial

Understanding Logistic Regression in Python

Learn about logistic regression, its basic properties, and build a machine learning model on a real-world application in Python using scikit-learn.

Avinash Navlani

10 min

tutorial

Python Machine Learning: Scikit-Learn Tutorial

An easy-to-follow scikit-learn tutorial that will help you get started with Python machine learning.

Kurtis Pykes

12 min

tutorial

Naive Bayes Classification Tutorial using Scikit-learn

Learn how to build and evaluate a Naive Bayes Classifier using Python's Scikit-learn package.

Abid Ali Awan

13 min

tutorial

Detecting Fake News with Scikit-Learn

This scikit-learn tutorial will walk you through building a fake news classifier with the help of Bayesian models.

Katharine Jarmul

15 min

See More See More

Importing Data

Data Cleaning and Preprocessing

batting_df

fielding_df

awards_df

allstar_df

hof_df

player_stats

appearances_df

master_df

Feature Engineering: Creating New Features

Selecting Error Metric and Model

Logistic Regression

Random Forest

Your Future Sports Analytics Projects

Scikit-Learn Tutorial: Baseball Analytics Pt 1

Random Forest Classification with Scikit-Learn

Understanding Logistic Regression in Python

Python Machine Learning: Scikit-Learn Tutorial

Naive Bayes Classification Tutorial using Scikit-learn

Detecting Fake News with Scikit-Learn

.css-1531qan{-webkit-text-decoration:none;text-decoration:none;color:inherit;}Supervised Learning with scikit-learn

Unsupervised Learning in Python

Introduction to Importing Data in Python

Scikit-Learn Tutorial: Baseball Analytics Pt 1

Random Forest Classification with Scikit-Learn

Understanding Logistic Regression in Python

Python Machine Learning: Scikit-Learn Tutorial

Naive Bayes Classification Tutorial using Scikit-learn

Detecting Fake News with Scikit-Learn

`batting_df`

`fielding_df`

`awards_df`

`allstar_df`

`hof_df`

`player_stats`

`appearances_df`

`master_df`

Supervised Learning with scikit-learn