Die Summe der Quadrate verstehen: Ein Leitfaden für SST, SSR und SSE

Die Summe der Quadrate ist ein komplexes statistisches Maß, das bei der Regressionsanalyse eine wichtige Rolle spielt. Sie beschreibt die Variabilität der abhängigen Variable und kann in drei Komponenten zerlegt werden - die Summe der Quadrate insgesamt (SST), die Summe der Quadrate der Regression (SSR) und die Summe der Fehlerquadrate (SSE) -, die zusammen helfen, die Leistung eines Regressionsmodells zu bewerten.

In diesem Artikel werden wir die drei Komponenten der Quadratsumme sowie das R-Quadrat besprechen. Zuerst geben wir einen Überblick über jede Summe der Quadrate einzeln. Als Nächstes werden wir die mathematische Beziehung zwischen ihnen betrachten. Schließlich werden wir den Zusammenhang zwischen SST, SSR und SSE und dem R-Quadrat, einer wichtigen Kennzahl für die Modellbewertung, untersuchen.

Was sind SST, SSR und SSE?

Zunächst wollen wir definieren, was SST, SSR und SSE sind, wie jedes Maß die Gesamtvariabilität widerspiegelt und wie jedes von ihnen hilft, die Anpassungsfähigkeit eines Regressionsmodells zu bewerten. Außerdem werden wir sehen, wie die Summe der Quadrate bei einer einfachen linearen Regression mit einer abhängigen und einer unabhängigen Variable aussieht.

Wenn du die Definitionen durchgehst und dich mit Statistik beschäftigen möchtest, ohne dabei zu kodieren, dann schau dir unseren Kurs Einführung in die Statistik an. Für Einführungskurse in die Statistik, die in einer bestimmten Technologie verankert sind, haben wir verschiedene Optionen, darunter Einführung in die Statistik in Google Sheets, Einführung in die Statistik in Python und Einführung in die Statistik in R.

Gesamtsumme der Quadrate (SST)

Die Gesamtsumme der Quadrate (SST) ist die Summe der quadrierten Differenzen zwischen jedem Wert der beobachteten abhängigen Variable und dem Mittelwert dieser Variable. Sie ist auch bekannt als die Gesamtsumme der Quadrate (TSS). 

Die Summe der Quadrate stellt die Gesamtvariabilität der abhängigen Variable dar, einschließlich der durch das Regressionsmodell erklärten und unerklärten Anteile der Variabilität. Der SST spiegelt naturgemäß die Gesamtstreuung der einzelnen Werte der beobachteten abhängigen Variable von ihrem Mittelwert wider.

Im Folgenden findest du die mathematische Formel zur Berechnung des SST:

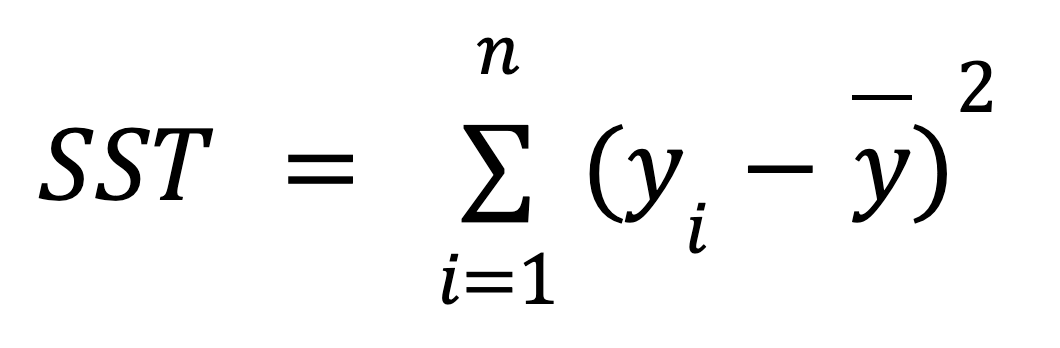
wo:

• y_i ist der Wert der beobachteten abhängigen Variable für jeden der n Datenpunkte.
• ȳ ist der Mittelwert der beobachteten abhängigen Variable.

Das folgende Diagramm für eine einfache lineare Regression veranschaulicht die Bedeutung der obigen Formel grafisch:

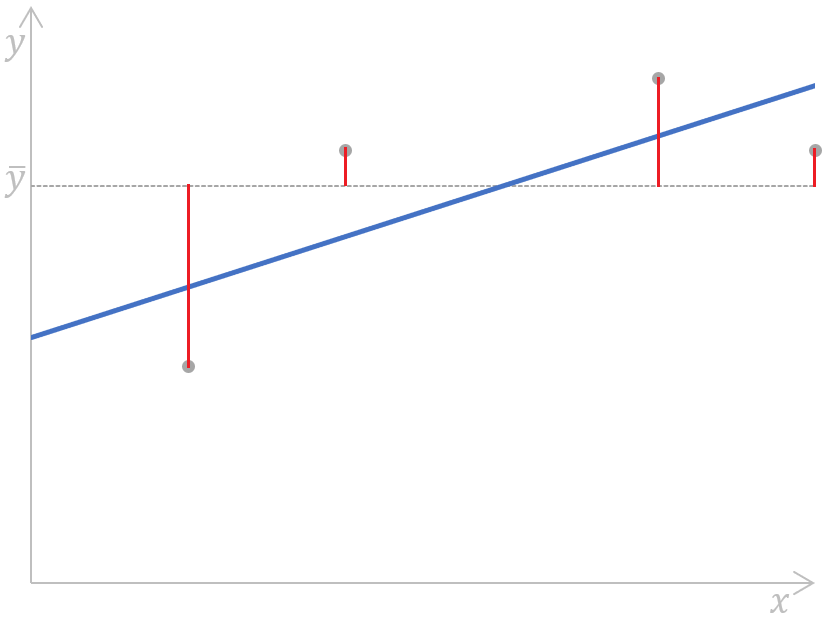
Berechne die Summe der Quadrate für eine einfache lineare Regression. Bild vom Autor

Wie wir sehen können, werden die Abstände (die roten Segmente auf dem Diagramm) zwischen dem Mittelwert (die graue gestrichelte Linie) der beobachteten abhängigen Variable und jedem Wert (die grauen Punkte) dieser Variable gemessen, quadriert und aufsummiert. Außerdem zeigt diese Grafik deutlich, dass der SST nicht vom Regressionsmodell abhängt, sondern nur von den beobachteten y-Werten und dem Mittelwert der beobachteten abhängigen Variable.

Summe der Regressionsquadrate (SSR)

Die Summe der Regressionsquadrate (SSR) ist die Summe der quadrierten Differenzen zwischen jedem Wert der abhängigen Variable , der durch ein Regressionsmodell für jeden Datenpunkt der unabhängigen Variablevorhergesagt wird, und dem Mittelwert der beobachteten abhängigen Variable. Andere Bezeichnungen für diese Metrik sind: Regressionsquadratsumme, Summe der Quadrate aufgrund von Regression und erklärte Quadratsumme. Es gibt sogar noch eine andere Abkürzung dafür: ESS. 

Die Regressionsquadratsumme erfasst den Anteil der Gesamtvariabilität der abhängigen Variable, der durch das Regressionsmodell erklärt wird (daher einer der alternativen Begriffe - erklärteQuadratsumme). Wir können ihn auch als den durch das Regressionsmodell reduzierten Fehler betrachten.

Um die SSR zu berechnen, verwenden wir die folgende Formel:

wo:

• y_i ist der Wert der abhängigen Variable, der durch ein Regressionsmodell für jeden der n Datenpunkte der unabhängigen Variable vorhergesagt wird,
• ȳ ist der Mittelwert der beobachteten abhängigen Variable.

Wir können diese Formel anhand der folgenden einfachen linearen Regressionskurve veranschaulichen:

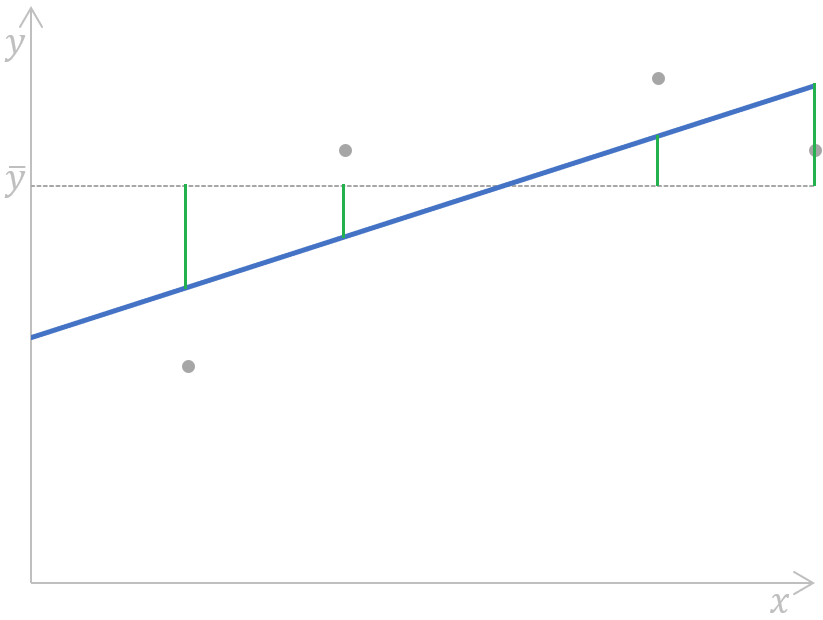Berechnen der Regressionsquadratsumme für eine einfache lineare Regression. Bild vom Autor

Vereinfacht gesagt, werden die Abstände (die grünen Segmente auf dem Diagramm) zwischen dem Mittelwert (die graue gestrichelte Linie) der beobachteten abhängigen Variable und jedem Wert der abhängigen Variable, der durch ein Regressionsmodell (die blaue Linie) für jeden Datenpunkt der unabhängigen Variable vorhergesagt wird, gemessen, quadriert und aufsummiert.

Bei der Regressionsanalyse trägt die SSR dazu bei, die Anpassung eines Regressionsmodells zu messen, indem sie dabei hilft, festzustellen, wie gut das Modell Datenpunkte vorhersagt. Wir werden später in diesem Lernprogramm ein klareres Bild davon haben, wie das passiert, wenn wir die Beziehung zwischen den drei Metriken der Quadratsumme besprechen.

Fehlersumme der Quadrate (SSE)

Die Summe der Fehlerquadrate (SSE) ist die Summe der quadrierten Differenzen zwischen jedem Wert der beobachteten abhängigen Variable und dem Wert der abhängigen Variable , der durch ein Regressionsmodell für denselben Datenpunkt der unabhängigen Variablevorhergesagt wird. Mit anderen Worten: Diese Kennzahl misst die Differenz zwischen den tatsächlichen und den vorhergesagten Werten der abhängigen Variable. 

Der Fehler der Quadratsumme wird auch als Fehlersumme der Quadrate, Residualsumme der Quadrate, Residualsumme der Quadrate oder unerklärte Summe der Quadrate bezeichnet. Neben SSE kann sie auch als RSS, ESS oder sogar SSR abgekürzt werden - im letzten Fall kann sie leicht mit der bereits erwähnten SSR verwechselt werden, die für die Summe der Quadrate der Regression steht.

Die Summe der Fehlerquadrate spiegelt den verbleibenden Fehler oder die unerklärte Variabilität wider, d.h. den Anteil der Gesamtvariabilität der abhängigen Variable, der nicht durch das Regressionsmodell erklärt werden kann (deshalb wird sie auch als unerklärte Summe der Quadrate).

Wir können die folgende Formel verwenden, um den SSE zu berechnen:

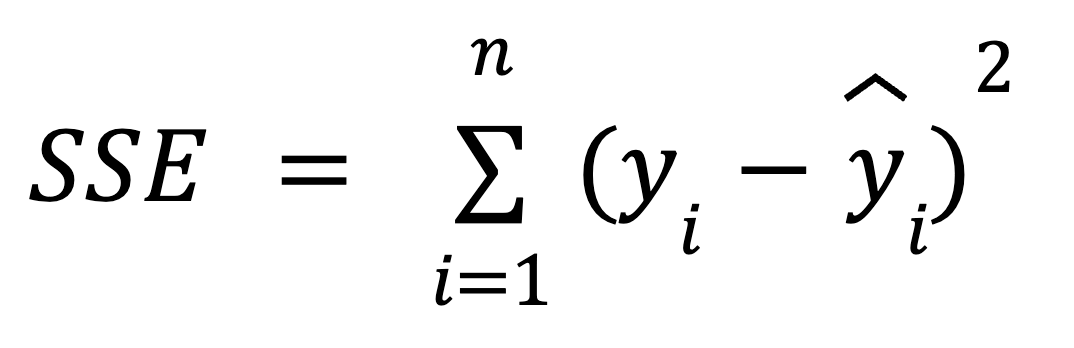
wo:

• y_i ist der tatsächliche Wert der abhängigen Variable für jeden der n Datenpunkte der unabhängigen Variable.
• ŷ ist der vorhergesagte Wert der abhängigen Variable für jeden der n Datenpunkte der unabhängigen Variable.

Grafisch kann diese Formel wie folgt dargestellt werden:

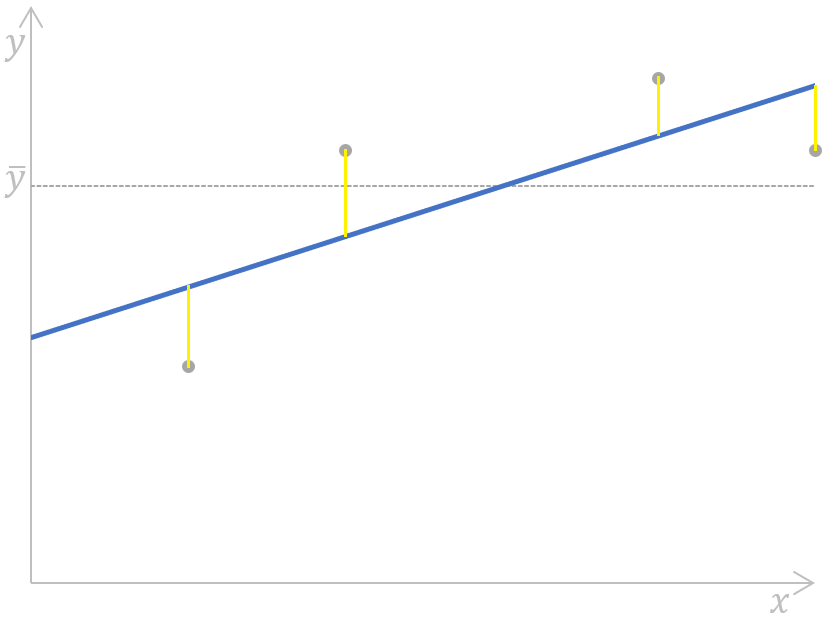Berechnung der Summe der Fehlerquadrate für eine einfache lineare Regression. Bild vom Autor

Hier werden die Abstände (die gelben Segmente auf dem Diagramm) für jedes Paar aus tatsächlichen und vorhergesagten Werten der abhängigen Variable gemessen, quadriert und summiert.

Bei der Regressionsanalyse ist die Minimierung des SSE der Schlüssel zur Verbesserung der Genauigkeit des Regressionsmodells, und wir werden im nächsten Kapitel eine Intuition dafür entwickeln.

Wir haben auch eine Sammlung von technologie-spezifischen Tutorials, die dir helfen, einfache lineare und logistische Regressionsmodelle zu erstellen. Dazu gehören Essentials of Linear Regression in Python, How to Do Linear Regression in R und Linear Regression in Excel: Ein umfassender Leitfaden für Einsteiger.

Mathematische Beziehung zwischen SST, SSR und SSE

Die mathematische Beziehung zwischen dem SST, dem SSR und dem SSE wird durch die folgende Formel ausgedrückt:

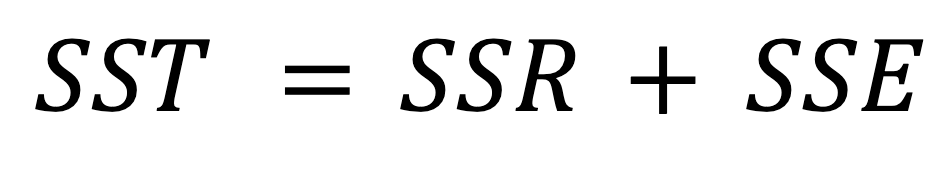
Wir haben bereits erwähnt, dass sich die Gesamtvariabilität (SST) sowohl aus der erklärten Variabilität (SSR) als auch aus der unerklärten Variabilität (SSE) zusammensetzt, was sich in der obigen Formel widerspiegelt.

Wie wir bereits gesehen haben, hängt der SST nicht vom Regressionsmodell ab, während die anderen beiden Messgrößen dies tun. Das bedeutet, dass die Verbesserung der Genauigkeit des Modells mit Änderungen der SSR oder SSE zusammenhängt - insbesondere durch die Minimierung der SSE und damit die Maximierung der SSR. Aus der obigen Formel können wir ableiten, dass die SSR umso näher an der SST liegt, je kleiner der SSE ist und je besser unser Regressionsmodell zu den beobachteten Werten der abhängigen Variable passt. 

Wäre der SSE gleich 0, würde der SSR mit dem SST übereinstimmen, was bedeuten würde, dass alle beobachteten Werte der abhängigen Variable perfekt durch das Regressionsmodell erklärt werden, d. h. sie würden alle genau auf der Regressionslinie liegen. In der Realität wird das nicht passieren, aber wir sollten versuchen, den SSE zu minimieren, um ein zuverlässigeres Regressionsmodell zu erhalten.

Geometrische Interpretation

Da die SST die Gesamtvariabilität der Daten darstellt, zerlegen wir diese Gesamtvariabilität in zwei Teile, wenn wir ein Regressionsmodell anpassen: SSR und SSE. Diese Zerlegung ist geometrisch interessant, weil sie den Satz des Pythagoras in einem hochdimensionalen Raum widerspiegelt. Das liegt daran, dass die Gesamtvariabilität in zwei orthogonale Komponenten aufgeteilt wird: die durch das Modell erklärte Variabilität und der unerklärte Fehler. Diese Interpretation macht Sinn, denn bei der Regression geht es im Wesentlichen darum, Daten auf einen niedriger-dimensionalen Raum zu projizieren, und das ist der Raum, der von unseren Prädiktoren aufgespannt wird. Nimm an unserem Kurs Lineare Algebra für Datenwissenschaft in R teil, um mehr über Konzepte wie Unterräume zu erfahren.

Wenn SST nicht gleich SSR + SSE ist

Bei der Ridge- und Lasso-Regression folgt die Zerlegung der SST in SSR und SSE nicht der gleichen Beziehung. Das liegt daran, dass sowohl Ridge als auch Lasso Regularisierungsterme oder Strafen zu ihren jeweiligen Kostenfunktionen hinzufügen, wodurch sich die Beziehung ändert. Bei den regularisierten Versionen der Regression ist der SST immer noch gut definiert, aber die erklärte Variabilität und die Restvariabilität summieren sich aufgrund des Regularisierungsterms nicht mehr zum SST. Lies unser Regularization in R Tutorial: Ridge, Lasso und Elastic Net um mehr zu erfahren.

Summe der Quadrate und R-Quadrat

Das R-Quadrat, auch bekannt als Bestimmtheitsmaß, ist ein wichtiges statistisches Maß zur Bewertung der Anpassungsqualität eines Regressionsmodells und damit seiner Vorhersagekraft. Sie gibt den Anteil der Variabilität der abhängigen Variable an, der durch die unabhängige Variable erklärt werden kann. Das R-Quadrat kann durch Quadrieren des Korrelationskoeffizienten r berechnet werden, und es kann auch nach dieser Formel berechnet werden:

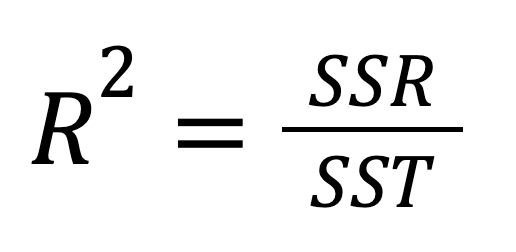
Oder, alternativ:

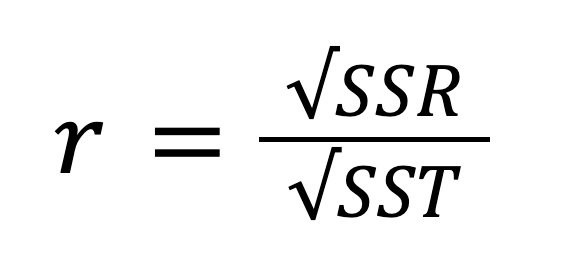
Unter Berücksichtigung der Beziehung zwischen SST, SSR und SSE kann die obige Formel wie folgt umgeschrieben werden:

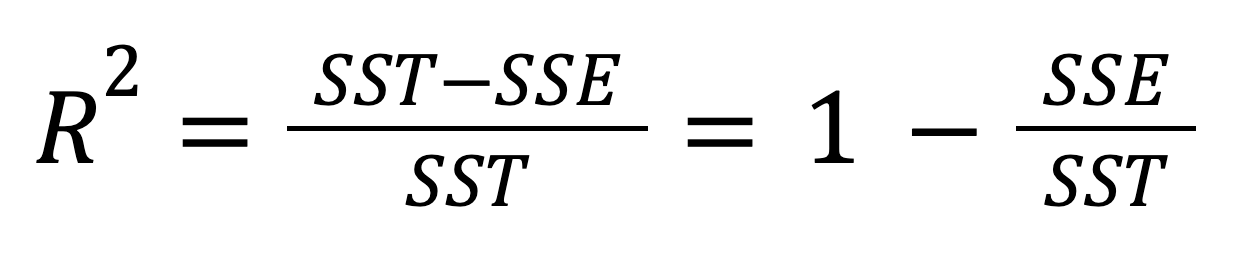
Der Wert des R-Quadrats kann von 0 bis einschließlich 1 reichen. Wenn R² = 0, bedeutet das, dass unser Regressionsmodell überhaupt keinen Teil der Variabilität der abhängigen Variable erklärt. Stattdessen, wenn R² = 1, bedeutet das, dass unser Regressionsmodell die gesamte Variabilität der abhängigen Variable perfekt erklärt. In der Praxis ist es fast unmöglich, diese extremen Werte zu erreichen - höchstwahrscheinlich werden wir in der Praxis etwas dazwischen finden.

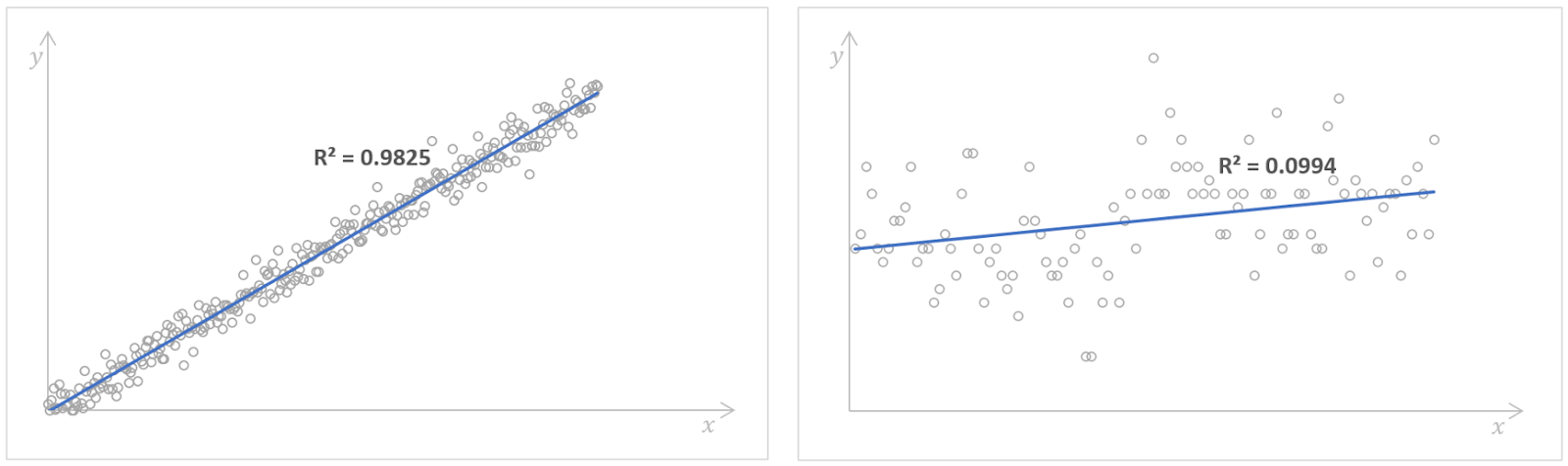
Regressionsmodelle mit hohen (links) und niedrigen (rechts) Werten für das R-Quadrat. Quelle: Kaggle Anzahl der gelesenen Bücher und Kaggle Possum Regression. Bild vom Autor.

Ein hoher Wert des R-Quadrats deutet auf eine gute Modellleistung hin, was bedeutet, dass die abhängige Variable durch die unabhängige Variable mit einer hohen Genauigkeit vorhergesagt werden kann. Es gibt jedoch keine Faustregel dafür, welcher Wert des R-Quadrats als gut genug angesehen werden sollte. Das hängt von jedem einzelnen Fall ab, von den Anforderungen an die Genauigkeit eines Regressionsmodells und davon, wie viel Variabilität wir in den Daten erwarten. Oft hängt es auch von dem Bereich ab, auf den sich unsere Regressionsanalyse bezieht. In wissenschaftlichen Bereichen würden wir zum Beispiel einen Wert des R-Quadrats von mehr als 0,8 anstreben, während in den Sozialwissenschaften ein Wert von 0,3 bereits gut genug sein könnte. 

Abschließend sei gesagt, dass wir bei der multiplen linearen Regression, also der Regression mit mehr als einer unabhängigen Variable, stattdessen oft das bereinigte R-Quadrat betrachten, das eine Erweiterung des R-Quadrats ist, die die Anzahl der Prädiktoren und die Stichprobengröße berücksichtigt.

Fazit

Auch wenn wir SST, SSR und SSE heute in den meisten Statistikprogrammen und Programmiersprachen einfach und schnell berechnen können, lohnt es sich, ihre Bedeutung, ihren Zusammenhang und vor allem ihre Bedeutung in der Regressionsanalyse zu verstehen. Das Verständnis der Beziehung zwischen den drei Komponenten der Variabilität und dem R-Quadrat hilft Datenanalysten und Datenwissenschaftlern, die Modellleistung zu verbessern, indem sie die SSE minimieren und gleichzeitig die SSR maximieren, sodass sie fundierte Entscheidungen über ihre Regressionsmodelle treffen können.

Um eine solide Grundlage in Statistik zu schaffen und leistungsstarke statistische Techniken zu erlernen, indem du mit realen Daten arbeitest, solltest du die folgenden ausführlichen und anfängerfreundlichen Skill Tracks in Betracht ziehen: Grundlagen der Statistik in Python und Grundlagen der Statistik in R. Wenn du dich dafür interessierst, wie die Regressionskoeffizienten berechnet werden, schau dir unser Tutorial zur Normalen Gleichung für lineare Regression und QR-Zerlegung im maschinellen Lernen an: Ein detaillierter Leitfaden.