RMSE Erklärt: Ein Leitfaden zur Genauigkeit von Regressionsvorhersagen

RMSE (Root Mean Squared Error) ist eine häufig verwendete Metrik zur Bewertung der Genauigkeit in der Regressionsanalyse, die die durchschnittliche Größe der Fehler in einem Regressionsmodell misst.

Im Gegensatz zum R-Quadrat, das die erklärte Varianz quantifiziert, liefert der RMSE ein direktes Maß für den Vorhersagefehler in denselben Einheiten wie die Antwortvariable. Das macht sie besonders nützlich, wenn es darum geht, die Fehlergröße zu minimieren und die Leistung des Modells in der realen Welt zu interpretieren.

In diesem Artikel befassen wir uns mit der Bedeutung, der Berechnung, der Interpretation und den häufigsten Missverständnissen rund um den RMSE. Wir werden auch Beispiele in Python und R durchgehen, um zu sehen, wie sich der RMSE unter verschiedenen Modellierungsbedingungen verhält.

Was ist RMSE?

Der RMSE ist die Quadratwurzel aus dem Durchschnitt der quadrierten Unterschiede zwischen beobachteten und vorhergesagten Werten. Es ist eine weit verbreitete Regressionskennzahl, die uns sagt, wie viel Fehler wir im Durchschnitt bei unseren Vorhersagen erwarten können. 

Die mathematische Formel zur Berechnung des RMSE lautet:

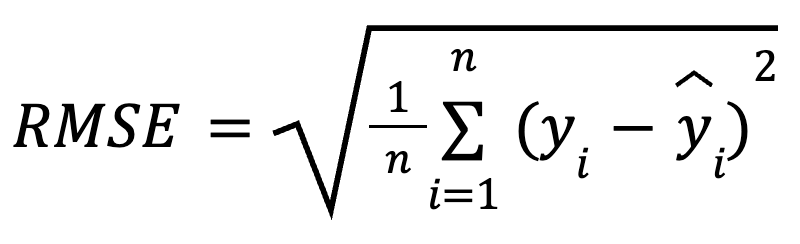
hier:

• y_i ist der tatsächliche Wert für die Beobachtung i,
• _ŷ, ist der vorhergesagte Wert für die Beobachtung i,
• n ist die Gesamtzahl der Beobachtungen.

Da die Residuen vor der Mittelwertbildung quadriert werden, bestraft der RMSE größere Fehler stärker als kleinere. Diese Empfindlichkeit macht sie zu einer guten Wahl, wenn große Vorhersagefehler besonders unerwünscht sind. Der RMSE ist immer nicht-negativ und niedrigere Werte bedeuten, dass das Modell besser passt.

Drei gleichwertige Möglichkeiten zur Berechnung des RMSE

Der RMSE ist einfach zu berechnen. Es geht einfach darum, die Residuen zu berechnen, sie zu quadrieren, den Mittelwert zu ermitteln und die Quadratwurzel zu ziehen.

Betrachten wir ein paar verschiedene Möglichkeiten, sie zu berechnen.

Residuen verwenden

Bei dieser Methode ziehen wir zunächst die Vorhersagen von den tatsächlichen Werten ab, um die Residuen zu erhalten. Als Nächstes quadrieren wir jedes Residuum, bilden den Durchschnitt aller Residuen und ziehen schließlich die Quadratwurzel.

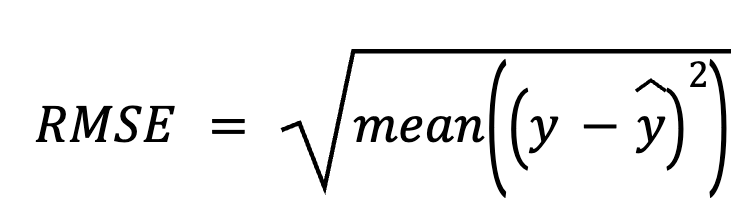
hier:

• y ist der Vektor der tatsächlichen Werte,
• ŷist der Vektor der vorhergesagten Werte.

Dieser direkte Ansatz hebt die Vorhersagefehler selbst hervor.

Verwendung des mittleren quadratischen Fehlers (MSE)

Das fühlt sich wie eine Wiederholung an, aber in Wirklichkeit steckt mehr dahinter: Der RMSE ist einfach die Quadratwurzel des MSE. 

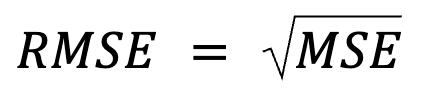
wo:

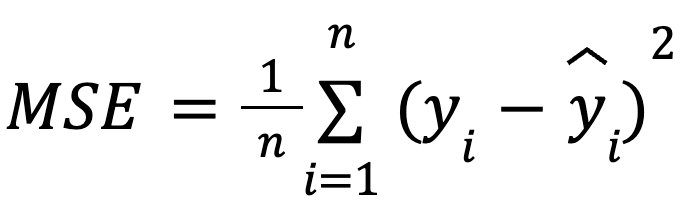
mit:

• y_i als den tatsächlichen Wert für die Beobachtung i,
• ŷ, als den vorhergesagten Wert für die Beobachtung i,
• n als die Gesamtzahl der Beobachtungen.

Diese Formulierung ist nützlich, weil der MSE eine gängige Verlustfunktion bei der Modelloptimierung ist. Diese Äquivalenz ist besonders wichtig beim maschinellen Lernen, wo die MSE oft die Verlustfunktion ist, die beim Training durch Gradientenabstieg minimiert wird. 

Mehr dazu: Gerade weil der RMSE eine Quadratwurzel einführt, entscheiden sich viele Algorithmen für maschinelles Lernen dafür, den RMSE während des Modelltrainings nicht zu berücksichtigen. MSE wird für diese Optimierungen bevorzugt, weil es einfachere Ableitungen hat (wiederum, weil die Quadratwurzel eine Nichtlinearität einführt). Der RMSE wird dann oft post hoc verwendet, um die Leistung in interpretierbaren Einheiten anzugeben.

In Matrixform

Bei der multiplen Regression kann der RMSE auch mithilfe der Matrixalgebra aus dem Residuenvektor abgeleitet werden:

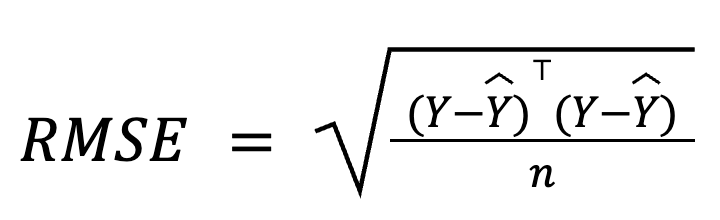
wo:

• Y ist der Spaltenvektor der tatsächlichen Werte,
• ŷ ist der Spaltenvektor der vorhergesagten Werte,
• n ist die Anzahl der Beobachtungen.

Diese matrixbasierte Formulierung ist besonders kompakt und recheneffizient, vor allem bei großen Datensätzen oder Modellpipelines. Wir haben einen speziellen Kurs für lineare Algebra, wenn du dich mit Mathematik beschäftigen willst.

RMSE interpretieren

Der RMSE wird als der durchschnittliche Vorhersagefehler interpretiert, der die Vorhersagegenauigkeit des Modells bestimmt. Einfach ausgedrückt, zeigt sie im Durchschnitt an, wie weit die Vorhersagen von den tatsächlichen Werten entfernt sind, und zwar in der gleichen Skala wie die Ergebnisvariable.

Ein niedriger RMSE deutet auf kleinere durchschnittliche Vorhersagefehler und damit auf genauere Vorhersagen hin, aber der "akzeptable" RMSE hängt ganz vom jeweiligen Kontext ab. Ein RMSE von 2 kann zum Beispiel gut sein, wenn es um die Vorhersage der Mandelgröße in Millimetern geht, aber nicht so überzeugend, wenn es um die Vorhersage der jährlichen Mandelernte in Tonnen geht.

Um aussagekräftig zu sein, sollte der RMSE zwischen Modellen verglichen werden, die auf denselben Daten trainiert wurden, oder durch Benchmarking der historischen Leistung.

Wann wird der RMSE verwendet?

Der RMSE ist in diesen Szenarien besonders hilfreich:

• Wenn absolute Vorhersagegenauigkeit entscheidend ist
• Wenn du Modelle mit demselben Datensatz vergleichst
• Wenn Modellfehler normal verteilt sind
• Wenn unser Ziel ist, große Fehler zu minimieren
• Wenn die Interpretation von Fehlern in natürlichen Einheiten wichtig ist

Der RMSE hat jedoch auch seine Nachteile:

• Sie ist empfindlich gegenüber Ausreißern. Einige wenige große Residuen können den RMSE überproportional beeinflussen und ihn irreführend machen.
• Sie ist nicht normalisiert. Das bedeutet, dass kein Vergleich zwischen verschiedenen Datensätzen und Zielskalen möglich ist, solange die Zielvariable nicht skaliert ist.

RMSE-Beispiele in Python und R

Wir zeigen dir jetzt, wie du den RMSE sowohl in Python als auch in R berechnen kannst, indem wir den Kaggle-Datensatz zur Klassifizierung von Mandelarten verwenden. Obwohl der Datensatz ursprünglich für die Klassifizierung gedacht ist, werden wir ihn hier für die Regression umfunktionieren , indem wir die Kerndicke als kontinuierliche Variable auf der Grundlage anderer physischer Attribute vorhersagen.

Wir werden zwei Modelle in jeder Programmiersprache erstellen und dann den RMSE für jedes Modell berechnen:

• Modell 1: Verwendet relevante Prädiktoren (Länge und Breite).
• Modell 2: Fügt einen zufälligen, irrelevanten Prädiktor hinzu.

Python Beispiel

Beginnen wir mit Python.

import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from math import sqrt

# Load data
data = pd.read_csv("almond_dataset.csv")

# Model 1
X1 = data[['Length', 'Width']]
y = data['Thickness']
model1 = LinearRegression().fit(X1, y)
preds1 = model1.predict(X1)
rmse1 = sqrt(mean_squared_error(y, preds1))
print("Model 1 RMSE:", round(rmse1, 3))

# Model 2 with an irrelevant predictor
np.random.seed(42)
data['random_noise'] = np.random.randn(len(data))
X2 = data[['Length', 'Width', 'random_noise']]
model2 = LinearRegression().fit(X2, y)
preds2 = model2.predict(X2)
rmse2 = sqrt(mean_squared_error(y, preds2))
print("Model 2 RMSE:", round(rmse2, 3))

Model 1 RMSE: 0.251
Model 2 RMSE: 0.253

Wir sehen, dass der RMSE nach dem Hinzufügen eines irrelevanten Prädiktors in Modell 2 gestiegen ist. Modell 2 mag zwar komplexer erscheinen, aber seine tatsächliche Vorhersagegenauigkeit kann sich verschlechtern (und zwar erheblich!), da wir nur zufälliges Rauschen hinzugefügt haben.

Um deine Regressionsfähigkeiten in Python zu verbessern, melde dich für diese Kurse an:

• Einführung in die Regression mit statsmodels in Python
• Mittlere Regression mit statsmodels in Python

R Beispiel

Versuchen wir es jetzt in R.

# Load data
almonds <- read.csv("almond_dataset.csv")

# Model 1
model1 <- lm(Thickness ~ Length + Width, data = almonds)
preds1 <- predict(model1)
rmse1 <- sqrt(mean((almonds$Thickness - preds1)^2))
print(paste("Model 1 RMSE:", round(rmse1, 3)))

# Model 2 with an irrelevant predictor
set.seed(42)
almonds$random_noise <- rnorm(nrow(almonds))
model2 <- lm(Thickness ~ Length + Width + random_noise, data = almonds)
preds2 <- predict(model2)
rmse2 <- sqrt(mean((almonds$Thickness - preds2)^2))
print(paste("Model 2 RMSE:", round(rmse2, 3)))

[1] "Model 1 RMSE: 0.251"
[1] "Model 2 RMSE: 0.253"

Hier habe ich dasselbe Beispiel in R umgestaltet. Der RMSE steigt, wenn wir einen irrelevanten Prädiktor in R einbeziehen. Das bestätigt, dass der RMSE steigen kann, wenn ein Modell unnötig komplex wird und die Generalisierungsfähigkeit des Modells sinkt.

Wenn du Probleme hattest, deinen R-Code zu kompilieren, oder wenn du Schwierigkeiten hattest, das Ergebnis zu interpretieren, versuche unsere Kurse:

• Einführung in die Regression in R
• Zwischenregression in R

RMSE vs. Verwandte Metriken

Der RMSE ist Teil einer breiteren Familie von Regressionsfehlermetriken. Wir wollen sie kurz mit anderen vergleichen, die Unterschiede zwischen ihnen klären und aufzeigen, wann sie am nützlichsten sind.

RMSE vs. MAE

Der RMSE bestraft große Fehler stärker, weil er die Residuen quadriert und dadurch empfindlicher auf Ausreißer reagiert. MAE (mittlerer absoluter Fehler) ist dagegen robuster gegenüber Ausreißern, behandelt alle Fehler gleich und eignet sich besser zur Messung der typischen Fehlergröße, wenn Ausreißer keine Rolle spielen. Während RMSE den quadratischen Verlust minimiert, minimiert MAE den absoluten Verlust.

Im Allgemeinen sollten wir den RMSE verwenden, wenn große Fehler besonders kostspielig sein können, und den MAE, wenn wir eine medianähnliche Ansicht des Fehlers wünschen, die weniger anfällig für Ausreißer ist.

RMSE vs. R-Quadrat

Der RMSE gibt den durchschnittlichen Fehler in Originaleinheiten an, was ihnfür die praktische Interpretation intuitiver macht. Stattdessen beschreibt das R-Quadrat, wie viel Varianz durch das Modell erklärt wird, gibt aber keinen Hinweis auf die Größe des Vorhersagefehlers.

Sie werden oft zusammen verwendet: R-Quadrat für die relative Anpassung und RMSE für die absolute Leistung.

RMSE vs. MSE

Der RMSE ist nur die Quadratwurzel des MSE, was die Interpretation erleichtert, da er in denselben Einheiten wie die Ergebnisvariable angegeben wird. 

Abgesehen von der reinen Interpretation ist MSE jedoch besonders nützlich für die Optimierung beim Training für maschinelles Lernen. Denke daran, dass die Quadratwurzelfunktion bei einer Optimierung nach RMSE bedeutet, dass das Modell größeren Fehlern mehr Bedeutung beimisst. Da die MSE eine glatte Ableitung hat, funktioniert sie gut mit gradientenbasierten Algorithmen wie dem stochastischen Gradientenabstieg und ermöglicht eine effiziente Konvergenz während des Modelltrainings. Kurz gesagt, der RMSE ist einfacher zu interpretieren, weil wir die Ergebnisse auf der Skala der Daten betrachten, aber wir sollten wissen, dass Deep Learning oft den MSE und nicht den RMSE optimiert.

RMSE vs. MAPE

MAPE (mittlerer absoluter prozentualer Fehler) gibt die Fehler in Prozent an, was für den Vergleich verschiedener Datensätze praktisch ist. Es bricht jedoch zusammen, wenn die tatsächlichen Werte nahe bei Null liegen, was es instabil macht. Der RMSE umgeht dieses Problem und ist zuverlässiger, wenn kleine Zielwerte vorhanden sind.

RMSE vs. log-likelihood

Hier ist eine weitere interessante Beziehung: Der RMSE ist formal gleichbedeutend mit der negativen Log-Likelihood unter Gaußschen Fehlern. Vielmehr sollten wir vielleicht sagen, dass Minimierung des RMSE gleichbedeutend ist mit der Maximierung der Log-Likelihood (eines Regressionsmodells) unter der Annahme normalverteilter Fehler (mit konstanter Varianz). Ich behaupte nicht, dass der RMSE allein die volle logarithmische Wahrscheinlichkeit schätzt, aber ich sage, dass die Minimierung desRMSE implizit die logarithmische Wahrscheinlichkeit unter der Annahme eines normalen Fehlers maximiert.

Wenn die Fehler jedoch schief sind oder Ausreißer aufweisen, können Alternativen wie Huber oder Quantil Loss besser abschneiden. In jedem Fall sollten wir die Wahl der Metrik als eine Entscheidung bei der Modellentwicklung betrachten, nicht als nachträgliche Überlegung.

Häufige Missverständnisse über den RMSE

Klären wir einige weit verbreitete Mythen über den RMSE auf:

• "Ein niedriger RMSE garantiert eine gute Generalisierung des Modells." Das ist nicht unbedingt richtig. Ein Modell kann bei den Trainingsdaten einen niedrigen RMSE-Wert haben, aber bei neuen, ungesehenen Daten aufgrund von Überanpassung trotzdem schlecht abschneiden. Um die Generalisierung effizient zu bewerten, müssen wir eine Kreuzvalidierung durchführen oder eine separate Testmenge verwenden.
• "Der RMSE kann feststellen, ob ein Modell überangepasst ist. Der RMSE allein reicht nicht aus. Er muss zwischen Trainings- und Validierungsdatensätzen verglichen werden: Wenn der Trainings-RMSE niedrig, der Validierungs-RMSE aber viel höher ist, bedeutet das meist eine Überanpassung.
• "Es gibt einen festen universellen Schwellenwert für einen guten RMSE." Nein, gibt es nicht. Ob der RMSE-Wert "gut" ist, hängt ganz vom Kontext, dem Bereich und den Einheiten der Ergebnisvariablen ab. Mit anderen Worten: Die RMSE-Werte sind ohne Kontext bedeutungslos.

Fazit

Zusammenfassend lässt sich sagen, dass der RMSE ein praktisches, interpretierbares und intuitives Maß für die Vorhersagegenauigkeit ist, das den durchschnittlichen Vorhersagefehler in den Einheiten der Zielvariablen angibt. Sie ist eine wichtige Kennzahl für die Bewertung der Regressionsleistung, vor allem wenn es auf die Höhe der Fehler ankommt.

Der RMSE sollte jedoch zusammen mit anderen Metriken wie R-Quadrat, MAE und Kreuzvalidierung verwendet werden, um ein umfassenderes Bild der Modellqualität zu erhalten. Wir sollten uns nicht blind auf dieses Maß verlassen, sondern immer den Maßstab, den Kontext und die Komplexität des Modells berücksichtigen. Außerdem kann die Verknüpfung des RMSE mit visuellen Diagnosen helfen, Verzerrungen aufzudecken. 

Kurz gesagt, der RMSE sagt uns, wie falsch unser Modell im Durchschnitt wirklich ist, und das ist ein wichtiger Aspekt bei der Entwicklung von Vorhersagesystemen.

Wenn etwas in diesem Artikel verwirrend war, mach dir keine Sorgen: Wir haben viele tolle Ressourcen, die dir helfen können: 

• Einfache lineare Regression: Alles, was du wissen musst tutorial
• Die Summe der Quadrate verstehen: Ein Leitfaden für SST, SSR und SSE tutorial
• Einführung in die Regression mit Statsmodels in Python
• Kurs Einführung in die Regression in R