Curso
Ao interpretar dados, escolher a medida certa de tendência central pode fazer toda a diferença na sua análise. Entre as métricas mais comuns estão amédia e a mediana , que são dois conceitos aparentemente simples, mas que têm implicações profundas na interpretação dos dados. Enquanto a média nos dá a média aritmética, a mediana é o ponto central em um conjunto ordenado de valores, de modo que metade das observações fica em cada lado. Mas qual deles é mais confiável? A resposta geralmente depende da distribuição dos seus dados, da presença de valores atípicos e da história que você está tentando contar.
Neste artigo, vou explicar as diferenças entre média e mediana, seus pontos fortes e fracos, e como escolher a opção certa para diferentes cenários. Também explorarei como distribuições distorcidas e valores atípicos afetam essas medidas, fornecendo exemplos práticos e recursos visuais para ajudar você a entender esses conceitos fundamentais. Também vamos dar uma olhada em ideias mais avançadas.
Definições de média e mediana
Para entender bem as diferenças entre a média e a mediana, vamos dar uma olhada em cada uma dessas medidas e destacar suas principais propriedades.
Qual é a média?
A média pode ser vista como o “ponto de equilíbrio” (ou centro de massa) dos dados. O considera todos os pontos de dados em um conjunto de dados e fornece um único valor que representa a média. Mais exatamente, o tque ele quer dizer é calculado somando todos os valores em um conjunto de dados e depois dividindo pelo número de valores.
O que é a mediana?
A mediana é o valor do meio quando os dados são organizados. Diferente da média, é mais resistente a valores atípicos, oferecendo uma medida melhor da tendência central para dados assimétricos.
Qual é o modo?
A moda é outra medida de tendência central, que mostra o valor que aparece mais vezes num conjunto de dados. Vamos ver um exemplo:
3, 3, 6, 8, 9Aqui, o modo é 3 porque aparece duas vezes, enquanto todos os outros valores aparecem apenas uma vez.
Como calcular a média e a mediana
Ler uma definição é uma coisa, mas calcular é outra. Nesta seção, vou explicar as etapas para calcular cada medida e destacar suas diferenças computacionais.
Como achar a média
A média é a média aritmética de um conjunto de dados e é calculada assim:
- Some os valores: Some todos os números do seu conjunto de dados.
- Divida pelo número total de valores: Pega o total e divide pelo número de valores.
Aqui está o processo representado como uma equação geral:
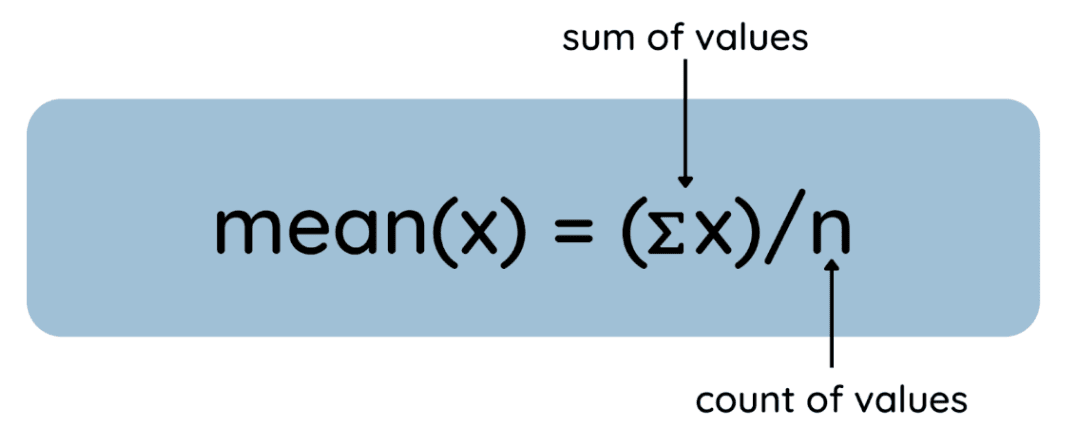
Como achar a média. Imagem do autor
Por exemplo, pense num conjunto de dados de notas de exames:
78, 85, 92, 88, 70- Passo 1 (Soma): 78 + 85 + 92 + 88 + 70 = 413
- Passo 2 (Dividir): 413 ÷ 5 = 82,6
A pontuação média é 82,6.
Como achar a mediana
A mediana é o valor do meio de um conjunto de dados quando eles estão organizados em ordem crescente. Veja como encontrar:
- Organizar os dados: Organize os valores do menor para o maior.
- Identifique o valor médio: Se o conjunto de dados tiver um número ímpar de valores, a mediana é o valor do meio; se o conjunto de dados tiver um número par de valores, a mediana é a média dos dois valores do meio.
E aqui estão essas etapas representadas como equações:
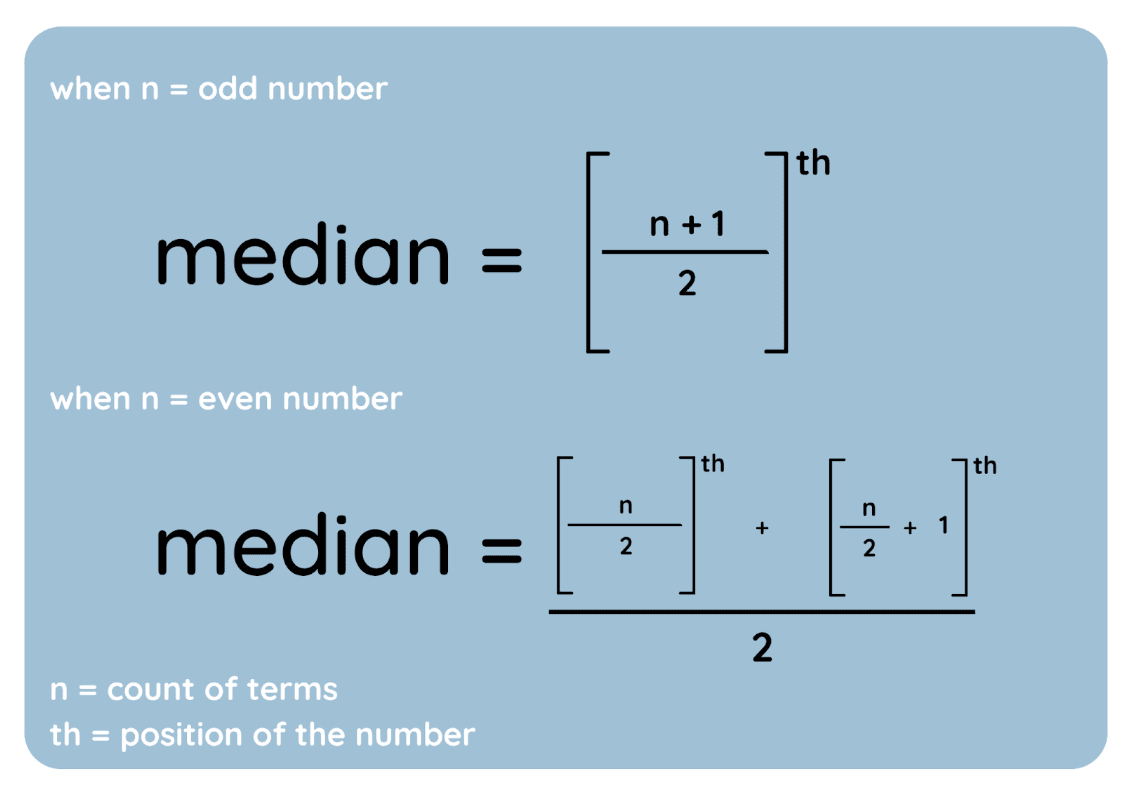
Fórmula mediana. Imagem do autor
Também criei um visual para destacar o processo.
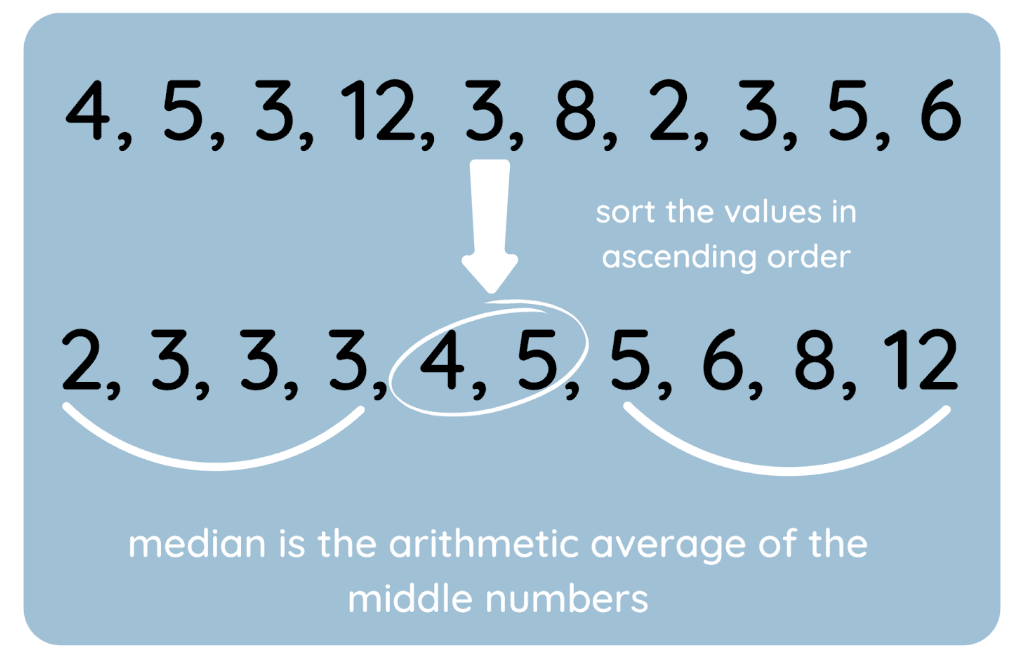
Como achar a mediana. Imagem do autor
Aqui está um exemplo de conjunto de dados com um número ímpar de valores:
70, 78, 85, 88, 92- Passo 1 (Classificar): Já está resolvido.
- Passo 2 (Valor médio): O terceiro valor é 85.
A mediana é 85.
Aqui vai outro exemplo, mas com um número par de valores:
70, 78, 85, 88- Passo 1 (Classificar): Já está resolvido.
- Passo 2 (Média dos valores médios): (78 + 85) ÷ 2 = 81,5
A mediana é 81,5.
Por que a diferença é importante: Outliers e Skew
Embora tanto a média quanto a mediana descrevam o centro de um conjunto de dados, o comportamento delas muda bastante quando tem valores atípicos e distribuições assimétricas. Entender essa diferença é muito importante para interpretar os dados com precisão e evitar conclusões enganosas.
Impacto dos valores atípicos
Outliers são valores que são bem mais altos ou mais baixos do que o resto dos dados. Eles podem influenciar bastante a média, mas têm pouco ou nenhum efeito na mediana.
Vamos pensar num conjunto de dados de rendimentos mensais (em milhares):
3, 3.5, 4, 4.5, 5, 6, 50A renda média aqui é de 10,85 mil, o que é bem distorcido pelo valor extremo de 50 mil.
Por outro lado, o valor mediano é 4,5 mil, o que, na minha opinião, é uma representação muito mais típica da renda desse grupo.
Distribuições assimétricas
A média e a mediana também são diferentes na forma como mostram os dados em distribuições assimétricas (conjuntos de dados que não são simétricos).
Por exemplo, em distribuições assimétricas à direita (por exemplo, renda ou preços de imóveis), a maioria dos valores está agrupada na extremnas distribuições com inclinação para a direita (por exemplo, renda ou preços de imóveis), a maioria dos valores está agrupada na extremidade inferior, com alguns valores extremos puxando a cauda para a direita.
- Média: Mudanças na cauda, resultando em um valor maior que a mediana.
- Mediana: Fica mais perto do conjunto de valores típicos, refletindo melhor o caso “típico”.
Pense nos rendimentos:
30k, 35k, 40k, 45k, 50k, 100k, 200k- Média: 71,4 mil (com um aumento de 100 mil e 200 mil).
- Mediana: 45 mil (mais próximo da maioria dos rendimentos).
Por que isso é importante
- Em dados distorcidos: A mediana costuma ser mais representativa de um ponto de dados “típico” porque não é influenciada por valores extremos.
- Em dados simétricos: A média e a mediana serão quase iguais, então qualquer uma delas pode ser usada como medida de tendência central.
Uma coisa que você deve levar em conta é que é importante sempre dar uma olhada na distribuição dos seus dados antes de decidir se vai usar a média ou a mediana. Ferramentas como histogramas e gráficos de caixa podem ajudar a visualizar a assimetria e identificar valores atípicos. Vamos falar sobre isso mais tarde. Além disso, quero dizer que examinar a diferença entre a média e a mediana é uma forma de avaliar a assimetria.
Quando usar a média versus a mediana
Ao analisar dados, decidir se você vai usar a média ou a mediana depende das características do seu conjunto de dados e das informações que você está tentando extrair. Abaixo está uma tabela de referência rápida para te ajudar a escolher:
| Use a média quando | Use a mediana quando |
|---|---|
| A distribuição dos dados é mais ou menos normal (simétrica). | Os dados são bem distorcidos (por exemplo, renda, valores imobiliários). |
| Os valores atípicos são mínimos ou irrelevantes para a análise. | Existem valores atípicos que podem distorcer os resultados se forem incluídos. |
| Você precisa de uma medida que seja sensível a cada ponto de dados, como em modelagem preditiva ou ao calcular totais. | Você quer mostrar o valor “típico” em vez do “centro matemático” do conjunto de dados. |
Aqui vai uma dica prática que vai te ajudar bastante: Comece sempre com uma análise visual dos seus dados (por exemplo, um histograma ou gráfico de caixa) para verificar a simetria, a assimetria e a presença de valores atípicos. Isso vai te ajudar a decidir se a média ou a mediana é mais adequada para o seu caso.
Visualizando média versus mediana
As visualizações são ferramentas poderosas para entender o comportamento da média e da mediana em diferentes conjuntos de dados. Elas podem mostrar claramente como essas medidas lidam com valores atípicos e distribuições distorcidas, ajudando a tomar decisões melhores com base nos dados.
exemplo de gráfico de barras
Imagina um pequeno conjunto de dados de rendimentos em milhares:
30, 35, 40, 45, 50, 55, 1000O gráfico de barras a seguir mostra como um único valor extremo pode afetar drasticamente a média, enquanto deixa a mediana relativamente estável. Nesse caso, a maioria dos pontos de dados se agrupa entre 30 e 55, mas a presença de um valor atípico (1000) eleva a média.
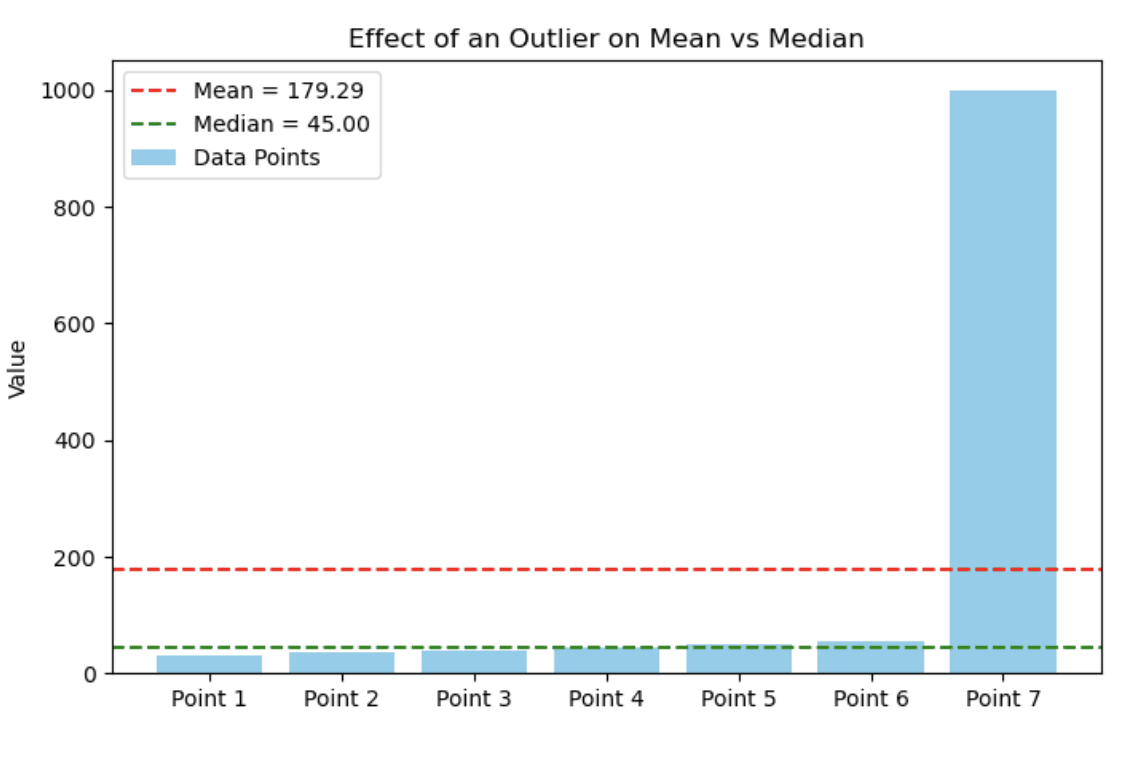
Gráfico de barras mostrando o efeito de um valor atípico na média versus mediana. Imagem do autor
Exemplo de histograma
Em uma distribuição direita (como renda ou preços de imóveis), a média costuma ser puxada para a cauda longa dos valores altos, enquanto a mediana fica mais perto do ponto de dados “típico”. Isso faz com que a mediana seja uma medida melhor da tendência central nesses casos.
O histograma abaixo mostra uma distribuição de renda simulada em que a média (linha tracejada vermelha) é bem maior que a mediana (linha tracejada verde) por causa da assimetria.
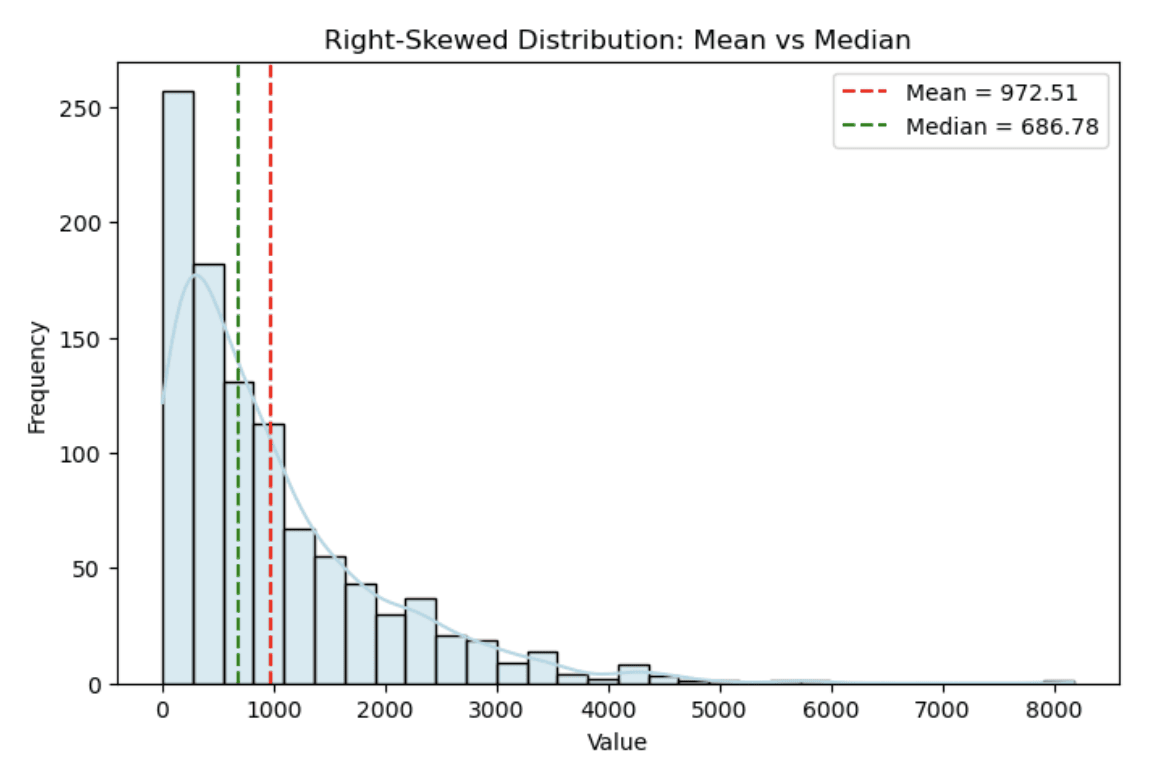
Histograma mostrando uma distribuição assimétrica à direita. Imagem do autor
Dá pra ver como a assimetria à direita estica a cauda, criando uma diferença clara entre a média e a mediana.
Exemplo de gráfico de caixa
Um gráfico de caixa é uma maneira excelente de visualizar o impacto dos valores atípicos na mediana. Abaixo, comparamos dois grupos: um com valores atípicos e outro sem. A mediana (linha vertical dentro da caixa) continua estável mesmo com a presença de valores extremos, mas o intervalo geral dos dados é fortemente afetado pelo outlier.
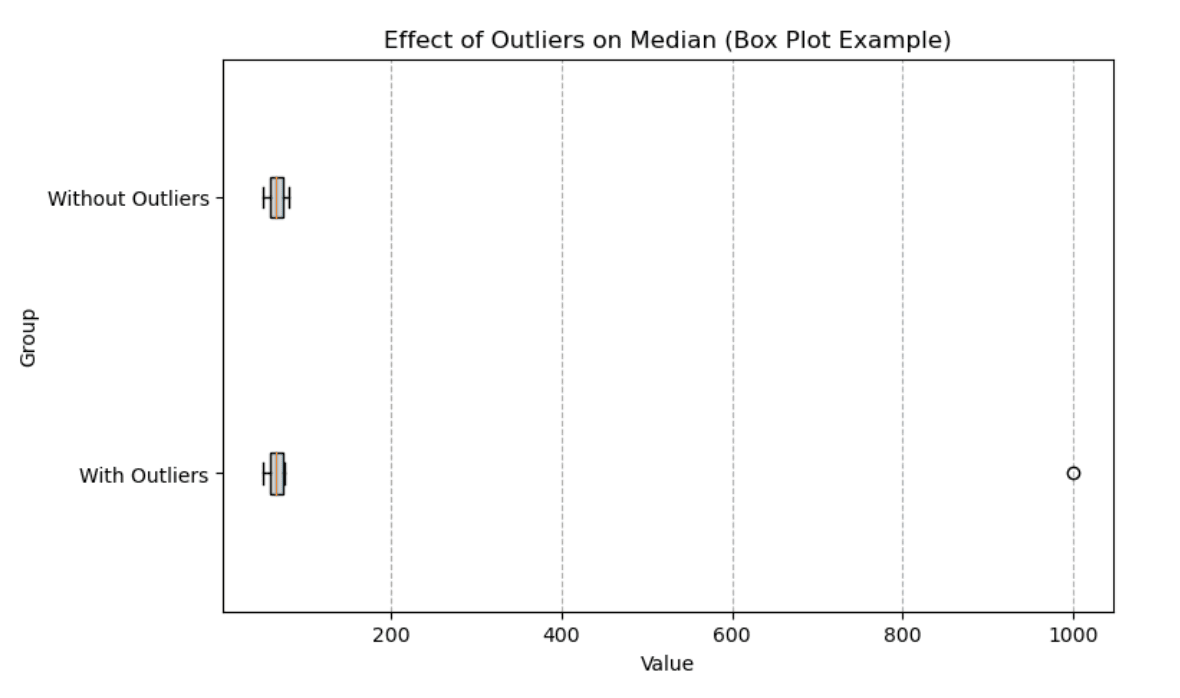
Gráfico de caixa mostrando o efeito dos valores atípicos na mediana. Imagem do autor
Essas visualizações mostram como a média e a mediana reagem a diferentes características dos dados, deixando claro quando usar cada medida. Seja analisando dados distorcidos, conjuntos de dados propensos a valores atípicos ou comparando grupos, recursos visuais como esses podem tornar relações complexas muito mais fáceis de entender.
Tópicos avançados e melhores práticas modernas
Agora vamos ver algumas ideias mais avançadas, caso você queira saber mais.
Imputação da média e da mediana
Agora, se você é um cientista de dados e precisa preencher lacunas nos seus dados, talvez precise escolher um método de imputação. Você deve estar se perguntando agora: qual é a diferença prática entre imputação média e mediana?
Como você pode imaginar, a imputação média substitui os valores ausentes pela média dos dados disponíveis, que, como já falamos, podem ser distorcidos por valores extremos. Já a imputação mediana substitui os valores que faltam pelo valor do meio do conjunto de dados.
Uma boa dica é dar uma olhada na distribuição dos seus dados. Se a distribuição dos seus dados estivesse distorcida com muitos valores ausentes e você tivesse usado a imputação da média, poderia ter alterado a distribuição dos seus dados!
MasMas lembre-se também que a imputação de valor único (média ou mediana) pode reduzir a variância e enfraquecer as relações entre as variáveis. Se a falta de dados for grande, pense em usar imputação múltipla ou imputação baseada em modelo para preservar melhor a incerteza e a estrutura.
Métodos paramétricos e baseados em classificação
Em muitos métodos paramétricos, a média (e a variância) são parâmetros centrais. Por exemplo, um modelo de regressão linear simples assume que os erros são normalmente distribuídos em torno de uma média. Quando seus dados seguem a suposição de normalidade, a média amostral é um estimador natural e se encaixa bem em estruturas paramétricas.
Agora, a mediana é frequentemente usada em configurações robustas e não paramétricas, e é uma escolha comum quando os dados são assimétricos ou têm valores atípicos. Muitos testes, como o teste de Mann-Whitney, são baseados em classificações e comparam distribuições (muitas vezes interpretadas como uma mudança de localização sob certas suposições) em vez de médias, e nem sempre testam uma diferença nas medianas.
Tudo isso quer dizer que entender a diferença entre média e mediana não é só uma questão de descrever os dados corretamente, mas também é importante para testar hipóteses.
Estabilidade do bootstrap para média e mediana
Ao decidir se usar a média ou a mediana, uma questão importante é saber se nossas estatísticas são estáveis para um determinado conjunto de dados. O bootstrapping é uma opção que nos permite estimar empiricamente a distribuição amostral da média e da mediana através de repetidas reamostragens (com reposição) dos dados originais.
Você poderia destacar as diferenças na estabilidade média e mediana de forma empírica. Você pode colocar alguns valores atípicos num conjunto de dados e depois repetir um procedimento bootstrap, o que vai te deixar mostrar visualmente como a distribuição da média muda mais drasticamente do que a da mediana. Além disso, o bootstrapping pode tornar isso mais concreto, mostrando o quão grandes ou pequenos podem ser seus intervalos de confiança em cenários realistas. Dá uma olhada no nosso tutorial sobre como usar métodos bootstrap pra saber mais.
Perda quadrada e perda absoluta
Deixa eu te dar uma definição alternativa, mas igualmente verdadeira: A média é o valor que minimiza a soma dos desvios quadrados dos dados, enquanto a mediana é o valor que minimiza a soma dos desvios absolutos.
Dá uma olhada nessa equação:
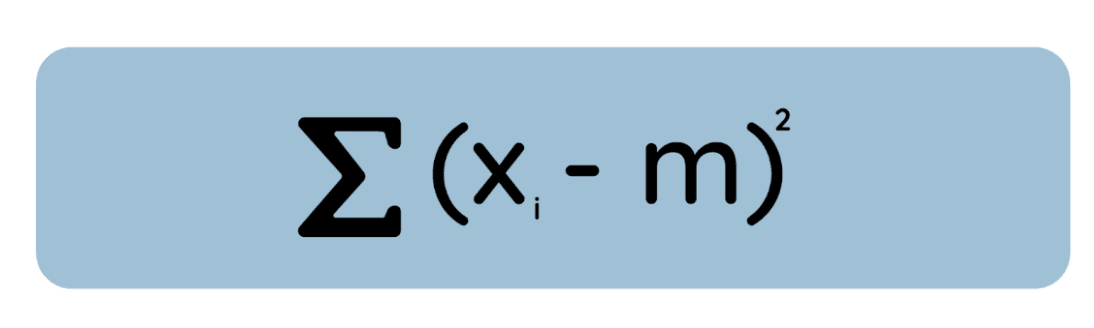
Se você derivar essa equação em relação a m, definir como zero e resolver, você descobrirá que o valor mínimo é simplesmente a média aritmética. Isso é importante porque, em muitos métodos estatísticos, como a regressão OLS, a gente minimiza os erros quadrados por conveniência matemática e para se adequar às suposições de erros normalmente distribuídos.
Agora, pense numa ideia diferente: Em vez de elevar ao quadrado cada desvio, medimos o erroabsoluto e e entre m e cada ponto de dados:
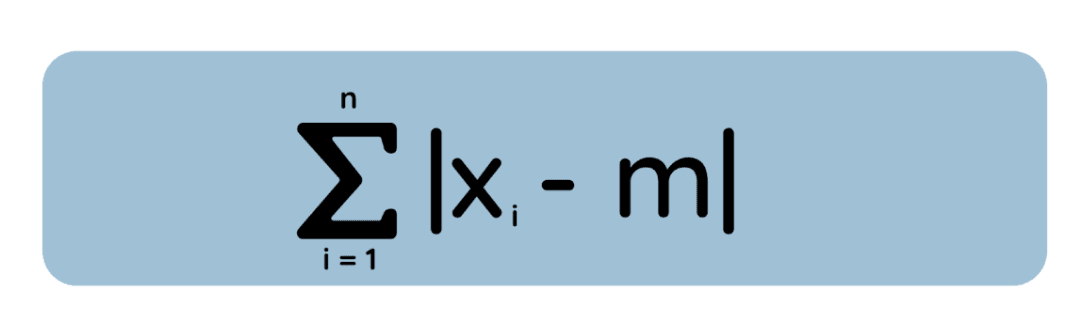
Aqui, queremos encontrar m que minimize esse desvio absoluto total. Acontece que (ao analisar a derivada da perda absoluta, ou por um argumento geométrico) a solução é amediana e e do conjunto de dados. (E quando você tem um número par de observações, qualquer valor entre os dois pontos médios minimiza o desvio absoluto total — portanto, o minimizador pode não ser único.)
Intuitivamente, se m está à esquerda da mediana, há mais pontos de dados à direita, puxando-o para se mover. Só a mediana é onde a atração da esquerda e da direita se equilibra, minimizando a distância absoluta total.
Média e mediana em escala
Por fim, vou dizer que a média é mais simples de calcular em grande escala. Isso quer dizer que você pode calcular isso aos poucos, conforme os dados vão chegando, sem precisar organizar nada.
A mediana é frequentemente calculada por meio de classificação na prática, o que pode ser caro em grande escala. Mas a mediana não precisa necessariamente de uma classificação completa (existem algoritmos de seleção) e, para conjuntos de dados muito grandes ou em streaming, algoritmos aproximados de esboço de quantis são normalmente usados para estimar a mediana de forma eficiente. Nosso curso Conceitos em Ciência da Computação é um ótimo recurso para aprender sobre essas coisas.
Próximos passos
Como você viu, a média é a média aritmética de um conjunto de dados, o que a torna sensível a valores extremos, enquanto a mediana representa o valor médio em um conjunto de dados ordenado. A escolha certa pode fazer toda a diferença, mas, dito isso, em análises do mundo real, muitas vezes é melhor relatar tanto a média quanto a mediana, junto com estatísticas adicionais, como moda, desvio padrão e percentis. Essa é a melhor maneira, porque dá uma visão geral.
Se você está ansioso para explorar mais a fundo os conceitos estatísticos, há várias áreas que valem a pena focar. Comece lendo sobre variações mais avançadas da média, como a média aparada, a média geométrica e a média ponderada, cada uma com sua finalidade específica. Eu também faria nosso curso de Introdução à Estatística, que não depende de nenhuma tecnologia específica.
Então, pra realmente se tornar mais um especialista, você vai querer escolher e dominar uma ferramenta. Nosso curso Introdução à Estatística em R e o programa de carreira de Estatístico em R são ótimos pontos de partida se você quer usar o R, que é uma linguagem popular para ciência de dados e estatística. Se você curte trabalhar com planilhas e uma linguagem de programação como Python, nossos cursos Introdução à Estatística no Google Sheets e Introdução à Estatística em Python oferecem uma abordagem prática para a análise estatística usando fórmulas e bibliotecas poderosas.
Profissional experiente em dados e escritor que tem paixão por capacitar aspirantes a especialistas no espaço de dados.
Média vs. Perguntas frequentes sobre a mediana
Qual é a principal diferença entre a média e a mediana?
A média é a média aritmética de todos os pontos de dados, enquanto a mediana é o valor do meio quando os dados são ordenados.
Quando devo usar a mediana em vez da média?
Use a mediana quando seus dados estiverem distorcidos ou tiverem valores atípicos que possam alterar a média.
A média e a mediana podem ser iguais?
Sim, eles podem ser iguais em uma distribuição perfeitamente simétrica, como uma distribuição normal.
Tem situações em que nem a média nem a mediana são suficientes?
Sim, para distribuições multimodais ou conjuntos de dados com vários picos, nenhum dos dois pode ser representativo. Nesses casos, medidas adicionais como moda ou percentis podem ser mais adequadas.
Por que a média é mais afetada pelos valores atípicos do que a mediana?
Para responder a essa pergunta, pense em como a média é calculada: A média é a soma de todos os valores dos dados dividida pelo número de observações. Um valor atípico (um valor super alto ou baixo) mexe bastante nessa soma, tirando a média do que a gente poderia chamar de um valor normal.
Agora, pensa em como a mediana é calculada: A mediana é o valor do meio em um conjunto de dados ordenado. Depende só da ordem dos dados — não do tamanho dos pontos individuais. Um único valor atípico não muda a posição do valor médio na lista ordenada e, por isso, quase não afeta a mediana.
O que você acha de escolher entre a média e a mediana?
Vamos ver algumas considerações importantes:
- Quando a precisão é fundamental: A média leva em conta todos os pontos de dados, o que a torna ideal para cálculos que precisam de todos os valores (por exemplo, consumo médio de combustível em todos os veículos).
- Quando é preciso robustez: A mediana é mais confiável em conjuntos de dados distorcidos ou quando valores extremos podem bagunçar a média. Por exemplo, a mediana é frequentemente preferida nos relatórios sobre rendimentos familiares para evitar distorções causadas por alguns indivíduos com rendimentos extremamente elevados.



