Curso
Análisis exploratorio de datos en R
4 h
115.1K
A la hora de interpretar datos, elegir la medida adecuada de tendencia central puede ser determinante para el éxito o el fracaso de tu análisis. Entre las métricas más comunes se encuentran lamedia y la mediana , dos conceptos aparentemente sencillos que tienen profundas implicaciones en la interpretación de los datos. Mientras que la media nos da el promedio aritmético, la mediana es el punto central de un conjunto ordenado de valores, de tal manera que la mitad de las observaciones se encuentran a cada lado. ¿Pero cuál es más fiable? La respuesta suele depender de la distribución de tus datos, la presencia de valores atípicos y la historia que quieras contar.
En este artículo, analizaré las diferencias entre la media y la mediana, sus puntos fuertes y débiles, y cómo elegir la más adecuada para cada situación. También exploraré cómo las distribuciones sesgadas y los valores atípicos afectan a estas medidas, proporcionando ejemplos prácticos e imágenes para ayudarte a comprender estos conceptos fundamentales. También abordaremos ideas más avanzadas.
Definiciones de media y mediana
Para comprender plenamente las diferencias entre la media y la mediana, veamos cada una de estas medidas y destaquemos sus propiedades clave.
¿Qué significa eso?
La media puede considerarse como el «punto de equilibrio» (o centro de masa) de los datos. considera todos los puntos de datos de un conjunto de datos y proporciona un único valor que representa la media. Más exactamente, tlo que tú quieres decir se calcula sumando todos los valores de un conjunto de datos y dividiéndolos por el número de valores.
¿Qué es la mediana?
La mediana es el valor medio cuando los datos están ordenados. A diferencia de la media, es más robusta frente a los valores atípicos, lo que proporciona una mejor medida de la tendencia central para los datos sesgados.
¿Cuál es el modo?
La moda es otra medida de tendencia central que representa el valor que aparece con mayor frecuencia en un conjunto de datos. Veamos un ejemplo:
3, 3, 6, 8, 9Aquí, el modo es 3 porque aparece dos veces, mientras que todos los demás valores solo aparecen una vez.
Cómo calcular la media y la mediana
Leer una definición es una cosa, pero calcular es otra. En esta sección, desglosaré los pasos para calcular cada medida y destacaré sus diferencias computacionales.
Cómo hallar la media
La media es la media aritmética de un conjunto de datos y se calcula de la siguiente manera:
- Suma los valores: Suma todos los números de tu conjunto de datos.
- Divide por el número total de valores: Toma la suma total y divídela por el número de valores.
Aquí se muestra el proceso representado como una ecuación general:
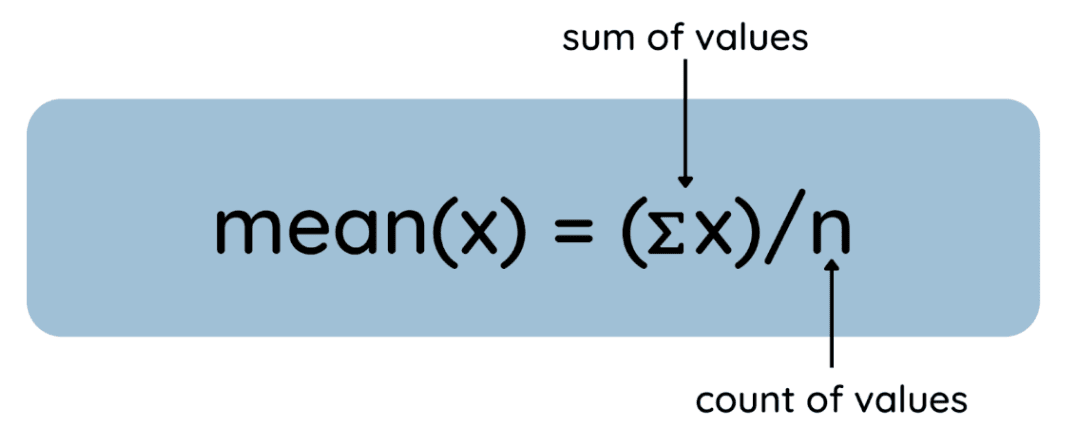
Cómo hallar la media. Imagen del autor
Por ejemplo, consideremos un conjunto de datos de calificaciones de exámenes:
78, 85, 92, 88, 70- Paso 1 (Suma): 78 + 85 + 92 + 88 + 70 = 413
- Paso 2 (Dividir): 413 ÷ 5 = 82,6
La puntuación media es 82,6.
Cómo hallar la mediana
La mediana es el valor medio de un conjunto de datos cuando se ordena en orden ascendente. Aquí te explicamos cómo encontrarlo:
- Ordenar los datos: Ordena los valores de menor a mayor.
- Identifica el valor medio: Si el conjunto de datos contiene un número impar de valores, la mediana es el valor del medio; si el conjunto de datos contiene un número par de valores, la mediana es la media de los dos valores del medio.
Y aquí están esos pasos representados como ecuaciones:
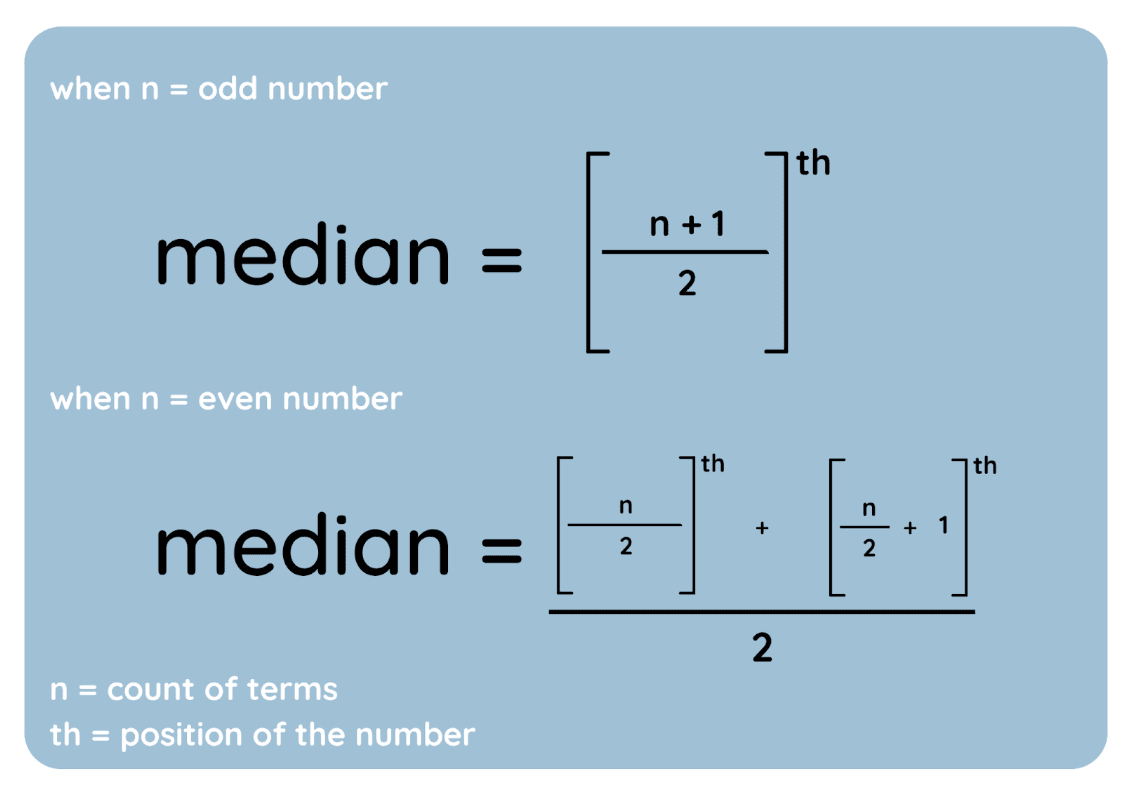
Fórmula mediana. Imagen del autor
También creé un gráfico para resaltar el proceso.
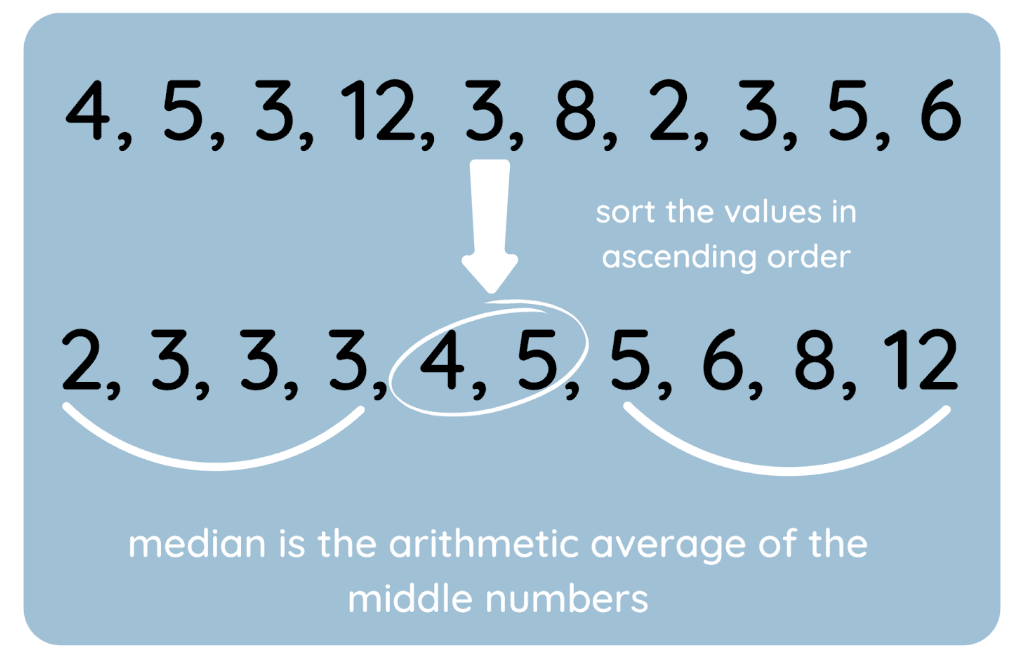
Cómo hallar la mediana. Imagen del autor
Aquí tienes un ejemplo de conjunto de datos con un número impar de valores:
70, 78, 85, 88, 92- Paso 1 (Ordenar): Ya está solucionado.
- Paso 2 (valor medio): El tercer valor es 85.
La mediana es 85.
Aquí hay otro ejemplo, pero con un número par de valores:
70, 78, 85, 88- Paso 1 (Ordenar): Ya está solucionado.
- Paso 2 (Promedio de los valores medios): (78 + 85) ÷ 2 = 81.5
La mediana es 81,5.
Por qué es importante la diferencia: Valores atípicos y sesgo
Aunque tanto la media como la mediana describen el centro de un conjunto de datos, su comportamiento diverge significativamente en presencia de valores atípicos y distribuciones sesgadas. Comprender esta diferencia es muy importante para interpretar los datos con precisión y evitar conclusiones erróneas.
Impacto de los valores atípicos
Los valores atípicos son valores que son significativamente más altos o más bajos que el resto de los datos. Pueden influir considerablemente en la media, pero tienen poco o ningún efecto en la mediana.
Consideremos un conjunto de datos de ingresos mensuales (en miles):
3, 3.5, 4, 4.5, 5, 6, 50El ingreso medio aquí es 10,85 mil, lo que se ve muy sesgado por el valor extremo de 50 000.
Por otro lado, el valor medio es 4,5 mil, lo que, en mi opinión, es una representación mucho más típica de los ingresos de este grupo.
Distribuciones sesgadas
La media y la mediana también difieren en su representación de los datos en distribuciones sesgadas (conjuntos de datos que no son simétricos).
Por ejemplo, enlas distribuciones sesgadas a la derecha (por ejemplo, los ingresos o los precios de la vivienda), la mayoría de los valores se agrupan en el extremo inferior, con unos pocos valores extremos que tiran de la cola hacia la derecha.
- Media: Desplazamientos hacia la cola, lo que da como resultado un valor superior a la mediana.
- Mediana: Se mantiene más cerca del conjunto de valores típicos, lo que refleja mejor el caso «típico».
Considera los ingresos:
30k, 35k, 40k, 45k, 50k, 100k, 200k- Media: 71,4 mil (con un aumento de 100 mil y 200 mil).
- Mediana: 45 000 (más cercano a la mayoría de los ingresos).
Por qué es importante
- En datos sesgados: La mediana suele ser más representativa de un punto de datos «típico», ya que no se ve influida por valores extremos.
- En datos simétricos: La media y la mediana serán casi idénticas, por lo que cualquiera de ellas puede utilizarse como medida de tendencia central.
Una cosa que debes recordar de esto es que es importante examinar siempre la distribución de tus datos antes de decidir si utilizar la media o la mediana. Herramientas como los histogramas y los gráficos de caja pueden ayudar a visualizar la asimetría e identificar valores atípicos. Hablaremos de esto más adelante. Además, quiero decir que examinar la diferencia entre la media y la mediana es una forma de evaluar la asimetría.
Cuándo utilizar la media y cuándo la mediana
Al analizar datos, la decisión de utilizar la media o la mediana depende de las características del conjunto de datos y de la información que se desee extraer. A continuación, te ofrecemos una tabla de referencia rápida para guiarte en tu elección:
| Utiliza la media cuando | Utiliza la mediana cuando |
|---|---|
| La distribución de los datos es aproximadamente normal (simétrica). | Los datos están muy sesgados (por ejemplo, ingresos, valor de las propiedades). |
| Los valores atípicos son mínimos o irrelevantes para el análisis. | Hay valores atípicos que podrían distorsionar los resultados si se incluyen. |
| Necesitas una medida que sea sensible a cada punto de datos, como en el modelado predictivo o al calcular totales. | Quieres reflejar el valor «típico» en lugar del «centro matemático» del conjunto de datos. |
Aquí tienes un consejo práctico que te será de gran ayuda: Comienza siempre con un análisis visual de tus datos (por ejemplo, un histograma o un diagrama de caja) para comprobar la simetría, la asimetría y la presencia de valores atípicos. Esto te ayudará a decidir si la media o la mediana se ajusta mejor a tu caso.
Visualización de la media frente a la mediana
Las visualizaciones son herramientas poderosas para comprender el comportamiento de la media y la mediana en diferentes conjuntos de datos. Pueden demostrar claramente cómo estas medidas responden a valores atípicos y distribuciones sesgadas, lo que ayuda a tomar mejores decisiones basadas en datos.
ejemplo de gráfico de barras
Imagina un pequeño conjunto de datos sobre ingresos en miles:
30, 35, 40, 45, 50, 55, 1000El siguiente gráfico de barras muestra cómo un solo valor extremo puede afectar drásticamente a la media, mientras que la mediana se mantiene relativamente estable. En este caso, la mayoría de los puntos de datos se agrupan entre 30 y 55, pero la presencia de un valor atípico (1000) eleva la media.
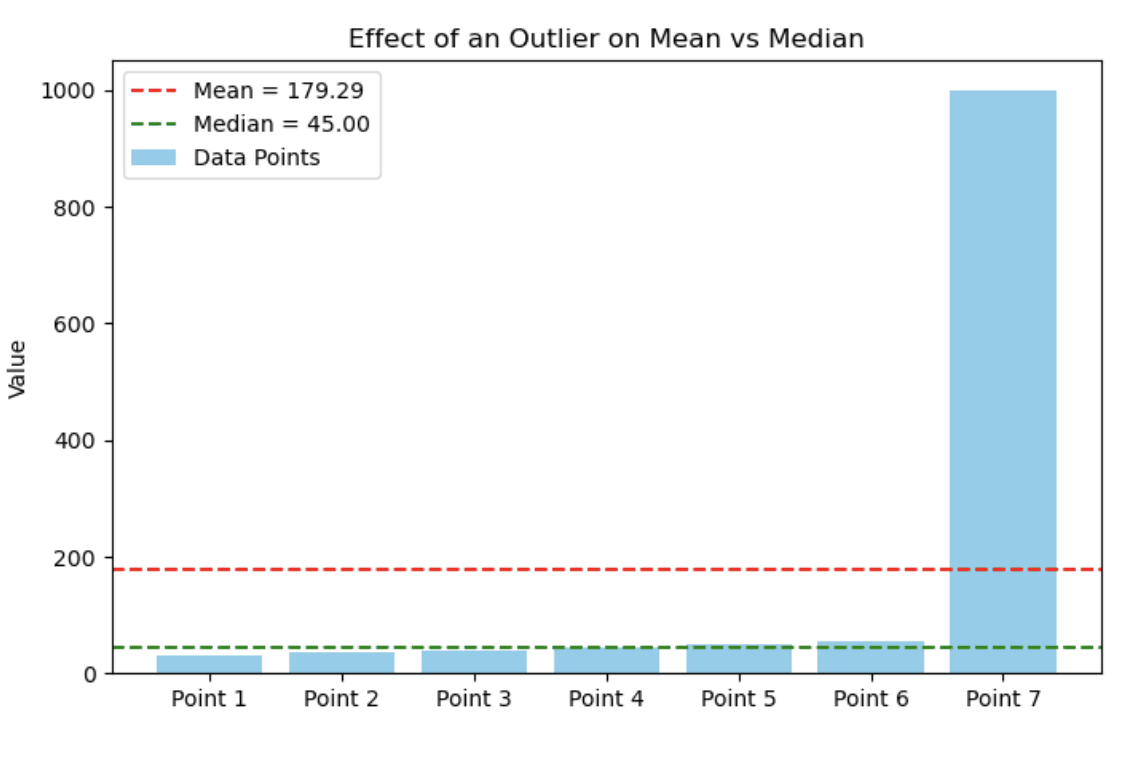
Gráfico de barras que muestra el efecto de un valor atípico en la media frente a la mediana. Imagen del autor
Ejemplo de histograma
En una distribución sesgada hacia la derecha (como los ingresos o los precios de la vivienda), la media suele desplazarse hacia la cola larga de valores altos, mientras que la mediana se mantiene más cerca del punto de datos «típico». Esto hace que la mediana sea una mejor medida de la tendencia central en estos casos.
El histograma siguiente muestra una distribución de ingresos simulada en la que la media (línea discontinua roja) es significativamente mayor que la mediana (línea discontinua verde) debido al sesgo.
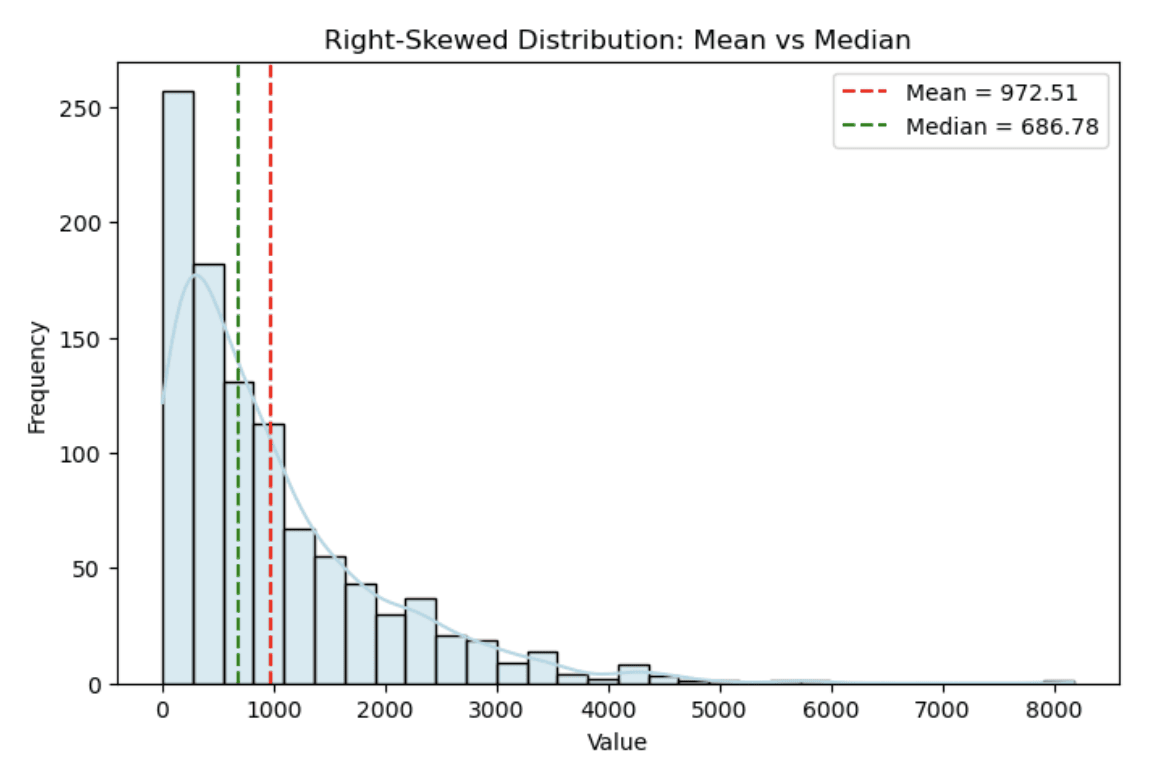
Histograma que muestra una distribución asimétrica a la derecha. Imagen del autor
Se puede observar cómo la asimetría a la derecha alarga la cola, creando una clara diferencia entre la media y la mediana.
Ejemplo de diagrama gráfico de caja
Un gráfico de caja es una forma excelente de visualizar el impacto de los valores atípicos en la mediana. A continuación, comparamos dos grupos: uno con valores atípicos y otro sin ellos. La mediana (línea vertical dentro del recuadro) se mantiene estable incluso con la presencia de valores extremos, pero el rango general de los datos se ve muy afectado por el valor atípico.
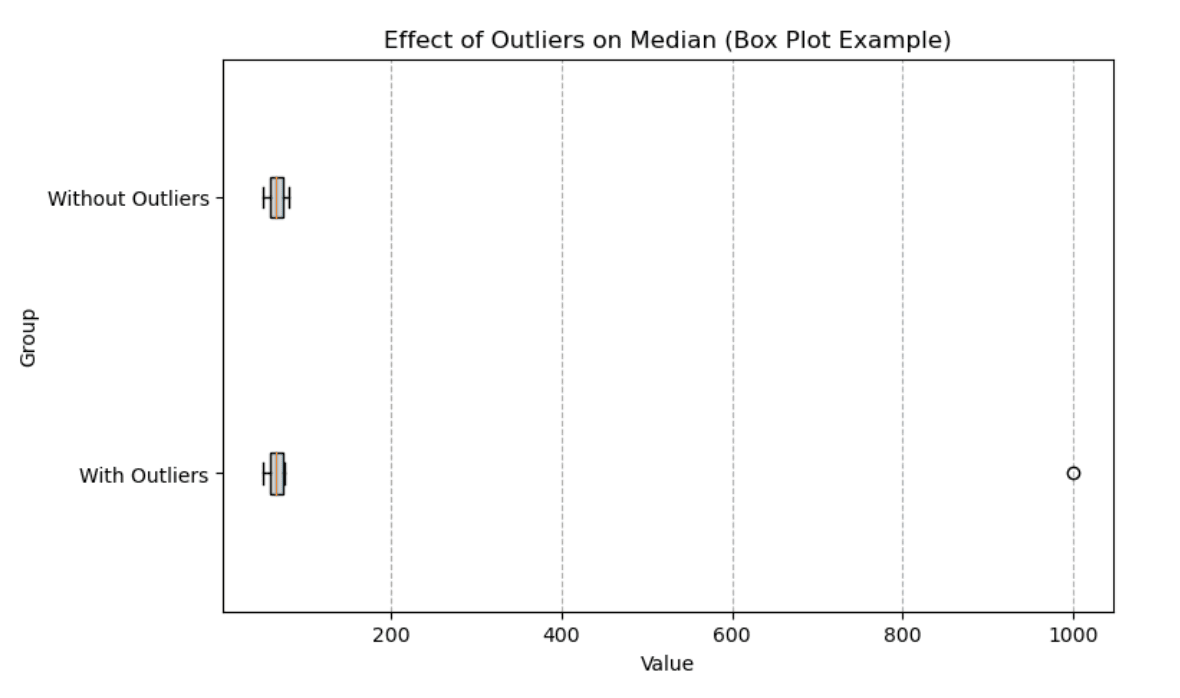
Gráfico de caja que muestra el efecto de los valores atípicos en la mediana. Imagen del autor
Estas visualizaciones resaltan cómo la media y la mediana responden a diferentes características de los datos, lo que proporciona claridad sobre cuándo utilizar cada medida. Ya sea para analizar datos sesgados, conjuntos de datos propensos a valores atípicos o comparar grupos, las ayudas visuales como estas pueden facilitar mucho la comprensión de relaciones complejas.
Temas avanzados y mejores prácticas modernas
Ahora veamos algunas ideas más avanzadas si tienes curiosidad por aprender más.
Imputación de la media y la mediana
Ahora bien, si eres científico de datos y necesitas completar los huecos en tus datos, es posible que tengas que elegir un método de imputación. Ahora te estarás preguntando: ¿cuál es la diferencia práctica entre la imputación de la media y la imputación de la mediana?
Como puedes imaginar, la imputación por la media sustituye los valores perdidos por la media de los datos disponibles, lo que, como hemos dicho, puede verse sesgado por valores extremos. La imputación mediana, por otro lado, reemplaza los valores faltantes con el valor medio del conjunto de datos.
Una regla general útil es observar la distribución de los datos. Si la distribución de tus datos estuviera sesgada con muchos valores perdidos y hubieras utilizado la imputación de la media, ¡podrías haber alterado la distribución de tus datos!
BPero recuerda también que la imputación de un solo valor (media o mediana) puede reducir la varianza y debilitar las relaciones entre variables. Si la falta de datos es considerable, considera la imputación múltiple o la imputación basada en modelos para preservar mejor la incertidumbre y la estructura.
Métodos paramétricos y basados en rangos
En muchos métodos paramétricos, la media (y la varianza) son parámetros centrales. Por ejemplo, un modelo de regresión lineal simple asume que los errores se distribuyen normalmente alrededor de una media. Cuando tus datos cumplen con la suposición de normalidad, la media muestral es un estimador natural y se ajusta bien a los marcos paramétricos.
Ahora bien, la mediana se utiliza a menudo en entornos robustos y no paramétricos, y es una opción habitual cuando los datos están sesgados o contienen valores atípicos. Muchas pruebas, como la prueba de Mann-Whitney, se basan en rangos y comparan distribuciones (a menudo interpretadas como un cambio de ubicación bajo supuestos) en lugar de medias, y no siempre comprueban una diferencia en las medianas.
Todo esto quiere decir que comprender la diferencia entre la media y la mediana no solo sirve para describir los datos correctamente, sino que también es importante para la comprobación de hipótesis.
Estabilidad de Bootstrap para la media y la mediana
A la hora de decidir si utilizar la media o la mediana, una cuestión clave es la estabilidad de nuestras estadísticas para un conjunto de datos determinado. El bootstrapping es una opción que nos permitiría estimar empíricamente la distribución muestral tanto de la media como de la mediana mediante un remuestreo repetido (con reemplazo) de los datos originales.
Podrías destacar empíricamente las diferencias en la estabilidad media y mediana. Podrías introducir algunos valores atípicos en un conjunto de datos y luego volver a ejecutar un procedimiento bootstrap, lo que te permitiría mostrar visualmente cómo la distribución de la media cambia de forma más drástica que la de la mediana. Además, el bootstrapping puede concretarlo mostrando lo grandes o pequeños que pueden ser tus intervalos de confianza en escenarios realistas. Lee nuestro tutorial sobre la aplicación de métodos bootstrap para obtener más información.
Pérdida al cuadrado y pérdida absoluta
Permíteme ahora ofrecerte una definición alternativa, pero igualmente cierta: La media es el valor que minimiza la suma de las desviaciones al cuadrado de los datos, mientras que la mediana es el valor que minimiza la suma de las desviaciones absolutas.
Echa un vistazo a esta ecuación:
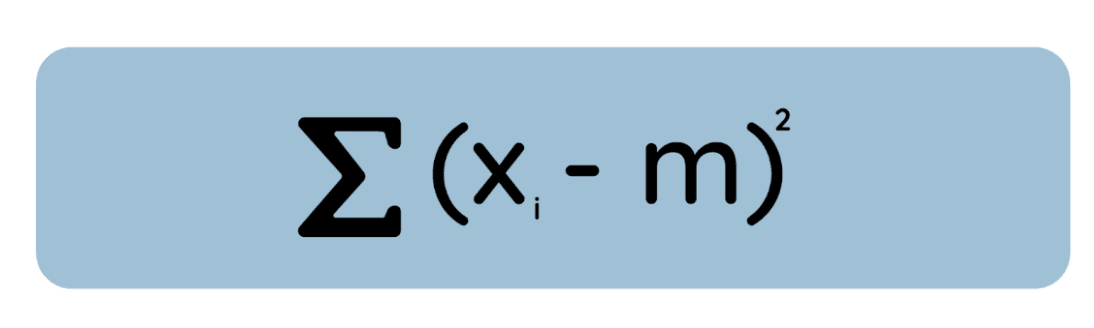
Si derivamos esta ecuación con respecto a , la pones a cero y la resuelves, verás que el valor mínimo es simplemente la media aritmética. Esto es importante porque en muchos métodos estadísticos, como la regresión OLS, minimizamos los errores al cuadrado por conveniencia matemática y para ajustarnos a los supuestos de errores distribuidos normalmente.
Ahora consideremos una idea diferente: En lugar de elevar al cuadrado cada desviación, medimos el errorabsoluto e e entre m y cada punto de datos:
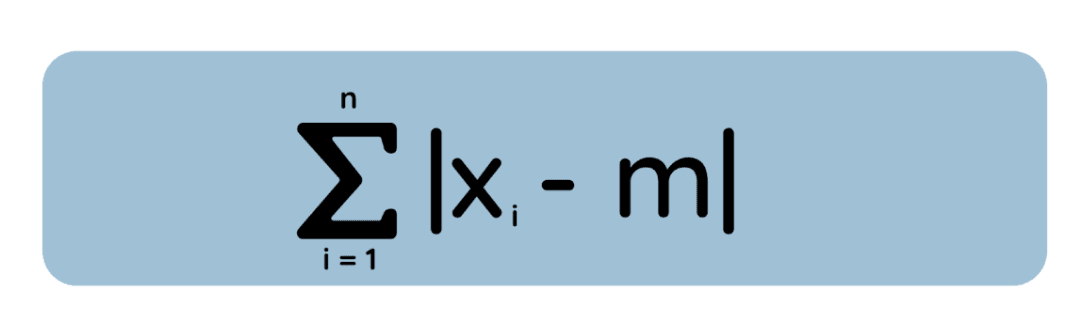
Aquí queremos encontrar m que minimice esta desviación absoluta total. Resulta (analizando la derivada de la pérdida absoluta, o mediante un argumento geométrico) que la solución es lamediana e e del conjunto de datos. (Y cuando tienes un número par de observaciones, cualquier valor entre los dos puntos medios minimiza la desviación absoluta total, por lo que el minimizador puede no ser único).
Intuitivamente, si está a la izquierda de la mediana, hay más puntos de datos a la derecha , lo que hace que se desplace hacia ese lado. Solo en la mediana se equilibran las fuerzas de izquierda y derecha, minimizando la distancia absoluta total.
Media y mediana a escala
Por último, diré que la media es computacionalmente más sencilla a gran escala. Esto significa que puedes calcularlo de forma incremental a medida que llegan los datos, sin necesidad de ordenarlos.
En la práctica, la mediana se calcula a menudo mediante la clasificación, lo que puede resultar costoso a gran escala. Sin embargo, la mediana no requiere necesariamente una clasificación completa (existen algoritmos de selección) y, en el caso de conjuntos de datos muy grandes o en streaming, se suelen utilizar algoritmos de esbozo cuantílico aproximado para estimar la mediana de forma eficiente. Nuestro curso «Conceptos de informática» es un recurso excelente para aprender sobre estos temas.
Próximos pasos
Como has visto, la media es la media aritmética de un conjunto de datos, lo que la hace sensible a los valores extremos, mientras que la mediana representa el valor medio en un conjunto de datos ordenados. La elección correcta puede marcar la diferencia, pero, dicho esto, en los análisis del mundo real, a menudo es mejor informar tanto de la media como de la mediana, junto con estadísticas adicionales como la moda, la desviación estándar y los percentiles. Esta es la mejor manera porque ofrece una visión global.
Si deseas profundizar en los conceptos estadísticos, hay varias áreas en las que vale la pena centrarse. Empieza por leer sobre variaciones más avanzadas de la media, como la media recortada, la media geométrica y la media ponderada, cada una de las cuales tiene su finalidad. También tomaría tu curso de Introducción a la Estadística, que es independiente de la tecnología.
Luego, para convertirte realmente en un experto, querrás elegir y dominar una herramienta. Nuestro curso Introducción a la estadística en R y el programa Estadístico en R son dos puntos de partida muy informativos si deseas utilizar R, un lenguaje muy popular en el ámbito de la ciencia de datos y la estadística. Si prefieres trabajar con hojas de cálculo y un lenguaje de programación como Python, nuestros cursos Introducción a la estadística en Google Sheets e Introducción a la estadística en Python ofrecen un enfoque práctico del análisis estadístico mediante fórmulas y potentes bibliotecas.
