Programa
Imagine que você está descendo uma colina, mas o terreno muda à medida que você avança - algumas partes são íngremes e outras são planas. Se você der um passo do mesmo tamanho todas as vezes, poderá ter dificuldades ou demorar muito para chegar ao final. No aprendizado de máquina, um desafio semelhante acontece com a descida de gradienteem que o uso da mesma taxa de aprendizado para todos os parâmetros pode tornar o aprendizado mais lento.
É aí que entra a Adagrad. Ele ajusta o tamanho da etapa para cada parâmetro com base no quanto ele foi alterado durante o treinamento, ajudando o modelo a aprender de forma mais rápida e eficaz, especialmente quando diferentes recursos têm escalas diferentes. Neste artigo, exploraremos como o Adagrad funciona e detalharemos a matemática por trás dele. Além disso, mostraremos a você como implementá-lo usando o PyTorch e o compararemos com outros otimizadores para que você possa escolher o melhor para seus projetos.
O que é Adagrad?
O Adagrad (Gradiente Adaptativo) é um algoritmo de otimização usado em aprendizado de máquinaespecificamente para o treinamento de redes neurais profundas. Ele foi projetado para adaptar a taxa de aprendizado de cada parâmetro com base em seus gradientes históricos. Essa abordagem permite que a Adagrad melhore a eficiência dos modelos de aprendizado de máquinaespecialmente em cenários com dados esparsos ou quando diferentes parâmetros têm taxas de convergência variáveis.
O Adagrad oferece taxas de aprendizado mais altas para recursos menos frequentes e taxas mais baixas para os mais frequentes, o que o torna adequado para trabalhar com dados esparsos. Além disso, ele reduz a necessidade de ajustar manualmente a taxa de aprendizado!
O algoritmo do Adagrad explicado
Vamos detalhar o algoritmo do Adagrad:
Etapa 1: Inicializar parâmetros
Primeiro, comece com:
- Os valores iniciais dos parâmetros,0que você deseja otimizar.
- Uma pequena constante ϵ para evitar a divisão por zero (geralmente é um número muito pequeno, como 10-8.
- A taxa de aprendizado inicial η, que determina o tamanho das atualizações de parâmetros no início.
Etapa 2: Calcular o gradiente
Para cada parâmetro 0t na etapa de tempo tvocê calcula o gradiente da função de perda em relação a esse parâmetro. Esse gradiente nos informa o quanto e em que direção devemos atualizar o parâmetro para reduzir a perda. Vamos chamar esse gradiente de gtonde t é a etapa de tempo atual.
Etapa 3: Acumular os gradientes ao quadrado
Em vez de atualizar os parâmetros diretamente, o Adagrad mantém o controle da soma quadrada dos gradientes de cada parâmetro. Para cada parâmetro ivocê calcula e acumula o gradiente quadrático em cada etapa de tempo. Esse gradiente acumulado é denotado como Gt.
Gt =Gt-1 + gt2
Aqui:
- Gt-1 é a soma dos gradientes ao quadrado até a etapa de tempo anterior.
- gt2 é o quadrado do gradiente atual do parâmetro.
Esse gradiente acumulado ajuda o Adagrad a ajustar a taxa de aprendizado de forma diferente para cada parâmetro com base no quanto ele foi atualizado.
Etapa 4: Atualizar os parâmetros
Agora que você tem o gradiente quadrático acumulado Gtpodemos atualizar cada parâmetro 0t. A regra de atualização do Adagrad é a seguinte:
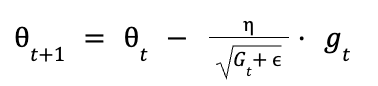
O que está acontecendo é o seguinte:
- η é a taxa de aprendizado inicial
- Gt são os gradientes quadrados acumulados até a etapa de tempo t.
- ϵ é um valor pequeno para evitar a divisão por zero.
- gt é o gradiente na etapa de tempo atual.
O termo:
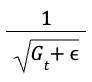
reduz efetivamente a taxa de aprendizado para parâmetros que têm um grande gradiente acumulado. Por outro lado, os parâmetros com gradientes acumulados menores terão uma taxa de aprendizado maior.
A fórmula do Adagrad adapta automaticamente a taxa de aprendizado, veja como:
- Atualizações frequentes (gradiente acumulado grande): Para parâmetros que são atualizados com frequência, Gt se torna grande, fazendo com que a taxa de aprendizado seja menor. Isso evita que o parâmetro mude muito drasticamente e estabiliza o aprendizado.
- Atualizações pouco frequentes (gradiente acumulado pequeno): Para parâmetros que são atualizados com menos frequência, Gt permanece pequeno, mantendo a taxa de aprendizado maior. Isso permite atualizações mais significativas quando necessário.
Implementação do Adagrad no PyTorch
PyTorch fornece uma implementação integrada do Adagrad, que pode ser acessada por meio do módulotorch.optim. Primeiro, instale o PyTorch usando o pip:
pip install torch torchvisionSaiba como criar sua primeira rede neural com nosso curso gratuito, Introdução à aprendizagem profunda com PyTorch.
Aqui está um guia passo a passo para você implementar o otimizador Adagrad no PyTorch:
Etapa 1: Importar as bibliotecas necessárias
import torchimport torch.nn as nnimport torch.optim as optimEtapa 2: Definir uma rede neural simples
class SimpleNN(nn.Module): def __init__(self): super(SimpleNN, self).__init__() self.fc1 = nn.Linear(10, 5) self.fc2 = nn.Linear(5, 2) def forward(self, x): x = torch.relu(self.fc1(x)) x = self.fc2(x) return xEtapa 3: Inicializar o modelo e o otimizador
model = SimpleNN()criterion = nn.CrossEntropyLoss()optimizer = optim.Adagrad(model.parameters(), lr=0.01)Etapa 4: Loop de treinamento
for epoch in range(10): # loop over the dataset multiple times inputs = torch.randn(1, 10) # random input tensor labels = torch.tensor([1]) # target labels # Zero the parameter gradients optimizer.zero_grad() # Forward pass outputs = model(inputs) loss = criterion(outputs, labels) # Backward pass and optimize loss.backward() optimizer.step() print(f'Epoch {epoch+1}, Loss: {loss.item()}')Nesse código, um modelo linear simples é treinado usando o otimizador AdaGrad. A taxa de aprendizado é definida como 0,01, mas o AdaGrad a ajustará para cada parâmetro com base nos gradientes quadrados acumulados.
Execute o código e você verá um resultado semelhante a este:

A saída mostra a perda após cada época, o que indica o grau de aprendizado do modelo. Inicialmente, a perda é maior, mas, à medida que o treinamento avança, a perda geralmente diminui, o que significa que o modelo está melhorando. Algumas flutuações são normais, especialmente com entradas aleatórias, mas, de modo geral, o modelo está aprendendo gradualmente a fazer previsões melhores.
Se você quiser descobrir a aprendizagem profunda e explorar como esse ramo da aprendizagem de máquina está mudando o mundo. Confira nosso curso sobre Aprendizado profundo em Python.
Adagrad vs. Outros otimizadores
Vamos comparar o Adagrad com outros otimizadores, como Adam, SGDe RMSProp.
Adagard vs. Adão
Adaptação da taxa de aprendizado
Tanto o Adagrad quanto o Adam adaptam a taxa de aprendizado para cada parâmetro, mas fazem isso de maneiras diferentes. O Adagrad dimensiona a taxa de aprendizado com base na soma dos gradientes quadrados, o que pode levar à diminuição das taxas de aprendizado ao longo do tempo. Por outro lado, o Adam usa o primeiro e o segundo momentos dos gradientes, o que lhe permite manter uma taxa de aprendizado mais estável durante o treinamento.
Manipulação de dados esparsos:
O Adagrad é particularmente adequado para lidar com dados esparsos devido à sua capacidade de atribuir taxas de aprendizado maiores a recursos pouco frequentes. Isso o torna uma boa opção para aplicativos como processamento de linguagem naturalem que gradientes esparsos são comuns. O Adam, embora também seja capaz de lidar com dados esparsos, é geralmente preferido por sua robustez e eficiência gerais em uma variedade maior de aplicativos.
Convergência e desempenho
Adam é frequentemente preferido por sua convergência mais rápida e desempenho superior na prática, especialmente em modelos de aprendizagem profunda com grandes conjuntos de dados. Seu uso de correção de momentum e viés ajuda a evitar que você fique preso em mínimos locais e pontos de sela, o que pode ser uma limitação para o Adagrad.
Aprenda sobre arquiteturas fundamentais de aprendizagem profunda, como CNNs, RNNs, LSTMs e GRUs para modelar imagens e dados sequenciais. Confira nosso curso Aprendizagem profunda intermediária com PyTorch.
Adagrad vs. outros algoritmos de descida de gradiente
Vamos comparar o Adagrad com o SGD e o RMSProp
AdaGrad vs. Descida de Gradiente Estocástico (SGD)
Descida de gradiente estocástica é um algoritmo básico de otimização que atualiza os parâmetros do modelo usando o gradiente da função de perda em relação aos parâmetros. Ele é conhecido por sua simplicidade e facilidade de implementação. No entanto, o SGD tem uma taxa de aprendizado constante, o que pode ser uma limitação ao lidar com dados esparsos ou escalas de recursos variáveis.
AdaGrad vs. RMSProp
O RMSProp é uma extensão do AdaGrad que aborda o problema da taxa de aprendizado decrescente introduzindo um fator de decaimento. Esse fator de decaimento permite que o RMSProp mantenha uma taxa de aprendizado mais estável durante todo o processo de treinamento.
Vamos resumir os prós e contras do Adagrad, SGD e RMSProp:
Otimizador | Prós | Contras |
Adagrad | 1. Adapta automaticamente as taxas de aprendizado para cada parâmetro. 2. Eficaz para dados esparsos. 3. Elimina a necessidade de ajuste manual da taxa de aprendizagem. | 1. A taxa de aprendizado diminui com o tempo, o que pode levar à convergência prematura. 2. Pode se tornar muito lento nas etapas posteriores do treinamento. |
SGD | 1. Simples e fácil de implementar. 2. Eficaz para escapar de mínimos locais devido à natureza estocástica. | 1. A alta variação nas atualizações pode levar à instabilidade. 2. Requer um ajuste cuidadoso da taxa de aprendizado e da dinâmica. |
RMSProp | 1. Adapta as taxas de aprendizado com base na média móvel dos gradientes quadrados. 2. Adequado para ambientes não estacionários. | 1. Requer um ajuste cuidadoso dos hiperparâmetros. 2. Não incorpora inerentemente o momentum. |
Casos de uso comuns e limitações
Vamos explorar os casos de uso e as limitações do AdaGrad em vários contextos.
Casos de uso do Adagrad
A capacidade exclusiva do Adagrad de adaptar as taxas de aprendizado para cada parâmetro o torna ideal para vários cenários:
- Processamento de linguagem natural (NLP): Uma das aplicações mais significativas do Adagrad é o processamento de linguagem natural (NLP). Na PNL, as incorporações de palavras são componentes essenciais, e o Adagrad é usado para otimizar essas incorporações, adaptando as taxas de aprendizado de cada parâmetro.
- Sistemas de recomendação: Nos sistemas de recomendação, o Adagrad é usado para otimizar os pesos do modelo de recomendação. Isso é importante para prever a probabilidade de um usuário gostar de um determinado produto.
- Reconhecimento de imagens: Em reconhecimento de imagensO Adagrad é usado para otimizar os pesos das redes neurais profundas. Ao adaptar as taxas de aprendizado de cada parâmetro, o Adagrad garante que os pesos sejam atualizados adequadamente para a tarefa em questão, melhorando a precisão do modelo de reconhecimento de imagem
Limitações do Adagrad
Embora o Adagrad seja poderoso em determinadas situações, ele tem algumas limitações:
- Diminuição da taxa de aprendizado: Uma das principais limitações do Adagrad é sua tendência de reduzir a taxa de aprendizado de forma muito agressiva ao longo do tempo. Como o algoritmo acumula os gradientes quadrados desde o início do treinamento, a taxa de aprendizado efetiva pode se tornar muito pequena, levando a uma convergência lenta ou até mesmo fazendo com que o modelo pare de aprender completamente.
- Requisitos de memória: O Adagrad requer mais memória para armazenar os gradientes históricos de cada parâmetro, o que o torna menos eficiente para conjuntos de dados maiores. Isso pode ser uma desvantagem significativa ao trabalhar com modelos de aprendizado de máquina em grande escala, em que a eficiência da memória é crucial.
Estratégias para atenuar as limitações
Há várias estratégias que você pode usar para lidar com as limitações do Adagrad:
- Uso de AdaDelta e RMSProp: Para resolver o problema da diminuição das taxas de aprendizado, foram desenvolvidas extensões do AdaGrad, como o AdaDelta e o RMSProp.
- Combinando com o impulso: Outra estratégia para atenuar as limitações do AdaGrad é combiná-lo com métodos baseados em momentum. O otimizador Adam, por exemplo, combina a taxa de aprendizado adaptável do AdaGrad com o conceito de momentum, o que ajuda a acelerar a convergência e a melhorar o desempenho na prática.
- Ajuste de hiperparâmetros: O ajuste cuidadoso dos hiperparâmetros, como a taxa de aprendizado inicial e o valor epsilon usado para evitar a divisão por zero, também pode ajudar a atenuar algumas das limitações do AdaGrad.
Exercício prático: Otimização de um modelo com o Adagrad
Vamos criar uma rede neural simples, treiná-la usando o otimizador Adagrad e comparar seu desempenho com o de outros otimizadores populares.
Se você quiser saber mais sobre o PyTorch, consulte nosso guia em Tutorial do PyTorch: Criando uma rede neural simples do zero.
Vamos começar criando um modelo básico de rede neural no PyTorch. Projetaremos uma rede adequada para classificação binária em dados esparsos, onde o Adagrad se destaca.
import torchimport torch.nn as nnclass SparseNN(nn.Module): def __init__(self, input_size): super(SparseNN, self).__init__() self.fc1 = nn.Linear(input_size, 50) self.fc2 = nn.Linear(50, 1) self.activation = nn.ReLU() self.output_activation = nn.Sigmoid() def forward(self, x): x = self.activation(self.fc1(x)) x = self.output_activation(self.fc2(x)) return xEssa rede neural tem uma camada de entrada, uma camada oculta com 50 neurônios e uma camada de saída com um único neurônio. Usamos a ativação ReLU para a camada oculta e a ativação Sigmoid para a camada de saída, o que a torna adequada para a classificação binária.
Agora, vamos configurar nosso processo de treinamento usando o otimizador Adagrad. Criaremos uma função para lidar com o treinamento:
import torch.optim as optimfrom torch.utils.data import DataLoader, TensorDataset# Function to train the modeldef train_model(model, optimizer, criterion, train_loader, num_epochs=100): losses = [] for epoch in range(num_epochs): # loop for each training epoch for inputs, targets in train_loader: # Clear gradients before each batch to avoid accumulation optimizer.zero_grad() # Reset gradients to zero # Forward pass - get model predictions outputs = model(inputs) # Calculate loss based on predictions and targets loss = criterion(outputs, targets) # Backward pass - calculate gradients for parameter updates based on the loss loss.backward() # Update model parameters based on calculated gradients optimizer.step() # Track loss for monitoring training progress losses.append(loss.item()) return losses# Setup for trainingX, y = generate_sparse_data() # This function generates our sparse datasetinput_size = X.shape[1]train_size = int(0.8 * len(X))X_train, X_test = X[:train_size], X[train_size:]y_train, y_test = y[:train_size], y[train_size:]train_dataset = TensorDataset(X_train, y_train)train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)model = SparseNN(input_size)criterion = nn.BCELoss() # Assuming binary classification with BCE lossoptimizer = optim.Adagrad(model.parameters(), lr=0.01)# Train the modellosses = train_model(model, optimizer, criterion, train_loader)Nessa configuração, nós:
- Crie nosso modelo SparseNN.
- Defina a função de perda (Binary Cross Entropy).
- Inicialize o otimizador Adagrad com uma taxa de aprendizado de 0,01.
- Treine o modelo por 100 épocas, registrando a perda em cada época.
Agora, para avaliar o desempenho do nosso modelo, criaremos uma função de avaliação:
def evaluate_model(model, test_loader): model.eval() correct = 0 total = 0 with torch.no_grad(): for inputs, targets in test_loader: outputs = model(inputs) predicted = (outputs > 0.5).float() total += targets.size(0) correct += (predicted == targets).sum().item() accuracy = correct / total return accuracy# Evaluate the modeltest_dataset = TensorDataset(X_test, y_test)test_loader = DataLoader(test_dataset, batch_size=32)accuracy = evaluate_model(model, test_loader)print(f"Adagrad Accuracy: {accuracy:.4f}")Essa função calcula a precisão do nosso modelo no conjunto de teste.
Em seguida, vamos compará-lo com outros otimizadores populares: SGD, Adam e RMSprop. Criaremos uma função para executar o experimento para cada otimizador:
def run_experiment(optimizer_class, lr=0.01): model = SparseNN(input_size) criterion = nn.BCELoss() if optimizer_class == optim.SGD: optimizer = optimizer_class(model.parameters(), lr=lr, momentum=0.9) elif optimizer_class == optim.RMSprop: optimizer = optimizer_class(model.parameters(), lr=lr, alpha=0.99) else: optimizer = optimizer_class(model.parameters(), lr=lr) losses = train_model(model, optimizer, criterion, train_loader) accuracy = evaluate_model(model, test_loader) return losses, accuracy# Compare optimizersoptimizers = { 'Adagrad': optim.Adagrad, 'SGD': optim.SGD, 'Adam': optim.Adam, 'RMSprop': optim.RMSprop}results = {}for name, opt_class in optimizers.items(): losses, accuracy = run_experiment(opt_class) results[name] = {'losses': losses, 'accuracy': accuracy}print("Final accuracies:")for name, data in results.items(): print(f"{name}: {data['accuracy']:.4f}")Depois de executar esse código, obtemos os seguintes resultados:
Final accuracies:Adagrad: 0.9350SGD: 0.8950Adam: 0.9300RMSprop: 0.8600Esses resultados mostram que o Adagrad teve o melhor desempenho em nosso problema de dados esparsos, alcançando a maior precisão de 95,00%. Isso mostra que o Adagrad é adequado para cenários de dados esparsos. Adam ficou em um segundo lugar, enquanto SGD e RMSprop tiveram um desempenho inferior nesse caso específico.
Para visualizar o processo de treinamento, podemos traçar as curvas de perda:
import matplotlib.pyplot as pltplt.figure(figsize=(12, 6))for name, data in results.items(): plt.plot(data['losses'], label=f"{name} (Accuracy: {data['accuracy']:.4f})")plt.xlabel('Epochs')plt.ylabel('Loss')plt.title('Training Loss Comparison (Sparse Data)')plt.legend()plt.show()Vamos combinar todos os trechos de código e aqui está o código completo.
import torchimport torch.nn as nnimport torch.optim as optimfrom torch.utils.data import DataLoader, TensorDatasetimport matplotlib.pyplot as plt# Step 1: Generate sparse synthetic datadef generate_sparse_data(n_samples=1000, n_features=100, sparsity=0.95): X = torch.randn(n_samples, n_features) mask = torch.rand(n_samples, n_features) < sparsity X[mask] = 0 weights = torch.randn(n_features) y = (torch.matmul(X, weights) > 0).float().view(-1, 1) return X, y# Step 2: Define the neural networkclass SparseNN(nn.Module): def __init__(self, input_size): super(SparseNN, self).__init__() self.fc1 = nn.Linear(input_size, 50) self.fc2 = nn.Linear(50, 1) self.activation = nn.ReLU() self.output_activation = nn.Sigmoid() def forward(self, x): x = self.activation(self.fc1(x)) x = self.output_activation(self.fc2(x)) return x# Step 3: Train the modeldef train_model(model, optimizer, criterion, train_loader, num_epochs=100): losses = [] for epoch in range(num_epochs): for inputs, targets in train_loader: optimizer.zero_grad() outputs = model(inputs) loss = criterion(outputs, targets) loss.backward() optimizer.step() losses.append(loss.item()) return losses# Step 4: Evaluate the modeldef evaluate_model(model, test_loader): model.eval() correct = 0 total = 0 with torch.no_grad(): for inputs, targets in test_loader: outputs = model(inputs) predicted = (outputs > 0.5).float() total += targets.size(0) correct += (predicted == targets).sum().item() accuracy = correct / total return accuracy# Step 5: Main function to run the experimentdef run_experiment(optimizer_class, lr=0.01): # Generate sparse data X, y = generate_sparse_data() input_size = X.shape[1] train_size = int(0.8 * len(X)) X_train, X_test = X[:train_size], X[train_size:] y_train, y_test = y[:train_size], y[train_size:] # Create data loaders train_dataset = TensorDataset(X_train, y_train) test_dataset = TensorDataset(X_test, y_test) train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True) test_loader = DataLoader(test_dataset, batch_size=32) # Initialize model and training components model = SparseNN(input_size) criterion = nn.BCELoss() # Use default hyperparameters for each optimizer if optimizer_class == optim.SGD: optimizer = optimizer_class(model.parameters(), lr=lr, momentum=0.9) elif optimizer_class == optim.RMSprop: optimizer = optimizer_class(model.parameters(), lr=lr, alpha=0.99) else: optimizer = optimizer_class(model.parameters(), lr=lr) # Train the model losses = train_model(model, optimizer, criterion, train_loader) # Evaluate the model accuracy = evaluate_model(model, test_loader) return losses, accuracy# Step 6: Compare Adagrad with other optimizersoptimizers = { 'Adagrad': optim.Adagrad, 'SGD': optim.SGD, 'Adam': optim.Adam, 'RMSprop': optim.RMSprop}results = {}for name, opt_class in optimizers.items(): losses, accuracy = run_experiment(opt_class) results[name] = {'losses': losses, 'accuracy': accuracy}# Step 7: Plot resultsplt.figure(figsize=(12, 6))for name, data in results.items(): plt.plot(data['losses'], label=f"{name} (Accuracy: {data['accuracy']:.4f})")plt.xlabel('Epochs')plt.ylabel('Loss')plt.title('Training Loss Comparison (Sparse Data)')plt.legend()plt.show()print("Final accuracies:")for name, data in results.items(): print(f"{name}: {data['accuracy']:.4f}")Aqui está o resultado:
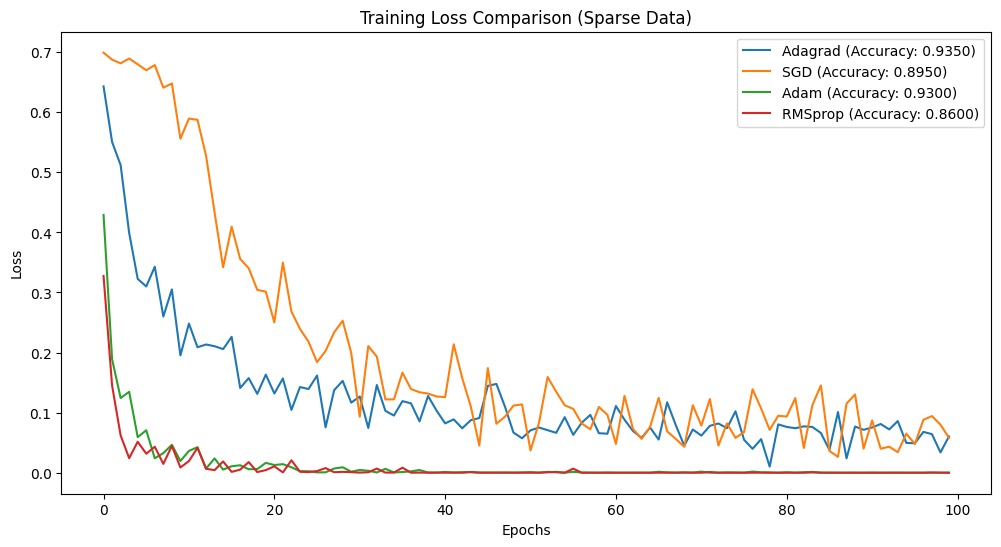
Conclusão
O Adagrad é útil ao trabalhar com dados esparsos devido à sua taxa de aprendizado adaptável. Criamos uma rede neural básica e a treinamos usando o Adagrad e, em seguida, comparamos seu desempenho com outros algoritmos de otimização conhecidos. Os resultados favoreceram fortemente o Adagrad, mostrando que ele lida melhor com dados esparsos.
Também escolhi a dedo alguns dos melhores recursos sobre PyTorch, aprendizagem profunda e outros algoritmos de otimização. Não deixe de dar uma olhada neles para saber mais a fundo:
- Tutorial do PyTorch: Criando uma rede neural simples a partir do zero
- Tutorial do Adam Optimizer: Intuição e implementação em Python
- Descida de gradiente estocástico em Python: Um guia completo para otimização de ML
- Introdução à aprendizagem profunda com PyTorch
- Aprendizagem profunda intermediária com PyTorch
- Aprendizagem profunda para imagens com PyTorch

