Método dos mínimos quadrados: Como encontrar a linha mais adequada

Imagine que você esteja tentando prever os preços de imóveis com base na metragem quadrada. Você tem pontos de dados de vendas recentes, mas eles não formam um padrão perfeito. Algumas casas são vendidas por mais do que o esperado e outras por menos. Como você encontra a melhor linha de tendência que reflete a relação geral entre tamanho e preço sem deixar que casas individuais atrapalhem sua previsão?

O método dos mínimos quadrados pode ser a solução que você precisa. Neste artigo, exploraremos os principais conceitos do método dos mínimos quadrados, suas variações e aplicações. Ao final, você terá uma sólida compreensão de como usar esse método e aplicá-lo a problemas reais.

O que é o método dos mínimos quadrados?

O método dos mínimos quadrados é uma técnica estatística usada para determinar a linha ou curva de melhor ajuste para um conjunto de pontos de dados. Ele funciona minimizando as diferenças quadráticas entre os valores observados e os previstos em um conjunto de dados. A diferença entre os pontos de dados reais e os valores previstos pelo modelo é chamada de resíduos. O objetivo é encontrar um modelo que minimize a soma desses resíduos ao quadrado, levando às previsões mais precisas possíveis.

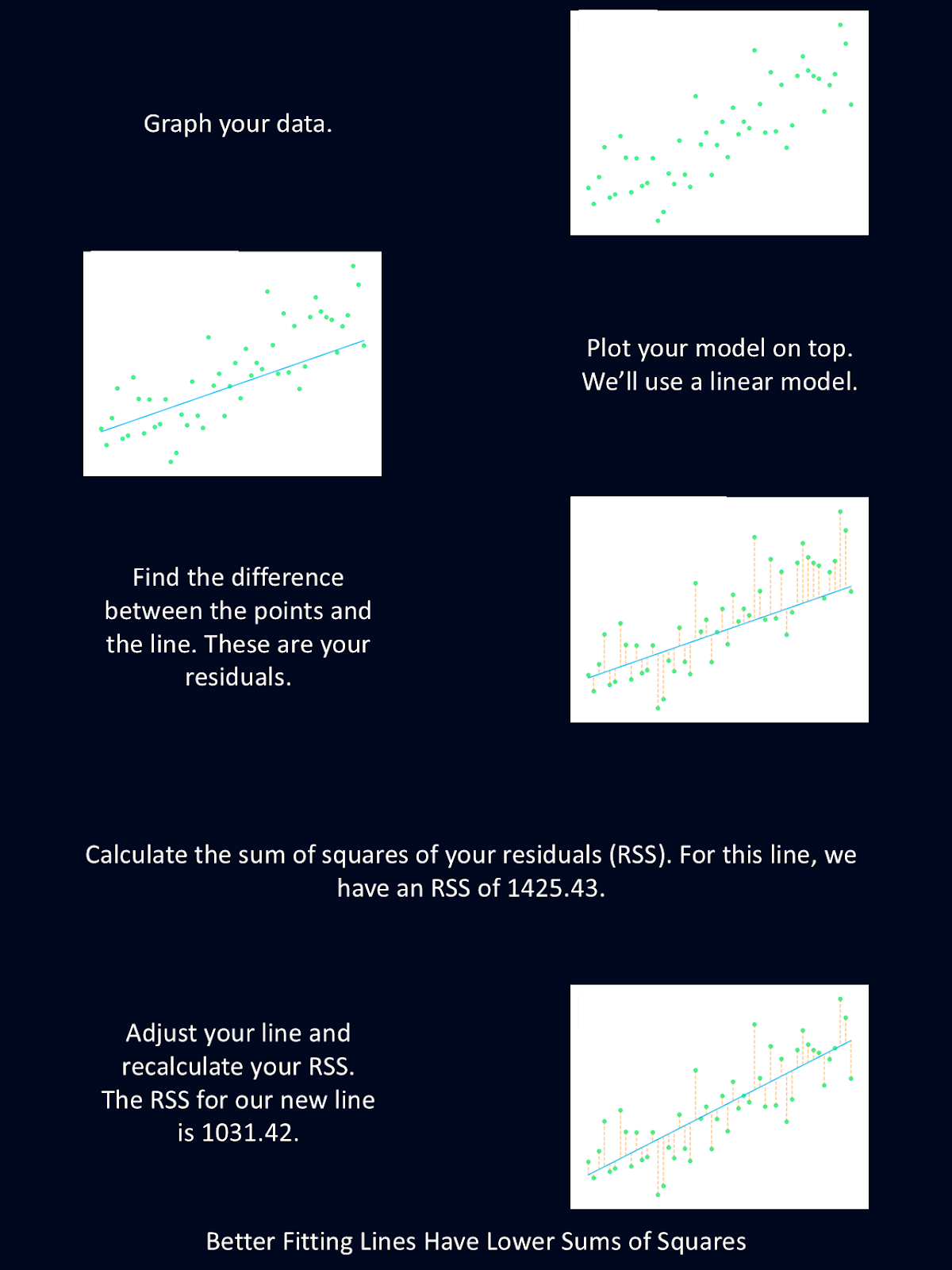
O diagrama acima fornece uma breve explicação das etapas do método dos mínimos quadrados.

Esse método foi criado por Carl Friedrich Gauss, de 18 anos, em 1895 (talvez você reconheça o nome dele pela distribuição gaussiana). Mais tarde, Adrien-Marie Legendre formalizou a técnica em 1805 e foi o primeiro a escrever um artigo usando o método dos mínimos quadrados para reconstruir a órbita de um asteroide. 

Como funciona o método dos mínimos quadrados

O método dos mínimos quadrados encontra a linha que melhor se ajusta a um conjunto de pontos, minimizando a soma das diferenças quadráticas entre os valores observados e os valores previstos. Isso é usado para encontrar os parâmetros do modelo com o ajuste mais próximo possível.

Vamos tentar isso com um conjunto de dados extremamente pequeno: apenas 10 pontos. Primeiro, precisamos escolher um modelo para ajustar nossos dados. Para este exemplo simples, escolheremos uma regressão linear simples, o que significa que estamos realizando uma regressão em que temos exatamente uma variável independente e uma variável dependente.

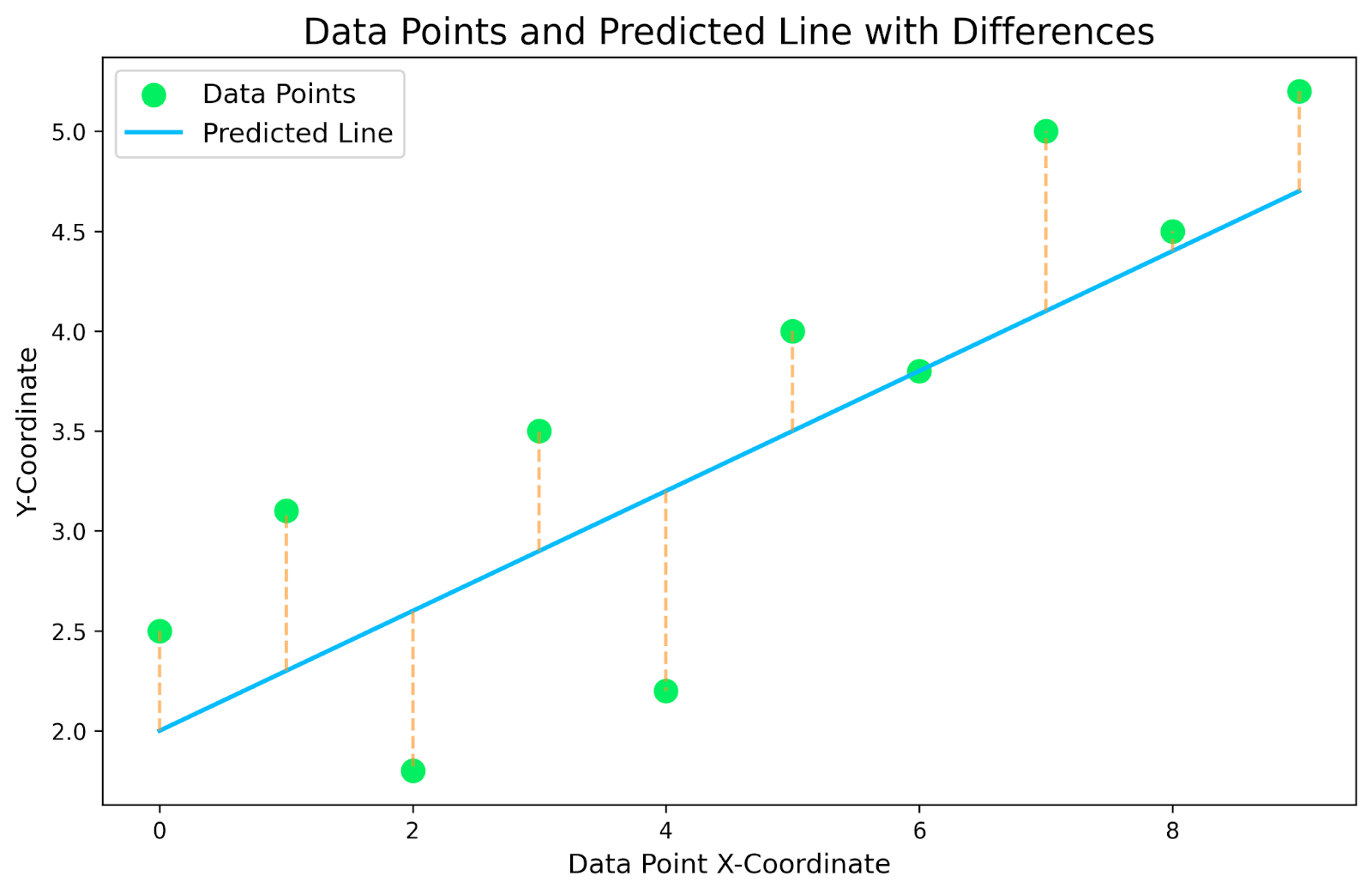
O gráfico acima é um gráfico de nosso pequeno conjunto de dados, com uma regressão linear plotada na parte superior. As linhas pontilhadas amarelas que conectam os pontos de dados com a linha prevista são os resíduos. O objetivo é encontrar o modelo de regressão linear que minimize essas linhas residuais pontilhadas em amarelo.

Para cada ponto de dados em nosso conjunto de dados, precisamos encontrar a diferença nas coordenadas y entre o ponto de dados e a linha. Esses serão os nossos resíduos. Em seguida, elevamos cada resíduo ao quadrado para remover quaisquer números negativos e obter a soma total. Isso nos dará uma noção de quão bem nossa linha se ajusta aos dados. Confira na tabela abaixo o detalhamento de nosso gráfico específico.

Agora que temos uma ideia de quão bem essa linha se ajusta aos nossos dados, podemos ajustar os parâmetros da linha, seja a inclinação ou a interceptação, e executar novamente nossos cálculos. A linha que tiver a menor soma de resíduos ao quadrado é a linha que melhor se ajusta aos nossos dados. Portanto, essa linha nos dará as melhores previsões.

Usando o método dos mínimos quadrados para encontrar a melhor linha

No exemplo acima, não encontramos a linha de melhor ajuste. Em vez disso, apenas calculamos a adequação dessa linha aos dados. Agora, podemos iterar por várias linhas potenciais e fazer o mesmo cálculo para encontrar as que se encaixam melhor. Ou podemos usar um pouco de álgebra para encontrar a melhor linha mais rapidamente. Vamos tentar isso.

Começaremos com a equação da regressão linear: y=mx+b, em que b é a interceptação y e m é a inclinação. Agora vamos criar alguns dados.

Primeiro, precisamos calcular a média dos valores X e Y. Eles servirão como nossos valores previstos:

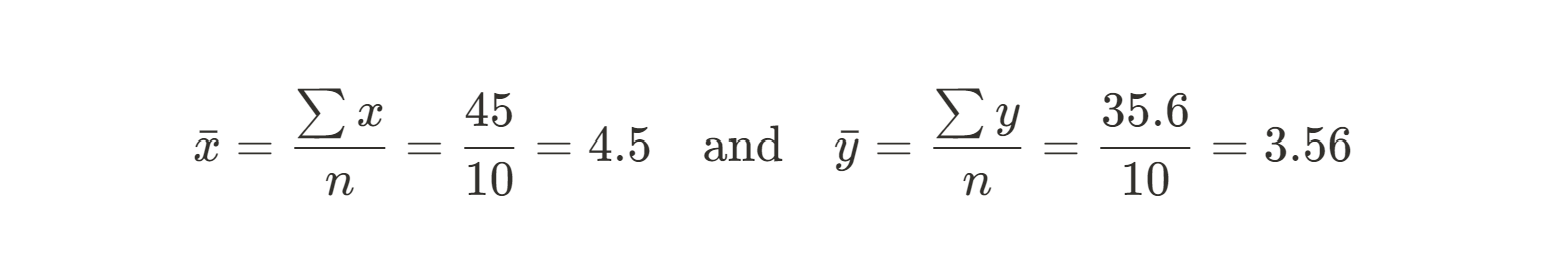
Em seguida, podemos usar a soma dos quadrados de nossos resíduos entre cada ponto de dados e nosso valor previsto (a média) para encontrar a inclinação. Aqui está a equação que usaremos:

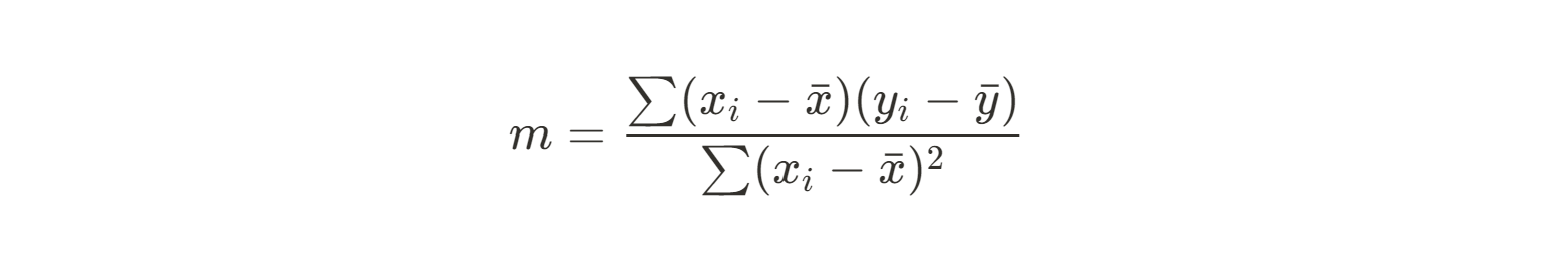
Como essa é uma equação bastante trabalhosa para ser feita manualmente, calcularemos o numeradore o denominador separadamente. Vamos começar com o numerador:

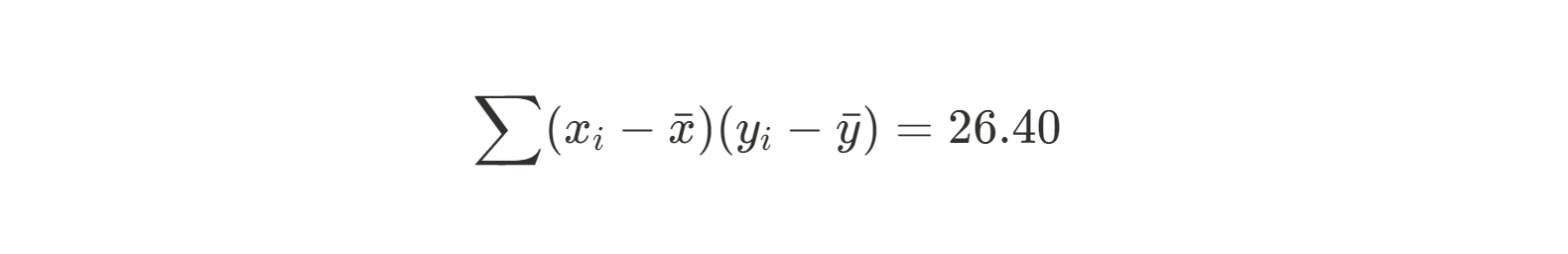
Agora vamos fazer o mesmo com o denominador:

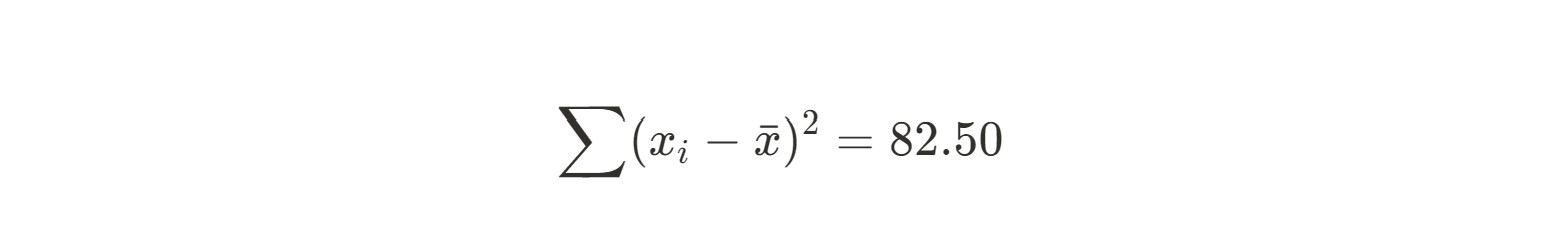
Agora podemos calcular a inclinação de nossa linha de melhor ajuste.

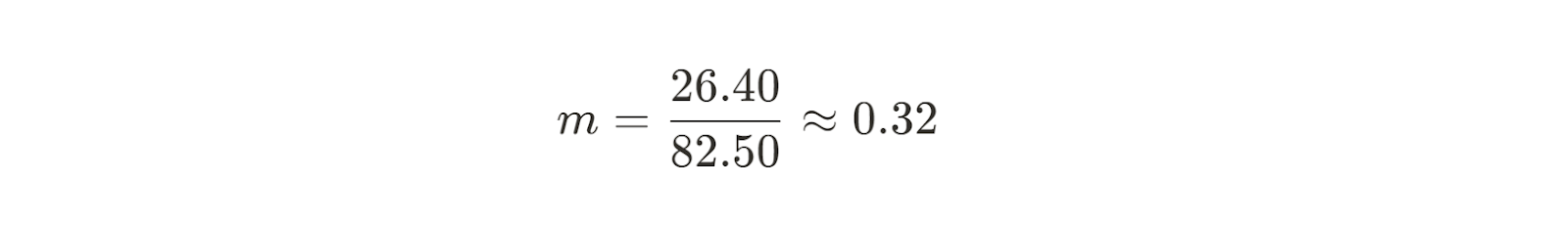
Portanto, agora sabemos a inclinação da linha que melhor se ajustará aos nossos dados. Em seguida, precisamos encontrar a interceptação y. A fórmula para o intercepto b é fácil de encontrar usando um pouco de rearranjo algébrico:

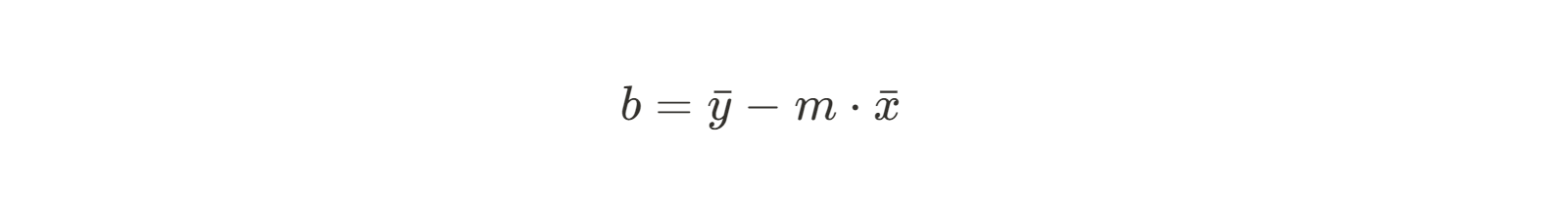
Como já sabemos a inclinação, podemos simplesmente inserir nossas médias x e y e resolver para b.

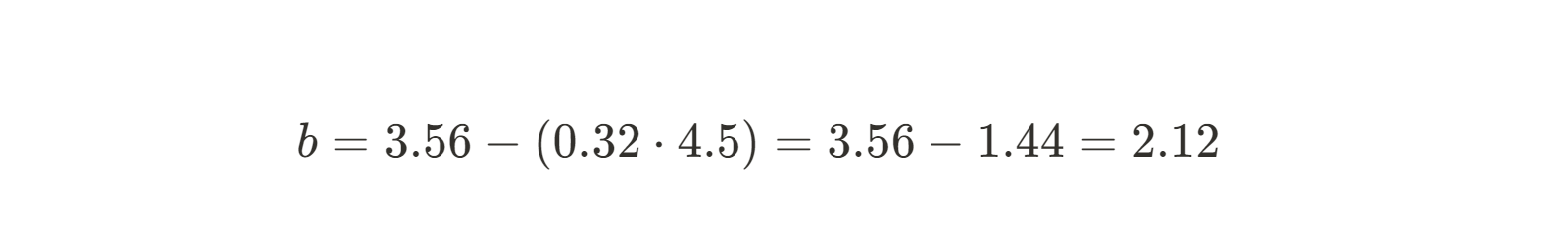
Agora que temos m e b, podemos escrever a equação da linha de melhor ajuste:

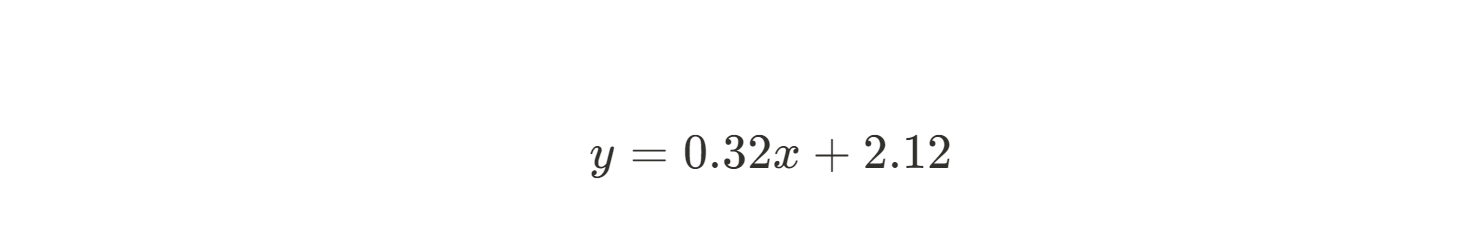
O método dos mínimos quadrados nos permitiu derivar de forma rápida e fácil a melhor linha de regressão linear, mesmo manualmente! Obviamente, quanto mais dados você tiver, mais difícil será fazer isso manualmente. Felizmente, como a matemática é bastante direta, é muito simples implementar esse método em Python ou R. Para obter explicações detalhadas sobre como fazer isso, consulte Essentials of Linear Regression in Python e How to Do Linear Regression in R.

Fundamentos matemáticos do método dos mínimos quadrados

Acima, usamos um exemplo com regressão linear simples e encontramos a inclinação e a interceptação usando equações de forma fechada e modelamos a variável dependente como uma função da variável independente: y=mx+b.

No entanto, as equações que mostrei acima só funcionam quando você tem uma variável independente. Outra maneira de encontrar os coeficientes de uma regressão é usar o que é conhecido como equação normal, que fornece uma solução baseada em matriz para o problema dos mínimos quadrados. A equação normal refere-se à equação da matriz que resulta da minimização da soma dos resíduos quadrados usando o método dos mínimos quadrados. Geometricamente, e usando a linguagem da álgebra linear, a solução de mínimos quadrados pode ser visualizada como a projeção ortogonal do vetor de dados observados no espaço de colunas da matriz do modelo. Simplificando, isso significa apenas que os erros são minimizados de forma a garantir que os valores previstos estejam o mais próximo possível dos dados observados, dadas as restrições do modelo.

Nos casos em que a matriz não é invertível (o que significa que o sistema de equações não tem uma solução única), o pseudoinverso de Moore-Penrose oferece uma maneira de calcular uma solução de mínimos quadrados. Isso nos dá a flexibilidade para lidar com situações em que o sistema é subdeterminado (o que significa que há mais incógnitas do que equações) ou sobredeterminado (o que significa que há mais equações do que incógnitas).

Se você precisar de uma atualização em álgebra matricial, recomendo o curso Linear Algebra for Data Science in R.

Tipos de métodos de mínimos quadrados

Até agora, falamos apenas sobre o uso do método dos mínimos quadrados com um estimador de mínimos quadrados ordinários. No entanto, é uma ferramenta versátil que pode ser adaptada a muitos cenários, dependendo da natureza do problema que você está enfrentando. Vamos explorar alguns tipos de métodos de mínimos quadrados, o que os torna únicos e seus usos práticos.

Mínimos quadrados lineares

A esta altura, você deve estar bastante familiarizado com os mínimos quadrados lineares (também chamadosde mínimos quadrados ordinários). É usado com modelos que têm coeficientes lineares, como naregressão linear simples ou múltipla . O objetivo é encontrar a linha (ou hiperplano, no caso de regressões lineares múltiplas) que minimize a soma dos resíduos ao quadrado.

Esse tipo de mínimos quadrados pressupõe que os resíduos tenham uma variância constante e que não haja outliers significativos nos dados. Ela pode ser aplicada à maioria das coisas que têm uma relação linear. Por exemplo, você pode usar isso para estabelecer relações entre a duração da gestação e o peso ao nascer ou entre os gastos com anúncios e a receita de vendas. Esse é o tipo de mínimos quadrados que uso com mais frequência e sobre o qual mais ouço outras pessoas falarem.

Mínimos quadrados ponderados

Os mínimos quadrados ponderados são uma extensão desse método que funciona quando a variação dos resíduos não é constante. Ao atribuir pesos a cada ponto de dados, os mínimos quadrados ponderados dão mais importância às observações com menor variação. A equação para isso é semelhante à soma de quadrados anterior, mas com um peso (w_i) aplicado a cada resíduo:

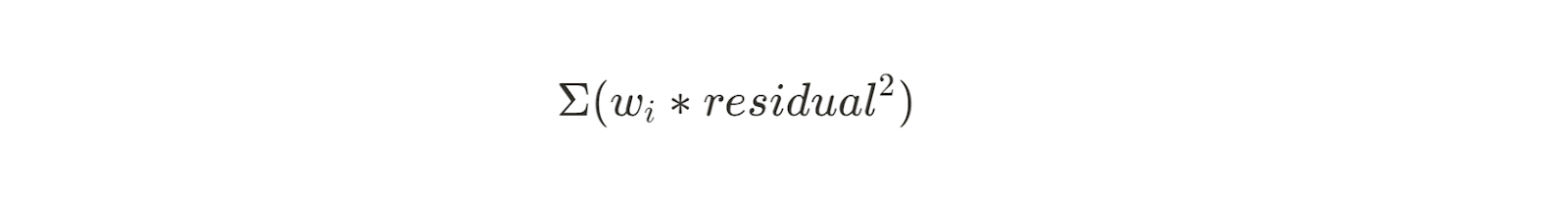
Esse método é útil para conjuntos de dados em que o erro de medição varia entre as observações, por exemplo, na calibração de sensores. Normalmente, os pesos são o inverso da variância de cada observação.

Mínimos quadrados robustos

Os mínimos quadrados robustos são projetados para lidar com conjuntos de dados com outliers que podem influenciar desproporcionalmente os resultados dos mínimos quadrados comuns. Ele usa técnicas de reponderação iterativa para reduzir o impacto dos valores discrepantes.

Nos mínimos quadrados robustos, você pode usar métodos como os resíduos mínimos absolutos (LAR) ou pesos bisquadrados para ajustar iterativamente os pesos e minimizar a influência dos outliers.

Um exemplo de quando você pode usar isso é na modelagem financeira, em que você quer levar em conta as quedas extremas do mercado. Se você tiver um conjunto de dados em que não deseja remover os valores discrepantes, mas ainda deseja considerá-los, os mínimos quadrados robustos podem ser o caminho a ser seguido.

Mínimos quadrados não lineares

Os mínimos quadrados não são usados apenas com regressões lineares. Os mínimos quadrados não lineares são usados quando o modelo que você está aplicando é não linear em seus coeficientes. Isso é mais complicado do que os mínimos quadrados lineares e pode exigir técnicas de otimização iterativas (como Gauss-Newton ou Levenberg-Marquardt) para encontrar o melhor ajuste.

É importante que você tenha cuidado com os mínimos quadrados não lineares. O cálculo pode ser sensível a estimativas de parâmetros iniciais, bem como a problemas de convergência. Exemplos de quando você pode usar isso incluem a modelagem do crescimento exponencial de vírus em um corpo durante uma infecção ou a modelagem de taxas de reação química no laboratório.

Mínimos quadrados totais

Até agora, falamos principalmente de instâncias em que apenas a variável dependente apresenta erros. E estamos minimizando as distâncias verticais entre o nosso modelo e os nossos dados. Mas e se você também tiver erros em suas medições independentes?

Os mínimos quadrados totais são úteis quando as variáveis independentes e dependentes têm erros de medição. Esse método leva em conta os erros em todas as variáveis. Isso pode ser especialmente útil em campos como astronomia e geodésia (o campo que mede a forma e o campo gravitacional da Terra), em que os erros de medição estão presentes em todas as dimensões devido ao alto nível de precisão necessário. Os mínimos quadrados totais são frequentemente usados em conjunto com a decomposição de valor singular.

Mínimos quadrados generalizados

Os mínimos quadrados generalizados são uma extensão do método dos mínimos quadrados que aborda os desafios apresentados por resíduos correlacionados. Com os mínimos quadrados generalizados, transformamos os dados em um formato em que os mínimos quadrados comuns podem ser aplicados. Essa transformação envolve o uso da matriz de covariância dos resíduos para levar em conta sua estrutura de correlação, permitindo estimativas de parâmetros mais precisas.

Isso pode ser particularmente útil em situações como análises de séries temporais, em que os resíduos podem apresentar autocorrelação. 

Aplicações do método dos mínimos quadrados

O método dos mínimos quadrados é uma técnica estatística amplamente usada com aplicações em vários campos.

Na estatística e na ciência de dados, os mínimos quadrados são usados para criar modelos de regressão linear e não linear para fazer previsões com base em entradas conhecidas. Também é útil para analisar tendências, principalmente em dados de séries temporais.

Em finanças, os mínimos quadrados são usados na análise de desempenho de ações, ajudando a determinar a relação entre o desempenho de uma ação e os índices de mercado. Por exemplo, ele pode ser usado para calcular a sensibilidade de uma ação aos movimentos do mercado. Ele também ajuda na modelagem de riscos, ajustando modelos a dados financeiros históricos para estimar o risco e o retorno.

Os engenheiros usam mínimos quadrados na calibração de sensores para ajustar modelos aos dados observados e minimizar os erros de medição. Ele também é aplicado no processamento de sinais para filtragem e redução de ruído, permitindo uma interpretação mais clara dos dados.

Obviamente, os mínimos quadrados tiveram seu início na astronomia; seu primeiro uso foi feito por Carl Friedrich Gauss para prever a órbita do asteroide Ceres. Também é usado na geodésia para modelar a forma da Terra com base em dados de observação, o que é essencial para medições geográficas precisas.

Se você já se interessou por machine learning, reconhecerá o método dos mínimos quadrados como um método para minimizar a função de perda durante o treinamento de modelos de regressão linear. Você também pode tê-lo usado durante a seleção de recursos para identificar as variáveis mais importantes que contribuem para o modelo.

Ela também tem uma função em muitas das outras ciências exatas, como física e química. Ele pode ser usado para ajustar curvas a dados experimentais, como taxas de reação ou medições físicas, e ajudar a minimizar erros em configurações experimentais.

O método dos mínimos quadrados é uma ferramenta estatística versátil. Pessoalmente, usei esse método para calibrar sensores de pressão, fazer previsões com base em meus dados experimentais e durante o treinamento de machine learning. A capacidade de modelar relacionamentos de forma confiável e minimizar erros é um recurso que oferece valor a muitas disciplinas diferentes.

Suposições e diagnósticos

O método dos mínimos quadrados faz algumas suposições importantes sobre seus dados e o modelo que está sendo usado. É importante que você entenda essas suposições, pois violá-las pode levar a resultados tendenciosos ou não confiáveis. Portanto, vamos discutir essas suposições, bem como a forma de diagnosticar e resolver possíveis problemas.

Uma suposição é a independência dos erros, o que significa que os resíduos não devem estar correlacionados. Se os erros estiverem correlacionados entre si, especialmente em dados sequenciais ou espaciais, as estimativas poderão ser distorcidas. O teste Durbin-Watson pode detectar autocorrelação nos resíduos, especialmente para conjuntos de dados dependentes do tempo. Se você encontrar uma correlação, poderá usar os mínimos quadrados generalizados para considerá-la.

Outra suposição é que a variância dos resíduos permanece constante em todos os níveis da variável independente. Se os resíduos apresentarem uma dispersão em forma de funil quando plotados em relação aos valores ajustados, essa suposição provavelmente foi violada. Para resolver esse problema, você pode usar os mínimos quadrados ponderados para atribuir pesos apropriados às suas observações. Como alternativa, você pode usar transformações como ajustes logarítmicos ou de raiz quadrada para estabilizar a variação desigual e corrigir quaisquer problemas de heterocedasticidade.

Como em toda modelagem, é importante que a estrutura reflita a relação subjacente entre as variáveis. Se isso não acontecer, não importa o quão otimizado seja o seu ajuste; os resultados ainda serão enganosos. Gráficos residuais e métricas de qualidade de ajuste, como ^R², podem ajudar você a determinar se o modelo escolhido captura os padrões nos dados. 

O método padrão de mínimos quadrados pressupõe que as variáveis independentes sejam medidas sem erros. Portanto, é importante que você conheça a precisão de sua medição independente. Você deve ter uma ideia da precisão dessa medição observando os métodos de coleta. Se houver erros de medição em seu preditor, certifique-se de usar o método de mínimos quadrados totais para atenuar as imprecisões em sua modelagem.

Por fim, a distribuição dos erros residuais desempenha uma função importante, principalmente no teste de hipóteses e na estimativa do intervalo de confiança. Os mínimos quadrados pressupõem que os erros seguem uma distribuição normal (gaussiana), e os desvios da normalidade podem afetar a inferência. Os histogramas e os gráficos Q-Q ajudam a avaliar se os resíduos estão alinhados com as distribuições esperadas. Se você tiver desvios significativos da normalidade, as técnicas de regressão robusta ou os métodos de bootstrapping podem fornecer estimativas mais confiáveis que são menos sensíveis a valores discrepantes.

Vantagens e desvantagens dos mínimos quadrados

O método dos mínimos quadrados é uma ferramenta amplamente usada na análise de dados. Mas isso não significa que ele deva ser usado em todos os conjuntos de dados.

O método dos mínimos quadrados oferece várias vantagens. É bastante fácil de calcular, especialmente para modelos lineares. Ele é facilmente interpretável por públicos técnicos e não técnicos. Além disso, há diferentes estilos, como regressão ponderada, robusta e não linear, o que o torna altamente versátil. E, o que é mais importante, ele tem uma base teórica sólida fornecida pelo teorema de Gauss-Markov. Tudo isso faz com que os mínimos quadrados sejam amplamente aplicáveis e usados em campos que vão da economia à engenharia.

No entanto, o método é sensível a valores discrepantes, que podem afetar desproporcionalmente os resultados do modelo. Ele também pressupõe que não há erros nos preditores, o que pode não ser verdade em dados do mundo real. Além disso, os mínimos quadrados podem ser limitados pela multicolinearidade. Isso significa que preditores altamente correlacionados podem levar a coeficientes instáveis e, portanto, a estimativas não confiáveis. Ele também exige uma variação constante dos resíduos, uma condição que nem sempre pode ser atendida.

É importante examinar atentamente o seu conjunto de dados e o seu objetivo antes de você decidir que o método dos mínimos quadrados é a melhor ferramenta para a sua situação.

Conclusão

O método dos mínimos quadrados é uma ferramenta fundamental para qualquer analista de dados. Ao encontrar o melhor ajuste para nossos dados, podemos fazer previsões mais precisas e encontrar tendências mais perspicazes.

Para ler mais sobre a medição de linhas retas no espaço euclidiano, recomendo o site Understanding Euclidean Distance: Da teoria à prática tutorial. Além disso, não deixe de se inscrever em nossos cursos de regressão para se tornar realmente um especialista. 

• Introdução à regressão com statsmodels em Python
• Introdução à regressão em R